Rhythmogenic neuronal networks, emergent leaders, and k-cores

Abstract

Neuronal network behavior results from a combination of the dynamics of individual neurons and the connectivity of the network that links them together. We study a simplified model, based on the proposal of Feldman and Del Negro (FDN) [Nat. Rev. Neurosci. 7, 232 (2006)], of the preBötzinger Complex, a small neuronal network that participates in the control of the mammalian breathing rhythm through periodic firing bursts. The dynamics of this randomly connected network of identical excitatory neurons differ from those of a uniformly connected one. Specifically, network connectivity determines the identity of emergent leader neurons that trigger the firing bursts. When neuronal desensitization is controlled by the number of input signals to the neurons (as proposed by FDN), the network's collective desensitization—required for successful burst termination—is mediated by k -core clusters of neurons.

I. INTRODUCTION

A neuronal network is a group of interconnected neurons functioning as a circuit. Each neuron receives electrical signals via its treelike dendrites, connected via synaptic inputs from other neurons. The neuron responds, based on some function of its input signals, by either doing nothing or by “firing,” i.e., by producing an action-potential output pulse that is transmitted to connected neurons via synapses [1]. In a highly simplified excitatory neuron, the electrical potential of the cell body, i.e., soma, always increases by an amount ΔV when the cell receives a synaptic input. The potential of the cell is an integral of the signals from other connected neurons. The firing probability of a neuron depends sensitively on its electrical potential, leading to threshold behavior. For a simple case, the neuron can be considered to be either in a quiescent state characterized by rare, sporadic firing if the cell potential is large and negative (“hyperpolarized”), or in an active state, with a significant increase in firing rate over the quiescent state when at higher potentials (“depolarized”).

The preBötzinger Complex (preBötC), a cluster on the order of 300 essential neurons located in the brain stem [2,3], provides an example of a network with nontrivial collective dynamics. The preBötC produces the neuronal activity that appears to drive the rhythm of mammalian breathing. Specifically, the timing of the inspiratory phase of the breathing cycle is set by the collective output of the preBötC in the form of periodic bursts of action potentials with a period on the order of a second, which is about 10³ times longer than the time scale associated with single action potentials in individual neurons. This scenario has been generally believed to be due to activity dependent adaptation that shuts down the collective burst, combined with the action of pacemakers that initiate it. In the “individual pacemaker” hypothesis, synchronization of neuronal firing in the preBötC is orchestrated by a subset of preBötC neurons that are able to oscillate autonomously between periods of firing and quiescence—intrinsic pacemakers. Simple and effective “mean-field” theories [4] have been developed for periodic bursting neuronal networks based on these or related features [5].

Feldman and Del Negro (FDN) have put forward a different description of preBötC rhythmic bursting that introduces two significant modifications to the above picture. First, they suggested that burst synchronization does not rely critically on the presence of intrinsic pacemakers [6]; rather, the oscillations are a collective property of a large group of sparsely connected neurons that need not oscillate in isolation. They refer to this as the “group pacemaker” hypothesis. This hypothesis is based on experiments that showed that preBötC oscillations persist even when the intrinsic pacemaker's neurons are “turned off” [7]. In this view, oscillations disappear when the number of neurons drops below a threshold where they can no longer maintain collective phase coherence. Indeed, when more than 80% of the neurons of the preBötC are destroyed, the rhythm in the intact mammal is interrupted [8]. Second, following experiments on neurons with buffered somatic Ca²⁺ [9], Feldman, Del Negro, and collaborators proposed that the Ca²⁺-mediated modulation of neuronal properties occurs primarily in the dendrites rather than in the soma of the neuron. When a dendrite receives a synaptic input, certain receptors are activated leading to a local increase in the Ca²⁺ concentration [10]. This rise generates a Ca²⁺-dependent nonspecific current that further depolarizes the membrane potential. Here we consider that this local change in dendritic nonspecific cation conductance also induces changes in other conductances that effectively shunt synaptic input to ground rendering the cell less responsive to subsequent incoming signals and that this process underlies the termination of each burst of activity. In the FDN model a neuron's desensitization is related to the number of action potentials it receives, i.e., it is synaptic in origin, rather than the number of action potentials it produces, as previously suggested. We show that this seemingly minor change in the dynamical model of individual neurons leads to profound changes in the collective dynamics of the system.

A full theory, based on the FDN description, would be very challenging since it would require a complete (or at least extensive) consideration of the complex electrophysiological structure of the dendrites of preBötC neurons. In this paper, we present a simplified “two-compartment” version (i.e., with soma and dendrites treated as two electrically communicating and uniform compartments with different Ca²⁺ concentrations) that incorporates dendritic synaptic activity-based modulation of excitability in response to synaptic input [9]. The principal contribution made by this paper is to show that the FDN model, which proposes that synaptic activity based modulation of excitability occurs in the dendrites rather than in the soma, leads to profound changes in the collective dynamics of the system. By making the desensitization of the neurons depend on incoming signals and thus a collective property of the network rather than an inherent property of the individual neurons, the mean-field description (formerly valid—see above) now fails at a fundamental level. Specifically, we show that a simplified network of identical but randomly connected neurons supports periodic synchronized bursts triggered by neurons that are characterized by being linked to a large number of neurons that are similarly well connected, forming the information transmitting backbone of the network. In this model, the minimum number of neurons required for rhythmogenesis is determined by a sequence of magic numbers that depends solely on the adjacency matrix and which can be calculated using simple graph-theoretic methods [11,12].

In Sec. II, we introduce our simplified model of the FDN description. In Sec. III, we analyze the dynamics of a fully connected network of FDN neurons. In Sec. IV, we study a randomly connected network and show that mean-field theory fails dramatically for the transition to high activity while remaining a valid description of the transition to stable oscillations. We also show the existence of a subpopulation of leader neurons that drive the initiation of each burst. Finally, in Sec. V, we summarize our results.

II. MODEL

In the two-compartment model, each neuron is represented by two dynamical variables: the somatic potential V_i(t) and the average dendritic Ca²⁺ concentration C_i(t) of the ith neuron. The N neurons fire according to the 2N coupled nonlinear rate equations,

$$\frac{d{V}_i}{dt}=\frac{1}{{\tau }_V}(V_{\mathrm{eq}}-V_i)+\Delta V\left(C_i\right)\sum _{j\ne i}{M}_{ij}P\left(V_j\right)$$ (1)

$$\frac{d{C}_i}{dt}=\frac{1}{{\tau }_C}(C_{\mathrm{eq}}-C_i)+\Delta C\sum _{j\ne i}{M}_{ij}P\left(V_j\right),$$ (2)

where V_eq and C_eq are, respectively, the resting potential and the equilibrium Ca²⁺ concentration of a neuron with τ_V (10 ms) and τ_C (500 ms) [1] as the respective equilibration times. In this basic model, we have simplified the FDN proposal for the sequence of events associated with the effects on excitability of the rise in dendritic Ca²⁺ concentration. Here we model the calcium-mediated adaptation by requiring ΔV(C) to drop rapidly when C exceeds a threshold C*. The identification of the slow variable with Ca²⁺ concentration, while supported by Pace et al. [10], is not essential to the model; we require that this variable depend only on synaptic input. The neurons interact in a firing-rate model [13,14] in which a neuron's voltage-dependent firing rate P(V) replaces the (stochastic) series of individual action potentials. If V exceeds the threshold V*, then P(V) increases rapidly from a basal rate to a higher rate, here taken to be about 5 spikes/s at rest to about 75 spikes/s (these numbers being arbitrary but physiologically reasonable). In replacing the actual spike trains by P(V) in Eqs. (1) and (2), we have averaged over the short-time shot noise in the system—a feature explored in [15].

In what follows, we use a simple Fermi function of the form

$$P\left(V\right)=\frac{r_m-r_b}{1+e^{-(V-V\ast )∕g_V}}+r_b,$$ (3)

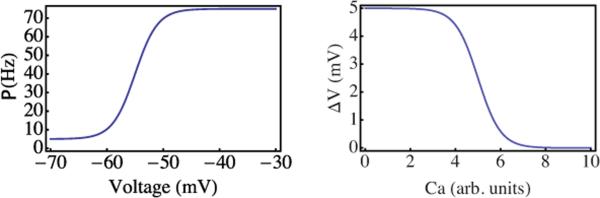
where r_m=75 Hz is the maximal firing rate, r_b=5 Hz is the basal spontaneous firing rate, and V*=−55 mV is the voltage at which a neuron transitions from ectopic to active firing. g_V=5 mV determines the steepness of the transition, and to obtain a sharp threshold we must certainly require g_V<V*−V_eq. The behavior of the model (other than moving around the phase diagram) does not depend critically on the choice of these parameters. This function is plotted in Fig. 1.

FIG. 1.

(Color online) Top panel: firing rate, P(V), as a function of somatic membrane potential V. The firing rate increases by one order of magnitude from a low basal rate near a threshold V*≃−55 mV. Bottom panel: voltage increment ΔV a neuron experiences upon receipt of an action potential. At a critical C*, the voltage increment drops rapidly to zero as the synaptic input is shunted.

Second, the calcium dependent voltage increment ΔV(C) must also have a sharp threshold from the low-calcium state in which the dendritic tree transmits postsynaptic signals to the soma efficiently to a high-calcium state in which those signals are shunted, leading to a strongly suppressed somatic voltage increase in response to an input signal. It is essential that the transition concentration C* is greater than the steady-state concentration (which by a suitable definition of C we may set to 0) so that the neurons in the absence of input signals are in the sensitive (i.e., not shunted) state. The basal value of the voltage increment, i.e., ΔV(C=0), is our control parameter for the excitability of the individual neurons. By setting (V*−V_eq)/ΔV(C=0), we are, in effect, setting the number of input action potentials required to drive the somatic potential from its basal, steady-state value to the firing threshold, and thus are setting the inherent excitability of each neuron. To capture these effects, we use

$$\Delta V\left(C\right)=\frac{\Delta V_{\mathit{max}}}{1+e^{(C-C\ast )∕g_C}},$$ (4)

where ΔV_max=5 mV. The critical concentration C*=10 is arbitrary and, in these units, g_C=3. This function is plotted in Fig. 1.

The entries of the adjacency matrix M_ij are equal to one if the output of jth neuron is an input to the ith and zero otherwise. In a one-compartment model, a similar pair of equations apply except that one would replace Σ_j≠iM_ijP(V_j) in Eq. (2) by P(V_i)

III. MEAN-FIELD ANALYSIS

We start with the simplest case of a model system composed of a homogeneous network where each neuron is linked to every other neuron: M_ij=1 for all i ≠ j. If the initial potentials and calcium concentrations also are the same for all neurons, then the 2N rate equations reduce to a single pair that describes all neurons,

$$\frac{dV}{dt}=\frac{1}{{\tau }_V}(V_{\mathrm{eq}}-V)+N\Delta V\left(C\right)P\left(V\right),$$ (5)

$$\frac{dC}{dt}=\frac{1}{{\tau }_C}(C_{\mathrm{eq}}-C)+N\Delta CP\left(V\right),$$ (6)

which can be analyzed by the standard methods of dynamical systems [16,17]. This pair of equations can also be viewed as a mean-field approximation for more complex networks [18]. In the mean-field theory of a homogeneous network, there is no difference between the one and two-compartment models, apart from a trivial scale factor. The resulting dynamical phase diagram is shown in the upper panel of Fig. 2.

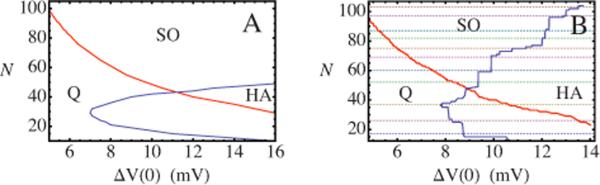
FIG. 2.

(Color online)(A) Phase diagram of a homogeneous N-neuron network with every neuron linked to every other neuron. The horizontal axis is the maximum somatic voltage jump of a cell following an input pulse, i.e., action potential. The red (light gray) decreasing line is the stability limit of a low-activity fixed point of Eqs. (5) and (6)(Q phase) while the blue (dark gray) line is the stability limit of a high-activity fixed point (HA phase). Cooperative limit-cycle oscillations are fully stable only in the region above the blue and red lines (SO phase). (B) Phase diagram of an inhomogeneous random N-neuron network with, on average, each neuron linked to N/6 other neurons. In the section labeled HA deterministic chaos, period doubling and intermittency are encountered. The dashed lines mark a sequence of magic numbers N_k determined by the adjacency matrix of the network.

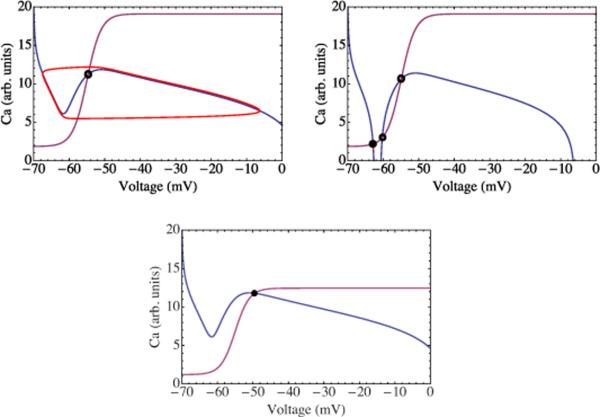
To determine these fixed points we plot the nullclines of this two equations—the set of points in the V-C plane for which either $\stackrel{.}{V}=0$ or $\stackrel{.}{C}=0$. In the parameter range corresponding to the stably oscillating phase, the former is shown in blue and the latter in purple in Fig. 3. The single intersection of these lines represents a stationary solution or fixed point, denoted by the open circle in the figure. Solutions not passing through this point evolve toward an oscillating limit cycle represented by the red curve in the same figure. These solutions generate the periodic bursting dynamics of the mean-field network and attendant out-of-phase calcium oscillation.

FIG. 3.

(Color online) Top panel: the phase portrait of the mean-field model in the SO phase. The curves represent the nullclines of the calcium and somatic voltage equations. Their intersection, marked by the open circle, is an unstable fixed point of the dynamics. Trajectories not starting there evolve toward the limit cycle shown in red. Middle panel: the phase portrait of the mean-field model in the quiescent (Q) phase. Trajectories not starting at these fixed points evolve toward the one stable fixed point corresponding to a highly polarized membrane potential and low dendritic calcium concentration. Here the neurons do not fire. Bottom panel: the phase portrait of the mean-field model in the HA phase. Their intersection, marked by the filled circle, is a stable fixed point corresponding to a depolarized membrane potential and significant calcium concentration. This state corresponds to the case in which the neurons should typically fire repeatedly.

In the parameter regime marked SO (“stable oscillation”), the neuronal potentials and calcium concentrations undergo a stable limit-cycle oscillation. For lower values of the input voltage jump at zero calcium concentration, ΔV(C=0), corresponding to weakly excitable neurons, the period of the oscillation increases and then diverges as the number N of neurons is reduced due to the appearance of a saddle node on an invariant cycle bifurcation [19]. A line of these bifurcations separates the SO phase from a quiescent phase, marked Q, where all neurons are permanently in a state of low activity. It must be noted that, since N—the number of neurons—can be varied only in integral steps, it may not be possible, at an arbitrary level of neuronal excitability [ΔV(C=0)], to tune the system to have arbitrarily long periods, but such an increase should be observable. This mean-field prediction, unlike those regarding the dynamics at the SO or high-activity (HA) phase boundary, remains valid for heterogeneously connected networks so that it should be observable in the slice preparation.

For higher values of ΔV(C=0), corresponding to highly excitable neurons, the unstable fixed point at the center of the limit cycle becomes stable as N is reduced. In the part of the phase diagram where this happens, marked HA, the neurons are permanently in a state of high activity. This mean-field HA phase does not show the complex firing pattern reported experimentally when the excitability was increased [20].

IV. HETEROGENEOUS NETWORKS

To examine the effect of connectivity on network dynamics, we consider a network with much sparser connections. Based on pairwise recordings of preBötC neurons, each excitatory preBötC neuron appears to be linked to, on average, (1/6)th of the other neurons [21]. To describe this, we use an Erdős-Rényi random adjacency matrix [22,23], assigning zeros and ones as the entries of M_ij with probabilities 5/6 and 1/6, respectively. Solution of the coupled rate equations on a typical example of a random graph produces the phase diagram shown in the lower panel of Fig. 2. Reducing the network connectivity clearly does not destroy its ability to produce robust synchronized stable oscillations, though note that the SO section of the phase diagram has been reduced in area as compared to the mean-field case.

Unlike the mean-field case, in the sparely connected network the firing pattern varies greatly from one neuron to the next. Superimposing the firing patterns of different neurons reveals an important feature [see Fig. 4(A)]. In the low-activity part of the cycle, the potentials of all neurons are below V*, but they rise more rapidly for a subpopulation; these reach the firing threshold first. Their increased firing rate pushes subthreshold neurons linked to them and passes the firing threshold as well. A chain reaction spreads over the network until all neurons are above threshold. Note that the least excitable neurons that crossed the firing threshold latest remain active over a longer period of time, producing a highly asymmetric pulse shape. Even though in our model all neurons are identical and none can oscillate autonomously, a subset of neurons, selected through the network connectivity, is timing the oscillations. This subpopulation of spike leaders can be interpreted as the “emergent” leaders of the network. The bursting does not require the activity of physiologically distinct independent pacemakers, thus the system behaves like a group pacemaker [24,25]. The lagging neurons effectively amplify the leader's actions.

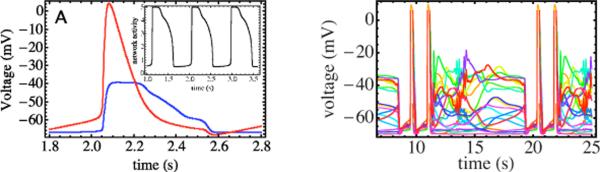
FIG. 4.

(Color online)(A) Periodic potential oscillations (SO phase) for a random 60 node network. We compare the voltage pulse generated by an emergent highly connected leader node in red (light gray, large pulse) with the voltage pulse produced by a poorly connected node in blue (dark gray, flat pulse). The emergent leader node first reaches the firing threshold of −55 mV. Note that the poorly connected node remains above threshold over a longer period of time. Inset: longer time trace demonstrating periodic bursting, illustrated by the total current output (in arbitrary units). (B) Time-dependent potentials in the high-activity phase. Each color represents an individual neuron. Multiple collective potential bursts alternate with an incoherent chaotic state. Note the different time scales in panels A and B.

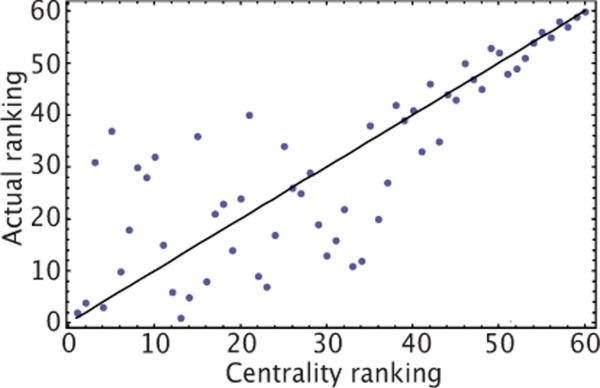
In order to identify the emergent leader nodes, we note that if P(V) in Eq. (1) was linearized, then the most rapidly growing mode, starting from a quiescent phase, would be the eigenvector of the matrix M_ij with the largest eigenvalue (Fig. 5). If one rank orders the nodes according to their eigenvector entry—known as “centrality ranking” in network theory—and compares with the actual firing order, one finds that centrality ranking predicts correctly the firing order of poorly connected nodes (see Fig. 3)._ The correlation is relatively poor for highly connected nodes, indicating a subpopulation of leader nodes that are all similarly well connected.

FIG. 5.

(Color online) Comparison of the firing order of a 60 node random network described in Eqs. (1) and (2)(vertical axis), with the firing order predicted by ranking nodes according to their entry in the eigenvector of the adjacency matrix M_ij with the largest eigenvalue (horizontal axis, centrality ranking). Note that only the higher firing orders can be reliably predicted based on this ranking. The correlation coefficient is r²=0.79.

Network degradation, i.e., randomly knocking out neurons [8], leads to complex changes in the set of these emergent group-pacemaker neurons. Removal of individual well-connected nodes does not lead to significant reduction of phase coherence. It does take longer for the network to reach threshold as N is reduced so the oscillation period increases. For lower values of ΔV(C=0), i.e., weakly excitable networks, the period diverges along the phase boundary between the SO and Q phases in Fig. 2(B), which agrees with the predictions of mean-field theory (see the supplement). For higher values of ΔV(C=0) the system enters the HA phase. Unlike mean-field theory, the HA phase of the random network exhibits complex dynamical behavior, with period doubling and deterministic chaos [20]. One example of this is shown in Fig. 4(B) where groups of high-activity bursts alternate with periods of deterministic chaos, forming a complex limit cycle.

The appearance of emergent leaders is a generic feature of excitatory interactions on an Erdős-Rényi graph independent of the two-compartment hypothesis. We now explore the SO↔HA threshold curve where the two-compartment FDN model causes the breakdown of mean-field theory. This threshold curve N_c(ΔV) has a surprising staircase dependence on ΔV differing dramatically from the continuous curve predicted by the mean-field theory (see Fig. 2) and the one-compartment model. These discontinuities define certain privileged numbers of neurons N_k below which the network fails to support stable oscillations. While certain numbers are privileged, the dynamics are collective and no neuron develops a specialized role in the burst termination. The values of these N_k's are independent of system parameters such as ΔC. The boundary of the SO regime makes discrete jumps between N_k's as the parameters (ΔC,ΔV) of the neuronal dynamical model are changed. The values of these magic numbers N_k vary between realizations of the random network, but their existence is generic. In contrast, the phase boundary separating the SO and Q phases in Fig. 2(B) largely follows mean-field predictions.

To understand these discontinuities in the SO or HA phase boundary, it is useful to introduce the concept of a k-core [26]. A k-core of a graph (for integer k) is a subgraph in which all nodes (i.e., neurons) have at least k inputs from other nodes in the subgraph. As the number of nodes increases in an Erdős-Rényi random network, k-core clusters appear with larger k values at sharply defined thresholds. As an example we show in Fig. 6(A) the k-cores of a symmetric random adjacency matrix. Nearly all nodes form a single five-core cluster. Deleting one node at random does not change this feature [Fig. 6(B)], but deleting two nodes at random produces a sharp transition in which the network is now dominated by a single system-sized four-core cluster [Fig. 6(C)]. Deleting an additional node does not alter the dominance of the four-core, as shown in Fig. 6(D). For the random network used to generate Fig. 2(B), these discontinuous transitions take place at N₃=17 when a three-core appears, at N₄=26 when a four-core appears, at N₅=37 when a five-core appears, and so on. The values of N_k for this realization of the random network are represented by dotted lines in Fig. 2(B). The locations of the discontinuities of the phase boundary as a function of N agree well, though not perfectly, with the k-core transition values N_k. The discrepancies are presumably due to the fact that a member of a k-core can have more than k input links, including links from non-k-core neurons. We emphasize that the k-core concept is inapplicable to the SO↔Q transition. Along the transition line, the neurons with the highest connectivity are able to trigger an excitation wave that spreads through the whole system. This transition is well described by mean-field theory because excitation is governed by a class of emergent leaders rather than a few select neurons, so removing one neuron does not have a dramatic effect.

FIG. 6.

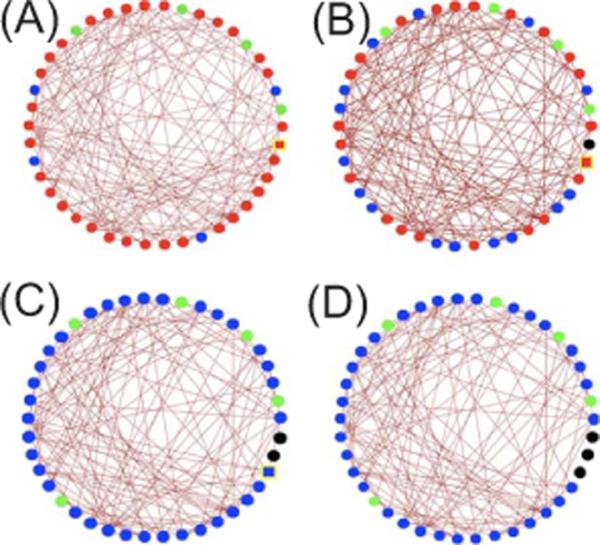
(Color online) k-cores of a symmetric N×N random adjacency matrix [27]. Nodes making up the five core are marked in red (medium gray), four-core nodes in blue (dark gray), three-core nodes in green (light gray), while removed nodes are marked in black. The yellow outlined square indicates the node to be removed on the subsequent panel. The four figures show a progressively decreasing network size: N_A=43, N_B=42, N_C=41, and N_D=40.

V. CONCLUSION

In summary, we have studied a simple version of the FDN description of rhythmogenic neuronal networks using a combination of excitable integrate-and-fire neurons modified by a slower process of activity-mediated desensitization. We showed that there is an asymmetry in the phase diagram between the transition from the stable bursting phase to the quiescent phase and the transition from the stable bursting phase to the HA phase. The first transition is well described by mean-field theory, while the staircase structure of the phase boundary of the second transition reflects the full nature of network connectivity. This asymmetry originates from the difference between the dynamics of a spreading wave of voltage-mediated excitation and collective desensitization. The asymmetry and the breakdown of mean-field theory in the FDN model are due to its identification of desensitization with the number of action potentials a neuron receives rather than produces. There are now unambiguous tests of the model: to examine the phase boundary one must move both vertically (changing N) and horizontally (changing the effective ΔV). Both are possible by changing the number of active neurons in their excitability, i.e., changing how many action potentials a neuron must receive to be stimulated to fire. Measuring the ΔV that first supports complex (chaotic) firing patterns as a function of N should directly reveal the predicted staircase structure of Fig. 2(B).