Abstract
Accurate quantification of the 15N-{1H} steady-state NOE is central to current methods for the elucidation of protein backbone dynamics on the fast, sub-nanosecond timescale. This experiment is highly susceptible to systematic errors arising from multiple sources. The nature of these errors and their effects on the determined NOE ratio is evaluated by a detailed analysis of the spin dynamics during the pair of experiments used to measure this ratio and possible improvements suggested. The experiment that includes 1H irradiation, is analyzed in the framework of Average Liouvillian Theory and a modified saturation scheme that generates a stable steady state and eliminates the need to completely saturate 1H nuclei, is presented. The largest source of error, however, in 1H-dilute systems at ultra-high fields is found to be an overestimation of the steady-state NOE value as a consequence of the incomplete equilibration of the magnetization in the so-called “reference experiment”. The use of very long relaxation delays is usually an effective, but time consuming, solution. Here, we introduce an alternative reference experiment, designed for larger, deuterated systems, that uses the fastest relaxing component of the longitudinal magnetization a closer approximation to the equilibrium state for shorter relaxation delays. The utility of the modified approach is illustrated through simulations on realistic spin-systems over a wide range of timescales and experimentally verified using a perdeuterated sample of human ubiquitin.
Keywords: Cross-Relaxation, Nuclear Overhauser Effect, Average Liouvillian Theory, Biomolecular Dynamics, Protein Dynamics
1. Introduction
The ability to characterize protein dynamics at atomic resolution is key to understand biological processes, such as enzymatic reactions, protein folding, the driving forces of interactions and allostery. Nuclear Magnetic Resonance (NMR) is a powerful tool to study protein dynamics over a wide range of timescales [1,2]. Hydrodynamic properties of proteins in solution and dynamics occurring faster than a few nanoseconds are usually measured by the quantitative analysis of 15N relaxation rates [2–5]. These rates depend both on the overall rotational diffusion in solution as well as fast backbone motions on a sub-nanosecond timescale through their effects on the spectral density functions [6–9]. Longitudinal and transverse relaxation rates largely sample the spectral density at low (15N Larmor frequency) and zero-frequency [6,7]. The accurate determination of the spectral density function at high frequencies (around the 1H Larmor frequency) relies on the accurate measurement of 15N-{1H} nuclear Overhauser effects (NOE)[10].
Several studies have underlined the effect on the measured value of the steady-state 15N-{1H} NOE of incomplete relaxation to the steady state, or equilibrium, 15N polarization in the pair of experiments with and without (reference) 1H saturation [11–13]. Ways to accelerate the evolution towards the equilibrium polarization have been found [11] and correction factors introduced [14]. However, Gong and Ishima [12] have recently shown that, on high-field spectrometers and particularly using highly deuterated proteins, cross-relaxation pathways due to the cross-correlation of chemical shift anisotropy (CSA) and dipole-dipole (DD) interactions could significantly slow down the recovery of equilibrium polarization. A simple way to overcome this problem is to introduce a longer relaxation delay in the reference experiment. This solution is simple to implement and is recommended for small, deuterated proteins. However, it is extremely time-consuming since durations above 10 s should be employed.
In this article, we introduce two modifications to commonly employed pulse sequences to reduce potential artifacts. These modifications are based on our theoretical treatment of the experiments. We first present a theoretical framework for the detailed analysis of spin-dynamics during the course of the steady-state 15N-{1H} NOE experiment using a realistic spin-system. Then, we analyze the saturated experiment in the framework of Average Liouvillian Theory [15,16]. We evaluate the effects of the sequence of pulses and delays in the saturation block and provide suggestions to reduce sources of errors in the measured steady-state NOE value. We examine the non-saturated experiment next and introduce a simple and effective modification to commonly employed sequences which accelerate recovery towards equilibrium. The use of this sequence is recommended for larger, deuterated proteins. The improvements in accuracy resulting from the new sequences set (saturated and reference) are evaluated on a sample of perdeuterated human ubiquitin at high fields (16.5 T and 21.1 T).
2. Theory
2.1 Definitions
For cases where the polarization does not evolve towards an effective zero steady-state [17], the homogeneous Master equation (HME) [15,16,18] provides the most convenient theoretical framework to describe longitudinal relaxation. For instance, Di Bari and Levitt [15] have shown that it was possible to create several kinds of steady-state terms under multiple-pulse experiments. These results are described elegantly and efficiently in the framework of Average Liouvillian Theory [15,16]. Using the notation of Ghose [16], one can write the HME:
| (1) |
where σ is the density operator and L̂(t) the Liouvillian superoperator, defined as:
| (2) |
Ĥ(t) is the Hamiltonian superoperator that contains all coherent terms, Γ̂(t) is the relaxation superoperator that accounts for the non-coherent evolution towards the steady state, and Θ̂(t) is the thermal correction superoperator. The steady state represents the state of thermal equilibrium in the absence of any significant perturbations to the Zeeman interactions.
In the present context, we treat coherent evolutions under radiofrequency (RF) fields as perfect instantaneous rotations, allowing the Liouvillian superoperators to be simplified to include only relaxation and thermal correction terms. All the relevant spin dynamics can then be analyzed using a simple 4-dimensional Liouville space for a two-spin system in the basis {E/2, Nz, Hz, 2NzHz}, where E is the identity operator. The Liouvillian superoperator, for an amide 1H, 15N spin pair can be written as:
| (3) |
where ρN is the longitudinal relaxation rate of the 15N nucleus, ρH is the longitudinal relaxation rate of 1H, ρNH is the auto-relaxation rate of the two-spin order, σNH is the auto-correlated dipolar cross-relaxation rate, δN (or δH) is the longitudinal cross-relaxation rate due to the cross-correlation of the 15N (or 1H) chemical shift anisotropy (CSA) and the 15N-1H dipole-dipole (DD) interaction. If one normalizes [19] the equilibrium 15N polarization to be 1, thermal correction terms can be written as:
| (4) |
2.2 Symmetry of the saturation block
The experimental scheme often employed for 1H saturation while observing the steady state on 15N is depicted in Figure 1a. The pulse applied on 1H is often a 2π/3 rotation, however, we will consider π rotations in this discussion for simplicity and this does leads to no loss of generality. An alternative symmetric saturation scheme is presented in Figure 1c. The scheme of Figure 1b is a formally identical expansion of the scheme of Figure 1a, and the schemes of Figure 1d and 1c are similarly identical. The average Liouvillian that describes the evolution of the density operator during the bracketed element of Figures 1b and 1d is given by:
| (5) |
with:
| (6) |
where R̂ represents the inversion due to a π 1H pulse:
| (7) |
Figure 1.

Schematic representation of 1H saturation elements to measure the steady-state polarization on the 15N nucleus. a–b: Two forms of a typical saturation sequence when π pulses are used on the 1H. c–d: Two forms of a symmetric saturation element.
Note that all odd-order terms in the average Liouvillian vanish, because the bracketed sequences (Figures 1b and 1d) are symmetric. The odd terms subspace, consisting of operators inverted by π 1H pulses (i.e. Hz and 2NzHz) is decoupled from the even subspace consisting of operators invariant under 1H pulses (i.e. E/2 and Nz). leads to a monoexponential evolution of 15N longitudinal polarization with a rate ρN towards the well-known steady-state polarization :
| (8) |
where is the equilibrium polarization of the 15N nucleus.
All higher order terms in the average Liouvillian may be neglected when the inter-pulse delay 2τ is short. The steady state described by Equation 8 will be reached after an integer number of saturation elements. One can notice that a delay τ after the last multi-pulse element, in Figure 1b, corresponding to one half of the inter-pulse delay is therefore not required and leads to an evolution of 15N polarization away from the steady-state towards equilibrium. This effect is often negligible when the steady-state and equilibrium polarizations are comparable and typical values of τ that range from 2.5 ms to 10 ms are used. However, systematic errors up to a few percent may be found for mobile residues with negative NOE ratios (Eq. 8 i.e when ) and typical longitudinal relaxation rates of the order of 1 s−1. It is therefore preferable that a symmetric saturation element like Fig 1.c be used, since no additional saturation period is required (in practical terms, an initial recovery delay is always employed to lock the magnetic field allowing the first delay τ to be deleted) but may suppress small systematic errors.
2.3. Is saturation of 1H polarization necessary?
It is quite remarkable that the degree of saturation of the 1H polarization does not appear in Equations 5–8. In fact, in an extreme case with no auto-relaxation of 1H nuclei and perfect π pulses (i.e. no saturation), the system evolves exactly towards the steady-state polarization. Indeed, during every element of Figures 1c–d, a 15N nucleus sees its neighboring 1H nucleus an equal amount of time as spin-up and spin-down. Thus, on average, the 1H polarization appears saturated to the 15N nucleus.
If the rate of pulsing on 1H is fast, the evolution of the 1H polarization during the inter-pulse (2τ) delay is very small. Therefore, during each saturation element, the 15N nucleus sees also, on average, a saturated 1H nucleus. There is thus no requirement for the 1H polarization to be saturated. In all simulations displayed in Fig. 2, the residual polarization of 1H is still larger than 5% of the equilibrium polarization after 5 seconds. Nevertheless, the 15N polarization is identically equal to the expected steady-state polarization when the inter-pulse delay (2τ) is short.
Figure 2.

Evolution of the 15N longitudinal polarization towards the steady-state under the application of the saturation sequence of Figure 1c with different values for the delay τ. For a rigid system (a), the Lipari-Szabo [20] form of the spectral density function was used with an order parameter S2 equal to 0.85 and the correlation time for local motions is 50 ps. For a mobile residue (b), the order parameter is 0.5 and the local correlation time is 200 ps. The inserts show the details of the last 500 ms of this evolution. As in the experimental situations, the system is allowed to relax from a fully saturated state for two seconds before the beginning of the saturation scheme. A small spherical deuterated protein was taken as an example: a single global rotation correlation time of 4.5 ns was used and the 15N-1H pair was supplemented with two 1H nuclei located at 290 pm of the 15N bound 1H. The relaxation superoperator used for this calculation is displayed in the Appendix.
When the 1H polarization is allowed to relax significantly towards equilibrium during the inter-pulse delay, the situation is more complex. On average, the polarization of 1H is different from zero and the 15N polarization does not evolve towards the “true” steady-state. Figure 2 illustrates this property. For both a mobile NH pair and a rigid one, a delay τ as long as 50 ms is only marginally detrimental to the accuracy of the steady-state shown in Eq. 8. If one uses a symmetric saturation scheme, as depicted in the inserts in Figure 2, the result is perfectly accurate. In the case of very long inter-pulse delays, the polarization of the steady-state is different from the one expected from Eq. 8. In the latter case, the 1H polarizations are closer to equilibrium before each pulse on 1H, so that, after the π pulse, the nitrogen polarization is driven towards −〈Nz〉eq. After half an interpulse delay, the system is still biased towards this state so that if the NOE ratio (Eq. 8) is larger than −1, the nitrogen longitudinal polarization expectation value is smaller than the steady state (Fig. 2). If the NOE ratio is smaller than −1, the expectation value is larger than the steady-state polarization (data not shown). One should notice that, under the conditions of the simulations, the system is significantly closer to the expected steady state after half an inter-pulse delay, validating the use of a symmetric saturation scheme.
Our simulations clearly show that the saturation of 1H polarization is not necessary if one chooses the proper symmetry properties for the saturation element. However, when one uses an asymmetric saturation scheme, the saturation of the 1H polarization may become necessary. Indeed, if the saturation is complete, the expectation value of operators inverted by the pulses on 1H is null: the longitudinal polarization of 1H and the two-spin order polarization are zero. Therefore:
| (9) |
where σss is the density operator at the steady-state. From Equations 6 and 9, it follows that:
| (10) |
where is the conjugate transpose of Nz. From Eqs. (1) and (10), one obtains:
| (11) |
The initial slope for the evolution of the longitudinal polarization of the 15N nucleus is zero.
In the case where the 1H polarization is fully saturated, i.e. the 1H polarization is zero, schemes presented in Figures 1a and 1c will provide identical expectation values for the longitudinal polarization of the 15N nucleus unless the delay τ is much longer than values typically employed in experiments (5 to 10 ms). The outcome of these two schemes will only be different in fast-relaxing systems (i.e. when τ is comparable to the relaxation rates) or when the 1H and two-spin order polarizations are significantly different from zero.
Nevertheless, complete saturation of the polarization of 1H may be difficult to achieve [13], particularly in cases where cross-relaxation or exchange with the slow-relaxing 1H nuclei from the solvent is efficient. By reducing the need for saturation of the 1H nuclei, the use of a symmetric saturation scheme, which comes at no cost, reduces one source of systematic errors. Even though the benefits may be limited is most cases, its use is recommended.
2.4. Relaxation in the reference experiment
As discussed in section 2.2, the effective relaxation of the 15N longitudinal polarization during the saturation scheme is a mono-exponential evolution towards the steady state. Relaxation during the reference experiment is much more complex.
As shown in the Redfield theory of relaxation [8], the secular approximation suppresses many of the possible cross-relaxation pathways. All longitudinal operators commute with the Zeeman and scalar coupling Hamiltonian operators. Therefore, in the absence of radio-frequency fields, all possible cross-relaxation pathways are active in the relevant Liouville subspace. The consequence is that relaxation towards equilibrium is potentially highly multi-exponential. As shown by Gong and Ishima [12], when small, highly deuterated proteins are under study at high fields, dipole-dipole/CSA cross-correlated cross-relaxation [21] is sufficient to lead to a very slow evolution towards equilibrium for the 15N longitudinal polarization. In larger non-deuterated proteins, the lifetime of the two-spin order 2HzNz is short, which significantly reduces this effect.
Nevertheless, deuterated proteins are excellent tools for relaxation studies, e.g. when basic 15N relaxation experiments are supplemented by experiments where the 1H polarization participates in the coherence being followed. For example, the characterization of chemical exchange parameters is significantly improved by the implementation of CPMG (Carr Purcell Meiboom Gill) schemes on amide 1H [22,23], and the measurement of cross-relaxation under the cross-correlation of dipolar and CSA interactions to complement typical 15N relaxation experiments allows an accurate determination of relaxation under chemical exchange [17,24]. The accuracy of the quantitative analyses of these experiments benefit strongly from deuteration. Thus in addition to large proteins, where the benefits of deuteration have been discussed at length elsewhere [25] and its application to relaxation studies demonstrated [26–28], deuteration of small proteins is also greatly beneficial especially when detailed, quantitative analyses are required to interpret data from relaxation experiments.
An accurate method to measure 15N-{1H} nuclear Overhauser effects adapted for deuterated proteins at high fields is, to the best of our knowledge, not available in the literature. A difficulty here is that manipulations of the spin system designed to alter cross-relaxation pathways would make the effective final state of the system different from the equilibrium state. In the absence of any manipulation of the spin system, it is still possible to accelerate the evolution towards equilibrium by an appropriate choice of the operator being followed. Indeed, the closer this operator is to the fastest relaxing relaxation modes of the density operator, the more efficient is its evolution towards equilibrium.
The development of spin-state-selective experiments [29–32] has made the manipulation of single-transition operators very convenient. Figure 3 compares the projections of three longitudinal operators that can be readily converted to observables: the longitudinal polarization of the 15N nucleus and the two single-transition longitudinal operators. The spin system employed for this calculation comprises additional protons (see Appendix), so that there are eight eigenvalues and not four, as expected from Eq. 3. It is quite remarkable that, for a rigid NH pair in a small protein (overall correlation time 5 ns) with a magnetic field of 21.1 T, the two single-transition operators are very close to either the slowest relaxing mode or the fastest relaxing mode of the spin-system, as can be seen in Fig. 5a. This is because the dominant contributions to relaxation rates are the 15N-1H dipole-dipole and 15N CSA, while the static field is close to its optimal value for relaxation interference [33]. This makes of the fast-relaxing single transition operator 2NzHβ the ideal operator to be followed in an experiment designed to reduce the recovery delay. In this study, we will refer to 2NzHβ as the fast-relaxing single-transition. This is consistent with the definitions of relaxation rates provided in the Appendix but may be in contradiction with part of the literature on the subject.
Figure 3.

Projection of the accessible observables 2HβNz 2HαNz and Nz on the eigenvectors of the Liouvillian superoperator that governs the evolution towards equilibrium. Eigenvalues are reported on the x-axis while the projections of the observables on the corresponding eigenvectors are reported on the z-axis. (a,b) For a rigid group with the same parameters as those used in Figure 2. (c,d) For a rigid group in a small mobile domain with the same parameters for local motions and a domain motion characterized by a correlation time equal to 10% of the overall tumbling time and an order parameter for slow motions of 0.3. The overall tumbling correlation time employed is (a,c) 5 ns and (b,d) 30 ns.
Figure 5.

Relaxation rates calculated for the simulations displayed in Figure 4. See the appendix for detailed expressions of the rates.
In a rigid NH pair in a large protein (Fig. 3b), however, the longitudinal polarization of the 15N nucleus is almost equal to the eigenvector with the lowest non-zero eigenvalue. The projections on fast-relaxing modes are only slightly larger for the 2NzHβ operator. In this case, 1H-1H cross-relaxation is the dominant mechanism for relaxation. One consequence is the effective decoupling of CSA/DD cross-relaxation pathways. If semi-local motions, such as small domain motions, occur on an intermediate time-scale (this assumes that the fast sub-nanosecond motions occur on two different timescales that differ by at least one order of magnitude), the projection of 2NzHβ on fast-relaxing modes increases significantly (Fig. 3d), so that this operator is, again, the most relevant “observable”. Overall, Figure 3 shows that this operator should relax faster than the other accessible operators.
To confirm this trend, we have simulated the evolution towards equilibrium of all three operators under three classes of local dynamics and over a wide range of overall tumbling times. Results are displayed in Figure 4 while the calculated rates are plotted in Figure 5. As illustrated by the bold line in all simulations, the same single-transition is the closest to equilibrium, under all simulated circumstances and all times. In small proteins, the advantage is dramatic. In larger systems, the difference between the relaxation properties of the three operators for rigid NH pairs (as illustrated by Fig 3b) and very mobile NH pairs becomes smaller, as expected from Fig. 3. Figure 5 illustrates the dominance of 1H-1H dipolar cross-relaxation in this regime. However, in the presence of small-domain motions the quantification of the operator 2NzHβ, provides a much closer estimate of the equilibrium polarization because it relaxes at a significantly faster rate than the other two operators over the entire range of overall tumbling times explored.
Figure 4.
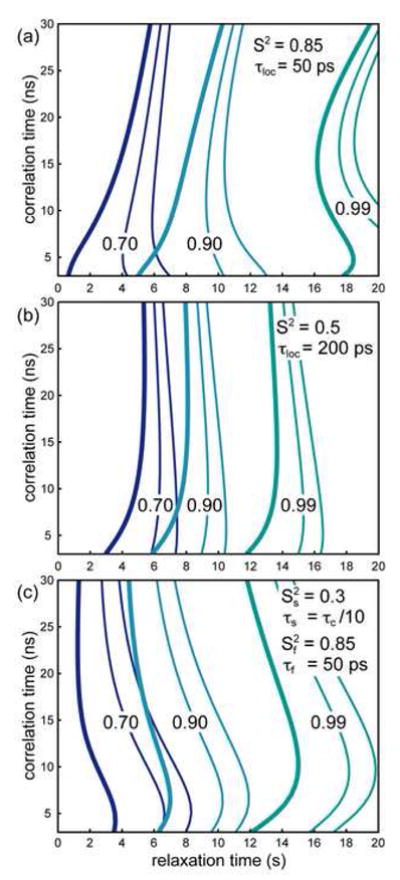
Evolution of 15N longitudinal polarization operators towards equilibrium from a fully saturated state. The bold contour lines correspond to the expectation value <2HβNz>. The thin line that carries the labels corresponds to the expectation value <Nz> while the second thin line represents the expectation value <2HαNz>. The parameters for local dynamics are displayed on each figure. They correspond to (a) a rigid NH pair, (b) a mobile NH pair and (c) a rigid NH pair in a mobile domain. Contour lines are plotted for a polarization equal to 70% (blue); 90% (cyan); and 99% (green) of its equilibrium value.
For example, in a large deuterated protein with an overall tumbling time of 20 ns, for which the use of this pulse sequence is recommended, we predict that, in a rigid system (S2 = 0.85 and τloc = 50 ps) studied on a 900 MHz spectrometer, 98 % of the equilibrium polarization is recovered after 14 seconds for the fast-relaxing single transition. For the same duration, 97.1 % of the equilibrium longitudinal 15N polarization is recovered, while 98 % would be obtained after 15.25 seconds. The difference for this system is not spectacular, but the reduction of 8 % of the relaxation delay should be welcome.
Figure 4 shows that, even if the advantage for the selection of one single-transition operator may be limited for specific cases, selection of this operator always leads to the closest estimate of equilibrium. Therefore, it should always be advisable to measure the polarization of the fast-relaxing longitudinal single-transition of the 15N nucleus as a standard for equilibrium in the experiment without 1H saturation when measuring the steady-state 15N-{1H} NOE with TROSY-based sequences.
3. Material and Methods
All simulations were performed using MATLAB (www.mathworks.com). The programs can be provided upon request and only a few major features are discussed here. The spin system considered comprised one 15N nucleus and three 1H nuclei. The distance between the 15N nucleus and its bound 1H nucleus is 102 pm. The distances between this 1H nucleus and its two neighbors are both 290 pm [30]). The 1H-1H cross-relaxation rate was added to the auto-relaxation rate of one of the two neighboring 1H nuclei to take into account the effect of cross-relaxation or exchange with 1H from the solvent. Values for the CSA of 1H and 15N nuclei are the average values provided by Loth et al. in their study of human ubiquitin [35]. The model-free form of the spectral density function was used to describe rigid and mobile residues [20]. The extended model-free form was employed to take into account small domain motions [36]. The spectral density function was adapted to include cross-correlated relaxation as in Loth et al. [35].
We have designed a new reference experiment, shown in Figure 6, where the element that suppresses all polarizations involving the 1H nucleus [26,37] (the element between points Asat and Bsat in the saturated experiment) is substituted by a conversion between the fast- and slow-relaxing components of the polarization. At point Aref, after a relaxation delay with a total duration Tlock + T, the expectation value <2NzHβ> is larger than <2NzHβ>. A composite π pulse on the on the 1H channel interconverts these two operators, so that, at point Bref in the sequence, the expectation value for 2NzHβ is closer to equilibrium. The latter operator is subsequently detected in a TROSY detection: a spin-state-selective transfer follows the 15N frequency labeling for the detection of a TROSY-like spectrum [31]. The conversion between the polarizations is achieved by a composite π pulse on the 1H channel to reduce effects of RF-field inhomogeneities flanked by two π/2 very selective pulses to ensure an efficient restoration of the water magnetization to the +z axis.
Figure 6.
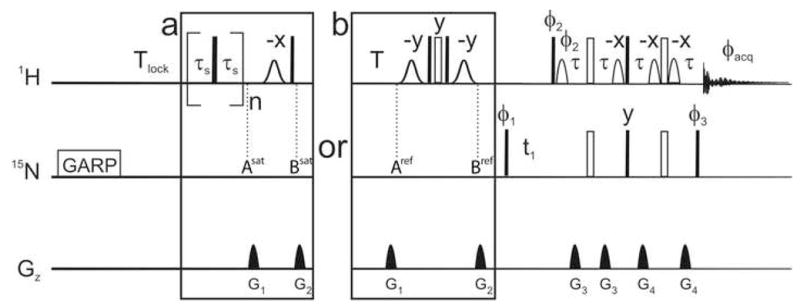
Pulse sequences used for recording steady-state 15N-{1H} nuclear Overhauser effects. In all experiments, a GARP [34] decoupling scheme was initially applied on the 15N channel for 60 ms followed by a 2 second recovery delay (Tlock) used to lock the magnetic field. Saturated and reference experiments were run in an interleaved manner with the boxed schemes (a) and (b) respectively. (a) A train of 2π/3 pulses was applied on the 1H channel for 4s with a delay τs equal to 5 ms. (b) A recovery delay T is followed by a composite pulse flanked by two water flip back pulses to invert all 1H polarizations but water 1H. The total recovery delay is Tlock+T. For comparison with the initial scheme for the reference experiment, bracketed saturation elements were replaced by the delay T. A classic TROSY detection follows for all experiments. Except in the saturation element, all narrow (filled) and (wide) open rectangles represent π/2 and π pulses respectively. Pulse phases are along the x-axis of the rotating frame unless otherwise mentioned. Gaussian shaped pulses are 2 ms and have a Gaussian shape truncated at 1% of the maximal amplitude. A longer duration of 3 ms is recommended if greater selectivity is required. Bell-shaped pulses are sinebell shaped pulses, of 1 ms. The delay τ is 1.792 ms. The phase cycles are φ1 = {y;−y; −x;x} used with φ2 = {y} and φ3 = {x}; and φ1 = {−y;y; −x;x} used with φ2 = {−y} and φ3 = {−x} alternated for every other free induction decay. The phase cycle for acquisition is φacq = {x; −x; −y;y}. The duration of acquisition is 120 ms. For the indirect dimension, 75 complex points were recorded with a spectral width of 34 ppm.
All experiments were performed on Bruker Avance NMR spectrometers operating at 1H Larmor frequencies of 500, 700 and 900 MHz equipped with TXI cryoprobes with z-axis gradients. A sample of perdeuterated, uniformly 15N-labelled ubiquitin (0.5 mM, in 50 mM ammonium acetate, 300 mM NaCl, pH 4.8) was used for all experiments. R1, R2 and 15N-{1H} NOE values (using the experiment presented here with a Tlock+T value of 8 seconds, 16 scans per transient) were obtained at 500 MHz. The following relaxation delays were used for the R1 and R2 experiments: R1: 5 ms (x2), 20 ms, 100 ms (x2), 300 ms and 600 ms; R2: 1 ms (x2), 50 ms, 100 ms (x2), 150 ms, 250 ms. A relaxation delay of 2 seconds was used between scans in the R1 and R2 experiments and 8 scans were collected per transient. All experiments were performed at 25° C. Analysis of the relaxation rates was performed in the usual way using the program DIFFTENS v2.0 [38] using an isotropic diffusion model and yielded a rotational correlation time of 4.48 ± 0.05 ns.
R1, R2 and 15N-{1H} NOE ratio were simulated using standard expressions [36] for a 15N-1H two-spin system using standard parameters for several motional models described in the legend to Figures 9 and 10. The “experimental” precisions of the R1, R2 and 15N-{1H} NOE ratio were assumed to be 2.5 %, 2.5 % and 5 % respectively. The microdynamic parameters were obtained assuming an isotropic overall motion and fitting to the 8 different motional models described in detail elsewhere using the DYNAMICS package[39].
Figure 9.
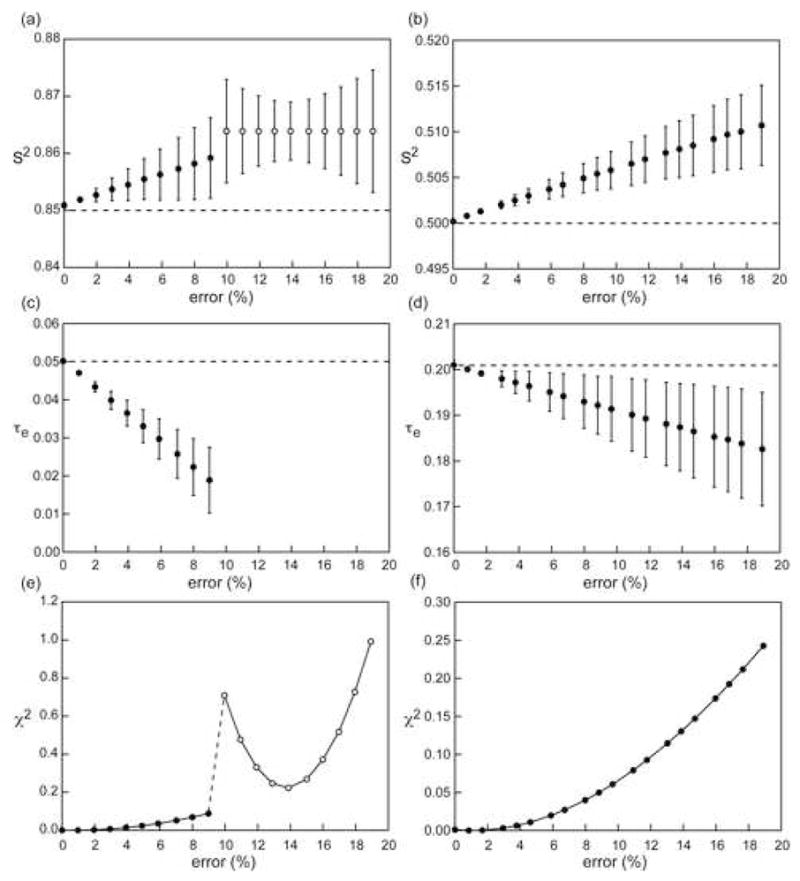
Influence of overestimation of the 15N-{1H} NOE ratio on derived Lipari-Szabo micro-dynamic parameters. Parameters were obtained from theoretical R1, R2 and 15N-{1H} NOE ratio at 700 MHz assuming an overall correlation time of 4.5 ns, S2=0.85 and τloc=50 ps (a,c,e) and S2=0.50 and τloc=200 ps (b,d,f). “Experimental” errors of 2.5 % for the R1 and R2 rates and 5 % for the 15N-{1H} NOE were assumed. Filled circles represent cases where the correct (input) model (S2, τloc) was selected based on the relaxation rates using a statistical F-test while open circles represent cases where the incorrect model (S2 only) was chosen. The dashed lines (panels a–d) represent the correct motional parameters.
Figure 10.
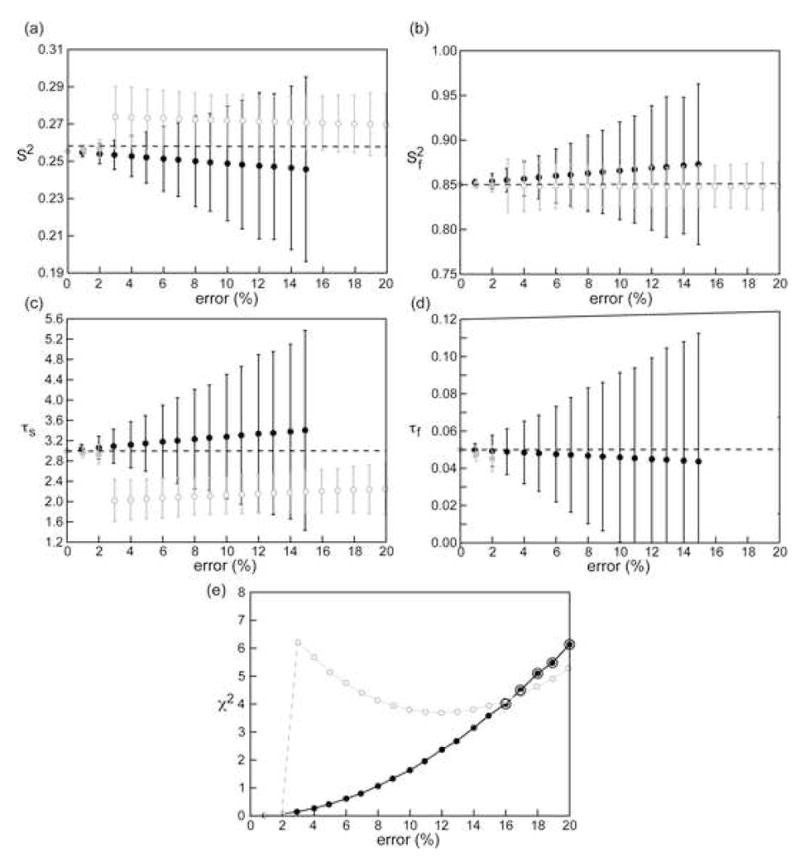
Influence of overestimation of the 15N-{1H} NOE ratio on Lipari-Szabo micro-dynamic parameters for a small rigid domain in a large protein. Parameters were obtained from theoretical R1, R2 and 15N-{1H} NOE ratio at 700 MHz and 900 MHz (analyzed simultaneously) assuming an overall correlation time of 30 ns, , τs =3 and τf = 50 ps. “Experimental” errors of 2.5 % for the R1 and R2 rates and 5 % for the 15N-{1H} NOE were assumed. Black circles represent the case where the NOE ratio at 700 MHz was overestimated and the correct value was used at 900 MHz, the reverse case is represented by gray circles. Filled circles represent cases where the correct model (S2, , τs, τf) was selected based on the relaxation rates using a statistical F-test while open circles represent cases where the incorrect model (S2, , τs only) was chosen. The dashed lines represent the correct motional parameters. The black concentric circles in (e) represent cases for which none of the possible dynamic models passed the goodness-of-fit test based on the corresponding χ2 distribution. The χ2 values for the most physical model in these cases have been displayed for illustration but the microdynamic parameters (which are erroneous) have not.
4. Results and Discussion
4.1. Quantification of the equilibrium polarization in the reference experiment
The scheme of Zhu et al. [37] as modified by Chill et al. [26] was compared to our present scheme, with the new reference experiment. Data obtained on a spectrometer with a 700 MHz Larmor frequency for 1H are displayed in Fig. 7. As can be seen from Fig. 7a, after 6 seconds of total recovery time neither the initial scheme nor the new one provide with an exact measurement of the polarization at equilibrium. However, the new scheme gives a closer estimate of the equilibrium polarization. For most NH pairs, the polarization is larger than 95% of the equilibrium polarization, assuming that the polarization is at equilibrium after a period of 12 seconds. For the initial scheme, many residues are still below 90% of the equilibrium polarization. Fig. 7b shows the NOE ratios derived from the two experimental approaches. As expected, ours provides smaller absolute values for the NOE ratio. This translates into larger values for the cross-relaxation rate σNH when the NOE ratio is positive and smaller values of σNH when the NOE ratio is negative (Figs. 7c,d).
Figure 7.

Comparison of the initial and new schemes for the reference experiment at 16.4 T. (a) Ratio of intensities after a total of 6 s and 12 s of recovery. The delay is Tlock + T. Tlock is 2 s in all experiments. (b–d) The durations of the delay T and of the saturation schemes are both 4 s. (b) NOE ratio. (c) ratio of the dipolar cross-relaxation rates and longitudinal auto-relaxation rate of the 15N nuclei derived from the NOE ratio of (b) as from Eq. 8. (d) Same as (c) with an expansion along the y-axis.
Since for most residues the NOE ratio is close to one, according to Eq. 8, a small error in this ratio may translate into large relative errors in the value of σNH: for several residues, this cross-relaxation rate can be underestimated by a factor of 2 (Fig. 7d). For very mobile residues that display a negative NOE ratio, the error is marginally attenuated, which explains why the dramatic error in the estimate of the polarization at equilibrium for the NH pair of residue 76 translates in a comparable error for σNH. The NOE ratios displayed in Fig. 7b for residue 36 deserve comment. These large values are due to the underestimation of the intensity in all reference experiments. The 1H signal of residue 36 is the closest to the water resonance, so that the 1H polarization is affected by 2 ms Gaussian water flip-back pulses. Therefore, in the original scheme, the polarization of the two-spin order is not properly suppressed, so that the slowly relaxing component has a major contribution to the detected signal. In our present scheme, the inversion of the polarization of the two-spin order is also not perfect, so that both single-transition polarizations are partially mixed. With the use of the same selective water flip-back pulses; the scheme introduced in this article is significantly more robust to this artifact than the original scheme.
Figure 8 presents experimental results obtained on a 900 MHz (1H Larmor frequency) spectrometer. This high magnetic field provides a close to maximum interference effect between the 15N CSA and 15N-1H dipolar interactions [33]. On average, our scheme provides a significantly larger intensity (i.e. closer to equilibrium) after a recovery delay as long as 8 seconds. The results depend significantly on the NH pair observed. Gly76 shows the most spectacular improvement, which can be linked to a high degree of flexibility. However, the preceding residues in the flexible C-terminal tail show very similar intensities in the two experiments, in spite of a large mobility.
Figure 8.

Comparison of intensities of the experiment of Zhu et. al.[37] as modified by Chill et al. [26] and the new scheme. Error bars are smaller than the symbols. Experiments were recorded on a 900 MHz spectrometer with a total relaxation delay of 8 s. Results of a linear regression are shown by the dashed line.
At both fields, the scheme introduced in this paper provides a better estimate of the equilibrium polarization for almost all residues. The number of residues for which the initial scheme provides a higher intensity is small and the extent of the difference is generally negligible. According to our simulations (Fig. 4) this tendency is verified under all dynamic regimes and all molecular masses explored. It is therefore recommended to employ the new TROSY-based scheme presented in Fig. 6, with more selective water flip-back pulses (for instance 3 ms Gaussian-shaped pulses truncated at one percent of the maximum amplitude at high fields).
Depending on the acquisition mode, the implementation of TROSY may lead to a loss of signal of a factor of 2 to if relaxation is negligible. 15N-{1H} NOE experiments are often signal-limited so that the use of TROSY for small proteins may not be the most appropriate method. It would indeed be more useful to employ twice longer relaxation recovery delays in the reference experiment with twice less scans and a conventional detection. That would lead to a good level of accuracy and more precision. On the other hand, if TROSY-based methods are to be used, which is the case for studies of large proteins or protein assemblies, the scheme discussed here should be favored.
4.2. Effect of the overestimation of the NOE on local dynamics parameters
The effect of the overestimation of 15N-{1H} NOE can lead to significant errors in the microdynamic parameters determined from an analysis of R1, R2 and 15N-{1H} NOE using the Lipari-Szabo or the extended Lipari-Szabo models. As seen in Figure 9, for simple models, the overestimation has a profound effect on a rigid system with errors greater than 60 % for the τe value even when the NOE value is overestimated by a mere 9 % (Figure 9(c)). When the overestimation is greater than 9 %, the timescale of the local motion can no longer be obtained and the incorrect motional model is selected based on a statistical F-test with very large increases in the χ2 value (Figure 9(f)). The effect is somewhat smaller in more dynamic systems. The transition point between different motional models being selected would necessarily depend on the software used to perform the Lipari-Szabo analysis and the particular algorithms utilized therein, however, the same general trends should be expected. The estimated S2 values are less affected by the NOE overestimation with the errors being approximately 2 % in both the rigid and dynamic cases. Additionally, when the NOE is overestimated, and the degree of overestimation is much larger than the experimental precision (i. e. the random error in the experimental data), the complete set of relaxation data ceases to be self-consistent and large errors are obtained in the fitted microdynamic parameters for the same level of experimental precision. The magnitude of these errors become larger when more complex motional models are considered (Figure 10) even though the average values of the fitted microdynamic parameters do not deviate significantly from the correct values. In extreme situations, for example, Figure 10(a–d), when the error in the NOE ratio exceeds 15 % at 700 MHz (the correct value is used at 900 MHz) for an extended Lipari-Szabo model, the goodness-of-fit criterion is no longer satisfied and no motional model is found to be appropriate for the set of relaxation data and no microdynamic parameters can be obtained.
5. Conclusion
We have introduced a new scheme for the measurement of 15N-{1H} NOE’s. We have shown that this experiment provides a better estimate of the equilibrium polarization than previous approaches even for long recovery delays (8 seconds at 900 MHz). We show that the use of this new scheme when TROSY detection is likely to avoid systematic errors. For small proteins, the use of long recovery delays for the reference experiment should provide better precision. Systematic errors arising from the underestimation of the 15N equilibrium polarization were shown to have variable impact on the parameters for local dynamics derived from a model-free approach. An improvement of the saturation schemes employed in the complementary experiment was introduced and evaluated through simulations. We are currently investigating in greater detail the nature of the saturation schemes utilized for 1H saturation in the saturated experiment.
Acknowledgments
This work has been supported by the following grants: MCB-0347100 from the National Science Foundation; 5G12 RR03060 towards support of the core facilities at the City College of New York and P41 GM-66354 towards partial support of the high-field NMR facilities at the New York Structural Biology Center from the National Institutes of Health, and R01 GM 47021.
Appendix
In this section, we present the expression of the Liouvillian superoperators used here for the simulation of the recovery of the spin-system towards equilibrium. The spin system consists of one 15N-1H pair supplemented by two neighboring 1H nuclei. One of these two 1H nuclei shows enhanced auto-relaxation rates to take into account cross-relaxation or exchange with solvent protons during the recovery.
We have neglected all DD/DD cross-correlation mechanisms, as well as all long-range DD/CSA cross-correlations. We have not taken into account any cross-relaxation mechanism between neighboring 1H nuclei and their 15N partner. Under these conditions, we can restrict the basis of the subspace of the Liouville space to: {E/2, Nz, Hz,2NzHz, }. The Liouvillian superoperator is:
| (A1) |
where the expressions of the relaxation rates are:
| (A2a) |
| (A2b) |
| (A2c) |
| (A2d) |
| (A2e) |
| (A2f) |
| (A2g) |
| (A2h) |
| (A2i) |
| (A2j) |
| (A2k) |
with: ; dN = ωNΔσN; dHx = ωH(σHxx − σHzz); dHy = ωH(σHyy − σHzz); ωN = − γNB0; ωH = − γHB0; μ0 is the permittivity of free space; γN and γH are the gyromagnetic ratio of 15N and hydrogen nuclei; rNH is the distance between the 15N nucleus and its neighboring 1H nucleus; rHH is the distance between two 1H nuclei; ΔσN is the chemical shift anisotropy of the 15N nucleus; σHxx, σHyy and σHzz are the three principal components of the 1H chemical shift tensor; B0 is the static magnetic field.
The spectral density functions employed make the assumption of uncorrelated isotropic local and global motions. A model-free form was employed for the case of local motions on one time-scale.
| (A3) |
where S2 is the generalized order parameter, τc the correlation time for the overall tumbling time and τe is defined from the correlation time for local motions τloc by: . The extended model-free form was used to describe the case of the motion of a small domain in a large protein:
| (A4) |
where and are the generalized order parameter for slow domain motions and fast local motions respectively; the time constants τes and τef are defined from the correlation times for slow domain τs and fast local τf motions by the relationships: and . Under isotropic global, domain and local motions, the spectral density functions for cross-correlated relaxation can be derived from auto-correlated spectral density functions by the relationship:
| (A5) |
| (A6a) |
| (A6b) |
where the angle θN describes the relative orientation of the NH vector and the principal axis of the axially symmetric 15N chemical shift anisotropy tensor; θHx and θHx describe the relative orientation of the NH vector and the x and y principal axes of the 1H CSA tensor respectively.
The values employed for the above-mentioned parameters are: rNH = 101 pm; rHH = 290 pm; ΔσN = 164 ppm; θN = 19°; σHxx = 14.6 ppm; σHyy = 8.2 ppm; σHzz = 2.1 ppm; θHx = 90°; θHy = 99°.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Mittermaier A, Kay LE. Review - New tools provide new insights in NMR studies of protein dynamics. Science. 2006;312:224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
- 2.Palmer AG., III NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 3.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational Diffusion Anisotropy of Human Ubiquitin from N-15 NMR Relaxation. J Am Chem Soc. 1995;117:12562–12566. [Google Scholar]
- 4.Fushman D, Tjandra N, Cowburn D. An Approach to Direct Determination of Protein Dynamics from 15N NMR Relaxation at Multiple Fields, Independent of Variable 15N Chemical Shift Anisotropy and Chemical Exchange Contributions. J Am Chem Soc. 1999;121:8577–8582. [Google Scholar]
- 5.Shapiro YE, Kahana E, Tugarinov V, Liang ZC, Freed JH, Meirovitch E. Domain flexibility in ligand-free and inhibitor-bound Escherichia coli adenylate kinase based on a mode-coupling analysis of N-15 spin relaxation. Biochemistry. 2002;41:6271–6281. doi: 10.1021/bi012132q. [DOI] [PubMed] [Google Scholar]
- 6.Bloembergen N, Purcell EM, Pound RV. Relaxation Effects in Nuclear Magnetic Resonance Absorption. Phys Rev. 1948;73:679–712. [Google Scholar]
- 7.Abragam A. Principles of Nuclear Magnetism. Oxford University Press; 1961. [Google Scholar]
- 8.Redfield AG. Theory of relaxation processes. Adv Magn Reson. 1965;1:1–32. [Google Scholar]
- 9.Favro LD. Theory of the Rotational Brownian Motion of a Free Rigid Body. Phys Rev. 1960;119:53–62. [Google Scholar]
- 10.Farrow NA, Zhang OW, Szabo A, Torchia DA, Kay LE. Spectral Density-Function Mapping Using N-15 Relaxation Data Exclusively. J Biomol NMR. 1995;6:153–162. doi: 10.1007/BF00211779. [DOI] [PubMed] [Google Scholar]
- 11.Grzesiek S, Bax A. The Importance of Not Saturating H2O in Protein NMR - Application to Sensitivity Enhancement and NOE Measurements. J Am Chem Soc. 1993;115:12593–12594. [Google Scholar]
- 12.Gong QG, Ishima R. N-15-{H-1} NOE experiment at high magnetic field strengths. J Biomol NMR. 2007;37:147–157. doi: 10.1007/s10858-006-9125-7. [DOI] [PubMed] [Google Scholar]
- 13.Renner C, Schleicher M, Moroder L, Holak TA. Practical aspects of the 2D N-15-{H-1}-NOE experiment. J Biomol NMR. 2002;23:23–33. doi: 10.1023/a:1015385910220. [DOI] [PubMed] [Google Scholar]
- 14.Skelton NJ, Palmer AG, Akke M, Kordel J, Rance M, Chazin WJ. Practical Aspects of 2-Dimensional Proton-Detected N-15 Spin Relaxation Measurements. J Magn Reson Ser B. 1993;102:253–264. [Google Scholar]
- 15.Levitt MH, Di Bari L. Steady-State in Magnetic-Resonance Pulse Experiments. Phys Rev Lett. 1992;69:3124–3127. doi: 10.1103/PhysRevLett.69.3124. [DOI] [PubMed] [Google Scholar]
- 16.Ghose R. Average Liouvillian theory in nuclear magnetic resonance - Principles, properties, and applications. Concepts Magn Reson. 2000;12:152–172. [Google Scholar]
- 17.Pelupessy P, Ferrage F, Bodenhausen G. Accurate Measurement of Longitudinal Cross-Relaxation Rates in Nuclear Magnetic Resonance. J Chem Phys. 2007;126:134508. doi: 10.1063/1.2715583. [DOI] [PubMed] [Google Scholar]
- 18.Jeener J. Superoperators in Magnetic-Resonance. Adv Magn Reson. 1982;10:1–51. [Google Scholar]
- 19.Levante TO, Ernst RR. Homogeneous Versus Inhomogeneous Quantum-Mechanical Master-Equations. Chem Phys Lett. 1995;241:73–78. [Google Scholar]
- 20.Lipari G, Szabo A. Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation In Macromolecules 1. Theory and Range of Validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- 21.Goldman M. Interference Effects in the Relaxation of a Pair of Unlike Spin-1/2 Nuclei. J Magn Reson. 1984;60:437–499. [Google Scholar]
- 22.Ishima R, Torchia DA. Extending the range of amide proton relaxation dispersion experiments in proteins using a constant-time relaxation-compensated CPMG approach. J Biomol NMR. 2003;25:243–248. doi: 10.1023/a:1022851228405. [DOI] [PubMed] [Google Scholar]
- 23.Korzhnev DM, Neudecker P, Mittermaier A, Orekhov VY, Kay LE. Multiple-Site Exchange in Proteins Studied with a Suite of Six NMR Relaxation Dispersion Experiments: An Application to the Folding of a Fyn SH3 Domain Mutant. 2005;127:15602–15609. doi: 10.1021/ja054550e. [DOI] [PubMed] [Google Scholar]
- 24.Kroenke CD, Loria JP, Lee LK, Rance M, Palmer AG., III Longitudinal and Transverse H-1-N-15 Dipolar N-15 Chemical Shift Anisotropy Relaxation Interference: Unambiguous Determination of Rotational Diffusion Tensors and Chemical Exchange Effects in Biological Macromolecules. J Am Chem Soc. 1998;120:7905–7915. [Google Scholar]
- 25.Gardner KH, Kay LE. The use of H-2, C-13, N-15 multidimensional NMR to study the structure and dynamics of proteins. Annu Rev Biopys Biomol Struct. 1998;27:357–406. doi: 10.1146/annurev.biophys.27.1.357. [DOI] [PubMed] [Google Scholar]
- 26.Chill JH, Louis JM, Baber JL, Bax A. Measurement of N-15 relaxation in the detergent-solubilized tetrameric KcsA potassium channel. J Biomol NMR. 2006;36:123–136. doi: 10.1007/s10858-006-9071-4. [DOI] [PubMed] [Google Scholar]
- 27.Hwang PM, Skrynnikov NR, Kay LE. Domain orientation in beta-cyclodextrin-loaded maltose binding protein: Diffusion anisotropy measurements confirm the results of a dipolar coupling study. J Biomol NMR. 2001;20:83–88. doi: 10.1023/a:1011226512421. [DOI] [PubMed] [Google Scholar]
- 28.Wang CY, Rance M, Palmer AG. Mapping chemical exchange in proteins with MW > 50 kD. J Am Chem Soc. 2003;125:8968–8969. doi: 10.1021/ja035139z. [DOI] [PubMed] [Google Scholar]
- 29.Sorensen MD, Meissner A, Sorensen OW. Spin-state-selective coherence transfer via intermediate states of two-spin coherence in IS spin systems: Application to E.COSY-type measurement of J coupling constants. J Biomol NMR. 1997;10:181–186. [Google Scholar]
- 30.Pervushin K, Riek R, Wider G, Wüthrich K. Attenuated T-2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci USA. 1997;94:12366–12371. doi: 10.1073/pnas.94.23.12366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pervushin KV, Wider G, Wüthrich K. Single transition-to-single transition polarization transfer (ST2-PT) in [N-15,H-1]-TROSY. J Biomol NMR. 1998;12:345–348. doi: 10.1023/A:1008268930690. [DOI] [PubMed] [Google Scholar]
- 32.Ferrage F, Eykyn TR, Bodenhausen G. Highly Selective Excitation in Biomolecular NMR by Frequency-Switched Single-Transition Cross-Polarization. J Am Chem Soc. 2002;124:2076–2077. doi: 10.1021/ja012452x. [DOI] [PubMed] [Google Scholar]
- 33.Pervushin K. Impact of Transverse Relaxation Optimized Spectroscopy (TROSY) on NMR as a technique in structural biology. Q Rev Biophys. 2000;33:161–197. doi: 10.1017/s0033583500003619. [DOI] [PubMed] [Google Scholar]
- 34.Shaka AJ, Lee CJ, Pines A. Iterative Schemes for Bilinear Operators - Application to Spin Decoupling. J Magn Reson. 1988;77:274–293. [Google Scholar]
- 35.Loth K, Pelupessy P, Bodenhausen G. Chemical Shift Anisotropy Tensors of Carbonyl, Nitrogen, and Amide Proton Nuclei in Proteins through Cross-Correlated Relaxation in NMR Spectroscopy. J Am Chem Soc. 2005;127:6062–6068. doi: 10.1021/ja042863o. [DOI] [PubMed] [Google Scholar]
- 36.Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. Deviations from the Simple 2-Parameter Model-Free Approach to the Interpretation of N-15 Nuclear Magnetic-Relaxation of Proteins. J Am Chem Soc. 1990;112:4989–4991. [Google Scholar]
- 37.Zhu G, Xia YL, Nicholson LK, Sze KH. Protein dynamics measurements by TROSY-based NMR experiments. J Magn Reson. 2000;143:423–426. doi: 10.1006/jmre.2000.2022. [DOI] [PubMed] [Google Scholar]
- 38.Ghose R, Fushman D, Cowburn D. Determination of the rotational diffusion tensor of macromolecules in solution from NMR relaxation data with a combination of exact and approximate methods - Application to the determination of interdomain orientation in multidomain proteins. Journal of Magnetic Resonance. 2001;149:204–217. doi: 10.1006/jmre.2001.2295. [DOI] [PubMed] [Google Scholar]
- 39.Fushman D, Cahill S, Cowburn D. The main chain dynamics of the dynamin pleckstrin homology (PH) domain in solution: Analysis of 15N relaxation with monomer/dimer equilibration. J Mol Biol. 1997;266:173–194. doi: 10.1006/jmbi.1996.0771. [DOI] [PubMed] [Google Scholar]


