The discovery of population differences in network community structure: New methods and applications to brain functional networks in schizophrenia

Abstract

The modular organization of the brain network can vary in two fundamental ways. The amount of interversus intra-modular connections between network nodes can be altered, or the community structure itself can be perturbed, in terms of which nodes belong to which modules (or communities). Alterations have previously been reported in modularity, which is a function of the proportion of intra-modular edges over all modules in the network. For example, we have reported that modularity is decreased in functional brain networks in schizophrenia: There are proportionally more inter-modular edges and fewer intra-modular edges. However, despite numerous and increasing studies of brain modular organization, it is not known how to test for differences in the community structure, i.e., the assignment of regional nodes to specific modules. Here, we introduce a method based on the normalized mutual information between pairs of modular networks to show that the community structure of the brain network is significantly altered in schizophrenia, using resting-state fMRI in 19 participants with childhood-onset schizophrenia and 20 healthy participants. We also develop tools to show which specific nodes (or brain regions) have significantly different modular communities between groups, a subset that includes right insular and perisylvian cortical regions. The methods that we propose are broadly applicable to other experimental contexts, both in neuroimaging and other areas of network science.

Introduction

The human brain network is modular in the graph-theoretical sense, containing nearly-decomposable functional communities. As revealed by an increasing number of resting-state fMRI studies of modularity (Meunier et al., 2010), anatomically similar functional communities have been found across a broad range of populations and experimental conditions (Fair et al., 2009; He et al., 2009; Meunier et al., 2009a). There is a high degree of correspondence between fMRI functional modules and the modules of structural networks, derived from either diffusion imaging (Hagmann et al., 2008) or interregional correlations in cortical thickness across a population (Chen et al. 2008). Hierarchical modularity has been been demonstrated in the human brain, with relatively large modules further divisible into many different, smaller sub-modules (Meunier et al., 2009b; Bassett et al., 2010).

In schizophrenia research, alterations in the topological characteristics of brain networks have been reported using a raft of methodological approaches, imaging modalities and patient populations (Liu et al., 2008; Bassett et al. 2009, 2008; Lynall et al., 2010; Van den Heuvel et al., 2010). Previously we tested the possibility of dysmodularity in schizophrenia, i.e., increased crosstalk between functionally segregated sub-communities in the brain (David, 1994). Using fMRI and graph-theoretical methods that quantify the extent of network modularity, by measuring the density of intra-modular connections, we found preliminary evidence for decreased modularity in a small sample of patients with childhood-onset schizophrenia (Alexander-Bloch et al., 2010).

But this finding leaves unanswered fundamental questions about the brain’s modular organization in schizophrenia. Given the blurring or increased crosstalk between topological modules, an outstanding question is whether, in affected individuals, the modules themselves are equivalent to those of experimental controls. In other words, does the decreased modularity simply reflect relatively more inter-modular connections and fewer intra-modular connections, between and within modules of a diagnostically unaffected community structure? Or does the community structure itself altered in schizophrenia, in terms of the assignment of specific brain regions to specific modules, and if so how?

It is striking that no statistical procedure seems to exist to determine whether the community structure is significantly different between groups of networks. The roles played by specific brain regions have been contrasted between young and aging adults (Meunier et al., 2009a), as quantified by their number of inter- and intra-modular connections (Guimerà and Amaral, 2005). The anatomical distance between nodes in the same functional module has been shown to increase during normal adolescence (Fair et al., 2009). In an MEG study of a small group of patients with epilepsy (N=5), the community structure was argued to be more stable and less variable than in a group of controls (Chavez et al., 2010a). But the community structure could be vastly different between two groups without affecting any of these metrics. In general, prior anatomical knowledge and labor-intensive human interpretation have informed descriptive claims about the different modular partitions found in the brain networks of different populations.

Here we use resting state fMRI in 20 healthy participants and 19 patients with COS, to test the hypothesis that the community structure is altered in schizophrenia, concomitant with a decrease in modularity. We use simple statistical procedures to demonstrate not only that the partition differs significantly between groups, but also which specific brain regions are responsible for network-level differences.

Materials and methods

Code to perform network analysis described in this paper is available online at http://sourceforge.net/projects/brainnetworks/files/.

Recruitment and demographics

Participants with childhood-onset schizophrenia (COS; N=23) and also healthy volunteers (HV, N=23) were recruited for the NIH study of COS and normal brain development. Patients with COS were recruited through nationwide referral and extensive prescreening. The institutional review board of the National Institutes of Health approved the study and written informed consent and assent were obtained from parents and children respectively. Diagnoses were made using unmodified DSM-IIIR/IV criteria for schizophrenia with the onset of psychosis before age 13. Any history of significant medical/neurological problems, substance abuse, or premorbid IQ below 70 was exclusionary. Seven participants (four COS and 3 HV) were excluded for excessive head motion during scanning (see Section Image acquisition and analysis), which resulted in final samples of 19 participants with COS and 20 healthy controls. The groups did not significantly differ in terms of maximum displacement due to motion (COS sample mean=.61 mm; HV sample mean=0.52 mm; t-test, P=0.51; 95% confidence interval −3.6 to 1.9), age (COS sample mean age=18.7; HV sample mean age=19.4; t-test, P=0.52; 95% confidence interval −2.2 to 4.3), or gender (10 female, 9 male COS; 9 female, 11 male, HV; chi-square test P=0.88).

Image acquisition and analysis

All participants were scanned with the 1.5 T General Electric Signa MRI at the NIH Clinical Center (Bethesda, MD). Image acquisition included one anatomical T1-weighted fast spoiled gradient echo MRI volume (echo time (TE) 5 ms; relaxation time (TR) 24 ms; flip angle 45°; matrix 256×256×124; FOV 24 cm) and two sequential 3-min EPI scans with participants lying quietly with eyes closed (TR 2.3 s; TE 40 ms; voxel 3.75×3.75×5 mm; matrix size 64×64; FOV 240×240 mm; 27 interleaved slices).

This study utilized the high-performance computational capabilities of the NIH Biowulf Linux cluster (http://biowulf.nih.gov). AFNI (Cox, 1996) and FSL (Jenkinson and Smith, 2001; Jenkinson et al., 2002) were used for image processing. The first 4 EPI volumes were discarded, and the scans were motion corrected, skull-stripped, and despiked to remove artifactual outliers in the voxel-wise time series. The maximum of the 6 motion parameters within any 10-s period was our measure of experimental motion, and an exclusion threshold was set at 2 mm (or degrees). Registration was performed via a two-step process: from each functional scan to that subject’s structural scan using 6 degrees of freedom transformation, and from each structural scan to MNI stereotactic standard space using 12 degrees of freedom transformation. All of the structural images were registered to the MNI adult brain template (Burgund et al., 2002; Kang et al., 2003). CSF and white matter were segmented from the structural images with a probability threshold of 0.8. Nuisance variables were defined as the 6 parameters from motion correction, the average CSF signal and the average white matter signal. The residuals after regressing each voxel’s time series against these nuisance variables were used for all further analysis.

Gray matter voxels in the brain were initially defined with FSL’s cortical and subcortical Harvard-Oxford probabilistic atlas, using a 25% threshold. Voxels without fMRI coverage in every subject were removed from this gray matter template, which was then down-sampled or sub-parcellated to ~275 approximately uniform regions (Fornito et al., 2010). This parcellation procedure attempts to maximize similarity in size and shape between brain regions, with the additional constraints that no regions spanned hemispheres or cortical lobes and the largest brain region was less than twice the size of the smallest, which resulted in 278 regions whose average time series were extracted for each functional scan. The maximal overlap discrete wavelet transform (MODWT) was used with a Daubechies 4 wavelet to filter the time series to the low frequency oscillations from 0.05 to 0.111 Hz. The wavelet coefficients from sequential scans were concatenated, resulting in a single series of 144 time points. Association matrices were constructed using the pairwise functional connectivity between all 38,503 pairs of anatomically defined regions, defined as the absolute wavelet correlation, 0≤|r|≤1.

Binary graph models of brain network connectivity were generated by thresholding the association matrices. In these models, brain regions included in the graph are defined as nodes, and the functional connections are edges. Sparse networks with relatively few edges were constructed using a minimum spanning tree (MST) followed by global thresholding (Alexander-Bloch et al., 2010). Graphs were constructed over a wide range of connection densities or costs, the percent of all possible edges included in the networks, from 1% to 50% at 1% intervals. We tested for a difference in modularity and for a difference in the community structure at every connection density, and sparse networks (composed of the strongest functional connections) were analyzed in more detail at 2% cost.

We note that it is theoretically possible for there to be more than one MST of a network. In unweighted networks for example, all spanning trees (connected graphs with no cycles that include every node) are minimum spanning trees. However, for networks where all of the connections have different weights, as is the case for the interregional correlations in all of our subjects, the MST is unique (Kruskal, 1956; Prim, 1957; Gallager et al., 1983).

Difference in modularity between groups

The measurement of modularity is non-trivial, as evidenced by the many different algorithms and approaches in current circulation (Danon et al., 2005). It can be thought of as a two-step process: determination of a value function and maximization of this value function. The value function determines, for a given partition of nodes into modules, how well the modules are self-contained or informationally encapsulated. The maximization process tries to find the partition that yields the highest value of this function, and this maximum is the modularity of the graph.

Here we use what is probably the most widely adopted value function (Newman and Girvan, 2004): the proportion of a network’s edges that fall within modules, subtracted by the proportion that would be expected due to random chance alone. This can be written as

$$Q(G,\text{Part})=\frac{1}{2\text{m}}\sum _{i\ne j}\left(A_{\text{ij}}-P_{\text{ij}}\right)\delta \left(M_i,M_j\right)$$ (1)

where Q is a function of a graph G and some partition of G’s nodes into modules; m is the total number of edges; A_ij =1 if an edge links i and j and 0 otherwise; δ (M_i, M_j)=1 if i and j are in the same module and 0 otherwise; and P_ij is the probability that there would be an edge between i and j, given a random graph with the same degree distribution as G,

$$P_{\text{ij}}=\frac{k_i{k}_j}{2m}$$ (2)

where k_i is node i’s degree (its number of edges) and m is the total number of edges in the network. To maximize Q by finding the best possible partition of nodes into modules, we use a simulated annealing algorithm (Reichardt and Bornholdt, 2006). G’s modular partition is the partition that maximizes Q, and this maximized value of Q is G’s modularity. To test for a group difference in modularity, we use a permutation test for the group difference in the means, using 10,000 permutations.

Difference in the community structure between groups

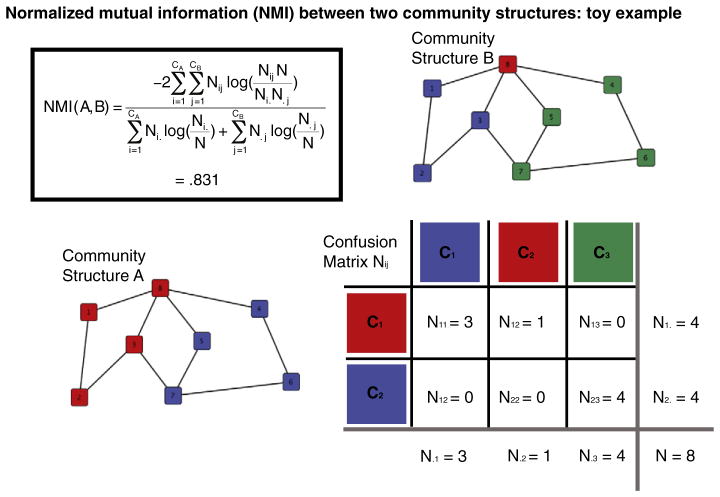
The similarity between two modular partitions or community structures can be quantified by their normalized mutual information (NMI; Kuncheva and Hadjitodorov, 2004; see Fig. 1 for an illustration):

$$\text{NMI}(A,B)=\frac{-2{\displaystyle \sum _{i=1}^{C_{\text{A}}}}{\displaystyle \sum _{j=1}^{C_B}}{N}_{\text{ij}}\mathit{log}\left(\frac{N_{\text{ij}}N}{N_{i.}{N}_{.j}}\right)}{{\displaystyle \sum _{i=1}^{C_{\text{A}}}}{N}_{i.}\mathit{log}\left(\frac{N_{i.}}{N}\right)+{\displaystyle \sum _{j=1}^{C_{\text{B}}}}{N}_{.j}\mathit{log}\left(\frac{N_{.j}}{N}\right)}$$ (3)

where A and B are the partitions of two graphs; C_A is the number of modules in partition A; C_B is the number of modules in partition B; N is the number of nodes, which is the same in both partitions; N_ij is the overlap between A’s module i and B’s module j, i.e. the number of nodes that the modules have in common; N_i. is the total number of nodes in A’s module i; N_.j is the total number of nodes in B’s module j; and this calculation follows the convention that 0×log(0)=0. The NMI ranges from 0 to 1, where 0 signifies that the partitions are totally independent and 1 that they are identical. This and related measures of pairwise similarity have been used largely to assess differences between community detection algorithms (Danon et al., 2005). In functional brain network studies, pairwise similarity has also been used to quantify the variability of a group of community structures: at different hierarchical levels (Meunier et al., 2009b); neurophysiological frequencies and instances in time (Chavez and Valencia, 2010); and in a group of epileptic patients compared to controls (Chavez et al., 2010).

Fig. 1. An illustration of the normalized mutual information (NMI) between two community structures, using toy networks.

In the NMI equation, C_A is the number of communities in structure A, and C_B is the number of communities in structure B; the “confusion” matrix, N_ij, measures the overlap between A’s community C_i and B’s community C_j; N_i. is the number of nodes in C_i; N_.j is the total number of nodes in C_j; and N is the total number of nodes over all communities. NMI(A,B) tends to be high when the N nodes are concentrated in a small number of entries in the confusion matrix. Note that NMI is not affected by the community labels, i.e., the numbers or colors corresponding to the specific communities, but matching the labels between networks is important for visual comparisons.

The NMI can be leveraged into a simple test for a group difference in the modular partitions. It is intuitive that the average within group pairwise similarity should be higher than the average between group pairwise similarity, if there is a genuine distinction between groups; but this cannot be tested directly because the individual similarity measures are not independent. An unbiased, nonparametric test of the same question is provided by a permutation procedure that compares the average within group similarity in the actual data with permutations where the group memberships are randomized. If the actual within group similarity almost always exceeds the permuted within group similarity, then it is unlikely that the modular partition is unrelated to the group assignment. The P value is simply the number of times that the permuted within group similarity is greater than the actual within group similarity, divided by the number of permutations (here 10,000).

Difference in the modular assignment of specific nodes

If there is a difference in the community structure between two groups, another question is which specific nodes are driving this difference. This question is related to the problem of how best to represent the modular partition of a group of subjects, which has in the past been solved by using the most representative subject in terms of NMI (Meunier et al., 2009b) or by finding the modular partition of a network based on the group mean functional connectivity matrix (Meunier et al., 2009a, Fair et al., 2009). While it is informative to simply list the differences between such group-level partitions, this approach has obvious limitations; because of the nontriviality of finding the modular partition and the fact that the modular assignment of some nodes can be less obvious than others, many differences could reflect random chance as opposed to a legitimate group difference. We propose two approaches to this problem.

Visualization of group-level differences

The first method visualizes the community structure at the group level by matching the modular partitions of individual subjects. The problem of matching two partitions arises because the labels assigned to different modules by community detection algorithms are arbitrarily different across subjects, such that even if two modules are quite similar, they do not necessarily have the same label. In practice this problem can be solved by manual intervention based on anatomical knowledge, but it is also possible to maximize an objective function such as the overlap between modules of the same label, while preserving the distinctions between different modules in each partition. Thus phrased it becomes a version of the “assignment problem” of combinatorics, which can be solved in polynomial time by several well-known algorithms (Papadimitriou and Steiglitz, 1982). In this fashion, all of the subjects in our study were matched to the single most representative subject in the population (as determined by pairwise NMI). Once the partitions have been matched, it is possible to look more precisely at the nature of the difference in the modular partition between groups. A “fuzzy” partition can be generated simply by labeling each node by the most frequently occurring label among the subjects in the group. A measure of confidence in the assignment of each node is provided by the frequency itself, which reflects the extent of agreement about the label of the node.

Statistical tests of regional differences

To more rigorously assess regionally specific differences in community structure between the two populations, we propose a second method that uses a permutation procedure similar to that described in section Difference in the community structure between groups but focused on a single node. For a given node X, the other 277 nodes are relabeled to reflect simply whether or not they belong to X’s module. These labels can then be compared across subjects: The similarity of two subjects, in terms of node X’s functional community, can be quantified as Pearson’s phi, − 1≤φ≤1, a statistic that is essentially the Pearson correlation of a dichotomous variable (Pearson, 1900). The phi coefficient can then serve the same role for node X that NMI served for the whole network. If there is a genuine difference in node X’s functional community between the patients and the controls, then the average within group phi coefficient should be higher than the average between group phi coefficients. This cannot be tested directly because the individual phi coefficients are not independent. However, the significance of the group difference can be assessed via a permutation procedure that compares the within-group average in the actual data to shuffled data, where the group memberships have been randomized. We performed this test for every one of the 278 nodes, using 10,000 permutations and an FDR correction for multiple comparisons.

Robustness to methodological variation

Because of concerns about the influence of particular preprocessing choices, we tested the robustness of the group difference in community structure using several methodological perturbations. First, as networks constructed from negative interregional correlations may be statistically “noisy” or topologically distinct from networks based on positive correlations (Wang et al., 2011; Schwarz and McGonigle, 2011), we limited the thresholded networks to only include positive correlations only, instead of the strongest connections in terms of absolute wavelet correlation. Secondly, we analyzed an alternative frequency band in the data, replacing the original scale 2 (0.05–0.11 Hz) wavelet correlations with scale 3 (0.03–0.05 Hz) wavelet correlations. Analysis was limited to these two frequency bands because of concerns about physiological noise contaminating higher frequencies, and because lower frequency scales are greatly affected by the boundaries of the relatively short fMRI time series (Percival and Walden, 2006). Thirdly, since heterogeneity in node size can distort community assignments (Butts, 2009; Wig et al., 2011), we reanalyzed the data while constraining the regions to be identical in volume. Rather than use anatomical regions of interest that were designed to maximize compactness (Fornito et al., 2010) while allowing the largest region to be twice as small as the largest (range=2128 mm³–4256 mm³), the edges of all of the regions were eroded until they were exactly 1600 mm³ in volume.

We also tested an alternative method to match the module labels across the population, in order to visualize the group-level partitions (see Section Visualization of group-level differences). The original method relies on matching every subject to the most representative subject in the population, which can result in suboptimal matching between the remainder of the subjects. For example, suppose that the most representative subject has 3 modules, subject A has 4 modules and subject B has 5 modules. As defined earlier, 3 of the 4 modules in subject A and 3 of the 5 modules in subject B are matched to the most representative subject. However, the left-over modules in the two subjects are not matched to each other. In our sample, on average 3% of the subjects’ nodes are left unmatched in this fashion. This number does not differ significantly between the clinical populations (Mean control=2.4%, Mean COS=3.6%, t-test, P value=0.23). The ideal scenario might be to directly maximize the overlap between module labels in the entire population, rather than for each subject to the most representative subject, which is an example of the NP-complete “multidimensional assignment problem” (Burkard et al., 1996; Burkard and Ela, 1999). In a supplemental analysis, we added a greedy algorithm to find a local maximum in the overlap of the entire population, increasing the matching between the remainder of the subjects after matching to the most representative subject.

Results

Group difference in modularity

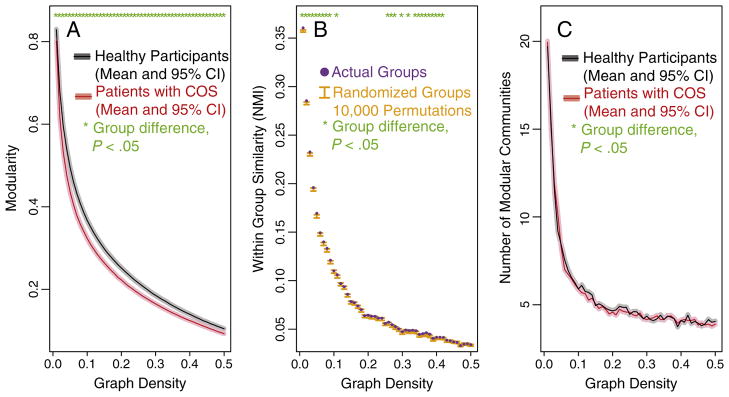
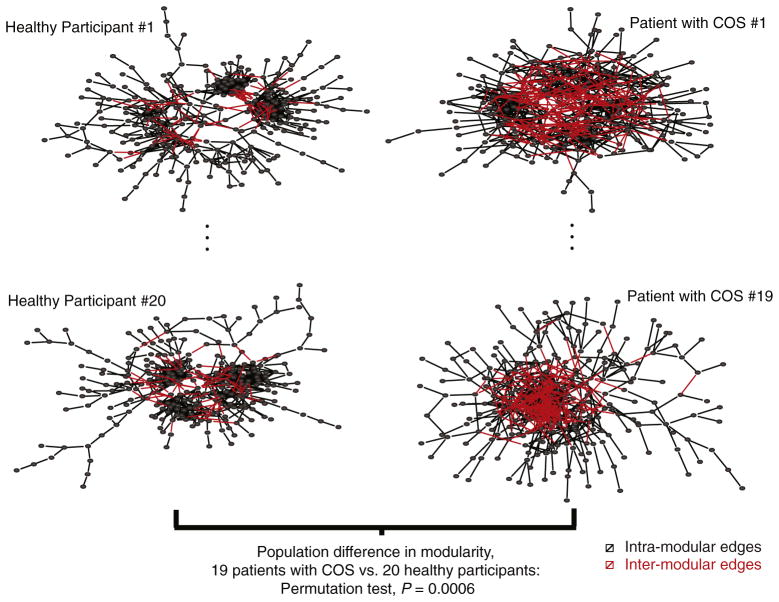
As we previously reported for a smaller sample of this same population (Alexander-Bloch et al., 2010), modularity is decreased in the functional networks of patients with childhood-onset schizophrenia (COS). At a sparse 2% connection density, for example, the mean modularity is significantly lower in the COS population compared to controls (patient mean=0.62; standard deviation=0.06; control mean=0.68; standard deviation=0.04; t-test, P value=0.0011; permutation test P value=0.0006). This group difference is robust to variation in the connection density of the thresholded networks (Fig. 2A). The reduction in modularity implies that there are relatively more connections between modules, and fewer connections within modules, in the patient population (see Fig. 3 for a graphical illustration).

Fig. 2. Group differences in modularity and community structure.

There is a significant difference in both modularity (A) and the community structure (B) of brain functional networks estimated from fMRI data on healthy participants and patients with childhood-onset schizophrenia (COS). A) For the full range of connection densities from 1% to 50%, the COS patients have decreased modularity. B) Over a more limited range that includes sparse networks thresholded at 1–10% connection density, there is a significant difference between the groups’ community structures, as assessed by the within-group similarity of the real data and permuted data. C) There is no significant difference in the number of modular communities, between the healthy participants and the COS patients.

Fig. 3. Group difference in modularity.

The group difference in modularity is illustrated with sparse graphs that include 2% of all possible edges, with the graphs represented in topological space using a forced-based algorithm (Fruchterman and Reingold, 1991), for two subjects in each clinical sample. Black edges represent intra-modular connections, between brain regions in the same functional community. Red edges represent inter-modular connections, between brain regions in different functional communities. On average there are more inter-modular connections and less intra-modular connections in the networks of patients with childhood-onset schizophrenia (COS) compared to healthy participants. The P value is based on a permutation test of the difference in modularity at the population level, 20 healthy participants vs. 19 patients with COS. For a version of this figure with the different modules demarcated by colors, please see Supplementary Fig. 1.

Group difference in the modular partition

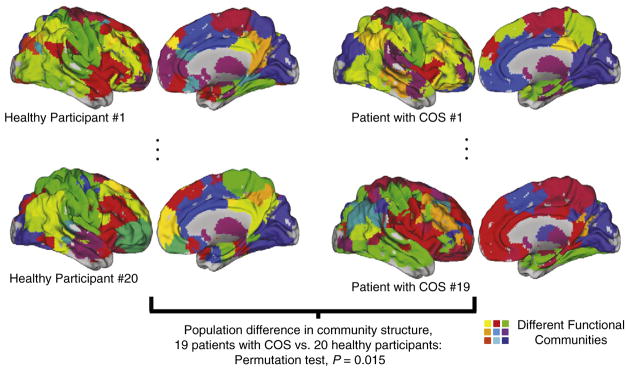
We find novel evidence for an alteration, in COS, in how the brain network is partitioned into functional communities. The within group similarity of the network partitions (the average normalized information [NMI] of pairs of subjects in the same clinical group) is higher than would be expected if the group difference were not significant (Fig. 2B). This difference is not as large as the difference in modularity, but it is especially clear for sparser graphs with only the strongest functional connections included as edges (at 2% connection density, for example: permutation test P value=0.0150). At sparser connection densities, brain networks also tend to be partitioned into greater numbers of modules (Fig. 2C; Alexander-Bloch et al., 2010). Although a difference in community structure could result because of a difference in the number of modules, there is no evidence that the number of modules differs significantly between the clinical groups (Fig. 2C). As opposed to the difference in modularity, which reflects the distribution of intra- and inter-modular edges, this alteration in community structures implies that the anatomical identity of the brain regions comprising specific functional modules is altered in schizophrenia (see Fig. 4).

Fig. 4. Group difference in the community structure.

The group difference in community structure, or the assignment of brain regions to modules, is illustrated with the modules of sparse graphs that include 2% of all possible edges, for two subjects in each clinical sample. The different functional modules are painted with different colors, with the colors between subjects algorithmically matched (see Materials and methods). The within-group community assignments are, on average, more similar than the between-group community assignments. CARET software (Van Essen et al., 2001) has been used to display the images. The P value is based on a permutation test of the difference in the community structure at the population level, 20 healthy participants vs. 19 patients with COS.

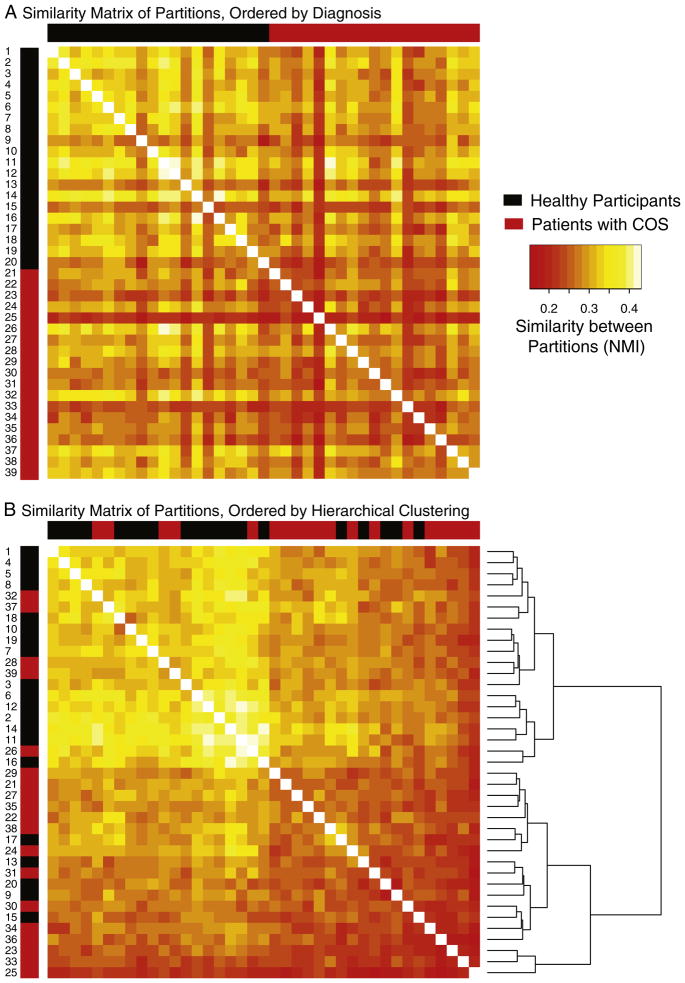
Using complete linkage hierarchical clustering to classify the subjects into “natural” groups, based on the NMI similarity matrix, there is a clear split between the two groups with ~75% of the subjects being correctly classified into their diagnostic group (Figs. 5A, B). Other clustering methods such as partitioning around medoids (Kaufman and Rousseeuw, 1987) and multidimensional scaling (Cox and Cox, 1994) did not improve on this performance. Because what is available to the classifier is fundamentally a measure of similarity between subjects as opposed to a distinct set of features, popular supervised learning approaches such as random forests and support vector machines are not readily applicable.

Fig. 5. The similarity of each pair of subjects’ community structures, between and within clinical groups.

Each element in the similarity matrix represents the normalized mutual information (NMI) measure of similarity between a pair of brain modular assignments like those illustrated in Fig. 4, although note that the NMI does not depend on the color-matching algorithm used for that figure. A) The layout of the similarity matrix is ordered only by clinical group, with the first 20 rows/columns (starting in the top right corner) representing healthy participants and the last 19 representing patients with schizophrenia. B) The same similarity matrix, except with the layout determined by complete linkage hierarchical clustering. Approximately 75% of the subjects are correctly classified into their actual groups using this unsupervised learning approach, signifying that the modular partitions contain information about diagnostic category.

The significant group difference between the populations is driven by the uniformity in the network partitions of the healthy participants. They are more similar to each other than they are to the patients with schizophrenia; in contrast, the patients with schizophrenia are no more similar to each other than they are to the healthy controls. This can be seen by direct visualization of the similarity matrices (Figs. 5A,B), and also quantitatively by performing the permutation test of within group similarity separately for each group. For example at 2% edge density, the significance of the overall group effect is P=0.015, which becomes P=0.002 for the effect of control group similarity treated separately, whereas P>0.5 for the COS group treated separately.

Group-level visualization and node-specific differences

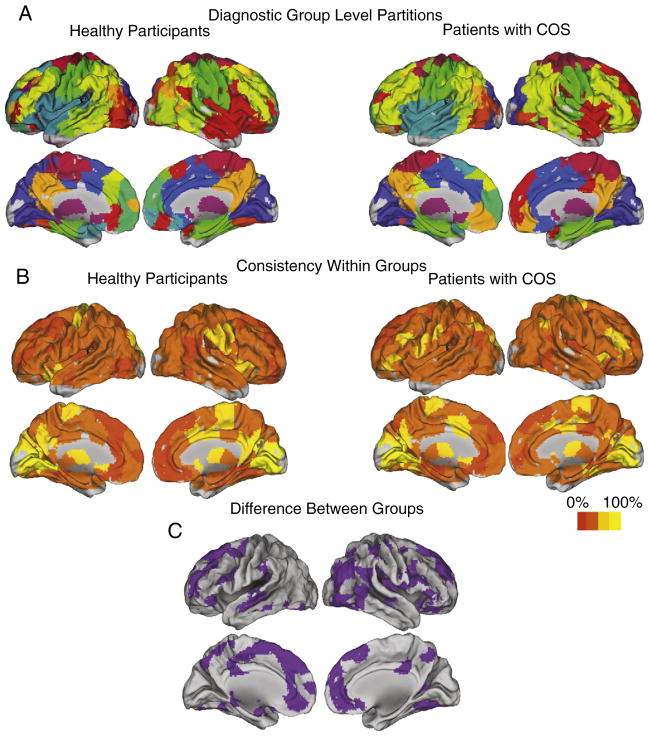
Fig. 6 shows the community structure at the group level for the two clinical samples. Note that the color-matching between the 2 groups was not done by hand, but reflects the most frequent label within each group after the partitions were algorithmically matched. Compared to representing the populations by their most representative subjects, these group-level partitions are substantially more similar to the subject partitions on average (within group NMI similarity=0.4 vs. 0.36). We can also visualize the intersubject consistency in the membership of specific functional communities (Fig. 6B). Among the most consistent modules are the occipital module, the subcortical module, and at least in the healthy participants the primary motor/somatosensory module.

Fig. 6. Group level community structurs and the difference between clinical samples.

A) The group-level community structures for each clinical population (20 healthy participants, 19 patients with schizophrenia). The color labels are determined by the most frequent label across all of the subjects, after they have been algorithmically matched by maximizing the overlap between all subjects and the single most representative subject as determined by average NMI. B) The consistency of the assignment of brain regions to modules, within each group. It is clear that our confidence in these assignments differs across nodes, with the greatest confidence in the modular assignment of subcortical areas, primary sensory areas and primary motor areas. C) The differences between the group-level community structures of the two clinical samples.

The difference in the diagnostic group partitions is driven by a minority of the nodes. Most notable is a discrepancy in the membership of a module that includes regions around the right anterior insula (colored red in Fig. 6A). Many of the differences between the HV group partition and the COS group partition are in nodes that belong to this module in one of the two groups (Fig. 6C).

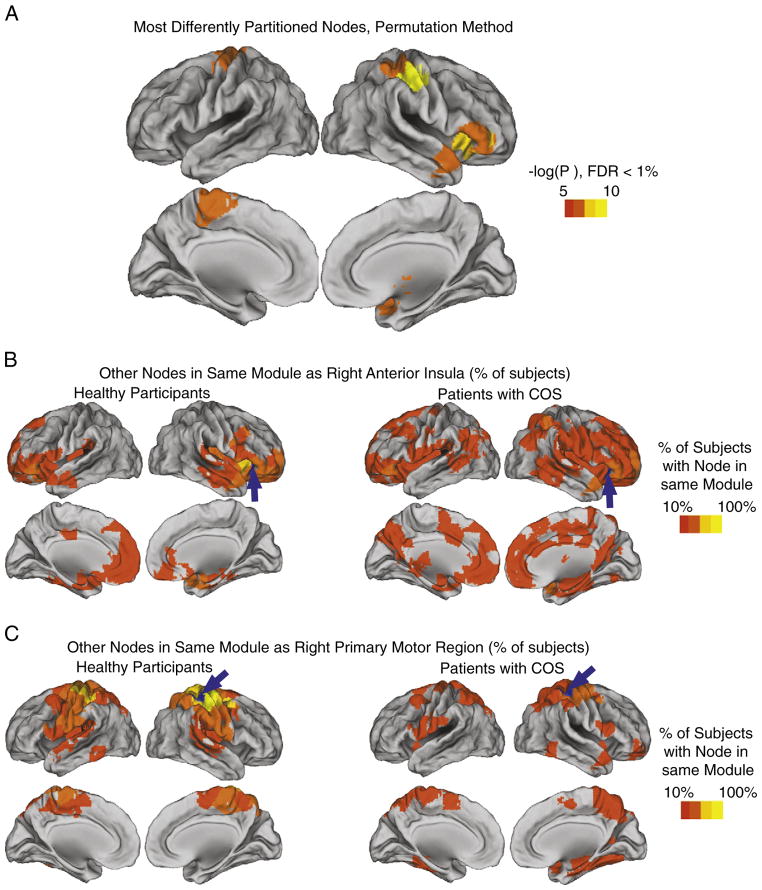
The complementary regional permutation test finds 8 regions with significantly different functional communities between the groups, using a 1% FDR correction for 278 multiple comparisons (Fig. 7A). Members of the right anterior insula module are indeed among these regions (Fig. 7B), as is the primary motor module (Fig. 7C) and the subcortical module. It is evident that in these significantly different nodes, the pattern is for the community to be more anatomically clustered and more uniform across subjects in the healthy controls, which gives way to a greater diversity (across anatomy and across subjects) in COS.

Fig. 7. Statistically significant differences in the community structure of specific nodes, between groups.

A) Regions displayed have significantly different communities between the healthy participants and the patients with childhood-onset schizophrenia (COS), in terms of the other brain regions that are found in the same module, as tested via a permutation procedure (see Materials and methods). All P values remain significant after correction for multiple comparisons, using a false discovery rate cutoff of 1%. The communities of two of these regions are illustrated, in both the healthy participants and the patients with COS, for B) a region in the right anterior insula and C) a region in right primary motor cortex.

Robustness to methodological variation

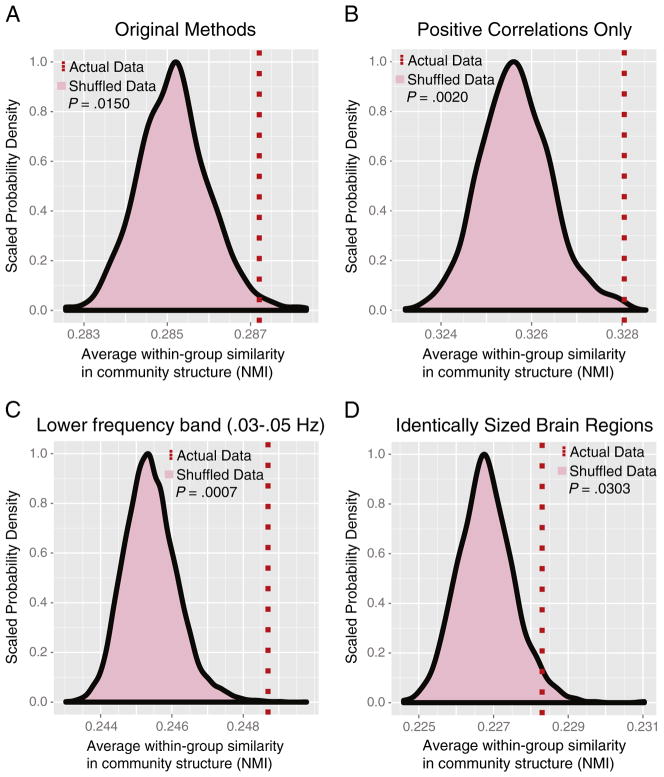
The methodological variations that we tested all preserved the group difference in community structure (Fig. 8). Using the following alternative preprocessing choices, at a sparse 2% network connection density, the within-group NMI was significantly higher in the clinical groups than in shuffled data where the group memberships were randomized: positive correlations only included in thresholded networks (permutation test P=0.0020; Fig. 8B); regional time series filtered to wavelet scale 3, 0.03–0.05 Hz (P=0.0007; Fig. 8C); regions of interest constrained to be identical in volume, (P=0.0303; Fig. 8D).

Fig. 8. Robustness of group difference in community structure to methodological variation.

A) The original methods: functional connectivity is defined as the absolute wavelet correlation at scale 2 (0.05–0.11 Hz), and anatomical regions were defined in order to maximize compactness while allowing some variation in volume (2128 mm³–4256 mm³). B) Only positive correlations included in the networks. C) Scale 3 frequency band (0.03–0.05 Hz). D) Regions constrained to be exactly the same size (1600 mm³). Permutation tests were conducted on sparse, 2% thresholded networks using 10,000 random permutations.

We tested another methodological variation, in the process of visualizing the population differences in modular community structure. After matching every subject’s module labels to the most representative subject, a greedy algorithm found a maximum by steepest ascent in the overlap of the module labels of the entire population. This additional, population-wide matching resulted in 5% greater overlap than the original method of simply matching to the most representative subject; however, compared to the original method, the resulting group-level “fuzzy” partitions were not more similar to the individual subjects (within group NMI similarity=0.4 in both cases). In terms of visualizing the group-level partitions and the group differences, the methods are grossly equivalent (see Fig. 7A; Supplementary Fig. 2A). Subtle differences are apparent, e.g., on reanalysis the right insular module in the patient group also included some left insular nodes, but low intersubject consistency indicates that these nodes lack a consistent modular assignment at the population level (Fig. 7B; Supplementary Fig. 2B).

Discussion

Our results show that both modularity and the modular community structure are quantitatively disturbed in patients with childhood-onset schizophrenia. The within-group similarity in the brain functional community organization is significantly higher than the between-group similarity. More specifically, it appears that the community structure is most consistent within the group of healthy participants; as opposed to displaying a similar amount of consistency about a different partition, the COS partition appears to fluctuate about this healthy norm. Anatomically, the difference in the modular partition is most striking for a module that consistently includes brain regions around the right anterior insula in healthy controls. In contrast, these regions are distributed over a number of other modules in the patient group.

The alteration of the community structure of brain networks in schizophrenia supports dysconnectivity theories of the disease. There is mounting evidence for a decrease in interregional functional connectivity, as well as topological disturbances that are reflected both in the global and nodal properties of the system (e.g. Lynall et al., 2010; Alexander-Bloch et al., 2010). The current results show dysconnectivity at the intermediate scale of brain modular organization, i.e., which brain regions form functional communities with each other. The lack of a consistent community structure across the patient group is consistent with randomization theories of the disease (Sporns, 2011), although other mechanisms could also result in such heterogeneity of the disease phenotype. The regional anatomy of the disorder in community structure, with a focus on the right insula, is intriguing given previous suggestions of schizophrenia-related alterations in insular cortex from both structural imaging studies (Wright et al., 1999; Kasai et al., 2003; Kim et al., 2003; Jang et al., 2006) and functional imaging studies (Curtis et al., 1998; Sommer et al., 2008; White et al., 2010; Corradi-Dell’acqua et al., in press).

Brain community structure has previously been analyzed at the level of groups, but prior methods could not address the specific questions of the current study. Group-level representations of the community structure have been used to visualize a pattern of group differences: Community detection can be performed on the group average correlation matrix (Kang et al., 2003, 2009a), or a population can be visualized via its single most representative subject (Meunier et al., 2009b). Resampling methods can also be used to generate estimates of the consistency of a partition, at the level of the individual subject or the group (Bellec et al., 2006; Bellec et al., 2010). A group-level partition can be back-projected onto individual networks, to ask whether these group-level modules or the nodes within them differ in terms of their interactions in individual subjects. Something like this back-projection procedure is for example used in group-level independent component analysis of fMRI (Calhoun et al., 2001; Erhardt et al., in press). In the broader field of complex network analysis, sophisticated methods have been suggested to generate confidence intervals on the partition of a network and its modules, mainly to account for the variability originating from the rugged nature of the landscape of possible modular partitions (Rosvall and Bergstrom, 2010); like much of complex network science, however, this approach is not directly applicable to experiments dealing with whole populations rather than single networks. A majority of the work on complex networks focuses on the analysis of single realizations of a network or the comparison of networks defined on different nodes, e.g., social networks composed of different people. None of the existing methods directly test for a difference in terms of which nodes belong to which communities, which is a pertinent question in many biological contexts.

Our novel approach exploits a simple permutation procedure, based on the pairwise normalized mutual information (NMI) between network partitions, to test whether the within-group similarity is significantly higher than the between-group similarity of communities. It is important to note that although increased variability in COS appears to drive the group difference in our data, the method would be sensitive to group differences in community structure without altered variability. Potential extensions include any situation where modular networks in different experimental samples are composed of the same nodes, e.g., comparing gene coexpression profiles across tissue samples. Rather than using the NMI, or another measure of the similarity between community partitions such as the adjusted Rand index (Kuncheva and Hadjitodorov, 2004; Vinh et al., 2010), an alternative would be to perform community detection via hierarchical clustering and generate pairwise similarity measurements between dendrograms (e.g. Waterman and Smith, 1978; Fowlkes and Mallows, 1983). Although applications are limited to contexts where there is a population of networks, as opposed to only one instantiation of the network of interest, “population” could be interpreted broadly to include many instantiations in time of the same network. The permutation procedure could also be extended to situations that include more than just two groups of interest.

The question of precisely how the groups’ functional communities differ is in many ways more difficult to address than simply whether there is a difference. Building on previous work described above, we suggest two novel approaches to this problem. Firstly, we use a community-matching algorithm to generate group-level partitions for each diagnostic group separately (Fig. 6). These group partitions have substantially higher similarity to the subject-level partitions than do even the most representative single subjects, and they represent the intersubject variability in terms of the consistency of the partition across subjects. However, a weakness of this approach is that everything downstream depends on the validity of the community-matching (see Materials and methods). While a useful heuristic to visualize the difference between the groups, there is an inevitable degree of arbitrariness in equating two modules in different networks. We suggest a more rigorous method to test whether specific nodes have differences in their community structure between the groups. Using a node-specific permutation procedure analogous to our method of testing for differences in the partition as a whole, many regions are found to be significantly different even after correcting for 278 multiple comparisons (Fig. 7).

The proposed methods to assess differences in community structure operate on substantially preprocessed fMRI data, which are the result of upstream methodological choices. To name just a few, the results could be affected by choices of motion correction procedure, nuisance-variable regression from the time series, bandpass-filtering, parcellation into regions of interest, graph construction and community detection algorithm. We have assessed the robustness of our main finding using several methodological variations: removing negative correlations from the brain networks, constraining the regions of interest to be identical in volume, filtering to a lower temporal frequency band, and thresholding the brain networks at a variety of different connection densities. One interesting preprocessing alternative, which we did not explore, would be to define regions of interest using a functional parcellation scheme (e.g. Craddock et al., in press). Extending the methods we propose here, future work could test for population differences at the level of the functional parcellation itself, in addition to assessing the impact on the community of structure of networks composed of interregional correlations.

Conclusions

This work introduces a suite of methods to determine whether and how populations of networks differ in their community structure. Applying these methods to functional brain networks derived from fMRI of healthy participants and patients with childhood-onset schizophrenia (COS), there is a significant difference between the groups, and this difference is focused on a subset of brain regions. In addition, we confirm our previous finding of an alteration in modularity, with proportionally fewer intra-modular connections in COS (Alexander-Bloch et al., 2010). The new methods we propose are applicable to diverse experimental contexts in brain imaging, neuroscience and other studies of complex networks.

Supplementary materials related to this article can be found online at doi:10.1016/j.neuroimage.2011.11.035.

Code to perform network analysis described in this paper is available online at http://sourceforge.net/projects/brainnetworks/files/.