A branching process model of ovarian cancer

Abstract

Ovarian cancer is usually diagnosed at an advanced stage, rendering the possibility of cure unlikely. To date, no cost-effective screening test has proven effective for reducing mortality. To estimate the window of opportunity for ovarian cancer screening, we develop a branching process model for ovarian cancer growth and progression accounting for three cell populations: Primary (cells in the ovary or fallopian tube), Peritoneal (viable cells in peritoneal fluid), and Metastatic (cells implanted on other intra-abdominal surfaces). Growth and migration parameters were chosen to match results of clinical studies. Using these values, our model predicts a window of opportunity of 2.9 years, indicating that one would have to screen at least every other year to be effective. The model can be used to inform future efforts in designing improved screening and treatment strategies.

1 Introduction

Ovarian cancer is the fifth leading cause of cancer death among women in the United States with one in 71 American women developing the disease during her lifetime. In 2012, 22,280 new cases are estimated to develop in the United States with 15,500 deaths expected [19]. Among cancers, ovarian cancer has a particularly low five-year survival at 43.8 percent. In the top ten most common cancers in the United States, only lung (15.6) has lower survival, whereas some like breast (89.1), prostate (99.4), and skin (91.2) have very high survival rates.

One explanation for this disparity in survival lies in the natural history of the disease: ovarian cancer often spreads readily to peritoneal surfaces and upper abdominal organs without prior evidence of lymphatic or hematogenous spread. This may explain why most ovarian cancers progress to an advanced stage prior to being detected clinically. Indeed, whereas breast, prostate, and skin cancers are detected in early (non-metastatic) stages 93, 93, and 92 percent of the time, respectively, only 32 percent of ovarian cancers are found early. Moreover, those cancers that are detected at an early stage are thought to be slower-growing and therefore less likely to impact cancer mortality. The inability to detect the aggressive but early-stage cancers while they are still curable is evidenced by the high mortality rate following diagnosis—patients with late-stage cancer have a five-year mortality of 26.9 percent.

To motivate our model, we begin by describing the four general stages used to classify the disease clinically:

1. Cancer confined to one ovary

2. Cancer involves both ovaries or has spread to other tissue within the pelvis

3. Cancer has spread to the abdomen

4. Cancer has spread to distant organs

According to the SEER database, the distribution of the stage at diagnosis is (roughly) I: 20%, II: 10%, III: 40%, and IV: 30%. Five year survival statistics based on stage at diagnosis are as follows: I: 90%, II: 65%, III: 25%, IV: 10%. [5]. Given these statistics, the ability to accurately detect early stage disease could improve ovarian cancer survival dramatically. However, no screening strategy has yet been proven to reduce mortality [4].

Several studies have evaluated the efficacy of screening for ovarian cancer. In 2011, results were published [17] of a study of 78,216 women aged 55–74 to evaluate the effects of screening on mortality. The intervention group underwent annual screening for the cancer antigen CA-125 for six years and annual transvaginal ultrasound for four years, while the control group received their usual medical care. The results, shown below, suggest that screening may not be very effective.

	n	diagnosed	death
Intervention group	39,105	212	118
Control group	39,111	176	100

Although 36 more women were diagnosed with ovarian cancer in the intervention group, there were also 18 more deaths. Given the costs associated with the procedures that the intervention group received, the authors concluded that the screening interventions evaluated in the study were not effective in reducing mortality. Furthermore, of the 3285 women in the intervention group with false-positive results, 1080 underwent surgical follow-up, and 163 experienced at least one serious complication as a result of the screening interventions.

Havrilesky and Myers, in collaboration with others in their group, have previously evaluated screening strategies for ovarian cancer using a Markov chain model to simulate the natural history of ovarian cancer in a cohort of women age 20 to 100 [10]. Parameters were chosen so that predicted lifetime incidence of ovarian cancer and deaths from it, as well as the stage distribution at diagnosis, closely approximated SEER data. They found that annual screening had the potential to result in up to a 43% reduction in ovarian cancer mortality but at an incremental cost of $73,500 per year of life saved in the general population (or $36,000 in the high-risk population). A follow-up study [11] which separated ovarian cancer cases into two phenotypes found less benefit from annual screening since a large percentage of the early-stage detections occurred for the less aggressive phenotype.

The Markov chain model used in the last two studies was very simple. There were eight states, {I, II, III, IV} × {U, D}, corresponding to the four stages listed above and whether the cancer was undetected or detected. In addition, there were four states for benign oophrectomy, ovarian cancer death, ovarian cancer survival, and death from other causes. A 12-state Markov chain has more than enough parameters to fit the data mentioned in the previous paragraph, but being able to fit the data does not guarantee that the model accurately reflects the underlying mechanisms. For example, in the Markov chain model, all stage residence times are exponentially distributed. For these reasons, we develop a mechanistic model rooted in the biology of ovarian cancer to assess screening efficacy. Our goal is to estimate the window of opportunity for screening, i.e., the time amount of time in which screening can help improve survival. More specifically, it is the amount of time during which the primary tumor is of a detectable size by transvaginal ultrasound while the amount of metastasis has not significantly increased the chance of mortality.

2 Methods

Ovarian carcinoma begins as a tumor on the surface of the ovary or fallopian tube, which we call the primary tumor. Metastasis occurs either by direct extension from the primary tumor to neighboring organs, such as the bladder or colon, or when cancer cells detach from the surface of the primary tumor via an epithelial-to-mesenchymal (EMT) transition. Once the cells have detached, they float in the peritoneal fluid as single cells or multicelluar spheroids. Cells then reattach to the omentum and peritoneum and begin more aggressive metastatic growth [15, 16]. We can therefore think of ovarian cancer as consisting of three general tumor cell subtypes: Primary (cells in the ovary or fallopian tube), Peritoneal (viable cells in peritoneal fluid), and Metastatic (cells implanted on other intra-abdominal surfaces).

To model this progression, we use a multi-type branching process that has been used in a number of studies: [13], [12], [2], [9], [7], and [8]. In this model, which is formulated in continuous time, type-i cells give birth at rate a_i and die at rate b_i for a net exponential growth rate of λ_i = a_i − b_i. In addition, cells of type i − 1 turn into cell of type i at rate u_i. In most applications, the u_i are mutation rates, but here they are migration rates: u₁ is the rate at which cells leave the primary tumor and u₂ is the rate at which cells in the peritoneal fluid attach to the omentum. The main biological events and associated parameters are summarized in the table below. Note that i = 0, 1 and 2 correspond to Primary, Peritoneal, and Metastatic, respectively.

Biological feature	Mathematical description
Primary tumor grows	Primary cells grow at rate λ0
Cells detach from surface	Primary cells on the surface mutate into Peritoneal cells at rate u1
Detached cells accumulate in peritoneal fluid	Peritoneal cells grow at rate λ1
Cells reattach to distant sites	Peritoneal cells mutate into type-2 cells at rate u2
Reattached cells grow	Metastatic cells grow at rate λ2 > λ0

To parametrize the branching process model, we use data from [3], which examined the incidence of unsuspected ovarian cancers in apparently healthy women who underwent prophylatic bilateral salpingo-oophrectomies. They estimated that ovarian cancers had two-phase exponential growth with λ₀ = (ln 2)/4 and λ₂ = (ln 2)/2.5 per month, i.e., in the early stage the doubling time is 4 months, while in the later stage it is 2.5 months. The growth rate λ₁ cannot be estimated from this data, so we will take it to be 0 and thereby get an upper bound on the window of opportunity for screening, which was described in words at the end of the introduction and will be defined more precisely in Section 3.2. With respect to the migration rates, there does not seem to be data to allow us to directly estimate u₁ and u₂. Fortunately, only the product u₁u₂ appears in our answers, so we can choose u₁u₂ = 10⁻⁴ to achieve agreement with observed quantities such as the size of the primary tumor when stage III is reached (see Figure 2 in [3] and Section 3.3 below).

In Section 3.1, we describe two known and one new result for the multi-type branching process that allow us to describe the behavior of Z_i(t) for the three cell subtypes. In Section 3.2, we use these results to compute the expected size of the window of opportunity, which we find to be 2.9 years, as well as to compute the distribution of the duration of the window. Finally, in Section 3.3, we use the model to compute the probability of metastasis given a primary tumor of known size.

3 Results

3.1 Branching process results

Type-0 cells are a branching process that grow at exponential rate λ₀ > 0. By well-known results (see, e.g., [1]), we have

Theorem 1. If λ₀ > 0 then as t → ∞, e^−λ₀tZ₀(t) → V₀ with

$$V_0\stackrel{d}{=}\frac{b_0}{a_0}{\delta }_0+\frac{{\lambda }_0}{a_0}\mathit{\text{exponential}}({\lambda }_0/a_0)$$

Here, δ₀ is a point mass at 0 corresponding to the event that the branching process dies out, a₀ represents the birth rate of the type-0 cells, and exponential(r) is the distribution with density function re^−rt.

We are not interested in the situation in which the type 0’s die out, so we consider the Z₀’s conditioned on nonextinction {Z₀(t) > 0 for all t}. In this case, we only have the second term. Time t represents the amount of time since the initial mutation that began the tumor. That event is not observable, so by shifting the origin of time we can

Assume Z₀(t) = e^λ₀t to get rid of V₀.

Type 1’s leave from the surface of the primary tumor at rate u₁ times the surface area. Ignoring the constant that comes from the relationship between the surface area and volume of a sphere, and letting γ₁ = 2λ₀/3, the mean is

$${\mathit{\text{EZ}}}_1(t)={\displaystyle {\int }_0^t}{u}_1{e}^{{\gamma }_{1}s}{e}^{{\lambda }_1(t-s)}\mathit{\text{ds}}=\frac{u_1}{{\gamma }_1-{\lambda }_1}(e^{{\gamma }_{1}t/3}-e^{{\lambda }_{1}t})~\left(\frac{u_1}{{\gamma }_1-{\lambda }_1}\right)e^{{\gamma }_{1}t}$$ (1)

where a(t) ~ b(t) means a(t)/b(t) → 1.

Since type 1’s are cells floating in the peritoneal fluid and have less access to nutrients, it is natural to assume that λ₁ < γ₁. To remove the unknown rate λ₁ from our calculations, we will later set λ₁ = 0. For the moment, we will proceed without that assumption.

Theorem 2. If γ₁ > λ₁ ≥ 0 then Z₁(t)/EZ₁(t) → 1 in probability as t → ∞.

Intuitively, this hold since the integral in (1) has its dominant contribution from times s near t when there are a lot of migrations. The results is easily shown by computing second moments. The proof is given in the appendix.

If we repeat the analysis of EZ₁(t) on EZ₂(t), then the resulting formula is not accurate.

$${\mathit{\text{EZ}}}_2(t)={\displaystyle {\int }_0^t}{u}_2\frac{u_1}{{\gamma }_1-{\lambda }_1}{e}^{{\gamma }_{1}s}{e}^{{\lambda }_2(t-s)}\mathit{\text{ds}}=\frac{u_1{u}_2}{({\gamma }_1-{\lambda }_1)({\lambda }_2-{\gamma }_1)}(e^{{\lambda }_{2}t}-e^{{\gamma }_{1}t})$$

However, now λ₂ > λ₀ > 2λ₀/3 = γ₁, so the dominant contribution comes from s near time 0, where there are very few mutations that make unrealistically large contributions to Z₂(t).

At time s, mutations occur to type-2 cells at rate u₂(u₁/γ₁)e^γ₁s, so we let

$$s_2=\frac{1}{{\gamma }_1}\text{log }(\frac{{\gamma }_1}{u_1{u}_2})$$ (2)

be the time at which the mutation rate is 1. The next result was proven in [9]. However, the version given here is somewhat different, so we give a new, simpler proof in the appendix.

Theorem 3. If λ₂ > γ₁ > 0 then e^{−λ₂(t−s₂)}Z₂(t) → V₂ where V₂ is the sum of points in a Poisson process with mean measure μ(x, ∞) = C₂x^−α₂ where α₂ = γ₁/λ₂,

$$C_2=\frac{1}{a_2}{\left(\frac{a_2}{{\lambda }_2}\right)}^{{\alpha }_2}\mathrm{\Gamma }({\alpha }_2)$$

and $\mathrm{\Gamma }(r)={\displaystyle {\int }_0^{\infty }}{t}^{r-1}{e}^{-t}\mathit{\text{dt}}$ is the usual gamma function.

Well-known results in probability theory (see, e.g., Section 3.7 in [6]) imply that V₂ is a stable law with index α₂ ∈ (0, 1). Stable laws have a power law tail P(V₂ > x) ~ C_x^−α, which implies EV₂ = ∞. This “pathology” derives from the fact that mutations at time s₂ − s occur at rate e^−λ₀s but produce a growing family that is e^λ₁s times as large as one that starts at time s₂.

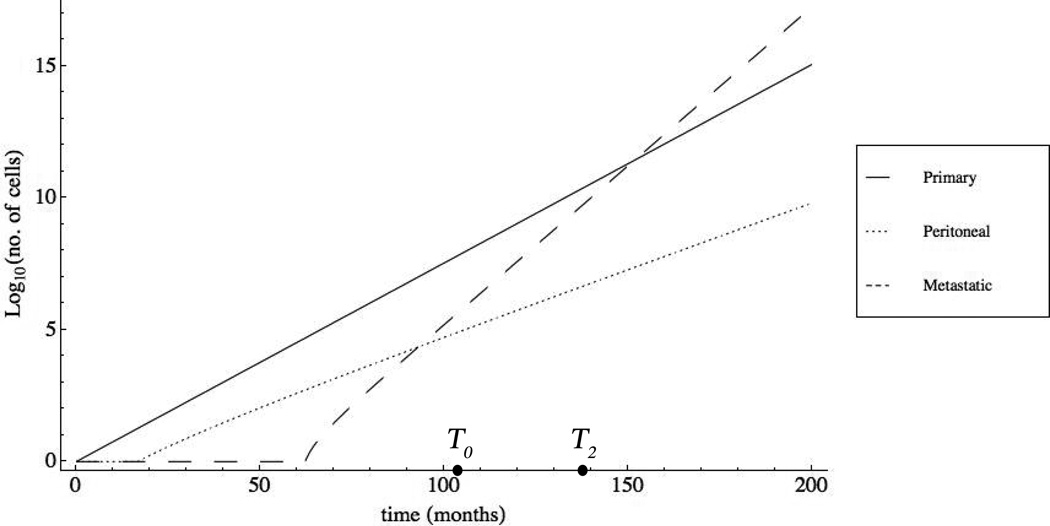
While the formulas in Theorem 3 are complicated, there is a simple conceptual picture. Figure 1 depicts the growth of each of the cell populations on a log scale. The plot matches well with our biological description of ovarian cancer: the Primary cells grow exponentially at time zero and give rise to the first Peritoneal cell at approximately t = 17 months. These cells grow at a slower rate and eventually give rise to the first Metastatic cell at roughly t = 61 months. By t = 145 months, the Metastatic population is larger than the Primary population and continues to grow at an aggressive rate.

Figure 1. Plot of the Primary, Peritoneal, and Metastatic cell subtypes on a logarithmic scale.

At time t = 0, the primary tumor begins to grow exponentially at rate λ₀ = ln(2)/4. At time t ≈ 19, a tumor cell detaches from the surface of the primary tumor and enters the peritoneal fluid, giving rise to a new cell population which grows at rate λ₁ = ln(2)/7. The peritoneal fluid becomes progressively more saturated, eventually giving rise to the Metastatic cell population at time t ≈ 61. This population grows at the most aggressive rate (λ₂ = ln(2)/2.5) and overtakes the primary cells at t ≈ 145.

3.2 Window of opportunity

In order to be able to compute the size of the window of opportunity, we need to have precise definitions of its two endpoints. For the upper bound, we define the time at which the patient enters stage III as T₂ = min{t : Z₂(t) = 10⁹}, where we have used the often-quoted rule of thumb that 10⁹ cells = 1 cm³ = 1 gram. For the lower bound, we focus on detection by transvaginal ultrasound, so we define T₀ = min{Z₀(t) = 6.5 × 10⁷}, corresponding to a spherical tumor of diameter 0.5 cm. These definition are based on somewhat crude estimates of detectability and “significant” metastasis; if the reader prefers different values, it is easy to recalculate the size of the window.

Using our growth rate parameters λ₀ = (log 2)/4 = 0.1733 and λ₂ = (log 2)/2.5 = 0.2772, we set

$$e^{0.1733T_0}=6.5\times {10}^7,\text{ which gives }{T}_0=\frac{1}{0.1733}\text{log}(6.5\times {10}^7)=103.8$$

months or 8.65 years. This may seem to be a very long time, but the estimate is consistent with calculations done for other types of cancers.

To make a crude calculation of T₂ ignoring the randomness in the growth of the 2’s, we note that by (2), mutations to type 2 occur at rate 1 at time

$$s_2=\frac{1}{{\gamma }_1}\text{ log }\left(\frac{{\gamma }_1}{u_1{u}_2}\right).$$

As one referee pointed out ${\displaystyle {\int }_0^{s_2}}{u}_2{Z}_1(s)\mathrm{\text{ds}}\approx 1/{\gamma }_1$ so the first mutation to type 2 may have occurred earlier. However, each mutation lives forever with probability γ₁, so the first surviving mutation occurs at time ≈ s₂. From this point, it will take roughly

$$\frac{1}{{\lambda }_2}\text{log}({10}^9)=74.76\text{ months}$$

for the 2’s to grow to size 10⁹. If we let u₁u₂ = 10⁻⁴ and note γ₁ = 0.1155, then

$$s_2=\frac{1}{.1155}\text{log}(1155)=61.05,$$

so T₂ = 7476+61.05 = 138.51 months, and the window of opportunity is T₂−T₀ = 34.7 months or 2.9 years.

To take the randomness of Z₂ into account, we use Theorem 3 to conclude that

$$Z_2(t)\approx e^{{\lambda }_2(t-s_2)}{V}_2.$$

Setting this equal to 10⁹ and solving, we have

$$T_2\approx s_2+\frac{1}{{\lambda }_2}\text{log}({10}^9/V_2)$$ (3)

and hence

$$T_2=138.51-\text{log}(1/V_2).$$

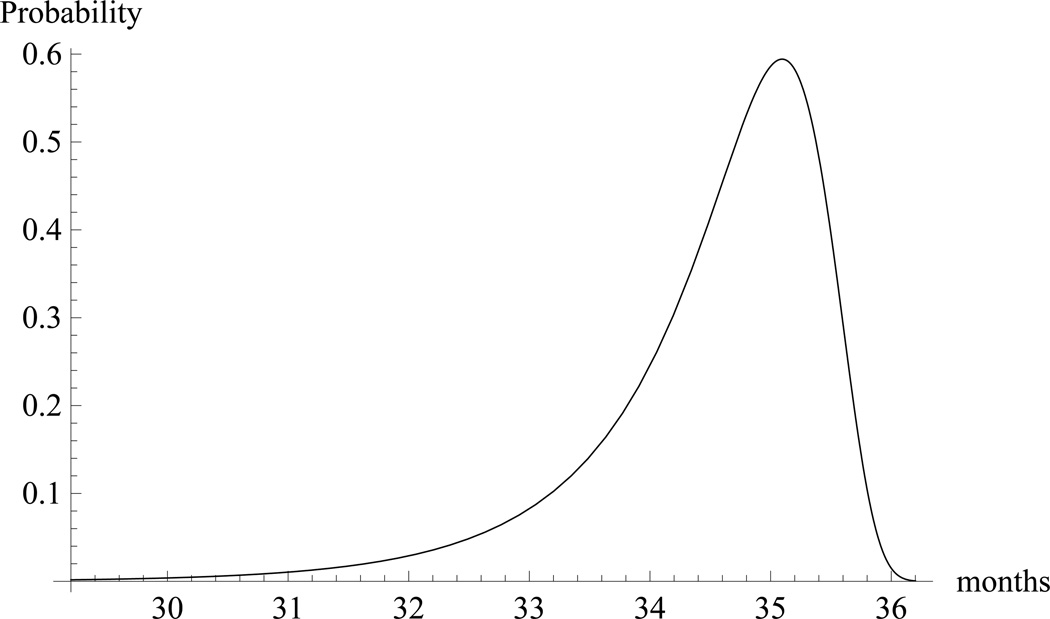
The distribution of the window, T₂ − T₀, is shown in Figure 2. Note that T₂ − T₀ is between 30 and 36 months with high probability.

Figure 2. Density function for the window of opportunity, T₂ − T₀.

Note that with high probability it is between 30 and 36 months in duration.

3.3 Primary tumor size at onset of metastasis

When tumors are found at an early stage and removed surgically, patients almost always undergo chemotherapy as the next step of treatment. Although chemotherapy is prescribed in part due to the possibility of residual tumor in the site of surgery, it is also done out of concern that some cells had already metastasized but had not yet grown to a detectable size. Here, we use our model to estimate the probability of metastasis given a primary tumor of known size.

We want to find the distribution for the size of the primary tumor at the onset of metastasis, i.e., at time T₂. Using (3), we have

$$Z_0(T_2)\approx \text{exp }({\lambda }_0[s_2+(1/{\lambda }_2)\text{ log}({10}^9/V_2)]).$$

Using (2) and recalling γ₁ = 2λ₀/3, λ₀/λ₂ = 5/8, we now have

$$Z_0(T_2)\approx {\left(\frac{{\gamma }_1}{u_1{u}_2}\right)}^{3/2}{(\frac{{10}^9}{V_2})}^{5/8}.$$

From this, we see that the size of the primary tumor at time s₂ is

$${\left(\frac{{\gamma }_1}{u_1{u}_2}\right)}^{3/2}\approx 4\times {10}^4,$$

which translates into a diameter of 0.84 mm. If we ignore randomness and take V₂ = 1, then the size of the primary at time T₂ is

$$4\times {10}^4\times {10}^{45/8}=1.686\times {10}^{10},$$

which translates into 3 cm, in agreement with results of Brown and Palmer. Figures 3 and 4 depict the distribution for size and a comparison with the results of [3], respectively.

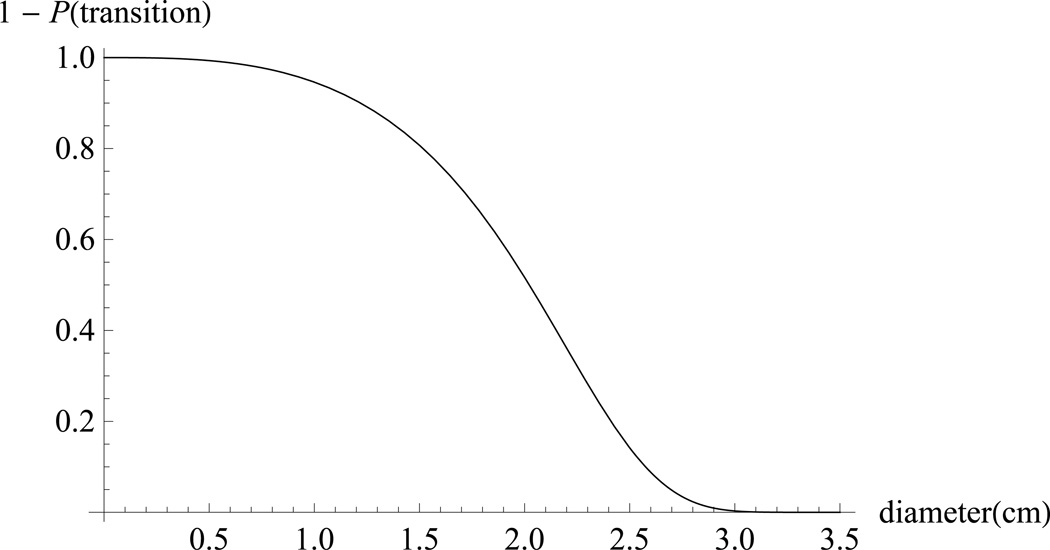
Figure 3. Tail distribution for transition to metastasis as a function of primary tumor size.

Our model predicts that a patient with a primary tumor of diameter 0.5 cm is very unlikely to have significant metastasis (where we define “significant201D as at least one gram). As we increase diameter, we predict that a patient with a primary tumor of diameter d = 2 cm is equally likely and unlikely to have metastasis. By d = 3, metastasis is predicted to be near-certain.

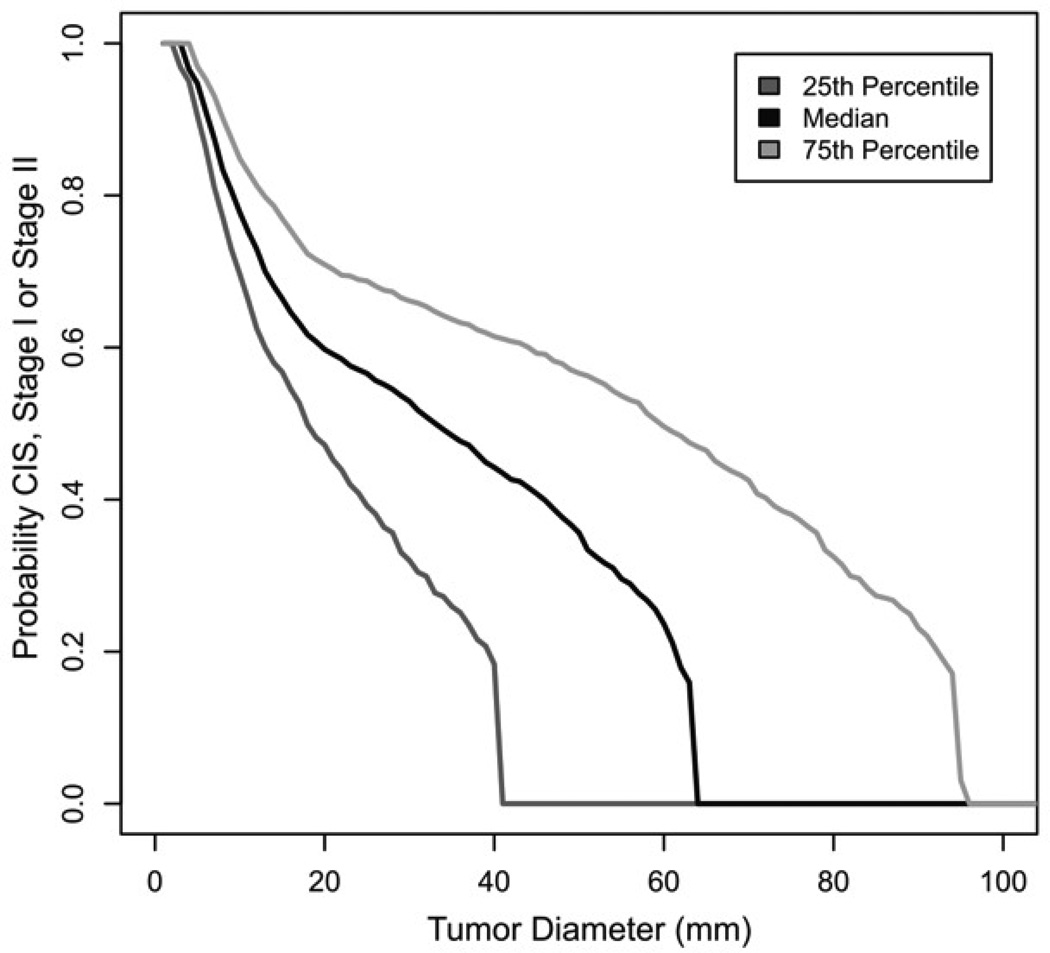
Figure 4.

Kaplan–Meier estimate of probability of progression to stage III as function of primary tumor size from Brown & Palmer [3].

There is an overall difference of factor two between the time at which the curves decrease to 0. This difference could be removed by adjusting our parameters. However, such an adjustment would not change the disagreement between the shapes of the early parts. We find the initial sharp drop of the curve surprising and think it might be an artifact of the way in which they analyzed data. In a typical Kaplan-Meier survival study, patients either leave the study or die. Deaths in such a study are observed when they occur. In the ovarian cancer study, in which a woman is observed to have stage III cancer, the progression occurred at some time in the past which must be estimated. The curve will be skewed if this is not done correctly.

4 Conclusions

We have created a mechanistic model of ovarian cancer in order to evaluate the possibility of developing effective screening strategies for ovarian cancer. Our model, with parameters chosen to match results from clinical studies, predicts a window of opportunity for screening of 2.9 years. Since the distribution of the time for a detectable tumor to metastasize is concentrated on the interval [30, 36] months, screening would need to occur at least every two years in order to have a significant effect. Given that our analysis assumes perfect detection of tumors greater than 0.5 cm in diameter and does not account for false negatives, biennial screens may still fail to measurably reduce mortality. A large clinical study [17] shows that false positives are also a serious problem since they result in unnecessary surgery with sometimes unfortunate consequences.

In order to obtain support for our parameter choices, we have used our model to calculate the distribution of the size of the primary tumor when metastasis occurs and the probability of metastasis as a function of the size of the primary tumor. These calculations can inform future efforts in designing improved screening and treatment strategies if one has faith in the values of the parameters used. Our long-term goal is to develop a well-calibrated model which can be used to evaluate such strategies in silico to complement the use of large (and expensive) clinical studies.

• A biologically accurate branching process model of ovarian cancer progression

• Uses parameters derived from clinical studies

• Predicts that the window of opportunity for screening is 30 to 36 months

• Screening needs to occur at least once every two years to be effective

Appendix

Here, we give the proofs of Theorems 2 and 3.

Theorem 2. If γ₁ > λ₁ ≥ 0 then Z₁(t)/EZ₁(t) → 1 in probability as t → ∞.

Proof. Let Z̄₁(t) be the contribution from mutations before time t − log t.

$$E{\mathrm{Z̄}}_1(t)={\displaystyle {\int }_0^{t-\text{log }t}}{u}_1{e}^{{\gamma }_{1}s}{e}^{{\lambda }_1(t-s)}\mathit{\text{ds}}$$

A little algebra and the asymptotic behavior of EZ₁(t) given in (1) shows that

$$E{\mathrm{Z̄}}_1(t)=e^{{\lambda }_1(\text{log }t)}{\mathit{\text{EZ}}}_1(t-\text{log }t)~e^{({\lambda }_1-{\gamma }_1)(\text{log }t)}{\mathit{\text{EZ}}}_1(t).$$

Since γ₁ > λ₁, EZ̄₁(t)/EZ₁(t) → 0.

Let Y₁(t) be the number of type 1’s at time t when we start our multitype branching process with one 1 and no 0’s. Using Theorem 1, there is a positive constant C so that

$$\text{var }(Y_1(t))~{\mathit{\text{Ce}}}^{2{\lambda }_{1}t}.$$

The process Z₀(t) is deterministic, so the contributions to Z₁(t) from different time intervals are independent. Thus, if we let Ẑ₁(t) = Z₁(t) − Z̄₁(t), we have

$$\text{var }({Ẑ}_1(t))~{\displaystyle {\int }_{t-\text{log }t}^t}{u}_1{e}^{{\gamma }_{1}s}{e}^{2{\lambda }_1(t-s)}\mathit{\text{ds}}.$$

Introducing the normalization and changing variables r = t − s in the integral, we have

$$\text{var }(e^{-{\gamma }_{1}t}{Ẑ}_1(t))~e^{-{\gamma }_{1}t}{\displaystyle {\int }_0^{\text{log }t}}{e}^{(2{\lambda }_1-{\gamma }_1)r}\mathit{\text{dr}}\le e^{-{\gamma }_{1}t}(\text{log }t)(1+t^{2{\lambda }_1-{\gamma }_1})\to 0,$$

where we have added 1 to take into account the possibility that 2λ₁ − γ₁ < 0. Since e^−γ₁tZ₁(t) converges to a positive limit, it follows that var (Ẑ₁(t)/EZ₁(t)) → 0. Combining this with the fact that EZ̄₁(t)/EZ₁(t) → 0 gives the desired result.

Theorem 3. If λ₂ > γ₁ > 0 then e^{−λ₂(t−s₂)}Z₂(t) → V₂ where V₂ is the sum of points in a Poisson process with mean measure μ(x, ∞) = C₂x^−α₂. Here α₂ = γ₁/λ₂,

$$C_2=\frac{1}{a_2}{\left(\frac{a_2}{{\lambda }_2}\right)}^{{\alpha }_2}\mathrm{\Gamma }({\alpha }_2)$$

and $\mathrm{\Gamma }(r)={\displaystyle {\int }_0^{\infty }}{t}^{r-1}{e}^{-t}\mathit{\text{dt}}$ is the usual gamma function.

Proof. Mutations to type 2 occur at time s₂ + s with rate e^γ₁s. Our result for the branching processes Theorem 1 implies a mutation at time s₂ + s will grow to size ≈ e^{λ₂(t−s₂−s)}W₂ by time t, where W₂ has distribution

$$W_2\stackrel{d}{=}\frac{b_2}{a_2}{\delta }_0+\frac{{\lambda }_2}{a_2}\text{exponential}({\lambda }_2/a_2).$$

To add up the contributions, we associate with each point s₂ + t_i at which a mutation occurs an independent random variable y_i with the same distribution as W₂. This gives us a Poisson process which on (−∞, ∞) × (0, ∞) (we ignore the points with y_i = 0) has intensity

$$e^{{\gamma }_{1}s}·{({\lambda }_2/a_2)}^2{e}^{-({\lambda }_2/a_2)y}.$$

Here, one of the two factors of λ₂/a₂ comes from P(W₂ > 0) and the other from the exponential density function.

A point (s₂ + t_i, y_i) makes a contribution e^−λ₂t_iy_i to lim_t→∞ e^{−λ₂(t−s₂)}Z₂(t). Points with e^−λ₂t_iy_i > x will contribute more than×to the limit. The number of such points is Poisson distributed with mean

$${\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{e}^{{\gamma }_{1}s}\frac{{\lambda }_2}{a_2}{e}^{-({\lambda }_2/a_2){\mathit{\text{xe}}}^{{\lambda }_{2}s}}\mathit{\text{ds}},$$

where one factor of λ₂/a₂ has disappeared since we are looking at the tail of the distribution. Changing variables, we have

$$\begin{array}{cc}\frac{{\lambda }_2}{a_2}{\mathit{\text{xe}}}^{{\lambda }_{2}s}=t,\hfill & \frac{{\lambda }_2}{a_2}x{\lambda }_2{e}^{{\lambda }_{2}s}\mathit{\text{ds}}=\mathit{\text{dt}}.\hfill \end{array}$$

Noticing s = (1/λ₂) log(ta₂/xλ₂) implies e^{(γ₁−λ₂)s} = (a₂t/λ₂x)^{(γ₁/λ₂)−1}, the integral above becomes

$$\begin{array}{c}={\displaystyle {\int }_0^{\mathrm{\infty }}}{\left(\frac{a_{2}t}{{\lambda }_{2}x}\right)}^{({\gamma }_1/{\lambda }_2)-1}{e}^{-t}\frac{\mathit{\text{dt}}}{{\lambda }_{2}x}\hfill \\ =\frac{1}{a_2}{\left(\frac{a_2}{{\lambda }_2}\right)}^{{\gamma }_1/{\lambda }_2}{x}^{-{\gamma }_1/{\lambda }_2}{\displaystyle {\int }_0^{\mathrm{\infty }}}{t}^{({\gamma }_1/{\lambda }_2)-1}{e}^{-t}\mathit{\text{dt}}\hfill \end{array}$$

and completes the proof.