Finding the probability of infection in an SIR network is NP-Hard

Abstract

It is the purpose of this article to review results that have long been known to communications network engineers and have direct application to epidemiology on networks. A common approach in epidemiology is to study the transmission of a disease in a population where each individual is initially susceptible (S), may become infective (I) and then removed or recovered (R) and plays no further epidemiological role. Much of the recent work gives explicit consideration to the network of social interactions or disease-transmitting contacts and attendant probability of transmission for each interacting pair. The state of such a network is an assignment of the values {S, I, R} to its members. Given such a network, an initial state and a particular susceptible individual, we would like to compute their probability of becoming infected in the course of an epidemic. It turns out that this and related problems are NP-hard. In particular, it belongs in a class of problems for which no efficient algorithms for their solution are known. Moreover, finding an efficient algorithm for the solution of any problem in this class would entail a major breakthrough in theoretical computer science.

1. Introduction

Mathematical modelling of epidemics is often traced to the celebrated SIR model of Kermack and McKendrick [1]. This model posits a population of constant size whose members fall into one of three classes: susceptible (S), infective (I) and removed (R). Approximating these as continuous and assuming well-mixing, i.e., each individual is in equal contact with and equally likely to infect each other individual, allows for an approximate description of the infection dynamics using ordinary differential equations (ODE).

Clearly, as it has been argued by many in theoretical [2, 3, 4] as well as experimental studies [5], the well-mixing assumption is not an accurate representation of real contact patterns. Thus, much recent work has focused on the role of the network of disease-transmitting contacts. (Reviewed in [6]. See also, [7, 8]. For a comparison of well-mixed and network-based models, see [9].) Indeed, Kermack’s and McKendrick’s ODE model arises as the limiting case as the number of people goes to infinity of a simplistic network model in which each individual has an equal chance of infecting every other. However, real-world social contact networks exhibit complex patterns of interconnection between individuals. Further, the probability of transmitting disease from one individual to another depends on the nature, frequency and duration of the contact as well as the immune competence of the target individual. This leads to a modelling formalism of social networks as a probabilistic graph 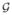= (G, Pr). Here G is the graph G = (V, E), each vertex u ∈ V is an individual, each edge e = (u, v) ∈ E records the fact that u might infect v and Pr : E → [0, 1] gives the probability that u infects v if u becomes infective while v is susceptible. In this formalism, 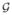is a fixed graph G = (V, E) with labelling Pr.

This relatively new modelling paradigm has triggered an enormous amount of research in theoretical epidemiology. The field has greatly benefited from approaches that range from applications of bond percolation theory and other techniques from statistical physics [10, 11, 3, 7, 12, 13, 14, 15, 16, 17, 18, 19] to large scale simulation endeavours [4, 20, 21, 22, 23]. Given that this mathematical formalism seems accurate and powerful to describe the spread of infectious diseases, the natural question arises as to whether calculations performed within this formalism can be used in practical situations to make useful predictions. Such calculations are based on potentially measurable parameters such as network topology and transmission probabilities [24]. For instance, one could attempt to calculate the probability that, given a social contact network 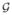, an epidemic starting with a set P of infectives results in the infection of an initially susceptible individual u. Are there any computational limitations when trying to calculate such magnitudes? If yes, how limiting are they? Fortunately, to address the computational issues associated with this and similar calculations, we don’t need to start from scratch, given that network engineers have already studied since the 1970s problems that are essentially the same.

In the era of electronically digitalized information and digital computers, communications networks have become the biggest and count among the most important networks. The size of these networks is exponentially increasing. For instance, the size of the Internet shows exponential growth since its creation in the early nineties (http://www.isc.org/). As the components of such networks are subject to failure, engineers face the problem of designing, constructing and operating networks that meet the required standards of reliability. Of particular interest is the estimation of how reliable a given network is in performing its function, provided some knowledge about the reliability of its components is available. In many cases, the functionality of the network can be expressed as the ability of its topology to support the network’s operation. In other words, the network is functional if and only if certain connectivity properties are fulfilled. Consider a network of computers which use this network to transmit messages. Let us suppose that each of these computers is reliable, but that each communication link has some chance of failure when called upon to transmit a message. We then encounter the same formalism explained above for social networks. A communications network is given by 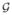= (G, Pr). Here G = (V, E) where each vertex u ∈ V is a computer, each edge e = (u, v) ∈ E is a communication link and Pr : E → [0, 1] is the reliability of the communication link from u to v. One might ask, given a communications network 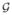, a set of computers P and a computer u ∉ P, if the computers in P all send a message, what is the chance it will reach u? We will see that this is the same problem we stated above in the context of epidemics on social contact networks.

It has long been known in the communications network literature that this problem is computationally intractable. A standard benchmark of computational complexity is the class of NP-complete problems. This class has the following properties:

• At present, no algorithm for an NP-complete problem is known to have a running time which is bounded by a polynomial. Indeed, many algorithms for NP-complete problems have exponential running time. It is unknown whether any NP-complete problem can be solved by an algorithm with polynomial running time.

• If any problem in this class can be solved by an algorithm whose running time is bounded by a polynomial, then every problem in this class can be solved by an algorithm whose running time is bounded by a polynomial.

In view of the second, it is considered unlikely that any NP-complete problem has a polynomial time solution. The communication among computers problem (and hence the epidemiology problem) listed above is known to be as hard as any NP-complete problem. Such problems are termed NP-hard. This is not the first problem in network epidemiology known to be NP-hard. Previously known examples include the following: Given a social contact network and limited resources

• What is the optimal strategy for vaccinating a limited number of individuals?

• What is the optimal strategy for quarantining a limited number of individuals?

• What is the optimal strategy for placement of a limited number of sensors for monitoring the course of an epidemic?

(See [25, 26, 27, 28].) These problems involve the search for an optimum among subsets of the vertices or edges of the given social contact network. It might be hoped that finding the probability of infection of a single individual would be computationally less demanding. As the engineers have taught us, this is not so. While this result has been recently reported in the physics and operations research community [29] and has recently been applied to the spread of influence on social networks [30], it seems almost unknown among epidemiologists.

This article is organized as follows: In Section 2 we give a very brief overview of the relevant concepts and methods in computational complexity. This provides the unacquainted reader with the basic tools for understanding the main message of this paper. Section 3 provides the elementary formal mathematical framework for studying SIR epidemics on networks, including the connection with percolation theory. In Section 4 we present a series of problems that have been studied in network engineering and demonstrate their structural isomorphism with certain problems concerning SIR epidemics on networks. Section 5 is devoted to studying the computational complexity of extended/generalized epidemiological problems. We finish in Section 6 with some concluding remarks.

2. Computational complexity

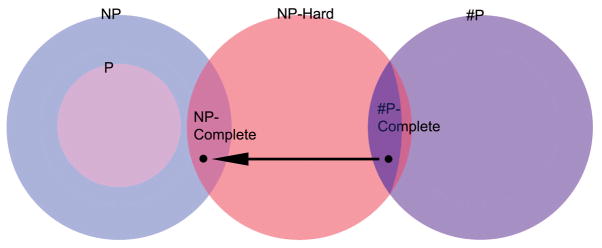
In this section we give a brief introduction to some of the major classes in the study of computational complexity. Perhaps chief among these is the class NP-complete which is used as a common benchmark for describing problems which are algorithmically soluble but computationally intractable. We start with a quick overview of the classes diagrammed in Figure 1³ and then proceed to fill in some of the mathematical details. For those wishing a fuller account we recommend [31].

Figure 1.

The class NP consists of decision problems, problems for which the answer is “yes or “no”. Within this class is the class P of problems which can be solved with polynomial running time and the class NP-complete of problems which are as hard as any other problem in this class. It is not known whether P = NP. This diagram is drawn under the assumption that these are not equal. The class #P consists of counting problems, problems for which the answer is a count, a non-negative integer. Within this class is the class #P-complete of problems which are as hard as any in #P. Every counting problem can be turned into a decision problem, namely, “Is the count larger than zero?” In this way some #P-complete problems become NP-complete problems, and thus all #P-complete problems (and all NP-complete problems) belong to the class of NP-hard problems, those which are as hard as any NP problem. The sliver to the right of the #P-complete problems indicates the possibility that (NP-hard) ∩ (#P) ⊊ #P-complete. This is currently unknown.

The classes P, NP and #P are defined by the running times of the algorithms that solve them and the capacities of machines these algorithms run on. The classes NP-complete and #P-complete play analogous roles in the classes NP and #P. They consist of the “hardest” problems of the class in the following sense: a solution for any NP-complete problem can be quickly transformed into a solution to any problem in NP. Accordingly, if there is an efficient solution to any NP-complete problem, there is an efficient solution to every problem in NP. (#P-complete problems play a similar role in #P.) It will be the work of this section to give more precise accounts of the terms problem, running time, transform and the classes of machines involved.

In describing the class NP-complete, it is useful to describe the class P, and necessary to describe the class NP.

The computational complexity of a problem Π is measured in terms of the running time necessary for an algorithm which solves Π. Defining these terms requires some preliminaries. First, note that a problem Π consists of a collection of instances, D_Π. Thus, “Determine whether 18 is composite” is an instance of the problem, “For any integer n, determine whether n is composite.” This is an example of a decision problem, that is, for each instance, the answer is either “yes” or “no”. A decision problem Π can be formalized as the pair (D_Π, Y_Π), where Y_Π ⊂ D_Π consists of the yes instances. In this example, D_Π is the set of integers and Y_Π is the set of composite integers. We will refer to this problem as Π_composite.

Notice that each instance π ∈ Π has a size, ℓ(π) and that the computational cost of solving the problem grows with the size of the problem. In this example, the size ℓ(n) of the instance n is the number of digits in n. If we then have an algorithm M which solves Π, we can consider the running time r_M (π) required by M when applied to the instance π. This could be measured in elapsed time or in terms of the number of steps carried out by M in this computation. We would like to know the worst (i.e., longest) running time for all instances of a given size. Now depending on the problem, there is no guarantee that there is at least one instance of every size. When no instance of size n exists we will take the worst running time for instances of that size to be zero. We refer to the function which gives the worst running time at each size to be the running time of M defined as follows:

$$r_M(n)=\{\begin{array}{ll}0\hfill & if\{\pi \mid \ell (\pi )=n\}=\varnothing \hfill \\ max\{r_M(\pi )\mid \ell (\pi )=n\}\hfill & \mathit{otherwise}\hfill \end{array}$$

The class P consists of those decision problems which can be solved with a polynomial running time. Stated formally, a decision problem Π belongs to the class P if there is an algorithm M which solves Π and a polynomial p(n) such that r_M (n) ≤ p(n). An example of a problem in the class P is Π_mult defined as follows: An instance of Π_mult is three integers, a, b and c. The size of an instance is the total number of digits in a, b and c. These constitute a yes instance if a × b = c. It is not hard to convince oneself that the amount of computation necessary to decide whether a × b = c is bounded by a polynomial in the total number of digits.

The class NP consists of non-deterministic polynomial time problems. That is, a decision problem is NP if a machine which is allowed to guess can verify a yes instance in polynomial time. Π _composite provides an example of a problem which is NP. Given an instance of Π_composite, i.e., an integer c, if c is, in fact, composite, a correct guess as to its factors a and b, can be verified in polynomial time by calling Π_mult. One can define this class in terms of the operation of non-deterministic Turing machines. See, for example, [32]. Clearly P ⊆ NP. In view of the perceived complexity of many problems in NP, it is generally believed that P ≠ NP, although no rigorous proof is known.

The class NP-complete consists of the hardest problems in NP. The problems in NP-complete have the following property: Suppose that Π₁ is NP-complete. Suppose that Π₂ is NP. Then there is an algorithm M which translates any instance π₂ of Π₂ into an instance π₁ of Π₁ such that π₁ is a yes instance of Π₁ if and only if π₂ is a yes instance of Π₂. Further, both the computational cost of translating π₂ into π₁ and the size ℓ(π₁) are bounded by a polynomial in ℓ(π₂). It follows that if any NP-complete problem can be solved (deterministically) in polynomial time, then every NP problem can be solved in polynomial time. Put another way, if any NP-complete problem can be solved in polynomial time, we will then have P = NP.

Hundreds of problems are known to be NP-complete [31]. These come from fields such as graph theory, number theory, scheduling, code optimization and many others. They are widely believed to be intrinsically intractable, but this remains an open question. Other problems which are not necessarily NP-complete (e.g., because they are not decision problems) are known to be at least as hard. This is because for such a problem, say Γ, there is an NP-complete problem Π that can be reduced to Γ, where the computational cost of this reduction is bounded by a polynomial in the length of the instance problem considered. Thus, Γ can be used to solve Π. These problems are called NP-hard. Since NP-complete problems transform to each other, all NP-complete problems can be solved by a reduction to any NP-hard problem. NP-hard problems are found in fields as diverse as epidemiology and origami [33].

Finally, we turn to the classes #P and #P-complete. The class NP consists of decision problems, e.g., Π_composite which asks whether a given integer c can be written as the product of two factors, a × b = c. The class #P consists of counting problems, e.g., given an integer c, how many different ways are there to write it as the product a × b = c? Let us call this ${\mathrm{\Pi }}_{\mathit{composite}}^{\#}$. Thus, for the instance 18 of Π_composite the answer is “yes”, while for the instance 18 of ${\mathrm{\Pi }}_{\mathit{composite}}^{\#}$, the answer is 4, as witnessed by the products 2 × 9 = 18, 3 × 6 = 18, 6 × 3 = 18 and 9 × 2 = 18.

We have seen that a problem Π is NP if there is a non-deterministic algorithm M which verifies the yes-instances of Π in polynomial time. M is allowed to make guesses. For each instance π of Π, we can ask how many different guesses M can make which will lead to the verification of π as a yes-instance. Of course, if π is not a yes-instance, this number is zero. Let us refer to this counting version of Π as Π^#. The problem Π^# belongs to the class #P if for every yes-instance π, every computation verifying π has length bounded by a polynomial in ℓ(π).

Clearly, any counting problem can be turned into a decision problem by asking whether the count is non-zero. In this way, every #P problem can be turned into a problem in NP. However, #P problems may well be strictly harder than NP problems in the following sense. Even if it turns out that P=NP, there may still be problems in #P that can’t be solved in polynomial time.

Among the problems in #P, there are some which qualify as being the hardest in the sense that a solution for any one of these can be quickly transformed into a solution for any problem in #P. These problems are referred to as #P-complete. Among the #P-complete problems are some which are the counting versions of NP-complete problems. It follows from this that every #P-complete problem is NP-hard. To see this, let ${\mathrm{\Pi }}_1^{\#}$ be any #P-complete problem, and let ${\mathrm{\Pi }}_2^{\#}$ be a #P-complete problem whose corresponding decision problem Π₂ is NP-complete. A solution to ${\mathrm{\Pi }}_1^{\#}$ can be transformed into a solution to ${\mathrm{\Pi }}_2^{\#}$, and this, in turn answers Π₂, hence any problem in NP. It follows that ${\mathrm{\Pi }}_1^{\#}$ is NP-hard. As we shall see below, some problems in network epidemiology are #P-complete and thus NP-hard.

3. SIR epidemics on networks

We start by describing a network SIR model in which both the population (which is finite) and the transmission probabilities between individuals are constant with respect to time. A network in question is a graph G = (V, E) where the vertices V represent individuals and the presence of an edge (u, v) ∈ E indicates that u and v have contact which would enable disease transmission from u to v. This transmission is probabilistic. Each edge (u, v) is labeled with the probability that u transmits the disease to v if u becomes infected while v is susceptible. We make no assumption as to the topology of this network. In this model, disease transmission takes place at discrete times t = 1, 2, 3 ….

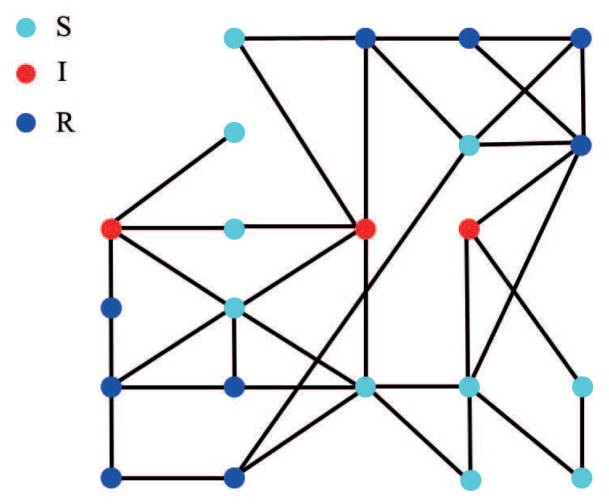
A state of this system is the assignment of each individual to one of the classes S (susceptible), I (infected) or R (recovered). (Figure 2 shows the state of a network at time t = 3.) Only susceptibles can become infective. Infected individuals remain so for one time step and then become recovered. These latter are assumed immune to further infection and play no further role in the spread of disease. The edges determine who can infect whom and consequently which states can follow a given state. The transmission probabilities on the edges determine the probability that any one of these states follows the given state. An epidemic is a sequence of states each of which is a possible successor of the previous state. We assume that the initial state consists of susceptibles and at least one infected, but make no assumption as to the number of people who become infected in the course of the epidemic. Given an initial state, we can speak of the probability that an epidemic evolves through a given sequence of states and the probability that it arrives at a particular state. Let us formalize this.

Figure 2.

The state of a social network on the third day of an epidemic which started at the lower left and upper right corners. Susceptibles are shown in cyan, infectives in red and recovereds in blue. Every infective is three edges from one of the two original infectives along some route of transmission. Each infective shares an edge with at least one recovered, namely the recovered that infected it. One susceptible will never become infected. The epidemic can continue for at most six more steps. We have omitted the probabilities on the edges.

As above, a social contact network is a pair 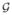= (G, Pr) where G = (V, E) is the graph with vertex set V and edge set E. Each edge has the form (u, v) with u, v ∈ V and u ≠ v. We make no assumption on the topology of this graph. The function Pr assigns a probability to each edge, that is Pr : E → [0, 1]. The states of 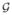are given by⁴

$$\text{St}(\mathcal{G})=\{\varphi \mid \varphi :V\to \{S,I,R\}\}.$$

Given states ϕ₁ and ϕ₂, the state ϕ₂ is a possible (immediate) successor of ϕ₁ if it satisfies the following conditions for each u, v ∈ V :

1. If ϕ₁(u) = R, then ϕ₂(u) = R. (Recovered individuals stay recovered.)

2. If ϕ₁(u) = I, then ϕ₂(u) = R. (Infected individuals recover in one step.)

3. If ϕ₁(u) = S, then ϕ₂(u) ∈ {S, I}. (Susceptible individuals either stay susceptible or become infected.)

4. If ϕ₂(u) = I, then ϕ₁(u) = S and there is a vertex q ∈ V\{u} and an edge (q, u) with ϕ₁(q) = I. (Infected individuals were susceptible and were infected by a neighbour.)

The requirement that individuals recover in exactly one time-step might appear to be a drastic oversimplification. However, the formalism is rich enough to accommodate patterns of latency and extended periods of infectivity. This can be done by replacing the individual represented by vertex u by a sequence of vertices u₁, u₂, … representing u on day 1, u on day 2, etc. See, e.g., [34].

An epidemic Φ is a sequence of states ϕ₁, …, ϕ_n where ϕ_i+1 is a possible successor of ϕ_i for i = 1, …, n − 1. We will assume that the initial state ϕ₁ consists of infectives and susceptibles. The length of this epidemic is ℓ(Φ) = n. Since individuals recover after one step and recovered individuals cannot be reinfected, infection must be transmitted or die out. As a consequence, no epidemic can be longer than the longest self-avoiding path in G = (V, E), for otherwise, it must infect some vertex twice, a contradiction. If we assume that each edge transmits or fails to transmit independently, then it is not hard to compute the probability that a susceptible individual is infected by its infected neighbours. This, in turn, allows one to compute the probability that a state ϕ₁ is followed by a particular successor state ϕ₂. Let us denote this probability by Pr(ϕ₂ | ϕ₁). This system enjoys the Markov property, that is, the probability of a given state depends only on the previous state. Thus given an initial state Φ₁, the probability of the epidemic Φ = ϕ₁, …, ϕ_n, is

$$Pr(\mathrm{\Phi }\mid {\varphi }_1)=\prod _{i=2}^{n}Pr({\varphi }_i\mid {\varphi }_{i-1}).$$

The probability that u becomes infected at the n^th step in the course of an epidemic starting with ϕ₁ is

$$Pr({\varphi }_n(u)=I\mid {\varphi }_1)=\sum _{\begin{array}{l}\{{\varphi }_1,\dots ,{\varphi }_n\mid \\ {\varphi }_n(u)=I\}\end{array}}Pr({\varphi }_1,\dots ,{\varphi }_n\mid {\varphi }_1).$$

Abusing notation, we denote the probability that u becomes infected in the course of some epidemic starting with ϕ₁ by

$$Pr(u\mid {\varphi }_1)=\sum _{j=1}^{n}Pr({\varphi }_j(u)=I\mid {\varphi }_1).$$

In this sum we consider each of these epidemics only up to the time at which u becomes infected. Because of this, no epidemic appearing in this sum is an initial sub-epidemic of another. Accordingly, these are disjoint cases and we can take the total probability to be the sum of the individual probabilities.

We will be interested in initial states ϕ₁ consisting only of infectives and susceptibles. In this case, we can identify ϕ₁ with the set of infectives $P={\varphi }_1^{-1}(I)$. This gives the notation Pr(u | P).

Let us formalize the problem Π_epidemic of finding Pr(u | P). An instance π of this problem consists of

• A graph G = (V, E).

• A labelling⁵ Pr : E → [0, 1] ∩ ℚ.

• An initial infective set P ⊂ V.

• An individual u ∈ V \ P.

A solution to π is the value Pr(u | P).

We take ℓ(Π) = |V|.

The epidemiological viewpoint we have just described follows the evolution of probabilities over time. If we ignore the order of events, we come to the simpler viewpoint of percolation. Percolation methods have been used in epidemiology. (See, for example, [36, 37, 34, 3, 12, 38]. The latter two contain extensive references.) Since an individual is only infected for one time step in the course of any epidemic, an edge can transmit at most once in the course of an epidemic. This allows us to consider a random variable that takes as values subgraphs of G. Given 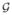, we take 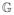to be the random variable which takes values in {G′ = (V, E′) | E′ ⊆ E}. The probability that 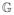takes the value G′ is given by

$$Pr(G^{\prime })=\left(\prod _{e\in E^{\prime }}Pr(e)\right)\left(\prod _{e\notin E^{\prime }}(1-Pr(e))\right).$$ (*)

We may think of E′ as determining whether e = (u, v) transmits in the course of an epidemic if that epidemic has a state ϕ with ϕ(u) = I and ϕ(q) = S. Given a path τ in G, we will abuse notation by writing τ ⊂ G and e ∈ τ for the edges of τ. Given a path τ, the probability that it appears in G′ = (V, E′) is

$$Pr\{G^{\prime }\mid \tau \subset G^{\prime }\}=\prod _{e\in \tau }Pr(e).$$

The following theorem is equivalent to observation (3) of [34, Lemma 3.5, pp 720–21]. The reference [34] uses ζ ∈ {0, 1}^E to induce a subgraph G′ = (V, ζ⁻¹(1)) of G = (V, E).

Theorem 1

Suppose 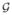is social contact network. Then

$$Pr(u\mid P)=Pr\{G^{\prime }\mid G^{\prime }\mathit{contains}a\mathit{path}\mathit{from}Ptou\}.$$

Corollary 1

Pr(u | P) is a finite sum of terms of the form (*). In particular, it is a polynomial in the values Pr(e) with integer coefficients and degree at most |E|.

This Theorem and its Corollary provide the link between epidemiology and communications networks. We will see that in the case where Pr is taken to have the single value p the polynomial of Corollary 1 corresponds to the reliability polynomial as described below (see also [35]).

4. NP-hard problems on communications networks: Consequences for epidemiological calculations

We assume that a communications network consists of a set of computers, each of which is reliable and a set of communication links each of which has a known likelihood of failure and that the communication links function or fail independently. There is no loss of generality in regarding each node as infallible, since a fallible computer can be modelled as a pair of nodes with a fallible link connecting its input to its output. Once again, we can formalize this as 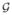= (G, Pr), where G = (V, E) represents installed capacity (V being the set of computers and E the set of communication links), Pr : E → [0, 1] the reliability of each link and 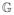is the random variable assuming values in {G′ = (V, E′) | E′ ⊆ E}. Each G′ = (V, E′) is the subnetwork of functioning links left after the failure of the edges e ∈ E\E′. Successful transmission of a message on this network depends on the connectivity of the subgraph realized by . Network engineers focus on several kinds of connectivity. We first examine two of the simplest.

The two-terminal reliability problem is defined as the calculation of the probability that there is at least one correctly functioning path in the network connecting a predefined source node to a predefined target node. An instance π of Π _{two terminal} consists of the following:

• A graph G = (V, E).

• A labelling Pr : E → [0, 1] ∩ ℚ.

• A source terminal u ∈ V.

• A target terminal v ∈ V \{u}.

A solution to π is the value Pr(v | u).

By Corollary 1 this value is given by an integer polynomial in the values Pr(e) for e ∈ E. If we restrict to the case where every edge takes the same value, this becomes an integer polynomial in one variable called the reliability polynomial. Thus a related problem is the following:

An instance π of Π_{rel poly} is

• A graph G = (V, E).

• A source terminal u ∈ V.

• A target terminal v ∈ V \{u}.

A solution to π is the coefficients of the reliability polynomial.

A number of additional network reliability problems have been studied (see [35], an excellent introduction to this field). These include

• k terminal reliability. This requires that k chosen terminals are mutually pair wise connected.

• Broadcasting, also known as all terminal reliability: This requires that all terminals are pair wise connected.

Note that while we have defined the reliability polynomial using the two-terminal problem. By Corollary 1 these also give polynomials in a similar way.

Naturally, in addition to the network reliability problems presented above, many other reasonable problems can be defined or could arise from practical applications. Formally, once a model = (G, Pr) of the network has been chosen, a general mechanism to define a reliability problem is the following: A network operation is specified by defining a set Op(G) ⊆ {G′ = (V, E′) | E′ ⊆ E} of states considered to be functional. The set Op(G) is sometimes called a stochastic binary system; the elements of Op(G) are termed pathsets. Specifying the pathsets for G determines the whole stochastic binary system, and therefore defines the network operation. The reliability problem consists of finding the probability Pr(Op(G)) that the probabilistic graph assumes values in the set Op(G).

A first naive algorithm to solve a network reliability problem formulated in this general manner is to enumerate all states of (i.e., the cardinality of the set {G′ = (V, E′) | E′ ⊆ E}), determine whether a given state is a pathset or not using some predesigned recognition procedure⁶, and sum the occurrence probabilities of each pathset. Due to the statistical independence assumed, the probability of occurrence of a pathset is simply the product of the operation probabilities of the edges in the pathset and the failure probabilities of the edges not present in the pathset. Complete state enumeration requires the generation of all 2^|E| states of , implying that the running time of this algorithm would exponentially depend on the number of links in the network.

A substantial amount of effort has been put into finding more efficient algorithms for exact calculation of network reliability problems (see [35]). However, efficient exact solutions seem unlikely as witnessed by [39, Theorem 1, p 158]:

Theorem 2

The problems Π_{two terminal} and Π_{rel poly} are NP-hard.

These problems belong to the class #P-complete [40, 41, 42, 43, 44, 35] and are thus NP-hard (see Section 2 above).

Corollary 2

The problem Π_epidemic is NP-hard.

To see this, notice that every instance of Π_{two terminal} is an instance of Π_epidemic, namely, an instance in which P consists of a single vertex.

More generally, despite dedicated efforts, no algorithm of polynomial running time has been found that allows for the exact calculation of the probability Pr(Op(G)) of a given set of pathsets Op(G), unless very specific assumptions are made on the topology of the underlying probabilistic network ([35, 45]). We consider it an open question as to which (if any) of these more general network reliability problems (defined through the choice of a suitable stochastic binary system Op(G)) correspond to epidemiological problems.

5. NP-hardness of extended problems in epidemiology

Epidemic on networks with time-varying transmission probabilities

As we have seen in the previous section, the seemingly simple problem of finding an individual’s chances of infection is NP-hard. This is even so in the case where the set of initial infectives is a single individual.

We can generalize Π_epidemic by allowing transmission probabilities to vary over time. We have seen that the length of any epidemic is at most the length of the longest self-avoiding path in G. Consequently, time-varying transmission probabilities can be encoded as

$$Pr:E\times \{1,\dots ,\mid E\mid \}\to [0,1].$$

In this case, percolation methods no longer apply. However, every instance of Π_epidemic can be mapped into an instance of this extended problem. Thus, the time-varying version of this problem is NP-hard.

Epidemic on networks with disease latency

One might also generalize Π_epidemic to allow patterns of latency and extended periods of infectivity⁷. We will take 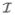to be a sequence of distinct states, {I₁, I₂, …, I_N }. We assume that for each stage I_i there is an infectivity μ_i and a probability of recovery ρ_i. We take ρ_N = 1. We now consider a social contact network and infectivity pattern 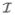. We refer to this as an S 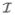R network. The states of this network are

$$\{\varphi \mid \varphi :V\to \{S\}\cup \mathcal{I}\cup \{R\}\}.$$

We modify the definition of possible successor states so that the allowable transitions are from S to I₁, from I_i to I_i+1 for i = 1, & mldr;, N − 1 and from I_i to R for i = 1, …, N. If ϕ(u) = I_i, u transitions to state R with probability ρ_i and to state I_i+1 with probability 1 − ρ_i. If e = (u, v) ∈ E and ϕ(u) = I_i, and ϕ(v) = S, then u infects v with probability Pr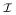(e, i) = μ_iPr(e). We assume that 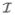is non-trivial in the sense that there is i with μ_i ≠ 0 and ρ_j ≠ 1. This ensures that at least one state is capable of transmitting infection and that an infected individual has a positive probability of reaching such an infective state. As before, under the assumption that transmissions and recoveries happen independently, we can develop an expression for Pr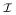(u | P).

Fix 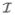. An instance of Π 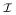is an instance of Π _epidemic.

A solution to Π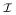 is the value Pr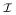(u | P)

Theorem 3

Given an non-trivial infectivity pattern 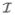, Π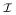 is NP-hard.

Lemma 1

Given 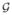= (G, Pr) and 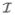= {I₁, …, I_N }, there is 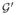= (G, Pr′) so that for each P ⊂ V and u ∉ P, Pr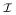(u | P) = Pr′(u | P).

Proof

Consider an edge e = (u, v). Suppose that ϕ₁(u) = I_i and ϕ₁(v) = S. What are the chances that v remains uninfected by u? (We assume for the moment that v is not infected by some other neighbour during the next N steps.) We take μ = Pr(e). Let us denote by ν_i the probability that u remains infected for i steps, but not i + 1 steps. We then have

$${\nu }_i={\rho }_i\prod _{j=1}^i(1-{\rho }_j).$$

The probability that v remains uninfected by u is

$${\tau }_{\mathcal{I}}(\mu )=\sum _{i=1}^N{\nu }_j\prod _{j=1}^i(1-{\mu }_j\mu )$$

We now define 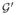= (G, Pr′) by taking

$${Pr}^{\prime }(e)=1-{\tau }_{\mathcal{I}}(Pr(e)).$$

This does what is required.

Proof (Proof of Theorem 3)

We will show that Π_{rel poly} is polynomially reducible to Π.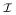

Fix 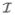to be a non-trivial pattern of infectivity. Suppose we are given an instance π of Π_{rel poly}. This consists of a graph G = (V, E) and source and target vertices u and v. Suppose also that we have a polynomial time algorithm for solving Π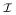. Let M be the degree of the reliability polynomial we are trying to find. This is bounded by the length of the longest self-avoiding path in G. We choose M + 1 arbitrary probabilities p₀, …, p_M+1. These give us M + 1 instances of Π 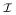by taking 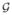_i = (G; Pr_i), where Pr_i takes the constant value p_i. By the previous lemma, solving these M + 1 instances of Π solves M + 1 distinct instances of Π_epidemic which consist of the graph G and differing constant functions ${Pr}_i^{\prime }$. These M + 1 values give us M + 1 independent linear equations whose unknowns are the coefficients of the reliability polynomial. Solving for these is a polynomial time problem.

Expected number of total infections

One might hope that while computing an individual’s probability of infection is NP-hard, there might be a way to compute the expected number of infections. This, too, is NP-hard. Let us formalize this.

An instance π of Π_expected is

• A graph G = (V, E).

• A labelling Pr : E → [0, 1] ∩ ℚ.

• An initial infective set P ⊂ V.

A solution to π is the expected number of infections,

$$\sum _{u\in V}Pr(u\mid P).$$

The following theorem was proved in [29, Theorem 1, p 483]. For the sake of completeness, we provide a proof here.

Theorem 4

Π_expected is NP-hard.

Proof

We will show that Π_epidemic can be polynomially reduced to Π_expected. Suppose we are given an instance π of Π_epidemic. Let π̃ be the instance of Π_epidemic which is formed from π by appending a single edge from u to v ∉ V and assigning Pr(u, v) = 1. It is clear that the expected number of infections in π̃ differs from the number of expected infections in π̃ by exactly Pr(u | P). Thus, if we had a polynomial time algorithm for finding the expected number of infections, we could find the probability of any individual becoming infected.

The fact that Π_{rel poly} is NP-hard suggests that the difficulty lies not in the probabilities Pr but in the topology of G. One problem which we have not addressed here is the question of calculating the probability of infection in an SIR network where the graph G_t = (V_t, E_t) changes over time due to stochastic births and deaths. It seems likely that this will also provide a source of NP-hard problems. However, this requires a reformulation of the underlying problem.

6. Discussion and conclusions

It has been the purpose of this paper to draw the attention of network epidemiologists to results in communications network reliability which shed light on questions regarding the computational aspects of epidemiology of SIR networks.

Theorem 2 and Theorem 4 tell us that generally, in the absence of a major break-through in computer science we cannot expect to be able to compute exact probabilities of infection or expected number of infection in large social contact networks. As [31] points out, problems do not go away simply because we have deemed them NP-hard.

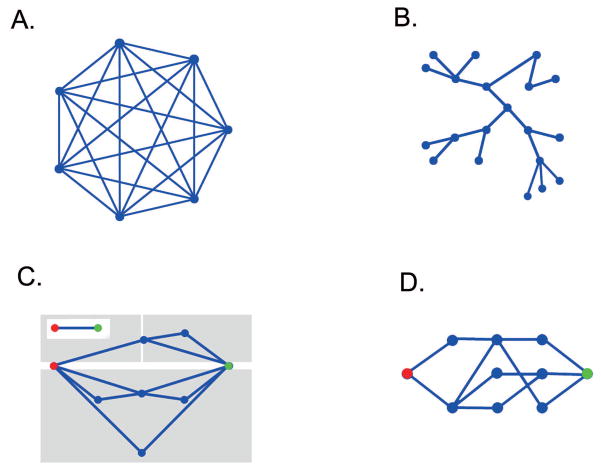
Since the network engineers have been here before us, it is tempting to ask whether their solutions will work for epidemiologists. While we consider the case open, the prospects seem mixed. Network engineers are often in the position of being able to choose the class of networks under consideration. As opposed to scale-free [8, 46] and small-world network structures [47, 48, 8], which frequently arise from a self-organization process during the spontaneous growth of a network, engineered or purposefully designed networks show rather different structures. Some of the classes that allow efficient calculations (exact or approximate) include trees, full graphs, series-parallel graphs [35], and channel graphs [45]. (See Figure 3.) Unfortunately, these classes of networks seem unrealistic as models of social contact networks.

Figure 3.

A. The full graph on seven vertices. Every edge is connected to every other. The Kermack-McKendrick model arises as the limit of the full graph as the number of vertices goes to infinity. B. Trees are connected graphs without loops. C. Series parallel graphs have a distinguished source and target vertex. They are built up from the graph which consists of two vertices and one edge (inset) by repeatedly combining smaller series parallel graphs either in series or in parallel. The grey rectangles indicate the last two moves in assembling this graph. The reader may wish to check that the three subgraphs are series parallel graphs. D. Channel graphs also have a distinguished source and target vertex. The vertices are partitioned into subsets and this set of subsets is ordered. Here each subset is grouped vertically. The first and last of these subsets each consist of a single vertex. Each edge connects vertices from adjacent subsets. While each of these classes of graphs allows for efficient computation of epidemic probabilities, none of them seem likely to be useful models of real world social networks.

Network engineers have turned to Monte Carlo simulation for the calculation of estimates of network reliability. We would like to give pointers into their literature [49, 50, 51, 52, 53, 54, 55, 29]. This approach has received increased attention in the last decade due to the power of modern computers and computing clusters. While Monte Carlo simulation only calculates an unbiased point estimator for reliability probabilities, increasing the number of simulated samples causes these estimates to converge to the actual value.

The fact that efficient and precise algorithms for computing infection probabilities are out of reach (see Theorems 2, 3 and 4) has real-world consequences. Designing a response to an emerging epidemic can depend on determining the kind of epidemiological probabilities we have been discussing [56]. The effectiveness of interventions during an emerging epidemic often crucially depends on timely implementation. Our results and those of [25] and [26] place an emphasis on the search for efficient and quick methods that give good approximations when applied to real-world social networks.

Highlight.

Communicaitons engineers have long studied transmission of messages in fallible networks. In its general form, exact solution of this problem is NP-hard and therefore presumed intractable. The communication problem is isomorphic to transmission of disease in social contact networks. In particular, exact computation of infection probabilities in social contact networks is also NP-hard.