Remote control of DNA-acting enzymes by varying the Brownian dynamics of a distant DNA end

Abstract

Enzyme rates are usually considered to be dependent on local properties of the molecules involved in reactions. However, for large molecules, distant constraints might affect reaction rates by affecting dynamics leading to transition states. In single-molecule experiments we have found that enzymes that relax DNA torsional stress display rates that depend strongly on how the distant ends of the molecule are constrained; experiments with different-sized particles tethered to the end of 10-kb DNAs reveal enzyme rates inversely correlated with particle drag coefficients. This effect can be understood in terms of the coupling between molecule extension and local molecular stresses: The rate of bead thermal motion controls the rate at which transition states are visited in the middle of a long DNA. Importantly, we have also observed this effect for reactions on unsupercoiled DNA; other enzymes show rates unaffected by bead size. Our results reveal a unique mechanism through which enzyme rates can be controlled by constraints on macromolecular or supramolecular substrates.

Quantification of enzyme rates is fundamental to mechanistic understanding of life processes. One often considers rates of enzyme activity to be dependent on properties of the molecules near the reaction site. However, conformational fluctuations of large molecules can be controlled by distant constraints on a molecule, which might in turn control activities of enzymes along that molecule that rely on conformational fluctuations of their substrates to reach their transition states. Large DNA molecules provide a prime candidate for realization of this effect. Tethering the ends of a chromosomal domain will constrain bending and twisting fluctuations of the DNA between the tether points. Changes in the tethering constraints will change the conformational kinetics of the intervening DNA, conceivably modifying rates of enzymes acting along it.

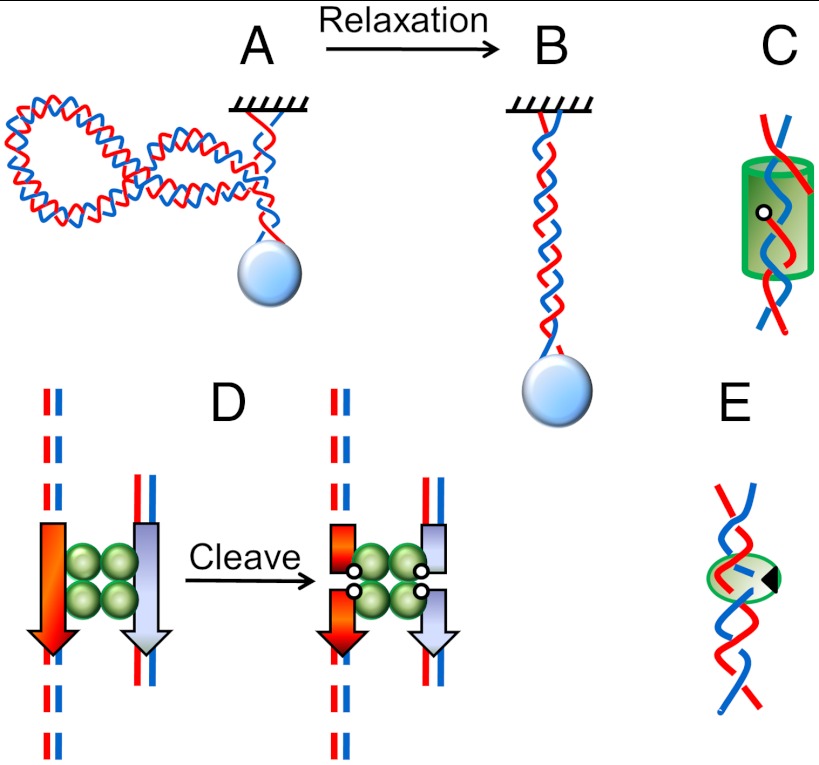
Here, we report in vitro single-molecule experiments showing this effect, through direct observation of variation of DNA-acting enzyme rates with changes in DNA end constraints. Our main focus is on enzymes that processively relax DNA supercoiling, although we have observed similar effects for single-step reactions on unsupercoiled DNAs. Single-DNA experiments (Fig. 1A) permit real-time observation of nucleic acid-acting enzyme activities, including those that change DNA supercoiling (1, 2). Such experiments are conveniently carried out using “magnetic tweezers,” where a paramagnetic bead attached to the end of the molecule is pulled by a constant force via a magnetic field gradient. Rotation of the magnets allows DNA to be supercoiled, reducing DNA extension (3) (Fig. 1A). This allows enzyme cleavage of one or both strands of a dsDNA to be observed (1, 2, 4) (Fig. 1B). When cleavage occurs, the particle at the end of the DNA moves as linking number is relaxed. We note that the bead orientation is fixed during DNA relaxation by the constant magnetic field direction.

Fig. 1.

Experiment setup and supercoil relaxation assay. (A) A supercoiled dsDNA is tethered between a surface and a paramagnetic bead. As plectonemic supercoils are introduced, DNA extension is reduced. (B) When supercoiling is relaxed, an increase in DNA extension is observed. (C) Relaxation mechanism for topo IB and topo V. Cleavage of one strand covalently links one end to the topo (open circle), and allows the other to rotate about the unbroken strand (blue), relaxing stored ΔLk. (D) Bxb1 integrase: A tethered dsDNA (dotted lines) with attP (red arrow) and a short DNA fragment with attB (blue arrow) form a synapse with two Bxb1 integrase dimers. Cleavage of all four strands is accompanied by covalent attachment of each 5′ end to an integrase subunit; supercoils on the tethered DNA then relax by rotation about the protein interface that holds the two halves of the complex together (21). Reactions in C and D are reversible (i.e., the cleaved strands may religate to recover the torsional stiffness of the dsDNA). (E) Nicking enzyme Nt.AlwI (9) binds to a dsDNA and cuts only one strand, producing irreversible nicking.

Enzymes that have been studied in this manner include topoisomerase (topo) IB (2) and topo V (4), which cleave and rejoin a single DNA strand (Fig. 1C); the site-specific DNA serine recombinase Bxb1 integrase (5), which makes reversible double-strand breaks (Fig. 1D); and a nicking endonuclease (2, 5), which irreversibly cleaves one strand of the double helix (Fig. 1E). Supercoil relaxation rates observed in such experiments have been argued to be limited by thermal fluctuation-driven barrier-crossing kinetics associated with DNA strand rotation at the DNA cleavage site (2, 4, 5). The “attempt rate” for barrier crossing in these experiments has been attributed to diffusive motion of the enzyme and the portion of DNA attached to it; however, it is conceivable that external constraints on the DNA can affect the rate at which the enzyme–DNA complex can reach its reaction transition state.

Here, we show that both the type of enzyme and the size of the paramagnetic particle, which controls the rate of fluctuation at the end of the DNA, affect supercoil relaxation rates for topo IB, Bxb1 integrase, and the nickase Nt.AlwI. We explain our observations using a simple model that indicates how fluctuations of the bead at the end of the DNA and the enzyme–DNA interaction energy landscape can combine to produce a relaxation rate for enzymes proportional to the diffusion constant of the bead at the end of the DNA; in effect, the “attempt rate” for barrier crossing can be controlled by the kinetics of the bead. We also show that other enzyme reactions mediated on long DNAs show bead size-dependent rates.

Results

Supercoil Relaxation by Topo IB Depends on Bead Size.

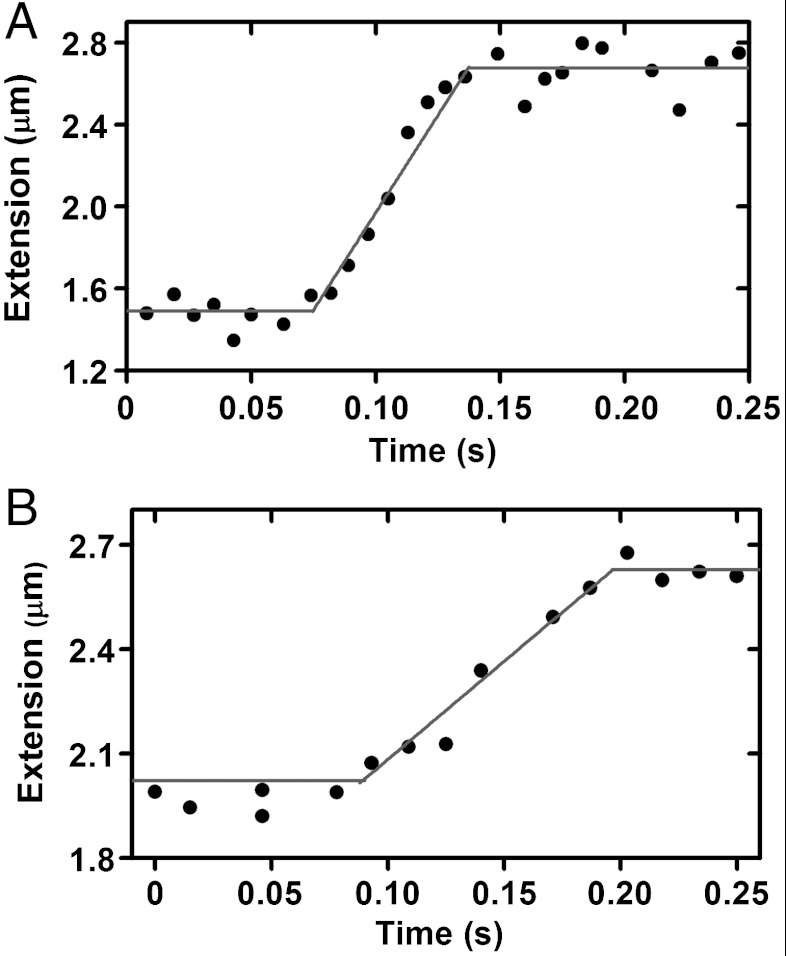
Fig. 2 A and B shows bead-tracking data for topo IB relaxation of a supercoiled 11.4-kb DNA (linearized pFOS1 with slight modifications; this DNA was used in all experiments of this paper). Before cleavage, force was adjusted to be 0.50 ± 0.05 pN and then held constant; this force is comparable to that generated by physiological DNA supercoiling (6). Linking number was set to ΔLk = -30, and then enzymes in solution were injected. Following cleavage, DNA extension returned to its torsionally relaxed value via a linear trajectory (Fig. 2, red lines). The slope of this trajectory was fit to obtain a relaxation velocity. Repeated velocity measurements for each force and bead size were carried out to obtain an average velocity.

Fig. 2.

Real-time traces for supercoil relaxation by topo IB (0.5 pN, ΔLk = -30). (A) A 1 μm-diameter bead; relaxation leads to bead velocity of 21 ± 1 μm/s. (B) A 2.8 μm-diameter tethered bead; relaxation occurs with bead velocity of 5.6 ± 0.4 μm/s.

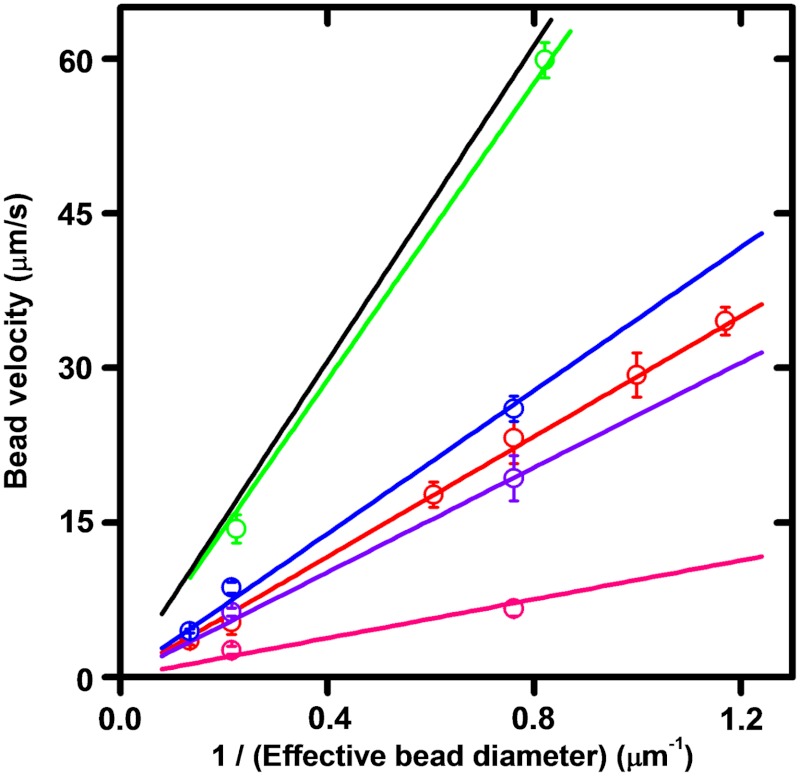
In experiments under identical conditions but with paramagnetic beads of varied size, the bead velocity during relaxation showed a striking linear dependence on the reciprocal of bead size [Fig. 3 (red) and Fig. S1; note correction of bead diameter for surface effects (ref. 7), Table S1]. Systematic errors in force calibration were ruled out by verifying that different-sized beads generate the same extension as a function of varied force and ΔLk (Fig. S2).

Fig. 3.

Dependence of supercoil relaxation velocity on the inverse of effective bead diameter (0.5 pN, ΔLk = -30). For each enzyme, a well-defined slope (in units of μm²/s) was obtained from a two-parameter linear fit to the velocities averaged over series of experiments. Bead diameters of 0.7 μm, 0.8 μm, 1.0 μm, 1.2 μm, and 2.8 μm were used; the slowest velocities were obtained using paired 2.8-μm beads (two beads stuck together). All error bars indicate standard errors determined from the number of measurements listed below. Pink: Bxb1 integrase. The slope of the velocity vs. effective bead diameter is 9.4 ± 0.8 μm²/s, lower than all other enzymes studied, indicating that Bxb1 integrase has the largest barriers to rotational relaxation among all enzymes studied in this paper. (Number of measurements: n = 7 and 26 for 1- and 2.8-μm beads, respectively). Purple: topo V, slope 25.4 ± 0.9 μm²/s (n = 11 and 23 for 1- and 2.8-μm beads, respectively). Red: vaccinia topo IB, slope 29.2 ± 0.8 μm²/s, close to that for topo V (n = 7, 5, 8, 5, 9, and 5 for 0.7-, 0.8-, 1.0-, 1.2-, and 2.8-μm beads, respectively; n = 5 for the double 2.8-μm bead). Blue: nicking enzyme Nt.AlwI, slope 35 ± 1 μm²/s, the highest among all supercoil relaxation enzymes studied, consistent with its having the lowest barriers to rotational relaxation (n = 10 and 8 for 1- and 2.8-μm beads, respectively; n = 9 for doublets of 2.8-μm beads). Green: bead release velocities obtained by cutting the dsDNA with restriction enzyme PvuII. Again, a simple linear dependence is found with slope 72 ± 2 μm²/s. As expected, this is higher than that of any supercoil relaxation experiments (n = 10 and 8 for 1- and 2.8-μm beads, respectively). Black: theoretical limit for bead release velocity based on estimated bead terminal velocity at 0.5-pN pulling force (constant in our experiments), water viscosity (6.9•10^-4 Pa·s for water at 37 °C), bead size, and proximity to surface (7). Expected velocity is linear in the inverse of effective bead diameter with slope 76.6 μm²/s, in accord with results for bead release (green).

The velocities found for topo IB were significantly less than the expected terminal velocity for a bead leaving the surface under the influence of a constant 0.5-pN force (Fig. 3, black line). To check this experimentally, and to establish that the topo IB velocities were limited by something other than the translational drag on the beads, “escape velocities” of free beads were determined by cutting the tethered DNA with the blunt-cutting restriction enzyme PvuII. The escape velocities (Fig. 3, green) are about three times faster than bead velocities during supercoil relaxation by topo IB, and are close to those expected from the drag coefficient of the bead (7) (Fig. 3, black, and Table S1).

The threefold lower slope of the topo IB relaxation rates (Fig. 3, red) relative to the free bead release data (Fig. 3, green) during supercoil relaxation by topo IB indicates that the drag force on the beads is only about one-third of the 0.5-pN external force being applied to the bead. Notably, the bead drag force is nearly constant for different bead sizes, indicating that bead drag force is not in itself limiting the supercoil relaxation rate as bead size is being made larger. Thus, supercoil relaxation in the topo IB experiments is slowed by something other than bead drag—i.e., crossing of energy barriers associated with the topo IB–DNA interaction energy landscape (2).

To check whether our results were comparable to prior single-DNA studies of topo IB, we carried out measurements for 1-μm beads (Fig. S3) and 0.2-pN force, recovering previously reported results (2) for bead velocities during relaxation of positive supercoiling by topo IB. In these experiments we used sufficient positive supercoiling so as to have the same initial extension as reported in ref. 2. When comparing these experiments, we do caution that the experiments of ref. 2 used 24-kb DNAs whereas we have used 10-kb DNAs; thus, these experiments are not precisely equivalent (see Fig. S3 legend for further discussion).

Supercoil Relaxation by Other Enzymes Depends on Bead Size.

Similar experiments (0.5 pN, ΔLk = -30) were carried out for topo V, an enzyme that relaxes DNA supercoiling in a manner similar to that of topo IB (4, 8), with the result that a similar bead-size effect was observed (Fig. 3, purple). As for topo IB, the topo V relaxation velocity was found to depend linearly on the inverse of the effective bead diameter. In an additional series of experiments with the site-specific DNA-nicking enzyme Nt.Alw1, which cuts one strand of a dsDNA at a specific target sequence allowing supercoil relaxation to occur (9), the same trend was observed (Fig. 3, blue).

We also measured supercoil relaxation rates for the Bxb1 phage integrase acting on a DNA carrying one specific recombination sequence (5, 10) (Fig. 3, pink). The recombination reaction requires a second target site, which we supply on oligomeric DNAs in solution. An oligomer forms a complex with the specific recombination sequence along the supercoiled tethered DNA and four molecules of Bxb1 integrase. Then, both DNAs are cleaved by the integrase, allowing supercoil relaxation to occur via rotation at the cleavage plane, with the tether held together solely by protein–protein interactions (5). The relaxation velocities for Bxb1 relaxation of DNA are significantly slower than those for the topoisomerases and the nicking enzyme, but still show a relaxation velocity that varies linearly in inverse bead diameter. The site for the recombination reaction is in the center of the tethered DNA (5), equidistant from the molecule ends, indicating that the bead-size effect can occur over at least a 5-kb sequence distance.

For each supercoil-relaxing enzyme studied, the rate of relaxation was proportional to the inverse of the effective bead diameter (Table S1), but with different rates for different enzymes. All velocities observed are slower than the “speed limit” of the free bead release experiments. Because the slopes of the curves in Fig. 3 are enzyme-dependent, the relaxation rates are determined by a combination of the bead size and the rotational kinetics of the enzyme–DNA complexes.

Friction Alone Cannot Explain the Data.

One might imagine that a combination of translational drag associated with bead motion and a simple molecular sliding friction model of the enzyme–DNA interaction might be sufficient to explain the data. However, this can be seen to be untenable by noting that in such a situation, one would expect the external (magnetic) force to balance the sum of bead drag and enzyme–DNA frictions, both of which should be proportional to bead velocity. In turn, this implies that the inverse of bead velocity should be linearly dependent on the bead drag coefficient—i.e., the effective bead size—with an enzyme-independent slope and enzyme-dependent intercept (SI Text). Fig. 3 data are plotted in this way in Fig. S4, which shows enzyme-dependent slopes. A sliding friction-only model cannot describe the experimental data.

Fluctuation-Assisted Barrier-Crossing Model for Bead-Size Effect.

The essential ingredient ignored in the sliding friction-only description is thermal motion. The time-averaged external (magnetic) force applied to the bead, and therefore to the DNA, is a constant 0.5 pN in the Fig. 3 experiments (see also Fig. S2). However, the kinetics of the bead are bead size-dependent (Fig. S5), and in turn, the Brownian forces applied to the DNA end have bead size-dependent kinetics. Because the bead fluctuation time is longer than the DNA conformational fluctuation time, tension and twist fluctuations generated by the bead are transmitted throughout the DNA. These stress fluctuations drive the enzyme–DNA complex over the barrier associated with relaxation of successive supercoils, with their correlation time setting the “attempt rate” for barrier crossing.

We can understand the bead-size dependence of the relaxation rates from a simple model. We consider, for simplicity, a single barrier crossing-limited reaction for an enzyme acting on a long DNA, with its reaction coordinate coupled to applied tension. The dynamics of force fluctuations in the DNA are determined by the net drag coefficient of the DNA and bead, ζ_bead + ζ_DNA (dominated by the bead in our experiments), and by the spring constant associated with length fluctuations of the DNA, k_DNA (11). Both ζ_DNA and k_DNA are dependent in general on force and linking number because of the nonlinear elasticity of DNA and the dependence of extension on linking number. Both ζ_DNA and k_DNA are also dependent on the precise location at which the enzyme acts along the DNA relative to the bead (they describe tension fluctuations in the DNA segment between bead and bound enzyme). However, for a given force, linking number, DNA length, and location of enzyme reaction point along the DNA relative to the bead, ζ_DNA and k_DNA may be considered to be fixed parameters. The relaxation time for extension and tension fluctuations (and therefore for torque fluctuations) is just τ = (ζ_bead + ζ_DNA)/k_DNA. Because ζ_bead = 3πηD, where D is the bead diameter and η is the solution viscosity, we expect a correlation time that, for sufficiently large beads, scales linearly with bead size. Given that we have observed this (Fig. S5), we conclude that we are in the regime where the bead is controlling the tension fluctuation correlation time.

This conclusion is in accord with an estimate based on prior experimental measurements of the longitudinal drag ζ_DNA for extended DNA (11); these experiments indicate ζ_DNA to be well-described by the rigid-rod result ζ_DNA = 2πηX/[ln(X/b)] (11), where X is the extension of the DNA and b = 2 nm is the DNA thickness. The ratio of the two relevant drag coefficients is ζ_bead/ζ_DNA = 1.5(D/X) ln(X/b); when this ratio is larger than one, the bead drag will dominate over the drag on the DNA molecule. For the 10-kb molecules used here, X is 3 microns at most (in most of the relaxation experiments, X is closer to 1 micron); for bead diameter D = 2.8 μm, this gives ζ_bead/ζ_DNA = 10.8; for D = 1 μm, one obtains ζ_bead/ζ_DNA = 3.7. For X = 1 μm, the two drag coefficients become equal for D approximately equal to 0.1 μm; for beads smaller than this characteristic size, the DNA drag will dominate. In the experiments of this paper, we thus expect the drag force on the bead to control tension fluctuations in the DNA.

The correlation time τ is approximately the time between successive uncorrelated “attempts” to cross the barrier of height E_b. The barrier height may have tension and torque dependences to it, but for given average force and linking number, it is a fixed parameter. During each attempt period τ, the probability of actually crossing the barrier is given by the Boltzmann factor exp[-E_b/(k_BT)], assuming that the waiting time to barrier crossing is long compared to equilibration of the enzyme itself. This allows us to estimate the waiting time for a single barrier-crossing event:

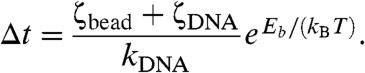[1]

This is essentially Kramer’s result for thermally excited barrier crossing for a viscosity-limited chemical reaction (12), but where the attempt time is not that for fluctuations of the enzyme bound to the DNA, and is instead the longer correlation time for force fluctuations in the entire DNA–bead–enzyme system.

In our supercoil relaxation experiments, a processive series of events gives rise to the motion of the bead with an apparent velocity. If the length released per barrier-crossing event is ℓ, then the net velocity will be ℓ/Δt, or:

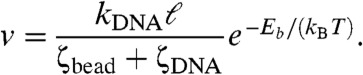[2]

Because ζ_bead is linearly dependent on bead diameter D, and we are in the regime where the bead is determining the relaxation time of the DNA, Eq. 2 indicates that the velocity of relaxation for the bead will depend inversely linearly on bead size in the regime where the bead is the dominant contributor to the total drag coefficient, as observed in Fig. 3.

For sufficiently small beads, the drag of the DNA itself will dominate, in which case tension fluctuations in the DNA will be determined by relaxation time of the molecule itself. Although we have not observed this regime, it may be possible to do so using small (< 0.1 μm) beads and fixed-force optical trapping. Eq. 2 also explains how different slopes of Fig. 3 arise from different enzymes, which have varied E_b, making the final factor in Eq. 2 enzyme-dependent. Finally, Eq. 2 indicates that the relaxation velocity will be inversely proportional to solution viscosity [through the viscosity dependence of ζ_bead + ζ_DNA, as previously noted in topo V experiments (4)].

This model describes a mechanism distinct from bead size-dependent entropic volume-exclusion forces associated with proximity of particles to the DNA-tethering surface (13, 14). For the experiments of this paper we estimate such volume-exclusion forces to be well below 0.1 pN and therefore irrelevant. We also note that for relaxation of supercoiling there is an additional contribution to the drag coefficient during relaxation from rotation of the plectonemic domain; however, a detailed study of this reached the conclusion that plectoneme drag was a negligible contribution to the total drag coefficient opposing relaxation (15) for topo IB relaxation experiments similar to those reported here.

Bead Size Can Affect Chemical Reaction Rates.

The experiments reported above establish a bead-size effect for the relaxation of supercoils by DNA topology-changing enzymes. Given the physical nature of those processes [rotational kinetics limited by thermally assisted barrier crossing (2)] and our model for them, one might suppose that this effect occurs only for reactions involving appreciable molecular motion, or supercoiling. However, we have also observed bead-size effects on rates of chemical catalysis of DNA by enzymes. A prime example of this is provided by our experiments on Bxb1 integrase, which revealed an influence of bead size on the rate of DNA religation.

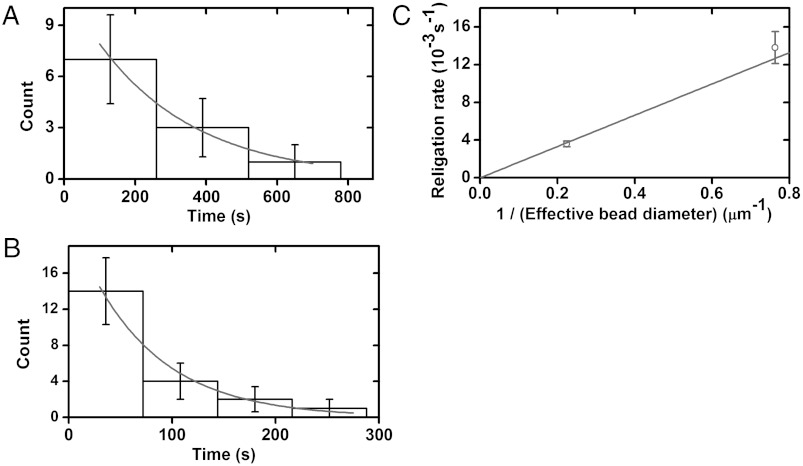
Religation times were measured by periodically testing for reappearance of torsional stiffness of the tethered DNA following relaxation events at a constant 0.5-pN force; their distribution was found to be exponential, indicating a one-step reaction (Fig. 4 A and B). We again observed a nearly linear dependence of the religation rate on the inverse of effective bead diameter (Fig. 4C), indicating that this effect can arise in reactions where there is no DNA torsional stress, DNA supercoiling, or large amounts of bead translational motion.

Fig. 4.

Religation times (“open” times) and corresponding rates for Bxb1 integrase depends on bead size. Following double-strand cleavage and supercoil relaxation, attP–Bxb1 integrase–attB–CT synapses usually religate, leading to recovery of torsional stiffness. A series of waiting times between relaxation and religation (constant 0.5-pN force) was measured and was well-fit by a exponential decay corresponding to a single-step chemical process. All error bars show standard errors. (A) Average waiting time for 2.8 μm-diameter beads was 225 ± 54 s. The exponential fit rate was 3.6 ± 0.3•10^-3 s^-1 (n = 11). (B) Average waiting time for 1 μm-diameter beads was 61 ± 17 s. The exponential fit rate was 14 ± 2•10^-3 s^-1 (n = 21). (C) Plot of religation rates indicates a linear dependence on the inverse of effective bead diameter.

The religation process corresponds to a single “hopping” event over one barrier rather than a series of events, but again, fluctuations at the end of the molecule determine the rate at which the transition state is visited. This barrier-crossing picture implies that for fixed bead size, there should be a force-dependent religation rate. Measurements of the religation rate for 2.8-μm beads at a larger force of 1.0 pN verify this (Fig. S6). Because the religation rate increases with force, the transition state for Bxb1 religation most likely slightly extends the synaptic complex, because there is no twist rigidity of the complex before religation.

We note that we have also observed a bead-size effect in the time to DNA cleavage by Bxb1 integrase (Fig. S7), consistent with the effect seen for the (reverse) religation process.

Bead-Size Effects on Loop Closure and Opening Kinetics.

We questioned whether there might not be similar effects for binding and catalytic reactions for enzymes that severely deform their target sites (e.g., by DNA bending or looping). Fig. S8 shows a bead-size effect for looping compaction and decompaction for DNA in the presence of the Escherichia coli chromosomal protein Fis (16). Although the dependence of the loop-formation rate on bead size might be expected, the dependence of the loop-opening rate on bead size was surprising. However, in light of the model, we can understand it in terms of larger beads slowing down the conformational fluctuations needed to traverse the energy barrier to disruption of protein–DNA interactions stabilizing the loops.

Some reactions do not show bead-size dependence. The PvuII DNA-cutting experiments used to trigger bead release (Fig. 3, green) show a cleavage rate with no dependence on bead size (Fig. S9). DNA cleavage by this enzyme likely involves diffusive search for the specific target along the DNA, followed by binding and cleavage with little or no dependence on DNA fluctuations, and hence a lack of dependence on bead size is reasonable. The mechanism we have outlined for a bead-size effect requires a reaction transition state that is coupled to external stress, through extension or twist distortion of the enzyme–DNA complex.

Discussion

We have shown how the Brownian dynamics of the end of a long DNA molecule can affect the operation of distant enzymes, using paramagnetic particles of varied sizes to control the rate of conformational motion at the DNA end. This effect appears to be common for enzymes that relax DNA supercoiling at rates limited by their rotational barrier-crossing kinetics: Topo IB, topo V, Bxb1 integrase, and a site-specific nickase all show the same effect, but with different rotational kinetics indicative of a dependence on the enzyme–DNA interactions.

We have proposed a simple model for this effect for supercoil-relaxing enzymes based on the idea that the rate of thermal fluctuations towards an enzyme–substrate transition state can be affected by molecular motions that are in turn influenced by distant mechanical constraints. The model shows how the supercoil relaxation rate is determined by a product of the inverse of the bead diameter, and a factor that depends on the energy landscape associated with the enzyme–DNA interaction, in accord with our experimental data. The relatively slowly moving bead controls tension and twist fluctuations in the DNA, in turn controlling the rate at which the barriers to relaxation at the DNA–enzyme interface are crossed.

We have also shown a similar effect for the rate of chemical religation of DNA by Bxb1 integrase, which establishes the bead-size effect for reactions on unsupercoiled (rotationally swiveling) molecules. We have observed the bead-size effect on the rate of closing and opening of DNA loops mediated by a bacterial chromosomal protein. Although these reactions involve only a single reaction step, the same mechanism of bead-controlled DNA fluctuation is likely to be the basis for the bead size-controlled rates we observe. The only requirement is that either tension or twist fluctuations in the DNA drive the enzyme–DNA complex towards its reaction transition state.

In application to single-DNA tethered-bead analyses of enzyme rates, we conclude that it is important that experiments with varied bead sizes be carried out to determine the relation between observed rates and reaction rates on nontethered molecules in vitro, or on the typically tethered chromosomal molecules found in vivo. In reactions involving sufficiently long untethered DNA molecules, it is conceivable that reactions might still be affected by overall molecule size (i.e., where the role of the bead is played by the dangling ends of a long DNA molecule or chromosome segment), and may occur on linear, nonsupercoiled molecules.

Our observation of the bead-size effect suggests that experiments with smaller particles might be able to observe rates that are intrinsic to interaction of enzymes with DNA a few microns long. We expect that for sufficiently small beads (not larger than 0.1 μm for the few-kb DNAs generally studied using micromanipulation methods), the drag coefficient for the DNA itself will control force fluctuations and enzyme reaction times. For the relatively large beads studied thus far we have not yet been able to observe this for any DNA substrate–enzyme pair, which would appear in Fig. 3 as a saturation of bead velocity for large 1/D (Fig. S10, green). However, a relatively weak bead-size effect has been observed in lac-repressor looping reactions with submicron-diameter beads; the effect weakness may reflect this small-bead limit (17).

We note that in the limit of very large and thus slowly moving beads, fluctuation of the bead becomes so slow that tension fluctuations induced by the bead occur on timescales longer than the enzyme action: In this case the bead will move at its terminal velocity following DNA relaxation (Fig. S10, red).

Our present model, although simple, does suggest that the spring constant of the DNA molecule should play a role in determining enzyme kinetic rates. This implies dependence on DNA length (11) and position of enzyme action along the DNA, which we have not yet investigated. More complete studies of force and torque fluctuation kinetics in supercoiled DNAs as a function of their length, including end-attached particle effects, are needed to obtain a more complete understanding of the bead-size effects we have observed. We note that although our experiments have been carried out with net tension applied to the DNA, we expect similar bead-size effects to occur even for zero applied tension: The rate of tension fluctuations in a DNA will depend on the diffusion rate of a tethered particle even when no external force is applied.

Enzyme rate dependence on substrate size or distant mechanical constraints is likely to appear in a wide variety of situations where enzymes act on large, thermally fluctuating substrates with internal degrees of freedom. Phenomena similar to those reported here may occur for enzymes that bind to and act on cytoskeletal filaments (actin, intermediate filaments, microtubules), for cell membranes, or even for chemical reactions occurring on synthetic macromolecules or supramolecular structures, if those enzyme–substrate complexes have reaction transition states that involve local deformations. Furthermore, one can expect to see the same kinds of effects in molecule-pulling experiments (e.g., protein unfolding) where beads and cantilevers of varied size are used. Finally, our observations of enzyme rate dependence on mechanical constraints of the substrate lead us to speculate that this effect may provide a means of regulation of proteins acting along a large molecule or complex. For example, the size of a chromosomal loop domain, along with other factors that affect conformational motion of that domain (such as crowding or attached macromolecular complexes), could affect rates of initiation of transcription or DNA replication on that domain.

Materials and Methods

DNA Constructs.

All experiments (supercoil relaxation and religation, DNA nicking, bead release, and nonspecific DNA looping) were performed with linear DNA fragments based on plasmid pNG1175 (5), which is a slight modification of pFOS1 (New England Biolabs). In brief, pFOS1 had a single Bxb1 attP site inserted between Mfe and BstX restriction sites, and was then was linearized by cutting at Spe and ApaI restriction sites. This linear molecule (9,702 bp) was ligated to approximately 900-bp PCR products carrying either biotinylated or digoxygenin-labeled nucleotides, with SpeI- and ApaI-compatible ends, respectively, resulting an 11.4-kb linear construct. The multiple labels at the ends constrain the two DNA strands sufficiently to permit supercoiling by rotation of the magnetic particle.

Magnetic Tweezers and Experiment Conditions.

Experimental setup, flow cell preparation, extension-force calibration, and ΔLk-time measurements were as described in refs. 4, 5, and 18. Force measurement was done as described in ref. 19. Nonspecific interactions between DNA, bead, and glass flow cell were suppressed using incubation with 0.4 mg/mL BSA–PBS solution.

For experiments with supercoil relaxation and religation, DNA nicking, and bead release, the 11.4-kb construct was tethered to an antidigoxygenin functionalized cover glass. A streptavidin-coated paramagnetic bead was attached to the other end of the DNA fragment (Dynal T1 and M280 for 1 μm- and 2.8 μm-diameter beads; MagSense Life Science particles for 0.7-μm, 0.8-μm, and 1.2-μm beads). Unless otherwise indicated, all supercoil relaxation experiments were performed under stretching force of 0.5 ± 0.05 pN and initial ΔLk = -30. Similarly, all torsional-stiffness restoration (religation) experiments were carried out under 0.5-pN force. Nonspecific DNA looping and unlooping were observed with stretching forces of 0.1 pN and 3 pN, respectively. Temperature of 37 °C was maintained for all experiments. Bead fluctuation and DNA extension–force responses were measured at room temperature, with the same 11.4-kb DNA construct.

Enzymes and Buffers.

Reactions with vaccinia topo IB (Epicentre Biotechnologies), Nt.AlwI (New England Biolabs), and PvuII (Promega) were performed in a buffer containing 50 mM potassium glutamate, 10 mM Hepes (pH 7.5), 1 mM MgCl₂, and 1 mM DTT. Reaction buffers, concentrations, and experimental methods for reactions with Fis (gift from R. C. Johnson, University of California, Los Angeles, CA), topo V (gift from A. Mondragon, Northwestern University, Evanston, IL), and Bxb1 integrase were as described previously (4, 5, 16).

Data Analysis.

Linear fitting for real-time reaction traces, such as Fig. 2 A and B, was done by χ-square minimization using a Monte Carlo method (software custom written in C). Four fit parameters, the initial extension, the final extension, and the times at which relaxation began and ended were used in the fits. MagSense beads with diameters of 0.7 μm, 0.8 μm, and 1.2 μm were measured by comparing images with 1-μm Dynalbeads using Adobe Photoshop. The drag coefficient for the double 2.8-μm bead was estimated by considering it to be a prolate ellipsoid moving along its minor axis direction with a minor radius of 1.4 μm and a major radius of 2.8 μm (20); this drag coefficient was then converted to an effective bead diameter (Table S1) using the Stokes drag formula for a sphere.