Building microscopic soccer balls with evaporating colloidal fakir drops

Abstract

Evaporation-driven particle self-assembly can be used to generate three-dimensional microstructures. We present a unique method to create colloidal microstructures in which we can control the amount of particles and their packing fraction. To this end, we evaporate colloidal dispersion droplets on a special type of superhydrophobic microstructured surface, on which the droplet remains in Cassie–Baxter state during the entire evaporative process. The remainders of the droplet consist of a massive spherical cluster of the microspheres, with diameters ranging from a few tens up to several hundreds of microns. We present scaling arguments to show how the final particle packing fraction of these balls depends on the dynamics of the droplet evaporation, particle size, and number of particles in the system.

Evaporation-driven particle self-assembly is an ideal mechanism for constructing micro- and nanostructures at scales where direct manipulation is impossible. For example, in colloidal dispersion droplets with pinned contact lines, evaporation gives rise to the so-called coffee stain effect (1): A capillary flow drags the particles toward the contact line to form a ring-shaped stain. Such a flow not only aggregates the particles, but is also able to organize them in crystalline phases (2–5). Similar mechanisms such as the convective assembly (6, 7) are currently successfully used to produce two-dimensional colloidal crystal films. To obtain three-dimensional clusters of microparticles, colloidal dispersion droplets can be dried suspended in emulsions (8–10), in spray dryers (11, 12), or kept in Leidenfrost levitation (13). The main drawback of these three-dimensional assembly techniques, however, is the lack of control on both the amount of particles and the particle arrangement in the remaining structures.

In this work, we devise a unique, controlled way of generating on-demand self-assembled spherical microstructures via droplet evaporation on a superhydrophobic surface (Fig. 1). We present scaling arguments to predict the particle arrangement in the microstructures formed, based on the dynamics of the evaporation process. To generate the microstructures, we evaporate colloidal dispersion droplets on a special type of superhydrophobic substrates. In most of the cases, a liquid Cassie–Baxter state drop evaporating on a superhydrophobic surface will eventually suffer a wetting transition into a Wenzel state, i.e., it will get impaled into the structure and loose its spherical shape (14, 15). Here, however, we use a surface that combines overhanging pillared structures (16, 17) with a hierarchical nanostructure (Fig. 2C). These surface properties impose a huge energy barrier for the wetting transition to occur, and therefore the droplet will remain almost floating over the structure in a Cassie–Baxter state during its entire life (18).

Fig. 1.

(A) A droplet of colloidal solution is left to evaporate on a superhydrophobic surface. As the solvent evaporates, the particle concentration increases. Once all the solvent has completely evaporated the colloidal particles have aggregated to form a spherical particle conglomerate: a colloidal supraball. (B) Top view of the resultant compact colloidal supraball left on the superhydrophobic surface after evaporation. The micropillars forming the structure are seen as circular objects around the supraball.

Fig. 2.

(A) Tilted view of the supraball in contact with the microstructure. (B) Detail of the contact area. (C) Magnified view of the micropillars forming the microstructure. (D) Close-up of the supraball surface. The distribution of crystalline patches resemble the pentagons in a soccer ball.

A typical result can be observed in Fig. 1 (see also Movie S1: A water droplet containing 1 μm soluble polystyrene particles (initial concentration 0.08% weight and initial volume 5 μL) evaporates on the superhydrophobic surface at room temperature and 30% humidity. After a typical evaporation time of 45 min, the solvent is completely evaporated and only the colloids are left upon the substrate. Remarkably, the particles (approximately 10⁷ in this particular case) are not just lying scattered on the pillars but they have aggregated and form a spherical macrocluster resting on top of the micropillars, which we call colloidal supraball. The final ball has a slightly oblate shape, with an ellipticity of approximately 10%. The final macroscopic contact angle with the structure is slightly (about 15%) lower than the initial one. Because the particles are fully wetted and do not have the tendency to accumulate at the interface, spontaneous shell formation (10) is not expected. Indeed, we do not observe shell formation during the evaporation of the droplets (11, 13, 19): The supraballs we obtain are solid, and present a high mechanical resistance and stability. To inspect inside the ball, we cut some of them open with the aid of sharp blades or microcapillaries. All the examined balls showed compact nuclei and no hollow structures (Fig. S1). Additionally, when looking closer at the surface of these particular colloidal supraballs as shown in Fig. 2D, one can identify crystalline flat patches which resemble the pentagonal patches present in a soccer ball. These crystalline patches are even observed close to the contact line (Fig. 2B), and at the bottom of the ball, where its shape is slightly flattened due to the contact with the pillars.

The system strongly differs from the particle deposition in the coffee stain problem (1, 5), where pinning of the droplet’s contact line causes a capillary-driven flow that brings the particles to the boundary. Pauchard and Couder (20) studied the drying of highly concentrated colloidal solutions of large droplets on hydrophobic surfaces, which is more similar to our system. However, in their case the contact line is also pinned, and as a consequence the droplet does not keep its spherical shape but shows strong deformations.

To understand the final structure of our present supraballs, it will turn out crucial to understand the dynamics of the droplet evaporation. The fact that we do not observe shell formation suggests that the particles do not influence the droplet evaporation. To test this hypothesis we compare the evaporation dynamics to that of a liquid drop that does not contain any particles. The evaporative mass loss from such a drop is typically governed by the diffusion of vapor molecules in the surrounding air (1, 21, 22). For diffusion-limited evaporation, the rate of volume change of the drop is given by

[1]

where R is the drop radius, D^′ = D_vaΔc/ρ, with D_va the diffusion constant for vapor in air, Δc the vapor concentration difference between drop surface and the surroundings, and ρ the liquid density (5). One might have expected the evaporation rate from the drop surface to be proportional to the droplet surface area approximately R². However, the vapor concentration gradient is proportional to 1/R, and therefore the total evaporation rate is proportional to R (23). If the droplet evaporates with a constant contact angle, we find that because V ∼ R³,

[2]

Here t_f is the total droplet lifetime in case no particles are present, for which the drop radius reaches zero. In the present case the drop radius saturates at a finite radius, R_ball, at a time , corresponding to the moment where the particles become densely packed. In Fig. 3 we plot the colloidal droplet radius versus t_f - t. The droplet radius is measured using a spherical/elliptical fitting from side-view images of the shrinking droplet during the experiment. Our experimental data for different number of particles are in very good agreement with the one-half power law. This result confirms that the particles do not influence the evaporation process until the final radius R_ball is reached. Hence, we see no indication that the particles form an impermeable shell during the evaporation of the drop. In previous studies, Sen et al. (11, 19) concluded that a shell would only form for fast evaporation or in extremely dilute cases. The absence of a shell also agrees with other well-known colloidal drop evaporation experiments in which particles do not tend to adsorb at the interface (1, 5), unless the colloids are specifically modified for that purpose (10, 24).

Fig. 3.

The radius of the droplet plotted against t_f - t with t_f the lifetime of the droplet and t the actual time. The triangle indicates the one-half power law, the dots represent the dataset for seven different experiments, where the number of particles was varied. For a certain the final ball size R_ball is reached. The final time was extrapolated as .

The scaling (Eq. 1) implies that the speed with which the interface is moving inward is given by dR/dt ∼ D^′/R. Hence, the interface speed increases dramatically as the droplet shrinks and the maximum speed reached in the experiment will be determined by the final radius R_ball. As we will show later, this increase in interface speed determines the particle packing inside the supraballs.

The final size of the ball depends on the number of particles inside the drop. The number of particles can be tuned by manipulating either the initial particle concentration or the droplet size. In our experiment, the ball size was in the range 100 < R_ball/R_p < 1,000, with R_p the particle radius. Clearly, the exact final size of the ball will not only depend on the amount of particles in the system but also on their packing fraction. We define the global packing fraction as

[3]

where N is the total number of particles in the droplet. The final supraball radius R_ball is accurately determined from SEM images. If the packing fractions were identical for all supraballs, one would expect that R_ball/R_p ∼ N^1/3. In Fig. 4A, however, we show that there is some deviation from the one-third scaling, especially for balls with a smaller number of particles.* In Fig. 4B we show that the packing fraction indeed strongly depends on the number of particles in the system.

Fig. 4.

(A) Supraball to microparticle diameter R_ball/R_p plotted against the total amount of particles N in the system. (B) The packing fraction Φ strongly depends on N. Blue dots represent experimental measurements and the red solid line corresponds to the most efficient particle packing Φ = 0.74 (hexagonal close packed), the dashed line marks Φ = 0.64, and random close packed. N_c is the critical number of particles, above which we find an ordered ball structure.

As the number of particles increases, the packing fraction approaches that of a perfect hexagonal close packing configuration, in which case one would find Φ = 0.74 (25), hence, we have an ordered particle packing inside the balls. On the other hand, the supraballs with a smaller amount of particles show remarkably low packing fractions, even below the random close packing (RCP) limit (Φ = 0.64) (26), corresponding to a disordered particle arrangement. The balls which show packing fractions below the RCP limit contain several empty cavities. Remarkably, the final configuration reached seems to depend on the number of particles in the system. In Fig. 4B we indicated the critical number of particles N_c ≈ 3·10⁶ when the packing fraction reaches that of an RCP. For N < N_c we get a loose, disordered particle packing in the supraball, whereas for N > N_c we get a densely packed, ordered supraball.

What causes the transition from ordered to disordered packings, and what determines the critical number of particles? In order to answer this question, we follow a similar approach as in Marín et al. (5): We compare the timescale on which particles can arrange by diffusion to the hydrodynamic timescale for the particle transport by convection, given by the inward motion of the liquid-air interface. If the diffusion time is small compared to the hydrodynamic time, particles can arrange into an ordered packing. The diffusive timescale for particles to find the best position in a crystalline phase is given by , with R_p the particle radius and D the diffusivity of the particles in the liquid (3, 5, 27). The hydrodynamic timescale is . Here R(t) is the droplet radius and L is the typical interparticle distance, which depends on the particle concentration as L = N^-1/3R, as long as the solution is dilute (L≫R_p). We define the ratio of both timescales as

[4]

where in the last step we used 1 to replace dR/dt ∼ D^′/R. Note that our definition of the interparticle distance L is a global average of the whole system. Locally, some inhomogeneities will be present, in particular close to the interface, but our scaling analysis will not be affected.

From Eq. 4 we observe that increases as the droplet radius becomes smaller during the evaporation (Fig. 3), until the limit R = R_ball is reached. A cross-over between the timescales is reached when the hydrodynamic time becomes equal to the diffusion time, hence when . If the cross-over is reached when R≫R_ball, the amount of crystalline clusters is still very small. From this point in time onward the interface speed is too high for the particles to further arrange in a crystalline way (5). Instead, they are pushed together in a random arrangement, with a low packing fraction. If the cross-over is reached when R ≤ R_ball, the particle packing is already dense and ordered, and we find a high packing fraction. For all droplets the evaporative mass loss, and hence the decrease in radius, is the same (Fig. 3), hence, the moment when the particle packing becomes sufficiently dense for particles to arrange depends solely on the number of particles in the droplet. If N is high (N > N_c), this moment is reached relatively early, i.e., well before , and we get an ordered particle packing inside the supraballs. Using that R_ball/R_p ∼ N^1/3 and considering , we find from Eq. 4 the critical number of particles above which we obtain ordered supraballs

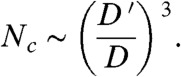[5]

This result emphasizes that the transition is governed by two diffusion processes: the diffusion of vapor, determining the speed of evaporation, versus the diffusion of particles inside the drop. The ratio of diffusion constants selects the critical number of particles. In our experiment D^′ = 3 × 10^-10 m²/s and D = 2 × 10^-13 m²/s, from which we find that N_c ∼ 10⁹. This prediction is two to three orders of magnitudes larger than the experimentally observed N_c. There are two reasons why this estimation is quantitatively off: First of all, we have neglected all prefactors, and the result is strongly (to the third power) dependent on the experimental parameters included in D^′, i.e., humidity, liquid density, diffusivity of vapor, and saturated vapor concentration. Secondly, in the analysis we have not taken into account which packing fraction is actually achieved when .

To verify whether the final packing fraction indeed depends on the spacing between the particles the moment the cross-over time is reached, we go back to our experimental data. We define the time-dependent packing fraction as N(R_p/R(t))³. As the droplet evaporates, this packing fraction will increase until it reaches its final value Φ. At the cross-over, defined by , the droplets will have a packing fraction Φ^∗. If this Φ^∗ is low, the amount of crystalline clusters is still very small. On the other hand, if Φ^∗ is high, we expect crystalline clusters to have formed already. After the cross-over time, the interface moves too fast to allow for further ordering, and it just presses the ordered particle clusters closer together. In Fig. 5 we show that droplets with a high Φ^∗ have a high Φ: When Φ^∗⪆0.1 we obtain a final packing fraction above the RCP limit.

Fig. 5.

Final packing fraction Φ_f versus the packing fraction at the cross-over time Φ^∗. Droplets below a certain Φ^∗ have a too low packing fraction at the cross-over time to achieve final packing fractions above the RCP limit. The particle packing can not only be obtained from the value of the packing fraction, but it can also directly be observed from the SEM images of the surface of the supraballs.

We cannot predict the critical Φ^∗ theoretically. However, we can, retrospectively, use the experimental critical Φ^∗ to compute N_c. Using that R_ball/R_p ∼ 0.1N^1/3 at the cross-over, we obtain N_c ∼ 10⁷, which is in the same order of magnitude as our experimental results (Fig. 4B).

The particle packing in the supraballs can not only be assessed by measuring the packing fraction, but it can also directly be seen in SEM images from the surface of the colloidal supraballs, as shown in Fig. 5. The size of the soccer-ball-like crystalline patches on the surface of the ordered supraballs depends on the ball size: Bigger balls will show larger patches due to the reduced curvature at their surfaces. To explain the size of the crystalline domains, we hypothesize that a crystalline patch will bend radially no more than a particle size. Then, it follows by simple trigonometry that the size of a patch S will be related to the ball radius R_ball and the particle size R_p via S/R_ball = arccos(1 - R_p/R_ball). This expression predicts a typical patch size of approximately15 μm for a ball with R_ball = 50 μm and R_p = 0.5 μm, which is in the right order of magnitude as one can observe in Fig. 2D.

In conclusion, in this work we devise a simple technique to create spherical colloidal supraballs relying only on droplet evaporation over a robust superhydrophobic surface. The supraballs show a highly ordered structure if the number of particles inside the drop is large enough to trigger early particle clustering. The critical number of particles required to obtain an ordered particle packing inside the balls depends on the parameters driving the droplet evaporation (through D^′) and the diffusivity of the particles. Hence, by controlling the humidity and ambient temperature the supraball packing fraction and hence size can be controlled. Massive fabrication of microcompact supraballs could easily be achieved by simply spraying a colloidal solution over the microstructure in a controlled atmosphere. By tuning the wetting properties of the particles one could also be able to generate the well-known colloidosomes (10) using the same proposed technique.