Vibrationally Assisted Electron Transfer Mechanism of Olfaction: Myth or Reality?

Abstract

Smell is a vital sense for animals. The mainstream explanation of smell is based on recognition of the odorant molecules through characteristics of their surface, e.g., shape, but certain experiments suggest that such recognition is complemented by recognition of vibrational modes. According to this suggestion an olfactory receptor is activated by electron transfer assisted through odorant vibrational excitation. The hundreds to thousands of different olfactory receptors in an animal recognize odorants over a discriminant landscape with surface properties and vibrational frequencies as the two major dimensions. In the present paper we introduce the vibrationally assisted mechanism of olfaction and demonstrate for several odorants that, indeed, a strong enhancement of an electron tunneling rate due to odorant vibrations can arise. We discuss in this regard the influence of odorant deuteration and explain, thereby, recent experiments performed on Drosophila melanogaster. Our demonstration is based on known physical properties of biological electron transfer and on ab initio calculations on odorants carried out for the purpose of the present study. We identify a range of physical characteristics which olfactory receptors and odorants must obey for the vibrationally assisted electron transfer mechanism to function. We argue that the stated characteristics are feasible for realistic olfactory receptors, noting, though, that the receptor structure presently is still unknown, but can be studied through homology modeling.

Introduction

Hearing, sight, touch, taste, and smell are the five basics senses that link animals and humans to their habitat. In particular, smell, or olfaction, endows animals and people with the ability to detect and distinguish different scents through volatile odorant compounds and, thus, provides a crucial ability to recognize food or evade predators. The five senses have been studied extensively [1] and are believed to be well characterized, but remarkably the fundamental mechanism of olfaction is still debated [2–5]. In this regard, the theory of electron transfer as pioneered by Rudolph Marcus [6] is playing a remarkable role, in this debate.

The mainstream theory of olfaction is based on the so-called lock-and-key model [5]. According to this theory, size, shape and functional groups of odorant compounds determine activation of olfactory receptors. Once an associated odorant molecule binds to an olfactory receptor, the receptor is activated and triggers a neural signal. Olfactory receptors have been identified as G-protein coupled receptors (GPCRs) [7]. Since most of the GPCRs, e.g., β-adrenergic agonists, are activated through binding of ligands and are highly sensitive to ligands’ conformation and surface properties [8], the lock-and-key mechanism seems to be a natural explanation of olfaction.

However, the lock-and-key mechanism as the sole discriminant was questioned after a sensory analysis of isotope effects of benzaldehyde and its derivatives (C₆(ring)-benzaldehyde, CHO-benzaldehyde and benzaldehyde-d₆) acting as odorants [9]. Based on the duo-trio test by 30 trained panelists, the authors reported a significant statistical odor difference of benzaldehyde-d₆ relative to non-deuterated benzaldehyde, evoking a shift of vibrational frequencies in the benzaldehyde samples [9]. Moreover, it was demonstrated recently that Drosophila melanogaster can distinguish between deuterated and regular odorant compounds, despite the fact that the shapes of such compounds are identical, while the only difference arises in the vibrational spectrum [10].

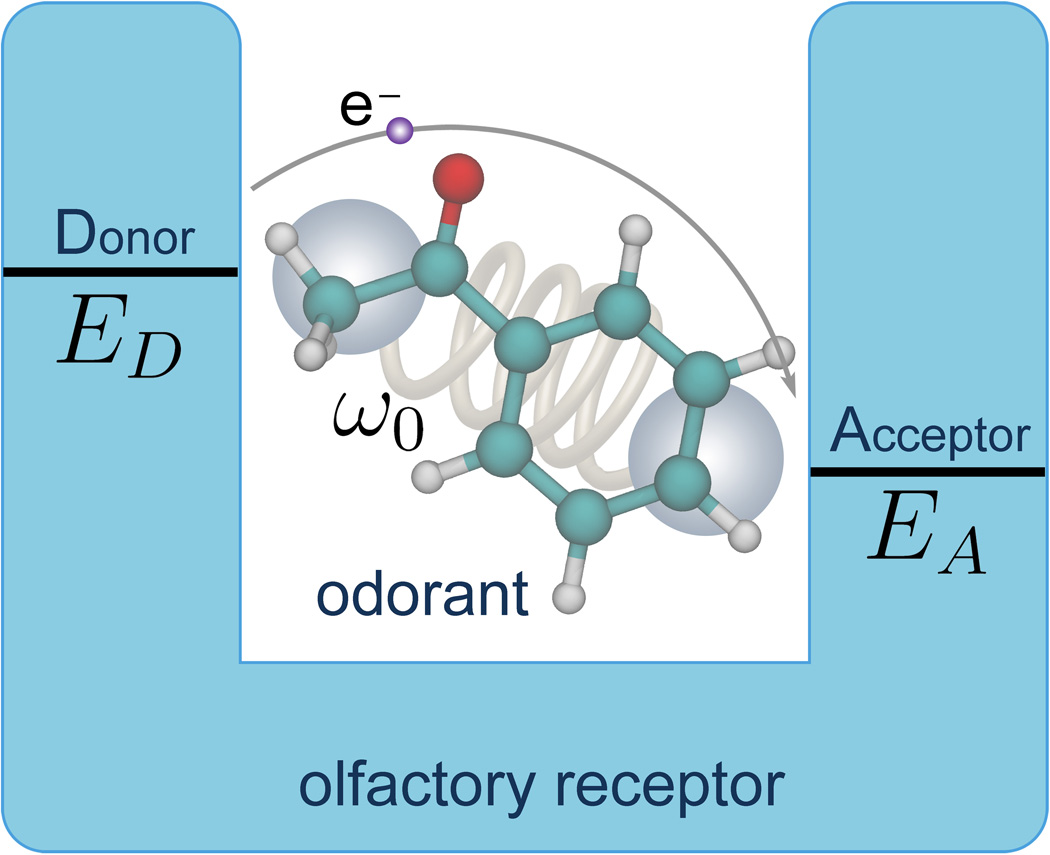
An alternative mechanism of olfaction had been suggested first in 1938 [11] and again in 1977 [12]. According to this mechanism the differences in key vibrational frequencies of odorant compounds contributes to odor perception. A plausible way of sensing the vibrational spectrum of an odorant is furnished through electron transfer in the olfactory receptor [3]. The mechanism is schematically illustrated in Fig. 1. Initially, an electron resides on the electron donor (D) site of the olfactory receptor. The receptor carries also an electron acceptor (A) site, but the D and A site redox energies differ by an amount Δε, too large to facilitate thermally assisted electron transfer on a relevant time scale, i.e., hundreds of nanoseconds or shorter, without presence of an odorant. However, once a suitable odorant binds to the receptor, the vibrational frequency of the odorant that matches Δε makes electron transfer possible, as the energy Δε can be released to the vibrational mode of the odorant. Odorant vibrations employed that way have particularly high frequencies. Thus, the key idea of the vibrationally assisted electron tunneling mechanism is to increase the tunneling rate in the olfactory receptor through vibrational excitation of the odorant, to make it larger than the elastic tunneling rate in the olfactory receptor, a rate that by itself is too small for olfactory reception. The vibrationally assisted mechanism inspired further studies and a microscopic picture leading to an electron tunneling rate estimate was proposed [4]. We like to emphasize that the stated mechanism complements, but does not replace, a lock-and-key mechanism of olfaction, i.e., both shape and vibrations should be significant for odor perception.

Figure 1. Principal of vibrationally assisted olfaction.

The odorant molecule with characteristic frequency ω₀ binds to the olfactory receptor binding pocket forming an electron-donor-acceptor complex with donor energy E_D and acceptor energy E_A. Electron tunneling from the donor site to the acceptor site of the olfactory receptor is enhanced if the vibrational frequency of the odorant molecule matches the energy difference Δε = E_D − E_A.

Although the structure of an olfactory receptor has not been determined, it is still possible to validate a mechanism of olfaction through an analysis of constraints imposed on the olfactory receptor. In this paper we focus on the principle possibility of the vibrationally assisted mechanism of olfaction and seek to understand under which conditions the mechanism can function in an actual olfactory receptor. The key focus of our study is the feasibility of vibrationally assisted olfaction and the needed physical characteristics on the side of olfactory receptor and oderant.

Below we describe the interactions between an olfactory receptor and different odorant molecules (acetophenon, citronellyl nitrile and octanol). The description is based on experimental measurements performed by others [10] and on quantum chemistry calculations performed by us. We calculate the electron tunneling rate in an olfactory receptor and elucidate the relationship between tunneling rate enhancement and odorant vibrational modes. Finally, we demonstrate for realistic physical characteristics of olfactory receptors a clear difference in the electron tunneling rate for non-deuterated and deuterated odorant compounds suggesting, thereby, new experiments to probe the vibrationally assisted mechanism of olfaction.

Theory

This section summarizes the theoretical description for the vibrationally assisted mechanism of olfaction. We derive key equations and explain the principle observables used to validate the mechanism in vivo or in vitro.

Vibrationally assisted olfaction

Electron transfer between donor and acceptor sites of an olfactory receptor (see Fig. 1) can be described through a model Hamiltonian H

$$H=H_R+H_{R-O}+H_{R-\mathit{\text{env}}}+H_T,$$ (1)

which accounts for the essential physical interactions in the system. Here H_R denotes the olfactory receptor Hamiltonian, H_R−O describes the coupling interaction between the olfactory receptor and an odorant molecule, H_R−env describes the coupling of the olfactory receptor to the thermal environment, and H_T accounts for electron tunneling from donor to acceptor sites of the olfactory receptor. Thus, the Hamiltonian H describes the entire olfactory system which consists of receptor, odorant, and molecular environment. The theory employed here had been employed successfully for the study of electron transfer in photosynthetic reaction centers as outlined in [13].

In the vibrationally assisted mechanism of olfaction, the olfactory receptor is a quantum mechanical system with two energy levels, which correspond to the electron donor and acceptor states. The Hamiltonian H_R can be written

$$H_R=E_D|D\rangle \langle D|+E_A|A\rangle \langle A|,$$ (2)

where E_D and E_A are the energies of donor state |D〉 and acceptor state |A〉, respectively. |D〉 and |A〉 describe the two states of the joined donor-acceptor (D − A) quantum system, so that the donor (acceptor) state refers to the state in which the electron resides on D (A) (see Fig. 1). The quantum mechanical “bra” 〈…| and “ket” |…〉 notations are used here to denote the possible quantum states in the olfactory receptor [14]. The coupling between olfactory receptor and odorant is described by Hamiltonian H_R−O that in the harmonic approximation is

$$H_{R-O}={\displaystyle \sum _{i=D,A}\hslash {\omega }_0|i\rangle \langle i|\left[u_i(a+a^{†})+\left(a^{†}a+\frac{1}{2}\right)\right]}.$$ (3)

Here a and a^† represent the quantum mechanical creation and annihilation operators of the odorant vibration [14] and ω₀ is the associated vibrational frequency; u_D is the coupling strength between odorant vibration and donor state of the receptor, while u_A is the analogous coupling strength for the acceptor state. Key for the present study is that we determine the coupling strengths u_A and u_D through quantum chemical calculations according to Eq. (18). The summation in Eq. (3) is performed over electron donor and acceptor states of the receptor.

Coupling of the receptor to the molecular environment, in particular the receptor interior, is represented through the Hamiltonian H_R−env and can be approximated as

$$H_{R-\mathit{\text{env}}}={\displaystyle \sum _{i=D,A}{\displaystyle \sum _q\hslash {\omega }_q|i\rangle \langle i|\left[u_{\mathit{\text{iq}}}(a_q+a_q^{†})+\left(a_q^{†}{a}_q+\frac{1}{2}\right)\right]}.}$$ (4)

Here the molecular environment is treated as an ensemble of harmonic oscillators with frequencies ω_q; u_Dq represents the coupling strength between the donor state of the olfactory receptor and a particular vibrational mode q; analogously, u_Aq denotes the coupling strength for the acceptor state. The summation in Eq. (4) is performed over the two possible quantum states of the olfactory receptor (D and A), as well as over all possible vibrational states of the molecular environment. All environmental vibrations, including those of the protein, are included in the Hamiltonian stated in Eq. (4) and through λ in the final equation (15). The effect of environmental vibrations (and by the same token, receptor vibrations) should be kept small as coupling to such vibrations does not discriminate odorants. As a result, an incorporation of receptor vibrations would be counterproductive in regard to the biological function of the receptors. There is another argument against a role of receptor vibrations partially absorbing the D − A redox energy difference: it is favorable to distinguish odorants through their feature of supplying high frequency vibrations to the reception process as such feature separates them from the background of other biomolecules; adding protein vibrations to the reception process would effectively lower the frequencies of odorants.

H_R−O and H_R−env describe competing interactions; H_R−O is essential for recognizing particular odorant vibrations, while H_R−env describes an indiscriminate coupling to a multitude of vibrational modes in the receptor and its interior. The odorant vibrations in (3) must “stand out” from the vibrations in (4) through their energy ℏω₀ (as stated above) as well as through strong coupling constants u_D and u_A.

Electron tunneling from donor to acceptor site of the olfactory receptor is governed by the Hamiltonian [15]

$$H_T=\gamma (|D\rangle \langle A|+|A\rangle \langle D|),$$ (5)

where γ is the hopping integral describing the coupling between donor and acceptor states.

The coupling of the olfactory receptor donor and acceptor states to the vibrations of the odorant molecule or of the environment in Eqs. (3)–(4) leads to a shift in the equilibrium position of the harmonic oscillators associated with the vibrations. Applying the displacement operators $a-a^{†}\text{ and }{a}_q-a_q^{†}$ of the vibrational modes [14], the eigenstate wavefunctions of the olfactory system can be written as

$${\mathrm{\Psi }}_{\mathit{\text{inX}}}=\text{exp }[u_i(a-a^{†})]\text{ exp }\left[{\displaystyle \sum _q{u}_{\mathit{\text{iq}}}(a_q-a_q^{†})}\right]|\mathit{\text{inX}}\rangle ,$$ (6)

where |inX〉 = |i〉 ⊗ |n〉 ⊗ |X〉 denotes the product state of (1) an electron localized at either donor (|i〉 = |D〉) or acceptor site (|i〉 = |A〉) of the receptor, (2) the n-th state of the odorant oscillator, |n〉, and (3) the vibrational state of the molecular environment, |X〉, characterized by a set of vibrational quantum numbers. |X〉 is defined through |X〉 = |n₁〉 ⊗ … ⊗ |n_j〉 ⊗ … ⊗ |n_q〉, with |n_j〉 being the n_j-th quantum number of the j-th vibrational mode of the molecular environment.

The energies corresponding to the eigenstates (6) are

$$E_{\mathit{\text{inX}}}=E_i+\hslash {\omega }_0\left(n+\frac{1}{2}-u_i^2\right)+{\displaystyle \sum _{q\in X}\hslash {\omega }_q\left(n_q+\frac{1}{2}-u_{\mathit{\text{iq}}}^2\right)}.$$ (7)

Here E_i describes the energy of the olfactory receptor with an electron occupying either the donor site (i = D) or the acceptor site (i = A); the next two terms describe the vibrational energies of the odorant molecule (assuming for the sake of simplicity a single mode) and of the molecular environment, respectively. The vibrational energies for odorant and molecular environment are quantized so that n and n_q are non-negative integers. The eigenstates (6) of the system allow one to calculate the vibrationally assisted electron tunneling rate from donor to acceptor site of the olfactory receptor. With |Ψ_D0X〉 and |Ψ_{AnX ′}〉 describing the initial and the final states of the receptor, respectively, the electron tunneling rate 1/τ_n can be deduced from Fermi’s golden rule [14] as

$$\frac{1}{{\tau }_n}=\frac{2\pi }{\hslash }{\displaystyle \sum _{X,X\prime }{P}_X{|\langle {\mathrm{\Psi }}_{\mathit{\text{AnX}}\prime }|H_T|{\mathrm{\Psi }}_{D0X}\rangle |}^2\delta (E_{\mathit{\text{AnX}}\prime }-E_{D0X})}.$$ (8)

Here the initial state |Ψ_D0X〉 is associated with an electron residing at the donor site of the olfactory receptor, while the odorant vibrates in its (n = 0) ground state. The subscript X denotes a set of initial state vibrational quantum numbers of the molecular environment which impact the electron transfer. In the final state, |Ψ_{AnX ′}〉, the electron is shifted to the acceptor, while the odorant molecule vibrates in its n-th state; the subscript X ′ represents the set of vibrational quantum numbers of the molecular environment in the final state. P_X in Eq. (8) denotes the Boltzmann weight to find the system in its initial state |Ψ_D0X〉 and δ(…) is the Dirac delta-function. The summation in Eq. (8) is performed over all possible vibrational states of the molecular environment before and after the electron transfer process.

Assuming the vibrations of the molecular environment have low frequencies, i.e., ℏω_q ≪ k_BT (k_B is the Boltzmann factor and T is the temperature of the molecular environment), Eq. (8) can be simplified

$$\frac{1}{{\tau }_n}=\frac{2\pi }{\hslash }\frac{{\gamma }^2{\sigma }_n}{\sqrt{4\pi k_{\mathrm{B}}T\lambda }}\text{ exp }\left(-\frac{{(\mathrm{\Delta }\epsilon -{\epsilon }_n-\lambda )}^2}{4k_{\mathrm{B}}T\lambda }\right).$$ (9)

Here γ is the hopping integral between the donor state |D〉 and the acceptor state |A〉 of the olfactory receptor defined already above; σ_n is the so-called Huang-Rhys factor [16] which describes the inelastic nature of the electron tunneling process due to the coupling between olfactory receptor and odorant molecule; following [16] it is defined as

$${\sigma }_n=\frac{{(u_D-u_A)}^{2n}}{n!\text{ exp }[{(u_D-u_A)}^2]}.$$ (10)

The reorganization energy λ in Eq. (9) describes the coupling of the olfactory receptor donor and acceptor states to the vibrations of the molecular environment and is

$$\lambda ={\displaystyle \sum _q\hslash {\omega }_q{(u_{\mathit{\text{qA}}}-u_{\mathit{\text{qD}}})}^2.}$$ (11)

Δε in Eq. (9) represents the energy difference between the olfactory receptor donor and acceptor states (see Fig. 1)

$$\mathrm{\Delta }\epsilon =E_D-E_A.$$ (12)

Finally, ε_n in Eq. (9) is the energy of the odorant in its n-th excited state gained through electron transfer accounting also for coupling to the odorant vibration, namely,

$${\epsilon }_n=n\hslash {\omega }_0+\hslash {\omega }_0(u_D^2-u_A^2),n=0,1,2,\dots$$ (13)

In the simplest scenario we consider electron transfer in the olfactory receptor assisted by only the first excited state of the odorant vibration. In this case, two characteristic rates for the electron tunneling process arise, namely, 1/τ₀, the elastic tunneling rate in the olfactory receptor, i.e., the rate in the absence of odorant vibrational excitation, and 1/τ₁, the inelastic tunneling rate assisted by the first excited vibrational state of the odorant. For the sake of simplicity, we omit below the subscript n = 1 for σ_n, ε_n, and τ_n and define

$${\sigma }_1\equiv \sigma ,{\epsilon }_1\equiv \epsilon ,1/{\tau }_1\equiv 1/\tau .$$ (14)

The elastic tunneling rate is denoted below as 1/τ₀, and the corresponding σ₀, ε₀ are calculated using Eq. (10) and Eq. (13), respectively, i.e. assuming n = 0.

As pointed out above, the couplings described by H_R−O and H_R−env compete with each other. This is evident from Eq. (9) where H_R−O enters through the term ε, while H_R−env enters through λ defined in Eq. (11). The competition arises in the term 1/τ ~ c_λ exp[−d_λ(Δε − ε − λ)²]. As long as λ ≪ Δε and λ ≪ ε, the coupling to a background of vibrational states does not affect discrimination of odorant vibrational excitations. It is also evident from Eq. (9) that sensitivity of the rate 1/τ is limited by λ, i.e., that the ε − dependence of 1/τ has a width of λ.

The energy ε and the Huang-Rhys factor σ depend on particular vibrational modes µ of the odorant. Therefore, to characterize vibrationally assisted tunneling, the tunneling rate 1/τ should include contributions from all vibrational modes of the odorant. At the level of perturbation theory (Fermi’s golden rule as stated in Eq. (15)) exercised here the contributions simply add and one obtains

$$\frac{1}{\tau }=\frac{2\pi }{\hslash }{\displaystyle \sum _{\mu =1}^N\frac{{\gamma }^2\sigma (\mu )}{\sqrt{4\pi k_{\mathrm{B}}T\lambda }}\text{ exp }\left(-\frac{{(\mathrm{\Delta }\epsilon -\epsilon (\mu )-\lambda )}^2}{4k_{\mathrm{B}}T\lambda }\right)},$$ (15)

where N is the total number of modes. The Huang-Rhys factors σ(µ), related through Eq. (10) to the coupling constants u_A and u_D, characterize how vibrational mode µ is coupled to electron transfer. The factors are determined computationally in this study according to Eq. (18) below and require that first the normal mode mass-weighted coordinates are determined quantum chemically for vanishing electrical field and for the relevant local electric field.

The odorant specific parameters (ε, σ) can be derived from ab initio calculations as demonstrated below, but the receptor specific parameters (Δε, λ, γ) possess a higher degree of uncertainty mainly due to the unknown receptor structure. Therefore, in this study, we consider the range of possible parameters in the latter case, to investigate the regimes in which the vibrationally assisted mechanism of olfaction is feasible, in principle, in realistic olfactory receptors.

Although Eq. (15) accounts for all key physical processes in the system, some uncertainties remain. One uncertainty stems from the model parameters employed that are built on three main assumptions: (i) The receptor is a quantum mechanical system with two relevant electronic states, donor state D and the acceptor state A. This assumption holds because other states in the receptor have higher energy than the D and A states and, therefore, are expected to contribute insignificantly to the electron transfer process. (ii) The donor and acceptor states are treated in the harmonic approximation. This assumption is reasonable because the olfactory receptor acts close to thermal equilibrium, where the harmonic approximation is valid. (iii) The effect of the thermal motion of the receptor is represented through a bath of low-energy (compared to k_BT) harmonic oscillators with energies significantly less than the characteristic vibrational energy of the odorant. This assumption holds since we are interested in the vibrationally assisted electron tunneling stimulated by the odorant. If relevant environmental oscillations become larger or comparable to the oscillations of the odorant, the electron tunneling would be facilitated by the environment and not by the odorant, and the olfactory receptor would become obviously dysfunctional in regard to odorant vibrational frequency discrimination.

Below we discuss all parameters in Eq. (15) in detail, and provide an estimate of their characteristic values.

Parameters of the vibrational theory of olfaction

In order to estimate the tunneling rates 1/τ₀ and 1/τ through Eq. (15) one needs to furnish the five parameters γ, σ, λ, Δε and ε. Here we suggest how these parameters can be estimated and what actual values to expect.

The vibrational frequency ω₀ of the odorant lies typically in the infrared (IR) range, i.e., corresponds to wavelengths of 750 nm − 1 mm. Thus, the associated vibrational excitation energy of the odorant is 0.001 − 1 eV. The actual energy can either be deduced from experimentally measured odorant IR spectra or taken from calculations, as done below for three different odorant molecules (acetophenone, citronellyl nitrile and octanol).

The Huang-Rhys factor, σ, can be estimated once the coupling strengths u_D and u_A between olfactory receptor and odorant are known. To estimate the coupling strengths one determines the electric field generated by the transferred electron localized at either the donor or the acceptor site of the olfactory receptor. The coupling of the odorant molecule with the olfactory receptor arises due to interaction of the odorant with this electric field through the odorant’s intrinsic dipole moment. In the simplest approximation the vibration of the odorant can be treated as a harmonic oscillator with a dipole moment linearly linked to the vibrational coordinate. Due to the presence of an electric field the equilibrium position of the harmonic oscillator is shifted. To calculate the coupling constants u_D and u_A one starts from the harmonic oscillator Lagrangian

$${ℒ}_{\mathit{\text{ocs}}}(\overrightarrow{E})={\displaystyle \sum _{\mu }\frac{1}{2}{\dot{\prod }}_{\mu }^2-\frac{1}{2}{\omega }_{\mu }^2{({\prod }_{\mu }+\sigma {\prod }_{\mu }(\overrightarrow{E}))}^2,}$$ (16)

where Π_µ denote the mass weighted normal vibration coordinates, ω_µ is the vibrational frequency of the µ-th mass weighted normal coordinate, and δΠ_µ(E⃗) represents the shift of the normal coordinate due to the electric field E⃗. The mass weighted normal coordinate shift $(\text{dimension is }\sqrt{\text{mass}}\times \text{length})$ is defined as

$$\delta {\prod }_{\mu }(\overrightarrow{E})={\prod }_{\mu }(\overrightarrow{E})-{\prod }_{\mu }(\overrightarrow{E}\equiv 0).$$ (17)

Once the vibrational spectrum {ω_µ} and the corresponding shifts of the mass weighted normal coordinates δΠ_µ(E⃗) for an odorant are known from ab initio calculations, the coupling strengths can be calculated through [17]

$$u_i(\mu )=-\sqrt{\frac{{\omega }_{\mu }}{2\hslash }\delta {\prod }_{\mu }({\overrightarrow{E}}_i),}$$ (18)

where E⃗_i indicates the electric field generated by the electron at either the donor (i = D) or acceptor (i = A) site of the receptor. The coupling strengths in Eq. (18) are key to define the Huang-Rhys factors σ(µ), i.e., the coupling strength between odorant and receptor in Eq. (15).

The Huang-Rhys factor is defined through Eq. (10), which in turn can be derived if one considers the matrix element 〈ψ_An|H_T|ψ _D0〉 of the Hamiltonian H_T defined in Eq. (5). Here, ψ_in = exp[u_i(a − a^†)]|in〉 is the wavefunction of the system in either the donor (i = D) or the acceptor (i = A) state without involvement of environmental vibrations (c.f. Eq. (6). Evaluating the matrix element for the first (n = 1) excited vibrational state of the odorant, and using the identity, $e^{\alpha a^{†}+\beta a}=e^{\alpha a^{†}}{e}^{\beta a}{e}^{-\frac{1}{2}[\alpha a^{†},\beta a]}$ with α and β being constants, one obtains the Huang-Rhys factor for a particular normal vibrational mode µ

$$\sigma (\mu )=\frac{{(u_D(\mu )-u_A(\mu ))}^2}{\text{exp}[{(u_D(\mu )-u_A(\mu ))}^2]},$$ (19)

where the coupling constants u_A(µ) and u_D(µ) are defined in Eq. (18). Note, that the Huang-Rhys factor is dimensionless; as will be demonstrated below, for typical odorants its value varies in the range 0.0 − 0.35.

The energy difference between donor and acceptor states of the olfactory receptor, Δε, should be comparable to ε in order for the vibrationally assisted mechanism to be functional, since otherwise the electron tunneling process becomes suppressed as can be seen from Eq. (15). Thus, Δε defines the frequency discrimination sensitivity of the olfactory receptor and must assume values in the range 10⁻³ eV − 1 eV. It is known that the number of different human olfactory receptors is large, namely about 347 [18]. Thus, a range of energy differences Δε should arise in different olfactory receptors. In the following, we treat Δε as a continuous variable within the stated range. We note, however, that shape selectivity could reduce drastically the number of receptors available for a certain odorant type.

The calculation of the hopping integral between donor and acceptor states of the olfactory receptor, γ, that arises in Eq. (15) is not trivial, since it is almost impossible to define a localized wavefunction for a donor and one for an acceptor in a system as complicated as the olfactory receptor; furthermore, the structure of the receptor is unknown and different methods for electronic-structure calculation do not provide consistent results when dealing with large biomolecules. However, since both electron tunneling rates 1/τ₀ and 1/τ are proportional to γ², the exact value of γ is not crucial for knowledge of the relative enhancement τ₀/τ of the electron tunneling rate.

An approximate value of γ can be estimated if one assumes that an olfactory receptor with E_D = E_A permits electron tunneling without the presence of an odorant. Expecting the size of the olfactory binding pocket to be ~ 5–15 Å [4], the tunneling rate should be about 10⁸ s⁻¹ as seen in photosynthetic redox proteins [19]. This rate value leads to an estimate of γ = 0.001 eV, which agrees with the value suggested in [4]. We note that for γ ≫ 0.001 eV, electron tunneling through the receptor is expected to occur very fast, e.g., on a picosecond time scale; for γ ≪ 0.001 eV, electron tunneling is occurring slow; in either case the relative enhancement of the electron tunneling rate, τ₀/τ, is not affected.

The reorganization energy λ cannot be stated precisely at present, again due to lack of a structure of the olfactory receptor. However its value is expected to lie in the range 0.03 – 0.05 eV, as reported for the photosynthetic reaction center of the bacterium Rhodobacter capsulatus; the latter protein complex exhibits electron transfer reactions in a hydrophobic environment similar in this regard to an olfactory receptor [4, 20]. A more rigerous treatment of electron transfer governed by Hamiltonians (1)–(5) in the photosynthetic reaction center is provided in [13].

Calculations of infrared spectra

The vibrational spectrum of the odorant molecules, characterized by a set of frequencies {ω_k} along with the associated mass weighted normal coordinates and electron transfer-induced equilibrium position shifts δΠ_i(µ), have been calculated for the present study using the Gaussian 09 quantum chemistry package [21]. We have carried out the respective calculations, determining also the IR intensities for all vibrations. Vibrations with the strongest IR intensities are accompanied by a significant change of dipole moment leading to a change in the corresponding normal coordinate due to an electric field and, therefore, should also be prominently involved in the vibrationally assisted mechanism of olfaction.

To determine vibrational properties of the three different odorant molecules of interest (acetophenone, citronellyl nitrile and octanol) we have used density functional theory based on the hybrid Becke-type three parameter exchange functional [22–25] paired with the gradient corrected Lee, Yang, and Parr correlation functional (B3LYP) [24–27]. We have utilized the 6-311+G(d) basis set of primitive Gaussian functions to expand the molecular orbitals in our computations [24]. The structures of odorant compounds were optimized using the B3LYP method and a standard vibrational analysis of the stable configurations was then performed.

Results

In the following the feasibility of the vibrationally assisted mechanism of olfaction is demonstrated. The key quantity for judging this mechanism is the electron tunneling rate 1/τ, defined in Eq. (15), which depends on several physical parameters describing intermolecular interactions in the system. We discuss the dependence of 1/τ on these parameters and determine them, where possible, through quantum chemistry calculations.

Odorant vibrational spectra

According to Eq. (15), the interaction of an odorant with the receptor, described through the Huang-Rhys factor σ, is key for the vibrationally assisted mechanism of olfaction. The Huang-Rhys factor can be calculated through Eq. (19), once the coupling strengths u_D and u_A are known. The coupling strengths can be evaluated, in turn, using Eq. (18) and depend on the vibrational spectrum of the odorant. The vibrational spectra for three odorant molecules of interest (acetophenone, citronellyl nitrile and octanol) were calculated using the ab initio density functional theory B3LYP/6-311+G(d) method.

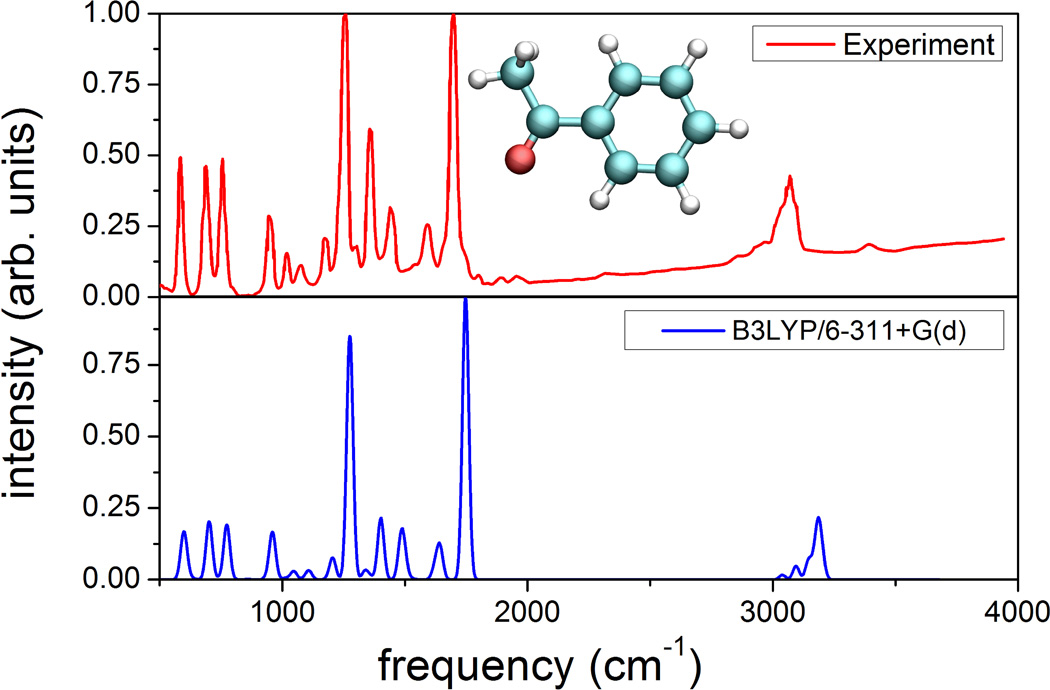
To demonstrate the accuracy of the theoretical method used for vibrational spectra calculation, Fig. 2 compares calculated and measured [28, 29] IR spectra for acetophenone. As expected from prior applications of B3LYP functionals to vibrational studies [30], all major experimentally resolved IR active vibrations are correctly described in the calculation; calculated and measured vibrational frequencies show almost perfect agreement, while in case of relative IR intensities the agreement is less accurate, but qualitatively satisfactory. The performed comparison clearly demonstrates that B3LYP/6-311+G(d) is a reliable method for calculation of vibrational spectra and, therefore, is employed in the further analysis.

Figure 2. Calculated and measured IR spectra.

Comparison of the measured infrared spectrum (top) for acetophenone [28, 29], the structure of which is shown in the inset, and the spectrum calculated from ab initio density functional theory as outlined in Methods.

Tunneling rate in the olfactory receptor

To calculate the coupling coefficients of odorant vibrations to olfactory receptor electron transfer, defined in Eq. (18), the electric field change created by the electron needs to be evaluated. The electric field at the odorant binding pocket is expected to be about 0.01 au. This characteristic field strength had been suggested earlier [4] and is arrived at, for example, if one considers a Zn⁺⁺ cation 15.4 Å away from the NE2 atom of a histidine residue; we note that histidine and zinc are discussed as putative electron donor-acceptor partners in the receptor [31]¹. Calculating the average electric field created between the Zn⁺⁺ cation and a histidine residue results in a value of 0.01±0.002 au, i.e., a value close to one estimated in [4]. Approximately the same electric field strength is obtained in an all-atom receptor model derived through homology modeling at the site of the putative odorant binding². For the stated electric field strengths the Huang-Rhys factor σ can be calculated directly using Eq. (19).

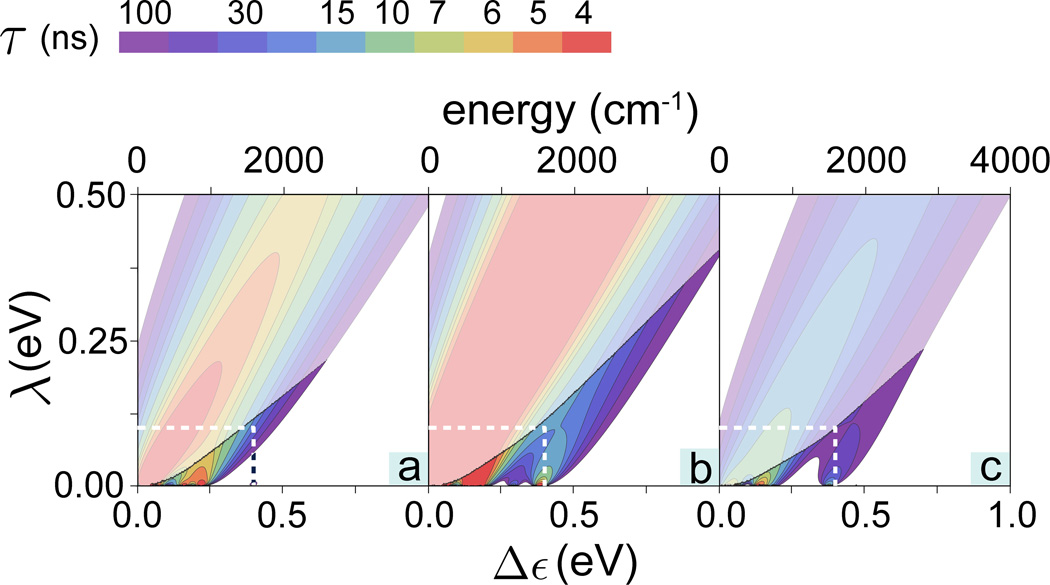
Using the Huang-Rhys factors, thus obtained, the electron tunneling rate 1/τ was calculated according to Eq. (15), assuming room temperature (T = 300 K). To characterize vibrationally assisted tunneling, the tunneling rate was calculated as a sum over individual rates for all vibrational modes of the odorants. Thus, the contour plots in Fig. 3 show the total electron tunneling rate 1/τ calculated as a function of the energy difference Δε and the reorganization energy λ for acetophenone, citronellyl nitrile and octanol. The typical times for intrinsic electron tunneling in biological systems occurring on a length scale of 5–15 Å are 10–100 ns [19, 32–35]. Accordingly, Fig. 3 shows only rates for which tunneling occurs faster than 100 ns.

Figure 3. Electron tunneling rates in an olfactory receptor.

Contour plots showing the calculated electron tunneling rates as a function of energy difference Δε and reorganization energy λ for (a) acetophenone, (b) citronellyl nitrile and (c) octanol. For convenience the color-code indicates the characteristic tunneling times of the electron in the receptor, i.e., the inverse of the tunneling rate. The endashed rates are shown in Fig. 4 in greater detail. The faded colors indicate regions where the inelastic tunneling rate 1/τ falls below the elastic tunneling rates, 1/τ₀.

The rates 1/τ for the three odorants studied, shown in Fig. 3a–c, behave similarly, although the maximal tunneling rates are slightly different. However for reorganization energies λ ≳ 0.5 eV, the tunneling rate shows only a weak dependence on the energy difference Δε, with a single peak at Δε ≈ 0.5 eV for all studied odorants. This λ-range renders then the vibrationally assisted mechanism impractical for resolving different odorant compounds, as all of them will act similarly on the receptor. This behavior can be readily understood from Eq. (15) where the key parameters involved in odorant recognition, Δε and ε, are accompanied by λ in the critical factor 1/τ ~ exp[−(Δε − ε − λ)²/4k_BTλ]. This factor shows that in case of λ ≈ Δε, ε the (Δε − ε) – dependence is washed out. In order to distinguish between different odorants through the vibrationally assisted mechanism, an olfactory receptor needs to adopt reorganization energy values λ ≪ Δε, ε, i.e., adopt values well below 0.1 eV. This condition has been already noted above.

A related argument for λ needing to be small to render a receptor functional arises from the requirement that the inelastic tunneling rate 1/τ has to be larger than the elastic tunneling rate 1/τ₀. If the inelastic tunneling falls below the elastic rate, i.e., for 1/τ < 1/τ₀, the receptor is actually insensitive to the respective odorant vibration. Figure 3 indicates the (Δε,λ)-regions where 1/τ is larger than 1/τ₀.

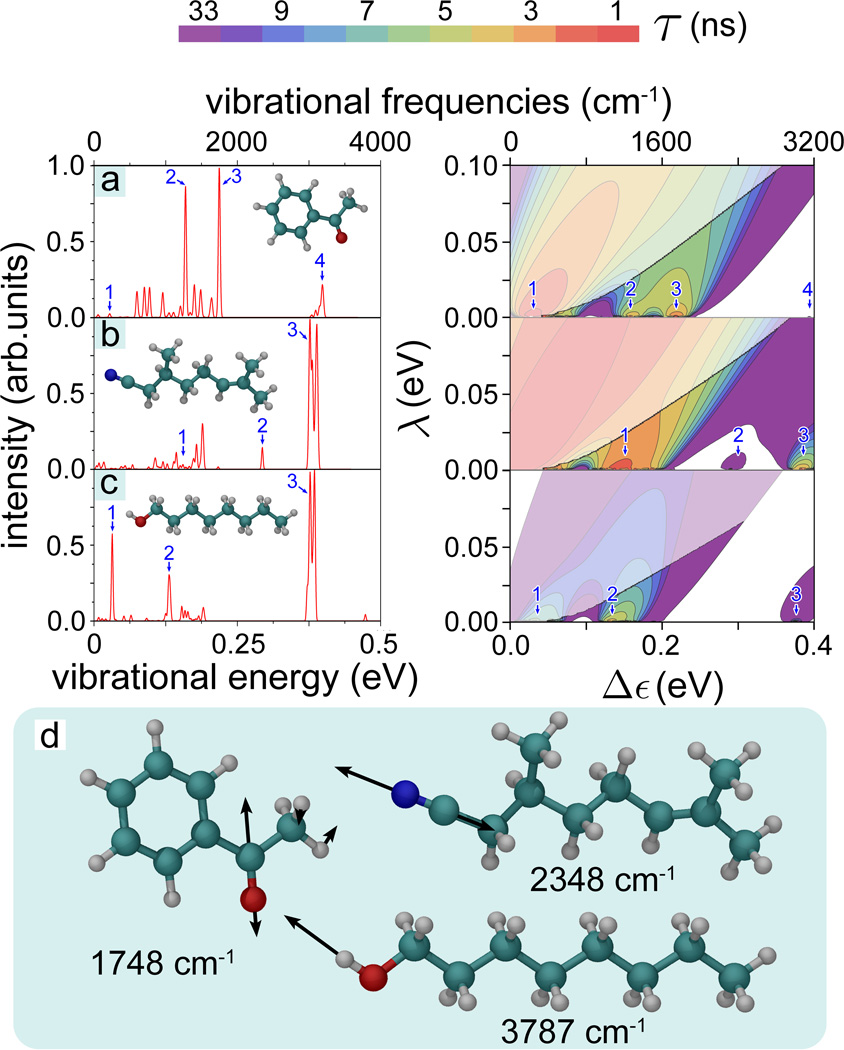
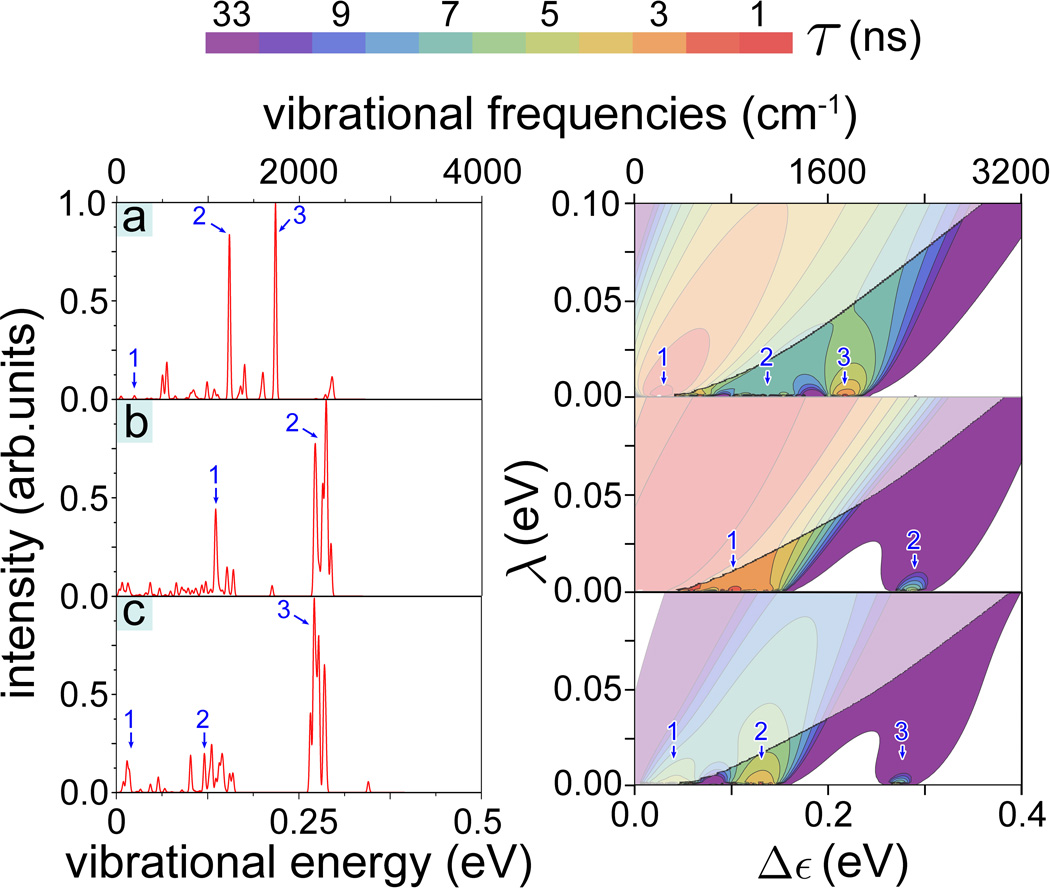
Figure 4 illustrates the differences in 1/τ calculated for acetophenone, citronellyl nitrile and octanol presenting 1/τ evaluated in the (λ, Δε)-range [0 ≤ λ ≤ 0.1 eV, 0 ≤ Δε ≤ 0.4 eV]. The 1/τ maxima at certain Δε values are related to the characteristic vibrational frequencies of the odorants. Thus, for example, citronellyl nitrile vibrations labeled 2 and 3 in Fig. 4b correspond to the maxima of the electron tunneling rate at Δε₂ = 0.29 eV and Δε₃ = 0.38 eV, respectively. Further inspection of Fig. 4 reveals that the energy dependence of the tunneling rate reflects the key IR active vibrations for the three studied odorants and, obviously, recognition of the odorants through the vibrationally assisted electron tunneling mechanism is feasible. The Huang-Rhys factor, describing the odorant-receptor coupling, is a critical parameter for this recognition; Tab. 1 lists the Huang-Rhys factors for the selected normal vibrations labeled in Fig. 4 in order to demonstrate the factor’s characteristic values and variation.

Figure 4. IR spectra and electron tunneling rates.

(Right) Contour plots of the calculated electron tunneling rates shown as a function of the energy difference 0 ≤ Δε ≤ 0.4 eV and reorganization energy 0 ≤ λ ≤ 0.1 eV for (a) acetophenone, (b) citronellyl nitrile and (c) octanol. The rates shown are taken from Fig. 3. For convenience the color-code indicates the characteristic tunneling times of the electron in the receptor, i.e., the inverse of the tunneling rate. The faded colors indicate regions where the inelastic tunneling rate 1/τ falls below the elastic tunneling rates 1/τ₀. (Left) Calculated normalized IR spectra for the three odorants with structures shown in the insets. Numbers 1, 2, 3, 4 label in the left and right panels corresponding IR vibrations. (d) Illustrative high-frequency vibrations in acetophenone, citronellyl nitrile and octanol involving odorant side-groups. The vibrational energies are indicated below the corresponding odorant molecule.

Table 1. Huang-Rhys factors for selected odorant vibrations.

Listed are vibrational frequencies and the corresponding Huang-Rhys factors for selected odorant vibrations labeled in Fig. 4, calculated for acetophenone, citronellyl nitrile and octanol.

Odorant	Peak label	Frequency (cm−1)	Huang-Rhys factor (σ)
Acetophenone	1	218	0.187
	2	1275	0.031
	3	1747	0.048
	4	3188	0.002
Citronellyl nitrile	1	1241	0.055
	2	2347	0.008
	3	3013	0.012
Octanol	1	255	0.007
	2	1050	0.026
	3	3015	0.010

It is worth noting that enhancement of the tunneling rate is not directly related to the IR intensity of the corresponding vibrations. Although, as can be discerned from Fig. 4, high values of the tunneling rate correspond to highly active IR vibrations, some non-active vibrations also assist electron tunneling. A strong enhancement of the tunneling rate is seen, for example, for citronellyl nitrile at Δε₁ = 0.154 eV, while the corresponding vibration of the molecule is barely IR active. What matters to make a vibration recognized through electron transfer is a sufficiently large σ value, which turns out to be 0.055 for that particular normal vibration (see Tab. 1). Figure 4 illustrates that although for some odorants (acetophenone, octanol) strong enhancement of the tunneling rates are expected for Δε < 0.1 eV, these tunneling rates are still smaller than 1/τ₀. Therefore, increases of 1/τ at low Δε are irrelevant for a vibrationally assisted mechanism of olfaction.

Isotope effect

Deuteration affects the vibrational frequencies of odorants due to substitution of hydrogen by the heavier deuterium. Deuteration offers an important test for the vibrationally assisted mechanism of olfaction as deuteration does not affect the surface properties of odorants. The electron tunneling rates for three deuterated odorants (acetophenone, citronellyl nitrile and octanol) were calculated with the approach described above. The dependencies of the electron tunneling rate on Δε and λ are shown in Fig. 5. The figure demonstrates that enhancement of this rate arises at different Δε values as compared to the non-deuterated odorant compounds. The shift of the peaks in the electron tunneling rates is due to the shift of the IR active odorant vibrations caused by deuteration (compare Fig. 4 and Fig. 5). The correspondence of some peaks in the IR spectra for the three odorants to enhancement of 1/τ in Fig. 5 is highlighted through the labels 1, 2 and 3.

Figure 5. IR spectra and electron tunneling rates for deuterated odorants.

IR spectra and electron tunneling rates calculated for deuterated (a) acetophenone, (b) citronellyl nitrile and (c) octanol. The presentation is analogous to that in Fig. 4.

An important result is observed for one particular vibrational mode in deuterated octanol (see Fig. 5c) and non-deuterated citronellyl nitrile (see Fig. 4b), where the increase of the electron tunneling rate occurs in either case around Δε ~ 0.29 eV (see peak 2 in Fig. 4b and peak 3 in Fig. 5c). The match of the electron tunneling rate at a certain vibrational frequency for two different odorants suggests that both odorants could activate the same olfactory receptor, namely the one tuned to detect this specific vibration, as long as odorants have both the proper shape. The enhancement of the tunneling rate at 0.29 eV (vibrational frequency of 2257 cm⁻¹) for deuterated octanol and non-deuterated citronellyl nitrile is in agreement with a recent experimental study performed on Drosophila melanogaster [10], where the authors reported that fruit flies react differently to natural octanol and citronellyl nitrile, while they show similar behavior if exposed to deuterated octanol and non-deuterated citronellyl nitrile. The authors in [10] related their observation to a shift of the coupled C-H stretch vibrations in deuterated octanol from ~3000 cm⁻¹ to ~2150 cm⁻¹, i.e., a wavelength at which citronellyl nitrile also experiences vibrations. Our calculations, yielding electron tunneling rates of 3 × 10⁷ s⁻¹ for both odorants at this frequency, support the experimental interpretation. The Huang-Rhys factor for the vibration of deuterated octanol at 2168 cm⁻¹, listed in Tab. 2, is about twice as large as the Huang-Rhys factor for the vibration of citronellyl nitrile at 2347 cm⁻¹ (see Tab. 1); indeed, at this particular frequency the tunneling rate for deuterated octanol is higher than the tunneling rate for citronellyl nitrile.

Table 2. Huang-Rhys factors for selected vibrations in deuterated odorants.

Listed are vibrational frequencies and the corresponding Huang-Rhys factors for selected normal vibrations labeled in Fig. 5, calculated for deuterated acetophenone, citronellyl nitrile and octanol.

Odorant	Peak label	Frequency (cm−1)	Huang-Rhys factor (σ)
Deuterated acetophenone	1	198	0.195
	2	1238	0.016
	3	1742	0.052
Deuterated citronellyl nitrile	1	1087	0.013
	2	2175	0.008
Deuterated octanol	1	119	0.010
	2	964	0.021
	3	2168	0.018

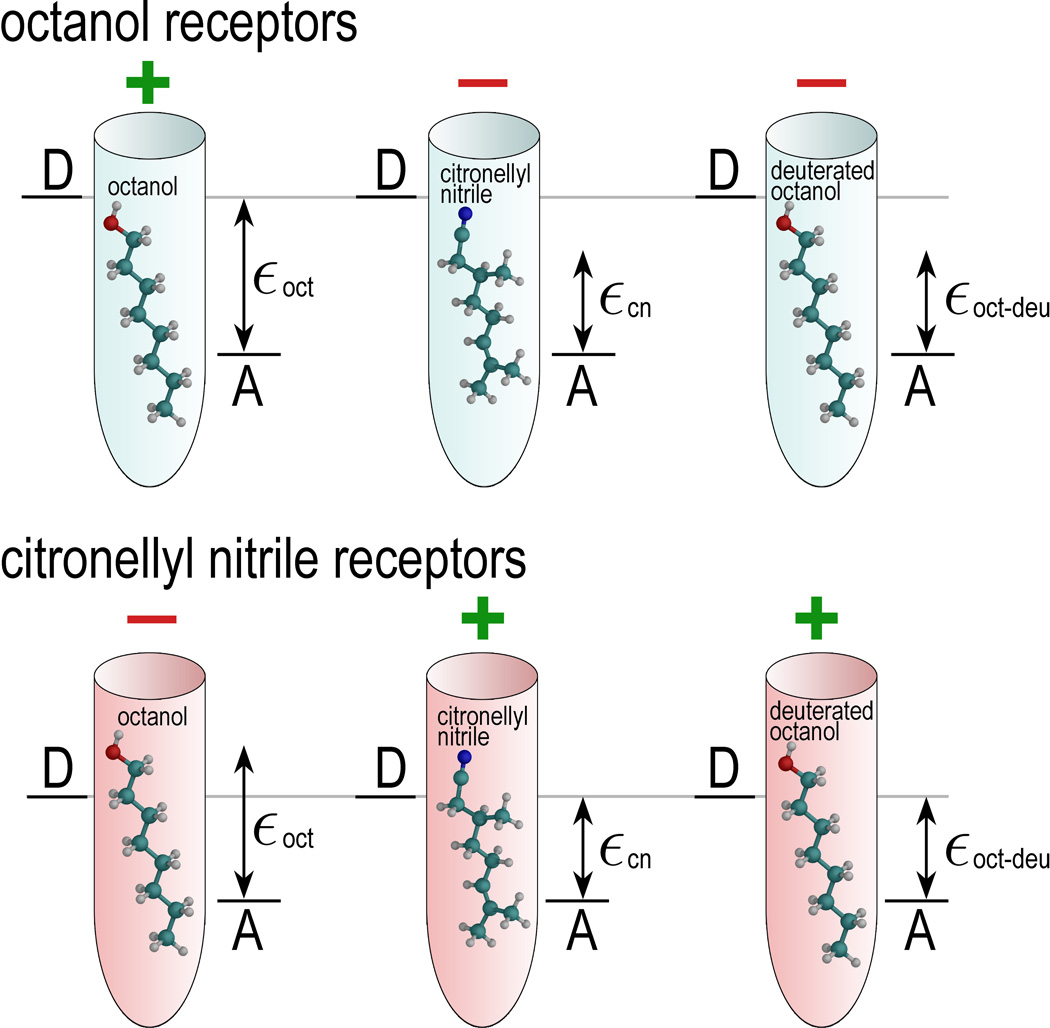
Figure 6 demonstrates the principle of odorant discrimination through shape and vibrational frequencies and, in particular, illustrates the similarity between deuterated octanol and non-deuterated citronellyl nitrile. Shape is a decisive factor to link odorants to a particular receptor. Figure 6 illustrates two types of odorant receptors, chosen to detect either octanol (light blue cones) and citronellyl nitrile (pink cones). Since the size of octanol and citronellyl nitrile is similar (the molecules have a length of about 11 Å, and are about 3–4 Å in diameter), both receptors could likely accommodate either molecule. Thus, the octanol and citronellyl nitrile can be recognized only through the vibrationally assisted electron transfer mechanism if the octanol (citronellal nitrile) receptor exhibits a Δε value characteristic for an octanol (citronellal nitrile) vibrational energy quantum, thereby enhancing the electron tunneling rate in the octanol receptor through the presence of octanol, and similarly in the citronellyl nitrile receptor through the presence of citronellyl nitrile.

Figure 6. textbfDiscrimination of deuterated odorant.

Illustrated is here the principle of odorant discrimination through shape and vibrational frequency. Octanol receptors (light blue) and citronellyl nitrile receptors (pink) accommodate octanol, citronellyl nitrile, and deuterated octanol. Since the shape of octanol and citronellyl nitrile is similar, both odorants fit into either receptor. The receptors possess different Δε, i.e., the energy between the donor state D and acceptor state A, tuned to a certain vibration of the odorant. The ability of a receptor to respond to odorant binding is denoted with a green “+” sign, while the red “−” sign shows that the receptor is passive to the corresponding odorant binding. The characteristic vibrational energy of octanol, citronellyl nitrile, and deuterated octanol are denoted as ε_oct, ε_cn, and ε_oct−deu, respectively.

Figure 6 illustrates also how electron transfer through the receptor is affected by deuteration. Deuteration of octanol decreases the vibrational frequency of some vibrational modes, and certain modes become energetically close to a vibrational mode in citronellyl nitrile. This results in the mismatch of the vibrational energy ε_oct−deu with Δε of the octanol receptor, but in a match of this energy to the Δε value of the citronellyl nitrile receptor such that deuterated octanol activates the citronellyl nitrile receptor.

Discussion

We have demonstrated that the vibrationally assisted mechanism of olfaction is feasible in olfactory receptors. Underlying this mechanism is electron tunneling, which has been modeled accounting for the key physical interactions in a receptor-odorant complex. We validated the vibrationally assisted mechanism of olfaction, suggested in [3, 4], through analysis of physical constraints imposed on the receptor and demonstrate that the vibrationally assisted electron transfer mechanism is feasible for a receptor reorganization energy λ in the range λ ≤ 0.1 eV and for an energy difference between receptor electron donor and acceptor states of Δε ≤ 1 eV, as well as a hopping integral γ of ~ 0.001 eV.

The expected values of the physical parameters which govern vibrationally assisted tunneling are summarized in Tab. 3. Given these parameters we have calculated the rates of electron tunneling in the olfactory receptor induced through odorant binding for three different odorant molecules (acetophenone, citronellyl nitrile and octanol). The results, in the case of favorable odorant-receptor interaction parameters, yield electron tunneling rates 1/τ as large as 10⁸ − 10⁹ s⁻¹, which corresponds to time scales typical for a sensory biological system [19, 32–35].

Table 3. Parameters of the vibrationally assisted mechanism of olfaction.

Listed are values of the five physical parameters Δε, ε, λ, σ, and γ expected for an odorant bound to an olfactory receptor to enable vibrationally assisted electron tunneling. The physical meaning and supporting references for each parameter are indicated. The range of values for the Huang-Rhys factor is estimated from our study of three odorants (acetophenone, citronellyl nitrile and octanol), and, in principle, can be wider for other odorant compounds.

param.	physical meaning	expected values	how estimated	role in mechanism
Δε	energy difference between donor and acceptor states in olfactory receptor	0 – 1 eV	matches odorant vibrational excitation energies; see Eq. (12)	selectivity filter for odorant vibrations
ε	odorant vibrational energy added to electron transfer	0 – 1 eV ε ≈ Δε	obtained from ab initio calculations; see Eq. (13)	discriminates vibrational fingerprint of an odorant
λ	general coupling of electron transfer to bath modes	0 – 0.1 eV λ ≪ ε, Δε	generalized from Rhodobacter capsulatus consistent with [4, 20]; see Eq. (11)	smears out detection of individual odorant vibrations
σ	coupling of odorant vibrations to electron transfer, Huang-Rhys factor	0 – 0.35	obtained from ab initio calculations; see Eq. (10)	enhances recognition of particular vibrations
γ	intrinsic strength of receptor electron transfer	~ 10−3 eV	estimated based on general assumptions; consistent with [4]	defines time scale of odor-free electron tunneling

Through comparison of calculated IR spectra and calculated vibrationally assisted electron tunneling for acetophenone, citronellyl nitrile and octanol we revealed a striking correspondence of characteristic vibrational modes in the IR spectra and enhancement of electron tunneling rates. The result leads us to conclude that due to differences in their vibrational spectra diverse odorants can selectively excite different olfactory receptors. Thus, the vibrationally assisted mechanism of olfaction provides a natural explanation how diverse odorants lead to different olfactory stimuli in animals, namely through a combination of surface properties recognition by receptor binding sites and vibrational frequency recognition through odorant assisted electron transfer. It is worth noting that the approach used here for studying odors of acetophenone, citronellyl nitrile and octanol can be applied to other molecules, revealing further odor-specific vibrations, which can then be tested in behavioral experiments, similarly to the study performed in [10].

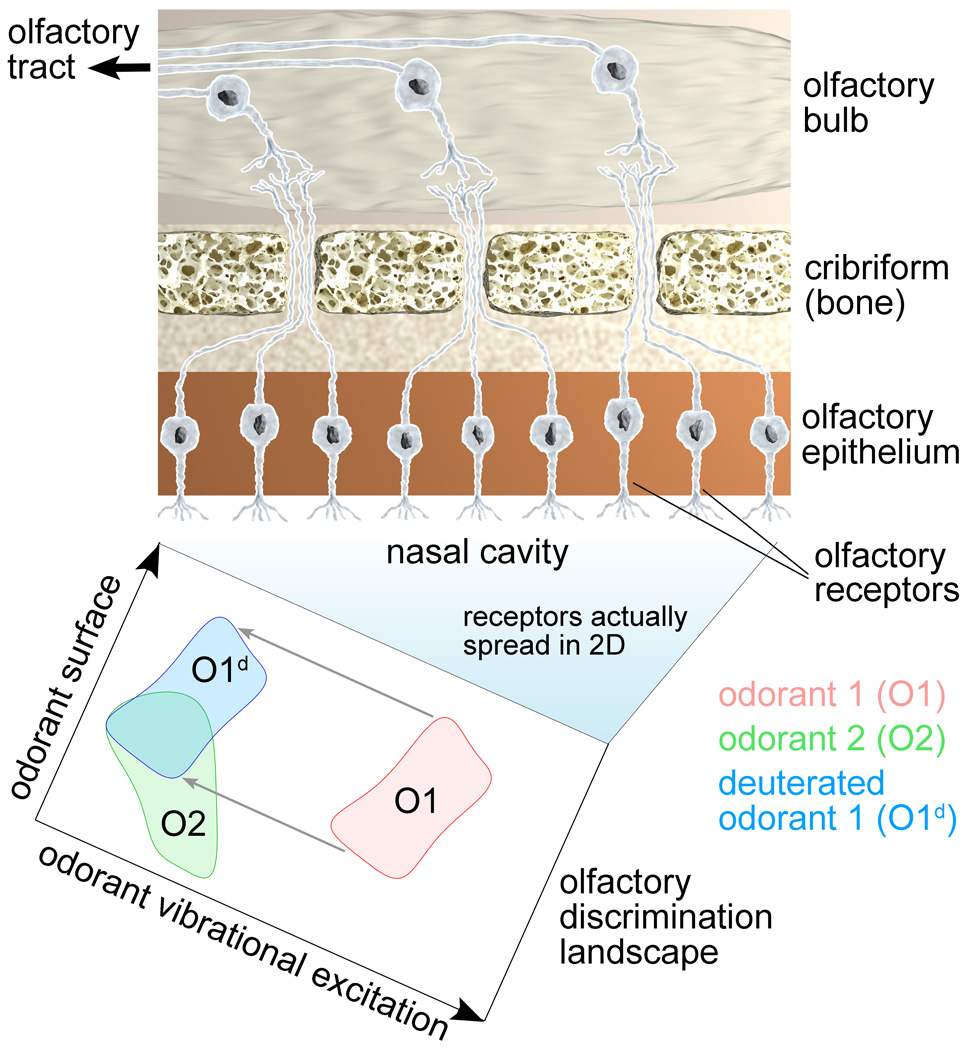
According to our suggestion the hundreds to thousands [18] of different olfactory receptors in an animal recognize odorants over a discriminant landscape with surface properties and vibrational spectrum as the two major dimensions. Figure 7 illustrates this idea by showing the olfactory discrimination landscape for two different odorants (red and green domains), acting on different receptors in the olfactory epithelium. Each odorant is attributed a certain activation domain on the olfactory discrimination landscape, i.e., a pattern which encircles generalized coordinates describing odorant’s surface properties and vibrational excitations recognized by receptors in the olfactory epithelium.

Figure 7. Olfactory discrimination landscape.

(Top) Schematic illustration of a part of the olfactory system consisting of olfactory epithelium, cribriform and olfactory bulb, responsible for detecting different odors. The olfactory receptors shown aligned in a row are actually spread over the two-dimensional nasal cavity. The cavity, through the different receptor properties, becomes an olfactory discrimination landscape. (Bottom) Schematic illustration of the olfactory discrimination landscape demonstrating odorant recognition through a combination of surface properties and vibrational excitations. Each odorant, a point in the x, y-plane surrounded by a neighborhood, is attributed an activation domain on this landscape, as illustrated for two examples (red and green domains). Odorant deuteration corresponds to a domain-shift along the odorant vibrational excitation coordinate (blue domain).

For an experimental verification of the vibrationally assisted mechanism of olfaction one should carry out studies of odorants with identical (or similar) surface properties inducing different responses in the olfactory system. Figure 7 illustrates how deuteration affects the olfactory discrimination landscape by shifting the odorant-specific activation domains along the odorant vibrational excitation coordinate (blue domain). The figure illustrates that in some cases deuteration leads to an overlap of activation domains for deuterated and non-deuterated odorants (see O2 and O1^d domain overlap in Fig. 7), thereby making odorant 2 receptors to become activated by deuterated odorant 1.

Above we demonstrated how deuteration of acetophenone, citronellyl nitrile and octanol impacts the electron tunneling rate through the olfactory receptor, i.e., we showed that the mechanism illustrated in Fig. 7 can occur in real systems. The deuteration-induced shift of odorant vibrational energies suggests a more general probe of the vibrationally assisted mechanism of olfaction, as artificial odorants with specific properties (i.e. similar vibrational bands) can be engineered to stimulate only specific olfactory receptors. Thus, through IR spectrum calculation (as done in the present study) one can propose specific compounds which are worth pursuing experimentally in behavioral studies, revealing odor selectivity.

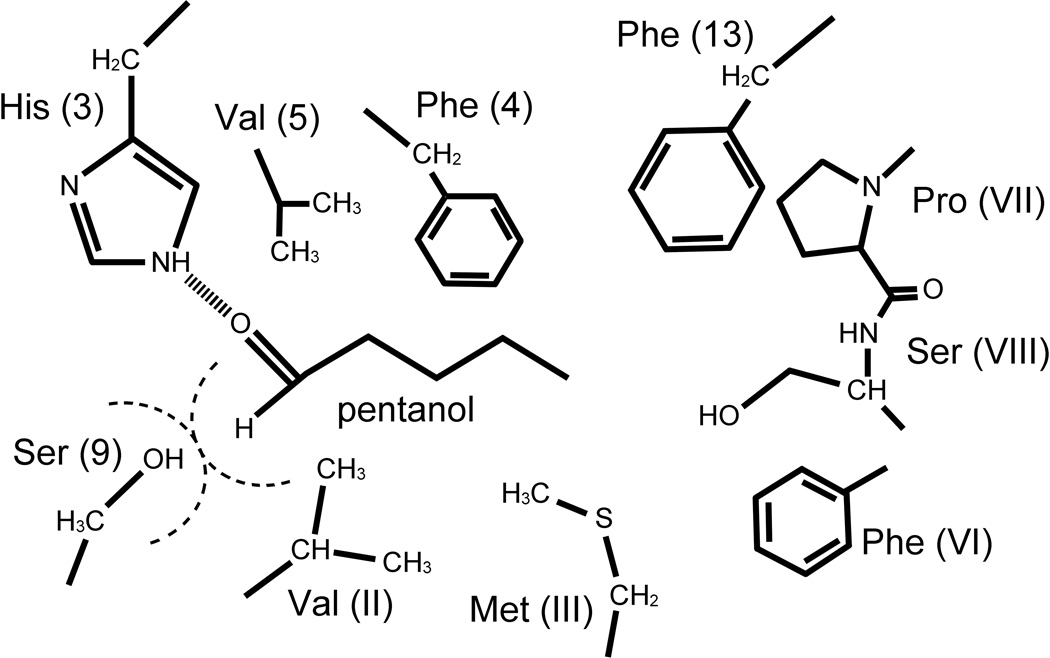
Although much speaks for the feasibility of the vibrationally assisted mechanism of olfaction, the fundamental mechanism depends on the atomic scale structure of the olfactory receptor and on an electron transfer process involving the odorant binding site. So far, structures for olfactory receptors have not been resolved crystallographically [36, 37], though structures of other G-protein coupled receptors are available [38–41]. Based on the available structures, models of olfactory receptors have been built, mainly by Goddard and coworkers [42–45], but also by others [46, 47]. In fact, models for a variety of odorants and receptors of different organisms were constructed; recently even automated modeling of mammalian olfactory receptors and docking of odorants has been reported [48]. A typical odorant binding site is illustrated in Fig. 8 that shows the types of amino acid sides groups in the immediate vicinity the an odorant. From the perspective of the vibrationally assisted electron transfer mechanism the presence of phenylalanine, tyrosine, and histidine side chains is of interest as they may serve as electron donor-acceptor partners. As illustrated in Fig. 4d, the high frequency modes are localized in the odorant and coupling to electron transfer can be achieved through direct contacts, e.g., hydrogen bonding with appropriate amino acid side chains.

Figure 8. Olfactory receptor binding site.

Putative binding site of an olfactory receptor around pentanol. The model is constructed based on homology modeling and site-directed mutagenesis experiments (Paolo Carloni, private communication).

The vibrationally assisted electron transfer mechanism requires provision of an electron. In this regard we note the suggestion that some olfactory receptors are actually metalloproteins involving, for example, zinc or copper ions, ligated to a receptor near its odorant binding site after odorant binding [31, 49]. The possible binding sites for the metal ions have been suggested, for example in [31], but will remain uncertain until the atomic-scale structure of the receptor is resolved. The idea that metal ions are involved in olfaction is very attractive, as such ions could readily function as a source for transferred electrons.