MANIFOLD LEARNING FOR ANALYSIS OF LOW-ORDER NONLINEAR DYNAMICS IN HIGH-DIMENSIONAL ELECTROCARDIOGRAPHIC SIGNALS

Abstract

The dynamical structure of electrical recordings from the heart or torso surface is a valuable source of information about cardiac physiological behavior. In this paper, we use an existing data-driven technique for manifold identification to reveal electrophysiologically significant changes in the underlying dynamical structure of these signals. Our results suggest that this analysis tool characterizes and differentiates important parameters of cardiac bioelectric activity through their dynamic behavior, suggesting the potential to serve as an effective dynamic constraint in the context of inverse solutions.

1. INTRODUCTION

There are several current clinical and research problems in which improved automated analysis of multichannel cardiac electrical recordings would be desirable. One example is deducing propagation parameters and tissue health from multi-electrode catheter electrograms during cardiac intervention procedures. Another is the inverse problem of electrocardiography, that is, localizing features of cardiac electrical activity from recordings by body surface electrodes or non-contact intra-chamber probes. A third is improving our understanding of the basic electrophysiology of disease states such as myocardial ischemia.

One major source of information in such recordings is the dynamical structure embedded in relationships between time waveforms, which stems from the electrophysiological constraints of cardiac bioelectric behavior. In particular, with data simultaneously recorded from many electrodes (typically 10’s to 100’s of electrodes may be used), the high data dimension can obscure lower-dimensional dynamical structure stemming from these constraints. Mapping (i.e. visualizations of these signals mapped to computer representations of the original anatomical surfaces) is commonly used to inspect and visually analyze the recorded data for such interdependencies. However, visual inspection is inherently subjective, and because of intrinsic variability in patterns from beat to beat, condition to condition, and individual to individual, it is a considerable challenge to identify subtle differences across multiple recordings.

In this paper, we start from the supposition that these signals follow trajectories traversing a much lower-dimensional nonlinear manifold in the measurement signal space. In particular, it is well known that electrical activity of the heart can be modeled by nonlinear reaction-diffusion partial differential equations (PDE) [1]. Our assumption of manifold behavior in the measured signals derives from this fact, but we avoid positing and solving an explicit PDE model. Instead we present an application of an existing data-driven technique for manifold identification and show how it can be used to reveal electrophysiologically significant changes in the underlying dynamics. We note that linear methods – mainly principal component analysis (PCA) – have long been used to extract dominant features of cardiac map data [2, 3], but are intrinsically unable to capture the nonlinear features that are critical to cardiac electrophysiology (e.g. refractory periods imply intersecting cardiac wavefronts annihilate rather than superimpose). A more recent example of a linear approach is the Isotropy method [4], which assumes statistical separability of spatial and temporal behavior and then uses a linear decomposition to find the dominant basis of the temporal correlation on the heart directly from body surface potentials.

In contrast, the method presented here directly identifies the dominant underlying nonlinear structure. Although there is no guarantee that this structure is electrophysiologically meaningful, we believe that the results we present here provide convincing initial evidence that this approach may be a compact and powerful way to identify those dynamics. We suggest that this method is not only useful in its own right to characterize and distinguish important aspects of cardiac bioelectric activity, but has the potential to serve as an effective dynamic constraint in the context of inverse solutions.

2. BACKGROUND AND METHODS

We first establish our nonlinear dynamical systems model, then describe the manifold learning algorithm employed and how we use it to reveal cardiac dynamics.

2.1. Nonlinear Dynamical Systems

We start with a combined model for time-variation of cardiac electrical potentials and observations on a remote surface (for convenience here we assume this is the outer surface of the body) using a standard nonlinear state-space formulation:

$$\stackrel{.}{x}(t)=f(x(t))$$ (1)

$$y(t)=Ax(t)+\eta (t)$$ (2)

where x describes the state of the electrical potentials on the relevant heart surface at any time t, f(·) describes their time evolution as governed by cardiac electrophysiology, A contains a numerical solution to Laplace’s Equation (the relevant PDE) and is thus the “forward model” relating heart surfaces potentials to body surface measurements, and η is IID noise. A is ill-conditioned as a consequence of the ill-posedness of the associated inverse problem [5]. Similar models have been used in the context of Kalman filtering approaches, either with a linear state evolution model [6, 7] or with our own group’s Wavefront Based Curve Reconstruction method [8]. However here, rather than posit an explicit state evolution model, we infer its dynamic properties from the differential geometric structure of heart surface or body surface measurements.

Since f defines a nonlinear dynamical system, if f is a diffeomorphism, then at each time instant the heart signals lie on a smooth manifold such that x(t) ∈ ⊆ ℝ^N. Despite A being ill-conditioned, if it is also a diffeomorphism, then the torso signals (perturbed by noise) also lie near a smooth manifold 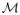⊆ ℝ^M.

2.2. Manifold Dynamics using Laplacian Eigenmaps

In recent years, the problem of learning manifolds from data has been an active area of research. Here we use a well-known method called Laplacian eigenmaps for this purpose [9]. Specifically, given a set of points $P={\{p_k\}}_{k=1}^K$, we have implemented the following version of this algorithm:

1. Calculate a matrix of pairwise distances between points R_i,j = ||p_i − p_j||₂ and choose a tuning parameter, σ (here set equal to the mean of R’s lower triangle).

2. Calculate a matrix $W_{i,j}=exp(-R_{i,j}^2/{\sigma }^2)$ and a degree matrix D = diag(Σ_i W_i,:) (where W_i,: denotes the i-th row of W).

3. Solve for the singular value decomposition of D⁻¹W = USV′. The columns of V are the new coordinates for the input points. That is: row i of V contains the Laplacian eigenmaps coordinates of the point p_i.

The singular values rank the significance of the new coordinates. The first column is typically discarded because it is constant. Here we refer to coordinates starting from the second column of V as the “relevant coordinates”.

To apply this method to high-dimensional cardiac electrical signals, measured either on the surface of the heart or on the surface of the torso, we simply define our points P as a collection of K time samples pooled across multiple beats. That is, for heart surface measurements we use $P={\{x(t_k)\}}_{k=1}^K$, and for body surface measurements we use y(t_k) instead of x(t_k). In what follows, we report our results by visualizing the first three relevant coordinates of the resulting Laplacian eigenmaps. In general, it may be useful to include more than just the first three in an analysis. Since we can trace each point on the manifold to its pre-image in the measurements, we can easily isolate subsets of P, such as recordings from a particular heartbeat or pacing site.

3. EXPERIMENTS

For our experiments, we applied our analysis technique to two datasets, one recorded on the ventricular surface of a canine heart, and the other on the torso of a human subject.

3.1. Heart Surface Signals

We analyzed electric potentials measured on the surface of a canine heart at the Cardiovascular Research and Training Institute (CVRTI) at the University of Utah. In this experiment, the electric potentials were recorded (1000 Hz sampling rate) from 247 “sock electrodes” that were wrapped around the ventricles of an in situ canine heart which was paced by electrically stimulating the right atrial appendage. After an initial rest period, 10 sequential ischemia interventions were conducted, each by total occlusion of blood flow in the left anterior descending artery, inducing supply ischemia, each followed by a recovery period. The duration of interventions increased as the experiment progressed. A total of 315 beats were analyzed.

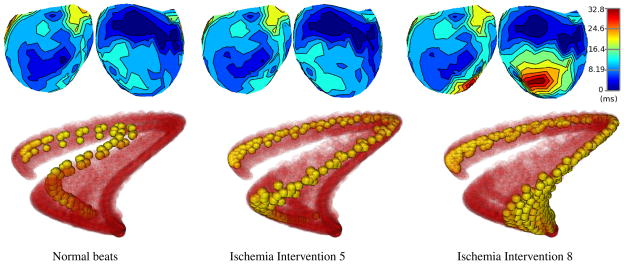
We restricted our analysis of the data to time samples during the QRS intervals. Fig. 1 shows each QRS time sample of the 315 beats as a solid red point in the first three Laplacian eigenmaps coordinates. We also show groups of beats corresponding to different stages of the ischemia experiment in Fig. 2 (bottom row), with the points of interest shown in solid yellow, and the remainder of the points from the experiment shown in semitransparent red. The average activation times for the same groups of beats are shown as isochronal maps in Fig. 2 (top row). Isochronal maps were produced by map3d, and manifold visualizations by SCIRun [10, 11].

Fig. 1.

Heart Signal Manifolds: three orthogonal views of points in the first three relevant coordinates of Laplacian eigenmaps from a collection of canine ventricular surface (epicardial) recordings during QRS. The mapping of each time instant in each beat is represented as a single red sphere.

Fig. 2.

Ischemia on Manifolds: comparison of activation times and trajectories on the manifold for three stages of a supply ischemia experiment. A total of 10 ischemia interventions were conducted, from which we show (left to right): normal beats, intervention 5, intervention 8. For each stage, the top row shows two opposite views of the average activation times as isochronal maps on the epicardial surface of the canine heart. These are level-set contours of activation wavefront arrival times, relative to the start of the QRS interval (blue is early, red is late). The bottom row shows manifold trajectories as yellow points for the corresponding stages of the experiment, along with the entire manifold in red, shown as in Fig. 1, but with transparency.

3.2. Torso Surface Signals

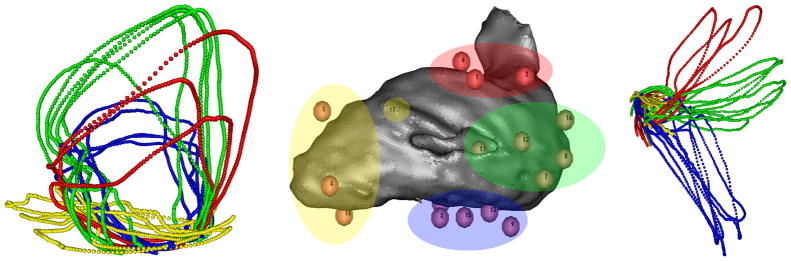
To demonstrate the method on torso surface measurements, we applied it to electric potentials recorded from a subject at the Charles University Hospital in the Czech Republic during a clinical procedure. The heart was paced by applying electrical stimuli to the interior wall of the left ventricular blood chamber at multiple sites with the tip of a CARTO ablation catheter. Measurements were recorded (2048 Hz sampling rate) from 120 torso leads. Multiple beats were recorded and averaged for each pacing site and our method was applied to the resulting data. Fig. 3 shows a volume visualization of the left ventricular blood chamber, along with the different pacing sites, as localized by the CARTO XP system. The pacing sites in Fig. 3 were separated in four groups, by spatial location, before our analysis, and labeled with a different color. The corresponding manifold trajectories in Fig. 3 have been colored according to the same pre-determined colors.

Fig. 3.

Torso Signal Manifold: visualizations of left ventricular (LV) sites paced in four groups, labeled by color (center), along with two views of the manifold trajectories (left, right) from the correspondinge torso surface data, with the same correspondence in color labels. Pacing as applied to the inner wall of the LV blood chamber, which is rendered as a gray volume, with pacing sites superimposed (#17 is behind the volume). The two manifold views were rotated to show pacing/trajectory groups more clearly (left: yellow, and right: red, green, blue).

4. DISCUSSION

Fig. 1 suggests that points sampled from the canine heart data indeed do lie on a nonlinear manifold structure, as represented in the first three Laplacian eigenmaps coordinates. For example, the fact that trajectories end QRS near where they started reflects this structure. In Fig. 2, beats from different stages of the ischemia experiment clearly traverse different regions of the manifold. Indeed the changes between the trajectories at each stage of the ischemia experiment are quite pronounced. By comparison, in the activation isochrone maps, changes between normal beats and intervention 5 are negligible, with the damage due to supply ischemia only becoming apparent in intervention 8. Intervening states, not shown, traverse intervening regions of the manifold. Thus the results indicate that we may be able identify signs of ischemia-induced damage via dynamic changes during QRS. This is in contrast to accepted clinical wisdom that relies only on changes later in the beat, in the ST segment, and at lower damage level in comparison to activation maps.

Perhaps even more intriguing, in Fig. 3 we also see a de-fined structure with torso surface data, including obvious similarities among manifold trajectories arising from the same pacing regions. We note that this separability of manifold trajectory groups is a result of differences between whole beats, and not just differences between locations of pacing sites, emphasizing the importance of using dynamics to compare beats. The forward model defines a map between heart and torso surface manifolds, suggesting that manifold constraints on dynamics in heart potentials based on torso measurements may be useful to regularize the inverse problem of electrocardiography.