Trigonal Mn₃ and Co₃ Clusters Supported by Weak-Field Ligands: A Structural, Spectroscopic, Magnetic, and Computational Investigation into the Correlation of Molecular and Electronic Structure

Abstract

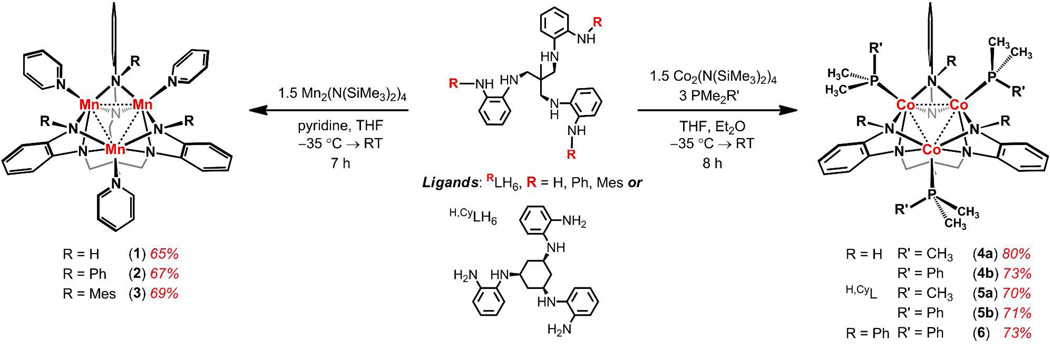
Transamination of divalent transition metal starting materials (M₂(N(SiMe₃)₂)₄, M = Mn, Co) with hexadentate ligand platforms ^RLH₆ (^RLH₆ = MeC(CH₂NPh-o-NR)₃ where R = H, Ph, Mes (Mes = Mesityl)) or ^H,CyLH₆ = 1,3,5-C₆H₉(NHPh-o-NH₂)₃ with added pyridine or tertiary phosphine co-ligands afforded trinuclear complexes of the type (^RL)Mn₃(py)₃ and (^RL)Co₃(PMe₂R’)₃ (R’ = Me, Ph). While the sterically less encumbered ligand varieties, ^HL or ^PhL, give rise to local square-pyramidal geometries at each of the bound metal atoms, with four anilides forming an equatorial plane and an exogenous pyridine or phosphine in the apical site, the mesityl-substituted ligand (^MesL) engenders local tetrahedral coordination. Both the neutral Mn₃ and Co₃ clusters feature S = 1/2 ground states, as determined by dc magnetometry, ¹H NMR spectroscopy, and low-temperature EPR spectroscopy. Within the Mn₃ clusters, the long internuclear Mn–Mn separations suggest minimal direct metal-metal orbital overlap. Accordingly, fits to variable-temperature magnetic susceptibility data reveal the presence of weak antiferromagnetic superexchange interactions through the bridging anilide ligands with exchange couplings ranging from J = −16.8 to −42 cm⁻¹. Conversely, the short Co–Co interatomic distances suggest a significant degree of direct metal-metal orbital overlap, akin to the related Fe₃ clusters. With the Co₃ series, the S = 1/2 ground state can be attributed to population of a single molecular orbital manifold that arises from mixing of the metal- and o-phenylenediamide (OPDA) ligand-based frontier orbitals. Chemical oxidation of the neutral Co₃ clusters affords diamagnetic cationic clusters of the type [(^RL)Co₃(PMe₂R)₃]⁺. DFT calculations on the neutral (S = ½) and cationic (S = 0) Co₃ clusters reveal that oxidation occurs at an oribital with contributions from both the Co₃ core and OPDA subunits. The predicted bond elongations within the ligand OPDA units are corroborated by the ligand bond perturbations observed by X-ray crystallography.

A. Introduction

Open-shell polynuclear clusters that feature close (ca. < 3 Å) M–M separations are utilized extensively in biology. Aside from the carbonyl/cyanide supported Fe-only hydrogenases,¹ nearly all of the polynuclear metallocofactors feature an open-shell electronic configuration. These clusters are used to mediate electron transfer ([Fe₂S₂] ferrodoxins, [Fe₄S₄] clusters, and [Fe₃S₄] aconitase),² reduction chemistry (FeMo, VFe, and Fe-only nitrogenases;³ Cu_Z site in nitrous oxide reductase⁴), and oxidation chemistry (Mn–O cluster in oxygen-evolving complex in photosystem II;⁵ Cu- and Fe-containing clusters in particulate⁶ and soluble⁷ methane monooxygenase, respectively). In an attempt to realize structural and functional models of these cofactors, researchers have utilized synthetic inorganic chemistry to prepare polynuclear molecular clusters where the protein superstructure has been replaced by organic ligands. However, the majority of ligands that support cluster formation induce low-spin configurations, often precluding the reactivity exhibited by native metalloenzymes.⁸

To synthesize open-shell cluster complexes meeting the aforementioned structural criteria, one can envision use of a flexible, multi-nucleating ligand comprised of weak-field binding sites to direct the formation of predesigned multinuclear architectures. In addition to synthetic tunability, this directed approach offers the distinct advantage of the ability to probe how the ligand scaffold influences the overall molecular symmetry and electronic structure. Towards this end, we recently reported the trinucleating platform, ^HLH₆,⁹ and its ability to direct the formation of trigonal planar Fe₃⁹ and octahedral Fe₆¹⁰ clusters, where steric modifications to the ligand platform have resulted in dramatic changes to the electronic structure (where ^RL = MeC(CH₂NPh-o-NR)₃; R = H,⁹ Ph,¹¹ SiMe₂tBu¹²). For instance, the proton-capped ligand (^HL⁶⁻) permits close metal-metal contacts giving rise to a low-spin ground state (S = 1) for (^HL)Fe₃(PMe₂R)₃.⁹ Appendage of large substituents onto the ligand’s peripheral anilide units gives rise to clusters with much larger spin ground states (i.e. S = 6 for (^PhL)Fe₃(thf)₃,¹¹ (^tbsLFe₃(thf)¹²; thf = tetrahydrofuran). Importantly, the open-shell configurations present in the Fe₃ clusters have led to facile reactivity with small molecule substrates. For example, reaction of the S = 6 complex (^tbsL)Fe₃(thf) was shown to activate azide to afford the cluster [(^tbsL)Fe₃(μ³-N)]⁻.¹² Given these initial results with iron, we sought to extend this methodology to include other 3d transition metals, in order to probe the correlation between molecular and electronic structure as a function of ligand type and transition metal employed.

Following a synthetic approach similar to that used for the trinuclear iron complexes, we present herein trinuclear complexes featuring divalent Mn and Co. Within this family of compounds, different ligand architectures give rise to different molecular symmetries. Following the successful expansion of our synthetic protocols to include Mn, Fe, and Co polynuclear complexes, this report will be directed toward addressing the following questions: (1) How does the overall molecular symmetry impact the electronic structure? (2) To what extent do the redox-active ligand components participate in the observed redox behavior characteristic of the trinuclear clusters? (3) What governs the nature of coupling between the metal centers in the trinuclear complexes?

B. Results

B.1 Synthesis of ^MesLH₆ and M₃ clusters

We have used hexadentate aniline-based ligands to assemble tri- and hexanuclear metal cores in the same proximal space.^9–11 The synthesis of the ligand platforms MeC(CH₂NHPh-o-NH₂)₃ (^HLH₆),⁹ 1,3,5-C₆H₉(NHPh-o-NH₂)₃ (^H,CyLH₆),¹² MeC(CH₂NHPh-o-NHPh)₃ (^PhLH₆)¹¹ have recently been reported by our group. Introducing phenyl substituents onto peripheral anilide of the base ^HLH₆ platform dramatically affected the ground state electronic structure observed within the trinuclear iron clusters.¹¹ Modification of the ^H,CyLH₆ to include large dimethyl-tert-butyl silyl substituents, affording ^tbsLH₆, changed both the electronic structure of the resulting trinuclear complexes as well as the local metal ion binding geometry.¹² To generate a ligand featuring even larger aryl substituents, ^HLH₆ was arylated with mesitylbromide using standard Pd cross-coupling methodologies (2.2% Pd₂(dba)₃, 6.6% rac-BINAP, 3.1 equiv bromomesitylene, 4 equiv NaO^tBu, toluene, 70 °C for 18h) to afford the ligand derivative MeC(CH₂NHPh-o-NH(2,4,6-Me₃C₆H₂))₃ (^MesLH₆) in 72% isolated yield.

Metallation of the ligand platforms was effected via transamination from the metal amide starting materials (M₂(N(SiMe₃)₂)₄, M = Mn, Co).¹³ For example, addition of 1.5 equivalents of Mn₂(N(SiMe₃)₂)₄ to ^RLH₆ and excess pyridine in thf at −35 °C, followed by standing in a mixture of thf and hexanes at −35 °C, afforded the trinuclear complexes (^HL)Mn₃(py)₃ (1, 65%), (^PhL)Mn₃(py)₃ (2, 67%), and (^MesL)Mn₃(py)₃ (3, 69%) as ¹H NMR silent, light yellow, crystalline products, akin to the previously reported complex (^HL)Mn₃(thf)₃.¹⁴ Note that complete transamination to the larger ^MesLH₆ required heating to 75 °C for 12 hours, as confirmed by monitoring HN(SiMe₃)₂ evolution by ¹H NMR spectroscopy.

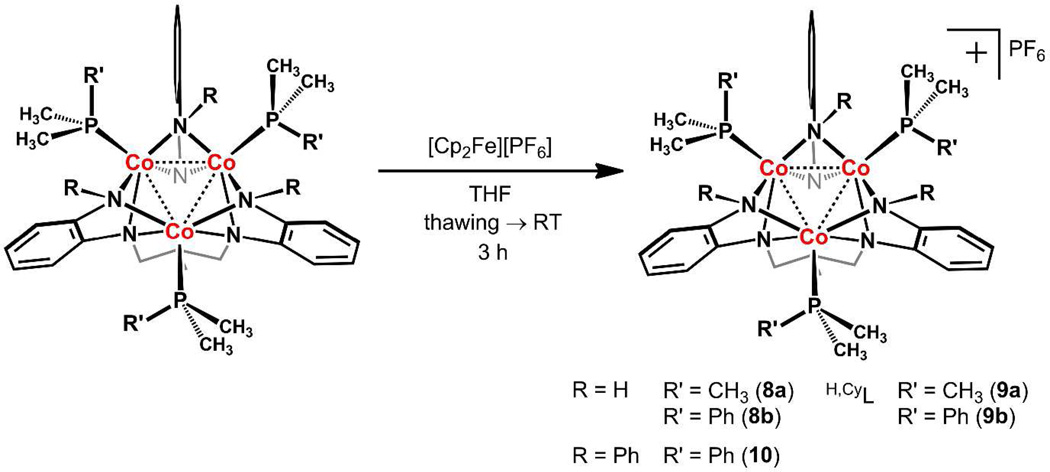
Installation of cobalt into the ligand scaffolds followed a similar protocol, where use of the tertiary phosphines PMe₂R (R = Me, Ph) in place of pyridine was necessary to generate isolable species. Specifically, reaction of ^RLH₆ with 1.5 equivalents of Co₂(N(SiMe₃)₂)₄ and three equivalents of PMe₂R (R = Me or Ph) in thf at −35 °C afforded the stable tricobalt complexes (^HL)Co₃(PMe₂R)₃ (R = Me (4a, 80%) or Ph (4b, 73%)), (^H,CyL)Co₃(PMe₂R)₃ (R = Me (5a, 70%) or Ph (5b, 71%)), and (^PhL)Co₃(PMe₂Ph)₃ (6, 73%) as dark red-brown solids in good isolated yields (see Scheme 1). Each of the Co₃ clusters shows a well-defined paramagnetically shifted ¹H NMR spectrum, typically exhibiting the appropriate number of proton resonances for complexes of C₃ symmetry. Addition of only two equivalents of PMe₂Ph in the reaction of 1.5 equivalents of Co₂(N(SiMe₃)₂)₄ with ^PhLH₆ afforded a new product that lacks C₃ symmetry, as assayed by ¹H NMR and EPR spectroscopy. Connectivity of this new species, (^PhL)Co₃(PMe₂Ph)₂ (7, 54%), was confirmed by X-ray crystallography.

Scheme 1.

B.2 Structures of M₃ clusters

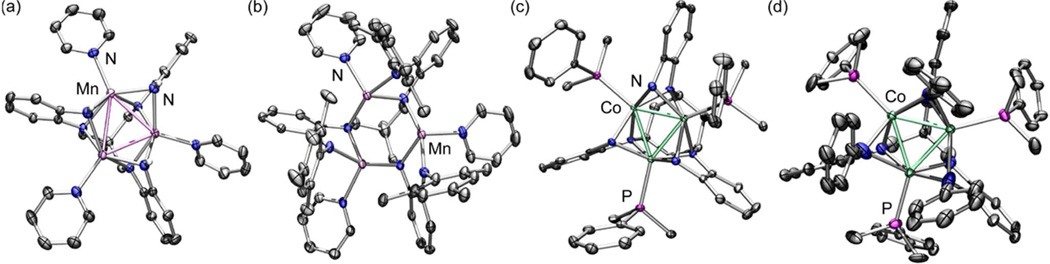
Crystals suitable for X-ray diffraction analysis of the Mn₃ clusters were grown from standing concentrated solutions in mixtures of thf, hexanes, and pyridine at −35 °C. Complexes 1 and 2 exhibit the same ligand binding modes as previously reported for the (^HL)Fe₃(PMe₂R)₃ redox series.⁹ Here, all six ligand anilides bridge two Mn ions (6-μ²), giving rise to a local square-pyramidal coordination environment about each metal, where a pyridine occupies the apical site, trans to a dimetal unit (see Figures 1 and S6 for representative structures and Table 1 for selected bond lengths and angles). Unlike the iron congener which exhibits very close Fe–Fe ion separation (d_Fe-Fe 2.299(2) Å), the average Mn–Mn separation in 1 (2.8550(5) Å) and 2 (2.8201(5) Å), like (^HL)Mn₃(thf)₃ previously reported,¹⁴ exceeds the van der Waals radius of Mn,¹⁵ suggesting little or no direct Mn–Mn interaction. Unlike 1 and 2, the steric bulk provided by the mesityl groups in 3 alters the local Mn coordination geometry. In particular, the three peripheral anilides no longer bridge adjacent metal sites giving rise instead to tetrahedral coordination at each Mn (see Figure 1b). This steric bulk also enforces even greater Mn–Mn separation (3.1252(7) Å), although the overall molecular C₃-symmetry is preserved. The range of Mn–Mn separations found in compounds 1–3 are similar to previously reported polynuclear Mn^II clusters.^16,17

Figure 1.

Solid-state structures for (^HL)Mn₃(py)₃ 1 (a), (^MesL)Mn₃(py)₃ 3 (b), (^H,CyL)Co₃(PMe₂Ph)₃ 5b (c), and (^PhL)Co₃(PMe₂Ph)₃ 6 (d), with thermal ellipsoids set at the 50% probability level. Hydrogen atoms are omitted for clarity; Mn pink, Co aqua-green, C gray, N blue, P magenta. Selected mean interatomic distances (Å) for 1: Mn1–Mn2 2.8229(4), Mn1–Mn3 2.8115(4), Mn2–Mn3 2.9267(5), Mn-N_base,avg 2.2062(7), Mn-NH_avg 2.1902(7), Mn-N_py,avg 2.186(2); 3: Mn1–Mn2 3.1354(11), Mn1–Mn3 3.1046(13), Mn2–Mn3 3.1357(12), Mn-N_base,avg 2.132(2), Mn-NMes_avg 2.088(2), Mn-N_py,avg 2.220(5); 5b: Co1–Co2 2.3978(7), Co1–Co3 2.3886(7), Co2–Co3 2.3702(7), Co-N_base,avg 2.021(4), Co-NH_avg 2.010(5), Co-P_avg 2.2302(13); 6: Co1–Co2 2.4265(17), Co1–Co3 2.4272(18), Co2–Co3 2.4274(18), Co-N_base,avg 1.987(8), Co-NPh_avg 2.149(9), Co-P_avg 2.253(3).

Table 1.

Selected bond lengths (Å) and angles (°) for complexes 1–3, 4b, 5b^a, 6^a, and 7^a.

	1	2	3	4b	5b	6	7
M1–M2	2.9117(4)	2.8104(4)	3.1365(9)	2.3820(4)	2.3978(7)	2.4265(17)	2.4377(7)
M1–M3	2.8665(4)	2.8542(4)	3.1045(11)	2.3796(4)	2.3886(7)	2.4272(18)	2.3368(7)
M2–M3	2.38650(4)	2.7960(4)	3.1371(10)	2.3965(5)	2.3702(7)	2.4274(18)	2.4385(7)
M1–N1	2.242(2)	2.200(1)	2.124(2)	2.089(2)	1.971(4)	1.988(7)	1.925(3)
M1–N2	2.207(2)	2.183(1)	2.144(2)	2.068(2)	1.999(3)	1.983(8)	1.921(3)
M2–N2	2.187(2)	2.181(1)	2.119(2)	1.979(2)	2.063(3)	1.992(7)	2.053(3)
M2–N3	2.212(2)	2.192(1)	2.139(3)	1.952(2)	2.042(4)	1.989(8)	2.042(3)
M3–N1	2.191(2)	2.188(1)	2.138(2)	1.956(2)	2.024(4)	1.981(7)	1.948(3)
M3–N3	2.187(2)	2.201(1)	2.124(2)	1.975(2)	2.026(3)	1.987(8)	1.984(3)
M1–N4	2.191(2)	2.206(1)	2.099(2)	2.085(2)	1.964(3)	2.174(9)	1.853(3)
M1–N5	2.172(2)	2.311(1)	–	2.112(2)	1.979(4)	2.120(9)	2.060(3)
M2–N5	2.201(2)	2.300(1)	2.084(3)	1.994(2)	2.027(4)	2.108(9)	2.029(3)
M2–N6	2.189(2)	2.186(1)	–	1.956(2)	2.060(4)	2.181(8)	2.053(3)
M3–N6	2.196(2)	2.304(1)	2.077(2)	1.958(2)	2.040(3)	2.173(9)	2.017(3)
M3–N4	2.214(2)	2.193(1)	–	1.990(2)	1.993(4)	2.136(9)	2.185(3)
M1–L1	2.2074(18)	2.1649(15)	2.214(2)	2.2026(6)	2.2358(12)	2.253(3)	–
M2–L2	2.1890(19)	2.1489(15)	2.213(3)	2.2298(6)	2.2277(12)	2.252(3)	2.2906(12)
M3–L3	2.1808(18)	2.1647(15)	2.248(4)	2.2309(6)	2.2271(13)	2.253(3)	2.2607(11)
M3–M1–M2	59.44(1)	59.15(1)	60.35(2)	60.44(1)	59.36(2)	60.02(5)	61.38(2)
M3–M2–M1	59.50(1)	61.21(1)	59.32(2)	59.73 (1)	60.13(2)	60.01(5)	61.35(2)
M2–M3–M1	61.06(1)	59.65(1)	60.33(2)	59.83(1)	60.51(2)	59.98(5)	57.27(2)
M2–N1–M3	82.49(6)	79.81(5)	93.50(9)	72.15(6)	73.35(12)	75.57(5)	74.30(11)
M1–N2–M3	80.80(6)	79.33(5)	94.73(10)	74.62(6)	70.87(11)	75.53(5)	74.29(11)
M1–N3–M2	80.09(6)	81.25(5)	94.77(10)	72.45(6)	72.80(11)	75.93(5)	75.76(11)
M2–N4–M3	80.56(6)	77.15(5)	–	72.15(5)	73.11(12)	67.83(5)	70.59(11)
M1–N5–M3	83.60(6)	76.98(5)	–	73.96(6)	72.24(12)	67.70(5)	69.95(11)
M1–N6–M2	80.94(6)	78.61(5)	–	71.43(6)	72.91(12)	67.70(5)	–
M–N–Mavg	81.43(7)	78.86(6)	94.33(11)	72.29(7)	72.55(13)	71.71(6)	72.98(12)

^aFrom representative molecule in asymmetric unit.

Crystals suitable for X-ray diffraction analysis of the Co₃ clusters were grown from concentrated hexane solutions at ambient temperature (4a,b) or via slow evaporation of benzene solution (5a,b, 6 and 7). Representative molecular structures are shown in Figure 1, and selected bond lengths and angles are listed in Table 1. In agreement with the respective ¹H NMR spectra, the molecular structures of 4–6 confirm the C₃-symmetry, and, like complexes 1 and 2, each of the cobalt atoms are bridged by four anilide units from the ligand. Each of the three cobalts reside in a distorted square pyramid that consists of four bridging anilides forming an equatorial plane, with the ancillary phosphine occupying the apical site, trans to a dicobalt unit. The average Co–Co separations (4b 2.3860(5) Å, 5b 2.3855(8) Å) show little variation with changing the tris-anilide backbone (^HL vs. ^H,CyL) and are longer than those in the isostructural iron congener (^HL)Fe₃(PMe₂R)₃ (average Fe–Fe distances are 2.299(2) Å).⁹ In contrast, the Co–Co separation for the ^PhL ligand variant in 6 (2.4270(19) Å) is contracted from the iron congener (^PhL)Fe₃(PMe₂Ph)₃ (2.5853(14) Å).¹¹ Although the average Co–Co separation in 6 is elongated by ~0.04 Å relative to 4b and 5b, the average distance is not beyond the van der Waals contact radius and is therefore consistent with metal-metal bonding interactions.¹⁵ The Co–Co interatomic distances are similar to those reported for trigonal cobalt cyclopentadienyl clusters,¹⁸ likely arising from overlap of metal-based σ and π orbitals (vide infra), akin to what has been previously proposed in trigonal Co₃ clusters.¹⁹

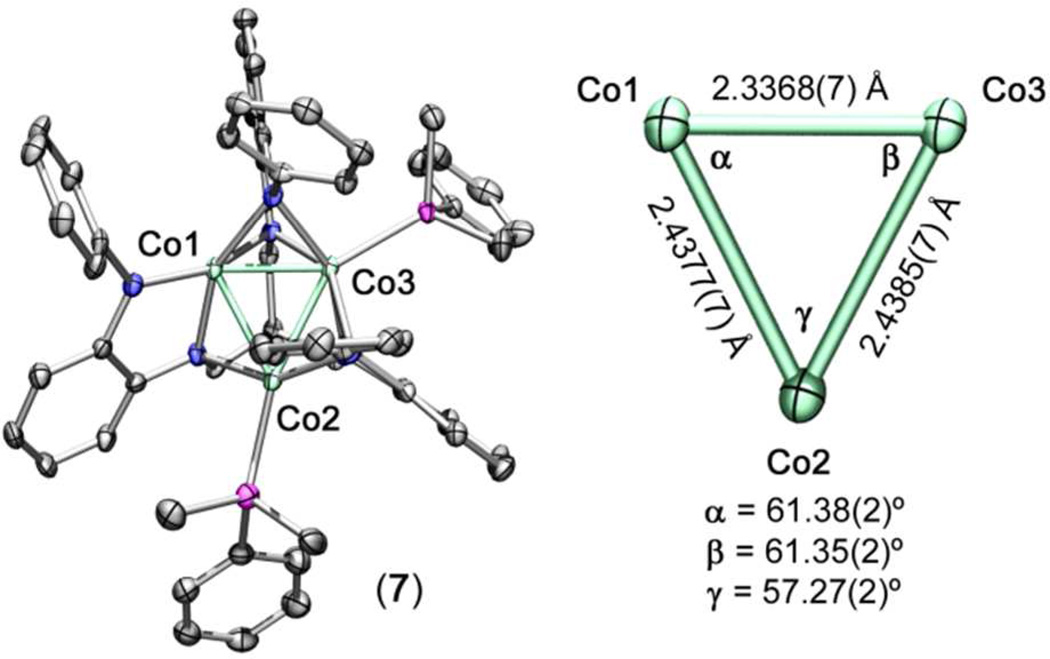
The presence of only two bound PMe₂Ph ligands in the crystal structure of 7 leads to a distinct coordination environment for each cobalt center and a loss of molecular C₃-symmetry. Two of the peripheral phenyl-anilides bridge adjacent metal sites in a μ²-fashion, while the third terminally binds Co3 only (see Figure 2). While Co1 retains the square-pyramidal coordination observed in 6, Co2 is bound by three anilides and one phosphine ligand in a distorted tetrahedral geometry (neglecting M–M interactions). Finally, Co3 resides in a distorted square planar environment that consists solely of four anilides from the (^PhL) ligand. Overall, this asymmetric ligand binding motif results in a significant distortion of the Co–Co separation relative to 6 (see Figure 2 inset). The Co1–Co3 distance is shortened to 2.3371(7) Å, 0.100(1) Å shorter than the Co1–Co2 and Co2–Co3 separations of 2.4377(7) and 2.4385(7) Å, respectively. The Co1–N4 distance (1.853(3) Å) is contracted relative to its bridging counterparts (Co–N_Ph (avg) = 2.045(3) Å).

Figure 2.

Solid-state structures for (^PhL)Co₃(PMe₂Ph)₂ 7 (thermal ellipsoids set at the 50% probability level; hydrogen atoms are omitted for clarity; Co aqua-green, C gray, N blue, P magenta).

B.3 Spectroscopic Characterization of Neutral M₃ Clusters

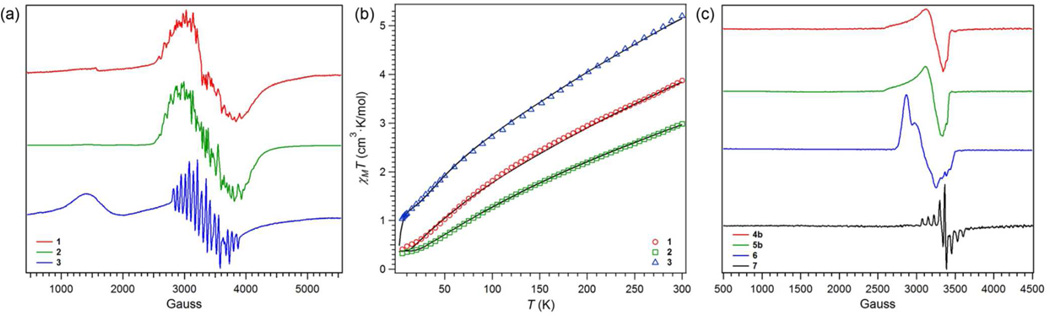
The X-band EPR spectra for the Mn₃ clusters 1–3 show strong transitions at 295 K, manifested as simple isotropic signals near g = 2.0, but exhibit fine structure when cooled to 3 K (see Figure 3a). Indeed, each of the spectra at low temperature exhibit substantial hyperfine coupling, presumably to the I = 5/2 ⁵⁵Mn nucleus and potentially to the I = 1 ¹⁴N nucleus. Complexes 1 and 2 show spectra exceeding the 16-line pattern expected for hyperfine coupling to all three Mn nuclei (2nI + 1; A_‖ = 118 MHz for 2 at 77 K; see Figure S1). In contrast, the spectrum for complex 3 shows a clean 16-line pattern (A_‖ 182 MHz, g = 2.04, see Figure 2a), despite exhibiting the largest Mn–Mn separation in the series of 1–3. The 16-line pattern, however, likely arises due to coupling of a single Mn center with N nuclei in different environments, though attempts to model the data using either coupling mechanism have failed to reproduce the spectrum obtained. The prominent transition centered at g ≈ 4.6 may correspond to a spin-allowed transition associated with the S = 3/2 excited state, which may exhibit some thermal population even at 3 K (vide infra). Note that the magnitude of the ⁵⁵Mn hyperfine coupling is similar to related Mn^II clusters (e.g. Mn₆(μ³-NPh)₄Br₄(thf)₆) that have been reported previously.^16d

Figure 3.

(a) Frozen toluene EPR spectra for (^HL)Mn₃(py)₃ 1 (red), (^PhL)Mn₃(py)₃ 2 (green), and (^MesL)Mn₃(py)₃ 3 (blue) obtained at 3 K (X-band, 9.380 GHz). (b) Variable-temperature dc magnetic susceptibility data for (^HL)Mn₃(py)₃ 1 (red circles), (^PhL)Mn₃(py)₃ 2 (green squares), and (^MesL)Mn₃(py)₃ 3 (blue triangles), collected in an applied field of 0.5 T. Solid black lines represent simulations using the parameters provided in the text. (c) Frozen toluene EPR spectra for (^HL)Co₃(PMe₂Ph)₃ 4b (red), (^H,CyL)Co₃(PMe₂Ph)₃ 5b (green), (^PhL)Co₃(PMe₂Ph)₃ 6 (blue), and (^PhL)Co₃(PMe₂Ph)₂ 7 (black) obtained at 3 K (X-band, 9.393 GHz).

To probe the magnetic behavior of the Mn₃ clusters, variable-temperature dc susceptibility data were collected in the temperature range of 5–300 K. The resulting plots of χ_MT vs. T for complexes 1–3 are shown in Figure 3b. At 300 K, χ_MT = 3.88, 2.99, and 5.20 cm³·K/mol for 1, 2, and 3, respectively. All three values are lower than the expected value of 13.1 cm³·K/mol for three magnetically isolated S = 5/2 Mn^II centers (g = 2.00), indicative of antiferromagnetic coupling between Mn^II nucleii. As the temperature is lowered, χ_MT steadily decreases to minima at 5 K of 0.408, 0.326, and 1.03 cm³·K/mol for 1, 2, and 3, respectively, close to the value of 0.375 cm³·K/mol expected for an S = 1/2 ground state.

Despite the approximate C₃ symmetry 1–3, the χ_MT vs. T data are poorly modeled using MAGPACK²⁰ according to the following spin Hamiltonian, which assumes an equilateral triangular arrangement of spins and one unique coupling constant (J):

$$Ĥ=-2J({\mathit{S}}_{\text{Mn}1}{\mathit{S}}_{\text{Mn}2}+{\mathit{S}}_{\text{Mn}2}{\mathit{S}}_{\text{Mn}3}+{\mathit{S}}_{\text{Mn}1}{\mathit{S}}_{\text{Mn}3})+g{\mu }_{\mathrm{B}}\mathit{S}·\mathit{B}$$ (1)

Rather, the data can be successfully modeled according to the following spin Hamiltonian considering an isosceles triangle, where two distinct coupling constants are employed:

$$Ĥ=-2[J_1({\mathit{S}}_{\text{Mn}1}{\mathit{S}}_{\text{Mn}2}+{\mathit{S}}_{\text{Mn}2}{\mathit{S}}_{\text{Mn}3})+J_2{\mathit{S}}_{\text{Mn}1}{\mathit{S}}_{\text{Mn}3}]+g{\mu }_{\mathrm{B}}\mathit{S}·\mathit{B}$$ (2)

Note that data for a related anilido-bridged Mn₃ cluster with an S = 1/2 ground state have been modeled analogously.^16f Moreover, closer inspection of the Mn–Mn separation in 1 reveals an asymmetry consistent with this formulation, which features two short and one long Mn–Mn distances (Mn1–Mn2 2.8229(4) Å, Mn1–Mn3 2.8155(4) Å, with Mn2–Mn3 2.9267(5) Å). Modeling the data accordingly provides exchange coupling constants of J₁ = −35(1) and J₂ = −27(1) cm⁻¹ (g = 2.00(2)) for 1, J = − 49(2) and J₂ = −39(1) cm⁻¹ (g = 1.99(3)) for 2, and J = −29.5(6) and J₂ = –17.5(3) cm⁻¹ (g = 2.00(3)) for 3. These values are considerably larger than those reported for related trigonal carboxylate- and amido-bridged Mn^II clusters, which exhibit J = −0.59 to −2.36 cm⁻¹,²¹ and J = −7.0 to −11.0 cm⁻¹ ,^16f respectively. Considering all trigonal Mn₃ clusters, the magnitude of antiferromagnetic exchange (J₁, J₂) track somewhat linearly with the Mn–N–Mn bond angle (see Figure S9), wherein the larger angle corresponds to weaker coupling between the metal centers.²²

The X-band EPR spectra of the Co₃ clusters 4b, 5b, 6 and 7, obtained for frozen toluene solutions at 77 K, are shown in Figure 3c. The EPR parameters for 4b (g = 2.035, 2.283) are similar to those observed for 5b (g = 2.043, 2.283). The large deviation from g = 2 is a feature that has been observed in other triangular tricobalt complexes.²³ Common to both previously reported examples, as well as to 4b, 5b and 6, the hyperfine interaction with the ⁵⁹Co nucleus (I = 7/2) is not the sole contributor to the hypefine observed. Nevertheless, hyperfine coupling to Cois indeed observed in the spectrum of 7, which displays a well-resolved eight-line pattern (A‖ = 68 G, g = 1.988; see Figure 3c), characteristic of a hyperfine interaction with one Co nucleus. One possibility to account for this spectral difference could be the desymmetrization of 7 relative to the trigonally symmetric 6. As highlighted in Figure 2, the close Co–Co separation of Co1 and Co3 (Co1–Co3 2.3368(7) Å, Co1–Co2 2.4377(8) Å, Co2–Co3 2.4385(7) Å) may indicate greater localization of the unpaired electron on Co2. Despite the difference between the C₃ symmetric species and 7, each of the complexes show metrical parameters consistent with the same S = 1/2 spin state formulation. Benzene solutions of 4–7 at 295 K were evaluated by the method of Evans to give solution magnetic moments (μ_B) of 1.79(4) for 4a, 1.74(6) for 5a, 1.95(3) for 6, and 2.02(6) for 7, indicative of an S = 1/2 formulation (1.73 μ_B spin-only) and consistent with the EPR spectra obtained for these complexes.

B.4 Redox Properties of Tricobalt Series

Cyclic voltammograms collected for complexes 1–3 all showed a cascade of irreversible oxidation events beginning near −1.2 V vs. [Cp₂Fe]^+/0 (see Figure S5). Accordingly, chemical oxidation of the Mn₃ clusters gave rise to intractable mixtures of products. In contrast, complex 4a exhibits several redox waves in the cyclic voltammogram (see Figure S5), reminiscent of the iron congeners.^9a The primary oxidation event for 4b occurs at −1.75 V vs. [Cp₂Fe]^+/0 (see Figure S5), suggesting a highly reducing species for a nominally all Co^II trinuclear complex. Chemical oxidation of 4, 5, and 6 with ferrocenium hexafluorophosphate resulted in the immediate generation of ferrocene, as ascertained via ¹H NMR, along with concomitant disappearance of the paramagnetic resonances and growth of new diamagnetic products. These spectral observations are consistent with the removal of one electron from each of the clusters to give the oxidized products [(^RL)Co₃(PMe₂Ph)₃][PF₆] (R = Me (8a) and Ph (8b)), [(^H,CyL)Co₃(PMe₂R)₃][PF₆] (R = Me (9a) and Ph (9b)), and [(^PhL)Co₃(PMe₂Ph)₃][PF₆] (10) (see Scheme 2). Oxidation of the neutral Co₃ clusters to cationic species was nearly quantitative, as assayed by ¹H NMR spectroscopy. In addition, 8, 9, and 10 could be isolated in 73–85% yield following crystallization from thf at −35 °C. The ¹H, ³¹P and ¹³C NMR spectra of the oxidized complexes displayed the expected resonances for the C₃-symmetric molecules. The visible spectra of the cationic complexes 8b, 9b, and 10 do not show any absorption in the region of 650–900 nm that is characteristic of ligand-to-ligand charge transfer bands, commonly associated with the one-electron oxidation of o-phenylenediamide ligands to the corresponding monoanionic π-radical o-diiminobenzosemiquinonate ligand (see Figure S4).²⁴

Scheme 2.

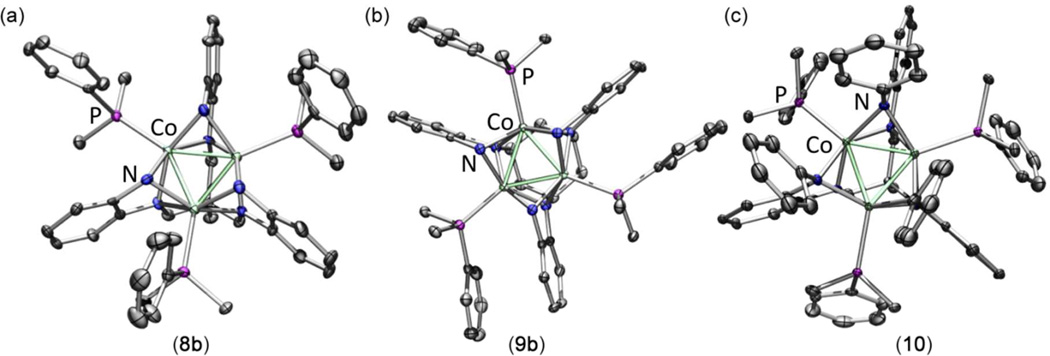
The solid-state molecular structures of 8b, 9b and 10 are shown in Figure 4, and selected bond distances and angles are provided in Table 2. The gross structural features of the cationic series are similar to their respective neutral starting materials. Like those in the neutral analogues, the bond metrics within each of the o-phenylenediamide ligand branches are characteristic of aromatic, closed-shell dianions (N–C_Ar 1.411(10); C_Ar–C_Ar 1.390(7) Å; Table S4), unchanged from the precursors and within the error of the measured bond lengths.²⁴ The Co–N bond distances for the cationic complexes are shorter than those in their respective neutral counterparts. For example, the Co–N_base and Co–N_R distances decrease 1.2–3.2% upon oxidation, reflective of the smaller ionic radius for the closed-shell cations relative to the open-shell neutral precursors. Aside from the change in Co–N bond lengths, the metal ion separation in the Co₃ core shows a contraction of similar scale to that observed for [(^HL)Fe₃(PMe₂R)₃]^+/0. The average Co–Co separation also decreases upon oxidation, as exemplified by a contraction in the Co₃ plane of 1.59–3.14% (see Tables 1 and 2), similar in magnitude to that observed in the [(^HL)Fe₃(PMe₂R)₃]^+/0 series (2.19% decrease in the area of the triangular Fe₃ plane).

Figure 4.

Solid-state structures for [(^HL)Co₃(PMe₂Ph)₃]⁺ 8b (a), [(^H,CyL)Co₃(PMe₂Ph)₃]⁺ 9b (b), and [(^PhL)Co₃(PMe₂Ph)₃]⁺ 10 (c) with thermal ellipsoids set at the 50% probability level; hydrogen atoms are omitted for clarity; Co aqua-green, C gray, N blue, P magenta). Selected mean interatomic distances (Å) for 8b: Co1–Co2 2.341(2), Co1–Co3 2.349(2), Co2–Co3 2.342(2), Co-N_base,avg 1.957(4), Co-NH_avg 1.968(4), Co-P_avg 2.235(2); 9b: Co1–Co2 (Co1–Co3, Co2–Co3) 2.3477(6), Co-N_base,avg 1.981(2), Co-NH_avg 1.955(2), Co-P 2.2308(7); 10: Co1–Co2 (Co1–Co3, Co2–Co3) 2.3905(7), Co-N_base,avg 1.965(4), Co-NPh_avg 2.096(4), Co-P 2.2806(8).

Table 2.

Selected bond lengths (Å) and angles (°) for complexes 8b, 9b, and 10.

	8b	9b	10
Co1–Co2	2.3406(17)	2.3477(6)	2.3905(7)
Co1–Co3	2.3494(15)	-	-
Co2–Co3	2.3418(17)	-	-
Co1–N1	1.953(4)	1.980(2)	1.962(3)
Co1–N2	1.972(4)	1.981(2)	1.968(3)
Co2–N2	1.960(4)	-	-
Co2–N3	1.960(4)	-	-
Co3–N1	1.952(4)	-	-
Co3–N3	1.947(4)	-	-
Co1–N4	1.964(4)	1.955(2)	2.072(3)
Co1–N5	1.978(4)	1.956(2)	2.119(3)
Co2–N5	1.971(3)	-	-
Co2–N6	1.971(4)	-	-
Co3–N6	1.947(4)	-	-
Co3–N4	1.974(4)	-	-
Co1–P1	2.234(2)	2.2308(7)	2.2806(8)
Co2–P2	2.244(2)	-	-
Co3–P3	2.227(2)	-	-
Co3–Co1–Co2	59.91(5)	60.00(1)	60.0
Co3–Co2–Co1	60.23(3)	-	-
Co2–Co3–Co1	59.86(5)	-	-

B.4 DFT analysis of [(^HL)Co₃(PMe₃)₃]^0/+

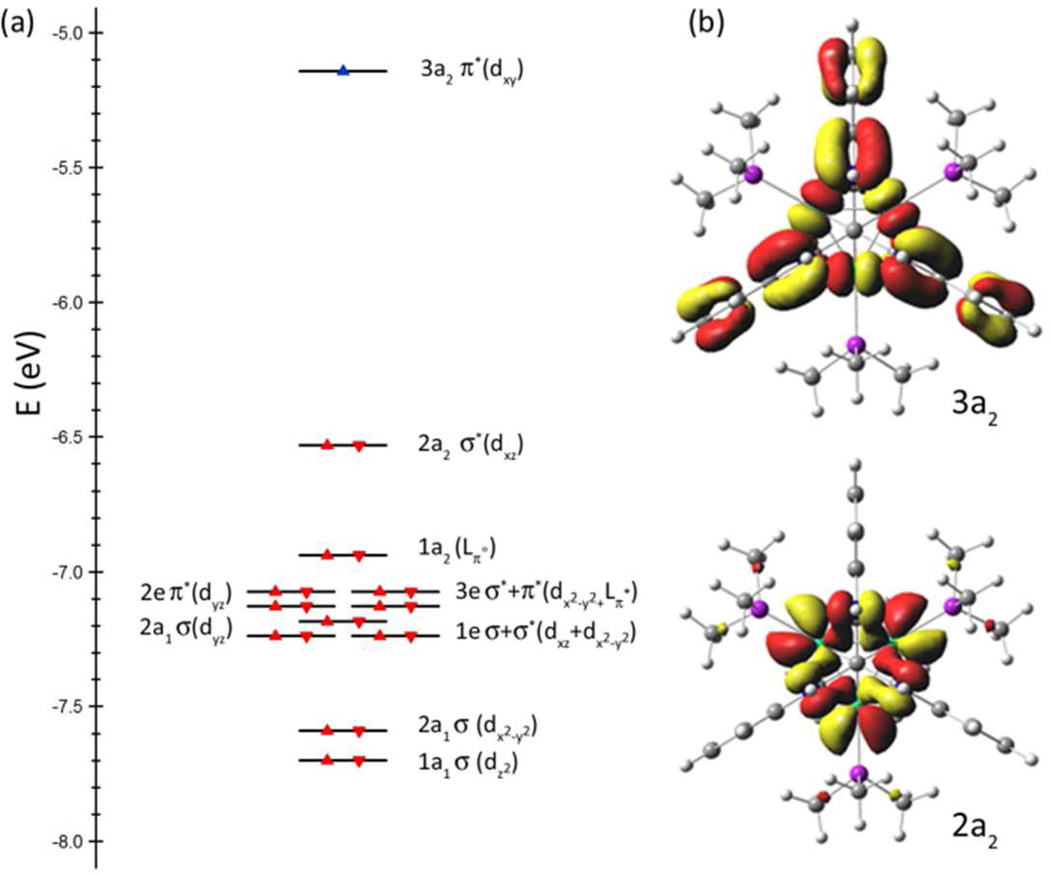
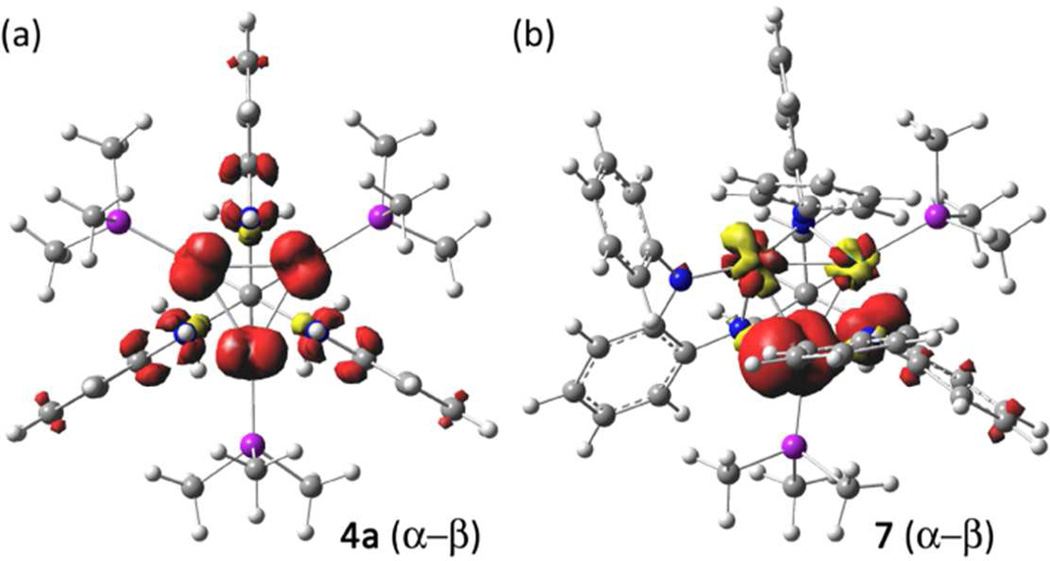
To further probe the electronic structure of [(^HL)Co₃(PMe₃)₃]^0/+, geometry optimizations with no symmetry restraints were performed on neutral 4 and 7 and cationic 8 (BP86/TZVP/SV(P)),^25,26 using coordinates from the X-ray data as an initial geometry. Comparison of the calculated bond lengths with those determined from X-ray analysis showed good agreement (see Table S5). The orbital energies for 4 and 8 are presented in Figure 5. The lowest unoccupied molecular orbital in 8 (or the singly occupied molecular orbital in 4) features both Co and ligand character. The 3a₂ orbital, pictured in Figure 5b, is comprised of a₂-symmetry combinations from the (^HL) ligand OPDA substituents and the a₂ combination of the three Co d_xy orbitals. This orbital combination features weak Co–Co π^* overlap and, more significantly, Co–Nσ^* interactions. The calculated bond metrics for neutral 4 and cationic 8 reproduced the decrease in the Co–Co separation and contraction of the Co–N interactions observed crystallographically, resulting from depopulation of the 3a₂ orbital. While both the frontier orbitals 1a₂ and 3e feature significant ligand contribution (see Figure S10), the remaining orbitals feature a larger component of cobalt parentage (see Figure S10). Despite the prominence of the OPDA contribution to the frontier orbitals in 4a, a spin density calculation (α–β) reveals that the primary spin density is located on the three Co ions, where the spin is equally distributed (for S = 1/2: Co1 0.25, Co2 0.26, Co3 0.27), with the remainder being ligand-borne (0.22). The spin density plot for 4a is illustrated in Figure 6a. As suggested by the EPR spectrum of 7, the lowered symmetry for the diphosphine complex produces two effects: (1) the conjugation between the OPDA subunits and the trinuclear core frontier orbitals is disrupted, and (2) the lowered symmetry and isosceles distortion of the trinuclear core suggests that the resultant spin is more localized on a single Co center (Co2 in Figure 2). The calculated spin density for 7 corroborates this assignment (for S = 1/2: Co1 −0.01, Co2 0.94, Co3 −0.01), which is illustrated in Figure 6b.

Figure 5.

(a) Computed orbital energies for (^HL)Co₃(PMe₃)₃ (4a) and [(^HL)Co₃(PMe₃)₃]⁺ (8a). (b) Molecular orbital representations for lowest unoccupied molecular orbital (LUMO, 3a₂) and highest occupied molecular orbital (HOMO, 2a₂) in 8a.

Figure 6.

Computed spin density (a–b) plots for 4a (a) and 7 (b).

C. Discussion

With the successful expansion of our synthetic approach to include Mn, Fe, and Co polynuclear complexes, several observations require address: (1) How does the overall molecular symmetry impact the molecular electronic structure? (2) To what extent do the redox-active ligand components participate in the observed redox behaviour of the clusters? (3) What governs the nature of coupling between the metal ions in the trinuclear complexes? These questions will act as guideposts as we set out to elucidate the correlation between molecular and electronic structure.

C.1 Structural considerations and molecular symmetry

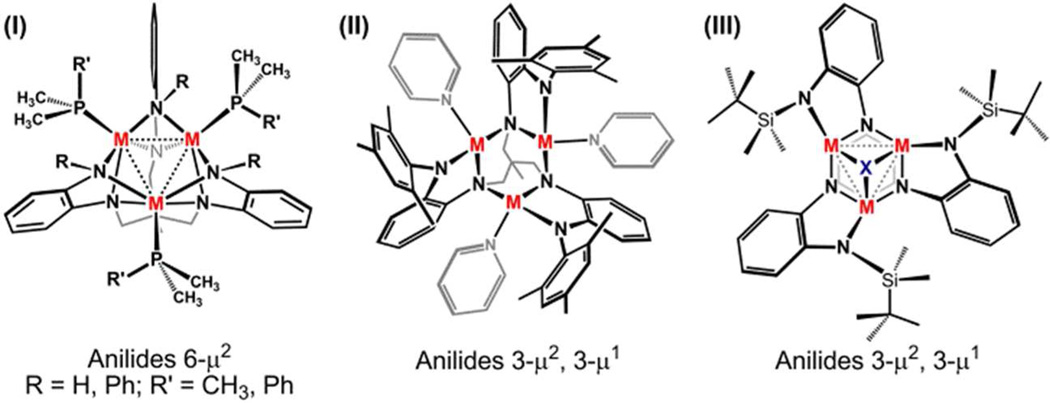
The polynuclear clusters employing the hexadentate ligand [^HL]⁶⁻ and its derivatives fall into three structure types, shown in Scheme 3, where the primary distinguishing characteristic of the structure types can be defined as the variation of angle between the planes defined by the M₃ core and each of the OPDA planes. In Type I structures, all six anilide groups are bridging (6-μ²) and the two planes are nearly orthogonal, with average dihedral angles (°) 89.04 (1), 86.67 (2), 89.56 (4b), 89.31 (5b), 88.91 (6b), 88.92 for (^HL)Fe₃(PMe₃)₃,⁹ 89.05 for (^PhL)Fe₃(thf)₃).¹¹ In Type II structures, only three anilides bridge (3-μ²), and the angle between OPDA and M₃ planes deviates significantly from orthogonality (e.g. 68.25° for 3). Finally, Type III structures show the greatest deviation (e.g., [(^tbsL)Fe₃(μ³-N)]⁻ 37.54°) and only occur upon bridging of a monoatomic ligand to the trinuclear core.¹²

Scheme 3.

The structural variation arises from the binding motif (μ¹ vs. μ²) of the peripheral anilide group, which changes as a function of the size of the anilide substituent. The proton- (^HL) or phenyl-capped (^PhL) ligand varieties permit bridging of the peripheral anilide group to adjacent metal ions (Type I), whereas o-substituted aryl (^MesL) and silyl (^tbsL) groups engender terminal binding to a single metal center (Types II and III, respectively). The larger substituents do not prevent the peripheral anilide unit from bridging exclusively, rather the substituents impede all three OPDA units from bridging adjacent metals. For example, the silyl-substituted complex (^tbsL)Fe₃(thf) features one silylanilide unit bridging two Fe sites (Type II).¹²

While the metal ion separation within the trinuclear core is affected by the type of supporting ligand, the M–M separation is more sensitive to the metal bound. Consistent with previously reported polynuclear Mn^II complexes,^16,27 complexes 1–3 do not feature close Mn–Mn interactions, suggesting an increased bonding interaction within the iron and cobalt analogues.²⁸ Further, within the trinuclear manganese complexes, the M–M separation is largely unaffected by changing the peripheral ligand anilide substituent from H to Ph. However, incorporation of the larger mesityl anilide units results in a significant increase in the Mn–Mn separation and a change in the local coordination environment at each metal center. Importantly, magnetic data for 1–3 can be modelled as stemming from superexchange between Mn^II ions through the bridging anilides, suggesting that direct Mn–Mn orbital interactions do not play a significant role in the exchange interactions. Complexes 1–3 all feature S = 1/2 ground states, where the strength of the superexchange interaction is most sensitive to the Mn–N–Mn angle, with the magnitude of J decreasing with increasing Mn–N–Mn angle (see Figure S9). This magnetostructural correlation is also manifested in the EPR spectra, where stronger coupling contributes to less resolved hyperfine coupling.

Unlike the Mn₃ clusters, employing larger ligand architectures in the Fe₃ clusters significantly increases Fe–Fe separation, which consequently impacts the resulting electronic structure. For instance, (^HL)Fe₃(PMe₃)₃, an example of a Type I structure, features an average Fe–Fe separation of 2.229(2) Å and an S = 1 ground state.⁹ Replacing (^HL) with (^PhL) to give (^PhL)Fe₃(PMe₂Ph)₃ leads to a dramatic increase in average Fe–Fe separation to 2.585(2) Å and an increase in spin ground state to S = 2.¹¹ Although a similar expansion of the Co ion separation is observed in the tricobalt series (see Table 1), complexes 4–7 all feature an S = 1/2 ground state. This observation suggests that the N₄P-coordination environment imparts a strong enough ligand field to enforce the Co₃ core into a low-spin regime.

C.2 Electronic structure considerations

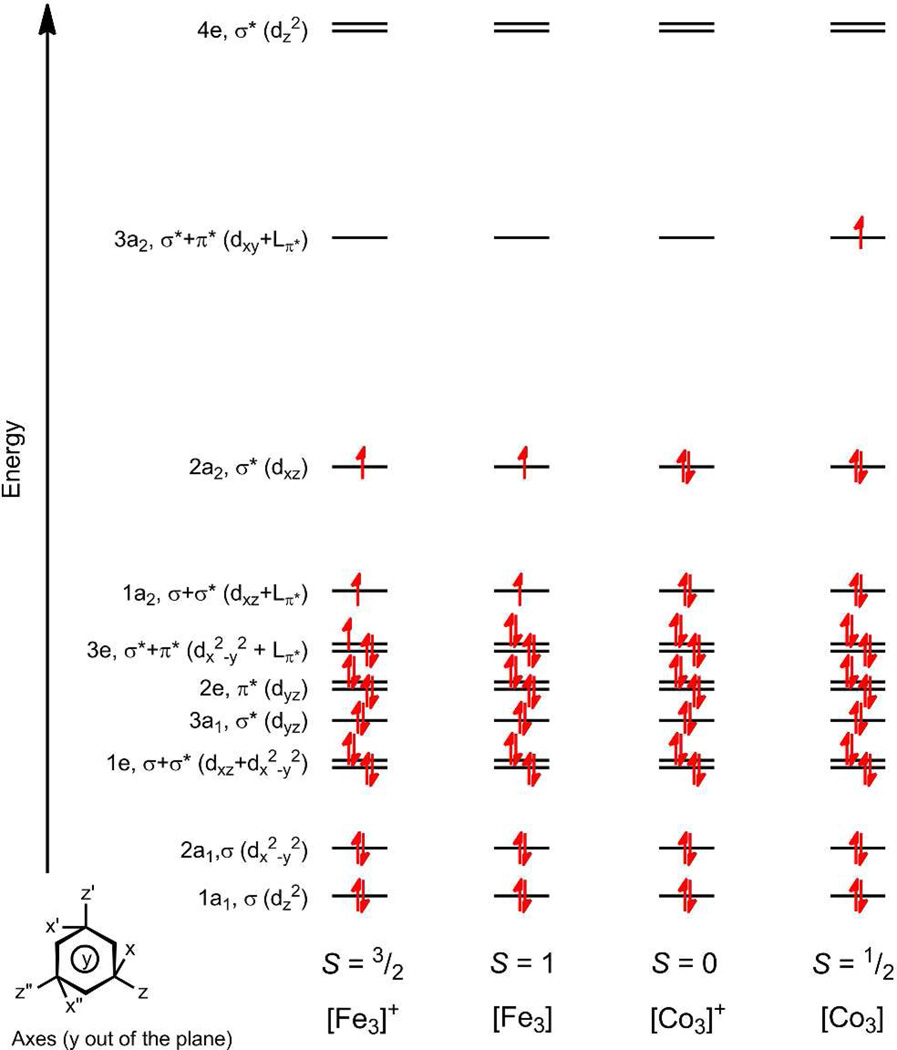
Given the data for all three sets of trinuclear clusters (Mn, Fe, and Co), spanning three structure types, we sought to establish how the structure type dictates electronic interactions between the redox-active components of the complex, the metal ions and OPDA substituents. The electronic structure of the Type I Fe₃ electron-transfer series focused exclusively on the M–M interactions in deriving a frontier molecular orbital scheme,⁹ analogous to the model first proposed by Cotton to rationalize the M–M bonding interactions within [Re₃Cl₉(μ₂-Cl)₃]³⁻.²⁹ Despite its simplicity, this model correctly predicts the ground spin state (S = 1/2) for the neutral Co₃ with a proposed electronic configuration of [(1a₁)_σ²(2a₁)_σ²(1e)_π⁴(3a₁)²(2e)⁴(1a₂)_σ*²(3e)_π*⁴(4e)_σ*¹], which will thus convert to a singlet ground state upon one-electron oxidation.

The DFT results for the redox pair 4a and 8a (and by extension, 5, 6 and [(^HL)Fe₃(PMe₂R)₃]^+/0) reveal a considerable energetic matching of the metal and ligand-based OPDA orbitals. Two of the three frontier orbitals described in Figure 5 exhibit substantial ligand contribution arising from the OPDA subunits. Specifically, the OPDA orbitals of a₂-symmetry that arise from mixing the π* orbitals mix with the metal-based orbitals of the same symmetry (d_xy in 3a₂, d_xz in 2a₂ and 1a₂). The electronic configuration within this orbital manifold reproduces the effects of oxidation exhibited by the conversion of 4a to 8a. Namely, the Co–Co distances decrease, and subtle structural changes within the OPDA units are also reproduced by the calculation (see Table S5). This mode of redox activity departs from the traditional electron transfer sequence of o-phenylenediamide → benzosemiquinonate → phenylenediimine exhibited by transition metal complexes featuring the redox active fragments.²⁴ Namely, the one-electron oxidation is borne by the trinuclear M₃ core and all three OPDA subunits. Thus, the traditional charge transfer bands assigned to the OPDA oxidation by Wieghardt and coworkers are either not present,^24c as in the oxidation of 4–6, or greatly attenuated as observed with [(^HL)Fe₃(PMe₂R)₃]⁺.⁹ While the structural changes in the [(^HL)Fe₃(PMe₂R)₃]^0/+ redox series were ascribed to depopulation of an antibonding orbital arising from the interaction of the M–based orbitals, the DFT results indicate the structural contraction arises from the depopulation of an orbital with M–L_N σ* symmetry (3a₂). For the [(^HL)Fe₃(PMe₂R)₃]^0/+ redox pair, the depopulation of an orbital exhibiting M–M σ* character (3e), in addition to removing electrons from 3a₂ and 2a₂, leads to trinuclear core contraction upon oxidation (see Figure 5).

The contribution of the OPDA subunits to the frontier orbitals of Co₃ series is also apparent in the EPR spectra obtained for complexes 4–6. The considerable ligand character in the S = 1/2 complexes manifests as broad features in the EPR spectrum without obvious hyperfine coupling to the Co nuclei in the temperature range 4–77 K. However, reducing the molecular symmetry of the Co₃ core in complex 7 effectively disrupts the conjugation of the Co₃ core and OPDA orbitals, thereby localizing the unpaired electron on a single Co center. This localization is evidenced by the sharp 8-line pattern of the EPR spectrum (Co, I = 7/2, Figure 2c bottom panel) and is further corroborated by the geometrical distortion that positions two Co atoms within close proximity of one another (Co1–Co3 2.3368(7) Å) relative to the longer distance to the spin-isolated Co2 (2.4377(7) and 2.4385(7) Å).

A similar phenomenon can be observed in the Mn₃ series. For complexes 1 and 2, which adopt a Type I structure, the EPR spectra exhibit hyperfine coupling that exceeds the 16-line pattern expected for the coupling to three Mn^II ions (I = 5/2). This phenomenon may arise due to the coordination mode change of the ligand scaffolds (6-μ² vs. 3-μ², 3-μ¹ anilide ligation), or it may suggest weak mixing of the Mn 3d orbitals with the OPDA subunits. Upon lowering the symmetry to the Type II structure in complex 3 (3-μ², 3-μ¹ anilide ligation), the OPDA units are not conjugated to the Mn orbitals of appropriate symmetry, thus the EPR transition exhibits well-defined hyperfine coupling to the Mn nucleii, giving the expected 16-line pattern without obvious contributions from the ligand framework.

C.3 Comparative magnetic coupling within Mn₃, Fe₃, and Co₃ cores

The M–M interactions observed in the trinuclear complexes investigated changes substantially in moving from Mn to Fe to Co. Indeed, the Mn₃ complexes exhibit coupling exclusively via superexchange through the anilide ligands, with no significant involvement of direct Mn–Mn orbital interactions. While structurally enforcing close Mn^II–Mn^II contacts can result in bonding interactions,²⁸ the Mn^II centers in complexes 1–3 exhibit greater separation. The contrasting behaviour of the Mn₃ clusters relative to the Fe₃ and Co₃ analogues may stem from the half-filled 3d orbital shell of the Mn^II ion. This electronic configuration represents an energy minimum, thus obviating the need for metal-metal interactions. In contrast, the low-spin Fe₃ and Co₃ complexes do indeed exhibit close M–M separation, within the range where direct M–M orbital overlap is possible. Moreover, calculations performed on the Co₃ series reveal electron delocalization within the frontier orbitals comprised of symmetry-allowed interactions between the three Co 3d orbitals. By extension, this description is also appropriate for the Fe₃ series (vide supra). The most significant difference between the Fe₃ and Co₃ series is that the Fe₃ complexes can span both low- and high-spin states (S = 1 → 6), depending on both supporting (e.g., ^HL, ^PhL, ^tbsL) and ancillary ligand (e.g., thf, py, PMe₂Ph), while all Co₃ clusters feature low-spin S = 1/2 ground states, regardless of the supporting ligand employed. Future ligand permutations will be aimed at accessing more sterically restricted local coordination environments, wherein variable open-shell configurations might be attainable for the Co₃ series.

D. Conclusions

This work demonstrates that the utility of tris(o-phenylenediamine) ligands in directing the formation of trigonal Fe₃ clusters can be extended to manganese and cobalt. A suite of spectroscopic and computational methods was applied to the resulting complexes, and the findings from these investigations are compared to properties previously reported for the Fe₃ analogues in order to probe the correlation of molecular and electronic structure. Particular attention is paid to the effects of constituent metal identity and steric effects imposed by both supporting and ancillary ligand substitution. Across the entire family of M₃ clusters, three distinct structure types are evident, with the types being primarily defined by the dihedral angle formed by OPDA and M₃ planes. While introduction of bulkier substituents onto the supporting ligand in the Mn₃ clusters can induce a change in structure type, the degree of metal ion separation in Mn₃ and Co₃ clusters is primarily dictated by the metal present in the M₃ core. In addition, while all Mn₃ and Co₃ clusters exhibit an S = 1/2 ground state, the ground state arises via different mechanisms: antiferromagnetic superexchange through the anilide ligands for the Mn₃ clusters, and via direct orbital overlap for the low-spin Co₃ clusters. The electronic differences between Co₃ and Mn₃ clusters may stem largely from the d⁵ electronic configuration of Mn^II, which already resides at an energetic minimum and therefore gains no added stabilization by engaging in metal-metal bonding interactions. The insight gained in this investigation will be employed to direct the formation of new metal clusters derived from poly(OPDA) ligand platforms, with the aim of synthesizing new high-spin, coordinatively unsaturated clusters for cooperative small-molecule activation.

Figure 7.

Frontier molecular orbital populations for (from left to right) [(^HL)Fe₃(PMe₂R)₃]⁺ (S = 3/2), (^HL)Fe₃(PMe₂R)₃ (S = 1), [(^HL)Co₃(PMe₂R)₃]⁺ (S = 0), and (^HL)Co₃(PMe₂R)₃ (S = 1/2).