Abstract
Adolescents engage in a wide range of risky behaviors that their older peers shun, and at an enormous cost. Despite being older, stronger, and healthier than children, adolescents face twice the risk of mortality and morbidity faced by their younger peers. Are adolescents really risk-seekers or does some richer underlying preference drive their love of the uncertain? To answer that question, we used standard experimental economic methods to assess the attitudes of 65 individuals ranging in age from 12 to 50 toward risk and ambiguity. Perhaps surprisingly, we found that adolescents were, if anything, more averse to clearly stated risks than their older peers. What distinguished adolescents was their willingness to accept ambiguous conditions—situations in which the likelihood of winning and losing is unknown. Though adults find ambiguous monetary lotteries undesirable, adolescents find them tolerable. This finding suggests that the higher level of risk-taking observed among adolescents may reflect a higher tolerance for the unknown. Biologically, such a tolerance may make sense, because it would allow young organisms to take better advantage of learning opportunities; it also suggests that policies that seek to inform adolescents of the risks, costs, and benefits of unexperienced dangerous behaviors may be effective and, when appropriate, could be used to complement policies that limit their experiences.
Keywords: aging, decision making, uncertainty, lifespan
Adolescents engage in more reckless, risky, and thrill-seeking behaviors than their younger and older peers (1–3); they have the highest rates of sexually transmitted diseases (4) and criminal behaviors (5) of any age group, and even drive faster than adults (6). The mortality and morbidity rates of adolescents are 200% greater than their younger peers, an increase that has been attributed to higher rates of what are traditionally called “risky behaviors.” Whatever psychological features give rise to these behaviors, they do not reflect flawed reasoning capabilities or generally poor decision-making skills—those are much improved in adolescents compared with younger children (7).
To protect adolescents from the consequences of their decisions, modern societies deploy a range of tools. Legally enforced age limits on gambling, drinking, driving, smoking, being able to open a bank account, and make medical decisions all limit adolescent engagement in high-risk behaviors. Educational programs inform adolescents of the risks and consequences of their behaviors in the hope that they will limit dangerous behaviors on their own.
We know that younger children show risk-related behaviors clearly distinct from those of adults (8–10). Why do adolescents make choices that dramatically increase their morbidity and mortality rates compared with younger children (11)? What feature of their decision making leads to these negative consequences? Do adolescents acquire a taste for risk that fades with age, or is a more subtle process at work?
To more fully understand behavior in risky situations, one can decompose decision making into the distinct behavioral subprocesses studied by psychologists and economists for nearly half a century. Tversky and Kahneman (12), for example, characterized decision making as the product of at least four distinct parameters: (i) attitudes toward risk per se; (ii) attitudes toward ambiguity; (iii) differential sensitivity to losses and gains; and (iv) impulsiveness (or patience). In parallel, the main theoretical approaches to the study of adolescent risk-taking in the psychology literature have been Reyna and Brainerd’s (13) fuzzy trace theory and imbalance theory (14, 15). Fuzzy trace theory identifies two basic processes: (i) a more precise form of risk-based analysis called “verbatim” thinking and (ii) a fuzzier “gist-based” method for reasoning about risk and reward. Fuzzy trace theory postulates that adolescents shift from verbatim to gist-based methods over development. Imbalance theory proposes that all decision makers rely on (i) a more precise frontocortical system and (ii) a less precise and emotionally driven limbic-based system. The theory hypothesizes that adolescents engage in more risky behaviors because the limbic-based system predominates during adolescence. Economists and psychologists have known for decades that one’s willingness to engage in an ambiguous, risky, and potentially costly behavior, like driving drunk, is determined by interactions among multiple processes. To more deeply understand why adolescents engage in risky behaviors it is necessary to examine each subprocess as a function of age.
Here we focus on two subprocesses, central to the economic approach, that have not been the subject of previous experimental decomposition in adolescents, and are widely acknowledged as central to understanding risk-related behaviors: a person’s taste for risk—henceforth, technical risk attitude—and her taste for ambiguity. The difference between risk and ambiguity in this technical sense is driven by the information available when a decision is made. As is standard practice in economics and psychology, we define a subject’s technical risk attitude as her willingness to accept offers when she knows the precise odds of each possible outcome. We define her ambiguity attitude as her willingness to accept offers when the precise odds of each possible outcome are not known. Most people exhibit technical risk aversion (16), preferring low risks to high risks, as well as ambiguity aversion (17), preferring known risks to unknown risks. Risk and ambiguity attitudes have been shown to be only weakly correlated across individuals (18, 19), and we do not know whether ambiguity contributes to adolescents’ risk-taking.
Results
To investigate risk and ambiguity attitudes in adolescents, we compared preferences for risky and ambiguous monetary lotteries in 33 adolescents (12–17 years old) and 32 adults (30–50 years old). All subjects completed a demographic form and a battery of personality and intelligence tests. These results were used as covariates to ensure that age-related differences in attitudes toward risk and ambiguity were not due to systematic differences in the underlying characteristics of the study participants.
Individual attitudes toward risk and ambiguity were assessed using a standard incentive-compatible technique widely used in economics (20) and neuroscience (19). In each of 160 choice trials, subjects had to choose between a certain payoff of $5 and a monetary lottery offering a chance to win more than $5 and a chance to win nothing. Across trials, the parameters of the lottery were varied systematically (in random order) to determine how the magnitude of the potential win, probability of winning, and ambiguity influenced a subject’s choices.
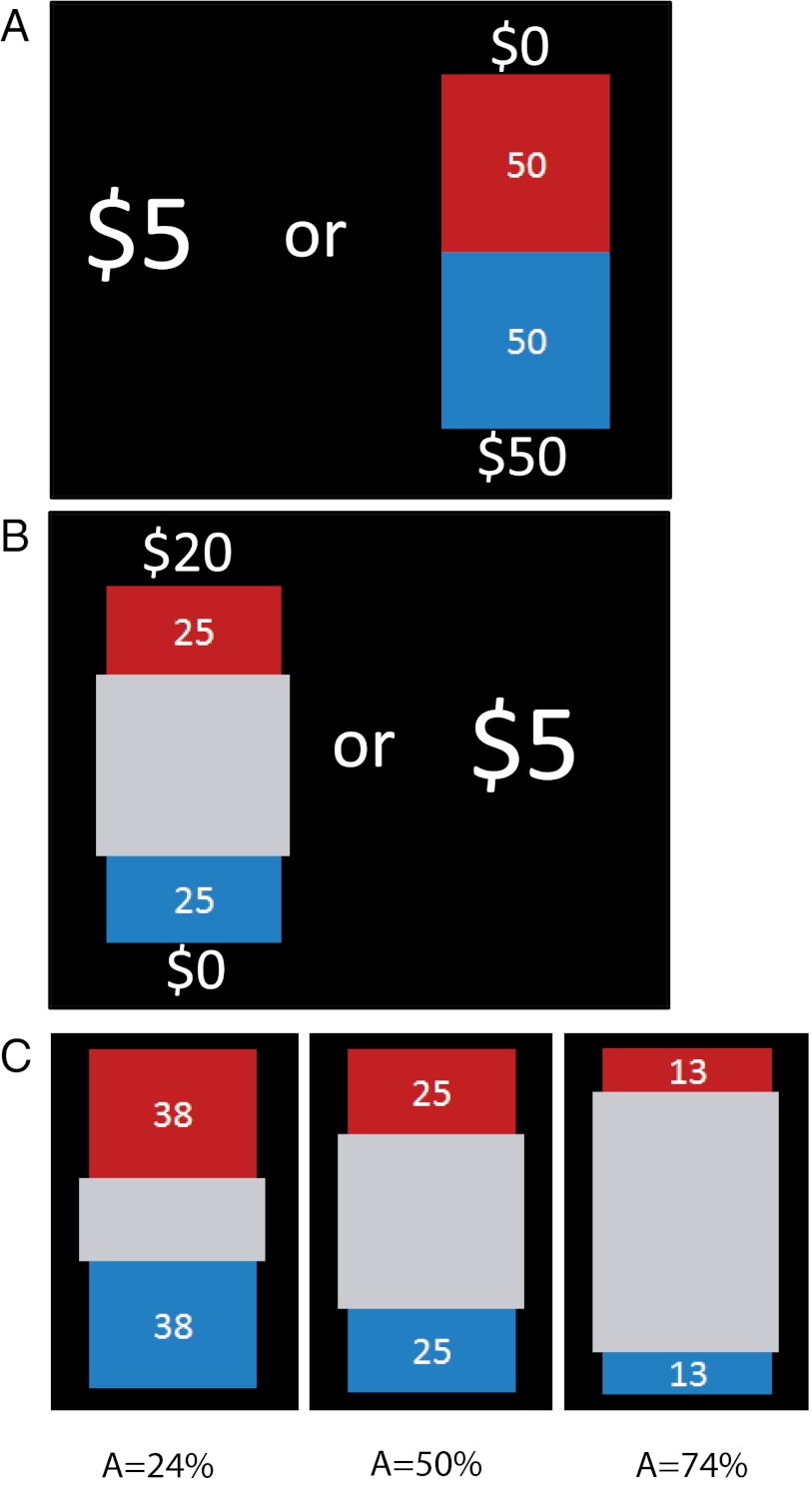
Each lottery was either technically risky or ambiguous, allowing us to assess each subject’s aversion to known (risky) and unknown (ambiguous) monetary risks. Fig. 1A depicts a technically risky trial. Here, a subject chooses between a certain $5, an option available on every trial, and a lottery with a 50% chance of winning $50 or $0. Subjects were told that each image depicted a stack of 100 poker chips, the number of chips of each color represented by the size of the corresponding colored area and the number written inside it. Because previous research has suggested that people may behave differently when their choices are hypothetical (21), we made the choices consequential. Subjects were informed that at the end of the experiment, one trial would be randomly selected and their decision on that trial would result in real monetary consequences. If they picked the certain payoff they would receive $5. If they picked a lottery they would reach into a bag filled with red and blue poker chips, and if they drew the winning color they would win between $5 and $125, depending on the lottery.
Fig. 1.
Experimental design. (A) Example of risky trial. The subject has a choice between $5 and equal chances of winning $50 or nothing. (B) Example of ambiguous trial. The subject has a choice between $5 and a lottery that pays $20, with a probability that is not precisely known. (C) All ambiguous lottery bags used in the experiment.
Fig. 1B depicts an ambiguous trial; a choice between a certain $5 or a lottery paying $20 or $0 with an ambiguous probability. To create ambiguity, a gray occluder covering 50 of the poker chips is displayed; the subject knows there are at least 25 red and 25 blue chips. The remaining 50 can be any combination of red and blue, implying that the odds of winning $20 can be anywhere from 25% to 75%. Fig. 1C presents the three possible ambiguous lotteries. Increasing occluder size reduces information about the contents of the bag, raising the level of ambiguity.
In our classical design (17), the objective winning probability in each ambiguous lottery is exactly 0.5, because each color (red and blue) is the winning color in half of the trials, and subjects do not know whether a red or blue trial will be selected for play (17, 22). Thus, an ambiguity-neutral person should view all of these ambiguous lotteries as the same as risky lotteries with a 50% chance of winning. An extremely pessimistic, or ambiguity-averse, individual would fear that the ambiguous offer (Fig. 1B) contains only 25 red chips. She would thus treat this as a risky lottery with a 25% chance of winning. An extremely optimistic, or ambiguity-seeking, individual would behave as if there are 75 red chips in the bag.
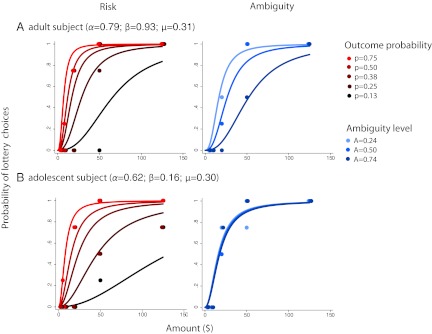
The simplest way to quantify technical risk and ambiguity attitudes is to calculate the proportion of times each age group chose a lottery over the certain option for each risk level. Fig. 2 depicts the proportion of trials in which subjects accepted the lottery as a function of lottery amount in technically risky (left) and ambiguous (right) trials. Both the adult and adolescent exhibited some risk aversion by choosing the certain amount over lotteries with higher average payoff. These subjects differed, however, in the level of their risk aversion. Though the adult always preferred the chance of $125 over the certain $5, the adolescent did not. Even more striking is the difference in ambiguous lottery choices. Recall that the objective winning probability for all of the ambiguous lotteries is 50%; a subject not affected by ambiguity should make similar choices regardless of the level of ambiguity. The adolescent subject in Fig. 2 indeed made almost identical choices under the three levels. The adult, however, showed a strong effect of ambiguity. This subject behaved as if the winning probability was the worst possible probability under each ambiguity level; his choices of lotteries at 50% ambiguity were similar to his choices of technically risky lotteries at a 25% winning probability.
Fig. 2.
Single subject choice behavior. The graphs represent the proportion of trials in which an adult (A) and an adolescent (B) chose the lottery over the sure amount (i.e., always equal to $5) as a function of the reward associated with the lottery, in risky (Left) and ambiguous (Right) trials. Dots indicate actual choice behavior. Smooth curves are a result of fitting the data to our choice model.
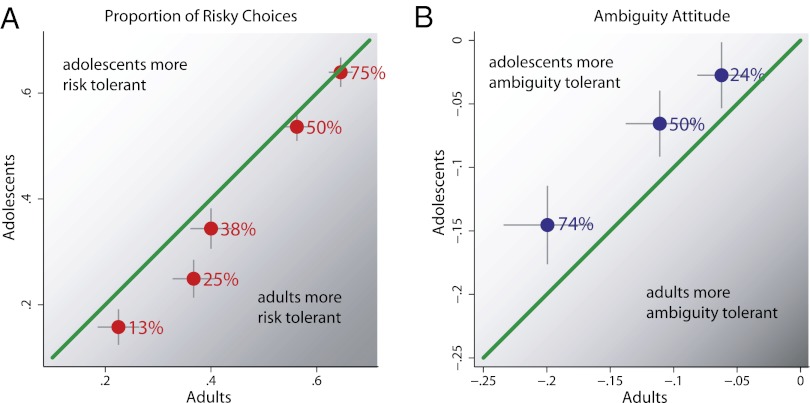
As Fig. 3 shows, these age-related differences were consistent in our subject populations. In Fig. 3A we plot the overall proportion of risky choices made by our adolescents against the same measure in our adults at each of the five risk levels we examined. If adolescents are more risk-seeking than adults in the technical sense, then these points should lie above the main diagonal of the graph. Fig. 3A shows that this is not the case; all of the points lie on or below the 45° line. Our adolescents unequivocally accept fewer risky lotteries than do their adult counterparts. A two-way ANOVA confirms that these overall age-related differences in technical risk attitude are statistically significant (P = 0.012) in our sample.
Fig. 3.
Comparison of risk and ambiguity attitudes in adolescents and adults. In A, each dot plots the average proportion of times that a risky lottery, characterized by a winning probability indicated next to the dot, was chosen over $5 for sure by adolescents (vertical axis) and adults (horizontal axis). In B, each dot plots the average ambiguity attitude of adolescents against the ambiguity attitude of adults at each level of ambiguity, indicated next to the dot. Error bars indicate SEM.
Assessing overall ambiguity attitudes is slightly more complicated because we must take into account the technical risk attitude of each individual before we calculate how much that risk attitude is altered by ambiguity; this is because the ambiguous lotteries offer a combination of both risk (at 50%) and ambiguity. We therefore computed the difference between the proportion of times that a lottery of each ambiguity level was chosen and the proportion of times that risky lotteries with a 50% chance of winning were chosen. These 50% lotteries serve as controls, differing only in the critical property of ambiguity. In Fig. 3B we plot the risk-corrected overall proportion of ambiguous choices made by our adolescents against the same measure in our adults at each of the three ambiguity levels. If adolescents are more ambiguity tolerant than adults, these points should lie above the main diagonal of the graph. As shown in Fig. 3B, this is the case. All data points lie above the 45° line. Our adolescents are more willing to accept ambiguous lotteries than are their adult counterparts. A two-way ANOVA confirms that these overall age-related differences in ambiguity attitude are statistically significant (P = 0.0139) in our sample.
This analysis suggests that adolescents are actually more technically risk averse than young adults, but we also know that they do take more risks in the real world. This paradox seems to be explained by an increased ambiguity tolerance. It is not that adolescents actually choose to engage in risks, but rather they are willing to gamble when they lack complete knowledge. Of course this simple analysis cannot control for socioeconomic or psychological factors. In what follows, we show that our results survive a structural estimation that uses socioeconomic factors and psychological scales scores as covariates.
We derived structural estimates of risk and ambiguity attitudes of the members of each age group by modeling the expected utility (U) of each option under consideration with a widely used power utility function that takes into account the effect of ambiguity on perceived winning probability. This particular parameterization was described originally by Gilboa and Schmeidler (23) and used in a similar manner by Levy et al. (19):
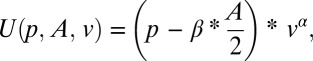 |
where v is the associated dollar amount, p is the winning probability, A is the ambiguity level, α is a measure of technical risk attitude, and β is a measure of ambiguity attitude. An individual with α = 1 would be risk neutral, and would switch from choosing the safe option to choosing a risky option when the latter option has a higher expected value. A risk-seeking subject would show an α > 1, a risk-averse subject would show an α < 1. A subject with a β = 0 would be ambiguity neutral; a pessimistic subject who viewed the uncertain component of any ambiguous lottery as reducing the probability of winning would show a β > 0; and an ambiguity-seeking, or optimistic, subject would show a β < 0. Ambiguity aversion as specified above is thus a concept that is very similar to pessimism.
Using maximum likelihood, we fitted choice data separately for teenagers and adults with the following probabilistic choice function:
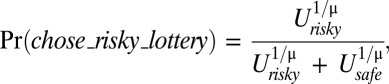 |
classically used by Luce (24) as well as by Holt and Laury (21), where μ is the noise parameter. Intuitively as the noise becomes large, choice becomes more random.
Fig. 2 presents this analysis for the two representative subjects in the fit lines. Fig. 4 presents group results. Because this analysis pools data within each subject group, the significance tests must respect the fact that the many choices in the dataset coming from each individual subject are nonindependent. Our statistical model therefore clustered SEs on individual subjects for the purpose of significance testing.
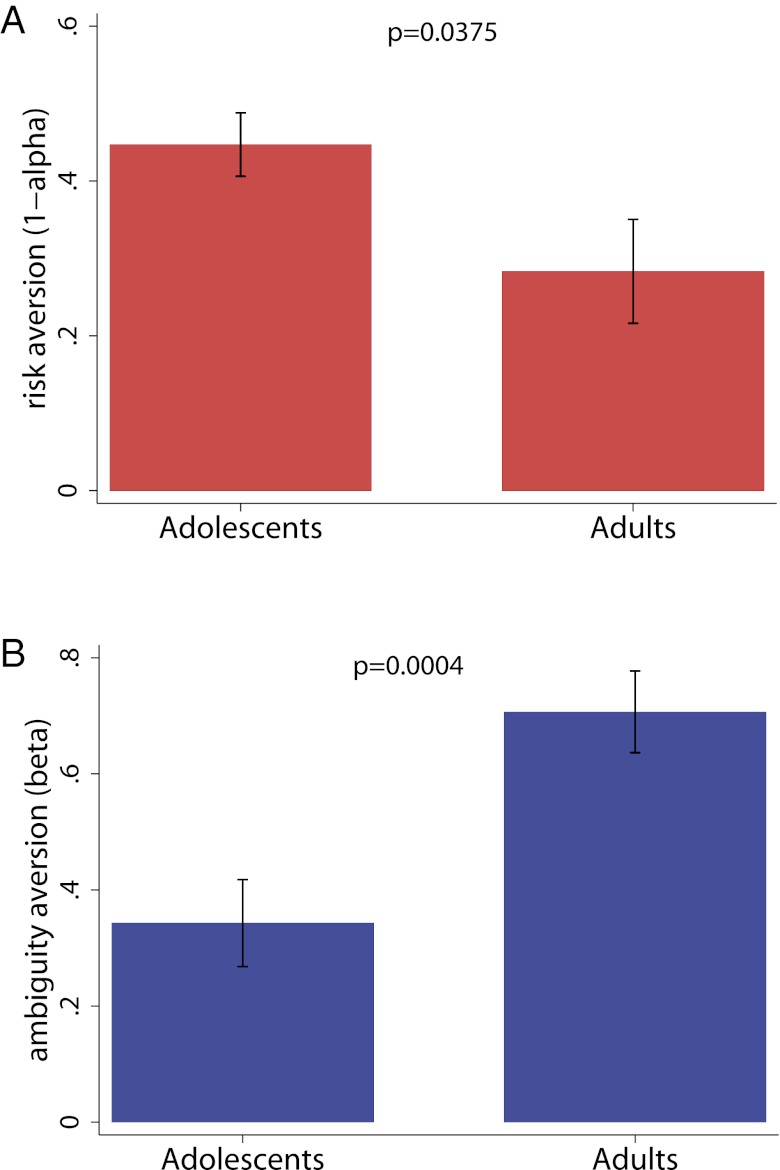
Fig. 4.
Estimated (A) risk aversion and (B) ambiguity aversion in adolescents and adults.
Fig. 4A plots the degree of technical risk aversion (1 − α) observed in adults (1 − α = 0.28 ± 0.07; mean ± SE) and adolescents (0.45 ± 0.04), with α = 1 (1 − α = 0), indicating risk neutrality. As in the nonparametric analysis, adolescents are more risk averse than adults (Wald test, P = 0.0375). An opposite pattern is observed in Fig. 4B, which plots the degree of ambiguity aversion (β). As in the nonparametric analysis, adolescents tolerate more ambiguity (β = 0.34 ± 0.08) than adults (β = 0.71 ± 0.07; Wald test P = 0.0004). Adolescents and adults exhibit the same degree of randomness in their behavior (μadolescent = 0.56 ± 0.06 vs. μadult = 0.57 ± 0.06, Wald test P = 0.830).
To control for socioeconomic and psychological factors, we next performed a series of more complicated procedures. In the first, we refit the structural model but included each individual’s psychological attraction to desired objects [known as behavioral approach scores (BAS); higher for less sensitive to rewarding stimuli] and each individual’s psychological propensity to avoid things that are unpleasant [behavior inhibition scores (BIS); higher for less sensitive to nonrewarding stimuli] (25) as covariates with the risk aversion parameter, the ambiguity aversion parameter, and the noise parameter. Previous results in the literature suggest that sensation-seeking and behavioral inhibition develop over the lifespan and correlate with experimental as well as self-reported real-life risk-taking practices (14, 26, 27). Our approach allowed us to ask whether there was an independent effect of age group on risk and/or ambiguity attitudes even when each individual’s BIS/BAS scores were controlled for in the fitting process. When these covariates were added, we found there was still a significantly greater tolerance for risk in the adults and for ambiguity in the adolescents. Detailed results are presented in Table S1.
We repeated the same type of analysis controlling for individual differences in impulsivity [using all nine measures of the Barratt Impulsiveness Scale (B11) as independent covariates] (28). We found that systematic differences in impulsivity characteristics between our groups do not drive the main result of the paper (Table S2). In a similar way, we found that adolescents are not more risk-seeking and are significantly more ambiguity tolerant than adults when we account for differences in sex, total household wealth, number of siblings, and IQ score (Table S3). [We replicate our major findings using continuous age variable (Table S4).]
To verify that adolescents in our sample did not differ on common measures of risk-taking from adolescents that have been previously studied, we administered the Adolescent Risk-Taking Questionnaire (ARQ) (2), a premier measure of adolescent risky behavior, to all of our adolescent subjects. Our adolescents’ behavior (Fig. S1) was well within 1 SD (and usually within just one-half of the SD) of the scores reported by Gullone et al. (2), confirming that our subjects were typical of their age group in this regard.
The ARQ measures individual perceptions of different types of behaviors and frequency of engaging in these behaviors, and it is therefore interesting to examine the relationships between responses on this questionnaire and our measures of technical risk and ambiguity attitudes. It should be noted, however, that this questionnaire does not control for or elicit individual beliefs about the possible consequences of the studied behaviors, their probabilities, and the precision of these probability estimates. The indicated responses might therefore represent either individual technical risk attitudes or ambiguity attitudes or both. It would be natural to expect ARQ scores to correlate with ambiguity attitudes in the domains where adolescents know little about the consequences of their actions; in the domains they are familiar with, we would expect a significant relationship with technical risk attitude. In Table S5, we present results of our model fit using ARQ scores as covariates. In line with intuition, we find that adolescents who engage more frequently in reckless behaviors (ARQ reckless) are significantly more ambiguity tolerant. Perhaps contrary to one’s intuition, those that perceive rebellious behaviors as more risky (ARQ rebel) are significantly more ambiguity tolerant in our measures. We also find that subjects less sensitive to rewarding stimuli (higher BAS reward score) are more ambiguity averse. To make sure that these results are robust, we control for the psychological scores that came up as significant predictors of risk and ambiguity attitudes in Tables S1–S3, as well as age and site effects.
Discussion
By separating the basic building blocks of what is commonly perceived as risky, we were able to gain a richer understanding of adolescent behavior. The evolution of risky behaviors across the lifespan is more complex than previously suspected, showing opposite patterns of age related changes in technical risk aversion and ambiguity aversion. Our data suggest that what is commonly viewed as increased risk-seeking in adolescents is driven not by preference for technical risk per se, but rather by a greater tolerance for options with consequences that have unknown probabilities. These results are robust to different data analytic approaches and remain significant when we control for systematic differences in psychological profiles and socioeconomic features.
Traditionally, research on the evolution of general risk attitudes over the lifespan has focused on differences in decision-making capacities (sensitivity to risk, probability estimation, etc.), emotional development, neurological and biochemical development, and social factors (29). All of these factors influence the likelihood that an individual will engage in risky behaviors, such as unprotected sex, drinking and driving, gambling, etc. (29), but the contribution of each factor to such behaviors changes as a function of age, with a pronounced effect of social and emotional factors on adolescents (14, 15, 30–32). We note that other studies, focused on technical risk, have found mixed evidence on age and risk-taking behavior. Though some studies confirm our findings that adolescents, at least those over 14 years of age, are not more technically risk-seeking than adults (33, 34), other important and well-regarded studies find that there are significant differences in risk-taking that depend on, among other things, the magnitude of the potential win (26, 27), providing compelling evidence that technical risk attitudes are distinct in adolescence. Our unique separation of ambiguity and risk at a within-subjects level allows us to contribute a unique perspective on the basic processes underlying the differences and similarities between adolescents and adults.
Some psychological research suggests that individual risk attitudes in domains such as financial, social, and health are uncorrelated (35). One could thus argue that risk and ambiguity attitudes in the monetary domain are not directly applicable to other everyday decisions. These previous reports, however, did not account for differences in subjects’ beliefs about outcome probabilities across domains (36). In support of this interpretation, Dohmen et al. (36) estimated that ∼60% of the variance in risk-taking in different domains can be explained by one common component, suggesting a stable risk attitude across all contexts. Compatible with this finding, a recent study by our group found very similar technical risk attitudes in choices about money, food, and water at the within-subject level (37). Moreover, a rich body of literature (38–41) has shown that the external validity of tasks developed in the laboratory to measure different subprocesses of risk-taking in the monetary domain is generally high. All of these studies lead one to conclude that differences in risk preferences are related to real-world risk-taking in adolescents.
What distinguishes our study from previous studies on adolescent risk-taking is that we focus on age-related differences in the response to known vs. unknown risks. Although technical risk aversion and ambiguity aversion might be thought of as one process, our data suggest that these two measures follow separate developmental paths. When we see young children engaged in risky actions we do not think about them as risk-takers, but rather we see them as curious about the world that surrounds them. This process of learning continues throughout life, and our results suggest that young people are equipped with a high tolerance for the unknown, a feature of this class of behavior.
Our results suggest that policies that aim to correct adolescent decision making under risk by providing a safe and supervised environment for learning by doing may in some cases be more effective than those that rely on prohibition (42). Good examples of tools that show great promise are drink-and-drive simulators that give participants complete experience from a sober perspective of driving while intoxicated. Decisions made in early childhood and adolescence establish patterns of behaviors that we carry throughout adulthood (43). Our data suggest the importance of understanding why adolescents make choices that are detrimental to their health and well-being.
Materials and Methods
Subjects.
A total of 65 subjects participated in the study: 33 adolescents (12–17 y old, 17 female) and 32 adults (30–50 y old, 17 female). Subjects were recruited in New York City and New Haven, CT, via traditional techniques such as fliers and recruitment e-mails sent to local online communities. We balanced the number of men and women in each age group and at each location. All participants signed an informed consent. This research project was approved by the University Committee on Activities Involving Human Subjects at New York University and the Human Investigation Committee at Yale University.
All potential subjects were screened for medications known to influence decision making under risk, such as medications for attention deficit disorder, depression, or anxiety. Any potential subject who had recently been medicated for one or more of these conditions was excluded from participating in the study. Only one person per household and family was allowed to participate.
Procedures.
Main task.
In the first session, we assessed individual attitudes toward risk and ambiguity using a standard incentive-compatible technique widely used in both economics (20) and neuroscience/neuroeconomics research (19). Upon arrival at the testing site, subjects were seated individually in front of private computer stations where they received extensive instructions and training. After they understood the task and had passed a detailed task comprehension test, they were allowed to proceed to the experiment itself.
The procedure consisted of 160 choice situations (trials) that presented a choice between one of two monetary options. One option was always a certain payoff of $5, the other was a lottery that might pay more than $5 but might also pay $0. On half of the trials, outcome probability was precisely specified (technical risk; Fig. 1A); on the other half, information about outcome probability was partially hidden, rendering the probability ambiguous (Fig. 1 B and C). Across trials, the details of the lottery were varied systematically (in random order) to determine how probability of winning (13%, 25%, 38%, 50%, and 75%), the magnitude of the potential win ($5, $8, $20, $50, and $125), and ambiguity about the probability of winning (24%, 50%, and 74% ambiguity around a probability of 50%) influenced choices. All potential rewards were fully crossed with each level of risk and ambiguity, yielding 40 unique lotteries. Each unique lottery was presented four times, counterbalancing the side where it appeared on the screen and the winning color, resulting in a total of 160 choice trials. Winning probabilities were chosen to be within a range where the probability weighting function has been previously shown to be relatively linear (12, 44, 45). In each trial, subjects made their choice using a computer keyboard. Two blocks of 80 trials each were presented interleaved with symmetrically structured blocks of loss trials, where the subject could choose to lose $5 for sure or play a lottery that would result in a loss (from $5 to $125) with the corresponding losing probabilities and ambiguity levels as in the gain trials. The order of gain and loss blocks was counterbalanced within each age group and site. Results from the loss trials will be reported elsewhere.
After making all 320 pairwise decisions, the subject drew a number out of a bag to determine for which trials she would be paid. If she picked the certain payoff on that trial, she received that amount. If she picked a lottery, she would reach into a bag filled with red and blue poker chips, and if she drew the winning/loosing color she would realize the amount specified by the lottery. We endowed subjects with $125 in the beginning of the study. Additionally, subjects received a $10 fee for participating in the experimental session and $30 for participating in the questionnaire session.
Subjects who chose $5 lotteries over getting $5 for sure more than half of the times were excluded from the parametric analysis because we cannot in principle infer their risk and ambiguity preferences (46). There were two such subjects, one adolescent and one adult.
General measures.
In a separate session, subjects completed an extensive demographic form and underwent a battery of psychological tests [BIS/BAS scales (25), the B11 Impulsivity Scale (28), the Domain-Specific Risk-Taking Scale for adults (35), and the ARQ (2)]. We estimated IQ using the nonverbal part of Kaufman Brief Intelligence Test 2. We measured numeracy skills using the numeracy module of the Health and Retirement Study done by the US Department of Health and Human Services (47). All measures were taken after subjects had performed the main task.
Adolescents: Special Procedures.
Each teenager provided a signed consent form from their parents. Accompanying parents and caregivers were compensated at a rate of $10/h. Teenagers filled out a different demographic form than adult subjects, and their parents or guardians were asked to complete a demographic form as well.
Supplementary Material
Acknowledgments
We thank two anonymous referees for their comments and suggestions. We also thank Samantha Shaw, Mariam Akbar, and Sana Samnani for their support in data collection. This research was supported by National Institutes of Health, National Institute on Aging Grant 5R01AG033406 (to P.W.G. and I.L.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1207144109/-/DCSupplemental.
References
- 1.Arnett J. Reckless behavior in adolescence: A developmental perspective. Dev Rev. 1992;12:339–373. [Google Scholar]
- 2.Gullone E, Moore S, Moss S, Boyd C. The Adolescent Risk-Taking Questionnaire: Development and psychometric evaluation. J Adolesc Res. 2000;15:231–250. [Google Scholar]
- 3.Spear LP. The Behavioral Neuroscience of Adolescence. New York: Norton; 2010. [Google Scholar]
- 4.Gittes EB, Irwin CE., Jr Sexually transmitted diseases in adolescents. Pediatr Rev. 1993;14:180–189. doi: 10.1542/pir.14-5-180. [DOI] [PubMed] [Google Scholar]
- 5.Arnett JJ. Sensation seeking, aggressiveness, and adolescent reckless behavior. Pers Individ Dif. 1996;20:693–702. [Google Scholar]
- 6.Jonah BA. Accident risk and risk-taking behaviour among young drivers. Accid Anal Prev. 1986;18:255–271. doi: 10.1016/0001-4575(86)90041-2. [DOI] [PubMed] [Google Scholar]
- 7.Reyna VF, Farley F. Risk and rationality in adolescent decision making: Implications for theory, practice, and public policy. Psychol Sci Public Interest. 2006;7:1–44. doi: 10.1111/j.1529-1006.2006.00026.x. [DOI] [PubMed] [Google Scholar]
- 8.Reyna VF, Ellis SC. Fuzzy-trace theory and framing effects in children’s risky decision making. Psychol Sci. 1994;5:275–279. [Google Scholar]
- 9.Levin IP, Hart SS. Risk preferences in young children: Early evidence of individual differences in reaction to potential gains and losses. J Behav Decis Making. 2003;16:397–413. [Google Scholar]
- 10.Crone EA, van der Molen MW. Developmental changes in real life decision making: Performance on a gambling task previously shown to depend on the ventromedial prefrontal cortex. Dev Neuropsychol. 2004;25:251–279. doi: 10.1207/s15326942dn2503_2. [DOI] [PubMed] [Google Scholar]
- 11.Dahl RE. Adolescent brain development: A period of vulnerabilities and opportunities. Keynote address. Ann N Y Acad Sci. 2004;1021:1–22. doi: 10.1196/annals.1308.001. [DOI] [PubMed] [Google Scholar]
- 12.Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty. J Risk Uncertain. 1992;5:297–323. [Google Scholar]
- 13.Reyna VF, Brainerd CJ. Fuzzy-trace theory: An interim synthesis. Learn Individ Differ. 1995;7:1–75. [Google Scholar]
- 14.Somerville LH, Jones RM, Casey BJ. A time of change: Behavioral and neural correlates of adolescent sensitivity to appetitive and aversive environmental cues. Brain Cogn. 2010;72:124–133. doi: 10.1016/j.bandc.2009.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Steinberg L. A social neuroscience perspective on adolescent risk-taking. Dev Rev. 2008;28:78–106. doi: 10.1016/j.dr.2007.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.von Gaudecker HM, van Soest A, Wengström E. Heterogeneity in risky choice behaviour in a broad population. Am Econ Rev. 2011;101:664–694. [Google Scholar]
- 17.Ellsberg D. Risk, ambiguity, and the savage axioms. Q J Econ. 1961;75:643–669. [Google Scholar]
- 18.Borghans L, Golsteyn GH, Heckman JJ, Meijers H. Gender differences in risk aversion and ambiguity aversion. J Eur Econ Assoc. 2009;7:649–658. [Google Scholar]
- 19.Levy I, Snell J, Nelson AJ, Rustichini A, Glimcher PW. Neural representation of subjective value under risk and ambiguity. J Neurophysiol. 2010;103:1036–1047. doi: 10.1152/jn.00853.2009. [DOI] [PubMed] [Google Scholar]
- 20.Cox J. In: Risk Aversion in Experiments. Harrison GW, editor. Bingley, United Kingdom: Emerald; 2008. [Google Scholar]
- 21.Holt CA, Laury SK. Risk aversion and incentive effects. Am Econ Rev. 2002;92:1644–1655. [Google Scholar]
- 22.Glimcher PW, Rustichini A. Neuroeconomics: The consilience of brain and decision. Science. 2004;306:447–452. doi: 10.1126/science.1102566. [DOI] [PubMed] [Google Scholar]
- 23.Gilboa I, Schmeidler D. Maxmin expected utility with non-unique prior. J Math Econ. 1989;18:141–153. [Google Scholar]
- 24.Luce RD. Individual Choice Behavior: A Theoretical Analysis. New York: Wiley; 1959. [Google Scholar]
- 25.Carver CS, White TL. Behavioral inhibition, behavioral activation, and affective responses to impending reward and punishment: The BIS/BAS scales. J Pers Soc Psychol. 1994;67:319–333. [Google Scholar]
- 26.Reyna VF, et al. Neurobiological and memory models of risky decision making in adolescents versus young adults. J Exp Psychol Learn Mem Cogn. 2011;37:1125–1142. doi: 10.1037/a0023943. [DOI] [PubMed] [Google Scholar]
- 27.Van Leijenhorst L, et al. Adolescent risky decision-making: Neurocognitive development of reward and control regions. Neuroimage. 2010;51:345–355. doi: 10.1016/j.neuroimage.2010.02.038. [DOI] [PubMed] [Google Scholar]
- 28.Patton JH, Stanford MS, Barratt ES. Factor structure of the Barratt Impulsiveness Scale. J Clin Psychol. 1995;51:768–774. doi: 10.1002/1097-4679(199511)51:6<768::aid-jclp2270510607>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 29.Boyer T. The development of risk-taking: A multi-perspective review. Dev Rev. 2006;26:291–345. [Google Scholar]
- 30.Casey BJ, Jones RM, Hare TA. The adolescent brain. Ann N Y Acad Sci. 2008;1124:111–126. doi: 10.1196/annals.1440.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gardner M, Steinberg L. Peer influence on risk taking, risk preference, and risky decision making in adolescence and adulthood: An experimental study. Dev Psychol. 2005;41:625–635. doi: 10.1037/0012-1649.41.4.625. [DOI] [PubMed] [Google Scholar]
- 32.Figner B, Mackinlay RJ, Wilkening F, Weber EU. Affective and deliberative processes in risky choice: Age differences in risk taking in the Columbia Card Task. J Exp Psychol Learn Mem Cogn. 2009;35:709–730. doi: 10.1037/a0014983. [DOI] [PubMed] [Google Scholar]
- 33.Harbaugh WT, Krause K, Vesterlund L. Risk attitudes of children and adults: Choices over small and large probability gains and losses. Exp Econ. 2002;5:53–84. [Google Scholar]
- 34.Burnett S, Bault N, Coricelli G, Blakemore S-J. Adolescents’ heightened risk-seeking in a probabilistic gambling task. Cogn Dev. 2010;25:183–196. doi: 10.1016/j.cogdev.2009.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Blais AR, Weber EU. A domain-specific risk-taking (DOSPERT) scale for adult populations. Judgm Decis Mak. 2006;1:33–47. [Google Scholar]
- 36.Dohmen T, et al. Individual risk attitudes: Measurement, determinants and behavioral consequences. J Eur Econ Assoc. 2009;9:522–550. [Google Scholar]
- 37.Levy DJ, Glimcher PW. Comparing apples and oranges: Using reward-specific and reward-general subjective value representation in the brain. J Neurosci. 2011;31:14693–14707. doi: 10.1523/JNEUROSCI.2218-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Galvan A, et al. Earlier development of the accumbens relative to orbitofrontal cortex might underlie risk-taking behavior in adolescents. J Neurosci. 2006;26:6885–6892. doi: 10.1523/JNEUROSCI.1062-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Galvan A, Hare T, Voss H, Glover G, Casey BJ. Risk-taking and the adolescent brain: Who is at risk? Dev Sci. 2007;10:F8–F14. doi: 10.1111/j.1467-7687.2006.00579.x. [DOI] [PubMed] [Google Scholar]
- 40.Lejuez CW, Aklin WM, Zvolensky MJ, Pedulla CM. Evaluation of the Balloon Analogue Risk Task (BART) as a predictor of adolescent real-world risk-taking behaviours. J Adolesc. 2003;26:475–479. doi: 10.1016/s0140-1971(03)00036-8. [DOI] [PubMed] [Google Scholar]
- 41.Parker AM, Fischhoff B. Decision-making competence: External validation through an individual-differences approach. J Behav Decis Making. 2005;18:1–27. [Google Scholar]
- 42.Centers for Disease Control and Prevention Youth risk behavior surveillance—United States, 2009. Morb Mortal Wkly Rep. 2010;59:1–148. [Google Scholar]
- 43.Ellickson PL, D’Amico EJ, Collins RL, Klein DJ. Marijuana use and later problems: When frequency of recent use explains age of initiation effects (and when it does not) Subst Use Misuse. 2005;40:343–359. doi: 10.1081/ja-200049356. [DOI] [PubMed] [Google Scholar]
- 44.Camerer CF, Ho TH. Violations of the betweenness axiom and nonlinearity in probability. J Risk Uncertain. 1994;8:167–196. [Google Scholar]
- 45.Wu G, Gonzalez R. Curvature of the probability weighting function. Manage Sci. 1996;42:1676–1690. [Google Scholar]
- 46.von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton, NJ: Princeton Univ Press; 1944. [Google Scholar]
- 47.Ofstedal MB, Fisher GG, Regula Herzog A. Documentation of Cognitive Functioning Measures in the Health and Retirement Study. 2005. HRS Documentation Report DR-006. Available at http://hrsonline.isr.umich.edu/sitedocs/userg/dr-006.pdf. Accessed July 25, 2012. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.