Programmed −1 frameshifting efficiency correlates with RNA pseudoknot conformational plasticity, not resistance to mechanical unfolding

Abstract

Programmed −1 frameshifting, whereby the reading frame of a ribosome on messenger RNA is shifted in order to generate an alternate gene product, is often triggered by a pseudoknot structure in the mRNA in combination with an upstream slippery sequence. The efficiency of frameshifting varies widely for different sites, but the factors that determine frameshifting efficiency are not yet fully understood. Previous work has suggested that frameshifting efficiency is related to the resistance of the pseudoknot against mechanical unfolding. We tested this hypothesis by studying the mechanical properties of a panel of pseudoknots with frameshifting efficiencies ranging from 2% to 30%: four pseudoknots from retroviruses, two from luteoviruses, one from a coronavirus, and a nonframeshifting bacteriophage pseudoknot. Using optical tweezers to apply tension across the RNA, we measured the distribution of forces required to unfold each pseudoknot. We found that neither the average unfolding force, nor the unfolding kinetics, nor the parameters describing the energy landscape for mechanical unfolding of the pseudoknot (energy barrier height and distance to the transition state) could be correlated to frameshifting efficiency. These results indicate that the resistance of pseudoknots to mechanical unfolding is not a primary determinant of frameshifting efficiency. However, increased frameshifting efficiency was correlated with an increased tendency to form alternate, incompletely folded structures, suggesting a more complex picture of the role of the pseudoknot involving the conformational dynamics.

Ribosomes synthesize protein by reading a messenger RNA in 3-nt steps to maintain a reading frame until a stop codon is reached. In programmed −1 ribosomal frameshifting (−1 PRF), the ribosome is forced backward by 1 nt, typically resulting in the bypass of a stop codon and the decoding of a new reading frame that specifies a different amino acid sequence (1, 2). Many RNA viruses from plants and animals use −1 PRF to express two proteins from a single mRNA in coordination at a defined ratio (1–4). Essential aspects of viral function, such as replication of the viral genome and packaging of the genome into a virion, depend critically on the tight regulation of the optimum expression ratio of the frameshifted proteins (5, 6). Also, −1 PRF occurs during the expression of cellular genes in a wide range of other organisms (4, 7–9).

Frameshifting depends on two specific components in the mRNA: a 7-nt “slippery sequence” at which −1 PRF occurs, and a stimulatory structure, usually a pseudoknot located 6–8 nt downstream (1, 2, 4, 10–12). The pseudoknot is a type of tertiary structure formed when nucleotides within the single-stranded loop of a hairpin base pair with complementary nucleotides outside of that loop (13) (Fig. S1). The slippery sequence can generate −1 PRF on its own, with some sequences increasing the intrinsic level of −1 PRF errors by up to 100-fold per codon; the pseudoknot component further stimulates frameshifting, 10–30 times the level produced by the slippery sequence alone (1). The detailed mechanism of −1 PRF remains unclear, however, and models have been proposed with −1 PRF occurring at various steps in the elongation cycle (1, 2, 14–17). A feature shared by several of these models is the role of tension in the mRNA, generated as the ribosome unwinds the pseudoknot. In one commonly cited model, the pseudoknot is viewed as a mechanical roadblock hindering ribosome translocation just when the slippery sequence is in registry with the A and P sites of the ribosome (17, 18). The strain from the mechanical resistance of the pseudoknot is thought to deform the P-site tRNA, weakening the codon–anticodon base pairing and promoting a −1 shift in reading frame. Interestingly, recent measurements of translocating ribosomes show that the ribosome actively generates tension in the mRNA to open the junction of structured RNAs and promote unwinding at the mRNA entry site (19, 20).

Given this mechanical model of pseudoknot-stimulated −1 PRF, where −1 PRF is dependent on tension induced in the mRNA when the translocating ribosome encounters a folded pseudoknot (16, 17), −1 PRF efficiency is expected to depend on how strongly the pseudoknot resists unfolding (21). However, −1 PRF efficiency seems to be unrelated to pseudoknot thermodynamic stability (22–24). A similar result is obtained when using duplexes formed by antisense oligos to induce −1 PRF (25), although there is conflicting evidence from −1 PRF induced by hairpin structures (26). Moreover, the extent of pseudoknot-induced ribosomal pausing is not strongly correlated with −1 PRF efficiency (18), as might be expected from this picture. On the other hand, base triples formed between loop 2 and the minor groove of stem 1 (Fig. S1), which should increase the pseudoknot stability, do stimulate efficient −1 PRF (27–35).

The possible correlation between the ability of pseudoknots to promote −1 PRF and their mechanical stability against unfolding was recently investigated directly using single-molecule force spectroscopy (SMFS) (34, 36–39), whereby tension is applied to the ends of the pseudoknot until it unfolds (40). This approach is particularly appropriate because the mode of unfolding mimics how the ribosome unwinds RNA structure, by actively applying force to the mRNA (19, 20). Moreover, SMFS yields not just the force needed to unfold the structure, but also the unfolding rates and characteristics of the unfolding energy landscape such as the location and height of the energy barrier (41–43). Two SMFS studies found a correlation between −1 PRF efficiency and pseudoknot unfolding force (34, 37) by studying the effects of destabilizing mutations, especially mutations disrupting major-groove base triples (34). In contrast, two other studies found no such correlation (36, 39), although slower unfolding rates were correlated with higher −1 PRF efficiency over a narrow force range (36), supporting a hypothesis that the rate of unfolding or barrier height might be important (16, 44). Each of these studies, however, was restricted to a single pseudoknot and its mutations; a broad survey of many different types of pseudoknots has yet to be made.

Here, we have made such a survey. To investigate possible deterministic correlations between frameshifting efficiency and pseudoknot resistance to mechanical unfolding, we used a panel of nine pseudoknots. We measured four retroviral pseudoknots, from the simian retrovirus-1, SRV1 (31); human endogenous retrovirus-K10, HERV (45); Visna–Maedi retrovirus, VMV (46); and mouse mammary tumor virus, MMTV (27, 47). Luteoviral pseudoknots from the pea enation mosaic virus-1, PEMV1 (32), and sugarcane yellow leaf virus, ScYLV, along with a ScYLV mutant (C27A) producing much reduced −1 PRF efficiency (33, 48), were also included, as was a pseudoknot from the severe acute respiratory syndrome (SARS) coronavirus (49). Finally, a nonframeshifting (2% efficiency) pseudoknot from the bacteriophage T2 gene 32, PT2G32 (50), which is structurally similar to the SRV1 pseudoknot (31), was included as a control. These pseudoknots were chosen for several reasons: (i) Most (SRV1, PT2G32, ScYLV, PEMV1, MMTV, HERV) have similar size and topology despite causing different −1 PRF efficiency; (ii) many have high-resolution structures; (iii) they allow exploration of the effects of larger size (VMV and SARS), long interstem elements (VMV), and different topology (three stems in SARS) (51, 52); and (iv) they represent a wide range of −1 PRF efficiencies, 2–30% as measured in rabbit reticulocyte lysate. The sequences and structural properties of all pseudoknots are summarized in Table S1 and Fig. S1.

Results

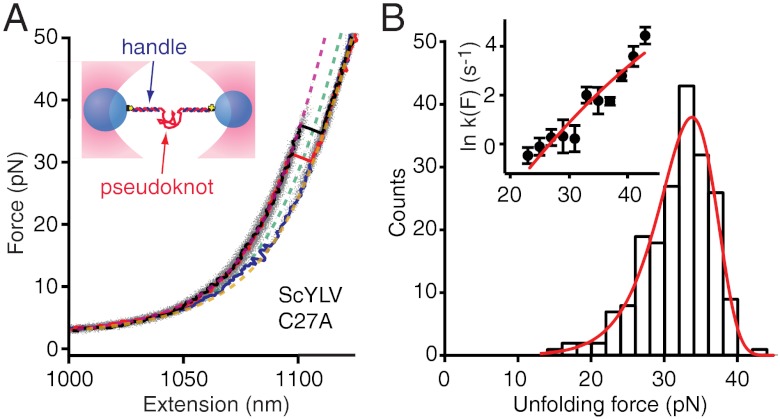
For each pseudoknot, RNA containing the pseudoknot sequence flanked on each side by kb-long “handle” sequences was transcribed in vitro, annealed to ssDNA complementary to the handles, and attached to beads held in optical traps (Fig. 1A, Inset), as described previously (53). The traps were held near zero force for 3–10 s to permit folding of the RNA, then separated at constant velocity to apply force to the RNA while the molecular extension was measured, generating force-extension curves (FECs). Representative FECs are shown in Fig. 1A for unfolding of the ScYLV C27A pseudoknot. Characteristically, the force rises nonlinearly with extension as the handles are stretched, until there is an abrupt extension increase and concomitant force decrease when the pseudoknot unfolds (40). Unfolding typically occurred at 20–40 pN as a two-state process, without intermediates (Fig. 1A, black and red). The change in contour length during unfolding, ΔL_c, was found by fitting the folded and unfolded branches of the FECs (Fig. 1A, purple and brown, respectively) to two extensible worm-like chains (WLCs) in series, one for the handles and one for the unfolded RNA (53). The result, ΔL_c = 13.9 ± 0.7 nm (all errors represent SEM), agreed well with the value (14.2 nm) expected from the NMR structure (48), indicating that the pseudoknot was natively folded. Very rarely, an unexpectedly short ΔL_c for unfolding was found in a FEC, indicating that the pseudoknot was not folded into the native structure before that pull and hence started from an alternate structure (Fig. 1A, blue; WLC fit, green).

Fig. 1.

Force spectroscopy of ScYLV C27A pseudoknot. (A, Inset) RNA containing the pseudoknot flanked by handle sequences was annealed to DNA strands complementary to the handles and attached to beads held in optical traps. Individual FECs (black, red, blue) are plotted above the aggregated data from 200 FECs (grey). Most FECs (black, red) show a monotonic rise of force with extension up to approximately 30 pN, at which point the extension increases abruptly as the RNA unfolds. A few FECs (blue) unfold at lower forces with a smaller length increase, indicating the RNA started in a different structure composed of fewer nucleotides. WLC fits to the elasticity of the handles, and unfolded RNA, used to determine the contour length change upon unfolding, are shown for three different states of the RNA: fully folded (purple); fully unfolded (brown); incompletely folded (green). (B) The distribution of unfolding forces from the natively folded pseudoknot FECs (black) is well-fit by Eq. 1 (red), yielding parameters describing the mechanical resistance to unfolding. (B, Inset) Unfolding rate as a function of force (black) is well-fit by Eq. 2 (red).

To quantify the resistance of the pseudoknot to mechanical unfolding, we examined the distribution of unfolding forces in the FECs, p(F) (Fig. 1B). The average unfolding force, here 32 ± 2 pN, provided the simplest measure of the mechanical stability. Other parameters related to the resistance to mechanical unfolding were obtained from fitting the shape of p(F) to a kinetic theory for FECs based on the unfolding energy landscape (41):

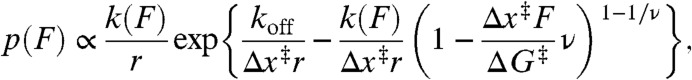[1]

where

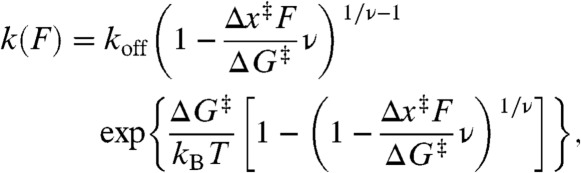[2]

k_off is the unfolding rate at zero force, Δx^‡ is the distance to the transition state from the folded state, ΔG^‡ is the height of the energy barrier, r is the loading rate, k_B is the Boltzmann constant, and ν parameterizes the shape of the energy barrier (ν = 1/2 for a cusp-like barrier, 2/3 for a linear-cubic potential). We averaged the results obtained under the two limiting cases for the shape of the energy barrier because this shape is unknown. As seen in Fig. 1B (red), p(F) was well-fit by Eq. 1. A complementary analysis of the kinetics based on the cumulative probability of unfolding (42) yielded the unfolding rate k(F) as a function of force (Fig. 1B, Inset), which was well-fit by the same type of landscape model using Eq. 2. Distributions measured at pulling rates ranging from 110–270 nm/s were analyzed by both methods and averaged, yielding log k_off = -4.1 ± 0.4 s^-1, Δx^‡ = 1.9 ± 0.2 nm, and ΔG^‡ = 49 ± 6 kJ/mol for this pseudoknot. There are no comparable measurements of ΔG^‡ for pseudoknots, but the values for k_off and Δx^‡ agree well with those for the infectious bronchitis virus (IBV) and telomerase pseudoknots, log k_off of approximately -4–5 s^-1 and Δx^‡ of approximately 1–2 nm (36, 38). The small Δx^‡ is typical of RNA tertiary structures (53–55), differing from the larger values seen for secondary structure alone (54, 56).

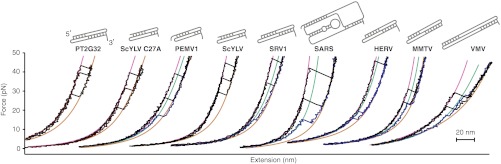
Similar measurements were made for each pseudoknot in the panel. The FECs displayed the same characteristic behavior as above (Fig. 2), sometimes unfolding from the native structure, sometimes starting from an alternate conformation. For several of the pseudoknots (PT2G32, PEMV1, ScYLV WT, and SRV1), ΔL_c values indicated that the pseudoknots were natively folded (Fig. S1 and Fig. 2, Insets) at the start of almost every FEC (Fig. 2, black), as for ScYLV C27A. For MMTV, HERV, SARS, and VMV, however, many FECs were observed in which the ΔL_c from folded to unfolded was less than expected for the native state (Fig. 2, blue), indicating that the pseudoknot started in an alternate conformation. The frequency with which unfolding occurred from such alternate states varied for different pseudoknots. The ΔL_c values expected from the native structure for each pseudoknot are listed in Table S2, along with the observed values.

Fig. 2.

Representative FECs for the nine pseudoknots. FECs from the different pseudoknots, arranged by increasing −1 PRF efficiency of the pseudoknot from left to right, show qualitatively similar unfolding. FECs in black show unfolding from the native structure, and those in blue, from alternate structures. States were distinguished primarily by the contour length changes upon unfolding, using WLC fits (purple: native structure; brown: unfolded; green: alternate structure). (Insets) Secondary structures of the pseudoknots. Available high-resolution structures are shown in Fig. S1.

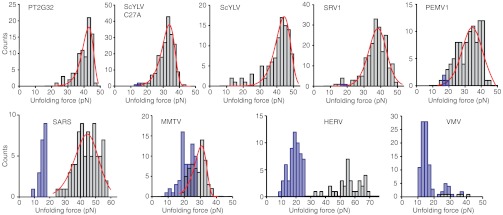
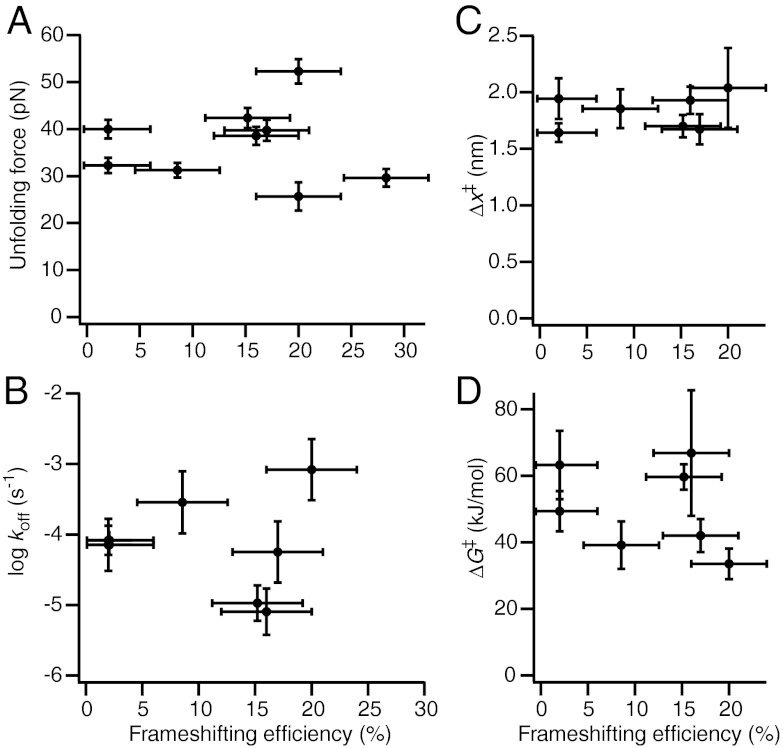
The unfolding force distributions were analyzed for each pseudoknot as described above for ScYLV C27A, including only those FECs in which the pseudoknot was natively folded as determined by ΔL_c (Fig. 3, grey). We first calculated the average unfolding force. Next, p(F) was fit to Eq. 1 (Fig. 3, red) and the rates k(F) were fit to Eq. 2, yielding the average values for k_off, Δx^‡, and ΔG^‡ (Table S2). In the case of HERV and VMV, it was not possible to obtain sufficient FECs showing unfolding of the native pseudoknot structure from a given molecule before it broke, hence the force distributions could not be fit reliably to obtain landscape parameters. The results are summarized in Fig. 4, plotting each quantity against the −1 PRF efficiency for the corresponding pseudoknot. No correlation is evident between the −1 PRF efficiency and the average unfolding force (Fig. 4A); indeed, the highest average force (for HERV) and the lowest (for MMTV) occurred for the same −1 PRF efficiency of 20%, and all other pseudoknots unfolded in the range 30–40 pN. Similarly, −1 PRF efficiency was not correlated with any of the other parameters describing the mechanical unfolding: k_off (Fig. 4B), Δx^‡ (Fig. 4C), or ΔG^‡ (Fig. 4D). The lack of correlation was confirmed by least-squares linear fits to the data in Fig. 4, which in each case yielded a slope of zero (within error).

Fig. 3.

Representative unfolding force distributions. The force distributions for unfolding the native structure of each pseudoknot (grey) were fit by Eq. 1 (red) to obtain parameters describing the energy landscape for unfolding. For some pseudoknots, significant numbers of FECs unfolded from alternate structures (force distributions shown in blue). All distributions measured at approximately 270 nm/s pulling speed.

Fig. 4.

Frameshifting efficiency is not correlated with mechanical stability parameters. The (A) average unfolding force, (B) unfolding rate at zero force, k_off, (C) distance to the transition state, Δx^‡, and (D) height of the energy barrier, ΔG^‡, were determined from the unfolding force distributions (as in Fig. 3) and fits to Eq. 1. All quantities are effectively constant as a function of −1 PRF efficiency of the pseudoknot, indicating that there is no correlation, and hence mechanical stability is not a primary determinant of −1 PRF efficiency. Error bars in the ordinate represent standard error; errors in the −1 PRF efficiency are an estimate of the variability in the values from the literature.

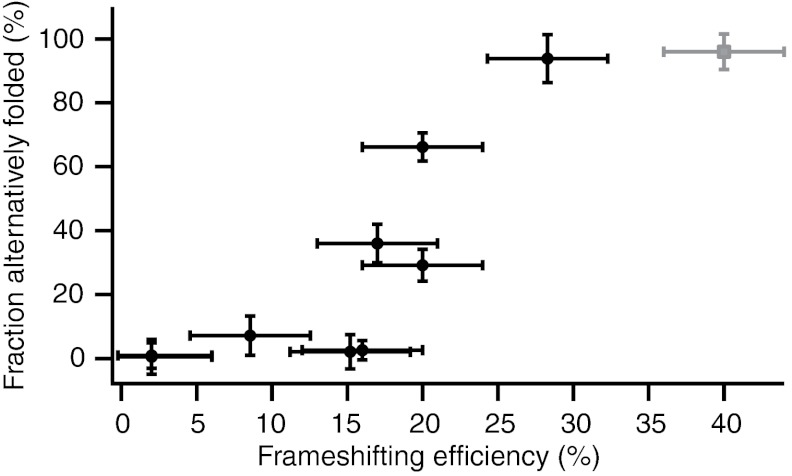
Unexpectedly, however, a different property of the FECs was found to correlate well with −1 PRF efficiency: the tendency of the pseudoknot to fold into alternate structures. The percentage of FECs in which the pseudoknot started in an alternate state was determined from the number of curves in which the total ΔL_c during unfolding did not match the value expected for the native state. The pseudoknots exhibiting low or intermediate −1 PRF efficiency tended to fold reliably into the native structure, when allowing 3 s for the RNA to refold at zero force between FECs; in contrast, pseudoknots stimulating higher −1 PRF efficiency tended to unfold more frequently from alternate structures (Fig. 5, black). For the three pseudoknots with the highest −1 PRF efficiency (MMTV, HERV, VMV), the fraction of FECs starting from alternate structures did not change when increasing the refolding time between measurements from 3 s to 10 s. Interestingly, this correlation extends to previous results for the telomerase pseudoknot, the only other pseudoknot for which alternate folding was similarly quantified (34). Although the telomerase pseudoknot is not naturally part of a frameshift signal, it stimulates −1 PRF efficiently and displays a correspondingly very high rate of folding into alternate conformations (Fig. 5, grey).

Fig. 5.

Frameshifting efficiency correlates with the formation of alternate structures. The fraction of FECs demonstrating unfolding from an alternate structure is generally higher for pseudoknots causing higher −1 PRF efficiency. The correlation extends to the telomerase pseudoknot measured in ref. 34 (grey square).

Discussion

Previous studies have provided contradictory evidence regarding correlations between −1 PRF efficiency and pseudoknot unfolding forces. The first to probe this question studied two near–wild-type pseudoknots derived from IBV having different unfolding forces. The one with higher unfolding force was found to be a more efficient −1 PRF stimulator (37), but the pseudoknots were likely not natively folded (shown by shorter-than-expected ΔL_c values), making the interpretation uncertain. This study was also contradicted by measurements on a related set of pseudoknots, a “minimal” near–wild-type IBV pseudoknot with shortened loop 2 (22) and three different mutants, which did not find any clear correlation between unfolding force and −1 PRF efficiency (36). A third study, on the beet western yellow virus (BWYV) pseudoknot and nonframeshifting mutants (39), again found little or no correlation between unfolding forces and −1 PRF efficiency, although it too showed a discrepancy between observed and expected ΔL_c values.

In contrast, measurements on the telomerase pseudoknot and a set of mutations that systematically disrupted the five base triples in the native structure (57), thereby reducing its mechanical stability, found a clear correlation between unfolding force and −1 PRF efficiency (34). The −1 PRF efficiency fell from approximately 40–50% for the wild-type pseudoknot to approximately 0% when all five base triples were disrupted, dropping exponentially as the unfolding force fell from 50 pN to approximately 20 pN. These results showed that mutations mechanically destabilizing the pseudoknot can decrease the efficiency of −1 PRF. This conclusion is corroborated by our measurements on ScYLV and the C27A mutation, which negatively affects the stacking of triple base pairs crossing the helical junction (48), reducing the unfolding force from 42 ± 3 pN to 32 ± 3 pN and decreasing the −1 PRF efficiency markedly from 15% to 2%. However, it is unclear from such measurements whether the lowered unfolding force in fact causes the −1 PRF efficiency reduction or is merely an incidental byproduct; for example, the change in −1 PRF efficiency could be caused by subtle structural changes and/or the prevention of specific contacts with the ribosome when key stabilizing interactions are removed (24, 29, 58, 59).

Our measurements test the correlation between −1 PRF efficiency and mechanical strength in a way that avoids these concerns, by determining whether wild-type pseudoknots producing different −1 PRF efficiencies also have different levels of resistance to unfolding. The result we find from our survey—that the −1 PRF efficiency is uncorrelated with unfolding force, rate, transition-state location, and barrier height—indicates that resistance to mechanical unfolding is not, in fact, a key determinant of −1 PRF efficiency. Deleting critical tertiary interactions in a given pseudoknot may decrease both −1 PRF efficiency and unfolding force, but the mechanical strength is generally a poor predictor of −1 PRF efficiency when comparing different pseudoknots. Extending our results to include previous measurements on the high-efficiency telomerase (wild-type) and IBV (near–wild-type) pseudoknots only reinforces this conclusion (Fig. S2). We cannot rule out the possibility of a weak correlation between efficiency and mechanical unfolding parameters (force, rate, …) that would only be apparent with a larger sample size, nor the possibility that these parameters may play a significant role for certain subsets of pseudoknots that we have not yet tested. However, the results are inconsistent with the idea that simple mechanical strength is a principal determinant. Instead, there is a clear trend that pseudoknots stimulating high −1 PRF efficiency tend to fold more frequently into alternate structures. The correlation in Fig. 5 is quite strong: The Spearman rank-correlation coefficient (testing monotonicity) is r_S = 0.94, whereas the Pearson correlation coefficient (testing linearity) is r_P = 0.87, both significantly above the 95% confidence level (0.63). It is also robust against uncertainty in the measurements of −1 PRF efficiency (SI Text).

How can these results be understood in terms of the role of pseudoknots in stimulating −1 PRF? This role is clearly more complex than simply providing a tuned mechanical resistance to unfolding by the ribosome. The pseudoknot is also likely acting as more than a passive roadblock for translation, given the suggestion from Fig. 5 that conformational dynamics are important. Indeed, other evidence supports a role for conformational plasticity in the pseudoknot. For example, NMR measurements found the nonframeshifting pseudoknot PT2G32 to be more conformationally rigid than pseudoknots derived from SRV1 and MMTV, with a much lower breathing frequency of the base pairs at the junction of the two stems (45), suggesting that a rigid structure prevents the pseudoknot from sampling a frameshift-competent conformation and leads to low −1 PRF efficiency. Recent work on the murine leukemia virus pseudoknot has also suggested that a dynamic equilibrium exists between alternate structures, only one of which is active in recoding translation, leading to a recoding efficiency proportional to the time spent sampling the active conformation (60). The fact that the correlation in Fig. 5 is not perfectly linear makes it unlikely that the alternate structures in our FECs are active (although they might lead to an active conformation when complexed with the ribosome); this view is supported by the fact that in several cases the alternate ΔL_c values are consistent with a hairpin formed from stem 1 (SI Text), which does not typically stimulate efficient −1 PRF. More likely, the correlation is an indirect reflection of the relevant behavior, with the alternate structure formation acting as a proxy for the property that does determine frameshifting efficiency.

One possibility is that the conformational fluctuations themselves, rather than specific structures, play an important role. It has been suggested that the ribosome senses the tension that it actively generates in the mRNA as structure is unfolded (19). A dynamic conformational equilibrium might then trigger frameshifting by causing fluctuations in this tension, which are communicated to the tRNA–mRNA complex, similar to the previous proposal that refolding of a partially unfolded pseudoknot during accommodation might induce a frameshift by pulling back on the mRNA (16). Measurements of pseudoknot extension under constant tension near the average unfolding force do show a dynamic conformational equilibrium. In the case of the telomerase (38), IBV (36), and SARS (Fig. S3) pseudoknots, the structural fluctuations occur on the ms–s timescale, likely rapid enough to affect the ribosome while it is paused at the slippery sequence. In the case of HERV, however, which also stimulates −1 PRF efficiently, the fluctuations are very slow (Fig. S4), suggesting that this explanation is incomplete. Complicating the picture, the ribosome is known to be an active helicase that interacts with the mRNA structure it is unwinding to facilitate melting (19). Such interactions may play an important role by biasing the dynamic equilibrium in favor of certain structures or speeding up the equilibration rates, but they are not probed in our measurements, which lack the ribosome.

A variety of evidence indicates a possible role for specific interactions with the ribosome in −1 PRF. Structural and functional studies suggest that triplex structures and unpaired, exposed-loop nucleotides may make or direct specific contacts to the ribosome that help determine −1 PRF efficiency, explaining why efficiency is reduced by removing or altering these structures (23, 27–35). Footprinting analyses of frameshift signals complexed with prokaryotic ribosomes indicate that specific contacts are indeed made with the pseudoknot when the slippery sequence is in the ribosomal decoding centre (61), but the details of these interactions and their role in regulation of −1 PRF efficiency are not well understood. Proteins at the mRNA entry tunnel of the ribosome, which could interact with the pseudoknot, have also been implicated in regulating −1 PRF efficiency (62). Again, however, we do not probe such interactions here. Programmed −1 frameshifting is clearly a complex phenomenon, regulated by many factors involving both the mRNA and the ribosome. The recent development of single-molecule assays of ribosome translocation along mRNA (19, 20) holds out the promise of directly observing interactions between the pseudoknot and ribosome during the actual frameshifting event, leading to a more complete understanding of −1 PRF mechanisms.

Methods

Sample Preparation.

Specific pseudoknot sequences (Table S1) were inserted into the pMLuc-1 plasmid between the SpeI and BamHI restriction sites. The resulting transcription template, containing a pseudoknot flanked by linker regions on either side, was amplified by PCR and transcribed in vitro using T7 RNA polymerase. Two ssDNA handles (one complementary to the 840 nt on the 3′ end of the transcript and labeled with biotin, the other complementary to the 2,280 nt on the 5′ end of the transcript and labeled with digoxigenin) were produced by asymmetric PCR from double-stranded DNA PCR products corresponding to the flanking handle sequences (53). The handles were annealed with the RNA transcript then incubated with 600-nm and 820-nm diameter polystyrene beads labeled with avidin DN (Vector Labs) and antidigoxigenin (Roche), respectively, to create dumbbells. Dumbbells were placed in measuring buffer [50 mM MOPS, pH 7.0, 130 mM KCl, 4 mM MgCl₂, 50 U/mL Superase•In RNase inhibitor (Ambion) and oxygen-scavenging system (40 U/mL glucose oxidase, 185 U/mL catalase, and 8.3 mg/mL glucose)] and inserted into a sample chamber on a clean microscope slide in the optical trap. Buffer ionic strength, which can affect unfolding energies, rates, and pathways (36, 39, 44), was chosen to be near-physiological, as required during translation.

Force Spectroscopy Measurements.

FECs were measured with a custom-built, dual-beam optical trap similar to one described previously (53). Briefly, two orthogonally polarized beams from a single 1,064-nm laser were steered independently with acousto-optic deflectors to create two traps. Motion of beads held in the traps was detected by collecting from two orthogonally polarized 830-nm laser beams aligned on the traps the light that was scattered by the beads onto position-sensitive diodes. Trap stiffnesses, 0.58 and 0.43 pN/nm, were calibrated as described (63). Data were sampled at 20 kHz and filtered online at 10 kHz with an 8-pole Bessel filter.

Contour Length Analysis.

The contour length changes expected during unfolding from the published NMR structures were calculated from 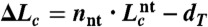, where d_T is the distance between the termini of the folded pseudoknot as measured from the NMR structure, n_nt is the number of nucleotides in the pseudoknot, and 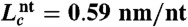is the contour length per nt (64). For most pseudoknots, d_T varied from approximately 2–5 nm. No structure has been solved for the HERV, SARS, and VMV pseudoknots; d_T was estimated from pseudoknots of similar size as approximately 4 nm (HERV), approximately 5 nm (VMV), or approximately 6 nm (SARS). Native and alternate structures were distinguished primarily by the difference in ΔL_c upon unfolding, using a threshold midway between the average value for the states.