Complexity of chromatin folding is captured by the strings and binders switch model

Abstract

Chromatin has a complex spatial organization in the cell nucleus that serves vital functional purposes. A variety of chromatin folding conformations has been detected by single-cell imaging and chromosome conformation capture-based approaches. However, a unified quantitative framework describing spatial chromatin organization is still lacking. Here, we explore the “strings and binders switch” model to explain the origin and variety of chromatin behaviors that coexist and dynamically change within living cells. This simple polymer model recapitulates the scaling properties of chromatin folding reported experimentally in different cellular systems, the fractal state of chromatin, the processes of domain formation, and looping out. Additionally, the strings and binders switch model reproduces the recently proposed “fractal–globule” model, but only as one of many possible transient conformations.

Understanding the interplay between genome architecture and gene regulation is one of the most challenging problems in biology. During mitosis, chromosomes are found in a condensed state, but decondense during interphase, when highly coordinated cellular processes such as transcription, DNA repair, and replication take place, creating cell-type–specific chromatin folding (1–3).

Chromosome organization occurs at different scales of genomic length to yield variable degrees of compaction (4). Linear nucleosome arrays fold into higher-order structures, first through local chromatin interactions, such as between promoters and enhancers, and then eventually giving rise to discrete chromosome territories (1).

Spatial genome organization is guided by intra-and interchromosomal interactions mediated by nuclear components that include transcription factors, transcription and replication factories, Polycomb bodies, and contacts with the lamina (5–8). However, how binding of diffusible factors to specific genomic regions drives chromatin folding remains poorly understood.

Imaging of single loci by FISH and genome-wide mapping of chromatin interactions by chromosome conformation capture (3C) approaches revealed a variety of chromatin architectures across genomic regions and cell types, and upon environmental cues (9–14) (Fig. S1A). In FISH experiments, chromatin folding is often measured by the mean-square spatial distance, R²(s), between two genomic regions as a function of their linear genomic distance, s (Fig. S1B), which usually exhibits scaling properties R²(s) ∼ s^2v. Although the behavior of R²(s) appears to depend on the genomic regions and cell types assessed (Fig. S1A), in general, at large genomic distances, R²(s) reaches a plateau (i.e., v = 0) that reflects the folding of chromosomes into territories (15).

A global analysis of genome-wide 3C (Hi-C) ligation products in human cells averaged across all chromosomes has been used to estimate the “contact probability,” P_c(s) (13). This measures how frequently two loci contact each other as a function of s (Fig. S1B). Measurements of P_c(s) have identified a power-law behavior, P_c(s) ∼ 1/s^α, with an average exponent α ∼ 1.08, at genomic distances 0.5–7 Mb. The observation of α of approximately 1.08 has led to the suggestion that chromatin behavior could be explained by a single folding structure, previously described in polymer physics by the “fractal–globule” (FG) model (16). Recent applications of Hi-C have found a lower exponent α in Drosophila (14), and revealed differing contact frequencies in human cells according to chromatin expression status (17). The observation that the exponent α may not be universal (see also Figs. S2–S4) or conserved, and the failure of the FG model to describe the plateauing of R²(s), prompted us to reconsider the fundamental underlying principles of chromatin folding.

Here, we explore how chromatin architectural patterns can arise and be regulated by using an alternative simple polymer physics model, first proposed in 2008 (18, 19). In our model, the “strings and binders switch” (SBS) model, nonrandom chromatin conformations are established through attachment of diffusible factors (binders) to binding sites. Binder-mediated interactions give rise to a variety of stable chromatin architectures that can coexist in the nucleus. Chromatin folding changes in response to changes in binding site distribution, binder concentration, or binding affinity, in a switch-like fashion across specific threshold values via thermodynamics mechanisms. Importantly, we show that the SBS model describes in a single framework all current experimental data on chromosome architecture from FISH, Hi-C and 3C approaches.

Results

The SBS Model: General Description.

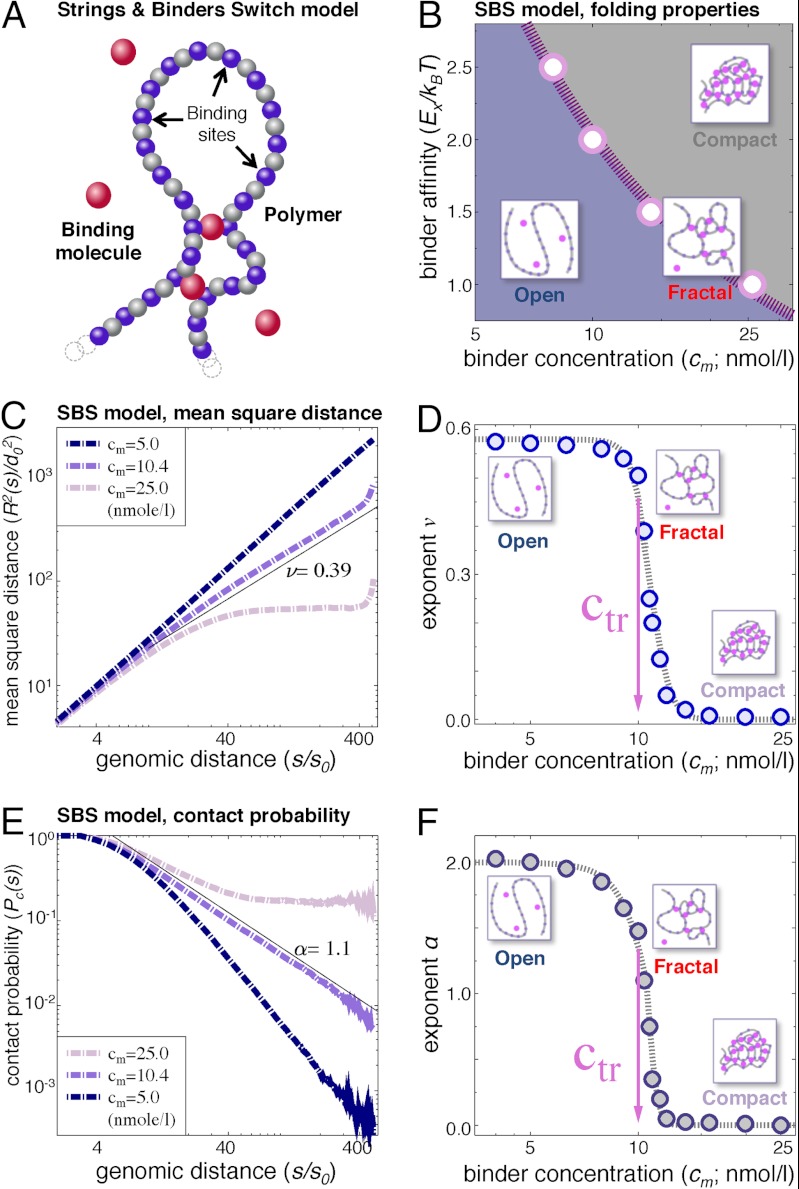
In the SBS model, a chromatin fiber is represented as a self-avoiding polymer bead chain (Fig. 1A), and binding molecules are represented by Brownian particles with concentration c_m. A fraction, f, of polymer sites can be bound by diffusing molecules with chemical affinity E_X. To investigate the system’s folding behavior, we evaluated the dynamics and equilibrium properties of the polymer using extensive Monte Carlo (MC) simulations in the known range of the biochemical values of c_m and E_X. In this instance, we chose a binding multiplicity of diffusing binders equal to six, as estimated for chromatin organizers such as CCCTC-binding factor (CTCF) or transcription factories (20, 21). This is a representative experimental condition because different binding multiplicities (≥2) promote similar patterns of folding (19).

Fig. 1.

The emerging stable states of the SBS model and the mechanisms of its self-organization. (A) Schematic representation of the SBS model. A chromatin filament is represented by a SAW polymer comprising n beads randomly floating within an assigned volume. A fraction, f, of beads (binding sites) can interact with Brownian molecules (magenta spheres; binders) with concentration c_m and binding site affinity E_X. In this example, f = 0.5 for an equal number of blue (binding) and grey (nonbinding) sites. Molecules bind more than one polymer site, allowing for loop formation. (B) Three classes of states exist. The phase diagram illustrates the conformational state of the system as a function of two main control parameters, c_m and E_X. The system is in an open randomly folded conformation below the transition line, C_tr(E_X) (dashed curve), it folds in a compact conformation above it, and it takes a different fractal structure at the transition point. (C) The polymer mean-square distance. R²(s) is the mean-square distance (in units of the bead linear length d₀) of two polymer sites having a contour distance s. R² is shown as a function of s for three values of the binder concentration, c_m = 5, 10.4, and 25 nmol/L, corresponding to below, around, and above the transition point (here, E_X = 2 k_BT). At large s, R²(s) has a power-law behavior R²(s) ∼ s^2v; at c_m = 10.4 nmol/L we find ν ∼ 0.39. For s/s₀ > 400, finite size effects are seen. (D) The power law exponent of R²(s) has three regimes. The exponent, ν, has a sigmoid behavior as a function of c_m, corresponding to different system states, with ν ∼ 0.58 for c_m < C_tr; ν ∼ 0.5 at C_tr = 10.0 nmol/L; and ν ∼ 0.0 at c_m > C_tr. (E) Site contact probability. P_c(s) is the contact probability of two sites with contour distance s along the polymer chain. It is plotted for c_m = 5, 10.4, and 25 nmol/L. At large s, a power law is found: P_c(s) ∼ 1/s^α. We find α = 1.1 at c_m = 10.4 nmol/L. (F) Power law behavior of P_c(s). The P_c(s) exponent α expressed as a function of c_m also displays three regimes: below, around, and above C_tr.

We first demonstrate how c_m affects the equilibrium compaction state of the polymer (Fig. S2). The extent of polymer folding is captured by measuring the squared radius of gyration, , which is the average squared distance of each bead to the center of mass of the polymer chain (Fig. S1B). 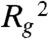attains a minimum when loops enclose the polymer into a compact state, and a maximum when the polymer is loose and randomly folded. The SBS model predicts that 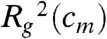has a sigmoid shape with two distinct regimes and a transition region, as a function of c_m (Fig. S2). When c_m is below a specific threshold value, C_tr, 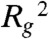has the same value found in the standard random self-avoiding walk (SAW) model (22), where the polymer is open and randomly folded. At the transition point, the conformations of the polymer are fractal (22). Above threshold, 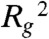harply decreases towards a value corresponding to a compact, collapsed structure. The threshold, C_tr, identified by the curve inflection point, corresponds to the polymer Θ transition (22). We find, for example, that for E_X = 2 k_BT, C_tr is approximately 10 nmol/L, a typical nuclear protein concentration (23).

The SBS model therefore explains that a polymer can undergo a switch-like conformational change to form or release loops by changing the concentration (and/or affinity, E_X) of binding molecules. Loops are stable only above C_tr, where the system undergoes a thermodynamic phase transition. By changing concentration or affinity across threshold, a thermodynamic switch is controlled to change reliably the polymer architecture (see ref. 19 for more details). The equilibrium folding state of the polymer across a wide range of E_X and c_m values is seen in the system phase diagram (Fig. 1B), which shows that the threshold concentration, C_tr(E_X), required for switching from open into compact states increases as E_X decreases.

The Conformational Self-Organization Mechanisms of the SBS Model and Its Emerging Stable States.

To assess the power of the SBS model in explaining the range of chromatin behaviors observed by FISH and Hi-C, we measured R²(s), the equilibrium value of the mean-square spatial distance, and the contact probability P_c(s) between loci separated by a distance s along the polymer (Fig. 1 C–F). In the SBS model, the shape of the two functions R²(s) and P_c(s) is sensitive to the concentration of binding molecules, c_m.

R²(s) is characterized by a power-law behavior, R²(s) ∼ s^2v, which defines the scaling exponent ν (at large s; Fig. 1 C and D). Importantly, we find that ν is a nonlinear sigmoid function of the concentration of binding molecules, c_m (Fig. 1D), which corresponds to a switch-like behavior in the architecture of the polymer. Three regimes exist corresponding to c_m: below, at, and above threshold. Analogous results are found when the binding affinity, E_X, or number of binding sites is varied (19). When c_m < C_tr, few chromatin contacts are present and the polymer is open; R²(s) increases as a function of s with an exponent ν ∼ 0.58, as expected for a randomly folded free polymer (the SAW random coil) (22). If c_m increases, more loops can be formed, but ν remains at approximately 0.58 until C_tr is approached. When c_m is around C_tr, the polymer architecture changes abruptly from open to a (stable) fractal-like conformation with ν of approximately 0.5. This exponent corresponds to the expected Θ-point exponent of the polymer coil–globule transition (22) and has been observed by FISH (11) (Fig. S1A). When c_m > C_tr, chromatin contacts are abundant and the polymer adopts a compact, nonfractal conformation. R²(s) shows a plateau behavior at large s, with an exponent v ∼ 0, also often observed in FISH data (9, 10) (Fig. S1A).

The shape of P_c(s) as a function of genomic distance, s, also reflects the three regimes described above (Fig. 1E). Similarly to R²(s), P_c(s) has a power-law behavior with P_c(s) ∼ 1/s^α, where the exponent α is also dependent on c_m (Fig. 1E). When c_m < C_tr, α = 2.1, which is the signature of the randomly folded (open) polymer (SAW model) (22). For c_m around C_tr, the scaling exponent changes in a range encompassing α = 1.08 found in Hi-C data (13); we find α = 1.5 at the transition Θ point. Distant loci are more likely to contact each other than in the free open polymer. When c_m > C_tr, the polymer shrinks into a compact mass manifested by a plateau of P_c(s) at large s, where the exponent becomes α = 0.0.

Comparison of the SBS and Other Models Against Experimental Data.

Before delving further into implications of the SBS model, we compare its predictions against experimental data and those of other models. The FG model represents the chromatin fiber as a noninteracting (free) polymer chain in a specific transient state. It was proposed in 1988 in the polymer physics literature as a knot-free state (16), and used recently to explain the behavior of P_c(s) from Hi-C data and to propose that chromatin is organized as fractal globules (13, 24).

The FG model seems attractive because it proposes that chromatin is found in a specific, unique fractal state that resembles the 1-Mb chromatin domains suggested earlier (15). Although the FG model only considers random chromatin interactions and not binder-mediated contacts as identified experimentally, it provides a P_c(s) with an exponent α of approximately 1, which is very close to the value of α estimated from some Hi-C average data (13). Thus, the FG model depicts chromatin as if it were all in a single conformational state. Importantly, it also predicts that R²(s) grows indefinitely with s with an exponent ν of approximately 0.33. However, although ν around 0.33 can be observed at some specific loci and cell types, it is not a general value found across most experimental datasets where a plateau in R²(s) is often observed (Fig. S1A). Furthermore, the FG state is only achieved using highly specific simulation conditions. For instance, the polymer must be initially forced into a highly compacted state without knots, before being released and becoming fully unfolded. The time window during which the polymer behaves as a FG only exists fleetingly, and the polymer converges to a different equilibrium state. This time window would become vanishingly small in the presence of key nuclear factors, such as DNA topoisomerases (24).

To compare predictions from SBS and FG models, we first considered available FISH data on R²(s) from different chromosomes and systems: on chromosome 12 in pro-B cells (0–3 Mb; Fig. 2A) (10), and on chromosome 11 in primary fibroblasts (0–80 Mb; Fig. S3) (9). The SBS model in the closed polymer state correctly fits all sets of FISH data, representing the early increase and plateau in R²(s) at shorter and longer genomic distances, respectively. In contrast, the FG predicts that R²(s) grows indefinitely with s (ν ∼ 0.33). Thus, the FG model accounts only for the early increase in R²(s) (Fig. 2A and Fig. S3), but fails to capture the leveling off at longer s. Interestingly, the R²(s) plateau across these two cell systems arises at different s, reflecting biological complexity (unless related to methodological differences).

Fig. 2.

The SBS model explains the range of experimental chromatin folding behaviors. (A) Mean-square distance of subchromosomal regions from FISH data. Mean-square distance, R²(s), from FISH data in pro-B cells chromosome 12, spanning 3 Mb (10). Superimposed dashed line indicates behavior predicted by the FG model; continuous line indicates behavior predicted by the SBS model in the compact state. (B–D) Contact probability from Hi-C data and SBS model. (B) Contact probability, P_c(s), was calculated separately for different chromosomes from published Hi-C dataset in human lymphoblastoid cell line GM06990 (13). Chromosomes 11 and 12 follow the average behavior reported (13) in the 0.5–7 Mb region (shaded in grey), with exponent α of approximately 1.08. Chromosomes X and 19 deviate from the average, with α exponents of approximately 0.93 to approximately 1.30, respectively. In a given system, different chromosomes can have different exponents. (C) P_c(s) was calculated for different chromosomes from published Hi-C dataset in human embryonic stem cell line H1–hESC (25). All chromosomes deviate from exponent α of approximately 1.08 in the 0.5–7 Mb region (shaded in grey), and have an exponent α of approximately 1.65, characteristic of open chromatin within the SBS interpretation. Different systems can have different exponents. (D) Mixtures of open and compact SBS polymers can model average Pc(s). Average P_c(s) is shown for mixtures of open and compact polymers in the SBS model (where α = 2.1 and 0.0, respectively). In each mixture, p and 1-p are the fractions of open and compact polymers, respectively. P_c(s) and α depend on p. For p of approximately 60%, α = 1.08 is found in a range of s about one order of magnitude long, as in Hi-C data. Simply changing the fraction of open chromatin can recover the entire range of Hi-C exponents of B and C.

We next investigated the generality of the value of α around 1.08 derived after averaging P_c(s) across all chromosomes in the human female lymphoblastoid cell line (GM06990) (13). Using the published Hi-C data, we calculated P_c(s) for different chromosomes separately (Fig. 2B and Figs. S4A and S5A). To investigate the effects of chromatin compaction, we chose to compare chromosomes 19 (gene dense with high gene expression) and X (one copy is silent in this female cell line). We show that chromosomes 19 and X deviate from the average behavior in the 0.5–7 Mb region, with α exponents ranging from 0.93 and 1.30, respectively. This is consistent with their average open and closed states, compared to chromosomes 11 and 12, which have α of approximately 1.08. We observed a similar deviation from the average P_c(s) in a different female lymphoblastoid cell line (GM12878) analyzed by either Hi-C or tethered conformation capture (TCC) (17), and in IMR90 cells characterized by Hi-C (25) (Fig. S4 B–D). Analogous comparisons between chromosomes 18 (gene poor) and 19 (gene rich) yield similar deviations from the average behavior, with chromosome 18 having larger α than chromosome 19 (Fig. S5).

Surprisingly, analyses of Hi-C data from the human embryonic stem cells (25) (H1–hESC) showed a striking deviation from the lymphoblastoid cells analyzed above. In H1–hESC, averaged Hi-C contact probabilities for all individual chromosomes analyzed resulted in a higher α of approximately 1.6 (Fig. 2C). This result agrees with previous findings that stem cell chromatin tends to assume more open conformations than in other cell types (26). Direct comparisons of genome-wide P_c(s) reveal different exponents α across the cell lines studied (Table S1 and Fig. S4F).

We stress that calculations of α for whole genomes or chromosomes reflect average chromatin folding behaviors that disregard the variety of conformations known to exist at specific loci. To illustrate this concept, we investigated whether the Hi-C–derived values of α could in principle be obtained by simple averaging over regions of open and closed chromatin, even in the absence of fractal folding states. Thus, we considered a mixture of SBS model systems containing a proportion of open and compact polymers (p and 1-p, with α = 2.1 and 0.0, respectively; Fig. 1F). The average P_c(s) of such mixtures has an exponent α that depend on the proportion p (Fig. 2D). Strikingly, α = 1.08 can be found for p of approximately 0.60, in a range of s that spans one order of magnitude, as observed in Hi-C data. When the fraction of open polymers is decreased to p = 0.45, α = 0.93 in the same s range, a value close to the one found for chromosome X in the female cell line GM06990 (13). Conversely, p = 0.80 gives α = 1.3, as it does for chromosome 19 in the same cell line.

This analysis illustrates the lack of power of the average α exponent alone to elucidate chromatin architecture. Taken together, our results strongly argue that an average α of approximately 1.08 does not describe a general principle of chromatin behavior, and show that the FG model is not a general description of chromatin folding principles. In contrast, the SBS model has the power to explain the whole range of α exponents identified experimentally (Table S1 and Figs. S1A, S2, S4, and S5). Nevertheless, the FG model may help explain specific transitional states for some genomic regions, as, for instance, rapid chromatin decondensation and chromatin looping out of chromosome territories during gene activation (27–31).

The SBS Model Reproduces the Organization of Chromatin in Topological Domains.

Chromatin domains or globules have been hypothesized as a basic unit of chromatin organization, based on the appearance of chromatin seen by electron microscopy, the size of chromatin loops, and evidence for chromatin associations derived by nuclear structures such as clustering of replicons in replication factories (3, 15, 32). Recent analyses of 3C-based studies are also consistent with the existence of approximately 1-Mb domains (25, 33).

To explore the formation of chromatin globules in the SBS model, we modeled a polymer containing two kinds of binding site (red and green), segregated in two separate halves of the polymer length, each with specific affinity to one kind of binder (red and green, respectively; Fig. 3A). In these conditions, the SBS model promptly produces separate domains, as demonstrated on single simulations (Fig. 3B) or by the average matrix of interactions (Fig. 3C). As expected, the P_c(s) of such a polymer has two different regions (Fig. 3D). At s shorter than the length of each domain, P_c(s) has a lower value of α, corresponding to a closed (globular) state. At larger s, it has a higher α, corresponding to an open state. The mean-square distance, R²(s), also has two regions, with an increase followed by a plateau as s increases (Fig. S6).

Fig. 3.

The SBS model captures the globular conformation of chromatin. (A) Schematic representation of the polymer system used to study formation of chromatin globules or domains. (B) Snapshots of chromatin domains formed after MC simulations of the SBS polymer model represented in A. (C) The steady-state “contact matrix” shows two separate chromatin domains. (D) The average P_c(s) shows two regimes: closed chromatin, at shorter s because of formation of globules; and open chromatin, at larger genomic regions because of the absence of interactions between the two domains.

As a final example of the power of the SBS model to simulate known chromatin behaviors, we investigated whether changes in binding site affinity upon domain formation could induce chromatin looping out from domains (27–31) (Fig. S7). We let the two globules reach equilibrium (as for Fig. 3), but subsequently changed the state of three (out of 11) contiguous sites from binding the red binders to no longer having affinity to binders (becoming blue). Red and green domains remained (red domains now of smaller dimension), but the polymer segment containing blue binding sites looped out from the red domain (Fig. S7). Analogously, associations between different domains can be explained by the action of common binders (SI Text).

Chromatin domains and looping can therefore be studied with the SBS model in conditions of full segregation or of partial mixing, depending on the binding site geography and binder properties. With appropriate experimental data of chromatin associations and epigenetic mapping, the SBS model has the power to describe principles that drive chromosome folding and the dynamic changes occurring during differentiation and in disease.

The SBS Model Reproduces the Dynamic Folding Behaviors of Chromatin.

As a final test to the power of the SBS model, we investigated the kurtosis 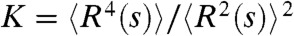, which is the ratio of the fourth and second moment of the spatial distance. K is a dimensionless quantity that allows for direct comparisons between polymer modeling results and experimental data (22). In principle, K carries information about genomic locus-to-locus and cell-to-cell variations. Interestingly, K has been measured experimentally by FISH (9, 34, 35) and found to vary between 1.5 and 4.4, depending on the locus and cell type studied (Fig. 4A).

Fig. 4.

The SBS model captures the full range of values of the distance kurtosis observed in FISH data. (A) The ratio of the fourth and second moment of the distance R between loci at the genomic distance s [i.e., the kurtosis; 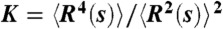] is plotted as a function of s. It provides a measure of the relative amplitude of fluctuations of the polymer conformations. K = 1.50 when R²(s) is randomly distributed as a self-avoiding polymer (horizontal dashed line). Experimental K values depart from 1.50; K values were first analyzed in ref. 35, and originate from human fibroblast chromosome 1 ridges or whole chromosomes 1 or 11 (9) (squares, open circles, and filled circles, respectively), and from pre/pro-B or pro-B cell murine immunoglobulin heavy chain locus (10) (light- or dark-blue diamonds, respectively). (B) The kurtosis measured in the SBS model is plotted as a function of c_m. K is close to 1.5 at low and high concentrations of binding molecules (open and closed chromatin). Around the binder threshold concentration, K exhibits a peak with values up to approximately 5. The range of values of K measured experimentally (A) matches the range found within the SBS model. It emerges that, beyond open and compact states, chromatin loci are likely to include also fractal conformations corresponding to the transition point.

Importantly, the SBS model produces a range of K values that span the same range of experimental K. In fact, K depends on c_m (Fig. 4B). K is approximately 1.5 at both low and high concentrations of binders (i.e., open and closed chromatin, respectively), but in the region around the threshold concentration K increases from 1.5 up to 5, encompassing all previously reported experimental measurements. To date, no other chromatin polymer model produces such a variety of behaviors and correspondence with experimental results.

The experimental observations (9, 34, 35) of loci where K = 1.5 (the value predicted by the SBS model for open and compact states; see Fig. 4A) and of loci with values between 1.5 and 5 (corresponding to the transition region between open and closed states) suggest that, indeed, chromatin exists in a complex mixture that includes fractal as well as open and closed states.

Measurements of K from previous models produce a constant value of K. The randomly folded polymer (SAW) model produces K = 1.5 (22). Previous polymer models that consider the effects of both specified chromatin loops at fixed lengths of 120 kb and 3 Mb (12, 36), and the possibility of chromatin loops of all sizes (37), also produce constant K values. Furthermore, although these models explain the plateau of the mean-square spatial distance, R²(s), at large s, they do not reproduce the behavior of the contact probability, P_c(s), observed in Hi-C data, as does the SBS model. More recently, the possibility of transient interactions across a polymer has been studied in the dynamic loop (DL) model, which, to mimic the effects of bridging molecules, assigns an attachment probability to genomic regions that randomly meet in space (35). In agreement with the SBS model, the DL model can also reproduce the Hi-C exponent of P_c(s). K has not been calculated for the FG model, but it will by definition give a constant K.

Discussion

Interphase nuclei exhibit dynamic chromatin structures that change in response to cellular signals and influence patterns of gene expression. We show that the SBS model can capture the key aspects of chromatin folding behaviors detected experimentally across different cell systems and by different technical approaches. The model describes how genomic architectures can spontaneously arise with a switch-like nature that can explain how a sharp regulation of nuclear architecture can be obtained reliably by simple strategies, such as protein up-regulation or modification, without the need to fine tune these specific parameters.

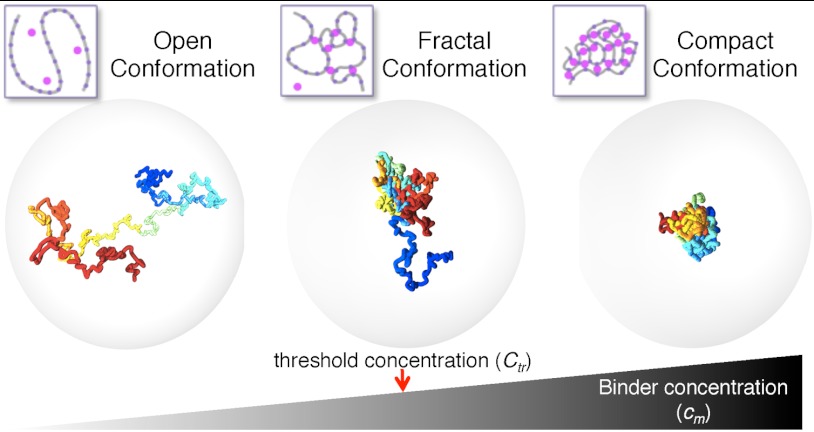
Under different initial conditions, the polymer displays a variety of transient conformations that evolve into specific stable states (Fig. 5): open polymers, closed polymers, and intermediate fractal states. In our scenario, the open polymer state represents open euchromatin (ν ∼ 0.58, α ∼ 2.1), whereas the compact state describes dense heterochromatin (ν ∼ 0, α ∼ 0). The region around the threshold fractal state includes states with exponents that fit with Hi-C–averaged data from human cells (α of approximately 0.9–1.6; Table S1), but also from Drosophila embryos (α of approximately 0.70 or 0.85 for open and closed chromatin, respectively) (14). However, Hi-C data inherently represent average behaviors across a population of cells and chromosomal loci. Although methodological variations could potentially be responsible for differences observed between datasets, the comparison of specific chromosomes within datasets yielded consistent behaviors, such as the deviation of chromosomes 18, 19, and X from the average genome behavior. Thus, our analysis strongly supports the conclusion that the principles of chromatin folding in interphase nuclei cannot be recapitulated by a single “universal” conformational state (and its given α).

Fig. 5.

Overview of the system states and their transitions. Representation of three classes of stable conformational states of the SBS polymer chain shown in Fig. 1: (Left) the open random coil (c_m = 5 nmol/L; c_m < C_tr), (Center) the transition-point fractal (c_m = 10 nmol/L; c_m around C_tr), and (Right) the compact globule state (c_m = 25 nmol/L; c_m > C_tr). The polymer conformations were obtained from MC simulations of the SBS model. For clarity, the polymer binding molecules are not shown and the surrounding transparent sphere represents the nucleus. Polymer and sphere sizes are proportional to the size of mammalian chromosomes and nuclei, respectively. Switch-like conformational changes occur, regulated by increasing c_m or E_X above precise threshold values marking thermodynamic phase transitions.

The simple SBS model considered here illustrates key physical concepts and basic required ingredients to explain chromatin folding in a variety of states identified in living systems. Although specific molecular details can be incorporated into more complex versions of the model (such as the presence of different binders or nonhomogeneous distributions of binding sites), the general range of folding behaviors will remain the same. Many complications arise in real nuclei, including chromatin entanglement effects that are resolved through the action of topoisomerases, self-interactions beyond steric hindrance, and interactions with the nuclear lamina. In reality, a variety of specific binding factors exist, and thus a complexity of folding states is present inside cell nuclei, where different regions can spontaneously fold into different chromatin states. Importantly, polymer scaling theory ensures that the exponents in R²(s) and Pc(s) are independent of the minute details of the system considered and reflect universal properties (22); these parameters are not affected by detailed mapping onto real chromosomes (e.g., the chosen coarse graining level used in the polymer models and the size of binding sites). Therefore, the general structural properties of our model are relevant to real chromatin.

It will be interesting in the future to use the SBS model to explore the behavior of two or more chromosomes when they are constrained in the cell nucleus. As additional genome-wide data become available, important issues that can be addressed with the SBS model include the extent and dynamics of chromatin intermingling and the effects of steric hindrance between chromosomes.

The SBS model can explain the nature of the mechanisms underlying chromatin self-organization whereby nuclear architecture is governed by a few core molecular ingredients and basic physical processes. More generally, the thermodynamic mechanisms discussed, which are robust and independent of specific molecular details, will be relevant to many cellular and nuclear processes requiring spatial organization (1, 2, 31).

Materials and Methods

Model and Its Parameters.

In the SBS model, a chromatin filament is represented as a self-avoiding polymer chain (19). Here, the chain is made of n = 512 spherical sites, each s₀ bases long (total length L = n·s₀). The polymer has binding sites for diffusing molecules (binders) with a concentration, c_m, that have an affinity E_X for polymer sites. The system is investigated by Metropolis Monte Carlo simulations. Full details of models and simulations can be found in SI Text.

Hi-C and TCC Data Analysis.

Hi-C and TCC contact probabilities were calculated genome-wide and/or for individual chromosomes with a method similar to the one described in ref. 13. Full details of datasets and analyses performed can be found in SI Text.