Assessment of a Three-Dimensional Line-of-Response Probability Density Function System Matrix for PET

Abstract

To achieve optimal PET image reconstruction through better system modeling, we developed a system matrix that is based on the probability density function for each line of response (LOR-PDF). The LOR-PDFs are grouped by LOR-to-detector incident angles to form a highly compact system matrix. The system matrix was implemented in the MOLAR list mode reconstruction algorithm for a small animal PET scanner. The impact of LOR-PDF on reconstructed image quality was assessed qualitatively as well as quantitatively in terms of contrast recovery coefficient (CRC) and coefficient of variance (COV), and its performance was compared with a fixed Gaussian (iso-Gaussian) line spread function. The LOR-PDFs of 3 coincidence signal emitting sources, 1) ideal positron emitter that emits perfect back-to-back γ rays (γγ) in air; 2) fluorine-18 (¹⁸F) nuclide in water; and 3) oxygen-15 (¹⁵O) nuclide in water, were derived, and assessed with simulated and experimental phantom data.

The derived LOR-PDFs showed anisotropic and asymmetric characteristics dependent on LOR-detector angle, coincidence emitting source, and the medium, consistent with common PET physical principles. The comparison of the iso-Gaussian function and LOR-PDF showed that: 1) without positron range and acolinearity effects, the LOR-PDF achieved better or similar trade-offs of contrast recovery and noise for objects of 4-mm radius or larger, and this advantage extended to smaller objects (e.g. 2-mm radius sphere, 0.6-mm radius hot-rods) at higher iteration numbers; and 2) with positron range and acolinearity effects, the iso-Gaussian achieved similar or better resolution recovery depending on the significance of positron range effect.

We conclude that the 3-D LOR-PDF approach is an effective method to generate an accurate and compact system matrix. However, when used directly in expectation-maximization based list-mode iterative reconstruction algorithms such as MOLAR, its superiority is not clear. For this application, using an iso-Gaussian function in MOLAR is a simple but effective technique for PET reconstruction.

1 Introduction

For a PET scanner, the system matrix is the discretized version of the scanner’s response function. It is an essential element in iterative PET image reconstruction and its accuracy has been considered to be crucial to achieving optimal resolution and noise properties in reconstructed images. There have been significant efforts on the subject of system matrix derivation and implementation by many groups, and various approaches have been published over the past 20 years [1-10].

The theory of the system matrix has been well established [4, 11]. An element in a system matrix represents the probability of the positrons in a particular image voxel contributing counts to a particular LOR; the physical factors that affect the probability are 1) the positron range before annihilation, 2) the annihilation-photons’ acollinearity, 3) the geometrical intersection between the image voxel and the LOR, 4) the annihilation photons’ depth of penetration into the detector, 5) the annihilation photons’ intra- and inter-detector scatter, and 6) the crystal mis-identification due to crystal light sharing and photo-multiplier tube (PMT) signal decoding variations, and 7) the mechanical and material irregularities that exist in the scanner system. Although modeling all these factors with high accuracy is intuitively appealing, given the increased complication of adding each factor into a huge system matrix, different strategies and compromises have been used to achieve a balance between performance (image quality and reconstruction speed) and practicality (ease in derivation, moderate requirements for computer hardware, etc). To introduce the approach we propose, we review briefly the existing methods for system matrix generation and implementation.

System matrices have been typically generated in 3 ways: 1) analytical calculation, 2) Monte Carlo simulation and 3) experimental measurement. Analytical methods account for only geometrical and photon-crystal penetration effects [1, 2, 6, 12]. In this case, the system matrix is calculated without the need for simulation or experiments, and the results are free of statistical noise. These methods therefore can be carried out on virtual scanners and are suitable for investigation of new system designs. However, the methods in this category do not account for several physical factors, such as positron range, which compromise the matrix’s accuracy.

The second approach, Monte Carlo based methods, can selectively incorporate all or some of the physical factors. This approach has been greatly facilitated by the continuous advancement of computer technology and recent developments in Monte Carlo simulation software [13, 14]. Currently, simulated experiments can be carried out with detailed realistic scanner-specific settings with established toolsets. The Monte Carlo approach has advantages that the scanner and emission source information are precisely known and accessible, and that the method is cost-effective in evaluating various system designs without the presence of the actual scanner [3, 4, 8]. The challenges for the Monte Carlo approach include determining the precise specifications of the actual PET system and having a high demand for computational resources.

Intuitively, experimental measurement such as scanning a point source throughout the field-of-view (FOV) of the actual system may be the most accurate way to obtain the system matrix [5, 7, 15], as this approach provides “one-stop-shopping” of the true system matrix, with all known or unknown factors included. The main drawback of this approach is the setup of measurements required for the point source scans. The system response extracted from the acquired data may be undermined by imperfections in point source positioning. Further, this approach is obviously not relevant for a system in the development stage. In addition, this approach may not be optimal for developing a new system matrix method, since the uncertainties about the specifications of the real PET system, such as detectors’ mechanical tolerance, may undermine the quality of the derived system matrix when compression or parameterization is used to reduce the matrix size.

Any system matrix generation strategy must be carried out by a computational implementation method, which is a non-trivial task for modern PET systems. The complexity stems from the large size of the system matrix, which has image voxel count in one dimension and LOR count in another dimension. Given the size of a high-resolution PET image and the number of LORs for today’s emission tomography systems, on the order of 10⁷ and 10⁹, respectively, the system matrix in its raw form is prohibitively large [8]. To handle this size, the most accepted approach is to decompose the system matrix into two sub-matrices: 1) a geometrical matrix that handles only the geometrical intersection of image voxels and LORs, and 2) a spread matrix that accounts for all other physical factors [4, 5, 9, 15]. Then, only the non-zero elements of the two sub-matrices are stored for reconstruction use. However, it is challenging to obtain the spread matrix, which is spatially variant and anisotropic [9, 10]. Some implementations used simplified blurring function parameterization (Alessio et al. 2006) and approximations in calculations, for example, axial compression and azimuthal meshing, to produce the final matrix [7].

In this work, our goal was to develop a new method for system matrix derivation and implementation. To have full control of the factors studied, we chose the method of Monte Carlo simulation for matrix generation. Based on the understanding that the challenges of system matrix implementation come from the conjuncture of image space and projection space in one matrix, we use a probability density function for each line of response (LOR-PDF) to model all the physical factors that involve the interactions between the image and the projection. This approach allows the inclusion of LOR depth-dependence and spatial asymmetries modeled in the system matrix for maximum accuracy. To our knowledge, this is the first time that LOR depth is directly modeled in a parameterized system matrix for PET. In addition, it allows for projection space parameterization, e.g., grouping LORs by their incident angles, thus permitting high efficiency implementation with matrix size reduction.

A small animal PET scanner was used as the test system for the method. However, the method is generally applicable to other PET scanners.

2 Materials and Methods

2.1 Animal PET Scanner

The animal PET scanner used in this study was a microPET Focus-120 system (Siemens Preclinical Solutions, Knoxville, TN). This scanner is manufactured with high accuracy in its detector construction and scanner integration, so the simulated scanner is expected to have a close resemblance to the true scanner. This is a critical factor for system matrices derived from a Monte Carlo based approach to be applied to real systems.

The scanner consists of 4 detector rings with 147.2 mm diameter and 76 mm axial extent [16]. Each detector ring has 24 detector blocks. Each block consists of a 12×12 array of Lutetium Oxyorthosilicate (LSO) crystals. The crystal size modeled in the simulation was 1.52×1.52×10 mm³. The gap between neighboring crystals is 0.07 mm and there is no gap between blocks. The energy window setting of 350-750keV and coincident timing window of 6 ns were used in all the simulations and experimental studies presented in this work.

2.2 3-D LOR-PDF

The variables and the corresponding definitions in this work are listed in Table 1.

Table 1.

Definitions of the variables used in this work, listed in the sequence of appearance.

Variables	Definitions
x, y, z	Coordinates of the PET image space reference frame XYZ.
r, u	The in-plane variables of the LOR-PDF function. The r and u axes are parallel to x and z axes, respectively.
d	The depth variable along LOR, starts from one predetermined (e.g., higher detector block index) end of LOR.
j, J	Image voxel index, and the number of image voxels, respectively.
i, I	LOR index, and the number of LORs, respectively.
Vi	The rectangular tube volume of LORi.
p()	Probability density function.
cij	Probability of emission from voxel j contributing to LOR i.
φ, θ	In-plane and out-of-plane orientation angle of LOR at the starting-side of LOR.
b	The separation between a LOR’s ending and starting side detector block indices.
N	The number of detector blocks in a detector ring.
L	Length of LOR
D	Diameter of detector ring

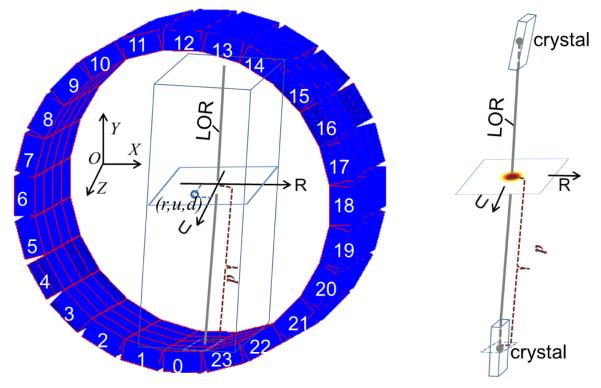
Figure 1 illustrates the LOR-PDF concept. First we define a fixed Cartesian coordinate system (x,y,z) as the reference of the scanner’s image space. The x, y, and z axes are in horizontal, vertical and axial directions, respectively. The center of the field of view (CFOV) is the origin. A LOR is defined as the line connecting the centers of the crystals of a coincident event. For consistent derivation and retrieval of LOR-PDFs, one end of each LOR is unambiguously identified (e.g., the side with higher detector block index), and named arbitrarily as the “starting-side”. For all LOR-PDF calculations, the detector block on the starting-side of the LOR is always rotated to the detector block 0’s position, i.e., at the bottom of the detector ring as shown in Figure 1. To model each LOR-PDF, we attach a reference frame of (r,u,d) to the rotated LOR. The r and u axes are parallel to the x and z axes and define a plane intersecting the LOR. The d (depth) axis begins at the starting-side of the LOR and is directed to the ending-side, (Figure 1).

Figure 1.

An illustration of the 3-D LOR-PDF concept. Left: The PET detector ring is shown with image-space and LOR-PDF-space reference frames (x,y,z) and (r,u,d), respectively. The rectangular tube with the LOR as central line is the 3-D volume of the LOR-PDF. The (x,y,z) origin is at the center of the scanner FOV, but is shown offset for clarity. Right: A sample LOR-PDF distribution in one r-u plane.

Consider an event along LOR i with activity contributions from the surrounding volume, the V_i probability of an emission from voxel j contributing to LOR i is

$$c_{ij}=p_i(r_{ij},u_{ij},d_{ij})j\in V_i$$ (1)

where p( ) is the LOR-PDF. The terms (r_ij, u_ij, d_ij) indicate the relative position of voxel j to the LOR i in the (r,u,d) frame. As only the voxels in the vicinity of the LOR make non-negligible contributions, V_i is an obliquely oriented rectangular box with LOR i as the approximate central line. A sample LOR-PDF distribution in one r-u plane is shown as an image in the right diagram of Figure 1.

2.3 Grouping LOR-PDFs by incident angle

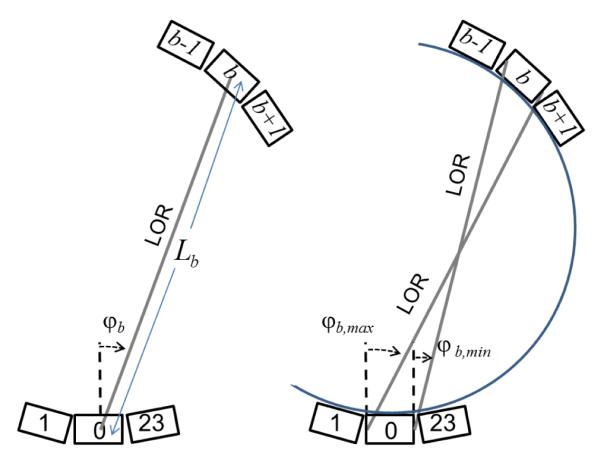
To reduce the number of LOR-PDFs and therefore reduce the size of system matrix, we group the LORs in terms of their incident direction onto the detector faces. The incident direction of a LOR onto its starting-side can be defined by an in-plane angle φ and an out-of-plane angle θ. Figure 2 illustrates the geometrical orientation of φ and θ. Without simplification, a LOR would require two sets of (φ, θ) from its two ends to describe its incident direction. However, with the cylindrical geometry of this PET scanner, and given that, in calculations, a LOR is first rotated so that its starting-side detector block is aligned to a fixed position, e.g., detector block 0, then the incident directions of LOR i can be uniquely identified by (φ_i, b_i, θ_i), where φ_i and θ_i are the angles on the starting-side of LOR, and b_i is the separation of detector block indices between the ending-side and starting-side of the LOR.

Figure 2.

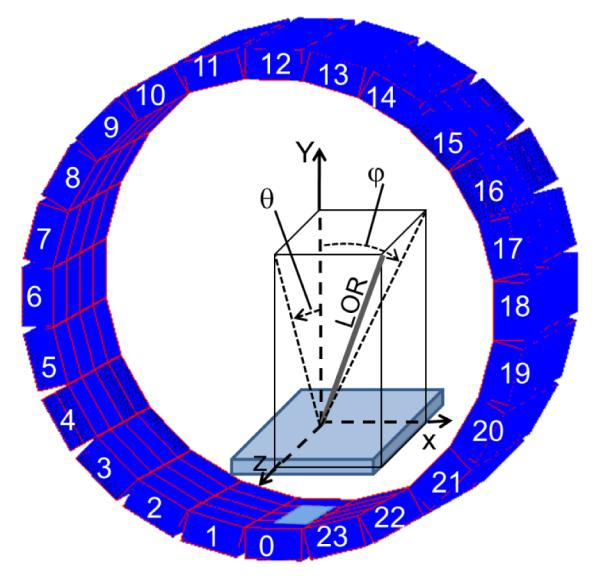
Reference frame for incident angle calculations for each LOR. The detector area on the starting-side of the LOR is enlarged to show the incident angle (φ,θ) definition. The angles φ and θ are always calculated from starting-side of LOR.

The LOR-PDF model can be generalized by replacing the function index i with (φ_i, b_i, θ_i) in (1), so the system matrix element can be written as

$$c_{ij}=p(r_{ij},u_{ij},d_{ij},{\phi }_i,b_i,{\theta }_i)j\in V_i$$ (2)

2.4 Sampling of the LOR tube volume and incident angles

With (2), the system matrix can now be expressed as a 6-dimensional histogram:

$$\begin{array}{cc}\hfill C& =\left[c_{ji}\right]{\mid }_{\underset{i\in I}{j\in J}}\hfill \\ \hfill & =\left[p(r_{ji},u_{ji},d_{ji},{\phi }_i,b_i,{\theta }_i)\right]{\mid }_{\underset{i\in I}{j\in V_i}}\hfill \\ \hfill & =\left[p(r,u,d,\phi ,b,\theta )\right]{\mid }_{r\in [r_{\min },r_{\max }],u\in [u_{\min },u_{\max }],d\in [0,d_{\max }],\phi \in [{\phi }_{b,\min },{\phi }_{b,\max }],b\in [b_{\min },b_{\max }],\theta \in [{\theta }_{\min },{\theta }_{\max }]}\hfill \end{array}$$ (3)

where [r_min, r_max], [u_min, u_max], and [0, d_max] define the span of the LOR volume V_i in the (r, u, d) are the frame, [φ_{η, min}, φ_{η, max}], [b_min, b_max], and [θ_min, θ_max] sampling ranges of the corresponding LOR incident direction variables.

Let φ_b be the angle of the LOR connecting the center of detector blocks 0 and b, as shown in the left diagram of Figure 3, then φ_b = (b · π/N-π/²), where N is the total number of detector blocks in the ring. The length of this LOR is L_b = D·cos(φ_b), where D is the detector ring diameter, i.e., the center-to-center distance between opposing crystals. For all the LORs between detector blocks 0 and b, the minimum and maximum in-plane incident angles are φ_b,min ≈ φ_b-π/N, φ_b,max ≈ φ_b+π/N and we use as L_b the average length of this group of LORs.

Figure 3.

The in-plane angle range of all LORs between detector blocks with a separation of b can be represented by [φ_b,min ,φ_b,max] centered about φ_b.

The sampling range of each variable in (3) is intrinsic to the system’s specific geometrical and physical design. For example, the block separation index range [b_min,b_max] is derived from the possible combinations of measured coincidences of the PET scanner, set by the scanner’s coincidence circuitry. The out-of-plane angle range [θ_min,θ_max] is calculated in a similar manner according to the scanner geometry. The range of r and u represent the widths of LOR-PDFs’ contribution volumes, which are determined by the LOR-PDF’s spread. As a result of depth of interaction, these values vary across LORs with different incident angles. For ease of implementation in the system matrix, we used only one set of r and u ranges for each positron emitter and attenuation material combination. So all LOR-PDFs had the same contribution volume, regardless their actual spread widths. The set of r and u range values chosen were large enough so that the widest LOR-PDFs, which are at the edge of the scanner’s FOV, were minimally truncated (truncated value was < 1% of the PDF maximum). When a LOR-PDF is retrieved from the system matrix and used in the forward and backprojections of reconstruction program, to confine the operation to the non-negligible portion of the LOR-PDF, a user-selectable parameter, e.g., 5% of the PDF maximum or a user-chosen fixed width, may be used to truncate the function to preserve computational efficiency (see Discussion).

The choice of the sampling size for each variable is a trade-off between the accuracy of the system matrix and the computational cost. Intuitively, finer sampling provides a more accurate system response function but leads to a larger system matrix, which requires increased system memory and higher overall statistics when generating the matrix. The sampling parameters reported in this work are shown in Table 2. This setting was determined empirically based on the reconstruction speed and image quality (see Discussion). The system matrix has ~74 million elements with the parameters chosen.

Table 2.

The sampling parameters of the Focus-120 animal PET scanner’s system matrices used for image reconstruction reported in this work. Note that the LOR lengths between different detector blocks vary. The specific descriptions of the γγ, ¹⁸F and ¹⁵O sources are described in section 2.5. The size of the final system matrix is 64×64×19×5×21×9 or ~ 74 million elements. To facilitate visual presentation, a different set of parameters was used for the LOR-PDFs shown in Figures 5-8.

Variable	Range	Number of samples	Sample size
r	[−5,5]mm for γγ ,18F; [−10,10]mm for 15O	64	~0.16mm for γγ,18F; ~0.32mm for 15O
u	[−5,5] mm for γγ, 18F; [−10,10]mm for 15O	64	~0.16mm for γγ, 18F; ~0.32mm for 15O
d	[0, Lb] mm, Lb ≈ 40.7 to 157.2	19	~2.1 to 8.3 mm
φ	[φb-7.5°, φb+7.5°	5	3°
b	[2, 22]	21	1 block index
θ	[−49.5°,49.5°]	9	11°

2.5 System matrix derivation from Monte Carlo simulation

In Monte Carlo simulation, the origin of positron emission of a detected event is known exactly, regardless of the emission source’s distribution. As compared to experimental measurements where this information is only available with limited accuracy when using point sources, simulation has a major advantage. Therefore, the data collection step can be achieved through a single uniform source simulation study. After collecting the simulated events, LOR-PDFs and the system matrix are obtained by simply histogramming the events in the (r,u,d,φ,b,θ) frame with the variable ranges and sample sizes described in Table 2. As the overall LOR sensitivity factor is handled by normalization which includes an adjustment for LOR solid-angle [17, 18], each (r,u) segment of a LOR-PDF is normalized to sum to unity. By excluding object scatter and random coincidences, the system matrix incorporates the effects of inter-crystal scatter, crystal penetration, positron range, and photon-pair acollinearity when applicable. PMT crystal mis-identification was not included in the Monte Carlo simulation (see Discussion).

To evaluate the core concept of the proposed system matrix and to assess the impact of positron range and annihilation photons acollinearity, three types of positron emitters were simulated. First is a back-to-back gamma (γγ) source, which only exists in simulation. There is no positron range or acollinearity effect involved. Rather, only geometry and photon-detector interactions are simulated for the system matrix generation. Second is an ¹⁸F source in water, i.e., a combination of the most frequently used PET radionuclide and the most encountered object material. Third is a source of ¹⁵O in water; since ¹⁵O has a high positron energy, we use this combination to evaluate the resolution recovery performance of the proposed system matrix with the nuclides with long positron range.

Monte Carlo simulations were performed with uniform source cylinders. The cylinders for the 3 radionuclides were slightly different in order to 1) minimize unnecessary attenuation so to improve simulation efficiency and 2) have adequate materials surrounding the source to ensure that each positron annihilates before escaping from the phantom. The size of the attenuating material was calculated so that the shortest distance from any point of the source distribution to the edge of the phantom is more than twice the effective-FWHM of the positron range. A larger volume of material was simulated for ¹⁵O to prevent its more energetic positrons from escaping the phantom and interacting with the detector system directly. Table 3 shows the parameters of the phantoms.

Table 3.

The size and composition of the simulated phantoms used for system matrix generation. Object scatter and random coincidences were excluded from the simulated counts and system matrix generation.

Nuclide	Nuclide cylinder (diameter and height, mm)	Material cylinder (diameter and height, mm)	PDF Counts (×106)	Simulation time (hours)
γ γ	30 ×76	130 ×76 air	3041	~14400
18F	75 ×68	79 ×76 water	250	~4400
15O	75 ×68	87 ×76 water	417	~6000

For the three simulations, the total activity in the cylinder was 0.25 mCi, emitted for 4 seconds in each acquisition. A total of 2400, 800 and 1600 acquisitions were simulated for back-to-back gamma, ¹⁸F and ¹⁵O radionuclides, respectively. The Monte Carlo simulation package GATE 6.0.0 [14] was used for emulating the virtual scanner. The simulated scanner geometry parameters were the same as the real system [16]. The detection efficiency of the γγ source described in Table 3 was (3041 × 10⁶ events)/(2400 acquisition. × 0.25 mCi × 4 seconds/acquisition), which is 3.4%.

The simulation tasks were distributed to computer nodes on a Linux cluster with random seeds pre-generated [19]. The simulation results generated on multiple computer nodes were collected to produce the system matrix. Each simulated acquisition required about 6 to 11 hours of computing time on a cluster unit (3.2GHz CPU, 2GB RAM). The number of acquisitions selected for a source-medium combination was based on the specific purpose of the study. For example, high statistics for γγ in air was used to test a range of PDF sampling options and to quantitatively compare the LOR-PDF with the iso-Gaussian system matrices. Lower numbers of acquisitions were simulated for the other two simulation configurations, since their purpose was to qualitatively demonstrate 1) the applicability of the simulated system matrix to real data, and 2) the effect of positron range in the system matrix, respectively.

2.6 Simulated hot-rod phantoms for resolution recovery evaluation

The uniform cylinder simulation data with 3 types of radionuclides from which the system matrices were generated were also used to produce simulated phantom data by reprocessing the simulated data to generate unique emission distributions. Specifically, only the events emitted from a predetermined phantom emission source geometry, i.e., a subset of the original distribution, were collected to form the phantom study data. This approach allows multiple uses of the simulated data and saves simulation time. We have compared this approach against using independent simulation data for system matrix generation and phantom studies, and no obvious differences were observed.

Three phantoms were extracted from the 3 positron-emitter datasets in Table 3 for evaluating the resolution recovery performance of the proposed system matrix. All the phantoms have 6 hot-rod sections with their transverse sections similar to the widely used Mini Hot Spot Insert (Data Spectrum Inc., Model ECT/DLX/MP, Hillsborough, NC). In each hot-rod section, the rods have uniform diameters, and the center-to-center distance between rods was twice that of the rod diameter. Hot-rod phantoms do not permit the study of axial resolution. However, initial simulations with point sources suggested that the axial and transverse resolution characteristics were similar, and it was thus simpler to study only transverse resolution.

For the first phantom, the rod diameters in the 6 sections were 1.2, 1.4, 1.6, 1.8, 2.0, and 2.2 mm, respectively. It was extracted from the γγ in air dataset. For the second and third phantoms, the hot-rod diameters in the 6 sections were 1.2, 1.6, 2.0, 2.4, 3.2, and 4.8 mm, respectively. The heights and the diameters of the non-radioactive material of the phantoms (see Table 3) were selected according to the positron energy of radionuclide used.

To focus on the resolution recovery effects of the system matrix, object scatter and random events were excluded in the emission data collection process for this phantom study. The total counts, i.e., the number of true plus detector scatter events, for the back-to-back gamma, ¹⁸F and ¹⁵O hot-rod phantoms were 79.6, 26.0, and 11.2 million, respectively. The count differences were due to different phantom configuration, acquisition time, and the number of simulations used.

2.7 Experimental phantoms for resolution recovery evaluation

To study the performance of the proposed simulation-based system matrix on experimental data, we used an acquisition from a Mini Hot Spot phantom (Data Spectrum Inc., Model ECT/DLX/MP, Hillsborough, NC) filled with ¹⁸F. The dataset had ~ 16.8 million prompt and 1.8 million random events. No attenuation correction information was obtained.

2.8 Simulated contrast phantom for quantitative assessment

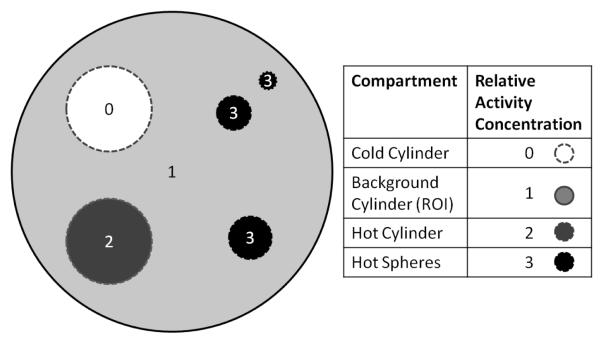
The γγ source in air uniform cylinder (Table 3) was used to extract a contrast phantom with multiple compartments to study the quantification accuracy of the reconstruction results. The relative intensity in different compartments of the phantom was obtained by selectively accepting a fraction of the events originated from the compartments; the fraction values were pre-determined. Figure 4 shows a transverse view of the phantom. The main body of the phantom was a cylinder of 75 mm diameter and 68 mm height. Within the main cylinder, there were 2 cylinders, each with 20 mm diameter and 68 mm height. One cylinder was filled with twice the background activity and the other was filled with no activity. There were 3 spheres with radii of 5, 4 and 2 mm, distributed in the main cylinder, centered on the same slice, and away from the two cylinders. The 3 spheres were all filled with radioactivity with a concentration of 3 times that of the background.

Figure 4.

An illustration of the compartments (small cylinders and spheres) of the contrast phantom. The regions of interest (ROI) used for evaluation had the same sizes as the corresponding compartments. The background ROI is the main cylinder volume with all other ROIs excluded.

Similar to the previous simulation, random events were excluded from the emission data simulation process. The choice of using back-to-back gamma in air was made to focus on the evaluation of effects of the system matrix on quantification.

A total of 280 million emission events were acquired for the contrast phantom study. The data were split into 20 equivalent sub-studies for quantification and noise analysis.

2.9 Image generation protocols

The simulated and experimental emission data were processed and reconstructed through three paths.

The first reconstruction path is named “ray-tracing”. In this path, list mode data were first histogrammed to form sinograms with a span of 3 and ring difference of 47. The sinogram was then processed with Fourier rebinning (FORE) followed by OSEM 2-dimensional (OSEM-2D) reconstruction provided by the manufacturer (microPET manager version 2.3.3.6, Siemens Pre-clinical Solutions, Knoxville, TN) with the default setting of 4 iterations and 16 subsets. This OSEM-2D algorithm uses a simple ray-tracing system model, with no resolution recovery. This path was used as a basic reference for reconstruction performance evaluation. The reconstructed image size was 256×256×95 (voxel size of 0.4mm × 0.4 mm × 0.796mm). The normalization coefficients were derived from simulated or experimental cylinder data using the normalization protocol provided by the manufacturer. For simulated studies, a 6-cm diameter uniform cylinder dataset was extracted from the γγ source in air simulation (Table 3) to derive the normalization coefficients.

Both the second and third paths were within the framework of the MOLAR list mode reconstruction algorithm [20]. The only difference between the two paths was the PDF used: the second path used a fixed Gaussian function to describe the PDFs of all LORs, thus named “iso-Gaussian”, and the third path used PDFs that were LOR-detector incident-angle dependent and LOR depth dependent, as described in sections 2.2 to 2.4. For reporting, we name the third path “LOR-PDF”. The full-width-at-half-maximum (FWHM) for the iso-Gaussian function was an estimated average transverse FWHM: 1.5 mm for both back-to-back gamma in air and ¹⁸F in water [16], and 2.9 mm for ¹⁵O in water [21]. For the second and third paths, the list mode data of the phantom studies were reconstructed with 6 iterations and 10 subsets. Subsets for MOLAR are determined in a modulo fashion by event order of arrival. The normalization coefficients were calculated from the singles efficiency of individual crystals derived from simulated and experimental uniform cylinder source data [17, 18]. For each LOR, a tube with a fixed cross-section size in the r-u plane was used for forward and back projection in MOLAR. The cross-section size was 2.5 mm × 2.5 mm for the back-to-back gamma in air and ¹⁸F in water studies, and 4.8 mm × 4.8 mm for the ¹⁵O in water study. The choice of using an adequately large but fixed-size section rather than a size chosen adaptively based on the non-negligible portions of LOR-PDF is considered in the Discussion section.

For simulated phantom studies, the contributions from object attenuation/scatter and random coincidences were excluded from acquisition, and thus no corrections were applied for scatter, attenuation or randoms. For the experimental hot-rod phantom experiment study, corrections for attenuation, scatter, and random were not applied.

2.10 Performance assessment

To assess the performance of the proposed LOR-PDF model, images of all the phantom studies were reconstructed through the three paths described in section 2.9. The resolution recovery performance of a reconstructed image was assessed by inspection of 1) the visibility of small hot-rod sections, and 2) the circular shape of the hot rods in the reconstructed images.

The quantitative performance was measured by the contrast recovery coefficient (CRC) values of selected ROIs, defined as

$$CRC=\frac{\left(\sum _i{M}_{ROI,i}∕\sum _i{M}_{bkg,i}\right)-1}{\left(T_{ROI}∕T_{bkg}\right)-1},$$ (4)

where i represent the reconstructed i^th replicate image, M_{ROI, i} and M_{bkg, i} are the mean values of the selected ROI and background ROI in the i^th reconstructed replicate image, and the T_ROI and are the T_bkg known true intensities of the selected ROI and the background ROI.

The noise performance was measured by the voxel coefficient of variance (COV) across replicates in selected ROIs.

$$COV=\frac{M_{ROI,std\mathrm{Img}}}{M_{ROI,mean\mathrm{Img}}},$$ (5)

where stdImg and meanImg are the standard deviation and mean images, respectively, calculated from the replicate images, respectively. The ROIs of the contrast phantom are shown in Figure 4. Each ROI, e.g., a cylinder, a sphere or the background, includes all the voxels in its corresponding compartment.

3 Results

3.1 3D LOR-PDF

The 3D distribution of a sample γγ in air LOR-PDF is shown in Figure 5. The LORs in this figure are from detectors directly facing each other across the FOV and therefore have minimal obliqueness in either in-plane or axial directions. Using the definitions in (3), these LORs have φ=[−2.5°,2.5°], b=12, θ=[−5.5°, 5.5°] and 9 depth segments. Note that these parameters, as well as the parameters used for Figs. 6, 7 and 8, are selected to facilitate the visual illustration of LOR-PDF’s characteristics. The total number of LORs for the Focus 120 animal PET scanner is ~ 8.4 × 10⁷. With a total of 3041 × 10⁶ counts simulated (see Table 3), the mean emission events recorded per LOR was (3041 × 10⁶)/(8.4 × 10⁷) = 36.2. The mean events recorded per LOR-group, with the grouping configuration for the PDF system matrix shown in Figs. 5-7, was (3041 × 10⁶)/(3 × 21 × 9) = 5.4 × 10⁶ events.

Figure 5.

The LOR-PDF of the group of LORs from detector blocks directly across the FOV, i.e. φ = [−2.5°, 2.5°], b =12, and θ = [−5.5°, 5.5°] according to (3). From left to right, the LOR-PDF segments are shown versus LOR depth from starting-side to ending-side with steps of 17.5 mm. The dimension of the images displayed is 4 mm in both r and u directions. The top row shows the LOR-PDFs using a common intensity scale while, in the bottom row, each 2D LOR-PDF segment is scaled to its own maximum. The (r,u) coordinate overlay is shown on the top-left image. The dashed line in the top-middle image is the profile for Figure 8.

Figure 6.

The LOR-PDF for LORs with ending-side that is two detector blocks to the right of the opposing detector block across the FOV, φ = [−2.5°, 2.5°], b =14, and θ = [−5.5°, 5.5°] . The top row shows the LOR-PDFs using a common intensity scale while, in the bottom row, each 2D LOR-PDF segment is scaled to its own maximum. The LOR-PDF of this LOR group is asymmetric in the r direction. Shape changes along the LOR depth from starting-side to ending-side (left to right) are also clear.

Figure 7.

The LOR-PDF for LORs with both in-plane and axial oblique incident angles. The range of the images displayed is 6 mm in both r and u directions. The top row shows the LOR-PDFs using a common intensity scale while, in the bottom row, each 2D LOR-PDF segment is scaled to its own maximum. Each LOR-PDF segment is scaled to its own maximum. Note the anisotropic distribution of LOR-PDF in all directions.

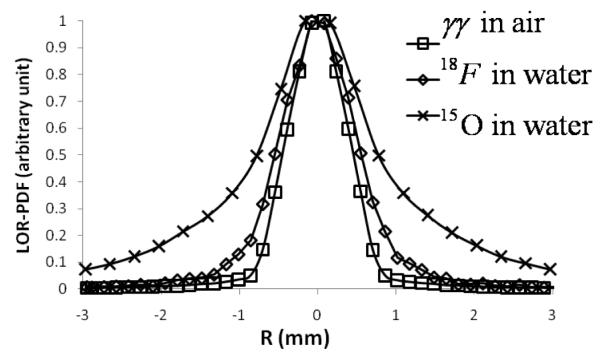
Figure 8.

Comparison of profiles for one LOR-PDF with different radionuclides and surrounding medium: γγ in air, ¹⁸F in water and ¹⁵O in water. Each profile was scaled to its own maximum. The LOR group is φ = [−2.5°,2.5°], b =12, and θ = [−5.5°, 5.5°] . The PDF’s depth index along LOR is 4 out of a total of 9 segments (central bin). The location of the profile is shown in the top-middle image in Figure 5. The PDF sample sizes for in air and ¹⁸F in γγ water are 0.16 mm, it is 0.32 mm for ¹⁵O in water to accommodate its broader spread.

In Figure 5, each image shown is the PDF in one r-u plane. From left to right, the LOR depth progresses from the starting-side to the ending-side. The two rows are from the same LOR-PDF but are displayed in different scales: the top-row uses the maximum of the entire LOR-PDF as the common scale for all the images, while the bottom row has each LOR-PDF segment displayed to its own maximum. The display setting of the bottom row helps visualize the variations of LOR-PDF shape, particularly for the ending segments of LOR where the overall intensity is much less than that of the central segments. That is, as emission location, d, moves away from the central FOV, there are less positrons contributing to the corresponding 2D segment of the LOR-PDF. The transition of the LOR-PDF’s shape from square to circular, and back to square is clearly seen; this corresponds to the classic understanding of PET geometrical response function [22]. The symmetries in r, u and d directions are consistent with the particular orientation of this group of LORs.

As compared to the LORs that formed LOR-PDF in Figure 5, the LORs for Figure 6 only differ in their detector block separation index b=14 , i.e., the ending-side of these LORs is two detector blocks away from a direct-opposite orientation (Figure 1), which corresponds to an in-plane obliqueness of 15°, i.e., φ_b =15° . The sequence and display settings of Figure 6 are the same as Figure 5. Here, the LOR-PDF is clearly asymmetric in the r direction, and the PDF is no longer centered, but is shifted to the left side (towards the CFOV). In addition, a clear elongation along the LOR’s incident direction is observed.

When a LOR is oblique in both in-plane and axial directions, the corresponding LOR-PDF shows anisotropic characteristics in all 3-directions, i.e., r, u and d. As an example, the LOR-PDF with φ=[−7.5°, −2.5°], b=15, and θ =[−27.5°, −16.5°] according to (3), is shown in Figure 7. Here both PDF width and shape varies for the different segments of the LOR. As a result of the skewed LOR orientation, the symmetries in r and u directions, as observed in Figures 5 and 6, do not occur, even in the PDF at the center of LOR.

3.2 Effect of positron range and annihilation photon acollinearity

The LOR-PDFs of ¹⁸F and ¹⁵O in water had similar characteristics to those of the γγ in air presented in Figures 5, 6 and 7, except that positron range and annihilation photon acollinearity broadened the LOR-PDF. Figure 8 shows a comparison of LOR-PDF section profiles from the 3 radionuclides with different positron ranges and acollinearities (the middle image in the top row of Figure 5 shows the location of the profile). The LORs for this figure have the orientation defined by φ = [−2.5°, 2.5°], b =12, and θ = [−5.5°, 5.5°] , and d = 4 (the central depth bin for a total of 9 LOR depth samples). The increased spread of ¹⁸F and ¹⁵O are clearly visible. The PDFs for ¹⁸F and ¹⁵O have less statistics than that of γγ due to the attenuation medium object surrounding the radionuclide. This can be improved by 1) performing a longer Monte Carlo simulation to collect more events; 2) filtering the LOR-PDF; and 3) reducing the number of LOR-PDFs by using a smaller number of LOR groups, i.e., using larger grouping bins.

3.3 Resolution recovery

The resolution recovery performance of the proposed LOR-PDF model was assessed by comparing the reconstructed images of simulated hot-rod phantoms from ray-tracing, iso-Gaussian, and LOR-PDF paths (section 2.9). The results are shown in Figures 9-12. In each figure, the ray-tracing image is on the left, the iso-Gaussian image is in the middle, and the LOR-PDF image is on the right. The images were summed over 60 mm in the axial direction to minimize the visual effect of statistical noise. Each image is displayed scaled to its in-plane maximum and results from one iteration/subset pair are shown.

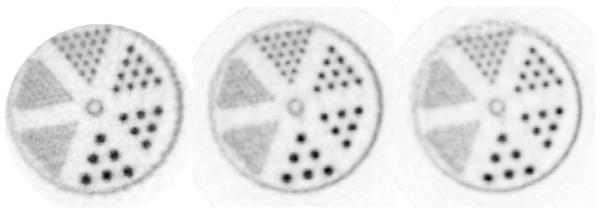
Figure 9.

Comparison of the simulated γγ hot-rod in-air phantom reconstructed with the ray-tracing OSEM-2D (left), iso-Gaussian (middle) and LOR-PDF (right) algorithms. All images were summed over 60mm in axial direction to reduce statistical noise. Each image is scaled to its in-plane maximum. These settings also apply to Figures 10-12.

Figure 12.

Comparison of the experimental ¹⁸F hot rod in-water phantom reconstructed with the ray-tracing OSEM-2D (left), iso-Gaussian MOLAR (middle), and LOR-PDF MOLAR (right) protocols. The images were summed over 20mm in axial direction, the axial extent of the hot-rod section, to reduce statistical noise effects.

The hot-rod phantom of Figure 9 had γγ as the radioactive source and air as the phantom medium. Both the iso-Gaussian and LOR-PDF images show clearer rod separation and more circular rod shapes than the ray-tracing method, which are exemplified in all the sections. The LOR-PDF image shows slightly higher resolution recovery in the quadrants with the smallest sources (rod diameter of 1.2 mm), although individual rods are not differentiable.

In Figure 10, the phantom consisted of ¹⁸F hot rods and water medium. Consistent with the results in Figure 9, the iso-Gaussian and LOR-PDF images show that the round shapes of the rods are better defined and the rods are better separated, as compared to the ray tracing OSEM 2D reconstruction. This can be seen in all 3 sections of the left half of the phantom images. As a result of including annihilation photons’ acolinearity and positron range, the section with the smallest rods is now further blurred and the lines are not differentiable. The iso-Gaussian shows clearer hot-rod separation and higher contrast than that of LOR-PDF for the upper right section, while other sections are similar.

Figure 10.

Comparison of the simulated ¹⁸F rods in water phantom reconstructed with the ray-tracing OSEM 2D (left), iso-Gaussian (middle) and LOR-PDF (right) protocols.

In Figure 11, the radionuclide of the hot-rod phantom is ¹⁵O. The apparent higher noise and distorted circular shapes in the ray-tracing OSEM-2D protocol image (left) as compared to the iso-Gaussian MOLAR (middle), and the LOR-PDF MOLAR images (right) clearly shows the impact of more accurate system matrix with the consideration of positron range effect for this phantom study. Note here the fixed FWHM used was 2.9 mm for the isoGaussian function, a median value selected from published resolution data [21]. This is expected as the ray-tracing model on the animal PET scanner does not take into account and resolution effects for all cases or the significant contribution from the energitic positrons of ¹⁵O in this case. Thus, the simple ray-tracing OSEM-2D, with severely distorted image pattern (9 o’clock segment) and significantly magnified noise, is not suitable for ¹⁵O radionuclide reconstruction. The LOR-PDF shows better resolution recovery than the reference method in terms of the lower activity between rods for the 3 largest rod segments, which is more visible with lower statistics data (not shown). In this case, the iso-Gaussian image achieves the best resolution recovery for the 4 larger rod segments.

Figure 11.

Comparison of the simulated ¹⁵O rods in water phantom reconstructed with the ray-tracing OSEM-2D (left column), the iso-Gaussian MOLAR (middle), and LOR-PDF MOLAR (right) protocols.

Fig. 12 presents the reconstructed images of an experimental ¹⁸F hot-rod phantom study obtained with the three reconstruction paths. According to the Monte Carlo simulation for the corresponding phantom, the scatter and random fractions were 26% and 11%, respectively. As scatter and random corrections were not implemented, the effects of these events were equivalent to background activity and therefore slowed algorithm convergence [23]. To avoid complicating the assessment with additional factors, no corrections for attenuation, scatter, or randoms were applied. Both the iso-Gaussian and the LOR-PDF images (middle and right) show tighter circular shape and cleaner rod separation. The iso-Gaussian image shows better contrast than that of LOR-PDF. This is most visible with the 12 o’clock segment. Another observation is that the top part of the outer hot-ring (outside the hot rod quandrants) shows a more consistent shape in the iso-Gaussian image than that in the LOR-PDF image. This was likely due to the lower amount of radioactivity in the area, as a result of phantom placement, which was aggravated by the slower convergence of the broader LOR-PDFs near the edge of FOV. The other parts of the outer ring, e.g. the 3 o’clock segment, do show sharper definition of the ring with LOR-PDF, which is expected with the better modeling of LOR-PDF.

As compared to simulated results in Fig. 10, the images in Fig. 12 have lower spatial resolution. This is evidenced by the rods in the 10 o’clock section that are not differentiable, and the separation between rods is less well defined for all three methods. This may be due, in part, to the inclusion of uncorrected object scatter and random events in the data, as well as other unmodeled errors such as crystal misidentification errors.

3.4 Contrast phantom study

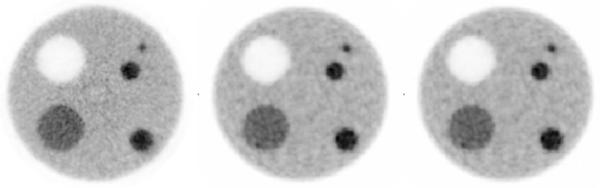
Figure 13 shows the visual appearance of the images obtained through the three image reconstruction paths – ray tracing, iso-Gaussian and LOR-PDF. Each image is a mean over the 20 replicates reconstructed. As is commonly seen in comparing reconstructions without and with resolution recovery, in both background and hot-sphere regions, the image from ray-tracing OSEM-2D looks most noisy. Here, the iso-Gaussian and LOR-PDF images look similar.

Fig. 13.

Central plane of the replicates’ mean images. From left to right are images from ray-tracing OSEM-2D (4 iterations of 16 subsets), iso-Gaussian (1.5mm FWHM, 6 iterations of 10 subsets) and LOR-PDF (6 iterations of 10 subsets).

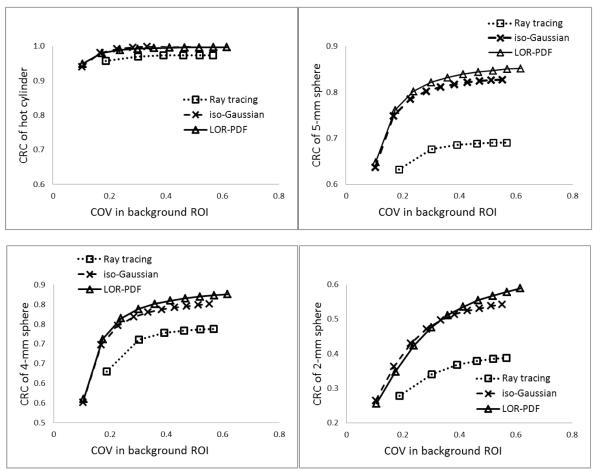
Figures 14 shows the comparison of the combined contrast recovery, CRC, and noise, COV, performance of the contrast phantom generated with the three reconstruction protocols. As defined in (4) and (5), CRC and COV were calculated from the replicate contrast phantom images. The CRC values in the 4 graphs of Figure 14 were from the hot-cylinder, the 5-mm, 4-mm and 2-mm radius spheres, respectively. The noise indices for all graphs were from the background ROI. From left to right, the data points of each curve correspond to incremental OSEM reconstruction iteration numbers. The OSEM iteration number, which is the product of iteration and subset numbers, of the ray-tracing curve start from 16 and increment by 16. For the two other curves, the OSEM iteration numbers start from 10 and increment by 10. The iteration numbers were selected so that the maximum iteration numbers roughly match.

Figure 14.

Contrast recovery coefficients (CRC) of the hot cylinder, and 5-, 4-, and 2-mm radius spheres versus the COV values in the background ROI. Given same level of CRC for 5- and 4-mm radius spheres, the noise in the background ROI was higher for the iso-Gaussian reconstructed images than those of LOR-PDF protocols.

Regardless of the sizes of the hot regions evaluated, the MOLAR reconstruction algorithms with either LOR-PDF or iso-Gaussian function showed, given similar noise level, consistently higher contrast recovery coefficients than the ray tracing path, as expected. This is consistent with the results shown in Fig. 9. Between iso-Gaussian and LOR-PDF, they have nearly identical curves for the hot cylinder region; to achieve same level of CRC with the 5-mm and 4-mm spheres, the iso-Gaussian yields images with higher noise, or in other words, iso-Gaussian achieves lower contrast recovery if the noise level were matched. With the 2-mm radius sphere, the LOR-PDF and iso-Gaussian curves crossed, with LOR-PDF achieving higher recovery (CRC) for 50 OSEM iterations or higher.

4 Discussion

For emission image reconstruction, there have been many system matrix derivation methods reported. This work is distinguished from other approaches in its implementation of the probability density function (PDF) concept. Each event along a LOR is related to a possible distribution of emission sources. Addressing the same subject of the widely used point spread function (PSF), but from a different perspective, the PDF concept provides a model that follows the natural sequence of PET event generation to describe the stochastic physical nuclide decay, annihilation photon emission and LOR detection process. With each LOR having its own PDF, the accuracy of the system matrix is ensured, yet the complexity of the system matrix is scalable as the LORs can be handled efficiently in the projection space.

The key techniques that enabled the LOR-PDF implementation was the concise parameterization of system matrix as described in (3): 1) the voxel-to-LOR positions, (r,u), replaced the conventional approach of calculating the intersection volume of voxel-to-LOR; 2) the LOR-depth, d, explicitly included this effect in the system model; and 3) using LOR-detector incident angles provided a simple analytical approach to take advantage of the in-plane and axial geometrical symmetries. The explicit modeling of LOR resolution vs. depth for PET in this work, to our knowledge, is new. As shown in Figs. 5, 6 and 7, it provides a complete model for this well-known physical concept.

With the parameterization, the 3-D LOR-PDF encapsulated all the interactions between image and projection space, therefore the system matrix could be decomposed into two modules: the LOR-PDF module and LOR module. The decoupled LOR module simplified the use of symmetries. For example, rotational symmetry, i.e., rotation of the starting-side of each LOR to a fixed position to sort the LORs was used in this work. This alone gave, in the case of the animal PET scanner used here, a 12-fold reduction of possible detector-block pair combinations. Other symmetries, such as in-plane and axial directions, may also be considered.

The significant variations observed in the LOR-PDFs over the range of LOR-detector incident angles, as shown in Figures 5-7, implies that using a fixed function to model the system response introduces discrepancies between the reconstruction model and the true system response. Despite these substantial effects, we found that using the iso-Gaussian function, with its approximate FWHM selected from the wide range of PSFs reported in literature, showed surprisingly good performance. In terms of resolution recovery, it is only slightly inferior to LOR-PDF in the large target regions of the back-to-back gamma in air phantom studies, but visibly better when the effects of positron range and annihilation photon acolinearity were involved (Figs. 10, 11 and 12). The superiority became more prominent when positron range effects were more significant. It should be noted, though, the significance of the observations in Figs. 9-12 may be compromised by the fact that these results reflect the image characteristics at a particular iteration. Given the high statistics we used for the γγ system matrix and the large section size of the LOR tube in all MOLAR reconstructions, some possible reasons for iso-Gaussian’s success are as follow: 1) The shape of LOR-PDF, especially when the long-tail positron range function [24] is included, although being a more accurate description of the system response, was not optimal for resolution recovery. For a target volume, the wider spread of the LOR-PDF includes more surrounding activity into the computation, which can slow down the convergence speed of the target region’s reconstruction [23]. 2) The resolution values used for the iso-Gaussian functions were average values estimated from literature [16, 21]. Knowing that a wider iso-Gaussian kernel would force the reconstructed image to have a higher resolution and vice versa, the net effect would be dependent on the iso-Gaussian resolution value in relation to a) the overall distribution of LOR-PDFs and b) the object distribution. 3) The statistical properties of different LOR-PDFs varies as the counts collected in each LOR-PDF group depends on geometry of the system and the phantom. The statistical noise in the low-count segments of the LOR-PDF system matrix may propagate into the reconstructed image and undermine image quality. 4) The artificial difference, or step-wise transition, of LOR-PDFs between neighboring LORs introduced by the LOR grouping mechanism (3) may have also contributed to reduced performance of the LOR-PDF approach. Apparently, the iso-Gaussian method does not have this issue. 5) All resolution-recovery reconstructions produce voxel values that are more correlated to their neighbors than those without resolution-recovery. Therefore, while voxel noise is an important measure, when ROI assessments are considered, the voxel-to-voxel correlation is also important and yet to be evaluated. It is possible that some combination of the above factors cancel out the benefit of the accuracy of LOR-PDF. While improving the statistics of the LOR-PDF system matrix is attainable, albeit computationally expensive, further investigation of the root cause of the recovery and noise behavior of the LOR-PDF is in progress.

With the LOR-PDF concept and the LOR grouping strategy, the issue of system matrix size requires decisions on the sample sizes of the variables involved, as listed in (3) and Table 1. The irregular shape of the PDFs, as in Figure 7, makes it difficult to extract parameterized functions to guide the selection of sample sizes, so we used an empirical approach to find the sample sizes for each variable. For example, we compared the reconstructed images for a few in-plane angle (φ) sample sizes (1°, 3°, 5°) while keeping other settings unchanged, and concluded that having in-plane (φ) and out-of-plane (θ) angle sample size of 5° and 11°, respectively, provides good image quality with reasonable reconstruction/simulation time.

We used a fixed width LOR cross-section, (r,u) for the LOR volume, for forward and backprojection. For γγ in air and ¹⁸F in water, it was 5 mm × 5mm. For ¹⁵O in water, it was 9.6 mm × 9.6 mm. The widths were selected so that there was minimal (<5%) truncation of the LORs contributing to the FOV. This approach ensured there was no over-truncation of the LOR-PDFs, but was not computationally optimal due to the significant variation of LOR-PDFs. The typical approach of using a cutoff threshold to control the effective tube-size of the LOR was tested and the results were not different from what is reported here. If the superiority of the LOR-PDF is confirmed, the LOR cross-section width may be adaptively selected to improve reconstruction speed.

Using the detector block separation index b combined with the in-plane and out-of-plane angles to represent the incident direction of each LOR was a useful approach to analyze the LOR-PDFs and to reduce system matrix size. A more straightforward approach would be to define the direction of each LOR directly, requiring φ and θ values for the two ends of a LOR. This would introduce 4 variables to the system matrix and the combination of these 4 variables forms a large and very sparse space. Given the cylindrical geometry of the scanner of this study (and of most PET scanners), the use of the (φ,b,θ) LOR indexing system is a more efficient approach.

To include the positron range effect [21], an attenuating medium must be present for annihilations to occur. The attenuation of a large object, which is needed for the generation of a complete system matrix, significantly increases the Monte Carlo simulation time, as demonstrated by the number of counts and simulation time for ¹⁸F and ¹⁵O in Table 3. Instead of including an attenuating medium, a more efficient alternative for generating a system matrix with the positron range effect included is to combine the γγ in air LOR-PDF with isotope-specific point spread functions, which include positron range and annihilation photons acollinearity effects. Further, attenuation medium-dependent positron range, rather than assuming the medium is uniform, can be implemented in the reconstruction algorithm [25]. This approach can be readily implemented whenever the imaging object’s attenuation coefficient map is available.

Crystal mis-identification, which can occur due to crystal light sharing and PMT signal decoding variations, was not included in the Monte Carlo simulation. This should not affect the assessment of the LOR-PDF method with simulated studies, as the system matrix and study have matching conditions. However, for the system matrix to be applied to a real imaging system, this factor should be included, either by including the PMT stage in the simulations, or by using an analytical model to modify the system matrix. In addition, mechanical and material irregularities that exist in real scanner system but without prior knowledge cannot be included in the Monte Carlo system matrix generation approach that we propose here.

In addition to performing long Monte Carlo simulations to increase LOR-PDF statistics, we also tested using median filtering and 2-D Gaussian fitting of the LOR-PDFs to compensate for low statistics. We found that noise performance after filtering or fitting was slightly improved, but the resolution recovery advantage as shown for the 2-mm spheres in Figure 14 was compromised. While increasing computation time by performing more simulations is possible, fitting the LOR-PDFs with appropriate non-Gaussian functions is another option that may reduce noise induced by the system matrix without affecting resolution.

Depth dependent LOR-PDFs suggest that there are large resolution differences towards the edge of the FOV. Thus for centered objects, we might expect to see the smallest advantages of the LOR-PDF method. Therefore, additional studies are required to evaluate the potential improvement of LOR-PDF for objects on the edge of the FOV.

The LOR-PDF system matrix was incorporated into the parallelized MOLAR list mode reconstruction software [20] which was implemented on a Linux computer cluster. The events from the list mode data file were assigned to multiple compute nodes by the arrival sequence instead of LOR incident angle; this required that the full system matrix be stored on each node. An alternative approach is to have a larger system matrix and store segments of it on individual nodes. With 2 or 4 GB RAM memory on each node of the cluster, it was observed that the reconstruction time increased several fold when the system matrix size exceeded 0.5GB, presumably due to disk swapping. Therefore, the system matrix size was kept small. Note that a small system matrix has the benefit of requiring a shorter time for simulation to achieve the same level of statistical precision, which directly affects the reconstructed image quality [26].

5 Conclusions

We developed a system matrix that is based on the probability density function for each line of response (LOR-PDF). The LOR-PDFs derived from Monte Carlo simulation showed LOR-detector angle, coincidence emitting source and medium-dependent anisotropic and asymmetric characteristics, which aligned well with common PET physical principles.

The application of iso-Gaussian and LOR-PDF based system matrices to simulated and experimental phantom studies showed better image quality than that of the OSEM-2D algorithm provided on the scanner. The comparison of the iso-Gaussian function and LOR-PDF revealed that 1) the LOR-PDF achieved consistent higher recovery when positron range and annihilation photon acolinearity effects were not involved, and 2) with positron range and acolinearity effects, the iso-Gaussian achieved similar or better resolution recovery depending on the significance of the positron range effect.

We conclude that the 3-D LOR-PDF is an effective approach to generate an accurate and compact system matrix. However, when used directly in expectation-maximization based listmode iterative reconstruction algorithms such as MOLAR, the superiority of this method was not evident. Thus, using an iso-Gaussian function with an average resolution parameter in MOLAR is currently a simple but effective technique for PET reconstruction. Substantial additional work is required to optimize the use of the LOR-PDF and to determine to what extent it can produce substantive advantages over isoGaussian reconstructions.