Changing spatial epidemiology of pertussis in continental USA

Marc Choisy; Pejman Rohani

doi:10.1098/rspb.2012.1761

. 2012 Sep 26;279(1747):4574–4581. doi: 10.1098/rspb.2012.1761

Changing spatial epidemiology of pertussis in continental USA

Marc Choisy ^1,^*, Pejman Rohani ^2,³

PMCID: PMC3479730 PMID: 23015623

Abstract

Prediction and control of the geographical spread of emerging pathogens has become a central public health issue. Because these infectious diseases are by definition novel, there are few data to characterize their dynamics. One possible solution to this problem is to apply lessons learnt from analyses of historical data on familiar and epidemiologically similar pathogens. However, the portability of the spatial ecology of an infectious disease in a different epoch to other infections remains unexamined. Here, we study this issue by taking advantage of the recent re-emergence of pertussis in the United States to compare its spatial transmission dynamics throughout the 1950s with the past decade. We report 4-year waves, sweeping across the continent in the 1950s. These waves are shown to emanate from highly synchronous foci in the northwest and northeast coasts. In contrast, the recent resurgence of the disease is characterized by 5.5-year epidemics with no particular spatial structure. We interpret this to be the result of dramatic changes in patterns of human movement over the second half of the last century, together with changing age distribution of pertussis. We conclude that extrapolation regarding the spatial spread of contemporaneous pathogens based on analyses of historical incidence may be potentially very misleading.

Keywords: pertussis, spatial dynamics, infectious disease re-emergence

1. Introduction

Over the past decade, the high-profile introduction and geographical spread of novel pathogens, such as SARS [1] and foot-and-mouth disease [2], and the ever-present threat of a devastating influenza pandemic [3] have emphasized the urgent need to better understand the spatial transmission of infectious diseases and their attendant control implications [4,5]. However, making predictions about the spatial dynamics of such diseases is hampered by the absence of data, precisely because they are emerging pathogens. Much progress in spatial epidemiology has resulted from studying long-term notification records of familiar infectious diseases, such as measles [6], seasonal influenza [7] and dengue [8]. It is important to determine, however, whether conclusions drawn from historical studies of particular infectious agents can inform the epidemiology of a modern day and novel pathogen threat.

To explore this issue, we examine case reports of whooping cough (or pertussis) in continental USA, where concerted immunization programmes in the 1950s led to a drastic reduction in incidence over the subsequent three decades [9]. Since 1980s, however, a significant and poorly understood upsurge in cases has been reported [10–12]. The fluctuating fortunes of pertussis control efforts in the US afford us a unique opportunity to study the spatial ecology of an infectious disease in the same localities but in two eras separated by many decades.

Whooping cough is a respiratory disease caused by the bacterium Bordetella pertussis. Historically, the onset of immunization programmes in developed countries were instrumental in the reduction of pertussis incidence [13,14]. It remains, however, one of the key microparasitic diseases of childhood and adolescence, with a significant annual burden of infant mortality [15], especially in developing nations [16]. The well-publicized resurgence of pertussis reports in several countries that boast high vaccine uptake has been the subject of much debate [10–12,17] and has highlighted major gaps in our understanding of its epidemiology [18,19].

Here, we analysed monthly whooping cough incidence in the 49 continental US states (including the District of Columbia) from January 1951 to December 2010. In order to take into account large temporal differences in incidence, and in particular the near-absence of cases from 1970s to 1990s, our analyses proceeded by splitting the data into three different time periods, focusing exclusively on the early (1951–1962) and the recent (2002–2010) eras (see §2 and the electronic supplementary materials for the rationale for these specific eras). To quantify patterns in the data, we used wavelet decomposition, a technique that is particularly well suited to non-stationary time series [20,21].

2. Material and methods

(a). Pertussis incidence reports

Pertussis monthly notifications were collected at the state level for the 49 continental states (i.e. including the District of Columbia) from 1951 to 2010. These data were obtained from the National Notifiable Disease Surveillance System and are fully anonymized. In the absence of detailed state-specific vaccine uptake estimates, we are unable to infer the fraction of infected reported, though analysis of hospital records suggests a reporting probability of 11.6 per cent [22].

(b). Population sizes and spatial locations

Population size estimates by state and year from 1951 to 2010 are freely available from the US Census Bureau (http://www.census.gov/popest/archives). Given that our epidemiological data are resolved by state, we make the pragmatic choice to define a population as the number of inhabitants within a given state. Because of the strong aggregation of populations into high-density urban centres, our definition is defensible. For the goegraphical location of each state population, we considered its centroid defined as the point on which a rigid, weightless map would balance perfectly, if the population were represented as points of equal mass. In this study, we used the coordinates (in degrees) of these centroids for the year 2000. These are freely available from the US Census Bureau (http://www.census.gov/geo/www/cenpop/statecenters.txt).

(c). Wavelet transforms

Prior to wavelet decomposition, time series were square-root transformed in order to stabilize the variance. Time series were then centred and reduced in order to allow comparisons of their qualitative features (i.e. periodicity) from state to state. Wavelet decompositions were performed using a Morlet wavelet with a non-dimensional frequency ω₀ = 6 (see [6,20,21] for mathematical expressions). Before wavelet transforms, time series were padded with zeros up to the nearest power of 2. Analyses with no padding gave very similar results (not shown). Filtering over a given frequency range is performed by summing the local wavelet power spectrum over this frequency range. Time series were smoothed by filtering over the frequencies where most of their power (i.e. variance) stands. A major advantage of complex wavelets such as the Morlet one is that they enable the quantification of phase angles of the time series. These phase angles give information on the timing of the epidemics. Phase angles were calculated after filtering and expressed, for each state, by taking their residuals in a linear model regressing phase angle of all states as a function of time (see the electronic supplementary materials and its figure S2 for more detailed explanations). They are thus called ‘residual phase angles’ in the rest of the text.

(d). Longitudinal speed of propagation

The longitudinal speeds of disease propagation were estimated from the slopes of the piecewise linear regression between phase angles in radians and longitude in degrees. The radians were first transformed into years, based on the period around which the time series were filtered. Taking into account the Earth's curvature, one longitude degree represents about 84 km at the latitude of 40° (the average latitude of the continental US).

(e). Critical community size

Critical community sizes (CCS) were estimated on a given time period by plotting, for each state, the proportion of months with zero disease notification during this time period against its mean population size over the same time period. Then, an exponential decay curve y(x) = Ae^−Bx was fitted to these 49 data points, and the value of the CCS was defined as the value of x where y is equal to a proportion that represents one month over the considered time period.

(f). Spatial synchrony

The assessment of spatial synchrony was based on pairwise (i.e. inter-state) correlation coefficients. Contrary to phase angle analyses which account only for the qualitative features of periodicity, synchrony is strongly dependent on the quantitative features of the time series, especially the amplitude (and thus is more affected by potential changes in the reporting rate). The two approaches are complementary [6,7]. The relations between synchrony and Euclidian distance were estimated by the NCF library for R [6]. In particular, the spatial correlation functions were estimated using the non-parametric spline covariance function and 1000 bootstraps to generate 95% confidence intervals (CIs) [23].

(g). Time period definition and robustness

The US pertussis incidence time series are characterized by strong non-stationarity, with a central era (1970–1990) during which very few cases were reported across the country. The rationale was thus to focus our analyses on the earlier segment of the data when the estimated vaccination coverage was still low [9] and pertussis incidence relatively high. Selecting a portion of the data on which analyses are performed naturally leads to concerns over the arbitrariness of the choice and its impact on the robustness of the results. We addressed these concerns by examining the behaviour of the distribution of the pairwise correlation coefficients, the number of states above and below the CCS, the spatial correlation functions and the global wavelet spectra, all calculated on the 1951 − x time periods, when x varies between 1951 and 2010 (see the electronic supplementary materials). These analyses identified a sharp transition around 1963 with constant behaviour before and after this transition (see the electronic supplementary material, figure S1b,d). The results presented for the first era with x = 1962 are robust with respect to x as long as x < 1970. Similarly, a second transition was identified around 2002, defining the second era but the results were less robust with respect to this choice (see §3). Finally, choosing the 1951 − x time period before or after the wavelet decomposition did not significantly affect the results.

3. Results

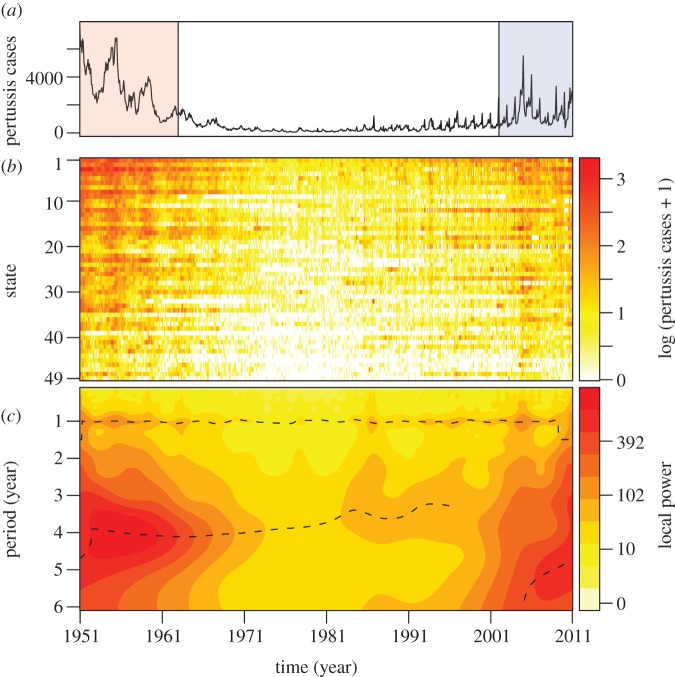
The previously mentioned decrease in pertussis incidence during the 1960s is illustrated in figure 1a,b, followed by the recent rise in case notifications across states. In figure 1c, we display the mean local wavelet power spectra of the 49 states. This figure indicates that most variance in pertussis fluctuations is centred around the period of 4 years in the first era (1951–1962) and between 5 and 6 years in the most recent era (2002–2011). The figure also shows that wavelet decomposition fails to identify significant periodicity during the 1970s because of the paucity of reported cases.

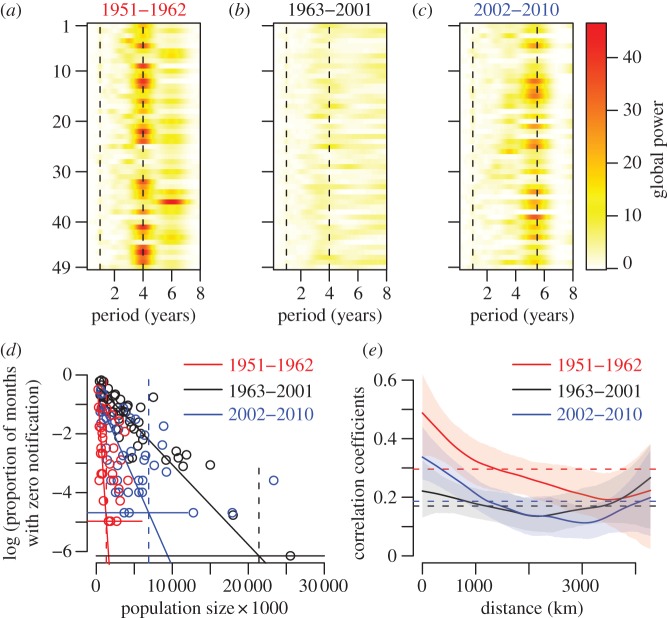
Additionally, we carried out standard Fourier spectral analyses of pertussis incidence in each era for all states. Consistent with the mean wavelet results, we found that most states in the early and recent eras exhibit a pronounced statistically significant 4- and 5.5-year period, respectively (figure 2a,c), whereas there is no detectable periodicity in the time series from 1963 to 2001 (figure 2b). The extinction profile of pertussis—defined using the CCS concept [24]—is also different in the three eras (figure 2d). Importantly, in the early era, in more than two-thirds of the states, the population size exceeded the CCS, with no pertussis extinctions. In the middle era, however, extinctions were frequently observed, while pertussis is endemic in 12 states in the recent era. The three epochs are also characterized by differences in their spatial synchrony [23,25] (figure 2e), with early and recent eras showing much more pronounced decay in synchrony with distance—characteristic of dispersal-driven synchrony [26]—than the intermediate period (figure 2e).

Figure 2. — Periodicity, CCS and spatial correlation for the three time periods considered (1951–1962, 1963–2001, 2002–2010). (a–c) Global wavelet power spectra for each state and colour-coded according to the scales on the left for (a) 1951–1962, (b) 1963–2001 and (c) 2002–2010. The vertical dashed lines show the 1-, 4- and 5.5-year periods. The states are ranked alphabetically. (d) Estimates of the CCS for the three periods: 1.3 million for early era (red vertical dashed line) with 34 states above it; 21.4 million for the middle era (black vertical dashed line) with 48 states below it; and 6.9 million for the recent era (blue vertical dashed line) with 12 states above it. Horizontal lines correspond to one month with zero notification over the considered time period. The intersections of these thresholds with the regression lines define the CCS. (e) Spatial synchrony with 95% CIs, same colour code as for (d). The horizontal lines are the mean correlation coefficients. (d,e) Red solid line, 1951–1962; black solid line, 1963–2001; blue solid line, 2002–2010.

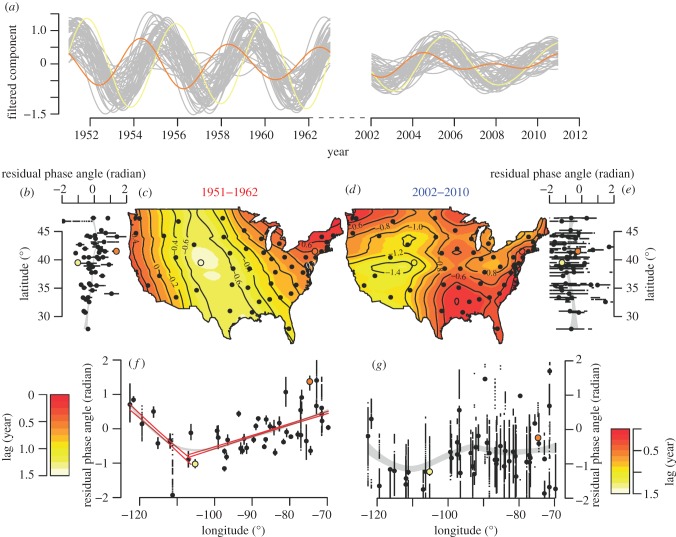
To examine relationships among epidemics in different states, we filtered the time series for each state in the early and recent eras around the dominant periods 4 and 5.5 years, respectively (figure 2a,c). A striking feature that emerges is the systematic gradient in the timing of epidemics in the early era, as illustrated in figure 3a. However, this organization among states appears different in the two eras as exemplified by the reconstructed incidence in New York and Colorado (highlighted in orange and yellow, respectively). In the early era, these two states show epidemics that are out of phase with a lag of almost 2 years, with outbreaks in New York leading the country, while epidemic cycles in Colorado trail. In contrast, the dynamics in these states are almost in synchrony in the recent era. Calculation of the residual phase angles of the filtered time series in the two eras allowed us to quantify the lags observed between epidemics in each state.

Mapping the early era residual phase angles (figure 3c) reveals spatially organized travelling waves, with two discernible foci, and this pattern is robust respective to the number of years used to define the early era (see the electronic supplementary material, figure S2f together with accompanying movies of the spatial dynamics of filtered signals). Epidemics in the northeastern and northwestern states are strongly in phase, despite the substantial geographical separation; a feature that is also apparent in figure 2e (red curve), with increasing spatial correlation functions for distances in excess of 3000 km. Thus, northern states on the east and west coasts appear to act as foci, driving epidemic waves that spread southwest and southeast, respectively. When phase lags are regressed against the geographical location of states, we find longitude is a strong and significant predictor of the epidemic timing (figure 3f). This translates into a longitudinal progression speed westward from the northeast (323 km per month, 95% CI, 311–336 km per month) that is almost three times as fast as the eastward wave from the northwest (113 km per month, 95% CI, 106–120 km per month). For comparison, the radial speed of the dengue haemorrhagic fever waves emanating from Bangkok in the 1980s–1990s was estimated at 148 km per month (95% CI, 114–209 km per month) [8], while the waves of measles in the pre-vaccine era were estimated to spread from London to nearby environs at 20 km per month [6]. Latitude, on the other hand, has much less effect (figure 3b).

In the recent era, in contrast, we find surprisingly little spatial organization (figure 3d). As we demonstrate in the electronic supplementary materials, while the earlier era is characterized by consistent phase hierarchy among states through time (see the electronic supplementary material, figure S2f), the later era exhibits substantial variability without any systematic structure (see the electronic supplementary material, figure S2m). Additional support for this clear difference between the eras is provided by the lack of robustness with respect to the length of time series used to define the recent era (see the electronic supplementary material, figures S1b,d), again confirming that there is no clear spatial organization in this era. Finally, by presenting the unfiltered time series ordered according to longitude, we confirm the spatial structure of pertussis dynamics in the first era (see the electronic supplementary material, figure S3a), together with its unravelling in the recent era (see the electronic supplementary material, figure S3b).

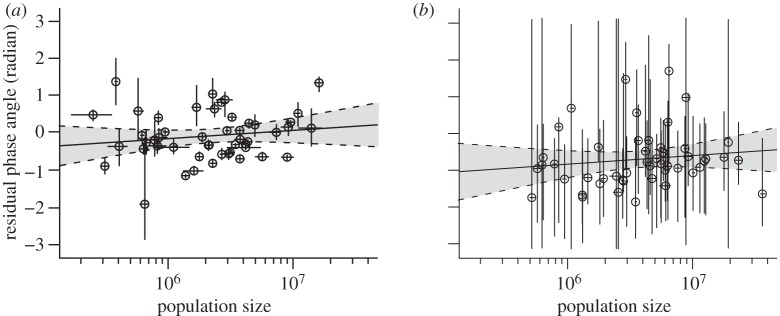
Finally, we examined whether residual phase angles depicted in figure 3 are associated with state population sizes and found no significant relationship (figure 4, F_1,47 = 1.14, p = 0.29 for the first era and F_1,47 = 0.85, p = 0.36 for the second era). This is in contrast with the relationship documented for measles in England and Wales [6]. Furthermore, no relationship was observed between phase correlations and population size products (see the electronic supplementary material, figure S4), in contrast to seasonal influenza waves in the US [7]. In the discussion section, we propose different lines of explanation for these observations.

Figure 4. — Relationships between residual phase angles and decimal logarithm of population sizes for the early (a, 1951–1962) and recent (b, 2002–2010) eras. Horizontal and vertical bars show, for each state, the extent (over the considered time periods) of population size and residual phase angles, respectively. Open circles show the means, for each state, of the population sizes and residual phase angles. Full lines and grey areas show linear regressions and their 95% CIs. The slopes of these regressions are not significantly different from zero: F_1,47 = 1.14, p = 0.29 for the first era and F_1,47 = 0.85, p = 0.36 for the second era.

4. Discussion and conclusions

To date, three distinct mechanisms have been identified to explain the spatio-temporal morphology of infectious disease systems.

I. Diffusive spread from a point source. This can result from the localized introduction of a pathogen into a virgin population, as documented in the systematic expansion of raccoon rabies [27] and West Nile virus [28] in the US and the Ebola virus in Zaire [29].

II. Source-sink dynamics and gravity coupling. Measles epidemics in the pre-vaccine era in England and Wales have been shown to be the result of recurrent waves emanating from large populous centres (sources) that percolate through the rural hinterland (sinks) [6]. These waves are consistent with ‘gravity coupling’, whereby the epidemiological exchange between two centres is determined by their distance and their respective population sizes [30]. Similar patterns have been noted in the spatial hierarchies of annual influenza epidemics across the US [7] and waves of dengue haemorrhagic fever in Thailand, pulsing across the country from Bangkok [8].

III. Environmental gradients. In contrast, the waves of seasonal influenza epidemics across Brazil are not thought to be driven by population density or patterns of movement. Influenza epidemics originate in northern Amazonian regions, where population density and movement rates are low, spreading to the more densely populated southern subtropical states over a three-month period [31]. Climatological variables (including temperature and absolute humidity [32]) are thought to be the leading candidates for generating this wave [33].

In this study, we find clear spatial organization of pertussis epidemics in the 1950s and the conspicuous absence of such structure after its re-emergence half a century later. Among the two above-described mechanisms relevant to recurrent epidemics (mechanisms II and III), we can tentatively rule out mechanism III because if environmental factors were the primary drivers of patterns reported in figure 3c, then we would expect approximately similar geographical structuring in the recent era (figure 3d).

A rigourous evaluation of the role of mechanism II in the spatio-temporal dynamics of pertussis in the early era would require the use of statistical inference methods, applied to coupled state-specific mechanistic transmission models [30]. Unfortunately, the absence of state-level vaccine uptake information in the 1950s precludes such an approach. Therefore, we resort to proximate indicators of gravitational coupling. Given that population sizes in most states in the early era exceeded the extinction threshold (CCS, figure 2d), the observed spatial waves are unlikely to have resulted from strict source–sink dynamics, where frequent local extinctions are followed by reignition from large reservoir states. We tested the effect of population size on the hierarchy of epidemic timings by two previously published methods (see figure 4 and electronic supplementary material, figure S4) and failed to observe any significant relationship, in contrast to measles in England and Wales [6] and influenza in the US [7].

A fourth hypothesis that may explain the patterns reported here for US pertussis in the 1950s is the ‘pacemaker’ mechanism, which has been readily predicted in theoretical studies [34,35] but has not been documented in large-scale epidemiological (or ecological) systems, so far. Here, the foci—or pacemakers—would be a collection of geographically clustered populations with highly synchronous epidemiological dynamics acting as local rhythm generators, such as states in the northeast and northwest in the 1950s. The factors that would determine the precise location of these foci are not yet understood. In mathematical models, however, pacemakers have been shown to arise in regions exhibiting higher than average connectivity [35], or—in spatially homogeneous systems—to emerge with no predictable location [34,36]. In epidemiological systems, regional population demography, patterns of localized movement and vaccine uptake levels are likely to play an important role in the spatial pattern formation. Theoretical work to identify the processes that may generate pacemaker dynamics and the impact of disease-specific epidemiological and immunological traits is clearly timely.

Over the 60 years of our dataset, we have documented major shifts in pertussis epidemiological dynamics. First, the inter-epidemic period shifted from 4 (figure 2a) to 5.5 years (figure 2c), which may be attributable to a decrease in the rate of susceptible recruitment either owing to a lower per capita birth rate or increased vaccine uptake. However, we point out that because of the brevity of the time series in the recent era (only 9 years), observed patterns need to be interpreted with caution, especially given the large CIs in figure 4b and variability in phase angles for some states in electronic supplementary material, figure S2l. Second, since the 1950s, there have undoubtedly been changes in pertussis reporting probability, likely attributable to changes in the surveillance system and improved diagnostic capabilities [37]. However, such changes, if they can affect the quantitative aspects of the dynamics (such as mean incidence), are expected to have very limited effects on qualitative aspects of the dynamics (such as periodicity and phase) on which our analysis is based. We thus expect our results on spatial dynamics to be insensitive to changes in the reporting fidelity.

The precise mechanisms generating different pertussis metapopulation dynamics in these eras are not known. We speculate, however, that the extent of pertussis-specific spatial coupling between states is likely to have altered substantially over the time span of these data. This would have arisen for two reasons. First, it would be uncontroversial to point out that human mobility patterns have changed dramatically over the past 6 decades. In the 1950s, the majority of trips were made by ground transportation, with air travel still rare apart from coast-to-coast exchange [38]. This verbal hypothesis can explain the spatial phase structure observed in figure 3f: rapid between-coast air connections would synchronize the two coasts and slow terrestrial diffusion on the road/rail network would be responsible for the linear phase-longitude association. The westward speed of propagation being almost three times as fast as the eastward one may have resulted from a road network being denser and straighter in the flat east part of the USA than in its mountainous Western counterpart, and also from higher population density in the east. The dramatic increase of air travel all over the continent together with rapid population growth in the central US may be responsible for the disruption of this spatial structure in the contemporary re-emergence of pertussis. The second potential factor in the changing spatial epidemiology of pertussis relates to the age distribution of pertussis incidence. It has been shown that, in recent years, pertussis is affecting older individuals [39,40], with increasing number of reports observed in adolescent and adult age groups [41,42]. Hence, compared with the 1950s, the spatial exchange of pertussis across states would have changed both because of changing underlying movement patterns in the population, but also because of a shift in the age classes affected. From a pragmatic perspective, our findings suggest that analyses of historical data may be much less informative about modern epidemiological systems than could a priori be expected.

Acknowledgements

We thank Aaron King and two anonymous reviewers for comments on this paper. M.C. was funded by IRD and CNRS. M.C. and P.R. were supported by the Vaccine Modeling Initiative of the Bill and Melinda Gates Foundation and the Research and Policy in Infectious Disease Dynamics program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, National Institutes of Health, and by a grant from the National Institutes of Health 1R01AI101155.

References

1.McLean A. R., May R. M., Pattison J., Weiss R. A. 2005. SARS: a case study in emerging infections. Oxford, UK: Oxford University Press [Google Scholar]
2.Keeling M. J., et al. 2001. Dynamics of the 2001 UK foot and mouth epidemic: stochastic dispersal in a heterogeneous landscape. Science 294, 813–817 10.1126/science.1065973 (doi:10.1126/science.1065973) [DOI] [PubMed] [Google Scholar]
3.Webby R. J., Webster R. G. 2003. Are we ready for pandemic influenza? Science 302, 1519–1522 10.1126/science.1090350 (doi:10.1126/science.1090350) [DOI] [PubMed] [Google Scholar]
4.Riley S. 2007. Large-scale spatial-transmission models of infectious disease. Science 316, 1298–1301 10.1126/science.1134695 (doi:10.1126/science.1134695) [DOI] [PubMed] [Google Scholar]
5.Keeling M. J., Rohani P. 2008. Modelling infectious diseases. Princeton, NJ: Princeton University Press [Google Scholar]
6.Grenfell B. T., Bjørnstad O. N., Kappey J. 2001. Travelling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 10.1038/414716a (doi:10.1038/414716a) [DOI] [PubMed] [Google Scholar]
7.Viboud C., Björnstad O. N., Smith D. L., Simonsen L., Miller M. A., Grenfell B. T. 2006. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312, 447–451 10.1126/science.1125237 (doi:10.1126/science.1125237) [DOI] [PubMed] [Google Scholar]
8.Cummings D. A. T., Irizarry R. A., Huang N. E., Endy T. P., Nisalak A., Ungchusak K., Burke D. S. 2004. Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature 427, 344–347 10.1038/nature02225 (doi:10.1038/nature02225) [DOI] [PubMed] [Google Scholar]
9.Simpson D. M., Ezzati-Rice T. M., Zell E. R. 2001. Forty years and four surveys: how does our measuring measure up? Am. J. Prev. Med. 20(Suppl 4), 6–14 10.1016/S0749-3797(01)00286-0 (doi:10.1016/S0749-3797(01)00286-0) [DOI] [PubMed] [Google Scholar]
10.Cherry J. D. 2003. The science and fiction of the ‘resurgence’ of pertussis. Pediatrics 112, 405–406 10.1542/peds.112.2.405 (doi:10.1542/peds.112.2.405) [DOI] [PubMed] [Google Scholar]
11.Halperin S. A. 2007. The control of pertussis: 2007 and beyond. N. Engl. J. Med. 356, 110–113 10.1056/NEJMp068288 (doi:10.1056/NEJMp068288) [DOI] [PubMed] [Google Scholar]
12.Rohani P., Drake J. M. 2011. The decline and resurgence of pertussis in the US. Epidemics 3, 183–188 10.1016/j.epidem.2011.10.001 (doi:10.1016/j.epidem.2011.10.001) [DOI] [PubMed] [Google Scholar]
13.Bass J. W., Stephenson S. R. 1987. The return of pertussis. Pediatr. Infect. Dis. J. 6, 141–144 10.1097/00006454-198702000-00001 (doi:10.1097/00006454-198702000-00001) [DOI] [PubMed] [Google Scholar]
14.Rohani P., Earn D. J. D., Grenfell B. T. 2000. Impact of immunisation on pertussis transmission in England and Wales. Lancet 355, 285–286 10.1016/S0140-6736(99)04482-7 (doi:10.1016/S0140-6736(99)04482-7) [DOI] [PubMed] [Google Scholar]
15.Winter K., Harriman K., Zipprich J., Schechter R., Talarico J., Watt J., Chavez G. 2012. California pertussis epidemic, 2010. J. Pediatr. [DOI] [PubMed] [Google Scholar]
16.Crowcroft N. S., Stein C., Duclos P., Birmingham M. 2003. How best to estimate the global burden of pertussis? Lancet Infect. Dis. 3, 413–418 10.1016/S1473-3099(03)00669-8 (doi:10.1016/S1473-3099(03)00669-8) [DOI] [PubMed] [Google Scholar]
17.Crowcroft N. S., Pebody R. G. 2006. Recent developments in pertussis. Lancet 367, 1926–1936 10.1016/S0140-6736(06)68848-X (doi:10.1016/S0140-6736(06)68848-X) [DOI] [PubMed] [Google Scholar]
18.Wearing H., Rohani P. 2009. Estimating the duration of pertussis immunity using epidemiological signatures. PLoS Pathog. 5, e1000647. 10.1371/journal.ppat.1000647 (doi:10.1371/journal.ppat.1000647) [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Broutin H., Viboud C., Grenfell B. T., Miller M. A., Rohani P. 2010. Impact of vaccination and birth rate on the epidemiology of pertussis: a comparative study in 64 countries. Proc. R. Soc. B 277, 3239–3245 10.1098/rspb.2010.0994 (doi:10.1098/rspb.2010.0994) [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Torrence C., Compo G. P. 1998. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78 [Google Scholar]
21.Cazelles B., Chavez M., Berteaux D., Mnard F., Vik J., Jenouvrier S., Stenseth N. 2008. Wavelet analysis of ecological time series. Oecologia 156, 287–304 10.1007/s00442-008-0993-2 (doi:10.1007/s00442-008-0993-2) [DOI] [PubMed] [Google Scholar]
22.Sutter R. W., Cochi S. L. 1992. Pertussis hospitalizations and mortality in the United States, 1985–1988 evaluation of the completeness of national reporting. JAMA 267, 386–391 10.1001/jama.1992.03480030064038 (doi:10.1001/jama.1992.03480030064038) [DOI] [PubMed] [Google Scholar]
23.Bjørnstad O. N., Falck W. 2001. Nonparametric spatial covariance functions: estimation and testing. Environ. Ecol. Stat. 8, 53–70 [Google Scholar]
24.Bartlett M. S. 1957. Measles periodicity and community size. J. R. Stat. Soc. A 120, 48–70 10.2307/2342553 (doi:10.2307/2342553) [DOI] [Google Scholar]
25.Rohani P., Earn D. J., Grenfell B. T. 1999. Opposite patterns of synchrony in sympatric disease metapopulations. Science 286, 968–971 10.1126/science.286.5441.968 (doi:10.1126/science.286.5441.968) [DOI] [PubMed] [Google Scholar]
26.Bjørnstad O. N., Bolker B. M. 2000. Canonical functions for dispersal-induced synchrony. Proc. R. Soc. B 267, 1787–1794 10.1098/rspb.2000.1211 (doi:10.1098/rspb.2000.1211) [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Smith D. L., Lucey B., Waller L. A., Childs J. E., Real L. A. 2002. Predicting the spatial dynamics of rabies epidemics on heterogeneous landscapes. Proc. Natl Acad. Sci. USA 99, 3668–3672 10.1073/pnas.042400799 (doi:10.1073/pnas.042400799) [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Mundt C. C., Sackett K. E., Wallace L. D., Cowger C., Dudley J. P. 2009. Long-distance dispersal and accelerating waves of disease: empirical relationships. Am. Nat. 173, 456–466 10.1086/597220 (doi:10.1086/597220) [DOI] [PubMed] [Google Scholar]
29.Walsh P. D., Biek R., Real L. A. 2005. Wave-like spread of Ebola Zaire. PLoS Biol. 3, e371. 10.1371/journal.pbio.0030371 (doi:10.1371/journal.pbio.0030371) [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Xia Y., Bjørnstad O. N., Grenfell B. T. 2004. Measles metapopulation dynamics: a gravity model for epidemiological coupling and dynamics. Am. Nat. 164, 267–281 10.1086/422341 (doi:10.1086/422341) [DOI] [PubMed] [Google Scholar]
31.Alonso W. J., Viboud C., Simonsen L., Hirano E. W., Daufenbach L. Z., Miller M. A. 2007. Seasonality of influenza in Brazil: a traveling wave from the amazon to the subtropics. Am. J. Epidemiol. 165, 1434–1442 10.1093/aje/kwm012 (doi:10.1093/aje/kwm012) [DOI] [PubMed] [Google Scholar]
32.Shaman J., Pitzer V. E., Viboud C., Grenfell B. T., Lipsitch M. 2010. Absolute humidity and the seasonal onset of influenza in the continental United States. PLoS Biol. 8, e1000316. 10.1371/journal.pbio.1000316 (doi:10.1371/journal.pbio.1000316) [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Finkelman B. S., Viboud C., Koelle K., Ferrari M. J., Bharti N., Grenfell B. T. 2007. Global patterns in seasonal activity of influenza A/H₃N₂, A/H₁N₁, and B from 1997 to 2005: viral coexistence and latitudinal gradients. PLoS ONE 2, e1296. 10.1371/journal.pone.0001296 (doi:10.1371/journal.pone.0001296) [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Sasaki A., Hamilton W. D., Ubeda F. 2002. Clone mixtures and a pacemaker: new facets of red-queen theory and ecology. Proc. R. Soc. Lond. B 269, 761–772 10.1098/rspb.2001.1837 (doi:10.1098/rspb.2001.1837) [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Litvak-Hinenzon A., Stone L. 2009. Spatio-temporal waves and targeted vaccination in recurrent epidemic network models. J. R. Soc. Interface 6, 749–760 10.1098/rsif.2008.0343 (doi:10.1098/rsif.2008.0343) [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Rohani P., Lewis T. J., Grünbaum D., Ruxton G. D. 1997. Spatial self-organisation in ecology: pretty patterns or robust reality? Trends Ecol. Evol. 12, 70–74 10.1016/S0169-5347(96)20103-X (doi:10.1016/S0169-5347(96)20103-X) [DOI] [PubMed] [Google Scholar]
37.Campbell H., Amirthalingam G., Andrews N., Fry N. K., George R. C., Harrison T. G., Miller E. 2012. Accelerating control of pertussis in England and Wales. Emerg. Infect. Dis. 18, 38–47 10.3201/eid1801.110784 (doi:10.3201/eid1801.110784) [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Goetz A. R. 1992. Air passenger transportation and growth in the US urban system, 1950–1987. Growth Change 23, 217–238 10.1111/j.1468-2257.1992.tb00580.x (doi:10.1111/j.1468-2257.1992.tb00580.x) [DOI] [Google Scholar]
39.Güriş D., Strebel P. M., Bardenheier B., Brennan M., Tachdjian R., Finch E., Wharton M., Livengood J. R. 1999. Changing epidemiology of pertussis in the United States: increasing reported incidence among adolescents and adults, 1990–1996 Clin. Infect. Dis. 28, 1230–1237 [DOI] [PubMed] [Google Scholar]
40.Lavine J. S., King A. A., Bjørnstad O. N. 2011. Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure. Proc. Natl Acad. Sci. USA 108, 7259–7264 10.1073/pnas.1014394108 (doi:10.1073/pnas.1014394108) [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Skowronski D. M., De Serres G., MacDonald D., Wu W., Shaw C., Macnabb J., Champagne S., Patrick D. M., Halperin S. A. 2002. The changing age and seasonal profile of pertussis in Canada. J. Infect. Dis. 185, 1448–1453 10.1086/340280 (doi:10.1086/340280) [DOI] [PubMed] [Google Scholar]
42.Rohani P., Zhong X., King A. A. 2010. Contact network structure explains the changing epidemiology of pertussis. Science 330, 982–985 10.1126/science.1194134 (doi:10.1126/science.1194134) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C1] 1.McLean A. R., May R. M., Pattison J., Weiss R. A. 2005. SARS: a case study in emerging infections. Oxford, UK: Oxford University Press [Google Scholar]

[RSPB20121761C2] 2.Keeling M. J., et al. 2001. Dynamics of the 2001 UK foot and mouth epidemic: stochastic dispersal in a heterogeneous landscape. Science 294, 813–817 10.1126/science.1065973 (doi:10.1126/science.1065973) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C3] 3.Webby R. J., Webster R. G. 2003. Are we ready for pandemic influenza? Science 302, 1519–1522 10.1126/science.1090350 (doi:10.1126/science.1090350) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C4] 4.Riley S. 2007. Large-scale spatial-transmission models of infectious disease. Science 316, 1298–1301 10.1126/science.1134695 (doi:10.1126/science.1134695) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C5] 5.Keeling M. J., Rohani P. 2008. Modelling infectious diseases. Princeton, NJ: Princeton University Press [Google Scholar]

[RSPB20121761C6] 6.Grenfell B. T., Bjørnstad O. N., Kappey J. 2001. Travelling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 10.1038/414716a (doi:10.1038/414716a) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C7] 7.Viboud C., Björnstad O. N., Smith D. L., Simonsen L., Miller M. A., Grenfell B. T. 2006. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312, 447–451 10.1126/science.1125237 (doi:10.1126/science.1125237) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C8] 8.Cummings D. A. T., Irizarry R. A., Huang N. E., Endy T. P., Nisalak A., Ungchusak K., Burke D. S. 2004. Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature 427, 344–347 10.1038/nature02225 (doi:10.1038/nature02225) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C9] 9.Simpson D. M., Ezzati-Rice T. M., Zell E. R. 2001. Forty years and four surveys: how does our measuring measure up? Am. J. Prev. Med. 20(Suppl 4), 6–14 10.1016/S0749-3797(01)00286-0 (doi:10.1016/S0749-3797(01)00286-0) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C10] 10.Cherry J. D. 2003. The science and fiction of the ‘resurgence’ of pertussis. Pediatrics 112, 405–406 10.1542/peds.112.2.405 (doi:10.1542/peds.112.2.405) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C11] 11.Halperin S. A. 2007. The control of pertussis: 2007 and beyond. N. Engl. J. Med. 356, 110–113 10.1056/NEJMp068288 (doi:10.1056/NEJMp068288) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C12] 12.Rohani P., Drake J. M. 2011. The decline and resurgence of pertussis in the US. Epidemics 3, 183–188 10.1016/j.epidem.2011.10.001 (doi:10.1016/j.epidem.2011.10.001) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C13] 13.Bass J. W., Stephenson S. R. 1987. The return of pertussis. Pediatr. Infect. Dis. J. 6, 141–144 10.1097/00006454-198702000-00001 (doi:10.1097/00006454-198702000-00001) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C14] 14.Rohani P., Earn D. J. D., Grenfell B. T. 2000. Impact of immunisation on pertussis transmission in England and Wales. Lancet 355, 285–286 10.1016/S0140-6736(99)04482-7 (doi:10.1016/S0140-6736(99)04482-7) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C15] 15.Winter K., Harriman K., Zipprich J., Schechter R., Talarico J., Watt J., Chavez G. 2012. California pertussis epidemic, 2010. J. Pediatr. [DOI] [PubMed] [Google Scholar]

[RSPB20121761C16] 16.Crowcroft N. S., Stein C., Duclos P., Birmingham M. 2003. How best to estimate the global burden of pertussis? Lancet Infect. Dis. 3, 413–418 10.1016/S1473-3099(03)00669-8 (doi:10.1016/S1473-3099(03)00669-8) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C17] 17.Crowcroft N. S., Pebody R. G. 2006. Recent developments in pertussis. Lancet 367, 1926–1936 10.1016/S0140-6736(06)68848-X (doi:10.1016/S0140-6736(06)68848-X) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C18] 18.Wearing H., Rohani P. 2009. Estimating the duration of pertussis immunity using epidemiological signatures. PLoS Pathog. 5, e1000647. 10.1371/journal.ppat.1000647 (doi:10.1371/journal.ppat.1000647) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C19] 19.Broutin H., Viboud C., Grenfell B. T., Miller M. A., Rohani P. 2010. Impact of vaccination and birth rate on the epidemiology of pertussis: a comparative study in 64 countries. Proc. R. Soc. B 277, 3239–3245 10.1098/rspb.2010.0994 (doi:10.1098/rspb.2010.0994) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C20] 20.Torrence C., Compo G. P. 1998. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78 [Google Scholar]

[RSPB20121761C21] 21.Cazelles B., Chavez M., Berteaux D., Mnard F., Vik J., Jenouvrier S., Stenseth N. 2008. Wavelet analysis of ecological time series. Oecologia 156, 287–304 10.1007/s00442-008-0993-2 (doi:10.1007/s00442-008-0993-2) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C22] 22.Sutter R. W., Cochi S. L. 1992. Pertussis hospitalizations and mortality in the United States, 1985–1988 evaluation of the completeness of national reporting. JAMA 267, 386–391 10.1001/jama.1992.03480030064038 (doi:10.1001/jama.1992.03480030064038) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C23] 23.Bjørnstad O. N., Falck W. 2001. Nonparametric spatial covariance functions: estimation and testing. Environ. Ecol. Stat. 8, 53–70 [Google Scholar]

[RSPB20121761C24] 24.Bartlett M. S. 1957. Measles periodicity and community size. J. R. Stat. Soc. A 120, 48–70 10.2307/2342553 (doi:10.2307/2342553) [DOI] [Google Scholar]

[RSPB20121761C25] 25.Rohani P., Earn D. J., Grenfell B. T. 1999. Opposite patterns of synchrony in sympatric disease metapopulations. Science 286, 968–971 10.1126/science.286.5441.968 (doi:10.1126/science.286.5441.968) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C26] 26.Bjørnstad O. N., Bolker B. M. 2000. Canonical functions for dispersal-induced synchrony. Proc. R. Soc. B 267, 1787–1794 10.1098/rspb.2000.1211 (doi:10.1098/rspb.2000.1211) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C27] 27.Smith D. L., Lucey B., Waller L. A., Childs J. E., Real L. A. 2002. Predicting the spatial dynamics of rabies epidemics on heterogeneous landscapes. Proc. Natl Acad. Sci. USA 99, 3668–3672 10.1073/pnas.042400799 (doi:10.1073/pnas.042400799) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C28] 28.Mundt C. C., Sackett K. E., Wallace L. D., Cowger C., Dudley J. P. 2009. Long-distance dispersal and accelerating waves of disease: empirical relationships. Am. Nat. 173, 456–466 10.1086/597220 (doi:10.1086/597220) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C29] 29.Walsh P. D., Biek R., Real L. A. 2005. Wave-like spread of Ebola Zaire. PLoS Biol. 3, e371. 10.1371/journal.pbio.0030371 (doi:10.1371/journal.pbio.0030371) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C30] 30.Xia Y., Bjørnstad O. N., Grenfell B. T. 2004. Measles metapopulation dynamics: a gravity model for epidemiological coupling and dynamics. Am. Nat. 164, 267–281 10.1086/422341 (doi:10.1086/422341) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C31] 31.Alonso W. J., Viboud C., Simonsen L., Hirano E. W., Daufenbach L. Z., Miller M. A. 2007. Seasonality of influenza in Brazil: a traveling wave from the amazon to the subtropics. Am. J. Epidemiol. 165, 1434–1442 10.1093/aje/kwm012 (doi:10.1093/aje/kwm012) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C32] 32.Shaman J., Pitzer V. E., Viboud C., Grenfell B. T., Lipsitch M. 2010. Absolute humidity and the seasonal onset of influenza in the continental United States. PLoS Biol. 8, e1000316. 10.1371/journal.pbio.1000316 (doi:10.1371/journal.pbio.1000316) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C33] 33.Finkelman B. S., Viboud C., Koelle K., Ferrari M. J., Bharti N., Grenfell B. T. 2007. Global patterns in seasonal activity of influenza A/H₃N₂, A/H₁N₁, and B from 1997 to 2005: viral coexistence and latitudinal gradients. PLoS ONE 2, e1296. 10.1371/journal.pone.0001296 (doi:10.1371/journal.pone.0001296) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C34] 34.Sasaki A., Hamilton W. D., Ubeda F. 2002. Clone mixtures and a pacemaker: new facets of red-queen theory and ecology. Proc. R. Soc. Lond. B 269, 761–772 10.1098/rspb.2001.1837 (doi:10.1098/rspb.2001.1837) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C35] 35.Litvak-Hinenzon A., Stone L. 2009. Spatio-temporal waves and targeted vaccination in recurrent epidemic network models. J. R. Soc. Interface 6, 749–760 10.1098/rsif.2008.0343 (doi:10.1098/rsif.2008.0343) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C36] 36.Rohani P., Lewis T. J., Grünbaum D., Ruxton G. D. 1997. Spatial self-organisation in ecology: pretty patterns or robust reality? Trends Ecol. Evol. 12, 70–74 10.1016/S0169-5347(96)20103-X (doi:10.1016/S0169-5347(96)20103-X) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C37] 37.Campbell H., Amirthalingam G., Andrews N., Fry N. K., George R. C., Harrison T. G., Miller E. 2012. Accelerating control of pertussis in England and Wales. Emerg. Infect. Dis. 18, 38–47 10.3201/eid1801.110784 (doi:10.3201/eid1801.110784) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C38] 38.Goetz A. R. 1992. Air passenger transportation and growth in the US urban system, 1950–1987. Growth Change 23, 217–238 10.1111/j.1468-2257.1992.tb00580.x (doi:10.1111/j.1468-2257.1992.tb00580.x) [DOI] [Google Scholar]

[RSPB20121761C39] 39.Güriş D., Strebel P. M., Bardenheier B., Brennan M., Tachdjian R., Finch E., Wharton M., Livengood J. R. 1999. Changing epidemiology of pertussis in the United States: increasing reported incidence among adolescents and adults, 1990–1996 Clin. Infect. Dis. 28, 1230–1237 [DOI] [PubMed] [Google Scholar]

[RSPB20121761C40] 40.Lavine J. S., King A. A., Bjørnstad O. N. 2011. Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure. Proc. Natl Acad. Sci. USA 108, 7259–7264 10.1073/pnas.1014394108 (doi:10.1073/pnas.1014394108) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20121761C41] 41.Skowronski D. M., De Serres G., MacDonald D., Wu W., Shaw C., Macnabb J., Champagne S., Patrick D. M., Halperin S. A. 2002. The changing age and seasonal profile of pertussis in Canada. J. Infect. Dis. 185, 1448–1453 10.1086/340280 (doi:10.1086/340280) [DOI] [PubMed] [Google Scholar]

[RSPB20121761C42] 42.Rohani P., Zhong X., King A. A. 2010. Contact network structure explains the changing epidemiology of pertussis. Science 330, 982–985 10.1126/science.1194134 (doi:10.1126/science.1194134) [DOI] [PubMed] [Google Scholar]

PERMALINK

Changing spatial epidemiology of pertussis in continental USA

Marc Choisy

Pejman Rohani

Abstract

1. Introduction