A test of maternal human chorionic gonadotropin during pregnancy as an adaptive filter of human gestations

Abstract

The risk of abnormalities and morbidity among live births increases with advanced maternal age. Explanations for this elevated morbidity invoke several maternal mechanisms. The relaxed filter stringency (RFS) hypothesis asserts that mothers, nearing the end of their reproductive lifespan, reduce the stringency of a screen of offspring quality in utero based on life-history traits of parity and interbirth interval (IBI). A separate line of research implicates human chorionic gonadotropin (hCG) during pregnancy as a signal of offspring quality. We test the RFS hypothesis directly by examining whether the difference in gestational hCG across consecutive live births varies positively with the mother's number of previous live births but inversely with her most recent IBI. We applied multivariable regression methods to a unique dataset of gestational hCG for over 500 000 live births from 2002 to 2007. The difference in gestational hCG across mothers' consecutive live births varies positively with both mothers' parity and IBI. These associations remain similar among older mothers (35+ years). Findings support the RFS hypothesis for the parity expectation but not for the IBI expectation. Further evidence for the RFS hypothesis among contemporary human gestations would have to invoke screening mechanisms other than hCG.

1. Introduction

Pregnancy serves as an important period for selection in that an estimated 30–70% of human conceptions do not survive to birth [1]. Population-based research also finds substantial losses in later trimesters, in that 20 per cent of intended pregnancies that progress to the second trimester end in spontaneous abortion [2]. Scholars argue that the production of more conceptuses than those carried to term may serve an adaptive function in that natural selection may have conserved mechanisms by which mothers screen for offspring quality [3]. Such mechanisms may trigger the spontaneous loss of chromosomally abnormal, malformed or other gestations that, if born, exhibit a low likelihood of surviving to reproductive age. According to theory, the ability to identify and terminate these gestations would allow the mother to invest her limited resources in either existing children or reproduction of offspring with a higher probability of yielding grandchildren [4].

The presumed existence of a maternal screen implies that the foetus somehow signals its hardiness to the mother over the course of gestation, and that the mother carries to term only those gestations whose signal exceeds a certain criterion. Research of the candidate signals implicates gestational human chorionic gonadotropin (hCG) in maternal serum as one component of the screen [5–8]. As early as the second week after fertilization, hCG promotes maintenance of the corpus luteum and stimulates progesterone secretion from the placenta; both processes prevent miscarriage [9]. Low levels of hCG, moreover, predict spontaneous abortion [6,7,10,11], and clinical administration of hCG has been attempted to reduce the risk of spontaneous abortion [12]. Evolutionary biologists propose that hCG signals offspring quality, although with some error [9]. Forbes [4], for example, contends that the maternal screen may act conservatively by terminating not only ‘defective’ but also a fraction of normal gestations that fall below a critical threshold of hCG.

A related literature finds that the incidence of chromosomally abnormal live births and adverse perinatal outcomes increases with advancing maternal age [13–18]. One explanation for this observation invokes the relaxed filtered stringency (RFS) hypothesis [4,19,20]. RFS asserts that mothers, faced with the end stage of their reproductive lifespan, may relax the screen against gestations that, if born, exhibit a low likelihood of surviving to reproductive age. According to RFS, adaptive relaxation of the screen serves as a fitness-maximizing strategy in that the gravid female, nearing reproductive senescence and faced with the prospect of yielding either sub-optimal offspring or no additional offspring, would prefer the former. RFS does not preclude other, non-adaptive explanations for the positive association between maternal age and the incidence of chromosomally abnormal births (e.g. increased error rates during meiosis with increasing age) [21,22].

Neuhauser & Krackow [20] build on RFS and hypothesize that the incidence of ‘low fitness’ live births should vary according to characteristics of the mother's reproductive history. The authors reason that, as mothers approach the end of their reproductive lifespan, they autonomically adapt the screen according to parity and interbirth interval (IBI). The authors assume that the expected value of fitness is greater than zero for a gestation that falls below the maternal criterion for spontaneous abortion, owing to the potential of the screening mechanism acting conservatively (i.e. eliminating some normal gestations). In this circumstance, the mother would stand to improve reproductive success by relaxing the screen only if she had relatively fewer previous live births in which to invest. Moreover, they argue that the production of new offspring necessarily detracts from investment in other children, and that competition for maternal resources varies inversely with birth spacing between siblings. Closely spaced births reportedly lead to increased strain of scarce maternal resources and predispose children to an increased risk of malnutrition and morbidity [23,24]. Given the higher maternal fitness costs of shorter (relative to longer) IBIs, the authors hypothesize that the stringency of the maternal screen would rise as the IBI narrows. A recent archival analysis supports the hypothesized associations between maternal reproductive history and the incidence of chromosomally abnormal (i.e. ‘low fitness’) births [20].

Although the literature offers tentative support for RFS, we know of no research that tests the biochemical mechanisms through which the adaptive maternal screen may operate. The RFS hypothesis, however, offers testable predictions of how a biomarker for the maternal screen would vary according to maternal reproductive history (see figure 1, modified from Forbes [4]). Population-based prenatal screening programmes may provide an opportunity to test potential biomarkers of the maternal screen. These programmes measure endocrine markers thought to predict foetal health (i.e. fitness), including hCG. Evidence for hCG as a screening mechanism includes its predictive value for spontaneous abortion.

Figure 1.

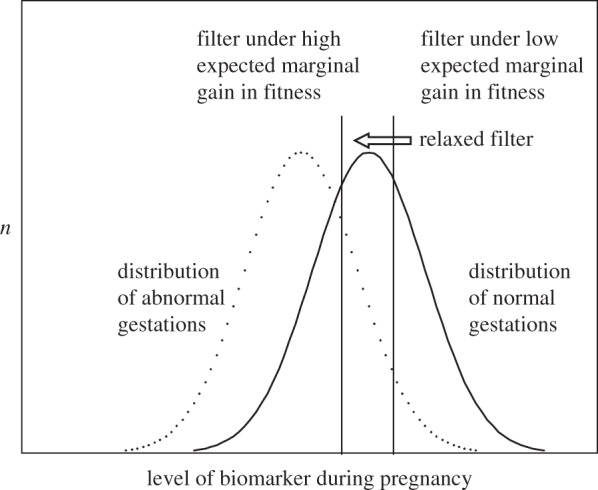
Schematic of the relaxed filter for spontaneous abortion. Right vertical line indicates a biomarker threshold by which a gravid mother screens for gestation quality. Only gestations to the right of the threshold survive to term. A ‘low expected marginal gain in fitness’ condition could include a birth to a mother of high parity. According to relaxed filter stringency, this threshold may relax, or ‘left-shift’, to the left vertical line if the expected marginal gain for carrying the gestation to term is relatively high (e.g. mother has no previous children). This relaxed filter condition would result in a relatively lower mean level of the biomarker among live births but a higher incidence of abnormal gestations carried to term. Adapted from Forbes [4].

If low levels of maternal serum hCG predict spontaneous abortion, and if RFS holds that the criterion for spontaneous abortion varies by parity and IBI, then the hCG of gestations that survive to birth should also vary according to parity and IBI. We examine this hypothesis directly by using maternal serum hCG measurements, assayed in the 14th through to the 21st week of gestation, for over 500 000 infants born in California from 2002 through to 2007.

We test two propositions. First, hCG (as measured during gestation) among subsequent live births will vary positively with the mother's number of previous live births. Second, hCG among subsequent live births will vary inversely with the mother's most recent IBI. Our dataset permits control for innate biological characteristics of the mother, as well as the independent influence of other factors (e.g. infant sex, maternal age) on hCG, by comparing consecutive births to the same mother over time. Evidence in support of these associations would implicate hCG as a component of the maternal screen of foetal fitness and provide empirical evidence of a biological mechanism for RFS.

2. Methods

(a). Data and availability

We acquired maternal serum hCG values from California's genetic disease screening programme (GDSP). By law, GDSP offers testing for the risk of chromosomal abnormalities to all women in prenatal care by the 140th day of gestation. This testing includes assessment of maternal hCG as well as other serum biomarkers. Approximately two-thirds of gravid women in California undergo testing with this service. GDSP contracts with regional laboratories to analyse the serum biomarkers for gravid women who decide to participate. The laboratories use a uniform assay protocol that includes an automated analytical system [25,26].

Researchers with GDSP have linked maternal hCG scores from the prenatal screening programme to live births in California occurring from January 2002 to December 2007. The California Department of Public Health birth registry contains all live births occurring in or to residents of California. The probabilistic linkage of the hCG scores to the birth file matches combinations of mother's/father's/child's names (first two letters, NYSIIS phonetic codes, and whole names), street address, phone numbers, residential ZIP code, mother's birth date (year only and whole dates), estimated date and date of birth. Approximately 92 per cent of prenatal screening records matched to a subsequent birth record.

These data include personal health identifying information that, by California and Federal Law, cannot be made ‘open access’ to the public. However, all data are publicly available in that GDSP provides the data to researchers after an application process, consistent with rules and regulations set forth by the State of California's Committee for the Protection of Human Subjects. These rules protect the rights of the human subjects under study (for data enquiries, please contact the California Department of Public Health or the corresponding author).

(b). Variables

The prenatal screening programme assays maternal serum hCG (measured in international units per litre) in the 14th through to the 21st week of gestation. Consistent with conventions in the prenatal diagnosis field, GDSP converted the raw hCG score into an adjusted ‘multiple-of-the-median’ (MoM) score [27]. The MoM hCG score standardizes all values to a median hCG value and statistically adjusts for other factors known to predict hCG. The adjustment variables included the following: gestational age (in days) at test as measured by ultrasound or date of last menstrual period, maternal race/ethnicity, maternal weight during pregnancy, gestational diabetes and changes in hCG assay ‘kit’ over time. Obstetricians use this standardized MoM hCG value in conjunction with other markers to assess the probability of foetal chromosomal abnormalities.

The key independent variables, implied by the RFS hypothesis, that may covary with MoM hCG values include the number of previous live births and the most recent IBI. We acquired data on parity, defined as the number of previous live births reported by the mother, directly from the linked California birth file. Derivation of IBI required identifying birth records from mothers with hCG scores on more than one pregnancy that resulted in a live birth from 2002 to 2007.

(c). Analysis

An ideal study design to test hCG as a gauge of RFS would prospectively follow mothers over their entire reproductive lifespan and compare the hCG of all gestations. We know of no such dataset. The GSDP data, however, allow linkage of mothers' reproductive history and hCG scores for her live births from January 2002 to December 2007. Linkage of these pregnancies permits the analysis of hCG scores by parity and IBI within mother across her pregnancies.

Scholars argue that analyses of birth outcomes and child development by parity suffer from bias in that women who deliver, for instance, five children fundamentally differ from women who deliver two children [28–30]. Selection into higher parity may arise from a complex set of biological and behavioural characteristics that could covary with hCG and confound our tests [31]. To control for this bias, we compare hCG within mother but across sibling gestations from separate pregnancies. Using the mother's previous pregnancy hCG score as a baseline comparison confers the benefit of removing bias owing to characteristics—unique to that mother—that predict levels of hCG and/or fecundity.

The logic of our analytic strategy requires linkage of data across two consecutive live births for mothers with more than one birth event during the 72 months for which we had data. We, therefore, excluded mothers with only one pregnancy. We then retained only singleton gestations because of the lower hCG screening rate for multiple gestations. In addition, maternal serum screening of multiple gestations appears much less common than for singletons (53% compared with 65%). We excluded births with a missing hCG score or with a value outside the credible range, and restricted the analysis to births of parity less than seven (99.4% of singleton births).

We calculated the IBI as the difference (in months) between the second and first birth date for the mother's two consecutive live births in which she received a gestational hCG measure. We excluded three or more births to the same mother over the analysis period (i.e. each mother contributes no more than one IBI observation). In addition, we excluded mothers with implausible values for IBI (i.e. fewer than nine months or greater than the length of the surveillance period). This process left us with 286 809 mothers―each with two births over the test period (n = 573 618 births).

We included the control variables of infant sex and maternal age given their documented association with both the independent and dependent variables. As recommended in the statistical literature, we used a ‘difference score’ dependent variable that adjusts for the mother's hCG score at baseline [32,33]. We estimated the following ordinary-least-squares regression:

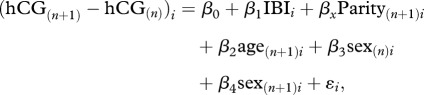where (hCG_(n+1) − hCG_n)_i is the difference, for mother i, between the MoM hCG score of the live birth to the (n + 1)th pregnancy and the live birth to the (n)th pregnancy from 2002 to 2007. This difference serves as our dependent variable.

β₀ is a constant.

IBI_i is the interbirth interval (in months) for mother i between birth (n) to the first pregnancy and birth (n + 1) to the second pregnancy over the test period.

β₁ is the coefficient for IBI.

Parity_i is a categorical variable for completed parity of mother i at her second linked pregnancy (n + 1) over the test period, with a range from two to six.

β_x is the coefficient for parity.

age_(n+1)i is a continuous variable for maternal age (in years) of mother i at delivery n + 1.

β₂ is the coefficient for the maternal age variable.

sex_(n)i is a binary variable for sex of infant born to mother i during the first pregnancy n over the test period, scored ‘1’ for male and ‘0’ for female.

β₃ is the coefficient for the sex of infant variable.

sex_(n+1)i is a binary variable for sex of infant born to mother i during the second pregnancy n + 1 over the test period, scored ‘1’ for male and ‘0’ for female.

β₄ is the coefficient for the sex of infant variable.

ɛ_i is the error term for mother i.

For the parity and IBI tests, we conducted additional analyses to assess the stability of results to alternative functional forms, specifications and assumptions.

3. Results

As described in §2, our analysis requires that a mother deliver at least two births over our test period (January 2002 to December 2007). The analytic sample, therefore, represents a subset of the two million births with hCG measures from the 14th to 21st week of gestation in California. The mean hCG of the mothers' subsequent live birth (mean = 1.11) is lower than that of the index birth (mean = 1.15), which indicates that hCG, on average, declines across consecutive pregnancies. The Pearson correlation coefficient of the mothers' hCG across the index and subsequent live birth is 0.37 (p < 0.001). The sex and racial/ethnic distribution of births for our analytic sample appears representative of all California births (table 1). The analytic dataset, however, includes a smaller proportion of mothers over 35 years of age. We attribute the difference in age distribution to the availability of amniocentesis and other diagnostic tests targeted to women 35 years or older.

Table 1.

Descriptive characteristics of the analytic sample and all live singleton births in California, 2002 to 2007. (Row totals may not sum to 100% owing to missing values, rounding and non-exhaustive categories.)

	analytic sample (n = 573 618)a	California births (n = 3 198 764)
mean hCG MoM (s.d.)	1.13 (0.60)	—
median hCG MoM	1.01	—
mean IBI in months (s.d.)	28.61 (11.88)	—
hCG difference (n + 1th pregnancy – nth pregnancy), mean MoM (s.d.)	−0.043 (0.67)	—
male sex (%)	51.2	51.2
race/ethnicityb
non-Hispanic white (%)	28.2	29.0
non-Hispanic black (%)	4.2	5.6
Asian (%)	12.2	7.3
Hispanic (%)	51.0	51.6
age (years)b
15–19 (%)	3.3	9.4
20–24 (%)	21.6	23.1
25–29 (%)	29.2	26.3
30–34 (%)	32.3	24.3
35–39 (%)	12.4	13.4
40–50 (%)	1.4	3.3
parity (total no. live births)b
1 (%)	—	39.5
2 (%)	64.1	31.5
3 (%)	23.0	17.2
4 (%)	9.2	7.2
5 (%)	2.8	2.7
6 (%)	0.9	1.9

^aIncludes 286 809 mothers, each with two births from 2002 to 2007.

^bFor mothers at the n + 1th pregnancy (for analytic sample) and at previous live births + 1 (for California births).

Table 2 (model 1: full sample) displays results of the test of parity, IBI and hCG difference score, controlling for maternal age and infant sex. The negative intercept coefficient indicates that, on average, hCG declines across consecutive live births. Consistent with previous reports, maternal age varies positively, whereas male sex varies inversely, with hCG.

Table 2.

Regression results predicting difference in serum human chorionic gonadotropin (hCG; in multiples of the median) across consecutive pregnancies for live births to mothers with at least two live births in California from 2002 to 2007. (*p < 0.05; ***p < 0.0001.)

	model 1: full sample (n = 286 809)	model 2: mothers ≥35 years (n = 38 544)
	coefficient (s.e.)	coefficient (s.e.)
intercept	−0.16*** (0.0077)	−0.25*** (0.068)
parity	0.024*** (0.0015)	0.020*** (0.0034)
IBI (in months)	0.0012*** (0.0001)	0.0016*** (0.0003)
maternal age (at birth n + 1)	0.0018*** (0.0002)	0.0045* (0.0018)
male infant (referent : female)
first birth	0.055*** (0.0025)	0.047*** (0.007)
second birth	−0.073*** (0.0025)	−0.079*** (0.007)

^ahCG score adjusted for gestational age (in weeks) at test, maternal race/ethnicity, weight gain during pregnancy, maternal smoking, gestational diabetes and changes in hCG assay kit over time.

Regarding the RFS hypothesis, the difference in hCG score between mothers' (n + 1)th and nth live birth varies positively with parity (coeff.: 0.024; s.e. = 0.0015, p < 0.0001). This positive relationship supports the RFS hypothesis in that the coefficient implies a relatively smaller (i.e. less stringent) hCG change with lower parity. To help the reader gauge the magnitude of the findings, the expected difference in hCG score of completed parity at four relative to parity at two is about 75 per cent of the size of the well-documented hCG deficit of male relative to female live births.

We detect a positive relation between IBI and the difference in hCG score between mothers' (n + 1)th and nth live birth (coeff.: 0.0012; s.e. = 0.0001, p < 0.0001). This result does not support the RFS hypothesis in that a longer IBI moves with a relatively higher hCG score among the (n + 1)th birth. The coefficient implies that an interval of an additional 12 months between live births (e.g. 36 months instead of 24 months) corresponds with a relative increase of 0.013 in hCG for the last live birth.

(a). Sensitivity tests

We conducted additional analyses to test whether discovered findings appear sensitive to the choice of maternal age range. Predictions arising from the RFS hypothesis pertain primarily to women at or near the end of their reproductive lifespan. We, therefore, repeated our regression analyses but included births only to mothers at or older than 35 years (an age range consistent with previous literature on RFS) [20]. Results (see model 2: mothers in table 2; n = 38 544 mothers) remain similar to those of the original test, as the hCG difference between the mothers' (n + 1)th and nth live birth varies positively with parity and IBI.

A key purpose of the GDSP prenatal screening involves the detection of gestations with chromosomal abnormalities (e.g. Down syndrome) with hCG levels outside the normal range. Because our dataset includes only live births, therapeutic or spontaneous abortion of foetuses with unusually high or low hCG scores may bias our results [34,35]. To test this possibility, we re-analysed the data but included only live births with an hCG score within the normal range (i.e. 0.5–2.0 MoM) that would yield a low probability of a chromosomal abnormality and/or spontaneous or therapeutic abortion. Inference for the coefficients in the multivariate regression did not change in that parity and IBI vary positively with hCG change score. We then re-analysed births to mothers both 35 years and above and with an hCG score in the normal range (n = 26 937 mothers). Results remain substantively similar to those reported in the initial test, although the coefficients for both parity and IBI are attenuated by about 50 per cent (coeff. for parity: 0.010, s.e. = 0.0027, p < 0.001; coeff. for IBI: 0.0005; s.e. = 0.0002, p < 0.05).

We then converted hCG to its logarithm (base 10) value (given the negatively skewed distribution of hCG scores) and repeated all analyses to assess whether findings could arise from misspecification of the model's functional form [27,36–38]. For all tests, statistical inference for the parity and IBI coefficients did not change (results available upon request).

Figures 2 and 3 display parity and IBI coefficients from a multivariate regression analysis identical to that shown in table 2 (model 1: full sample) except that we now classify these variables as categorical values. Figure 2 indicates a large within-mother difference in hCG across subjects of completed parity at three (referent category, coefficient fixed at 0) relative to those of completed parity at two. By contrast, the positive relation of IBI and hCG change appears relatively monotonic across the range of IBIs (save for months 60 through to 71).

Figure 2.

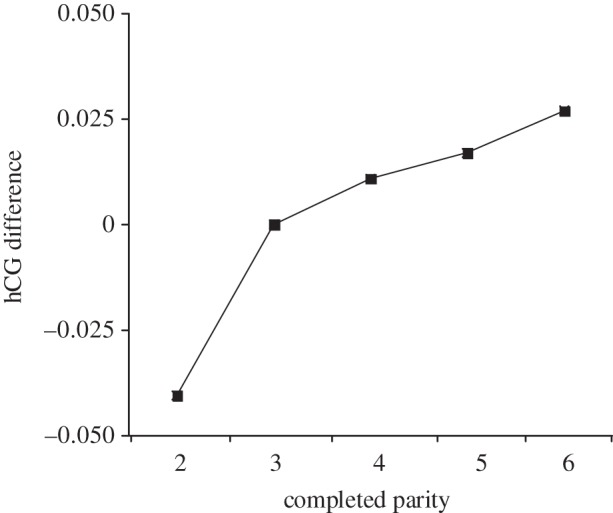
Parity coefficients predicting the difference between hCG of the mothers' (n + 1)th and nth live birth, with completed parity = 3 as the referent group (coefficient fixed at 0).

Figure 3.

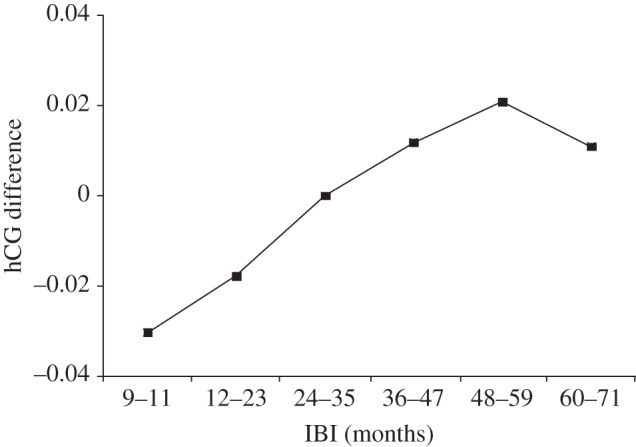
Interbirth interval (IBI) coefficients predicting the difference between human chorionic gonadotropin of the mothers' (n + 1)th and nth live birth, with IBI from 24 to 35 months as the referent group (coefficient fixed at 0).

4. Discussion

We tested the adaptive RFS hypothesis that gravid mothers autonomically shift the selectivity of their screen of gestations based on the expected incremental fitness gained by carrying a gestation to term. We specified maternal serum hCG, measured in the early second trimester, as a candidate biomarker for this screen. According to RFS, lower parity and a relatively long IBI (holding maternal age constant) represent two circumstances in which the mother who approaches reproductive senescence may relax the screen for a viable gestation. Results for over 500 000 births in California support RFS for the parity expectation but not for the IBI expectation. We observe greater hCG change among live births with greater parity and longer IBI. Findings offer partial support for the role of second trimester maternal hCG as an adaptive screening mechanism of RFS.

The relatively large hCG difference across completed parities two and three (figure 2) supports RFS in that the hCG change score falls to its lowest point at the lowest parity we examined. We view the relaxed maternal filter at low (relative to high) parities as consistent with RFS. IBI results, however, diverge from RFS predictions. According to theory, a shorter (relative to longer) IBI implies a more intense sibling conflict for maternal resources and a higher maternal reproductive fitness cost. For this reason, the stringency of a maternal screen in utero should increase as the IBI narrows [20,39]. We observe no such relationship. Rather, hCG varies positively with length of IBI. We know of no evolutionary explanation for this finding. We, however, offer two post hoc explanations. First, in developed countries such as the United States with near replacement fertility rates, parity more than birth spacing may serve as the relevant ‘decision rule’ for autonomic parental investment decisions [31]. Any biomarker that gauges adaptive filters during gestation, therefore, may be detectable more clearly across parity. Second, if RFS holds among contemporary human gestations, the theory would have to invoke screening mechanisms other than second trimester maternal hCG.

A key strength of our study includes population-based biomarker data on a large cohort of gravid women. In addition, our analytic strategy compares hCG scores within mother but across pregnancies, which adheres to the logic of RFS in that the hypothesis implies adaptive trade-offs in reproduction relative to each mother's own fertility history. This approach differs from previous work on RFS that compares ‘low fitness’ births by parity across mothers and assumes a physiological similarity across different mothers with high and low parity [20]. Findings, moreover, remain robust to several alternative specifications in which we analysed only mothers 35 years and older.

The literature reports that 20 per cent of intended pregnancies spontaneously end in the second and third trimester, which implies important selection after mothers take the California-sponsored hCG test [2]. A key limitation of our dataset, however, involves the absence of hCG information on embryos not carried to the 14th week of gestation and foetuses lost after the second trimester hCG measurement. Serum hCG plays a critical role in maintaining the corpus luteum and the endometrial lining as early as 9 days after fertilization. Its potential role as a maternal screen of embryo quality may diminish after the first trimester [9]. An ideal dataset would allow longitudinal measurement of hCG and other biomarkers of pregnancy as soon as fertilization becomes clinically detectable. Such information would permit tests of hCG as a mechanism of RFS among the large fraction of conceptuses that do not survive to birth, as well as a careful examination of the inter-relation among spontaneous foetal loss, IBI and parity progression. We know of no such dataset but anticipate that increased clinical attention devoted to early pregnancy may yield such information in the future.

Our analytic sample does not include mothers who sought prenatal testing using other diagnostic methods. Women aged 35 years or older may directly seek amniocentesis and other diagnostic tests that provide greater sensitivity and specificity than does the triple marker screening to detect chromosomal abnormalities. We await replication of results among gravid women elsewhere to determine the external validity of our findings. In addition, the use of an hCG difference score as the dependent variable, while appropriate for testing RFS, gauges the trajectory of hCG across a mother's pregnancies but not her hCG level at either birth. As such, we caution against using our regression estimates to predict the hCG level for any specific pregnancy.

The clinical observation that advancing maternal age corresponds to a lower risk of chromosomally normal foetal loss but a greater risk of chromosomally abnormal live births has stimulated several hypotheses regarding the nature of a maternal screening mechanism during pregnancy [4,9,16,19,20,40]. The search for such a mechanism, and its potential restoration especially among older gravid mothers, could hold considerable public health implications. Our results offer mixed support for the role of hCG as a mechanism of the adaptive filter. We acknowledge that findings hold limited clinical relevance given the small magnitude of the hCG coefficients and our focus on variables other than infant morbidity. We, however, view our work as encouraging refinement of hypotheses about the adaptive role of hCG for mothers at or near reproductive senescence and stimulating work on other candidate biomarkers that may signal foetal fitness.