Footprints in time: comparative quantitative trait loci mapping of the pitcher-plant mosquito, Wyeomyia smithii

Abstract

Identifying regions of the genome contributing to phenotypic evolution often involves genetic mapping of quantitative traits. The focus then turns to identifying regions of ‘major’ effect, overlooking the observation that traits of ecological or evolutionary relevance usually involve many genes whose individual effects are small but whose cumulative effect is large. Herein, we use the power of fully interfertile natural populations of a single species of mosquito to develop three quantitative trait loci (QTL) maps: one between two post-glacially diverged populations and two between a more ancient and a post-glacial population. All demonstrate that photoperiodic response is genetically a highly complex trait. Furthermore, we show that marker regressions identify apparently ‘non-significant’ regions of the genome not identified by composite interval mapping, that the perception of the genetic basis of adaptive evolution is crucially dependent upon genetic background and that the genetic basis for adaptive evolution of photoperiodic response is highly variable within contemporary populations as well as between anciently diverged populations.

1. Introduction

One of the fundamental connections sought in contemporary evolutionary biology is the link between genotype and phenotype. What genes are responsible for the evolution of ecologically relevant (adaptive) traits in changing environments or over environmental gradients in nature? Part of the difficulty is that the ‘interesting’ traits often involve the expression of many genes of varying effect [1–3]. Success in connecting genotype with phenotype has most often come when evolution has involved few changes in well-defined pathways [4–8]. Even in these cases, gene discovery has started with top-down or forward-genetic approaches, usually initiating with the mapping of quantitative trait loci (QTL).

At its origins [9–11], QTL mapping was targeted at identifying regions of the genome that accounted for a significant proportion of the phenotypic variance of a polygenic trait between lines or populations. In these experiments, the null hypothesis is that there are no QTL, and only QTL that exceed some likelihood threshold are considered ‘significant’. Several problems arise. First, QTLs represent regions of the genome, not individual genes, and a single QTL typically encompasses multiple genes [2]. Second, unless the number of markers used, and the number of individuals phenotyped and genotyped are large, this approach overestimates the effect size of the QTL and underestimates the number of QTL contributing to genetic divergence of the trait [3,12,13]. Third, if genetic divergence between populations involves the cumulative contribution of many genes of small effect, or even an exponential distribution of effect sizes [1], this approach is likely to miss some or most of the genetically important regions of the genome contributing to the evolution of the trait [14,15]. In short, most QTL mapping studies are biased towards discovering (and overestimating) large effect alleles.

Herein, we consider the evolution of photoperiodic response among three natural populations of the pitcher-plant (Sarracenia purpurea) mosquito, Wyeomyia smithii. Photoperiodism is the ability to use the length of day to regulate the timing of seasonal activities. In W. smithii, photoperiodism controls the onset, maintenance and termination of larval dormancy (diapause). Photoperiodic response varies with geography, and possessing the correct response to day length is essential in maintaining fitness [16]. We take two approaches to explore genetic differences in photoperiodic response among populations along a selection gradient in nature. First, we use the usual composite interval mapping (CIM) approach to identify major regions of the W. smithii genome in three QTL maps: one map compares a population that persisted near the front of the Laurentide Ice Sheet with a post-glacial population; the other two maps compare reciprocal crosses from a southern population from an unglaciated region with the same post-glacial population over a 15-fold greater time of divergence (see the electronic supplementary material). Second, we use individual marker regression coefficients as analogues of genes of small effect contributing to the evolution of photoperiodic response to make these same comparisons.

The mosquito W. smithii completes its entire pre-adult development within the water-filled leaves of the purple pitcher plant (S. purpurea). The range of the mosquito follows that of its host plant from the Gulf of Mexico to northern Canada [17]. Populations are divided into two major, fully interfertile clades: an ancestral southern clade along the Gulf Coast and the Carolina coastal plain (30–35° N), and a derived northern clade extending from Maryland to Newfoundland and west to northern Alberta [17–19]. We focus on three populations: an unglaciated, ancestral population in southern Alabama (AL), a derived population in New Jersey (NJ) that persisted near the glacial front during at least the Wisconsin glaciation, and a derived population that colonized northern Maine (ME) since recession of the Laurentide Ice Sheet (see the electronic supplementary material, table S1). Of 10 polymorphic allozyme loci [18], two show fixed differences between the southern and the northern clade (600 and 1100 individuals per locus, respectively). Three alleles present at 3–5% in three loci in 11 NJ populations (550 individuals per locus) are all absent in six ME populations (300 individuals per locus). We therefore conclude that there has been vanishingly little, if any, recent gene flow among populations in AL, NJ and ME.

Throughout its range, W. smithii uses photoperiod to initiate, maintain and terminate hibernal dormancy or diapause [17]. The day length used to switch from active development to diapause, or from diapause back to active development, is termed the critical photoperiod. Winter arrives earlier at longer day lengths in the north than in the south, a fact that impacts the timing of seasonal life-history events in literally thousands of photoperiodic species from rotifers to rodents [20]. Consequently, critical photoperiod increases with latitude and altitude and in W. smithii, with r² repeatedly greater than or equal to 0.92 [21]. In our three focal populations, critical photoperiod increases five phenotypic standard deviations from AL to NJ and three standard deviations from NJ to ME [22]. Across this range, the standard deviation of critical photoperiod remains constant so that the evolution of photoperiodic response represents directional evolution on a continental scale and stabilizing selection on a local scale [22].

In this study, we pursue several general questions. First, are the same regions of the genome involved in the genetic divergence of photoperiodic response over long (unglaciated versus glaciated) as over short (post-glacial) time spans? Second, do marker regression coefficients identify regions of the genome not identified by CIM that contribute to the evolution of photoperiodic response? Third, how complex is the genetic mechanism and regulation of photoperiodic response likely to be—what is the relative importance of polymorphism within when compared with between populations?

2. Material and methods

(a). Hybrid lines and phenotyping

Our approach was to make outbred crosses that we treated as inbred F₂ crosses among three single populations from AL, NJ and ME (see the electronic supplementary material, table S1). We established three mapping lines by mating a NJ male with a ME female (NJ × ME), a different AL male with a different ME female (AL × ME) and its reciprocal, an AL female with a ME male (ME × AL). The hybrid offspring from each line were reared through seven generations before phenotyping critical photoperiod (see the electronic supplementary material, table S2). Each hybrid generation was reared on short days (10 L : 14 D) at 21°C to initiate larval diapause and to synchronize the population. After all of a given generation's offspring were in diapause, they were transferred to long days (18 L : 6 D) and with a 13–35°C sine-wave thermoperiod to reinitiate development and generate the next generation.

Diapausing seventh generation hybrid individuals were exposed at 23°C to a ramped day length that started with larvae on short days that then incremented by 3 min per day as in nature [23]. Each individual interpreted the increased day length as long, reinitiated development and then pupated. The day length on the day of pupation was scored as that individual's critical photoperiod (see the electronic supplementary material, figure S1). In the seventh hybrid generation, we phenotyped 1682 individuals in the NJ × ME cross, 1886 individuals in the AL × ME cross and 1176 individuals in the ME × AL cross. We then chose for genotyping an equal number of males and females to minimize the effects of sex linkage [23] and chose individuals of both sexes spread evenly throughout the distribution of critical photoperiods to maximize discriminating power (see the electronic supplementary material, figure S1).

(b). Single nucleotide polymorphism identification

Restriction-site associated DNA (RAD) libraries were created using pre-established protocols [6,24–26]. Briefly, genomic DNA was isolated from individual mosquito pupae using DNeasy columns with RNase-A treatment (Qiagen) and digested with SbfI-HF (New England Biolabs). Digested DNA samples were individually barcoded by adding a ‘forward’ adaptor with a unique 5 bp sequence [24]. Libraries were then prepared by pooling 16 distinctly barcoded individuals, shearing digested DNA, ligating on a common ‘reverse’ adaptor and size-selecting libraries of 300–500 bp. These libraries were then amplified via a small number of PCR cycles. Each library was quantified by qPCR (Illumina protocol SY-930-10-10) and sequenced in a single lane of an Illumina GAIIx.

Genomic loci were assembled and single nucleotide polymorphisms (SNPs) within those loci were identified using the software package Stacks [27]. This package uses a maximum-likelihood model to determine SNP genotypes and haplotypes at each RAD locus. RAD loci were retained as markers for the linkage map if they showed fixed differences among parents (codominance) and showed no evidence of segregation distortion (see the electronic supplementary material, table S3). The quality-filtered sequences are deposited at the National Center for Biotechnology Information short-read archive (accession no. SRA057681).

(c). Linkage map construction

Linkage map construction was performed using packages R/qtl and onemap for the statistical programming environment R [28–30]. From the linkage map created using Seriation in OneMap, we chose seven equally spaced markers. We then removed all but these seven markers and, using the Try algorithm, individually placed each of the other markers back on to the linkage map so as to maximize the likelihood of the marker belonging in that place on the linkage map. After every 10 marker additions, Ripple was used to search the nearby space of marker order combinations for orders of higher likelihood with a window size of seven [31]. As these are advanced intercross lines, it is assumed that recombination interference is negligible. The genetic distance was calculated from recombination frequency using Haldane's [32] mapping function. Genome length was estimated by averaging the estimates resulting from two established methods described in Mathias et al. [23]. Marker dispersion was tested for departure from random spacing using a one-dimension nearest-neighbour test [33].

(d). Quantitative trait loci analysis

Individual marker regression coefficients were determined by regressing critical photoperiod on marker genotype, assuming no dominance or epistasis. Homozygous southern alleles (AL or NJ, depending on the mapping line) were given a value of 0, heterozygotes a value of 1 and homozygous ME a value of 2. In this way, positive regression coefficients paralleled the evolution of critical photoperiod from south to north, i.e. from short to long critical photoperiods. Marker regressions and CIM were performed using QTL Cartographer [34]. CIM was performed as for an F₂ cross, with a window size of 8.75 Centimorgan (cM) and allowing for 10 marker covariates. Significance levels were determined by 1000 bootstraps of the data. All estimates of QTL effects were also performed within QTL Cartographer.

To test for bi-marker-epistasis affecting critical photoperiod, we first performed a two-way ANOVA for each marker pair, modelling critical photoperiod as a function of the genotypes at the two markers. Two-way epistatic interactions were evaluated from the p-values associated with the interaction term from each ANOVA [23]. Second, we used the scantwo module from R/qtl, which calculates a log(odds ratio) (LOD) score for epistasis by comparing the likelihood of a two-qtl model including an interaction term to a two-qtl model without an interaction term ([28] and see the electronic supplementary material, figure S3).

Marker regressions represent the regression of the critical photoperiod of all individuals in a cross on marker genotype assuming no dominance or epistasis (independent variables = A1A1, A1A2, A2A2), where A1 is the marker allele from the southern parent, and A2 is the marker allele from the northern parent. Hence, there is a marker regression coefficient for each marker. To determine which of the marker regression coefficients were contributing to the higher than expected numbers in the former two crosses, we applied Storey & Tibshirani's [35] false discovery rate test to the regression coefficients in each cross to account for multiple comparisons.

The sex locus was mapped using a binary one-dimensional interval map in R/qtl [28].

3. Results

(a). Linkage and resulting composite interval-mapping maps

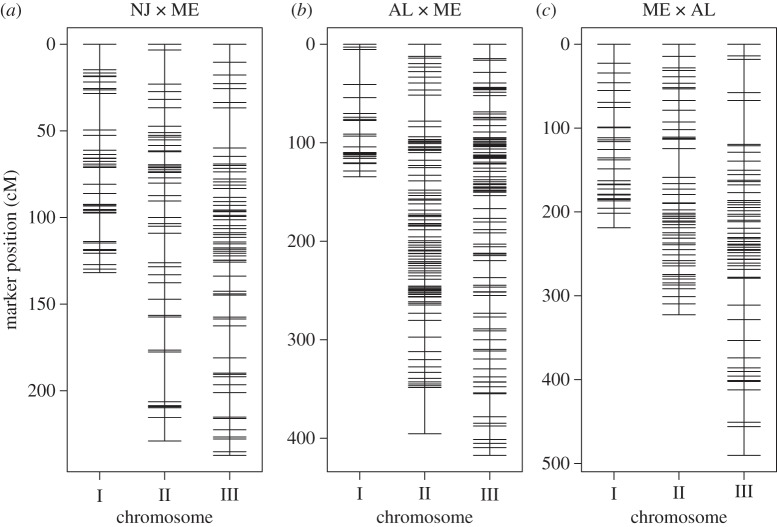
In concordance with Mathias et al. [23], the linkage group with the sex locus is designated as chromosome I, the linkage group with WsUbcD4 is designated as chromosome II, and the linkage group with Wstimeless as chromosome III (figure 1). In all three crosses, the spacing in cM between markers does not depart significantly from random expectation and greater than 95 per cent of the genetic map resides within a window size of 10 cM (see the electronic supplementary material, table S4). In the results below, effects follow geography. Positive effects are in the direction of longer critical photoperiods of the northern parents, whereas negative effects are in the direction of longer critical photoperiods of the southern parents. For each cross, RAD-tag loci were included in the analysis if they: (i) contained SNPs that were homozygous within each parent and variable between parents, (ii) were genotyped in more than 150 offspring, and (iii) showed no strong evidence of segregation distortion (see the electronic supplementary material, table S3).

Figure 1.

SNP-based linkage maps of Wyeomia smithii based on RAD genotyping of the F₇ hybrid generation of a single pair cross between populations having evolved over a (a) shorter or (b,c) longer evolutionary time span; (b) and (c) represent reciprocal crosses.

The NJ × ME linkage map is based on 223 individuals and consists of 181 markers (figure 1), totalling 618.5 cM with an average interval length or marker spacing of s = 3.4 cM (see the electronic supplementary material, table S4). There are two significant QTLs, one on chromosome II and the other on chromosome III (figure 2), accounting for 6.7 per cent and 6.1 per cent of the variance in critical photoperiod, respectively. In both cases, the additive effects were positive and the dominance effects negative; the dominance : additive ratios fell between 0 and 1, indicating partial dominance (table 1). There was no evidence for any significant bi-marker epistatic interaction (see the electronic supplementary material, figures S2 and S3).

Figure 2.

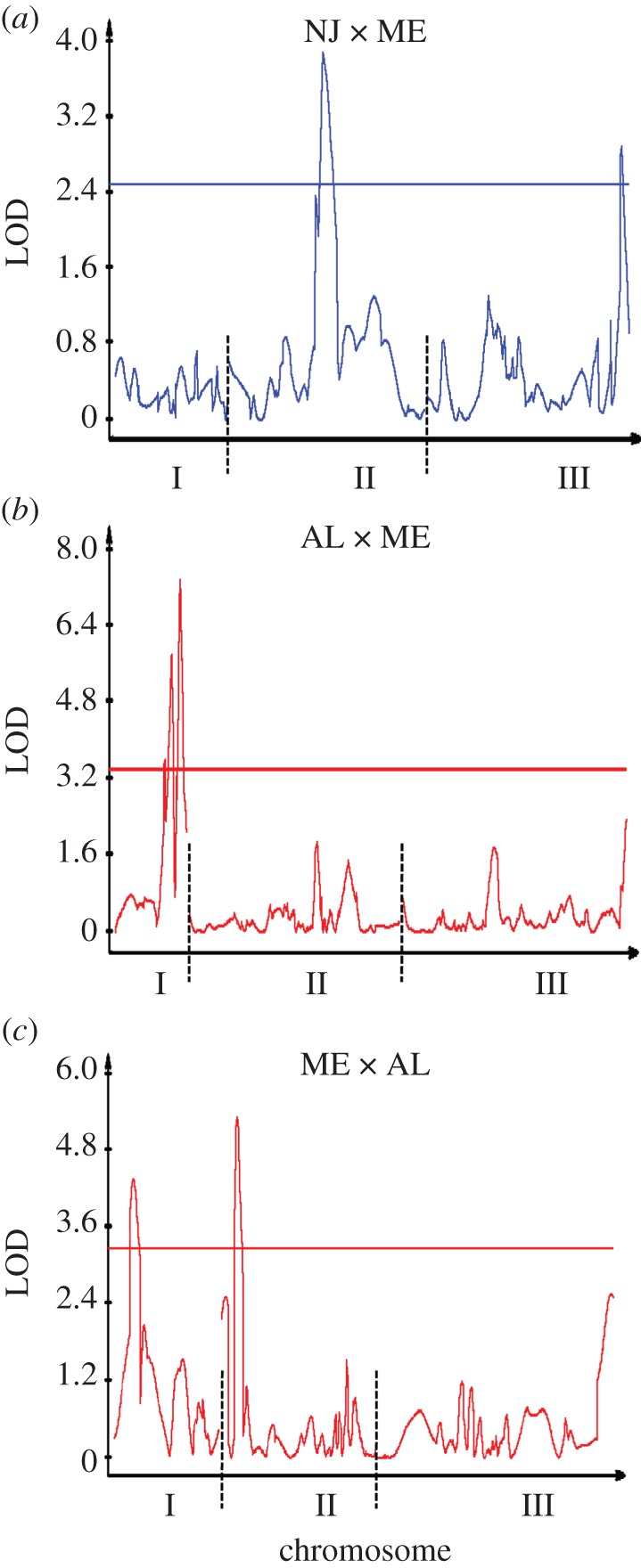
Composite interval map for the divergence of critical photoperiod over a (a) shorter or (b,c) longer evolutionary time span; (b) and (c) represent reciprocal crosses.

Table 1.

Composite interval map analysis. (Position in cM. LR, likelihood ratio; a, additive effect; d, dominance effect; r², percentage of variation accounted for by the QTL. |d/a|, absolute value of the ratio of dominance to additive effects; a QTL is considered overdominant when this ratio > 1, completely dominant when this ratio = 1, partially dominant when this ratio is between 0 and 1, and additive when the ratio = 0.)

cross	QTL	chromosome	position	LR	a	d	|d/a|	r2 (%)
NJ × ME	1	II	109	17.9	0.39	−0.27	0.69	6.7
	2	III	227	13.3	0.57	−0.12	0.21	6.1
AL × ME	1	I	92	16.4	0.56	0.63	1.13	12.8
	2	I	105	26.7	−1.57	0.58	0.37	15.9
	3	I	121	33.9	1.24	0.35	0.28	18.7
ME × AL	1	I	40	20.1	0.18	0.40	2.22	6.8
	2	II	34	24.6	0.68	0	0	9.3

The AL × ME linkage map is based on 224 individuals and consists of 303 markers (figure 1) totalling 947.3 cM with an average interval length or marker spacing of s = 3.2 cM (see the electronic supplementary material, table S4). There are three QTLs, all on chromosome I (figure 2), accounting for 12.8 per cent, 15.9 per cent and 18.7 per cent of the variance in critical photoperiod (low to high cM; table 1). The sequence of additive effects was +0.56, −1.57 and +1.24 (low to high cM) while all dominance effects were positive. The dominance : additive ratios indicated slight overdominance for the first QTL and partial dominance for the second and third QTLs. There was no evidence for any significant bi-marker epistatic interaction (see the electronic supplementary material, figures S2 and S3).

The ME × AL linkage map is based on 279 individuals and consists of 177 markers (figure 1) totalling 1031.8 cM with an average interval length or marker spacing of s = 5.9 cM (see the electronic supplementary material, table S4). There are two QTLs, one on chromosome I and the other on chromosome II (figure 2), accounting for 6.8 per cent and 9.3 per cent of the variance in critical photoperiod, respectively (table 1). The additive effects were +0.18 and +0.68 on chromosomes I and II, while the single dominance effect was on chromosome I and indicated strong overdominance. There was no evidence for any significant bi-marker epistatic interaction (see the electronic supplementary material, figures S2 and S3).

(b). Individual marker regressions

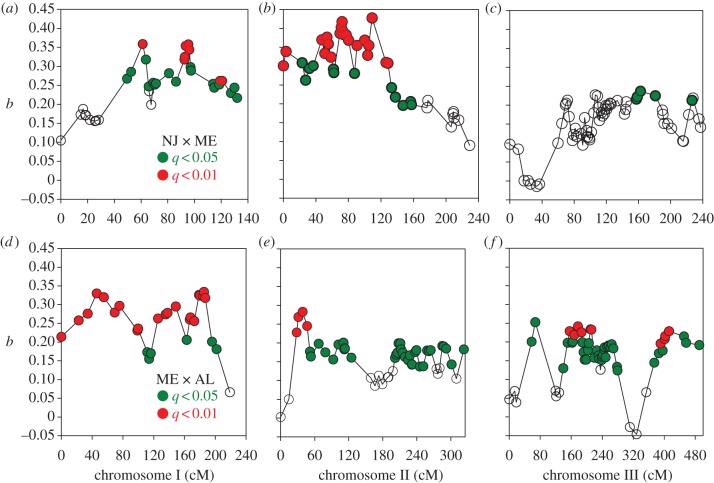
This test indicated that none of the marker regression coefficients was significant in the AL × ME cross (all q > 0.20). In the NJ × ME cross, 84/181 and 35/181 marker regression coefficients were significant at q < 0.05 and q < 0.01. Significant marker regression coefficients occurred in all three chromosomes (figure 3). There were clearly two and possibly three peaks of positive regression coefficients on chromosome I, two and possibly four peaks on chromosome II and two peaks on chromosome III. In the ME × AL cross, 166/177 and 40/177 marker regression coefficients were significant at q < 0.05 and q < 0.01. There were possibly two peaks on chromosome I, one and possibly two peaks on chromosome II and two clear peaks on chromosome III.

Figure 3.

Patterns of marker regression coefficients b, in the (a–c) NJ × ME and (d–f) ME × AL crosses and their associated significance after a posteriori correction for multiple comparisons using false discovery rates. The number of peaks depends upon whether one scores as independent two clusters of significant coefficients separated by non-significant coefficients (q ≥ 0.05, open circles), or clusters with q < 0.01 (red) separated by coefficients with 0.05 > q > 0.01 (green).

4. Discussion

(a). Genetic architecture underlying the evolution of photoperiodic response

Differences in CIM maps or marker regression patterns between the crosses could have two nonexclusive bases. First, these differences may represent variation in evolutionary time among the parent populations; second, these differences may be owing to polymorphisms within the parent populations. Only multiple, replicated lines could determine the relative importance of these two alternatives. With three maps, if differences in CIM maps were owing primarily to evolutionary time, we would expect the two AL/ME maps to be similar and the NJ × ME map to be distinctly different. If differences in CIM maps included a significant effect of polymorphisms within populations, we would expect dissimilarities among all three maps. Our results point to a combination of these alternatives. First (figure 2), none of the three CIM peaks in the AL × ME cross on chromosome I appear in the ME × AL cross and there is a significant peak on the chromosome II in the latter but not in the former. Second, there are no significant (q > 0.05) marker regression coefficients in the AL × ME cross but an abundance of significant marker regression coefficients (q < 0.01) in the ME × AL cross (figure 3). At the same time, there are distinct CIM peaks (figure 2) in the NJ × ME cross on chromosomes II and III that do not appear in either the ME × AL or AL × ME cross. Finally, in our first QTL map of photoperiodic response [23] of F₂ hybrids between northern Alberta and Florida (54° N, 31° N), there were multiple peaks spread across all three chromosomes. We therefore conclude from QTL mapping that genetic variation underlying photoperiodic response is highly variable within as well as between populations of W. smithii.

This conclusion is supported by components of genetic variation revealed in line crosses among and within populations. Among populations [22,36,37], crosses between the southern (ancestral) and northern (derived) populations [18,19] consistently revealed genetic differences in photoperiodic response involving epistasis but varied among crosses in the components of digenic epistasis (additive × additive, additive × dominance, dominance × dominance). A cross between the AL population used in this study and a Florida population at the same latitude involved dominance, maternal additive, maternal dominance and epistatic effects. A cross between the ME population used in this study and a Wisconsin population at the same latitude involved additive and dominance effects alone. Within the same NJ population used in this study [38], three separate subpopulations were sampled within a 200 m radius and subjected to divergent selection on photoperiodic response. Line crosses between divergent lines within each subpopulation revealed genetic differences owing to epistasis, but the components of digenic epistasis differed among the separate subpopulations. Hence, parallel phenotypic evolution of photoperiodic response among populations in eastern North America or in response to selection within the single NJ population involved different elements of the underlying genetic architecture.

Genetic background of individuals used in the QTL mapping, in specific populations along the climatic gradient of North America or in specific lines within the NJ population, has been crucially important in evaluating regions of the genome or the genetic architecture underlying the evolution of photoperiodic response in W. smithii, and should be an important factor in the experimental design of any comparative study involving adaptive evolution.

(b). The importance of marker regressions

In all three crosses, we failed to identify any significant bi-marker epistatic interactions (see the electronic supplementary material, figure S2). This result contrasts with our previous QTL analysis [23] that identified several epistatic interactions in an Alberta × Florida cross, using exactly the same analytical methodology. More strikingly, the lack of bi-marker epistasis in the ME × AL and AL × ME crosses contrasts with line crosses that consistently identify the effects of epistasis in genetic divergence of photoperiodic response between southern and northern populations [22,36,37] and despite the conservative nature of line-cross analysis that only detects net directional epistasis [39]. However, owing to the integration across the genome, line-cross analysis can provide greater statistical power to detect epistasis than ANOVA of marker pairs [40], as illustrated by W. smithii.

As discussed in §1, interval-mapping approaches are biased towards discovering (and overestimating) large effect regions in the genome; yet much of the variation that contributes to response to selection may depend on many loci of small effect. We have used individual marker regressions to probe the W. smithii genome to identify regions that, although not significant by CIM standards, are likely to contribute to the evolution of photoperiodic response. We fully acknowledge that individual marker regressions from the same chromosome are not necessarily independent because ‘significance’ may be biased by linkage to a locus or QTL of major effect, even after adjusting for multiple comparisons. However, if linkage is responsible for several marker regression coefficients to register as significant after adjusting for multiple comparisons, then the associated markers should be clustered at a specific region of the chromosome and both the regression coefficients and their significance should decline with increasing distance up or down the chromosome. For example, in the NJ × ME cross, CIM (figure 2a) identifies a significant peak on the second chromosome that coincides with a cluster of significant marker regressions (figure 3b). Both the magnitude and significance of marker regressions then decline with distance (cM) from this cluster. We therefore discuss clusters of significant marker regressions that reside on different (unlinked) chromosomes or that are separated by clusters of non-significant marker regressions on the same chromosome.

CIM identifies a significant QTL near the end of chromosome III in the NJ × ME cross (figure 2a) but not in the ME × AL cross (figure 2c). In the ME × AL cross, marker regressions indicate two significant clusters separated by non-significant regression coefficients that differ in sign (figure 3f). We interpret this pattern to indicate that two regions of chromosome III contribute to the genetic variation in photoperiodic response, even though no significant QTLs were identified by CIM (figure 2c).

CIM does not identify a significant QTL in the NJ × ME cross on chromosome I (figure 2a) but marker regression coefficients show two clusters separated by non-significant marker regression coefficients on the same chromosome (figure 3a). Whether or not this pattern represents two independent regions or one linked region of the genome, the presence of multiple significant marker regressions on chromosome I in figure 3a indicates that genetic differences between the NJ and ME parents include regions of this chromosome.

The important point is that CIM with sample sizes under 1000 is prone to overestimating the effect size of the significant QTL and to underestimating the number of QTL contributing to genetic divergence of a trait [3,12,13,15]. Yet, in all cases, the QTL identified by CIM accounted for less than 50 per cent of the genetic difference in photoperiodic response between the parents (table 1). We have shown that clusters of marker regressions can be used to identify regions in the genome that are ‘overlooked’ by CIM and, that, in using QTL as an exploratory, forward-genetic tool, both approaches should be used in parallel with each other.

(c). Implications for evolution in seasonal environments

There are two major rhythms of the biosphere: the daily and seasonal rhythms of light, moisture and temperature. Plants and animals possess an internal circadian clock that keeps track of daily time and a photoperiodic timer that keeps track of seasonal time. Following the first identification of a circadian clock gene in Drosophila [41], there followed three decades of intense research on the genetic basis of circadian rhythmicity in flies and mice and, to a lesser extent, in other animals [42–45]. This research identified many homologous genes between insect and mammalian circadian clocks; however, even within insects, individual genes exhibit functional variation within circadian clockworks [46]. Similar progress has not been made on the genetic basis of photoperiodism in animals. In part, this lack of progress may be owing to the multiple neuronal and hormonal cascades that intervene between the translation of day length into overt development, dormancy, reproduction or migration that are initiated by photoperiod [47,48]. Lack of progress may also be owing to a persistent, myopic effort to find a causal link between circadian rhythmicity and photoperiodism, rather than using a circadian-unbiased forward-genetic approach [20,49–51]. Importantly, it is clear that even within a single species, W. smithii, the genetic basis of photoperiodic response is highly complex, not only across climatic gradients though evolutionary time, but within populations as well. Identification of specific genes involved in photoperiodic time measurement among different species of insects, much less genetic commonalities between arthropods and mammals, is going to be far more elusive than the historical progress in circadian rhythmicity.