The dynamics of food chains under climate change and nutrient enrichment

Abstract

Warming has profound effects on biological rates such as metabolism, growth, feeding and death of organisms, eventually affecting their ability to survive. Using a nonlinear bioenergetic population-dynamic model that accounts for temperature and body-mass dependencies of biological rates, we analysed the individual and interactive effects of increasing temperature and nutrient enrichment on the dynamics of a three-species food chain. At low temperatures, warming counteracts the destabilizing effects of enrichment by both bottom-up (via the carrying capacity) and top-down (via biological rates) mechanisms. Together with increasing consumer body masses, warming increases the system tolerance to fertilization. Simultaneously, warming increases the risk of starvation for large species in low-fertility systems. This effect can be counteracted by increased fertilization. In combination, therefore, two main drivers of global change and biodiversity loss can have positive and negative effects on food chain stability. Our model incorporates the most recent empirical data and may thus be used as the basis for more complex forecasting models incorporating food-web structure.

1. Introduction

Current changes in our planet's ecosystems have the potential to cause species extinctions [1]. The changes in nutrient availability (enrichment) and temperature (climate warming) were identified by the Millennium Ecosystem Assessment as two major direct drivers of biodiversity loss [2]. They predict the impact of both these drivers to increase very rapidly in all biomes [3, p. 9]. To predict accurately the community effects of enrichment and warming, it is important to understand their interactive impact on biological rates. This helps in developing community protection measures and in conserving important ecosystem functions.

Both enrichment and warming have wide-ranging implications for food-web and ecosystem structure, many of which are mediated by changes in population dynamics [4–11]. Rosenzweig [6] analytically investigated the effect of increased energy input on the dynamics of a predator–prey system and coined the term ‘paradox of enrichment’: enrichment drives a predator–prey system from stable equilibria into oscillations and finally into extinction when population minima hit extinction boundaries [6]. This has recently been generalized as the principle of energy flux: any process increasing energy fluxes relative to consumer loss rate will destabilize systems by shifting biomass up the trophic levels [12]. This moves the isoclines of the species towards unstable equilibria. Interestingly, when consumer mass systematically increases with trophic levels [13], the destabilizing effects of enrichment are ameliorated [11].

Warming has profound effects on biological rates such as organism metabolism [14–16], growth [17], feeding [18,19] and death [20]. However, the interplay of these physiological effects at the population level is not yet entirely clear, and there are several possibilities. Warming might simply accelerate population dynamics. In a seminal study of population dynamics, Vasseur & McCann [5] found that increasing temperature destabilizes systems and increases the amplitudes of oscillations. These findings are based on assumptions such as temperature invariance of the system carrying capacity (the maximum biomass the system can support) and the consumer's half saturation density. While the former is certainly not supported by empirical data [21], the latter characterizes the consumer's efficiency at attacking resources and more recent studies showed that it is likely to change with temperature [19,22,23]. Additionally, Vasseur & McCann [5] assumed that in most natural communities, the species ingestion increases more with warming than does their metabolism. However, feeding interactions among terrestrial and marine invertebrates indicate the opposite [18,19,24]. These studies found that warming increases species metabolism more strongly than ingestion rates. The decreasing energetic efficiencies (the ratio of ingestion rate to metabolism) lead to increasing energetic restrictions for predators and decreasing predator biomasses. This stabilizes the system dynamics and reduces biomass oscillations. These studies emphasize the possibility of predator starvation at high temperatures when metabolism exceeds ingestion rates [18,19]. However, dynamic model analyses of these empirical patterns are still lacking.

Here, we fill this void by developing a nonlinear bioenergetic population-dynamic model that includes empirical body-mass and temperature dependencies for the major biological rates affecting population dynamics such as carrying capacity [21], production [17], metabolism [16] and functional response parameters [25]. With this model, we numerically investigated the solitary and interactive effects of two major drivers of global change, enrichment and warming, on the population dynamics of a three-species food chain. We were particularly interested in the following questions: (i) What are the individual effects of enrichment and warming on the dynamics of the food chain? (ii) What are the combined effects of enrichment and warming on these dynamics? and (iii) Does the community size structure with systematically increasing body mass ratios influence these effects?

2. Methods

The bioenergetic dynamic model used is based on Yodzis and Innes' [26] consumer–resource model and is updated with allometric coefficients and temperature dependencies of the biological rates. In the three-species food chain, the basal species (B) is fed on by the intermediate species (I) which in turn is consumed by the top species (T). The biomass changes of the species (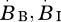 and 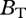, respectively) are described by the following differential equations:

2.1

2.2

2.3

Here, 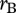is the basal species' mass and temperature-specific maximum growth rate, 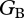is the basal species' logistic growth term and 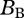is its population biomass density. The functional responses 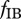and 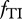describe the feeding dynamics of the feeding links in the food chain. The assimilation efficiencies (efficiency of conversion of prey biomass into predator biomass), 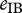and 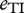, are both set to 0.85 because both species are carnivores [26]. The metabolism of the intermediate and top species, 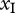and 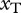, also depend on their masses and the temperature of the system.

We used a logistic growth term where the potential growth of the population depends on its current population biomass and its body-mass and temperature-dependent carrying capacity, :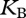

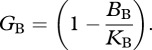2.4

The functional response, 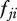, describes the feeding dynamics between consumer j and its prey i. It depends on the consumer's maximum consumption rate when feeding on species i, 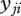, which depends on the body-masses of both species j and i and the temperature, the Hill exponent, h, which determines the shape of the function and the half saturation density 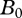. 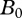gives the prey population density at which half the maximum consumption of the consuming species is reached and depends on the body-masses of species j and i and the temperature of the system:

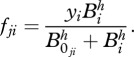2.5

The mass and temperature dependencies of the maximum growth rate of the basal species 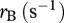is calculated as follows:

2.6

Here, 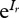is the rate-specific constant, calculated for a species' body mass of 1 g and a temperature of 20°C (= 293.15K). Its value is modified by the second term, the body-mass dependency, expressed by the mass of the species m and a rate-specific scaling coefficient, s. The term of the temperature dependency is an extended notation of the Arrhenius equation, where Ea is the activation energy (eV), T₀ the normalization temperature, T the temperature of the system and k (eV K 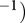the Boltzmann constant.

The mass and temperature dependent metabolism of the intermediate and top species 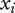( 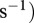and the carrying capacity of the basal species 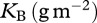are calculated accordingly:

2.7

and

2.8

Both terms of the functional response, the maximum ingestion, 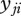, and the half saturation density, 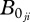, depend not only on the temperature of the system and the body mass of species i, but also on the body mass of its predator j:

2.9

and

2.10

Analyses of extensive databases [25] revealed additional dependencies of the parameters of the functional response. To understand these, it is best to refer to the traditional Holling type II functional response model [27]:

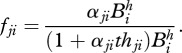2.11

Instead of using the maximum ingestion and half saturation density of the other notation (equation (2.5)), this uses 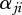, the attack rate of the consumer when it feeds on i, and the handling time, 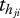, the time the consumer needs to process one prey item before it can start looking for another one. The attack rate and the handling time both show a hump-shaped relationship with the body-mass ratio of the consumer and its prey. The exponential equations for these dependencies follow the same principle as already introduced (see equations (2.6)–(2.10)):

2.12

and

2.13

Here, 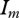is the intercept, and the consumer–prey mass ratio has a twofold influence on the feeding parameters: the slope s1 is the ratio's scaling coefficient in its simple form, whereas s2 is the scaling coefficient for its quadratic form.

The handling time also displays a hump shape with temperature:

2.14

These additional scaling relationships of the functional response parameters can be incorporated into the equations for the maximum consumption and half saturation density by using the interrelation of the parameters of the two different notations of the functional response:

2.15

and

2.16

This yields the following equations to express the body-mass and temperature scaling of the functional response parameters:

2.17

and

2.18

Inserting all equations accounting for the allometric and temperature scaling of the biological rates (equations (2.6)–(2.8), (2.17) and (2.18)) into the differential equations (2.1)–(2.3) yields a nonlinear bioenergetic population-dynamic model of a three-species food chain.

In this study, we modelled a food chain parametrized solely for invertebrates. Whenever possible, we incorporated values extracted from extensive empirical databases. These parameters represent a wide range of different species and ecosystem types. The scaling relationships for the biological rates and their sources are summarized in tables 1 and 2. Using these relationships yields a model with five free parameters: (i) the body mass of the basal species, (ii) the body-mass structure of the species in the food chain, (iii) the temperature of the system, (iv) the Hill coefficient shaping the functional response, and (v) the intercept of the carrying capacity (basic fertilization level). We used constants for the basal body mass (0.01 g) and the Hill coefficient (1, yielding type-II functional responses). A species was considered extinct and removed from the system when its biomass fell below 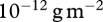. To investigate the individual and combined effects of enrichment and warming, we systematically varied the intercept of the carrying capacity (fertilization gradient, range from 1 to 20), temperature (range from 0°C to 40°C) and the size structure of the community in three levels: (i) all species equally sized (no size structure), or consumers (intermediate or top) are (ii) 10 times larger or (iii) 100 times larger than their resources. Every species started with a biomass density equal to half the carrying capacity of the system with that particular enrichment and temperature combination. All simulations ran for 100 000 years and we recorded species biomasses and survival.

Table 1.

The parameter values of the model's mass and temperature dependencies of the carrying capacity (K in 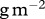), from Meehan (2006) [21], growth (r in 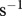), from Savage et al. [17], maximum ingestion (y in s⁻¹), from Rall et al. [25], half saturation density ( 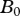in 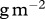), from Rall et al. [25] and metabolism (x in 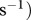, from Ehnes et al. [16]. Generally, the parameters scale with the body mass of the resource species (i) of the considered species pair; only the feeding parameters scale additionally with the body mass of the consumer species (j). The conversion factor used to transform the metabolism of the species from Joule per hour to 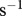was taken from Peters [28].

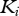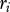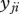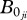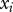intercept (I)		−15.68	−9.66	3.44	−16.54
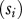
slope resource species i	0.28	−0.25	0.45	0.2	−0.31
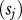
slope consumer species j			−0.47	0.33
activation energy (Ea)	0.71	−0.84	−0.26	0.12	−0.69

Table 2.

The parameter values for the body-mass ratio and temperature-dependent hump shape of the functional response parameters, attack rate and handling time. The mass ratio and temperature dependencies of the attack rate (in 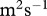, mass dependency 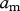) and handling time (in s, mass dependency 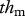, temperature dependency ).

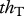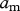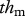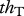intercept (I)	−1.81	1.92	0.5
slope term 1 (s1)	0.39	−0.48	−0.055
slope term 2 (s2)	−0.017	0.0256	0.0013

3. Results

(a). Single effects of enrichment and warming

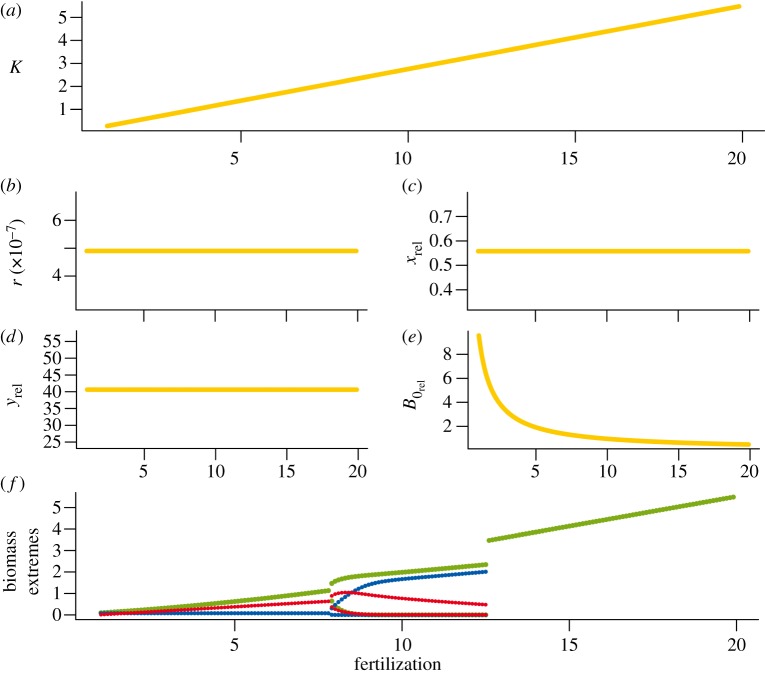
Increasing system fertility at a constant temperature increases the carrying capacity linearly (see figure 1a, for an example at 20°C). The growth rate, the relative metabolism of the species and its ingestion efficiency are not affected (figure 1b–d). However, there is an inverse proportional decrease in the half saturation density relative to the carrying capacity (figure 1e). This implies that fertilization increases the efficiency of consumers in attacking resources. The bifurcation diagram shows the classical pattern of the ‘paradox of enrichment'. At low fertility, all species coexist in an equilibrium at low densities; the equilibrium biomasses increase as fertility increases until the biomasses start cycling (figure 1f). The amplitude of these cycles increases until both the top and the intermediate species are driven into extinction and only the basal species survives, growing up to its carrying capacity. Increasing the fertility thus destabilizes the system. Both increasing bottom-up supply (figure 1a) and increasing top-down pressure (figure 1e) contribute to this progressive instability of the system.

Figure 1.

The mass- and temperature-dependent parameters of the model and a bifurcation diagram on a fertilization gradient. All parameter values are calculated for species with a body mass of 0.01 g at a temperature of 20°C. Shown are (a) the carrying capacity of the basal species (K (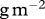)), (b) the growth rate of the basal species (r (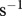)), (c) the metabolism of a consumer relative to the basal species' growth rate (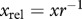, dimensionless), (d) the maximum consumption of the species relative to their metabolism (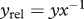, dimensionless), (e) the species' half saturation density relative to the carrying capacity (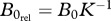, dimensionless) and (f) the biomass extremes of the three species (basal species: green; intermediate species: blue, top species: red, 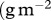) on a fertilization gradient.

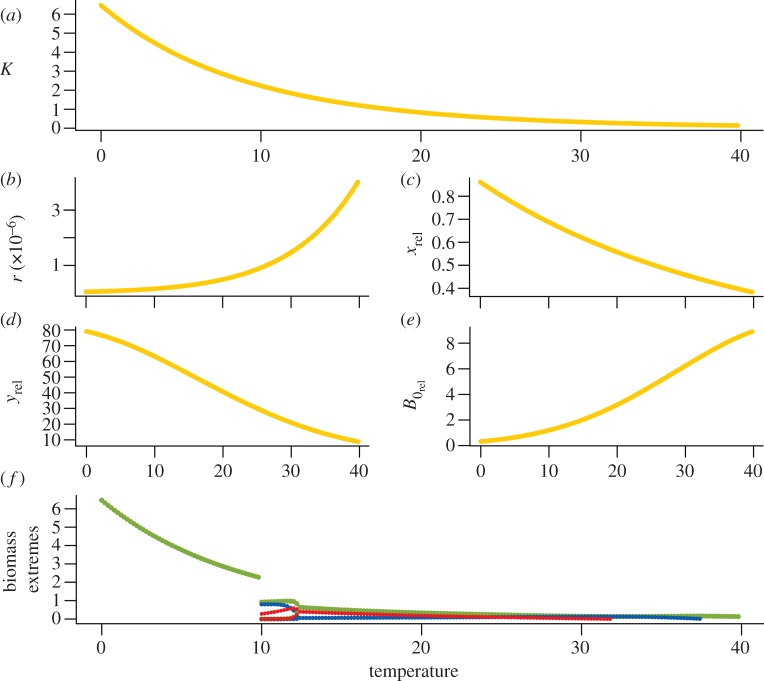
Increasing the temperature of the system at a constant fertilization level decreases the carrying capacity exponentially (see figure 2a for an example at a fertilization value of 3). At the same time, the growth rate of the basal species increases (figure 2b). The metabolism of the species increases with temperature at a slower rate, resulting in a decrease in the relative metabolism (metabolism relative to basal production) of the species (figure 2c). The ingestion efficiency (ratio of ingestion and metabolism of a species) decreases with temperature: a species' metabolism increases more strongly with temperature than its ingestion (figure 2d). At the same time, the relative half saturation density of the species increases (figure 2e). This results in a reduced flux of energy from the base to the top of the food chain. Warming has a marked effect on species biomasses (figure 2e). At low temperatures, only the basal species survives, growing up to its carrying capacity. At higher temperatures, the biomasses of the species oscillate with decreasing amplitudes along the temperature gradient. Finally, the system crosses over an inverse Hopf bifurcation and reaches equilibrium dynamics. A further temperature increase pushes the top species beyond the point where its ingestion cannot keep up with its metabolism and it dies as a result of a poor ingestion efficiency. At even higher temperatures, the same happens to the intermediate species and it also dies of starvation. Warming up the system thus stabilizes population dynamics, with a pattern of a reversed enrichment gradient, but very high temperatures can lead to the extinction of species.

Figure 2.

The mass- and temperature-dependent parameters of the model and a bifurcation diagram on a temperature gradient. All parameter values are calculated for species with a body mass of 0.01 g at an artificial fertilization level of 3. Shown are (a) the carrying capacity of the basal species (K (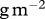)), (b) the growth rate of the basal species (r (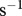)), (c) the metabolism of a consumer relative to the basal species' growth rate (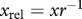, dimensionless), (d) the maximum consumption of the species relative to their metabolism (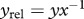, dimensionless), (e) the species' half saturation density relative to the carrying capacity (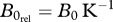, dimensionless) and (f) the biomass extremes of the three species (basal species: green; intermediate species: blue, top species: red, 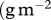)) on a temperature gradient.

(b). Interactive effect of enrichment and warming

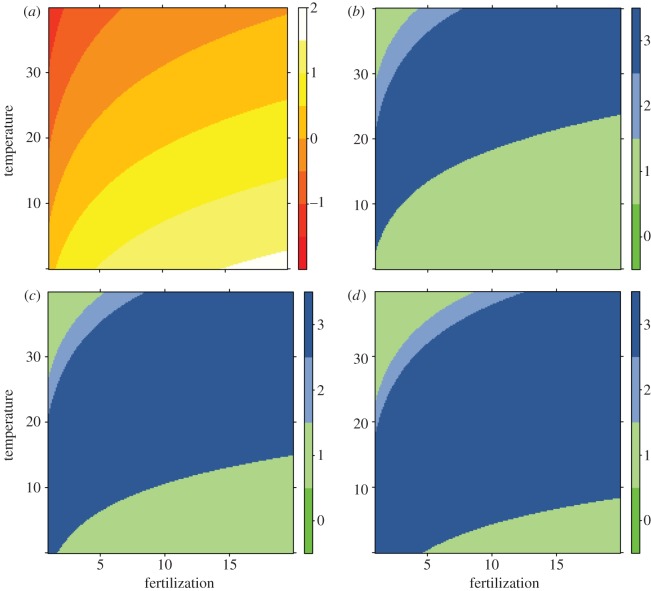
The carrying capacity increases with fertilization and decreases with warming. This leads to the highest carrying capacities at combinations of high fertilization and low temperature and the lowest carrying capacities at combinations of low fertilization and high temperature (figure 3a). The number of species extant after 10 000 years across all combinations of fertilization and temperature is shown in the remaining panels of figure 3. In the scenario without body-mass structure, increasing fertility at low temperatures leads to species extinctions (figure 3b). Warming counteracts these detrimental effects of enrichment: the higher the temperature, the more the system can be fertilized before it loses species. The exceptions are high temperature, low fertility systems (upper left corner, same panel) where warming decreases the relative ingestion and increases the relative half saturation density of the consumer, reducing its efficiency. Consequently, first the top and then the intermediate species cannot ingest as much energy as they need to survive and become extinct. These extinctions at high temperatures are prevented by higher levels of fertilization. The lower two panels show the surviving species in a scenario with size structure (figure 3c, consumer 10 times larger than its prey; basal species: 0.01 g, intermediate species: 0.1 g, top species: 1 g; figure 3d, consumer 100 times larger than its prey; basal species: 0.01 g, intermediate species: 1 g, top species: 100 g). A three-species food chain with a structured body-size distribution, as is likely in nature [13,29], is generally less susceptible to the paradox of enrichment, and at low temperatures, the extinctions are postponed to higher fertilization levels. The rescuing effect of warming that prevents extinctions caused by unstable oscillations is more pronounced in size-structured food chains, but the top and intermediate species are more vulnerable to starvation and, in the low fertility region, extinctions occur at lower temperatures. At high temperatures, it takes more fertilization to rescue the consumers from starvation due to lower ingestion efficiencies. Warming thus counteracts the paradox of enrichment at low temperatures but increases the starvation risk of species with higher trophic levels in high temperature, low fertility systems. At high temperatures, increasing fertility prevents consumer extinctions. The stabilizing and destabilizing effects of warming are more pronounced the larger consumers are.

Figure 3.

The 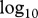of the carrying capacity of the three-species system ((a), colour-coded, see colour key) and the number of species surviving after 10 000 years ((b): no body-mass structure; (c): consumer 10 times larger than its prey; (d): consumer 100 times larger than its prey, colour-coded, see colour-key) on a combined gradient of fertilization (x-axis) and temperature (y-axis (°C)).

Increasing enrichment increases the carrying capacity and destabilizes the biomass dynamics of the species. Extinctions occur when the carrying capacity exceeds a certain threshold. Warming, in contrast, reduces the carrying capacity and stabilizes species biomass dynamics. No further extinctions occur when the carrying capacity falls below a certain threshold. If both enrichment and warming would act entirely through the carrying capacity (i.e. via bottom-up effects), these thresholds would be the same across all temperature and fertilization combinations. A carrying capacity value above this threshold would lead to extinctions, whereas none would occur at lower carrying capacities. We refer to this threshold as the maximum feasible carrying capacity: it is the maximum carrying capacity the system can be subjected to without losing species. However, instead of being constant, the maximum feasible carrying capacity follows a nonlinear curve with temperature, with a maximum at approximately 38°C (figure 4, all curves). This indicates a ‘top-down’ component in the impact temperature has on the dynamics of the system. Additionally, applying a body-mass structure to the food-chain increases the maximum feasible carrying capacity (no structure: 1.47–5.24; consumers ten times larger: 3.65–20.42; consumers 100 times larger: 10.09–92.04). Warming operates via both bottom-up and top-down effects. This increases the maximum carrying capacity that the system can tolerate without losing species. Again, the effect of temperature is more pronounced in size-structured food chains.

Figure 4.

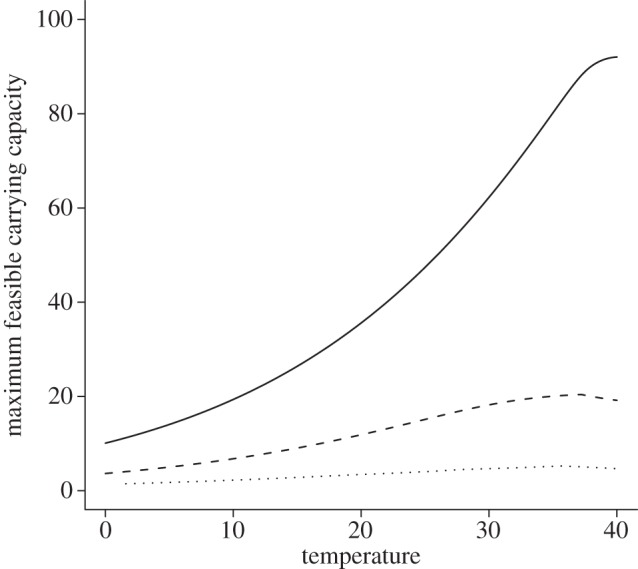
The maximum feasible carrying capacity able to sustain all three species in the system (y-axis), depending on the temperature (x-axis (°C)) for the approach without body-mass structure (dotted line), with the respective consumer 10 times larger than its prey (dashed line) and with the respective consumer 100 times larger (solid line).

4. Discussion

Using a nonlinear bioenergetic population-dynamic model for a three-species food chain parametrized with the latest body-mass and temperature dependencies for biological rates, we investigated the individual and combined effects of two main drivers of biodiversity loss, nutrient enrichment and warming, in food chains with different body size structures. Consistent with expectations [6,30], enrichment destabilizes the system and ultimately leads to extinctions. Warming stabilizes the system by reducing the carrying capacity and the ingestion efficiency and increasing the relative half saturation density of the species. When the ratio between maximum ingestion and metabolism of a species falls below a critical threshold, it becomes extinct as a result of starvation. Thus, high temperature surprisingly counteracts the destabilizing effects of enrichment. High temperatures, however, also increase the risk of consumers starving in oligotrophic and low fertility systems. Higher levels of fertilization, in turn, counteract these detrimental effects of warming. Larger consumer body masses enhance the stabilizing as well as the destabilizing effect of warming and postpone the effects of fertilization. Additionally, warming increases the maximum carrying capacity at which the system retains all its species, and again, increasing consumer body masses enhance this effect drastically. This implies novel interactions between two drivers of global change: nutrient enrichment and warming. Moreover, we found striking effects of the community size structure amplifying the impacts of warming.

(a). Single effects of enrichment and warming

The carrying capacity of the three-species food chain increases with enrichment. This decreases the ratio of half saturation density to carrying capacity and consequently increases the energy flux from the basal to the top species [5,26]. This direct conversion of bottom-up supply into top-down pressure destabilizes the system along the fertilization gradient and results in the biomass patterns of the ‘paradox of enrichment’ [6]. Consistent with prior studies [11], simulations with differently sized consumers and prey display a reduced severity of this effect (figure 3b–d). Inedible, invulnerable or unpalatable prey and inducible defences can alleviate the paradox of enrichment in natural and laboratory environments [31–35]. These are not accounted for in our model.

Warming stabilizes the biomass oscillations within the food chain, leading to a pattern of an inverse ‘paradox of enrichment’. This corroborates recent feeding studies of terrestrial arthropods [18,19] and is contrary to the predictions of Vasseur & McCann [5]. This discrepancy is explained by differences in the temperature dependencies of the biological rates. We assumed that the carrying capacity of the system decreases with temperature. Simultaneously, the half saturation density of the species relative to the carrying capacity increases with warming, decreasing the flux of energy to the top of the chain and stabilizing the dynamics. Vasseur & McCann [5] assumed the carrying capacity, the half saturation density and therefore also their ratio to be temperature independent. The parameter values of our system suggest that the growth rate of the basal species increases faster with warming than with the consumers’ metabolism. The increase in production outpaces the increasing metabolic demands of the consumers, enhancing the system's ability to keep energy at the lower trophic levels [5]. This reduces biomass oscillations. Also, the temperature dependencies of ingestion and metabolism [16,25] suggest that a species metabolism increases faster with warming than with its maximum ingestion, reducing its ingestion efficiency and thus biomass oscillations. Vasseur & McCann [5] discussed all possibilities but then assumed that warming induces faster increases in species metabolism than in basal species growth rate and the increase in ingestion to outpace the increase in metabolism. Together, this leads to the destabilization of the system they found. The parametrization of our study is well supported by empirical data [16,17,21,25], suggesting a broad generality of the results presented here. There are, however, cases where warming destabilizes population dynamics. Warming increased population oscillations of the rotifer Brachionus calyciflorus [36] and also induced the development of defensive spines [37]. Inducible defences thus might attenuate not only the detrimental effects of enrichment [33,35] but also the effects of temperature we found. Similarly, warming can disrupt species interactions [38] and thus dynamics in many ways, for example via changing developmental schedules [39] or dissimilar range shifts [40]. Our model is based solely on energetic considerations and does not account for other effects that can modify a system's response to warming.

At high temperatures, the metabolism of the consumers exceed their ingestion rates; so their metabolic demands are higher than the energy gained by ingestion. In consequence, they can be surrounded by prey but starve to death. This phenomenon was observed in terrestrial [18,19] and aquatic [8] microcosm experiments, where high trophic level species were found to be at risk of starvation at high temperatures. A three-species laboratory system involving plankton was destabilized at a high temperature [41,42]. The data indicate no oscillations though, and temperature-induced changes of population rates are likely to have led to consumer starvation [42]. Moreover, increased risk of starvation might help to explain the warming-induced shift towards smaller species in aquatic systems [43,44]. Through changing size distributions, warming can indirectly have profound effects on species communities and ecosystem functioning (see Brose et al. [45] and citations within).

(b). Interactive effect of enrichment and warming

Fertilization and warming together have interactive effects on the dynamics of the food chain. At low temperatures, warming counteracts the degrading effects of enrichment: both the onset of the oscillations and the occurrence of extinctions connected to increasing fertilization are delayed. Kratina et al. [46] corroborate our findings and showed for pond mesocosms that fertilization destabilized chlorophyll biomass dynamics at ambient temperature but not under three degrees of warming. Interestingly, this stabilizing effect of a small amount of warming was observed in a temperate seasonal environment with an annual range of about 20°C in daily average temperature. Moreover, Shurin et al. [47] found a negative interaction between nutrient content and warming in the experimental ponds: warming reduced the effects of eutrophication. A study of a host–parasitoid community, however, showed no interactive effect of temperature and nitrogen levels [48]. This might be due to the different nature of host–parasitoid feeding relationships and their different body-size structure. We found that the rescuing effect of temperature was more pronounced when the consumers were larger than their prey. Larger species are more susceptible to the effect of temperature on their biological rates. A fundamental difference between terrestrial (without interactive effect) and aquatic (with interactive effect) systems is not supported by our data because the parametrization of the model incorporates data of different ecosystems.

At high temperatures, higher fertility counteracts the detrimental effects of warming. Fertilization increases the attack efficiency of the consumers and can thus save species from warming-induced starvation. In size-structured communities, this rescuing effect is delayed to higher fertilization levels. The biological rates of large species react more strongly to warming and so need more fertilization to antagonize its effect. Laboratory studies could test this model prediction, but it should be kept in mind that at different temperatures, varying resource quality affects small species differently than larger species [49].

The increasing maximum feasible carrying capacity with warming is a sign for a top-down component in the effect of warming. Warming has been shown to strengthen top-down control in food webs [46,50,51], explaining the increase in the maximum carrying capacity. Also, warming has stronger effects on larger species. This increases the maximum feasible carrying capacity in size-structured food chains. Its slight decrease at high temperatures is caused by the curve of the maximum ingestion (maximum around 30°C). The decreasing maximum consumption at higher temperatures accelerates the decrease of the species' ingestion efficiency and decreases the maximum feasible carrying capacity after its maximum.

5. Conclusions

In this study, we show that it is important to understand the interactive effects of drivers of global change. On the basis of our simulations, we expect climate change to have different effects on nutrient-poor and nutrient-rich communities, and nutrient enrichment to act differently in different climates. Warming in both nutrient-poor and nutrient-rich communities generally decreases biomass oscillations and stabilizes population dynamics, with nutrient-poor communities being more stable at low temperatures than their nutrient-rich counterparts. At high temperatures, however, consumers in nutrient-poor communities run a risk of starvation because of an unfavourable ratio of ingestion to metabolism. This does not happen in nutrient-rich communities within the temperature range we simulated. Both the stabilizing and the destabilizing effect of increasing temperatures are more pronounced when the consumers are larger than their prey. Consequently, nutrient-poor biomes are fragile, and, especially, large consumers are at risk of starvation when temperatures increase. Nutrient-rich systems are stabilized by increasing temperatures. Enrichment has different effects on communities in cold and warm environments. In cold climates, nutrient enrichment has the detrimental effects described by the ‘paradox of enrichment’. This harmful impact of nutrient loading is attenuated by an increasing body-size structure in the food chain. Hence, large top consumers of cold climates are less prone to extinction by nutrient enrichment than small consumers. In warm environments, increasing nutrient levels save the consumer species from starvation, and we observe a beneficial effect of nutrient enrichment. Increasing consumer body masses delay the onset of this rescuing effect of enrichment. Therefore, a small body size is advantageous for consumers at high temperatures, but this advantage is lost with increasing enrichment.

With our simulations, we have taken an important step to disentangle the effects of two main direct drivers of global change. We have shown that the combined effects of warming and nutrient enrichment are far from trivial and can, depending on the situation, be supportive or detrimental for the stability of food chains. Increasing body-mass ratios generally accentuate the effects of changing temperatures. This knowledge will help us to develop conservation measures that are tailored to the specific conditions of the species environment.