Climate change effects on macrofaunal litter decomposition: the interplay of temperature, body masses and stoichiometry

Abstract

Macrofauna invertebrates of forest floors provide important functions in the decomposition process of soil organic matter, which is affected by the nutrient stoichiometry of the leaf litter. Climate change effects on forest ecosystems include warming and decreasing litter quality (e.g. higher C : nutrient ratios) induced by higher atmospheric CO₂ concentrations. While litter-bag experiments unravelled separate effects, a mechanistic understanding of how interactions between temperature and litter stoichiometry are driving decomposition rates is lacking. In a laboratory experiment, we filled this void by quantifying decomposer consumption rates analogous to predator–prey functional responses that include the mechanistic parameters handling time and attack rate. Systematically, we varied the body masses of isopods, the environmental temperature and the resource between poor (hornbeam) and good quality (ash). We found that attack rates increased and handling times decreased (i) with body masses and (ii) temperature. Interestingly, these relationships interacted with litter quality: small isopods possibly avoided the poorer resource, whereas large isopods exhibited increased, compensatory feeding of the poorer resource, which may be explained by their higher metabolic demands. The combination of metabolic theory and ecological stoichiometry provided critically important mechanistic insights into how warming and varying litter quality may modify macrofaunal decomposition rates.

1. Introduction

Two aspects of climate change [1], warming and elevated atmospheric CO₂ concentrations, can both influence soil organisms and their critically important ecosystem function of litter decomposition [2]. First, warming affects all levels of biological organization from individuals up to communities [3,4], because it directly accelerates the metabolic rates and biochemical processes of organisms as conceptualized by metabolic theory [5,6]. Eventually, this implies that warming should accelerate decomposition rates. Second, elevated atmospheric CO₂ concentrations increase the carbon content of plant tissues [2]. Ecological stoichiometry describes how the macroelements carbon (C), nitrogen (N) and phosphorus (P), and their ratios are critical for organisms to build biological structures and regulate physiological processes [7,8]. Interestingly, most animals need to maintain an elemental homeostasis, and thus stoichiometric mismatches between consumers and their resources, as caused by higher atmospheric CO₂ concentrations, can lead to decreased (avoidance) as well as increased (compensatory) levels of herbivory [9]. Moreover, these stoichiometric mismatches can strongly interact with species’ body masses in driving the strength of herbivory [9]. In consequence, the importance of ecological stoichiometry for decomposition processes was recognized [10,11] and related to relationships between stoichiometric litter quality and decomposer abundance [12]. However, mechanistic insights into how warming and modified litter stoichiometry interactively affect decomposition rates are still lacking [10,13].

The decomposition of litter depends on the interaction (trophic and non-trophic) of the microflora (bacteria and fungi) with primary and secondary decomposers [14–16]. Among these, the larger decomposers such as earthworms, millipedes and woodlice (macrofauna henceforth) contribute by consuming leaf litter (colonized by microflora), thereby shredding it into finer pieces and mixing the leaf fragments with other layers and components of the forest floor habitat [14–16]. These processes increase the leaf litter accessibility to the microflora and smaller decomposers [14–16]. Thus, the presence and activity of the macrofauna is crucially important for the energy transfer and decomposition speed of soil organic matter [14,16–18]. Previous climate change studies on macroarthropods concentrated on behaviour [19], physiology [20], life-history traits combined with resource quality [21–23], population density and phenology [24] or habitat specification and geographical distribution patterns (reviewed by David & Handa [25]). Quantitative predictions of how decomposer-feeding rates depend on warming and the lower stoichiometric quality of the litter resources have not been provided by previous studies.

In this study, we addressed how climate change alters decomposition rates by systematically varying temperature, decomposer body mass and litter quality in a laboratory experiment. By using the concept and methodology of nonlinear functional responses (nonlinear models relating feeding strength to resource density, see §2c) characterizing predator–prey interactions, we aimed to provide a novel mechanistic understanding of decomposer–litter feeding interactions. According to metabolic theory, we addressed whether consumption depends on (i) decomposer body mass, and (ii) temperature. While metabolic theory does not assume any relationship of feeding interactions with resource quality, stoichiometric theory suggests either compensation or avoidance if consumption rates on the poorer resource are increased or decreased, respectively. Furthermore, we aimed to address the entirely novel question of how these metabolic and stoichiometric constraints interact in determining decomposition. We used the parameters of the functional response, attack rate and handling time, to reveal a mechanistic understanding of decomposer feeding under the influence of climate change.

2. Methods

(a). Experimental design

We quantified the feeding rates of a common terrestrial woodlouse, Oniscus asellus L. (Isopoda: Oniscidae) across a full-factorial combination of three levels of environmental temperature (10°C, 15°C and 20°C) with a poor (hornbeam: Carpinus betulus L.) and a good litter resource (ash: Fraxinus excelsior L.). Litter quality was judged by the stoichiometric contents of the leaf species (see §2b). For each of these combinations, 18 trials across a continuous size range from small to large isopods (11.1–130.4 mg) were established leading to a total of 108 experimental units. Full-factorially replicated control units without animals exhibited only minimal leaf decay. Hence, a significant influence of micro-organisms on the leaf decay in our feeding experiments could be excluded.

We used glass jars (6.3 cm diameter, 7.5 cm height) as experimental units. Each jar had a 2 cm layer of plaster at the bottom to provide constant moisture during the experiment. Jars were covered with gauze mesh (100 µm) to allow gas exchange. Habitat structure was provided by 1 g (dry mass) of artificial leaves made of plastic cloth. A pre-test assured that these artificial leaves were not consumed by woodlice. Our experiment ran for a total of 115 days with a day–night rhythm of 12 L : 12 D in thermostatically controlled incubators and a relative air humidity of 70 per cent (±10%). In spring 2011, woodlice were collected in a deciduous forest and kept in closed plastic boxes at 15°C. Woodlice were weighed before and after the experiment to calculate the average individual body masses for all experimental units. All weight measurements were performed with a precision scale (LE225D, d = 0.01 mg, Sartorius AG, Göttingen, Germany). Three woodlouse individuals were placed in each experimental unit. Individuals were distributed across experimental units to minimize within-unit variation of body mass while maximizing the range in body masses across experimental units. Moreover, we ensured that a similar body-mass range was realized for each treatment combination of temperature with litter quality. Pilot studies on woodlouse consumption allowed calculation of the initial litter biomasses per experimental unit depending on consumer body mass, temperature and resource quality. Thus, initial litter density differed across treatments, which was necessary to enable robust fits of functional-response models to data with initially strong declines and subsequently saturating decreases. However, effects of these initial differences on their parameters (attack rate and handling time) are unlikely (see §4). On the basis of these relationships, we started with different initial litter biomasses per treatment (a range of 9.8–145.6 mg m⁻² for ash and 7.1–60.1 mg m⁻² for hornbeam; variation according to temperature and woodlouse body mass).

Leaf litter and plaster were moistened with water every day. Experimental units were aligned in the incubators in a random rotation after daily moistening to avoid any blocking effects. Dead animals were replaced, and faeces were removed daily to ensure that litter consumption was not influenced by fluctuating isopod numbers, necrophagic or coprophagic feeding [22]. During the experiment, leaf litter weights were measured every third day for each replicate independently to monitor the decay in litter biomass. Prior to weighing, experimental units were acclimatized for 1 h to the weighing room conditions that were held constant for the entire experimental time (relative air humidity 62 ± 3%, temperature 24.5 ± 1°C). All litter weights are fresh weights (litter was not dried prior to weighing), but note that it is not equivalent to the fresh weight of green leaf tissue.

(b). Litter material and quality

Litter material was obtained from deciduous forest stands located in the northeastern part of the Hainich National Park, Germany. Freshly fallen leaves were collected in autumn 2010. Litter was air-dried and separated into species. Woodlice prefer decomposed over freshly fallen leaf litter ([22] and citations therein). Thus, the sorted leaf material was exposed to natural conditions for eight weeks in open plastic vats (aperture: 0.29 m²) to ensure abiotic conditioning, including leaching and physical breakdown. Subsequently, the leaf litter was defaunated for 3 days at 60°C and stored at room conditions before usage.

Analyses of litter quality were based on two samples per species, each sample pooled three randomly taken leaves. Leaf sample preparations and analyses of initial nutrient concentrations were carried out according to published protocols [26]. Concentrations were measured as millimol per gram dry weight. A recent study demonstrated that woodlouse abundance is positively correlated to litter contents of calcium (Ca) [12]. Thus, we analysed the contents of carbon (C), nitrogen (N), phosphorous (P) and calcium (Ca).

In our study, nutrient concentrations in ash were: N = 1.37, P = 0.03 and Ca = 0.66 (mmol g⁻¹). These contents were higher than those in hornbeam: N = 0.80, P = 0.02 and Ca = 0.59 (mmol g⁻¹). The corresponding ratios to carbon (C) contents were 27.24 C : N and 1176.84 C : P for ash versus 47.10 C : N and 1816.55 C : P for hornbeam. Together, these stoichiometric data indicated that ash should be a better resource than hornbeam.

Several studies suggested that other chemical compounds of leaf litter such as lignin, cellulose and phenolic contents may affect the accessibility of leaf resources to decomposer animals [17,27]. Thus, it might be anticipated that decomposer feeding rates could respond to these leaf characteristics. However, contents of lignin or polyphenols in ash and hornbeam are so low [18,28,29] that differences among the two resources should be negligible in our study. Moreover, isopods are well adapted to tolerate phenolic litter contents [17,22]. Hence, these non-stoichiometric characteristics of the leaf resources should not account for the results presented here, though our approach would be flexible enough to incorporate these additional indicators of litter quality.

(c). Functional responses as mechanistic models of nonlinear interaction strengths

The functional response describes the per capita consumption rate F_ij of a consumer i in dependence of the density, N_j, of its resource j:

2.1

where a_ij is the per capita attack rate (also instantaneous rate of successful capture) and h_ij is the handling time needed to ingest and digest a resource unit [30]. Here, we extend this concept to decomposer–detritus interactions and replace resource abundance by biomass density of litter to predict quantitative decomposition rates.

Many biological rates such as attack rate, a_ij, and handling time, h_ij, follow power–law relationships with organism body mass, m_i (gram fresh weight), and exponential relationships with temperature, T (K) [5,6], expressed as an extended Arrhenius term [31,32]:

2.2

and

2.3

where h₀ and a₀ are normalization constants at temperature T₀ (15°C = 288.15 K equal to the average of our temperature gradient), s_h and s_a are the allometric scaling exponents for handling time and attack rate, respectively, E_h and E_a are the activation energies (eV) for handling time and attack rate, respectively, k (1 eV⁻¹) is Boltzmann's constant (8.62 × 10⁻⁵ eV K⁻¹) and T (K) is the absolute temperature. This allometric concept of species interactions has been implemented in simple model systems [31,33,34] and complex ecological networks [35].

(d). Statistical procedures

Data were analysed using the statistical program R (version 2.14.0) [36] with the additional package ‘emdbook’ [37]. Instead of varying the resource density similar to a traditional functional-response experiment, we used only one initial litter density per replicate and kept track of the decomposer feeding by measuring a highly resolved time-series. The statistical procedure, however, was the same as in traditional functional-response experiments using Rogers ‘random predator equation’ [38] as the integrated form of the functional response while correcting for decreasing prey density during the time of the experiment:

2.4

where N_e (Ind m⁻²) is the density of prey j eaten during the experiment, P is predator i's density (Ind m⁻²), τ is the experimental time (d), N_j is the initial prey density (Ind m⁻²), a_ij is the attack rate (m² d⁻¹) and h_ij is the handling time (d Ind⁻¹). Note that in our case N_e and N_j are expressed in mass (gram FW) instead of individuals.

We solved the recursive function (equation (2.4)) for final prey density N = N_j−N_e using nonlinear least square regressions (function ‘nls’ in R) yielding

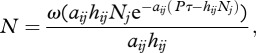2.5

where ω is the Lambert W function (see Bolker [37] and references therein for a detailed description). We applied the power-law and exponential relationships of handling time (h_ij) and attack rate (a_ij) with body mass and temperature, respectively, as described in equations (2.2)–(2.5).

We began by fitting the full functional-response model with all parameters (the scaling exponents of body mass and temperature in equations (2.2) and (2.3)) dependent on litter quality. Hence, the full model included different allometric exponents and activation energies for the two leaf resources, ash and hornbeam. Subsequently, we systematically simplified this model according to the lowest Akaike information criterion (AIC) [37] by removing the dependency of the parameters on litter quality. These AIC values (ΔAIC) describe the equality of models: models with ΔAIC < 2 are not distinguishable; ΔAIC values of 4–7 indicate slightly different models and models with ΔAIC >10 are severely different [37,39].

3. Results

(a). Litter decay

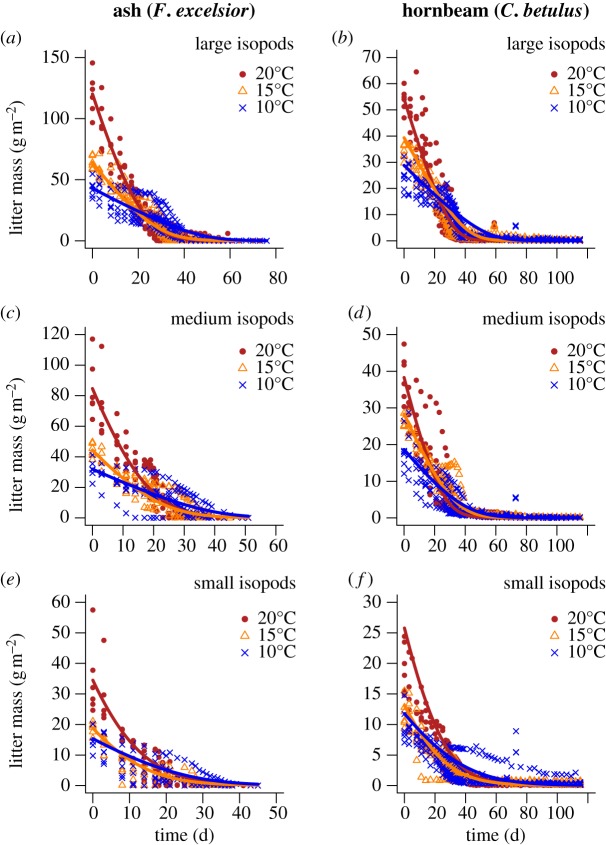
The amount of leaf litter exhibited a continuous and saturating decay in our experiment, which was terminated after 76 days for ash (figure 1a,c,e) and 115 days for hornbeam (figure 1b,d,f). As our control units without woodlice did not show a similar decay, we could assign these decreases in litter biomass to consumption by decomposers. Our experiment included a continuous body-mass spectrum of the woodlice (shown in discrete size classes as the three rows in figure 1 for clarity of presentation) and three different temperature levels (10°C, 15°C and 20°C; figure 1). This nonlinear decay in leaf litter resulting from feeding by woodlice was quantified by fitting type II functional-response models to the data (curves in figure 1). In general, the decline of litter mass became steeper with warming (e.g. red compared with blue curves, figure 1) and decomposer body mass (lower to upper row of figure 1), and it was shallower for the poor resource hornbeam (figure 1b,d,f) than for the good resource ash (figure 1a,c,e).

Figure 1.

Time-series of litter mass loss resulting from isopod consumption. Curves are based on the best-fitting functional-response model of isopods feeding on ash (a,c,e) and hornbeam (b,d,f) plotted as litter mass loss (g m⁻²) against time (day). We plotted panels with differently sized isopods: large (70–130 mg, (a,b)), medium (40–70 mg, (c,d)) and small (11–40 mg, (e,f)) to disentangle the size range of the isopods. (a–e) The overall trends for the three temperatures (blue line: 10°C, orange line: 15°C, red line: 20°C) are fitted to the six associated replicates. Note that we fitted a single model to the data while disentangling the data in this figure for clarity of presentation. See table 1 for model parameters.

(b). Choice of functional-response model

The lowest AIC value was achieved by the model with the mass-scaling exponent of the handling time, s_h, set independent of litter quality (table 1). Thus, this model has the same allometric exponent (s_h) for both litter resources (ash and hornbeam) and is more parsimonious than the full model. All other possible model simplifications were not warranted (ΔAIC > 2), suggesting that (i) attack rates and handling time depend on decomposer body mass and temperature, and (ii) litter stoichiometry affects the allometric and temperature relationships of attack rates, but only the temperature dependency of handling time. The subsequent results are based on this model.

Table 1.

Parameters of the functional-response model for decomposer interactions with a good (ash) and a poor resource (hornbeam): all parameters except for the mass-scaling exponent of handling time, s_h, depended on litter quality. Estimates of handling time, h₀ (d g⁻¹) and attack rate, a₀ (m² d⁻¹), allometric exponents s_a and s_h, activation energies, E_a and E_h and their s.e. were obtained by fitting the functional-response model (equation (2.5) including equations (2.2) and (2.3)).

litter species	parameter	estimate	s.e.	significance level (p)
	mass-scaling exponent of handling time (sh)	−1.65 × 10−1	4.83	<0.001
ash (Fraxinus excelsior)	normalization constant for handling time (h0)	2.07 × 102	2.61 × 101	<0.001
	activation energy of handling time (Eh)	−1.36	3.53 × 10−2	<0.001
	normalization constant for attack rate (a0)	2.74 × 10−4	4.46 × 10−5	<0.001
	mass-scaling exponent of attack rate (sa)	2.01 × 10−1	5.30 × 10−2	<0.001
	activation energy of attack rate (Ea)	2.30 × 10−2	6.71 × 10−2	>0.1
hornbeam (Carpinus betulus)	normalization constant for handling time (h0)	5.10 × 102	6.59e × 101	<0.001
	activation energy of handling time (Eh)	−8.60 × 10−1	4.77 × 10−2	<0.001
	normalization constant for attack rate (a0)	1.18 × 10−3	3.55 × 10−4	<0.001
	mass-scaling exponent of attack rate (sa)	7.45 × 10−1	8.42 × 10−2	<0.001
	activation energy of attack rate (Ea)	2.74 × 10−1	9.47 × 10−2	<0.01

(c). Functional-response parameters

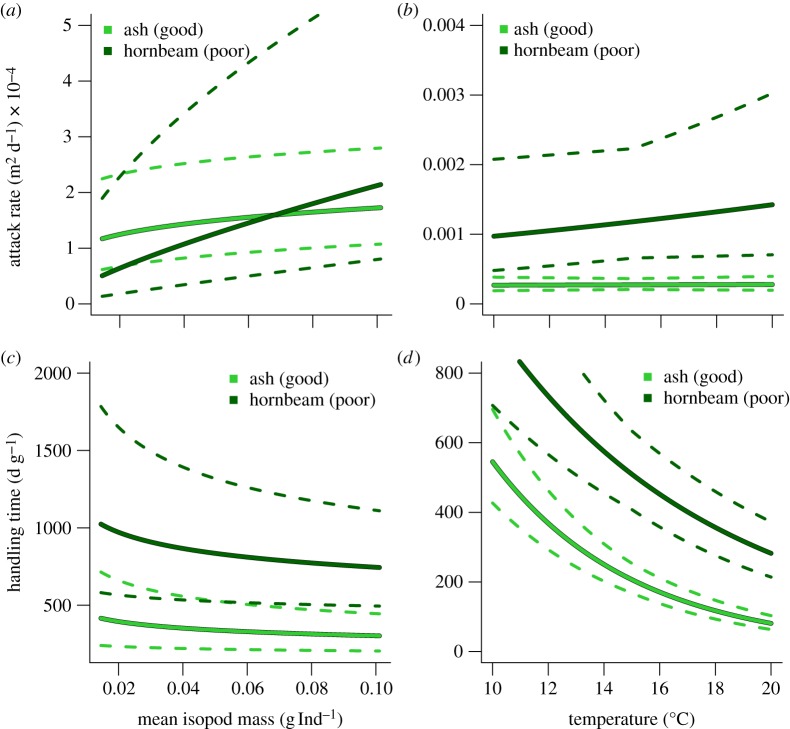
Consistent with our expectations, the most adequate functional-response model suggested significant dependencies of decomposer attack rates and handling times on decomposer body mass, environmental temperature and resource quality (table 1). The attack rates increased significantly with increasing isopod body mass (figure 2a) feeding on the good resource ash (power-law exponent: s_a = 0.201 ± 0.053, p < 0.001, table 1) as well as on the poor resource hornbeam (s_a = 0.745 ± 0.084, p < 0.001, table 1). These differences in attack rates between the two litter types are significant: the model with a single attack rate on both resources performed significantly worse (ΔAIC = 37.57, F-test for model comparison p < 0.001). Interestingly, the attack-rate curves across the isopod body-mass gradient intersect. This is because the allometric exponent for the poor resource is roughly 3.7 times larger than for the rich resource (figure 2a). While the attack rate on the poor resource (hornbeam) was lower than the attack rate on the good resource (ash) for isopods of small body masses, it was higher at higher body masses (figure 2a). This points to a compensatory feeding of large isopods, whereas small isopods seem to avoid the poor resource (hornbeam).

Figure 2.

Scaling of functional-response parameters: attack rates depended on isopod masses (a) and temperature (b); handling times depended on isopod masses (c) and temperature (d). The different leaf resources are indicated in light green (good) and dark green (poor). 95% CIs are shown by dashed lines. See table 1 for model parameters.

Following our expectations, attack rates increased with warming when feeding on the poor resource (hornbeam; activation energy E_a = 0.274 ± 0.095, p < 0.01, figure 2b and table 1). In replicates with the good resource (ash), however, attack rates did not increase significantly (E_a = 0.023 ± 0.067, p > 0.1, figure 2b and table 1). More generally, the attack rate on the poor resource (hornbeam; figure 2b) was higher than the attack rate on the good resource (ash; figure 2b). This difference increased with warming, suggesting accelerated compensatory feeding on the poor resource (hornbeam). Together, these results illustrate that effects on attack rates of consumer body mass, temperature and resource stoichiometry are not independent of each other.

Moreover, handling times decreased significantly with increasing isopod body mass (figure 2c). The power-law exponent of body mass was independent of litter species (s_h = −0.165 ± 4.827, p < 0.001, figure 2c and table 1). However, the normalization constants for handling time (parameter h₀ in equation (2.2) and table 1) differed for the litter species (figure 2c).

Handling time decreased with warming (figure 2d). The activation energies characterizing the strength of these relationships differed between litter types (good resource (ash): E_h = −1.363 ± 0.035, p < 0.001; poor resource (hornbeam): E_h = −0.860 ± 0.048, p < 0.001, table 1). In consequence, across our gradients in isopod body mass and temperature, we found that the handling time was higher on the poor resource (hornbeam; figure 2c,d) than the handling time on the good resource (ash; figure 2c,d). This was consistent with expectations, and the difference became more accentuated with warming (figure 2d).

4. Discussion

For the first time, this study successfully quantified consumption rates of terrestrial decomposers in the context of a consumer–resource functional response. Our analyses unravelled significant effects of decomposer body mass, temperature and resource quality on attack rates and handling times. Strikingly, litter quality interacted with metabolic constraints of body mass and temperature in driving decomposer-feeding rates, suggesting a synthesis of ecological stoichiometry and metabolic theory. This synthetic theory will be at the heart of obtaining a generalized understanding of how climate change will affect decomposition rates across ecosystems.

Consistent with metabolic theory [5,6], we found that attack rates increased and handling times decreased with (i) isopod body mass, and (ii) temperature. However, we also found surprising and entirely novel interactions with litter quality. Our results demonstrated higher handling time of the poorer resource, confirming assumptions that poorer resources require more time for digestion owing to longer biochemical processing of carbon-rich resources [21]. Moreover, we found a shift from possible avoidance of the poor resource by small isopods to compensatory feeding by large isopods, indicated by higher attack rates on the poor resource. However, lower attack rates of the small isopods on the poor resource might also be influenced by the limited foraging behaviour of the juveniles (e.g. slower moving speed or resource detection). Compensatory feeding implies increased feeding of poor resources to balance nutritional requirements for elements (e.g. N, P and Ca) that are necessary for the structural components of their body tissues. In addition to that, the resource quality (i.e. litter species) influenced the mass and temperature dependence of attack rates and the temperature dependence of handling times. These results imply an interplay among metabolic and stoichiometric constraints of decomposer feeding.

The power-law and exponential relationships with body mass and warming are consistent with similar scaling relationships found in predator–prey studies [31,33,34]. Moreover, similar relationships drive metabolic rates of invertebrates [40]. The inverse of handling time, the maximum consumption rate, describes consumers’ ability to balance their metabolic demands [41]. Consequently, we can compare handling times directly to the scaling of metabolic rates because they follow similar relationships [5,42]. The metabolism of isopods exhibits an activation energy E_i = 0.686 [40], which is substantially lower than the activation energies of handling times in our study when absolute values are considered (ash: E_h = 1.363; hornbeam: E_h = 0.86). This indicates that woodlouse consumption of both resources should increase more strongly with warming than metabolism. The resulting net energy gain suggests that warming may cause population growth of decomposers. These findings are contrary to predator–prey systems: a new meta-study on predator–prey functional responses reported that the activation energy of handling times for terrestrial invertebrates (E_h = −0.3) [41] is lower than that of metabolism (E_i ranging from 0.38 to 0.8) [40]. Hence, the increase in decomposer feeding rates with warming exceeded that of metabolism, whereas predators failed to cover their increasing metabolic demands with warming. Together, this may lead to increased population growth of decomposers owing to accelerated feeding and reduced top down pressure.

As for any laboratory study, potential caveats have to be discussed. We used initial litter densities that differed across treatments, which were necessary to enable robust fits of functional-response models. This came at the cost of potentially confounding temperature treatments with initial litter densities, and some of the conclusions drawn concerning effects of high temperature might have been driven by high initial litter density. However, this alternative explanation has the unlikely implication that higher consumption rates at high litter density (prior to intersection of curves in figure 1) would preclude saturation and lead to continuously higher consumption rates at low litter density (after intersection of curves in figure 1). Instead of this mechanistically dubious explanation, we interpret the steeper decreases in litter density at higher temperatures as a consequence of the increased metabolism of isopods forcing them to higher consumption.

5. Conclusions

Our results indicate an important interaction between decomposer body mass and compensatory feeding behaviour that may be explained by varying metabolic constraints. Small decomposers with a low metabolic rate exhibited lower attack rates on the poorer resource that can be interpreted as avoidance behaviour. By contrast, large decomposers showed compensatory feeding behaviour with a higher attack rate on the poorer resource. This may imply that small decomposers can avoid poor resources, whereas their substantially higher metabolic rate drives large decomposers into compensatory feeding behaviour. This argument is supported by the accelerated compensatory feeding on the poorer resource that is caused by warming. Ultimately, our results imply that metabolic theory and ecological stoichiometry interact with each other to constrain decomposition rates. Our results provide an important step towards an ‘overarching framework’ that integrates ‘from individuals to ecosystems’ [43] thus linking metabolic theory and ecological stoichiometry to a single synthetic theory. This multitrophic perspective will become critically important for predicting warming effects on population stability, species coexistence [41,44] and organic matter fluxes in food webs [45,46].

Because decomposition and climate change are multifactorial processes, other factors such as litter mixtures, species interference, moisture availability and dispersal should be of main concern in future studies testing the macrofaunal functional responses with warming [2,14,18,47]. Interestingly, warming may yield range shifts of macrofauna decomposers leading to increased invasions of prior-permafrost ecosystems of the cold biomes [47]. Contingently, our results suggest warming may accelerate decomposition rates, which could fuel carbon turnover and CO₂ release. Together, these findings suggest a possible positive feedback loop between warming and decomposition with the potential to push the world's ecosystems faster towards melting point.