Universal temperature and body-mass scaling of feeding rates

Abstract

Knowledge of feeding rates is the basis to understand interaction strength and subsequently the stability of ecosystems and biodiversity. Feeding rates, as all biological rates, depend on consumer and resource body masses and environmental temperature. Despite five decades of research on functional responses as quantitative models of feeding rates, a unifying framework of how they scale with body masses and temperature is still lacking. This is perplexing, considering that the strength of functional responses (i.e. interaction strengths) is crucially important for the stability of simple consumer–resource systems and the persistence, sustainability and biodiversity of complex communities. Here, we present the largest currently available database on functional response parameters and their scaling with body mass and temperature. Moreover, these data are integrated across ecosystems and metabolic types of species. Surprisingly, we found general temperature dependencies that differed from the Arrhenius terms predicted by metabolic models. Additionally, the body-mass-scaling relationships were more complex than expected and differed across ecosystems and metabolic types. At local scales (taxonomically narrow groups of consumer–resource pairs), we found hump-shaped deviations from the temperature and body-mass-scaling relationships. Despite the complexity of our results, these body-mass- and temperature-scaling models remain useful as a mechanistic basis for predicting the consequences of warming for interaction strengths, population dynamics and network stability across communities differing in their size structure.

1. Introduction

Feeding rates are closely related to interaction strengths [1,2], and thus any motivation for measuring interaction strengths, such as understanding the stability of populations and communities [3–6], the flows of energy in ecosystems [7] and the functional consequences of biodiversity loss [8], applies equally to estimating feeding rates. In particular, a mechanistic understanding of how temperature affects feeding rates will provide critically important information on the consequences of global warming for population and community characteristics [9–12]. In this study, we show how functional responses, i.e. quantitative models of interaction strengths, depend on temperature as well as consumer and resource body sizes.

Interaction strengths describe how changes in biomass of one species affect other species' biomass densities [13]. Although non-trophic interactions can be important drivers of population and community dynamics [14], important aspects of interaction strengths are driven by feeding interactions [2]. The strengths of these feeding interactions are highly variable across spatial and temporal gradients [15,16]. Functional responses capture some of this variability by describing how feeding rates vary with resource abundance (figure 1a,b): as such the common notion of a weak or strong interaction is resource-dependent and related to functional response parameters [4]. For example, high attack rates imply high feeding rates (all else being equal) and thus strong interactions. Hence, functional responses determine interaction strengths in analyses of consumer–resource population dynamics [17–20], the stability of complex food webs [20–23] and structural patterns of food webs [11,24,25].

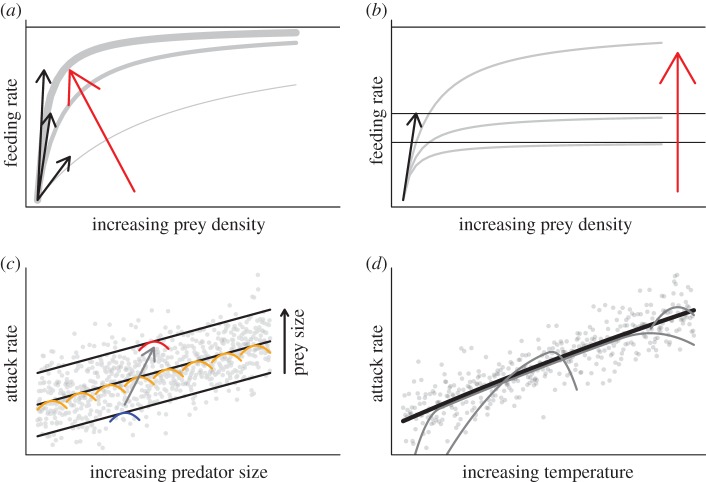
Figure 1.

Conceptual visualization of theoretical aspects. (a) Attack rates determine the initial increase in feeding rate at low resource abundance (aN, black arrows). At low resource densities, increasing attack rates (all else equal) correspond to higher feeding rates (red arrow). (b) Decreasing handling times lead to an increase in overall feeding rate (red arrow, horizontal lines correspond to maximum feeding rates F_max ∼ 1/h). Feeding rates additionally depend on consumer and resource body size (c) and temperature (d). On a global interspecific scale, the rates (here exemplified using the attack rate) increase linearly with consumer mass in a log–log space (c). Within particular taxonomic groups, hump-shaped relationships are expected (orange, blue and red humps). Assuming a constant resource mass and an increasing consumer mass leads to different optimal body-mass ratios forming a plethora of small humps along the line of the global model (orange humps). Assuming a constant body-mass ratio and an increasing resource mass leads to different optimal predator masses (grey arrow from the blue to the red hump). Similarly, species have different thermal windows (d). To detect these multiple overlaying humps, we adopted a nested statistical design that first investigates the global relationships and, in a second step, the humps as residual deviations from the global model.

Measuring a functional response requires sufficiently replicated feeding rates across a gradient of resource densities. Even for a small food web such as Broadstone Stream [26], comprising 131 species with 891 trophic interactions, quantifying functional responses for each of these interactions would be logistically impossible. Instead, systematic scaling relationships of functional responses with organism size [19,24,27] and temperature [11,28–30] can provide estimates of interaction strengths. Here, we present a novel and extensive analysis of the allometric and temperature scaling of functional responses, test their universality across ecosystems and metabolic types of species and check their consistency with theoretical expectations. These relationships will be, for example, useful for parametrizing models of community responses to biodiversity loss and environmental change [12].

(a). The anatomy of the functional response

The functional response describes the relationship between the per capita feeding rate of a consumer i, F_ij (individuals_i s⁻¹) and the density N_j (individuals_i m^{−2 or −3}), of the resource j being fed on. Density is measured in units of per metre squared or cubed, depending on whether the consumer is foraging on a surface or in a volume. The parameters of a functional response model (sensu Holling [31]) are attack rate, a_ij (m^{2 or 3} s⁻¹), and handling time, h_ij (s). Attack rates describe the initial increase in a functional response (figure 1a, black arrows), whereas handling time limits the maximum feeding rate (figure 1b, horizontal asymptotic lines), which yields a hyperbolic Holling type II curve [31]:

1.1

Biologically, handling time describes the time a consumer needs to fight, subdue, ingest [31] and digest a resource item [32]. The attack rate is the rate of successful attacks (also termed capture rate [33], instantaneous rate of successful search [31], maximum filtration rate [34] or maximum interaction strength [4]) and includes processes such as searching (e.g. movement), detection, encounter and success of the attack [27]. Some functional responses in our database exhibited a sigmoid shape (type III, not shown), where the attack rate increases with resource density, a ∝ N^q, with a nonlinearity described by q [21,35,36]. We followed Englund et al. [30] and used the attack rate at the half saturation density to include type III functional responses in our analyses.

(b). Body-mass dependence

Since the nineteenth century, biologists have reported biological rates to scale nonlinearly with organism body mass (i.e. allometric scaling) [37]. Allometric scaling of metabolic rates is perhaps the most widely studied [38–40], though other quantities have received considerable attention, e.g. growth rates, death rates and population abundances [38,39]. The size dependence of functional responses has been investigated for different specific taxonomic groups [36,41,42], but there is a lack of a unifying framework, and limited data collation over ecosystem types and physiological blueprints. In the following, we develop a null hypothesis for the allometric relationships for handling time and attack rate.

Handling times: We recast the functional response following Koen-Alonso [33] to the form of

1.2

where F_ij,max = 1/h_ij (figure 1b, asymptotic lines) is the maximum feeding rate, and f_ij = a_ijN_j/(F_ij,max + a_ijN_j) is a non-dimensional feeding level taking values between 0 and 1 that describes the proximity to maximum feeding capacity of the consumer [43]. Handling time as used here is a phenomenological description, including both physical handling (i.e. attacking, overwhelming and chewing a resource) and digestion [32,44]. Metabolic theory suggests that metabolic rate scales with a 3/4 power law of body mass [38]. Therefore, to persist, a predator at least needs to balance its food intake rate (via F_ij) to the metabolic rate, meaning that F_ij,max should share scaling relationship with metabolic rate, which subsequently means that handling time should scale as

1.3

Besides the Metabolic Theory of Ecology, other frameworks invoke more flexible theories that predict exponents from 0.66 to 1 for metabolic rates [45,46], leading to a continuum of expectations for the handling time scaling in the range from −0.66 to −1.

Resource size naturally also influences handling time, as it takes longer to handle larger prey. Classically, many bioenergetic models [19,20,22,23] and older functional response studies [34] assumed that resource mass is linearly proportional to digestion time leading to an isometric scaling. However, there is a more complex interplay between the degree to which time is devoted to ingestion and the subsequent digestion of the resulting resource pieces [32]. In the extremes, assuming that resource mass is negligible for the consumer, handling time does not depend on resource mass. Overall, this means that the resource-scaling exponent is expected to be in the range from 0 to 1:

1.4

Attack rates describe the feeding rate at low resource density where handling time is negligible (F_ij → a_ijN_j for N_j → 0 [4]). As a null model, we assume that the possibility of encounter of two individuals (consumer and resource) is proportional to the area or the volume that is searched per unit time while ignoring any movement of the resource (zero resource mass scaling) [47]. Following McGill & Mittelbach [47], we assume the speed of movement to scale with a 1/4 exponent [39]. The area or volume that is searched per unit time is given by the locomotive rate (distance per time, see exponent for movement) and (i) the visual search width for surface animals (assumed proportional to body length: 1/3 exponent) or (ii) the visual search area by animals hunting in volumes (assumed proportional to squared reaction distance: two-third exponent) [47]. Subsequently, the expected scaling exponents for consumer mass become 0.58 (1/4 + 1/3) and 0.92 (1/4 + 2/3) for consumers in two- and three-dimensional environments, respectively [47]. The visibility of the resource increases with resource body mass with a 1/3 to a 2/3 power law in dependence if the environment is two- or three-dimensional [47]. Moreover, typically environments are not purely two- or three-dimensional due to habitat structure [47] leading to a broad continuum of possible slopes:

1.5

Analogies similar to speed of movement and reaction distance/area apply for animals with different feeding strategies (e.g. filtrators, sit-and-wait, nocturnal or olfactorial consumers); different exponents may naturally be achieved. Furthermore, this simple null hypothesis neglects all behavioural aspects.

(c). Temperature dependence

Biological rates depend not only on body masses but also, as all chemical reactions, on temperature. The Metabolic Theory of Ecology [38] extends the allometric descriptions of metabolic rate, I, with the addition of the Arrhenius temperature dependence [48–50] such that: 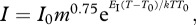where E_I (eV) is the activation energy describing the exponential increase in the metabolism with temperature, k (eV K⁻¹) the Boltzmann constant, T (K) is the absolute temperature and T₀ sets the intercept of the temperature relationship at T₀, rather than at zero Kelvin [11,29]. By applying the same idea to the handling time and attack rate relationships, equations (1.4) and (1.5) yield

1.6

and

1.7

where E_h and E_a refer to the activation energy of handling time and attack rates, respectively. Gillooly et al. [50] argue that for metabolic rates the expected range of activation energies fall in the range of 0.6–0.7 eV, as this is the average of all biochemical reactions. For simplicity, many studies normalize or test their data using the value of 0.65 (see Brown et al. [38] for an example). Other theories predict a larger range of possible activation energies ranging from 0.46 to 0.96 [51]. As the maximum feeding rate is the inverse of the handling time (see above), we expect an activation energy of from −0.96 to −0.46 for handling time. As there is no conceptional background for the temperature dependence of attack rate or movement, we use as a null expectation the average biological activation energy of 0.65 eV (ranging from 0.46 to 0.96 [51]) for the attack rate.

(d). Deviations from the global models: going to the extremes

Besides the log-linear ‘global’ models, many case studies document hump-shaped relationships for attack rates with consumer size or body-mass ratio [36,41,52–55] (figure 1c, humps). Also, humps with increasing temperature were reported for attack rates [56] and maximum feeding rates [57] as summarized by Englund et al. [30]. Especially, for attack rates in dependency of the body-mass ratio, humps are often reported [36,41,52–54], whereas they appear only in approximately 40 per cent of all studies for temperature [30]. Additionally, the parameters describing the humps such as optimal foraging mass ratio vary across consumer–resource pairs [52] and the shape of the humps with increasing temperature (also known as thermal windows [58,59]) even varies with ontogenetic stage. Moreover, these humps are hidden within a large scatter of data points (figure 1c) and can vary in width (figure 1d). Here, analyses of hump-shaped relationships were constrained to studies that were designed to investigate scaling with body mass or temperature.

(e). Expectations

We compiled and analysed the largest database of functional responses currently available. We investigated how handling times and attack rates depend on consumer mass, resource mass and temperature. Moreover, we collected data on the metabolic group of the consumers (endotherm vertebrates, ectotherm vertebrates, invertebrates and unicells), and the ecosystem types (freshwater, marine and terrestrial ecosystems), following Brose et al. [60]. With this dataset, we test the scaling relationships of attack rates and handling time with temperature, consumer and resource masses as described earlier. These analyses are carried out at global (pooling all data) and local resolutions (more fine-grained analyses).

2. Methods

(a). Data collection

We searched ISI Web of Science and Google Scholar for the keywords ‘functional response’, ‘feeding rates’ with ‘prey/resource density’ and ‘non linear interaction strength’. Additionally, we searched bibliographies of found publications for further literature. We included studies that provided information only about (i) temperature; (ii) consumer and resource identity; and (iii) the spatial size of the experimental units. If information on body masses was not provided, we searched for secondary literature to find average length or body masses of the species. If only length was given, we used allometric equations to calculate the mass of the organisms according to Peters [39]. We used studies that provided attack rates and handling times of type II and type III functional responses estimated via (i) Holling's functions [31], (ii) Rogers random equation [61,62], or (iii) time-series analyses (mainly occurring in Hansen et al. [34]). If a study included data that were not statistically analysed to provide values for attack rates or handling times, we refitted the data with Rogers random equation or Holling's function. The final functional response database included 648 functional responses from 86 studies including unicells (n = 22), invertebrates (n = 472), ectotherm vertebrates (n = 143) and endotherm vertebrates (n = 11) from marine (n = 86), freshwater (n = 273) and terrestrial (n = 288) ecosystems.

(b). Statistical procedures

We used the log-linear version of (1.6) and (1.7) yielding

2.1

and

2.2

to fit a linear model to the data. Units were K for T, mg for m, s for h_ij, m^{2 or 3} for a_ij and we set T₀ to 293.15 K. We applied a ‘random intercept model’ [63] using mixed effect models with a maximum-likelihood estimator (function ‘lme’ with ‘method = ML’ within the ‘nlme’ package [64] of the statistics program R [65]). To correct for differences between studies such as length of the experiment, moisture, pH, experimental procedure and the foraging dimension (two- versus three-dimensional), we used the study identity as a random factor in the handling-time model and a nested formulation of dimension/study identity as random factors in the attack-rate model. However, we could not apply a random intercept and slope model, because none of the studies included all three continuous variables (body mass of resource, consumer and temperature), and the majority of studies only provided few data points.

We fitted (2.1) and (2.2) starting with a model including free allometric slopes and a free activation energy and a full model including interactions of metabolic ecosystem type (including all possible combinations of ecosystem types with species metabolic types) with allometric slopes and activation energy. Then, we used the automated ‘stepAIC’ function [66]. This function adds or deletes automatically interactions or parameters from or to a model until the lowest AIC (Akaike information criterion) is reached, in order to find the most parsimonious model. We started with both models described earlier to avoid a local minimum.

Subsequently, we tested for hump-shaped deviations from the global model in allometry (figure 1c) and temperature (figure 1d) dependence. These deviations are assumed to occur at a narrow taxonomic range in allometry [52] and (at least for metabolism and growth) for temperature [58,59]. Moreover, these humps may be overlaid by the general global intra-taxonomic trend (figure 1c). Hence, we used only studies that were designed to investigate allometric or temperature scaling of functional response parameters. Hence, we saved residuals of the most parsimonious models and built (i) subsets only including studies that measured functional responses across a body mass gradient of a close taxonomic group with at least five measurements, and (ii) a subset including studies measuring functional responses on a temperature gradient with at least four functional responses. We fitted polynomial models, including a linear and a quadratic term to these subsets:

2.3

and

2.4

where ɛ_m and ɛ_T are the residuals from the body mass studies and from the temperature models, respectively, R is the consumer–resource body-mass ratio and T_C is the temperature in degree Celsius. We used the body-mass ratios instead of consumer or resource masses to normalize the independent variable. To correct for different linear deviations from the global intraspecific model while focusing on hump deviations, we applied a mixed effects model to the residual data. We used a ‘random intercept and slope model’ ([63], with ln(R) or T_C as random slope) using mixed effect models with a maximum-likelihood estimator (function ‘lme’ with ‘method = ML’ within the nlme package [64] of the statistics program R [65]) and the identity of the study as the random effect influencing the intercept and the linear slope of the model.

3. Results

(a). Global relationships

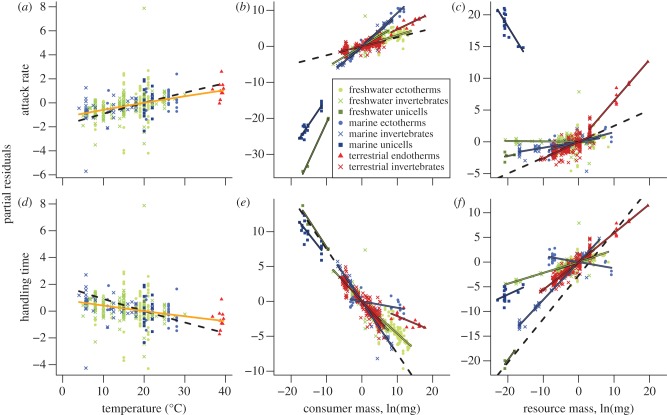
Across the entire dataset, higher temperatures were associated with higher attack rates and lower handling times (figure 2 and table 1). There was no evidence that the temperature scaling varied among metabolic and ecosystem types. Interestingly, attack rates increased less steeply than expected (figure 3a and table 1) and handling times decreased less than expected (figure 3d and table 1).

Figure 2.

Effects of temperature, consumer body mass and resource body mass (x-axis) on attack rates (a–c) and handling times (d–f) as estimated by the most parsimonious models. The y-axis refers to the partial residuals that only show the effect of either temperature, body mass of the consumer or body mass of the resource while being corrected by the other effects. The black dashed lines display the expected null hypothesis and the solid orange line shows the regression of rate versus temperature; the group-dependent regressions are explained in the legend (b).

Table 1.

Estimates for the within taxonomic group models. Total number of data points is n = 648.

ecosystem	metabolic group	ΔAIC	n(subgroup)	intercepta	p(intercept)	E	p	bi/ci	p	bj/cj	p
attack rate models
only slopes model
all	all	68.80	648	−16.82	<0.001	0.44	<0.001	0.47	<0.001	0.15	<0.001
full model
freshwater	ectotherm vertebrates	11.52	115	−11.69	<0.001	0.51	0.4554	0.31	<0.001	0.15	<0.001
	invertebrates		154	−19.03	<0.001	0.53	<0.01	0.58	<0.001	−0.01	0.9304
	unicells		5	−17.54	0.3795	−37.66	0.189	0.97	0.3325	0.03	0.9584
marine	ectotherm vertebrates		28	−18.77	<0.001	0.40	0.7831	0.93	<0.001	0.15	0.1719
	invertebrates		41	−21.29	<0.001	0.38	0.5283	0.85	<0.001	0.09	0.5323
	unicells		17	−28.13	<0.001	1.45	0.7918	1.45	<0.001	−0.91	<0.001
terrestrial	endotherm vertebrates		11	−20.99	0.1073	1.61	0.7532	0.48	0.1462	0.64	0.0818
	invertebrates		277	−16.27	<0.001	0.40	<0.001	0.24	<0.001	0.26	<0.001
most parsimonious model
			648			0.42	<0.001
freshwater	ectotherm vertebrates	0	115	−11.71	<0.001			0.31	<0.001	0.15	<0.001
	invertebrates		154	−19.09	<0.001			0.58	<0.001	−0.01	0.9176
	unicells		5	3.09	0.8089			2.12	<0.001	0.11	0.8299
marine	ectotherm vertebrates		28	−18.77	<0.001			0.93	<0.001	0.15	0.1685
	invertebrates		41	−21.23	<0.001			0.85	<0.001	0.09	0.5211
	unicells		17	−27.68	<0.001			1.45	<0.001	-0.91	<0.001
terrestrial	endotherm vertebrates		11	−18.19	<0.001			0.47	0.1489	0.65	0.0724
	invertebrates		277	−16.27	<0.001			0.24	<0.001	0.26	<0.001
handling time models
only slopes model
all	all	122.94	648	8.30	<0.001	−0.27	<0.001	−0.48	<0.001	0.34	<0.001
full model
freshwater	ectotherm vertebrates	8.83	115	5.69	<0.001	−0.28	0.5603	−0.46	<0.001	0.25	<0.001
	invertebrates		154	9.18	<0.001	−0.42	<0.01	−0.55	<0.001	0.22	<0.001
	unicells		5	10.43	0.476	−3.58	0.8556	−0.90	0.2232	0.98	<0.05
marine	ectotherm vertebrates		28	4.54	<0.01	1.15	0.2289	−0.02	0.8866	−0.14	0.0748
	invertebrates		41	9.92	<0.001	−0.72	0.877	−0.76	<0.001	0.76	<0.001
	unicells		17	0.47	0.9267	0.41	0.8978	−0.66	<0.05	0.33	<0.05
terrestrial	endotherm vertebrates		11	0.48	0.9582	2.40	0.5189	−0.20	0.4104	0.56	<0.05
	invertebrates		277	9.61	<0.001	−0.27	<0.001	−0.56	<0.001	0.56	<0.001
most parsimonious model
			651			−0.30	<0.001
freshwater	ectotherm vertebrates	0	115	5.69	<0.001			−0.46	<0.001	0.25	<0.001
	invertebrates		154	9.25	<0.001			−0.56	<0.001	0.22	<0.001
	unicells		5	12.48	0.1486			−0.78	<0.05	0.99	<0.01
marine	ectotherm vertebrates		28	4.57	<0.01			−0.09	0.4536	−0.13	0.112
	invertebrates		41	10.38	<0.001			−0.76	<0.001	0.76	<0.001
	unicells		17	0.72	0.8828			−0.64	<0.05	0.33	<0.05
terrestrial	endotherm vertebrates		11	6.84	<0.05			−0.21	0.3698	0.59	<0.01
	invertebrates		277	9.62	<0.001			−0.56	<0.001	0.56	<0.001

^aThe intercept is ln(a₀) for attack rates and ln(h₀) for handling times.

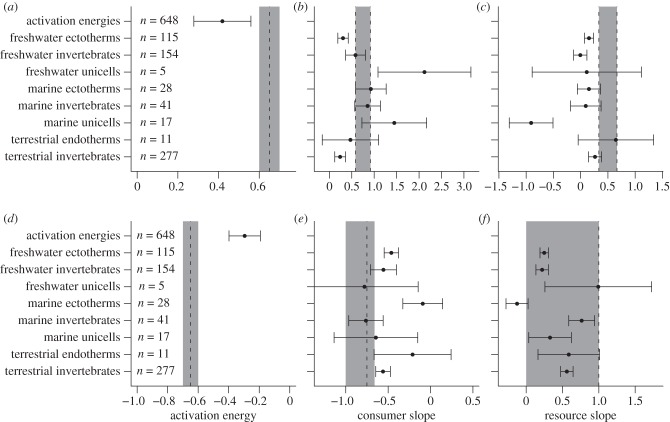
Figure 3.

(a–c) The estimated activation energies and allometric exponents for attack rates and (d–f) handling times. The points denote the estimate whereas the whiskers denote the 95% confidence values. The dashed vertical lines represent the different model expectations based on the Metabolic Theory of Ecology [38] and the foraging theory of McGill & Mittelbach [47]. Systematic mixing of these predictions is indicated by grey areas.

Also across the entire dataset, increases in consumer mass were associated with increased attack rates and decreased handling times (figures 2 and 3b,e). The scaling exponents, however, differed across metabolic and ecosystem types (figure 3b,e and table 1). The mass scaling exponents of freshwater ectotherms and unicells and terrestrial invertebrates deviated from expectations (0.58 and 0.92; figure 3b). Moreover, scaling exponents for consumer mass and handling time were lower than expected for freshwater and marine ectotherms and terrestrial invertebrates (figure 3e).

The scaling of attack rates with resource mass was most often shallower than expected (figures 2c and 3c), marine unicells exhibited significantly negative exponents. The exponent of terrestrial endotherms was most consistent with the prediction of 0.33 to 0.66, and the exponent distributions of the four other groups overlap the predicted range (figure 3c). All exponents estimated for the dependence of handling time on resource mass were lower than unity, and, as expected, we found a continuum of possible slopes ranging from 0 to 1 (figure 3f and table 1).

Together, these results suggest some general trends: (i) temperature influences functional response parameters less strongly than expected by metabolic theory, (ii) attack rates exhibited exponents deviating form theoretical predictions, and (iii) handling times decreased less with consumer mass and increased less with resource mass than expected.

(b). Local relationships

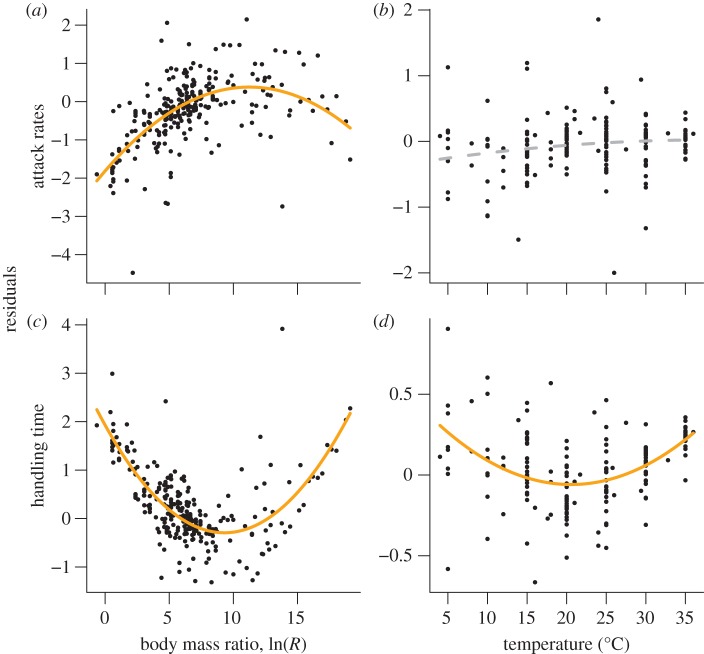
Attack rates followed hump-shaped relationships with increasing consumer–resource body-mass ratios (figure 4a, see legend for statistical outputs), whereas we found no significant deviation from the global model for the temperature dependence of attack rates (figure 4b). Handling times followed a negative hump-shaped relationship with increasing consumer–resource body-mass ratios (figure 4c) and temperature (figure 4d).

Figure 4.

Residual analyses of attack rates and handling times to identify nonlinear deviations (see figure 1c,d for a conceptional explanation). The exponent of the normalized residuals (residuals corrected for random effects of the consumer–resource pairs) is plotted as the dependent variable. (a) The attack rates exhibit hump-shaped relationships with consumer–resource body-mass ratios (residuals = −1.81** + 0.37** log(R) − 0.017* (log_n(R))²), (b) whereas attack rates do not deviate significantly from the global temperature model (residuals = −0.34^n.s + 0.02^n.s. T_C − 0.0003^n.s T_C²). The handling times follow a positive quadratic relationship with (c) body-mass ratios (residuals = 1.93*** − 0.48*** log(R) + 0.026*** (log(R))²) and (d) temperature (residuals = 0.51* − 0.055** T_C + 0.0013*** T_C²). The significance levels are ***p < 0.001, **p < 0.01, *p < 0.05, n.s. ≥ 0.05.

4. Discussion

Knowledge on the scaling of feeding interactions with species’ body masses and environmental temperature is crucial to explain and predict population stability and community persistence in nature. We analysed the currently largest database on functional responses including 648 entries from 86 studies. We found that functional responses followed universal scaling relationships with temperature, whereas body-mass dependencies, from analyses of diverse taxa ranging over nearly 20 orders of magnitude in body mass, varied among metabolic groups and ecosystem types. In addition to these results, more fine-grained residual analyses revealed hump-shaped relationships between (i) attack rates and handling times with consumer–resource body-mass ratios and (ii) handling times and temperature. Together, these results yield novel empirical relationships and scaling models relating consumer–resource interaction strengths to their body masses and the environmental temperature. These findings could fuel a new generation of population dynamic models. In addition, however, the systematic deviations from predictions also stress the need for novel mechanistic interaction models that go beyond simple and somewhat phenomenological metabolic considerations [47].

(a). Temperature dependence

Consistent with prior functional response studies [28,30], we found that the activation energies of attack rates (0.42) and handling times (−0.30) were lower than those found for metabolism (0.38–0.80 for invertebrates [67], 0.43–0.79 for unicells to mammals [50]). This suggests that feeding increases less strongly with temperature than metabolism, which supports prior conclusions that consumer biomass should decrease with warming [10]. Interestingly, this implies that warming should decrease interaction strengths at per capita (lower individual consumption rates relative to metabolism) and at population levels (lower consumer population densities). While these weaker interaction strengths may imply a higher stability of populations and more persistent communities [3,4,68], they may also cause consumer starvation [10,69].

Consistent with previous studies [30,56,57], our results suggest that the temperature dependence of functional response parameters is more complex than simple Arrhenius terms. While the positive quadratic deviation we found in the residual analyses for handling time supports these prior conclusions, we found no hump-shaped relationship of attack rates with increasing temperature. These and similar additional complexities found for metabolic scaling and growth rates [67,70] imply that temperature effects on organismic biology may go beyond simple thermodynamics [58,59]. Ultimately, more complex models accounting for biological processes under the influence of temperature need to be developed.

(b). The allometry

We found systematic scaling relationships of handling times and attack rates with consumer and resource masses. However, these empirical relationships differed significantly from predictions by simple concepts based on the allometry of metabolism and from more complex models based on visibility and movement. Focusing on the three groups that had the highest number of data points (n>100, terrestrial invertebrates, freshwater invertebrates and ectotherm vertebrates) reveals that all three groups exhibited exponents generally lower than expected by theory (0.58 for two-dimensional searchers to 0.92 for three-dimensional searchers; table 1 and figure 3 [47]). Also, the exponents for resource mass were lower than expected, only the exponent for terrestrial invertebrates was not different from 0.33. These two observations suggest that the scaling of attack rates with consumer and resource masses implies more than simple changes in movement speed, visual search width or area and visibility. One potential explanation for the disparity between theoretical predictions and empirical data could be that many of the studies included here added habitat structure and this may lead to the breakdown of the model predictions [47]. In addition to encounter, realized attack rates also depend on the success rates [27], and the interplay of these two components can yield hump-shaped relationships between attack rates and consumer–resource body-mass ratios [36,41,52]. Strikingly, our residual analyses confirmed these hump-shaped deviations from the allometric scaling models [36,41,52].

The handling times were expected to follow 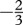to −1 power-law relationships with consumer mass [38,45,46]. We found that only half of the groups tested fall into this range, whereas the others were systematically higher. Interestingly, the groups represented by most data (n > 100, freshwater ectotherm vertebrates, invertebrates and terrestrial invertebrates; table 1) showed smaller exponents. We found a variety of exponents for the relationship between handling time and resource mass ranging from zero to unity. Traditionally, assuming two resource items each of 1 g will take the same time to handle as one resource of 2 g led to linear scaling models in functional response studies and theoretical models [19,20,22,23,34]. However, assuming digestion processes to be dependent (i) on the degree the resource is broken down into pieces or (ii) that digestion takes place only on the surface of the resource item, this relationship can be dampened. Moreover, handling not only includes digestion of the resource but also aspects of subduing that additionally could influence the exponent (see Jeschke et al. [32] for a detailed discussion on the components of handling time). Assuming that the time to subdue a resource is constant and independent of resource mass implies that it takes longer to handle two small resources than one large, because the time to subdue the resource is needed only once. Moreover, the large variation in the resource–mass slopes across the different combinations of ecosystem and metabolic types might be caused by substantial variation in morphological traits (e.g. external versus internal digestion, swallowers versus chewers) of the resource that is independent of allometry.

5. Conclusions

Altogether, our study enables a detailed understanding of the complex implications of warming for natural communities in experiments and field observations. The statistical models presented will also provide information for more detailed parametrizations of population dynamic [8,19–23,29] and topological [11,24] models that could be used to predict the effects of temperature change on ecological communities (but see Binzer et al. [71] for an applied example).

Moreover, the hump-shaped deviations from the global scaling models generalize the findings of recent studies [36,52,54,55,72] across ecosystem types. Interestingly, this more fine-tuned approach to predicting interaction strengths allows a more quantitative understanding of interaction strengths and the consequences of consumer loss for ecological communities and their functioning [73]. Future extensions of this approach may unravel systematic shifts in these humps such as those caused by different optimal body-mass ratios of consumers with different feeding strategies [36,52]. This will provide a novel mechanistic approach towards integrating phylogenetic constraints with allometric scaling of physiological parameters to predict species’ interaction strengths.

Our results have important implications for food-web structure and stability. Regarding food-web structure, the stronger temperature scaling of attack rate than handling time predicts a decrease in connectance with increasing temperature, assuming that consumers act independently to maximize the rate at which they gain energy [11], but see Lurgi et al. [74] for a review on this topic. Because a decrease in connectance is expected to stabilize population dynamics, we might expect, therefore, stabilizing effects of increases in temperature. Two other drivers of population stability and community persistence are (i) the ratio of the maximum feeding rate to the metabolic rate and (ii) the ratio of the half saturation density to the resource density of the system [19,20]. Our results imply that the ratio between the maximum feeding rate (the inverse of handling time, see §1 and Koen-Alonso [33]) and the metabolic rate should decrease with warming, which generalizes studies of terrestrial and marine arthropods [10,28,75] and suggests that population and food-web stability should increase [19,20]. Interestingly, our results also imply that the half saturation density (a⁻¹ h⁻¹, see Koen-Alonso [33]), expressing the efficiency of consumer attacks, decreases less steeply with warming (activation energy: −0.12) than population densities (activation energy: −0.71 [76]), which should also lower feeding rates. Both effects should lead to a strong decrease in interaction strength with warming as documented in a study of a rocky intertidal community [77]. Ultimately, this decrease in interaction strength may lead to consumer starvation [10,19,20], suggesting that higher trophic levels may be most prone to extinctions as shown in a microcosm study [69]. Our detailed analyses of how interaction strengths depend on temperature in size-structured systems may thus provide critically important predictions on the implications of climate change for natural ecosystems [12,71,78–80].