The yield of experimental yeast populations declines during selection

Abstract

The trade-off between growth rate and yield can limit population productivity. Here we tested for this life-history trade-off in replicate haploid and diploid populations of Saccharomyces cerevisiae propagated in glucose-limited medium in batch cultures for 5000 generations. The yield of single clones isolated from the haploid lineages, measured as both optical and population density at the end of a growth cycle, declined during selection and was negatively correlated with growth rate. Initially, diploid populations did not pay this cost of adaptation but haploidized after about 1000–3000 generations of selection, and this ploidy transition was associated with a decline in yield caused by reduced cell size. These results demonstrate the experimental evolution of a trade-off between growth rate and yield, caused by antagonistic pleiotropy, during adaptation in haploids and after an adaptive transition from diploidy to haploidy.

1. Introduction

Costs of adaptation are central to understanding the evolution of life-history traits and ecological niches. Disease, ageing and death are sometimes indirect effects of adaptation, both in theory [1] and in experiments [2–4]. Adaptation tends to limit performance because of trade-offs under a broad range of conditions [5–7]. Some of these costs of adaptation are transient and can be alleviated by compensatory evolution [8,9]. Other costs, however, are imposed by constraints on cellular metabolism and other forms of functional interference that generate trade-offs among fitness components. For example, the decline of metabolic efficiency associated with faster growth and reproduction is a life-history trade-off that is based on the first law of thermodynamics: energy allocated to accelerating the rate of biomass production is diverted from contributing to biomass yield [10–12]. Mutations that increase the speed but reduce the efficiency with which limiting resources are exploited may therefore prove adaptive even if those resources then support fewer individuals. Here, we test for the evolution of this evolutionary trade-off between growth rate and yield in experimental populations of the yeast Saccharomyces cerevisiae.

The experimental evolution literature offers extensive evidence of costs of adaptation, but only in a few cases was the cost demonstrated for traits that were relevant for fitness in the selective environment [13–15]. This is surprising because these costs can be the engine of further adaptation through compensatory evolution [16–18], and they can maintain genetic variance for traits correlated with fitness if negative frequency-dependent selection emerges [19]. In most studies, populations are selected under one set of conditions and assayed under others, with the common selective features of these environments from the point of view of the genotypes assayed being largely unknown [19–22]. A frequent approach is to select microbial populations in media that contain single sources of carbon and measure the indirect responses to selection in media containing a different carbon source or concentration [23–27]. Another strategy is to study the indirect response of a life-history trait to directional selection on another life-history trait (e.g. late-life and early-life traits [3]). However, costs of adaptation are more compelling and relevant for general theories of adaptation when they concern traits that may have been functionally relevant during adaptation [28]. Here, we test for a cost of adaptation in an environment that varies in time between feast and famine (i.e. batch cultures) and where the potential cost is expressed in that same selective environment.

We analysed clones from the haploid and diploid populations of the budding yeast S. cerevisiae that Zeyl et al. [29] selected for 5000 generations under daily population transfers in a glucose-limited medium. The original experiment reported that haploids adapted faster than diploids in large populations, but not in small ones, and that beneficial mutations fixed in haploids and diploids are partially recessive and partially dominant, respectively [29]. Under the selective regime, the experimental populations were expected to evolve to grow faster during the feast early in the selection cycle [10,11,30]. Here we ask whether faster growth was associated with a decline in the yield, or final biomass, of these populations. We found clear evidence that such a cost in productivity had evolved independently in all haploid populations, and in all diploid populations only when they spontaneously haploidized.

2. Methods

(a). Selection experiment

A single leucine-auxotroph strain of S. cerevisiae derived from the standard laboratory strain S288c was used as the founder of five haploid and five diploid selection lines [29]. Each population was initiated with a single clone, therefore all responses to selection relied on de novo mutations. The lines were propagated in minimal medium (5 g l⁻¹ ammonium sulphate, 2.5 g l⁻¹ glucose, 1.7 g l⁻¹ yeast nitrogen base, 0.06 g l⁻¹ leucine; incubation at 30°C) in which growth was limited by glucose, by serial transfers of 100 μl of 24-h cultures into 10 ml of fresh media. Selection was carried out for approximately 5000 generations at approximately 6.6 generations per day. Aliquots were sampled from each of the 10 selection lines every approximately 100 generations and preserved in 15 per cent glycerol at −80°C. Competitive fitness increased rapidly in the selective environment over the first approximately 2000 generations of selection, followed by slower, but still significant, adaptation over the next 3000 generations [29]. Our experiments on optical density, population density and cell size were performed with single clones isolated from 12 time-points for each lineage, spread over the 5000 generations of selection (every approx. 250 generations for the first 1000 generations, and every approx. 500 generations thereafter; 12 time-points × 10 replicate selection lines). The ploidy of all 120 clones was measured following Gerstein et al. [31].

(b). Assayed traits

Clone yield was measured as the optical density (O.D.) at the end of the growth cycle in the selective conditions for each clone. To assess the importance of cell mortality in stationary phase we also analysed maximal O.D., estimated for each clone as the highest of the O.D. values obtained every 3 h from hour 12 to hour 24 of the growth cycle. Clone yield may also be impacted by the inoculum size, the number of cells in the volume of culture transferred daily. Therefore, in another set of assays, inoculum size was equalized across all clones by transferring the same number of O.D. units into fresh media (that common inoculum size was set to the corrected O.D. of the culture with the fourth highest O.D. among the 120 cultures, while that culture was kept at the 100 μl transfer). Optical density was estimated by vortexing the cultures until they were visually homogeneous, transferring 200 μl into each of two separate wells of a 96-well plate, and reading the O.D. at 630 nm with a spectrophotometer (PowerWave XS2; BioTek Instruments, Winooski, Vermont). These O.D.s were corrected by subtracting the average O.D. of blank wells containing 200 μl of fresh media.

The O.D. is influenced by both population density and cell size, so we estimated these parameters at the end of the growth cycle for all 120 clones. Final population density is the per microlitre number of particles counted in 500 μl of a 10 per cent culture dilution in the diluent Isoton II using a Coulter Counter (Beckman Coulter, Inc.). Counted particles may be live or dead, so we also estimated final population densities of live cells for clones isolated from generation 500 and 5000 of each haploid selection line, by plating diluted cultures (unequalized inocula and with 10-fold replication) onto solid minimal medium (same recipe as above, plus 20 g l^–1 agar). To account for variation in plating efficiency, prior to plating each culture of a focal clone was mixed 1 : 1 (by volume, 50 μl each) with cultures from a standard strain marked with an antibiotic resistance allele. The live cell population density analysed is the ratio of the number of colonies of the focal clone to the total number of colonies on each plate (i.e. density relative to the standard, and ranging from zero to one).

Average cell size was estimated as the average ln(pulse width × pulse height) across all particles counted in a sample, with electrical pulses being generated by each cell crossing the aperture of the Coulter Counter. Each yeast population was differentiated along both the height and width axes of the electrical pulses, forming a bivariate bimodal distribution due to the cycle of growth and budding off of daughter cells. The average cell size (univariate variable) was also bimodal (see the electronic supplementary material, figure S1 [32,33]). Analyses of the univariate cell size distribution did not reveal a mode of particles larger than budding cells, suggesting that cell clumping is not an issue when interpreting our results. Clumps of cells would have also clogged the aperture (50 μm diameter) of the Coulter Counter repeatedly, but this did not happen. Average cell size was measured twice, at the time of transfer (hour 24 or 0) and 6 h into the growth cycle, allowing us to assess the effect of the change in average cell size during the early exponential phase on our estimates of clone growth rate.

Clone growth rate is the maximal rate of increase in O.D., which we estimated for each clone as the slope of the natural logarithm of O.D. in microwells of 96-well plates during the first 8 h of growth. Microwells in an incubating spectrophotometer allow for near-continuous measurements of O.D. giving much improved precision over disruptively sampling tubes at few time-points. We validated the conclusions drawn from these measurements in microwells by analysing growth rate in tubes (the selective environment), estimated by O.D. after 12 h of growth in tubes. Clones growing faster are expected to have a higher O.D. in mid-log phase (about 12 h). Because O.D. increases can be caused by increases in either population density or average cell size, we compared the O.D.-based estimates of clone growth rates with (i) the number of population doublings during the first 6 h of the cycle in tubes, and (ii) the change in average cell size (measured as above) during the first 6 h in test tubes. The number of population doublings is given by log₂(population density at 6 h/initial population density), where initial population density is 1 per cent of final population density. Population density was estimated using a Coulter Counter, as described earlier. The above data are available as the electronic supplementary material to this article.

3. Results

(a). Gradual trade-off in haploid selection lines

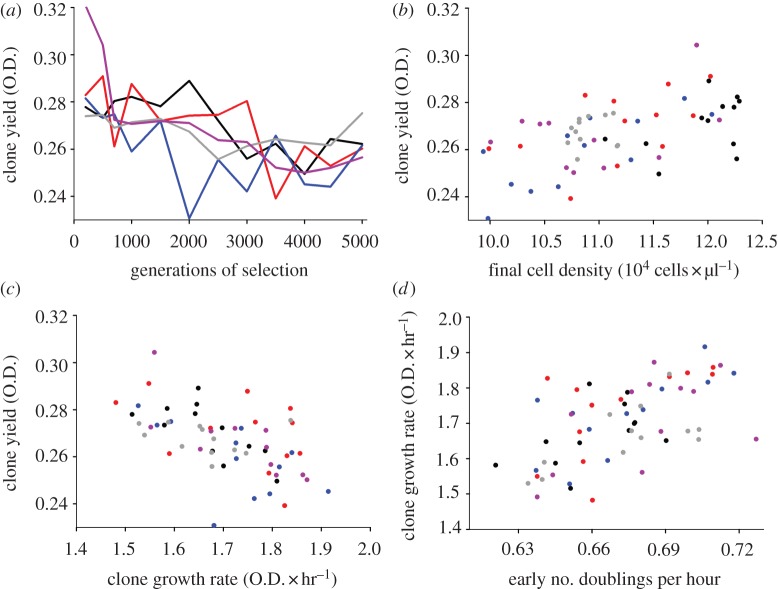
Final O.D., or clone yield, declined during selection in each of the five haploid replicate lines, albeit at varying rates (figure 1a, repeated-measure ANOVA, time F_11,5 = 15, p = 0.004; line F_4,15 = 3, p = 0.05; time × line F_44,21 = 2.6, p = 0.01). This decline in O.D. can be associated with a decline in population density, a reduction of cell sizes or both. We found that changes in final population density alone, as estimated by direct cell counts, explained clone yield (figure 1b, population density F_1,1 = 5.6, p = 0.02; line F_4,4 = 0.8, p = 0.5; density × line F_4,4 = 0.2, p = 0.9, model R² = 0.38). These direct cell counts included both live and dead cells, which is appropriate to assess how much resources and energy have accumulated in the population during growth. Nevertheless, we also observed that population density declined when only live cells were counted (by plating cultures); clones isolated at generation 500 gave on average 46 per cent more colonies on plates than clones sampled 4500 generation later (paired t-test, t = −5.2, d.f. = 4, p = 0.003). Cell size varied significantly among lines (cell size × line effect, F_4,4 = 4.4, p = 0.004, in a model also including main effects), thus we used multiple comparisons to test for an effect of average cell size on final optical density. That relationship was significantly negative in one line (F_1,1 = 7.7, p = 0.02), negative but not significant in three lines, and positive but not significant in the remaining line. Thus, if there was a trend at all, it was that lower clone yield coincided with larger cell size, the opposite of what would be expected if variation in clone yield was explained by cell size.

Figure 1.

Responses to 5000 generations of selection in haploid populations (colours indicate five independently selected lines). (a) Clone yield decreased during selection. (b) Clone yield is explained by population density, and (c) decreased with clonal growth rate. (d) Clonal growth rate correlates with the number of cell doublings.

Clone yield was negatively correlated with clonal growth rate as estimated in microwells, which we take as evidence for a trade-off between growth rate and yield (figure 1c and table 1). A multiple comparison test revealed that all rate-yield slopes were negative, and three out of five significantly so (p < 0.01). Changes in clonal growth rates in microwells were associated with the number of cell doublings during the first 6 h of growth in tubes (figure 1d), but not with changes in average cell size during that same period (early number of doublings: doublings F_1,1 = 22, p < 0.0001; line F_4,4 = 0.8, p = 0.6; doublings × line F_4,4 = 0.04, p = 1; early change in cell size: change in cell size F_1,1 = 1.1, p = 0.29; line F_4,4 = 0.5, p = 0.7; change in size × line F_4,4 = 1.5, p = 0.2). Thus, the dynamics of adaptation (i.e. faster growth) and one of its costs (i.e. decline in yield) were explained by changes in population density in the haploid lineages. Growth rates measurements in microwells are precise but may not reflect accurately population dynamics in the tubes in which selection was carried out. However a second, independent estimate of growth rate, the optical density of cultures after 12 h of growth in tubes was also negatively correlated with clone yield. (O.D. at 12 h, F_1,1 = 41, p < 0.0001; line, F_4,4 = 1.5, p = 0.2; O.D. at 12 h × line, F_4,4 = 3.8, p = 0.009; despite the significant interaction, all lines show a negative relationship between clone yield and O.D. at 12 h). These results support the view that the direct response to selection (that is, the acceleration of clonal growth rate) lowered clone yield.

Table 1.

ANOVA of two measures of clone yield in haploid lines as a function of growth rate and replicate selection line.

	growth rate		line		growth rate × line
	F1,1	p-value	F4,4	p-value	F4,4	p-value
final O.D.	28	<0.0001	2.1	0.1	2.3	0.07
final O.D. equalized	30	<0.0001	1.0	0.4	2.4	0.06

It is conceivable that the negative association between clone growth rate and yield was caused by variation in inoculum sizes if, for example, a smaller number of cells was transferred from low yield tubes and growth was strongly density-dependent even at low density, resulting in increased growth rates. If this were true, equalizing the yield of each clone to a common O.D. value would disrupt the negative relationship between growth rate and yield. However, we found a strong correlation between clone yields, whether or not inoculum size was equalized across cultures (linear regression across all 60 clones, t = 7.5, p < 0.0001, R² = 0.50). Clone yield with equalized inocula also correlated negatively with growth rate (table 1 for microwells; in tubes, O.D. at 12 h F_1,1 = 18, p < 0.0001; line F_4,4 = 1, p = 0.4; growth rate × line F_4,4 = 2.0, p = 0.1). Thus, feedback between clone yield, inoculum size and growth rate is not responsible for the negative rate-yield correlation we reported.

In conclusion, the haploid lines responded to selection by increasing the rate of production of biomass through increasing the rate of cell doublings early in the growth cycle, and this came at a cost in yield, as measured by final optical density or population density. Indeed, final population density is negatively correlated with the number of population doublings in the first 6 h (doublings F_1,1 = 17, p = 0.0002; line F_4,4 = 7.3, p = 0.0001, doublings × line F_4,4 = 1.8, p = 0.14).

(b). Trade-offs in the initially diploid lines

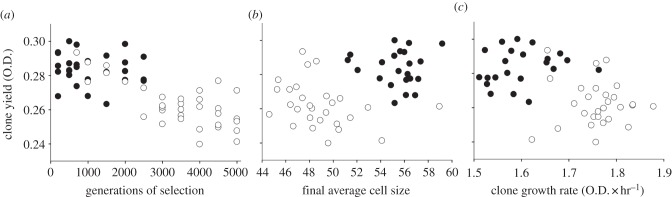
The five selection lines initiated with a diploid clone spontaneously haploidized after approximately 1000–3000 generations of selection (J.-N. Jasmin, A. C. Gerstein & C. Zeyl 2010, unpublished data). Diploid clones, on average, had a higher yield than haploids (figure 2a, ploidy F_1,1 = 7.4, p = 0.009; time nested in ploidy F_2,2 = 14, p < 0.0001; line F_4,4 = 1.9, p = 0.12), and yield declined during selection in the haploid but not the diploid lineages (figure 2a, factorial model with time and line, diploids, p > 0.35 for all effects; post-haploidization, time: F_1,1 = 14, p = 0.001, line F_4,4 = 3.2, p = 0.03, time × line F_4,4 = 0.3, p = 0.9). On average, the last diploid clone of a line had a higher yield than the first haploid clone (paired t-test, t = −2.8, d.f. = 4, p = 0.026), indicating that haploidization decreased yield. The above conclusions are unchanged when inoculum sizes are equalized across all clone; most importantly, haploidization still decreased clone yield (paired t-test, t = −2.4, p = 0.036).

Figure 2.

Responses to 5000 generations of selection in populations that were initially diploid and that changed to haploidy after 1000–3000 generations. Filled and empty symbols indicate diploid and post-haploidization haploid clones, respectively. Mainly as a result of haploidization, (a) clone yield decreased during selection; (b) clone yield is explained by average cell size; and (c) clone yield is negatively correlated with clone growth rate.

Haploidization reduced clone yield because it reduced cell size (figure 2b, paired t-test, t = −6.5, d.f. = 4, p = 0.0015), despite increasing final population density by about 20 per cent (paired t-test, t = 9.3, d.f. = 4, p = 0.0004). However, variation in clone yield was not associated with changes in average cell size while the lines were diploid, or during their evolution after haploidization (linear model with line, average cell size and average population density, and all interactions, all factors: diploids, p > 0.7; haploids p > 0.1; a reduced model also failed to reveal significant factors).

While reducing yield, haploidization also accelerated clone growth rate (figure 2c, paired t-test, d.f. = 4, growth rate in microwells: t = 1.9, p = 0.06; O.D. at 12 h in tubes, t = 3.7, p = 0.01), thus generating a negative correlation between growth rate and yield. Faster clone growth rate coincided with an increase in the change in average cell size during the first 6 h of the growth cycle (paired t = 5.2, d.f. = 4, p = 0.003), and was not associated with the number of population doublings early in the growth cycle (paired t = 1.3, d.f. = 4, p = 0.13). Clone growth rate also accelerated during selection in both the diploid (time F_1,1 = 12, p = 0.003; line F_4,4 = 0.83, p = 0.53, time × line F_4,4 = 1.3, p = 0.3) and post-haploidization haploid (time F_1,1 = 8.5, p = 0.008; line F_4,4 = 0.41, p = 0.80, time × line F_4,4 = 1.2, p = 0.3) phases of each lineage. Here faster growth resulted from increases in the number of cell doublings and the change in average cell size in the first 6 h of the cycle (respectively, with F_1,1 = 81 and 12, p < 0.0001 and 0.0009; see the electronic supplementary material, figure S2). Most importantly, clone yield was not correlated with clone growth rate among diploids, but it was in post-haploidization haploids (table 2). Thus, only diploids were spared the rate-yield trade-off in our experiment.

Table 2.

ANOVA of two measures of clone yield in the initially diploid lines as a function of growth rate and replicate selection line. 2n indicates diploid lines before haploidization, and n post-2n indicates haploid lines arising after the haploidization.

	growth rate		line		growth rate × line
	F1,1	p-value	F4,4	p-value	F4,4	p-value
2n final O.D.	0.09	0.8	0.9	0.5	0.4	0.8
2n final O.D. equalized	2.1	0.2	0.1	0.9	0.8	0.5
n post-2n final O.D.	5.3	0.03	1.4	0.3	2.2	0.11
n post-2n final O.D. equalized	8.2	0.008	0.1	0.9	1.1	0.4

In summary, haploidization increased clonal growth rate and reduced both yield and cell size. After haploidization, further increases in growth rate came at the expense of yield as they did all along in initially haploid lines and unlike those that had evolved while the lines were diploid.

(c). Stationary-phase mortality

It is possible that the negative correlation between growth rate and yield reported above for haploid lineages resulted from increases in stationary-phase mortality rates. We expect that fast growing clones will reach stationary phase sooner than slow clones (unless growth rate correlates positively with yield), leaving more time for cells to die before yield is measured. A positive correlation between growth rate and the amount of stationary-phase mortality may thus generate the observed negative correlation between growth rate and yield. We tested this idea by measuring the maximal yield attained by each clone during the 24 h growth cycle, which should be little, if at all, impacted by stationary-phase mortality. We did this by estimating maximal optical density (O.D.) in tubes from reads taken every 3 h from hour 12 to hour 24 of the growth cycle. In these assays, the size of the inoculum was equalized across all cultures to exclude inoculum size effects. Maximal O.D. was well correlated with final population density (haploids p < 0.0001, R² = 0.64; diploids p < 0.0001, R² = 0.53; post-haploidization haploids p < 0.0001, R² = 0.65). Like final O.D., maximal O.D. was negatively correlated with growth rate in the post-haploidization haploids, but not among the diploid clones (growth rate effect in diploids p = 0.3; post-haploidization haploids p = 0.08; electronic supplementary material, figure S3b). In the haploid lines, the relationship between growth rate and yield was quadratic (electronic supplementary material, figure S3a), with the growth rate-yield correlation being negative for all but the slowest growing clones of each line (full factorial model, growth rate, F_1,1 = 4.2, p = 0.04; growth rate², F_1,1 = 4.8, p = 0.03; line, F_1,1 = 1.7, p = 0.2; growth rate × line, F_4,4 = 2.5, p = 0.06; growth rate² × line, F_1,1 = 2.4, p = 0.06). Finally, haploidization reduced maximal O.D. in each of the five lines (paired t = −1.9, d.f. = 4, p = 0.066). In conclusion, a negative correlation between growth rate and yield persists even when stationary-phase mortality is circumvented experimentally.

4. Discussion

We tested experimental yeast populations for a cost of adaptation expressed in the selective environment, in the form of reductions in yield associated with the evolution of faster growth rates [11]. Initially, isogenic haploid populations independently evolved faster growth rates, at the cost of lower yield, as measured by the maximal and final O.D.s, as well as final population densities of all cells (figure 1) or live cells alone. Initially, diploid populations did not pay this cost of adaptation even though their growth rate also increased, until they spontaneously became haploid after approximately 1000–3000 generations of selection. Haploidization itself increased growth rate and final population density, while also lowering final and maximal O.D.s and average cell size (figure 2; see also [34,35]). The negative correlations between growth rate and yield in haploid lineages and during haploidization evolved de novo in our experimental populations, and they are similar to those that have been genetically engineered in previous work [36].

At least four non-exclusive mechanisms could underlie the negative rate-yield correlation in the haploid lineages: (i) the metabolic efficiency of growth could decrease, with less biomass being produced for a given amount of resource consumed [11]; (ii) fast growing clones could release more growth inhibiting molecules (such as ethanol) per cell division than their slower ancestors [36]; (iii) mortality rates late in the growth cycle could increase (akin to the growth-mortality trade-off in plants [37]); or (iv) the affinity for the limiting resource (here, glucose) could decline, leaving more resources unused at the end of the growth cycle (this trade-off is especially associated with trans-membrane sugar transporters [38]). Although we demonstrated that the negative correlation between growth rate and yield was genetic, these four scenarios are not explicit about whether the correlation is genetic or environmental. Indeed, a linear negative relationship between growth rate and yield (as measured either by dry weight or population density) occurs among isogenic cultures of S. cerevisiae when growth rate is experimentally manipulated by varying the resource supply rate in chemostats [39]. This happens because faster growth is achieved by diverting resources from respiratory to fermentative pathways, which are 10 times less efficient than respiration at converting glucose into ATP (scenario i). Although we cannot reject alternative scenarios, this metabolic trade-off very likely contributed to our observations, except that in our study, variation in growth rate was generated by genetic differences among clones rather than differences in culturing conditions. Increased fermentation relative to respiration may also increase the amount of ethanol released in the medium, which may in turn reduce yield (scenario ii [36]). The diversion of pyruvate from respiration to fermentation during glucose metabolism is the sort of mechanism thought to be responsible for the evolutionary trade-off between rate and yield in micro-organisms [10,11,20,40]. More broadly, in all four scenarios, the negative genetic correlation between growth rate and yield that we reported is caused by antagonistic pleiotropy.

Fitness costs in the selective environment, like the decline in yield reported here, have been most clearly demonstrated in evolutionary experiments in which populations were propagated both within and between patches of a heterogeneous environment. Lineages specializing on each patch type are expected to evolve if different phenotypes optimize fitness in the different patches [22]. These specialists demonstrate costs of adaptation in situ whereas a single generalist lineage does not. Most experiments implementing this design have shown evidence of costs of adaptation and the maintenance of specialists [14,19,41,42]. Two studies even found costs of adaptation when selection varied in time rather than in space [15,43], although temporal variation tends to favour generalists [44–46]. Our selective environment could also be thought of as varying in time because of the feast–famine cycle of batch cultures, but the local adaptation that evolved in the above studies is probably irrelevant for interpreting our results if one or more of the above scenarios (i–iii) are correct because these scenarios do not rely on environmental heterogeneity. Local adaptation is relevant only for scenario (iv), for example, if fast growing clones require more nutrients to sustain growth (have a higher half-saturation constant [38]) and thus cease growing earlier than their ancestor.

Declining yield was also reported by Adams et al. [47] for yeast clones from six successive fixation events in an unreplicated glucose-limited batch culture. These authors were surprised by their result as they expected the evolution of yield to be driven by the accumulation of conditionally neutral mutations, which does not predict such rapid decay. Paquin & Adams [48] also found that yield declined when their Saccharomyces populations adapted to a chemostat. Interestingly, drops in yield between time-points in their experiment did not coincide with increases in growth rate, but rather with the intensification of intransitive interactions (in which genotype A beats B, B beats C and C beats A, as in the rock–paper–scissors game). Other experiments have failed to find evidence for a trade-off between growth rate and yield. Novak et al. [20] analysed populations of Escherichia coli over 20 000 generations of selection in a glucose-limited environment and observed a trade-off among genotypes isolated from single samples (one replicate population at a single time-point), but not among 12 replicate populations after 20 000 generations of selection, nor across samples isolated at different time-points for each selection line (which was our strategy). These results are difficult to interpret because yield was estimated on microwell plates (200 μl) whereas selection was performed in 10 ml of media in Erlenmeyer flasks. Furthermore, Novak et al. [20] assayed whole-population samples to test for a decline in yield during selection, and the genetic variation along the rate/yield trade-off within the samples may have masked that trade-off.

We observed that the yield of diploid lineages was not affected by acceleration of growth, until they haploidized, which caused cells to become smaller and consequently populations to have a lower yield. The productivity of haploids also declined, but the decline was due to lower population density rather than to smaller cells. These results are consistent with an evolutionary trade-off between growth rate and yield in yeast populations selected to rapidly exploit a common pool of resources [10]. That the diploids (pre-haploidization) did not pay a cost of adaptation raises the possibility that diploid and haploid populations exploited different mechanisms when they accelerated their growth [49]. This difference may explain why competitive fitness increased much more slowly in diploids than in haploid [29] and may be relevant for understanding the evolution of ploidy in yeast.