Abstract
Exposure to low doses of pathogens that do not result in the host becoming infectious may ‘prime’ the immune response and increase protection to subsequent challenge. There is increasing evidence that such immune priming is a widespread and important feature of invertebrate host–pathogen interactions. Immune priming clearly has implications for individual hosts but will also have population-level implications. We present a susceptible–primed–infectious model—in contrast to the classic susceptible–infectious–recovered framework—to investigate the impacts of immune priming on pathogen persistence and population stability. We describe impacts of immune priming on the epidemiology of the disease in both constant and seasonal environments. A key result is that immune priming may act to destabilize population dynamics. In particular, when the proportion of individuals becoming primed rather than infected is high, but this priming does not confer full immunity, the population may be strongly destabilized through the generation of limit cycles. We discuss the implications of our model both in the context of invertebrate immunity and more widely.
Keywords: immunity, model, cycles, destabilization, bistability, seasonality
1. Introduction
Pathogens, also referred to as microparasites, are ubiquitous in nature and by definition cause significant harm to their hosts. In response, hosts have evolved a range of resistance mechanisms, including behavioural avoidance, physical barriers and complex cellular and humoral immune responses [1]. The immune responses of invertebrates, though less well understood than that of vertebrates, are now widely studied [2,3]. Traditionally, invertebrates were thought to have no capacity for memory in their immune response to pathogens because they lack the immune cells that are responsible for vertebrate acquired immunity [4]. However, despite being mechanistically distinct to the vertebrate acquired immunity, growing empirical evidence suggests that invertebrates show immune memory and are more resistant to pathogen infection following previous exposure [3,5]. This form of memory in an invertebrate is termed ‘immune priming’, which is broadly defined as increased protection to a pathogen following previous exposure to a pathogen or an immune elicitor. Although recent work has investigated the impacts of immune priming on infection prevalence, host population size and population age structure using a stage-structured model [6], it remains unclear what impact this form of immunity has on the persistence and stability of host–pathogen systems in general.
Evidence for immune priming has been found in a number of different insect species and in response to a diverse range of pathogen species, indicating that this phenomenon may be widespread. For example, immune priming has been shown in Tribolium castaneum [7] and in the social insect Bombus terrestris in response to bacteria [8,9]; in the Lepidopteron, Plodia interpunctella in response to virus [10]; and in Tenebrio molitor in response to entomopathogenic fungi [11]. Furthermore, there is evidence for immune priming in other invertebrates such as crustaceans, including Daphnia magna [12], Penaeus monodon [13], Penaeus japonicus [14] and Litopenaeus vannamei [15]. Both within generation [7,10,11] and transgenerational priming [8,10,12], where protection is passed from parent to offspring, have been found. Although our mechanistic understanding of immune priming is limited and clearly requires further study [16], the phenomenon of immune priming seems to be conserved across many invertebrates.
Immune responses have implications for individual hosts, but they may also have implications for the host population as a whole. Mathematical modelling is a key tool in capturing infectious disease dynamics and can be used to infer the effect that different immune responses can have on host–pathogen interactions and population dynamics. Traditionally, epidemiological studies are in the form of susceptible–infectious–recovered (SIR) models [17,18], where following infectiousness, hosts recover to a completely immune state. Comparison of these SIR systems with susceptible–infectious–susceptible (SIS) models, where following infectiousness, individuals return to being susceptible, has highlighted the impact that immunity can have on population dynamics. SIR systems exhibit more prolonged and larger damped oscillations on approach to a stable equilibrium compared with SIS systems [19].
Factors important in disease dynamics are unlikely to be constant through time with seasonality in epidemiological and demographic parameters substantial in natural and human disease interactions [20]. Incorporating such variation into mathematical models therefore enables the more accurate representation and prediction of disease dynamics in nature. Seasonality in the SIR model tends to drive regular multi-annual epidemic disease outbreaks as is seen in childhood infections such as measles [21–23]. Vaccination has also been modelled as removal of individuals from the susceptible class directly to the immune class without an infectious stage and at a rate independent of pathogen density in the population [24,25]. However, these classic SIR-type models do not capture the population dynamics with immune priming, where a proportion of individuals do not become infectious but are primed following pathogen exposure and have reduced risk of becoming infectious on subsequent exposure. The immune priming process we consider is epidemiologically distinct from the acquired immunity more commonly assumed in classical SIR models, where immunity is gained only after hosts have been infectious for some period of time. Instead, we assume that hosts gain immunity following exposure to an infected host but without ever becoming infectious themselves.
Here, we develop and analyse a mathematical model that incorporates within generation immune priming and transgenerational immune priming into a disease system. We describe the implications of immune priming for the persistence and prevalence of the pathogen and the population dynamics in constant environments and under seasonal forcing.
2. Modelling
A general theoretical framework is developed to examine the impacts of both within generation and transgenerational immune priming on the dynamics and stability of the host–pathogen population. The host population is divided into three distinct classes: susceptible hosts with density S, primed hosts with density P and infectious hosts with density I (total density, H = S + P + I). We therefore call this model susceptible–primed–infectious (SPI). The dynamics of the population are represented by equations (2.1)–(2.3).
| 2.1 |
| 2.2 |
and
| 2.3 |
All hosts reproduce at rate a, which is reduced by factor h, owing to density dependence, so that increased population density results in a negative feedback on reproduction. Hosts are subject to a natural death rate b. The host population is therefore limited to a carrying capacity in the absence of disease making our model applicable to wildlife disease systems. The transmission coefficient is β and is assumed to be through direct contact between susceptible and infectious hosts, and is density-dependent. Following exposure to the pathogen, a proportion, p, of susceptible individuals become primed, and the remainder (1 − p) become infectious. Infectious individuals suffer increased death rate (pathogenicity, α) and do not recover. Primed individuals become infectious at a reduced rate q, with subsequent exposure to the pathogen. The degree of transgenerational immune priming in the system is determined by τ, with primed individuals giving birth to primed offspring at rate τ and susceptible offspring at rate (1 − τ). Primed and infectious individuals have reduced fecundity, fP and fI, respectively. Priming wanes over time so that primed individuals become susceptible again at rate c, with priming duration equal to host lifespan divided by c. Default parameters include a = 2 so that a host gives birth to two offspring in their lifespan, b = 1 so that a host's lifespan is on average one year and α = 1 so that an infectious host's lifespan is half that of a susceptible host's.
We investigate the ecological behaviour of the SPI system using the AUTO continuation software package [26], which identifies the location and stability of equilibria as parameters of the model are varied. Specifically, we focus on areas of parameter space where the pathogen cannot persist, where there is an endemic equilibrium and where there are endemic cycles. We examine the consequence of priming rate p, and degree of priming protection q, on the persistence of the pathogen and stability of the endemic state with and without transgenerational priming, when priming wanes and when demographic and epidemiological parameters (namely birth rate (a), transmission (β), pathogenicity (α)) are varied. By using the Odesolve package in R, we examine the dynamics of the SPI system in comparison with more traditional model frameworks and within the cyclic region. Our aim is to gain a general understanding of the population dynamical effects of immune priming.
We extend this model to include seasonality in birth rate and transmission rate by setting these parameters to be a function of the sine wave so that:
| 2.4 |
and
| 2.5 |
where δ is the amplitude of the seasonal variation and, the period of the oscillation is exactly 1 year.
We explore how seasonal fluctuation in birth rate and transmission rate affect the population dynamics of a system that exhibits immune priming.
3. Results
R0 for a pathogen is defined as the average number of secondary cases of disease that arise from one infectious individual in an otherwise susceptible population. Generally, if R0 > 1, then the pathogen can successfully invade a population, whereas if R0 < 1, then the pathogen cannot invade [27]. The expression of R0 for the SPI model is
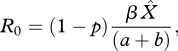 |
2.6 |
where 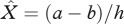 is the disease-free host equilibrium density. Clearly, the value of R0 depends on priming, p. From equation (2.6), it is clear that, rather intuitively, increasing the proportion of priming (p) reduces the ability of the pathogen to invade a susceptible host population because fewer hosts are becoming infected. It is important to note though that the level of protection which priming provides (q) and the rate at which priming wanes (c) does not influence the R0 value.
is the disease-free host equilibrium density. Clearly, the value of R0 depends on priming, p. From equation (2.6), it is clear that, rather intuitively, increasing the proportion of priming (p) reduces the ability of the pathogen to invade a susceptible host population because fewer hosts are becoming infected. It is important to note though that the level of protection which priming provides (q) and the rate at which priming wanes (c) does not influence the R0 value.
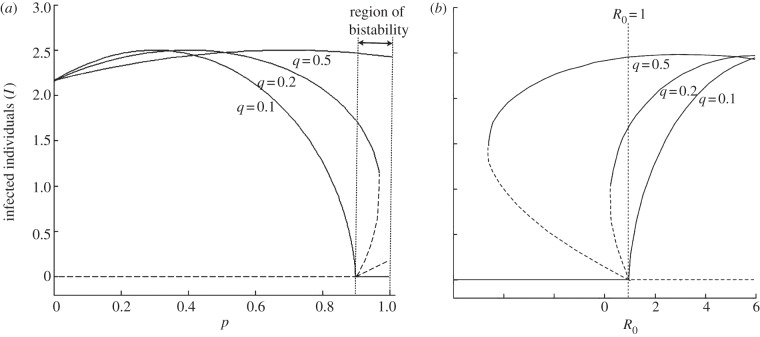
In this system, the host and pathogen may also coexist when R0 < 1. When priming is high (despite R0 < 1), both the disease-free and endemic equilibrium are stable, i.e. the system is bistable (figure 1). Whether the disease-free or endemic equilibrium is reached depends on the initial conditions of the system and the level of protection that priming provides (q). Independent of q, when priming is high and the pathogen is initially absent, the pathogen cannot invade and the system settles at the disease-free equilibrium. However, if the pathogen is already present, it may persist depending on the value of q. When q is low, so that the protection provided by priming is high, the pathogen cannot persist when R0 < 1, but when q is high, so that the priming protection is low, the pathogen can persist at R0 < 1. Therefore, in a system that experiences high rates of priming, the persistence criteria and the invasion criteria of the pathogen are distinct.
Figure 1.
Bistability in the susceptible–primed–infectious system when there are no fecundity costs of infectiousness and priming. (a) Region of bistability, when priming rate (p) is high, is dependent on priming protection (q). When priming protection is high (q = 0.1), there is no bistability, but when priming protection is less (q = 0.5), the pathogen can persist even when all susceptible individuals become primed (p = 1). (b) Bistability plot in terms of R0. R0 < 1 when p = 0.9 for the model parameters used. When q > 0.1, the number of infected can be positive, with the system at an endemic equilibrium, even if R0 < 1. Therefore, higher levels of priming protection result in persistence of the pathogen below R0 < 1. (Parameters: a = 2, b = 1, h = 0.1, α = 1, β = 2, τ = 0, c = 0, fY = 1, and fP = 1. Solid lines represent a stable population and dashed lines represent an unstable population).
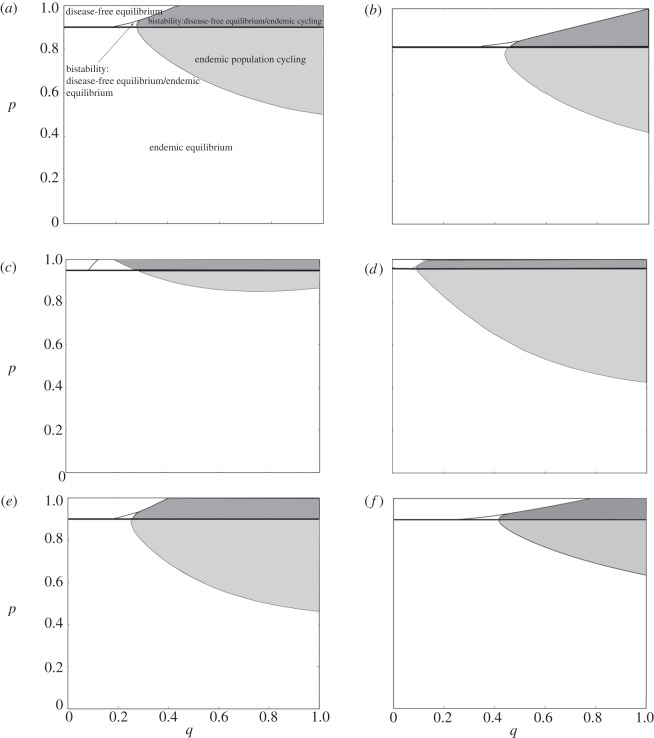
A key result from the numerical simulations performed in AUTO and R is that high levels of immune priming destabilizes the host–pathogen population. However, the destabilizing effects of priming are seen in systems where only infectiousness results in reduced fecundity and is stronger if primed individuals also have reduced fecundity. When the rate of immune priming is low, the SPI system mimics the traditional SIR system and reaches an endemic equilibrium following damped oscillations. However, when the proportion of priming is high, the SPI system may exhibit prolonged limit cycles. Limit cycles produce repeated increases and crashes in the densities of the population classes. Therefore, in a system characterized by endemic limit cycles, we see periods of disease outbreak followed by near-absence of disease. The range of priming rates and priming protection where instability is found depends on specific parameters of the model (figure 2). In particular, increased fecundity costs of infectiousness and priming are important and increase the range of priming rate and priming protection over which cycles are exhibited. In addition, increased pathogenicity (figure 2b), increased birth rate (figure 2c) and waning of priming over time (figure 2f) lead to reduced chance of destabilization, while increasing transmission (figure 2d) and the addition of transgenerational priming (figure 2e) result in an increase in total cycling region and therefore further destabilization of the population.
Figure 2.
Regions in p (degree of priming), q (priming protection) parameter space where the disease-free equilibrium is stable, the endemic equilibrium is stable, the endemic population is unstable and there is bistability. (a) Default parameters. (b) Increased pathogenicity (α = 2.5) leads to a reduced range of q over which the endemic population cycles. (c) Increased birth rate (a = 3) also leads to a reduced region of p over which the endemic population cycles. (d) Increased transmission (β = 5) leads to a greater region of p, q parameter space over which the endemic population cycles. (e) The addition of transgenerational priming (τ = 0.5) leads to a slight increase in endemic population cycling region. (f) When priming wanes over time (c = 3) the region over which the endemic population cycles is reduced. (Default parameters: a = 2, b = 1, h = 0.1, α = 1, β = 2, τ = 0, c = 0, fY = 0.2, fP = 0.5.)
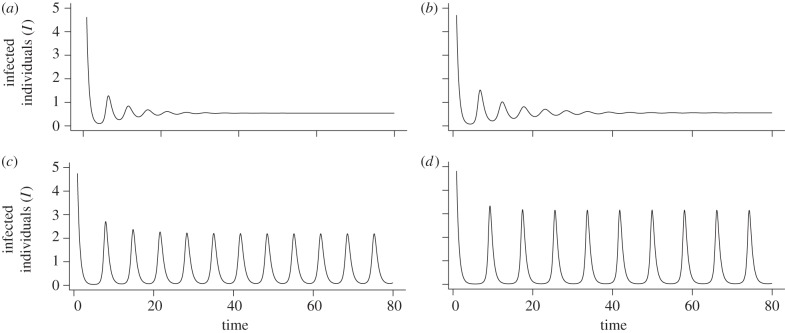
In addition to generating cyclic population dynamics, immune priming also modulates these cycles as it varies. Increasing the level of priming within the cycling region results in limit cycles of greater amplitude but reduced frequency (figure 3b,c) that translates into fewer, larger disease outbreaks over time. Furthermore, outside the region of limit cycles, the time taken for the cycles to dampen is longer under increased priming (figure 3a,b). Throughout then, it is clear that in a system which experiences high levels of immune priming, and fecundity costs of infection and priming, the population dynamics are more likely to be unstable.
Figure 3.
The nature of the SPI system dynamics. (Parameters: a = 2, b = 1, h = 0.1, α = 1, β = 2, τ = 0.5, c = 0, fY = 0.2, fP = 0.5.) (a) The endemic equilibrium is reached via damped oscillations when priming is low (p = 0.2, q = 0.5). (b) More prolonged damped oscillations occur when priming is increased within the stable endemic region (p = 0.4, q = 0.5). (c) Limit cycles occur when priming is increased again (p = 0.7, q = 0.6). (d) Limit cycles of greater amplitude but reduced frequency are evident when priming is increased further (p = 0.8, q = 0.6).
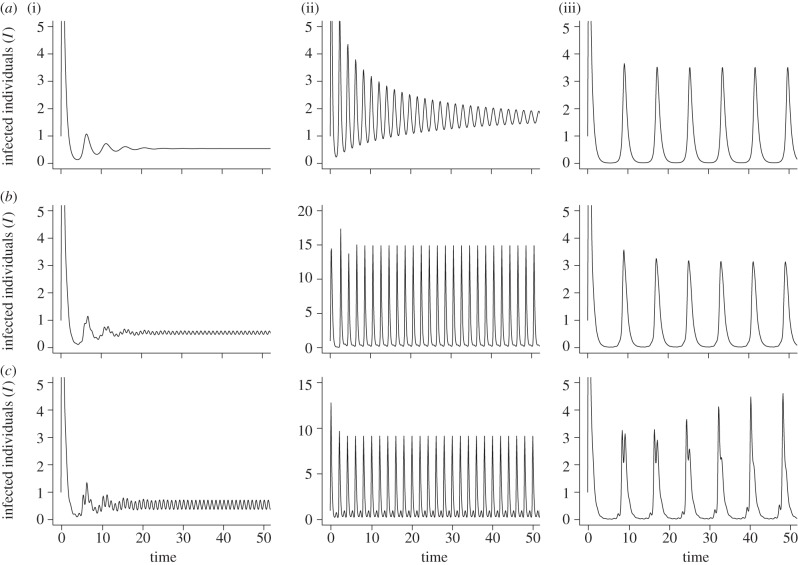
The addition of seasonality into the SPI model adds further complexity to the population dynamics. However, it appears that the forced dynamics can be accurately predicted from the non-forced dynamics (figure 4), so that small annual cycles occur in the forced system where there is a stable endemic equilibrium in the non-forced system (figure 4a), i.e. when priming rate is low. These small annual cycles are entirely owing to seasonal forcing, and are seen when both birth rate and transmission are forced. At intermediate priming rates, for specific model parameters, the non-forced system produces prolonged damped oscillations which, as in the SIR model, when combined with seasonality produce multi-year cycles (figure 4b). At high priming rates, the non-forced system and the forced birth rate system produce stable limit cycles. However, when transmission is forced, quasi-periodic solutions occur (figure 4c). These trajectories form a torus around the existing limit cycle and appear close to a regular cycle, but in fact never return to the same point and hence do not complete a true cycle [28].
Figure 4.
The dynamics of the SPI system with seasonality incorporated into the model. (i) Low priming rate (parameters: a = 2, b = 1, h = 0.1, p = 0.1, q = 0.2, α = 1, β = 2, τ = 0.2, c = 0, fY = 0.2, fP = 0.5). (ii) Intermediate priming rate (parameters: a = 5, b = 2, h = 0.1, p = 0.5, q = 0.7, α = 3.5, β = 2, τ = 0.5, c = 0, fY = 0.2, fP = 0.5), and (iii) high priming rate (parameters: a = 2, b = 1, h = 0.1, p = 0.8, q = 0.7, α = 1, β = 2, τ = 0.5, c = 0, fY = 0.2, fP = 0.5). (a) Original SPI model with fixed transmission and birth rate. Endemic equilibrium occurs at low priming, prolonged damped oscillations to endemic equilibrium at intermediate priming and endemic limit cycles at high priming. (b) SPI model with seasonal birth rate. Small annual cycles occur at low priming, multi-year cycles at intermediate priming and fewer, larger multi-year cycles at high priming. (c) SPI model with seasonal transmission rate. Annual cycles occur at low priming rate, large biennial cycles at intermediate priming rate and quasi-periodic cycles at high priming rate.
4. Discussion
By using a theoretical model, we have shown that immune priming alters the likelihood of persistence of a pathogen and has pronounced destabilizing effects on the dynamics of host–pathogen populations. Furthermore, we demonstrated that the effects of immune priming depend on: (i) the proportion of susceptible individuals that become primed; (ii) the level of protection on future exposure which immune priming provides, and importantly; (iii) the reproductive costs to the host of priming and infectiousness. In addition, seasonality in birth rate and, in particular, transmission further destabilize a system with immune priming. The difference in dynamics between traditional SIR-type models and the SPI model developed here highlights the need to consider immune priming, which may be a widespread phenomena, and the way in which immunity occurs more generally, when exploring and predicting infectious disease dynamics.
The focus of many host–pathogen studies is on the critical value of R0 = 1, where the pathogen is able to invade a disease-free host population. In traditional SIR models, this condition is identical to the condition of pathogen persistence in an endemic population. However, in the SPI system, we have shown that when a large proportion of hosts are immune-primed following exposure to a pathogen but priming does not result in full immunity, there can be bistability such that the pathogen can remain endemic when R0 < 1. This is owing to the ability of the pathogen to infect primed as well as susceptible hosts. To invade a disease-free population, the pathogen still requires R0 > 1 to spread quickly enough in the susceptible population to persist. However, if the disease is already endemic, even if the susceptible population is low such that R0 may be less than unity, the pathogen is still able to gain enough infections from primed hosts (albeit at a reduced rate) to persist in the population. This phenomenon is caused by a backward bifurcation at R0 = 1 and a subsequent fold bifurcation at a lower R0 value, and has also been found in models which consider vaccination strategies [29,30]. Clearly, this result has important consequences for disease control, because in a system that exhibits immune priming, simply reducing the pathogen R0 to less than unity, may not suffice to eradicate disease.
When disease affects fecundity in the SPI model, and priming rate is high, limit cycles occur, indicating instability. As primed individuals, as well as susceptible individuals can become infectious in the SPI system, the length of a disease epidemic may be longer than expected. This, combined with a reduction in replenishment of susceptibles owing to fecundity costs, means that instead of maintaining a stable endemic equilibrium, limit cycles occur where the population undergoes periodic crashes before increasing again. These limit cycles act as indicators of population instability as theoretically population crashes, with the addition of stochastic events, may result in epidemic fadeouts. In addition to systems exhibiting immune priming, limit cycles may also be found in systems where transmission is via free-living infectious stages [27], infection is sublethal [31] and there is latency between exposure and infection and immunity wanes over time [32]. However, limit cycles never result from basic classic models, including susceptible–infected, SIS or SIR even when fecundity costs of infection are present. Interestingly, while the advantages of immune priming at the individual level will probably be greatest for hosts that suffer a high reproductive cost of infection, results from the model suggest that the destabilizing effects of immune priming will be greatest in systems where the host incurs a high reproductive cost of infection. The duration for which hosts remain immune-primed is not well studied; however, the results of this model demonstrate that although limit cycles are most likely to occur when priming does not wane over time, limit cycles still persist in a population where organisms remain primed for only a short proportion of their lifespan. Specifically, cyclic population dynamics are seen when hosts remain primed for greater than one fifth of their lifespan (i.e. c < 5). Consideration of the population-level effects of priming as well as individual-level effects will be important when examining immune priming potential further and in an evolutionary context.
Seasonal fluctuations in environmental factors such as rainfall and temperature [33–35] influence host demographic factors such as birth and death rate [20,36] and epidemiological factors such as pathogen transmission and host immunity [37,38] and are well known to drive population dynamics. We have shown that the inclusion of seasonality in both birth rate and transmission add complexity to the population dynamics and add to the instability of the SPI system. Seasonal forcing in transmission rate has a greater impact on the dynamics than seasonal forcing in birth rate. This is concurrent with traditional human epidemiological models and is thought to be owing to the fact that changes in transmission effect the system over a shorter time period than changes in birth rate [20].
Evidence for a mechanism behind immune priming in invertebrates is limited. The presence of immune priming has been inferred empirically using many criteria including reduced fecundity costs of Pasteuria ramosa in D. magna from mothers exposed to this bacterium [12]. However, substantial evidence suggests that immune priming does result in reduced prevalence of the pathogen. Roth & Kurtz [39] showed that primed Porcellio scaber had greater phagocytotic activity leading to reduced prevalence of bacteria compared to controls. In addition, Tidbury et al. [10] found a reduced probability of infection with an obligate killer following previous exposure and therefore reduced prevalence of the pathogen in the population. Also, Sadd & Schmid-Hempel [9] showed increased clearance of bacteria in the haemolymph and therefore reduced prevalence in previously exposed B. terrestris compared with controls. Our model represents a natural form of immune priming where density-dependent exposure to pathogen in the environment does not always result in infectiousness but may increase protection on subsequent pathogen challenge. This model is therefore distinct from traditional human epidemiology models, including SIR models, where individuals are infectious prior to developing immunity, susceptible–exposed–infectious–recovered where there is a time lag between being exposed and becoming infectious, and vaccination models where individuals become immune independent of the abundance of the pathogen in the population. The damped oscillatory dynamics seen with traditional models compared with the cyclic dynamics seen with high priming in the SPI model reported here further highlight how different this model is from more traditional models. We do not investigate the implications of immune priming which may occur following recovery from infectiousness then subsequent exposure to a pathogen (i.e. S–I–S–P). However, we do not expect this to change the qualitative outcome of the SPI model but it presents an interesting avenue for further extension of the model.
For greatest clarity and applicability, some important features of insect–pathogen interactions have been excluded from the model. Often, there is a strong negative correlation between host development stage and susceptibility to pathogen infection, with early instar larvae being most susceptible and adults being completely resistant in some systems [6,40]. We find that transgenerational immune priming has less effect on disease prevalence than within generation immune priming, but the relative importance of within and transgenerational immune priming has been found to depend on the life-history-stage-specific nature of the host–pathogen interaction [41]. While there is no stage structure included in the SPI model, future investigations may benefit from the addition of stage structure. Also, we assume for simplicity, a single host–pathogen interaction but appreciate that complex multiple-host, multiple-pathogen interactions are common in nature [42]. There seems to be a lack of generality in the specificity of immune priming protection with some studies concluding that protection is general [43] while some studies find evidence for specificity of protection [9,39]. There is also evidence that immune priming to one pathogen may actually increase susceptibility to another pathogen [44]. The specificity of immune priming protection is likely to contribute to the population-level consequences of priming in complex interacting populations of hosts and pathogens, and requires further empirical and theoretical study.
Our primary focus has been on invertebrate systems, but priming of immunity may be more widespread. The key aspect of immune priming is that, when exposed to disease, hosts may quickly become immune and, crucially, without ever having become infectious. Exposure to a low level of pathogens that does not result in infectiousness is likely to feature in many host–pathogen interactions across multiple taxa. Although perhaps gaining little attention, instances may exist where humans and other animals test positive for pathogen antibodies without any evidence of infectiousness. There is therefore scope for this model to be applied to non-invertebrate systems including humans.
Immune priming has important implications for pathogen persistence and host–pathogen population dynamics. Immune priming, while beneficial for the individual host, may increase the persistence of pathogen and destabilize host–pathogen populations. This work has made general predictions of when this destabilization is likely to occur and we emphasize that immune priming needs consideration and inclusion into models of specific disease interactions in order to understand the host–pathogen dynamics accurately.
Acknowledgements
This work was funded by a Natural Environment Research Council studentship to H.T.
References
- 1.Murphy K., Travers T., Walport M. 2011. Janeway's immunobiology. New York, NY: Taylor and Francis [Google Scholar]
- 2.Rolff J., Reynolds S. E. 2009. Insect infection and immunity. New York, NY: Oxford University Press [Google Scholar]
- 3.Schmid-Hempel P. 2005. Evolutionary ecology of insect immune defenses. Annu. Rev. Entomol. 50, 529–551 10.1146/annurev.ento.50.071803.130420 (doi:10.1146/annurev.ento.50.071803.130420) [DOI] [PubMed] [Google Scholar]
- 4.Rowley A. F., Powell A. 2007. Invertebrate immune systems: specific, quasi-specific, or nonspecific. J. Immunol. 179, 7209–7214 [DOI] [PubMed] [Google Scholar]
- 5.Little T. J., Kraaijeveld A. R. 2004. Ecological and evolutionary implications of immunological priming in invertebrates. Trends Ecol. Evol. 19, 58–60 10.1016/j.tree.2003.11.011 (doi:10.1016/j.tree.2003.11.011) [DOI] [PubMed] [Google Scholar]
- 6.Tate A. T., Rudolf V. H. W. 2012. Impacts of life stage specific immune priming on invertebrate disease dynamics. Oikos 121, 1083–1092 10.1111/j.1600-0706.2011.19725.x (doi:10.1111/j.1600-0706.2011.19725.x) [DOI] [Google Scholar]
- 7.Roth O., Sadd B. M., Schmid-Hempel P., Kurtz J. 2009. Strain-specific priming of resistance in the red flour beetle, Tribolium castaneum. Proc. R. Soc. B 276, 145–151 10.1098/rspb.2008.1157 (doi:10.1098/rspb.2008.1157) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sadd B. M., Kleinlogel Y., Schmid-Hempel R., Schmid-Hempel P. 2005. Trans-generational immune priming in a social insect. Biol. Lett. 1, 386–388 10.1098/rsbl.2005.0369 (doi:10.1098/rsbl.2005.0369) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sadd B. M., Schmid-Hempel P. 2006. Insect immunity shows specificity in protection upon secondary pathogen exposure. Curr. Biol. 16, 1206–1210 10.1016/j.cub.2006.04.047 (doi:10.1016/j.cub.2006.04.047) [DOI] [PubMed] [Google Scholar]
- 10.Tidbury H. J., Pedersen A. B., Boots M. 2011. Within and transgenerational immune priming in an insect to a DNA virus. Proc. R. Soc. B 278, 871–876 10.1098/rspb.2010.1517 (doi:10.1098/rspb.2010.1517) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Moret Y., Siva-Jothy M. T. 2003. Adaptive innate immunity? Responsive-mode prophylaxis in the mealworm beetle, Tenebrio molitor. Proc. R. Soc. Lond. B 270, 2475–2480 10.1098/rspb.2003.2511 (doi:10.1098/rspb.2003.2511) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Little T. J., O'Connor B., Colegrave N., Watt K., Read A. F. 2003. Maternal transfer of strain-specific immunity in an invertebrate. Curr. Biol. 13, 489–492 10.1016/S0960-9822(03)00163-5 (doi:10.1016/S0960-9822(03)00163-5) [DOI] [PubMed] [Google Scholar]
- 13.Witteveldt J., Vlak J. M., van Hulten M. C. W. 2004. Protection of Penaeus monodon against white spot syndrome virus using a WSSV subunit vaccine. Fish Shellfish Immunol. 16, 571–579 10.1016/j.fsi.2003.09.006 (doi:10.1016/j.fsi.2003.09.006) [DOI] [PubMed] [Google Scholar]
- 14.Wu J. L., Nishioka T., Mori K., Nishizawa T., Muroga K. 2002. A time-course study on the resistance of Penaeus japonicus induced by artificial infection with white spot syndrome virus. Fish Shellfish Immunol. 13, 391–403 10.1006/fsim.2002.0414 (doi:10.1006/fsim.2002.0414) [DOI] [PubMed] [Google Scholar]
- 15.Pope E. C., Powell A., Roberts E. C., Shields R. J., Wardle R., Rowley A. F. 2011. Enhanced cellular immunity in shrimp (Litopenaeus vannamei) after ‘vaccination’. PLoS ONE 6, e20960. 10.1371/journal.pone.0020960 (doi:10.1371/journal.pone.0020960) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hauton C., Smith V. J. 2007. Adaptive immunity in invertebrates: a straw house without a mechanistic foundation. Bioessays 29, 1138–1146 10.1002/bies.20650 (doi:10.1002/bies.20650) [DOI] [PubMed] [Google Scholar]
- 17.Anderson R. M., May R. M. 1979. Population biology of infectious diseases. I. Nature 280, 361–367 10.1038/280361a0 (doi:10.1038/280361a0) [DOI] [PubMed] [Google Scholar]
- 18.Dietz K. 1967. Epidemics and rumours: survey. J. R. Stat. Soc. A Gen. 130, 505–528 10.2307/2982521 (doi:10.2307/2982521) [DOI] [Google Scholar]
- 19.Keeling M. J., Rohani P. 2008. Introduction to simple epidemic models. In Modeling infectious disease in humans and animals, pp. 15–53 Princeton, NJ: Princeton University Press [Google Scholar]
- 20.Altizer S., Dobson A., Hosseini P., Hudson P., Pascual M., Rohani P. 2006. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 9, 467–484 10.1111/j.1461-0248.2005.00879.x (doi:10.1111/j.1461-0248.2005.00879.x) [DOI] [PubMed] [Google Scholar]
- 21.Fine P. E. M., Clarkson J. A. 1982. Measles in England and Wales. I. An analysis of factors underlying seasonal patterns. Int. J. Epidemiol. 11, 5–14 10.1093/ije/11.1.5 (doi:10.1093/ije/11.1.5) [DOI] [PubMed] [Google Scholar]
- 22.Finkenstadt B. F., Grenfell B. T. 2000. Time series modelling of childhood diseases: a dynamical systems approach. J. R. Stat. Soc. C Appl. Stat. 49, 187–205 10.1111/1467-9876.00187 (doi:10.1111/1467-9876.00187) [DOI] [Google Scholar]
- 23.London W. P., Yorke J. A. 1973. Recurrent outbreaks of measles, chickenpox and mumps. 1. Seasonal variation in contact rates. Am. J. Epidemiol. 98, 453–468 [DOI] [PubMed] [Google Scholar]
- 24.Griffith D. A. 1973. Effect of measles vaccination on incidence of measles in community. J. R. Stat. Soc. A Stat. Soc. 136, 441–449 10.2307/2344999 (doi:10.2307/2344999) [DOI] [Google Scholar]
- 25.Heffernan J. M., Keeling M. J. 2009. Implications of vaccination and waning immunity. Proc. R. Soc. B 276, 2071–2080 10.1098/rspb.2009.0057 (doi:10.1098/rspb.2009.0057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Doedel E., Champneys A. R., Fairgrieve T. F., Kuznetsov Y. A., Sandstede B., Wang X. 1997. AUTO 97: user's guide. Montreal, Canada: Concordia University [Google Scholar]
- 27.Anderson R. M., May R. M. 1981. The population-dynamics of micro-parasites and their invertebrate hosts. Phil. Trans. R. Soc. Lond. B 291, 451–524 10.1098/rstb.1981.0005 (doi:10.1098/rstb.1981.0005) [DOI] [Google Scholar]
- 28.Rinaldi S., Muratori S., Kuznetsov Y. 1993. Multiple attractors, catastrophes and chaos in seasonally perturbed predator prey communities. Bull. Math. Biol. 55, 15–35 [Google Scholar]
- 29.Arino J., McCluskey C. C., Van den Driessche P. 2003. Global results for an epidemic model with vaccination that exhibits backward bifurcation. SIAM J. Appl. Math. 64, 260–276 10.1137/S0036139902413829 (doi:10.1137/S0036139902413829) [DOI] [Google Scholar]
- 30.Kribs-Zaleta C. M., Velasco-Hernandez J. X. 2000. A simple vaccination model with multiple endemic states. Math. Biosci. 164, 183–201 10.1016/S0025-5564(00)00003-1 (doi:10.1016/S0025-5564(00)00003-1) [DOI] [PubMed] [Google Scholar]
- 31.Boots M., Norman R. 2000. Sublethal infection and the population dynamics of host-microparasite interactions. J. Anim. Ecol. 69, 517–524 10.1046/j.1365-2656.2000.00417.x (doi:10.1046/j.1365-2656.2000.00417.x) [DOI] [Google Scholar]
- 32.Greenhalgh D. 1997. Hopf bifurcation in epidemic models with a latent period and nonpermanent immunity. Math. Comp. Model. 25, 85–107 10.1016/S0895-7177(97)00009-5 (doi:10.1016/S0895-7177(97)00009-5) [DOI] [Google Scholar]
- 33.Hoshen M. B., Morse A. P. 2004. A weather-driven model of malaria transmission. Malaria J. 3, 32. 10.1186/1475-2875-3-32 (doi:10.1186/1475-2875-3-32) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pascual M., Bouma M. J., Dobson A. P. 2002. Cholera and climate: revisiting the quantitative evidence. Microbes Infect. 4, 237–245 10.1016/S1286-4579(01)01533-7 (doi:10.1016/S1286-4579(01)01533-7) [DOI] [PubMed] [Google Scholar]
- 35.Waller P. J., Rudby-Martin L., Ljungstrom B. L., Rydzik A. 2004. The epidemiology of abomasal nematodes of sheep in Sweden, with particular reference to over-winter survival strategies. Vet. Parasitol. 122, 207–220 10.1016/j.vetpar.2004.04.007 (doi:10.1016/j.vetpar.2004.04.007) [DOI] [PubMed] [Google Scholar]
- 36.Pathak A. K., Boag B., Poss M., Harvill E. T., Cattadori I. M. 2011. Seasonal breeding drives the incidence of a chronic bacterial infection in a free-living herbivore population. Epidemiol. Infect. 139, 1210–1219 10.1017/S0950268810002311 (doi:10.1017/S0950268810002311) [DOI] [PubMed] [Google Scholar]
- 37.Bjornstad O. N., Finkenstadt B. F., Grenfell B. T. 2002. Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Ecol. Monogr. 72, 169–184 [Google Scholar]
- 38.Cattadori I. M., Boag B., Bjornstad O. N., Cornell S. J., Hudson P. J. 2005. Peak shift and epidemiology in a seasonal host–nematode system. Proc. R. Soc. B 272, 1163–1169 10.1098/rspb.2004.3050 (doi:10.1098/rspb.2004.3050) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roth O., Kurtz J. 2009. Phagocytosis mediates specificity in the immune defence of an invertebrate, the woodlouse Porcellio scaber (Crustacea: Isopoda). Dev. Comp. Immunol. 33, 1151–1155 10.1016/j.dci.2009.04.005 (doi:10.1016/j.dci.2009.04.005) [DOI] [PubMed] [Google Scholar]
- 40.Kirkpatrick B. A., Washburn J. O., Volkman L. E. 1998. AcMNPV pathogenesis and developmental resistance in fifth instar Heliothis virescens. J. Invertebr. Pathol. 72, 63–72 10.1006/jipa.1997.4752 (doi:10.1006/jipa.1997.4752) [DOI] [PubMed] [Google Scholar]
- 41.Tate A. T., Rudolf V. H. W. 2011. Impact of life stage specific immune priming on invertebrate disease dynamics. Oikos 121, 1083–1092 10.1111/j.1600-0706.2011.19725.x (doi:10.1111/j.1600-0706.2011.19725.x) [DOI] [Google Scholar]
- 42.Rigaud T., Perrot-Minnot M.-J., Brown M. J. F. 2010. Parasite and host assemblages: embracing the reality will improve our knowledge of parasite transmission and virulence. Proc. R. Soc. B 277, 3693–3702 10.1098/rspb.2010.1163 (doi:10.1098/rspb.2010.1163) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Siva-Jothy M. T., Moret Y., Rolff J. 2005. Insect immunity: an evolutionary ecology perspective. Adv. Insect Physiol. 32, 1–48 10.1016/S0065-2806(05)32001-7 (doi:10.1016/S0065-2806(05)32001-7) [DOI] [Google Scholar]
- 44.Sadd B. M., Schmid-Hempel P. 2009. A distinct infection cost associated with trans-generational priming of antibacterial immunity in bumble-bees. Biol. Lett. 5, 798–801 10.1098/rsbl.2009.0458 (doi:10.1098/rsbl.2009.0458) [DOI] [PMC free article] [PubMed] [Google Scholar]