Dynamic self-cleaning in gecko setae via digital hyperextension

Abstract

Gecko toe pads show strong adhesion on various surfaces yet remain remarkably clean around everyday contaminants. An understanding of how geckos clean their toe pads while being in motion is essential for the elucidation of animal behaviours as well as the design of biomimetic devices with optimal performance. Here, we test the self-cleaning of geckos during locomotion. We provide, to our knowledge, the first evidence that geckos clean their feet through a unique dynamic self-cleaning mechanism via digital hyperextension. When walking naturally with hyperextension, geckos shed dirt from their toes twice as fast as they would if walking without hyperextension, returning their feet to nearly 80 per cent of their original stickiness in only four steps. Our dynamic model predicts that when setae suddenly release from the attached substrate, they generate enough inertial force to dislodge dirt particles from the attached spatulae. The predicted cleaning force on dirt particles significantly increases when the dynamic effect is included. The extraordinary design of gecko toe pads perfectly combines dynamic self-cleaning with repeated attachment/detachment, making gecko feet sticky yet clean. This work thus provides a new mechanism to be considered for biomimetic design of highly reuseable and reliable dry adhesives and devices.

1. Introduction

Gecko feet are sticky on almost any surface, but in order to be functional through thousands of cycles of stick and release in natural environments, they must remain relatively free of dust and other debris. The extraordinary ability of gecko feet to be both sticky and clean presumably stems from their hierarchical fibrillar adhesive system, which consists of millions of micro-fibrils, called setae, with billions of nano-sized branches, terminating in small plates called spatulae [1–5]. Efforts to mimic gecko toe pad structure and function seek to develop a new class of advanced adhesives that are not only sticky, but also non-fouling. An impressive variety of synthetic mimics that capture the adhesive qualities of the gecko system has already been developed [6–15]. Some prominent examples include designs based on photoresist nanorods on solid micropillar-supported platforms and micropaddles [7,9], polyurethane microfibres with angled mushroom tips [10], micro- and nano-integrated hierarchical polymeric hairs [11], and carbon nanotube brushes/forests [14,15]. Notably, the adhesion of some synthetics has even reached up to 1000 KPa [15,16], about 10 times higher than what a gecko can achieve. Given this success, it is striking that the non-fouling performance of both the gecko and synthetic adhesive systems has received comparatively little attention. However, this non-fouling property is fundamental to the desire to produce innovative adhesives that work under circumstances where traditional pressure sensitive adhesives fail. It is therefore crucial to explore how geckos combine high adhesion and self-cleaning together within their toe pads.

A few possible self-cleaning mechanisms have been proposed, including: (i) an ultra-hydrophobic surface that resists unwanted adhesion [17–20], and (ii) the lotus effect [21,22]. These mechanisms, however, which arise from hydrophobic surfaces with micro- and nano-roughness combined topology, do not explain self-cleaning in gecko toe pads. More recently, it was suggested that setal self-cleaning occurs owing to an energetic disequilibrium between the adhesive force attracting a dirt particle to the substrate and those attracting the same particle to one or more spatulae [23]. In other words, small solid particles may bind more strongly to the substrate surface (e.g. a stone wall or glass) than to the constituents of toe pad (i.e. setae or spatulae), such that after pressing and dragging a contaminated setal array or toe pad against a clean surface, the particles are removed and deposited onto the opposing surface. However, this mechanism was proposed based on the empirical measurements of self-cleaning in isolated setal arrays and intact gecko toes by simulated ‘steps’. The natural pealing motion, digital hyperextension (DH), which many geckos use, was not included in their experiments because the rate at which toes move during DH was concluded to be too slow to measurably affect the rate of self-cleaning [23].

Here, we demonstrate that when walking naturally across a surface and scrolling their toe pads using DH, geckos clean their feet more rapidly than previously suggested. The rate and extent of the self-cleaning in unrestrained geckos are two times higher than those without DH or previously reported for arrays of setae isolated from geckos and extrinsically manipulated gecko toes [23]. We report an intrinsic dynamic self-cleaning mechanism that is associated with both the gecko toe pad structure and animal-induced motion. A mathematical model accounting for dynamics under the influence of DH explains the self-cleaning phenomena observed at the whole animal scale, and the general observation that gecko toes remain highly functional in free-ranging animals even when they move on dirty surfaces. The work here thus reveals a new direction for biomimetic design of highly reuseable and reliable dry adhesives and devices.

2. Material and methods

We obtained 10 Gekko gecko (Tokay gecko) from California Zoological Supply. Gekko gecko is a nocturnal gecko found in Southeast Asia. Geckos weighed between 56 and 100 g, with snout-vent lengths ranging between 12.9 and 15.2 cm. All geckos were housed and maintained as described in Niewiarowski et al. [24].

All experimental trials were conducted in a walk-in environmental chamber maintained at 25 ± 1°C and 55 ± 2 per cent relative humidity. We used a custom-designed apparatus with glass as a substrate to estimate maximum clinging force of individual geckos (for further explanation, see Niewiarowski et al. [24]). For all trials, the apparatus was held in a horizontal position, and shear forces were tested by pulling on the gecko in a direction parallel to the surface. Silica particles, ranging from 5 to 50 µm diameter, were used as a fouling agent for the gecko's feet. Clinging force was recorded as the maximum force immediately prior to all four feet of the gecko slipping. A trial consisted of placing a gecko on the clean glass of our force apparatus and measuring its clinging capacity under different conditions through multiple ‘pulls’ in quick succession. The first pull was with clean feet. Subsequent to the initial ‘clean’ pull, the gecko was slowly lowered onto a glass tray filled with silica dust until it supported its own body weight, and all four feet were in contact with the dust. A second ‘dirty’ pull was then immediately conducted identically to the ‘clean’ pull. To collect data for self-cleaning, trials were conducted as described earlier, except that following the fouling induced by exposure to silica dust, the gecko was lowered onto the clean glass substrate and induced to walk. Once at rest, the number of steps taken was recorded and clinging force measured as mentioned earlier. After each and every trial, the glass was cleaned with ethanol and allowed to dry. This sequence in protocols allowed us to estimate self-cleaning rate as in Hansen & Autumn [23], where clinging ability when fouled is compared directly with the clinging ability when clean. Finally, subsequent to any trial in which we applied silica dust to the feet of geckos, we thoroughly washed them with water to remove any remaining particles.

Trials with animals unable to use DH were conducted exactly as mentioned earlier but prior to the start of a trial, each gecko was fitted with custom-designed ‘gecko shoes’ (figure 1a,b). ‘Gecko shoes’ were constructed to restrict the extent of DH possible (figure 1c,d) without blocking access of toe pads to the substrate. Geckos fitted with ‘shoes’ could still walk, but only with minimal to zero capacity for DH. ‘Shoes’ were made from adhesive ends of BAND-AID Tough-Strips (each BAND-AID made two ‘gecko shoes’). Strips were applied to the dorsal surface of the foot and then a very thin, flexible, adhesive, aluminium strip was laid over the top of the BAND-AID. These ‘shoes’ were easily removed by peeling with no discernible effect on the underlying skin. The ‘shoes’ were also extremely lightweight.

Figure 1.

(a) Tokay gecko with fitted ‘braces’ (i.e. ‘gecko shoes’) that prevented digital hyperextension but allowed the animal to walk, adhere to the surface, and release. (b) Close-up of the ‘gecko shoe’ on the dorsal surface of a gecko foot. A gecko foot showing toes in (c) flat and (d) hyperextended positions without the ‘shoe’.

Statistical analyses were conducted to account for the experimental design in which every gecko was exposed to all possible treatment combinations, a repeated measures analysis of variance. Dependent variables were transformed when necessary to satisfy assumptions of parametric analysis.

3. Results

3.1. Self-cleaning of toe pads in unrestrained geckos

We assayed the self-cleaning ability of live geckos walking naturally across a horizontal, clean glass surface under two different conditions. After dusting gecko feet with silica particles, we allowed geckos to freely walk across a clean glass surface, with or without custom-fitted toe braces that prohibited toe scrolling (DH). In both cases, geckos were able to adhere to the glass such that we could measure the shear forces they generated [24] as a function of the number of steps taken before they voluntarily stopped. Data collected over a large number of trials allowed us to compare shear forces generated by geckos with dirtied feet after taking from one to up to eight steps. We used a recovery index (RI), the proportion of adhesion strength when feet are dirty relative to that when feet are clean, to estimate rate and extent of self-cleaning [23].

All geckos showed improved adhesion (self-cleaning) with each step taken (RI; F_3,10 = 12.7, p < 0.001; figure 2), but geckos that were able to use DH when they took steps experienced a self-cleaning rate that was approximately twice as fast as geckos that could walk but not use DH (steps × DH; F_4,7 = 5.26, p < 0.002; figure 2). Moreover, geckos using DH ended up with a greater degree of self-cleaning that approached 80 per cent of clean forces after just four steps. Note that after five steps, the 95% confidence interval of the average recovery rate is very close to 100 per cent recovery, suggesting that after just five or six steps with DH enabled, adhesion of self-cleaned toes would be statistically indistinguishable from toes that were never exposed to dust. On the other hand, the extent of self-cleaning levelled off for geckos not able to use DH, stalling at approximately 40–50% even after taking eight steps. In general, self-cleaning in geckos without DH began to level off after approximately four steps (figure 2). Rates and extent of self-cleaning for geckos without DH in our study are very comparable to previously reported self-cleaning rates in isolated setal arrays and intact gecko toes manipulated through simulated stick and release cycles [23].

Figure 2.

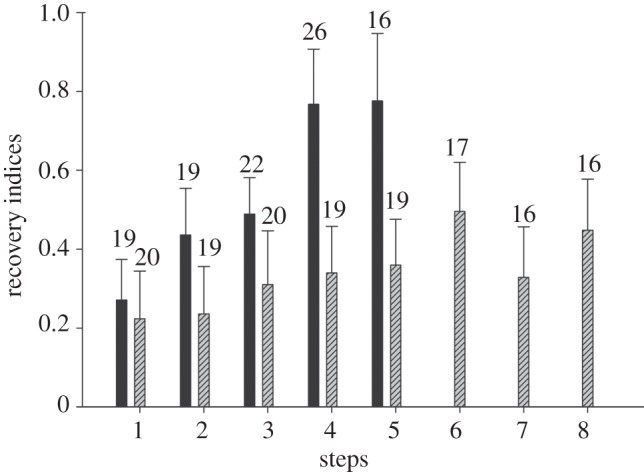
Recovery indices for trials with (black bars) and without digital hyperextension by steps (striped bars). Numbers above bars are sample sizes. Error bars represent ± 2 s.e.

Geckos with clean feet and the ability to hyperextend their toes were able to adhere to a glass substrate with an average force (15.7 ± 3.6 N; mean ± 2 s.e.) roughly equal to 20 times that required to support their body weight; however, the force decreased by nearly a factor of six with dirtied toes (2.59 ± 2.63 N). Geckos unable to perform DH generated force (5.8 ± 2.14 N) about one-third as great when clean without shoes, but still substantially higher than that required to support their body weight. When dirtied, adhesive force fell close to that required to support average body weights of the largest animals in our sample (0.85 ± 1.50 N). The absolute clinging force generated by geckos with clean feet and the ability to use hyperextension was greater than that generated by geckos with clean feet and lacking the ability to hyperextend. However, the rate at which self-cleaning occurred was not related to the magnitude of the clean clinging force recorded for an individual, only to whether toes could hyperextend or not (covariate = maximum clean adhesion in ANCOVA; F_1,10 = 1.6, p > 0.23; not significant). Thus, DH plays a major role in self-cleaning of gecko feet.

3.2. Observations of dirt particles on live gecko toe pads

We examined the toe pad structure of a live gecko using optical microscopy (Mitutoyo America Corporation, FS-70 Series 378-Microscope Unit). A gecko was coaxed to adhere to a glass plate allowing us to capture images when the foot was clean (never dirtied), right after it had been dirtied, and after it walked freely with DH through eight steps; we were also able to capture an image of the footprint after the first step was taken (figure 3). Although the effect of DH on self-cleaning could not be quantitatively evaluated by counting the particles removed for each step, significant removal of dirt particles was clearly evident (figure 3a–c). After eight steps of free walking, the toe pad returned nearly to its original state (figure 3a,c). Larger particles are more likely to be deposited onto the glass surface compared with smaller particles especially for those stuck in between lamellae: the footprint after one step contained many of the larger particles within the gap between setal arrays (figure 3d), while the remaining particles after self-cleaning appear substantially smaller (figure 3c).

Figure 3.

Optical micrographs of live gecko toe pads adhering to a glass surface when (a) it is clean (never dirtied), (b) right after dirtied, (c) self-cleaned by eight steps of free walking with digital hyperextension on clean glass substrate, and (d) the footprint after one step. Arrows in (c) point to some of the remaining dirt particles that can be easily identified after eight steps of self-cleaning.

4. Discussion

4.1. Gecko detachment mechanisms with and without digital hyperextension

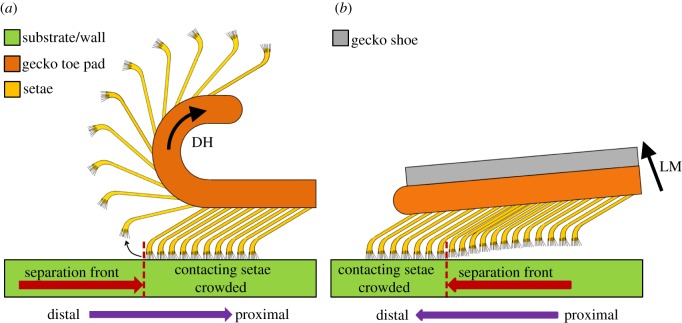
Our experimental results demonstrate that DH has a significant effect on the self-cleaning experienced by geckos walking on a smooth and clean substrate. Because self-cleaning occurs after each toe pad detachment (figure 2), analysing the detachment mechanisms with and without DH is crucial for understanding this strong correlation.

When walking naturally, before taking each step, geckos peel their toe pads from the substrate by scrolling their toes from a distal to a proximal direction under the action of DH (see figure 1c,d and the electronic supplementary material, movie S1). If we model toe pad scrolling as a rolling motion of a circle with setal arrays along a horizontal plane, where each seta is lifted sequentially, then its trajectory follows the corresponding cycloid (figure 4; e.g. from point A to A′). Specifically, the pad motion will sequentially exert on the setal roots, a vertical displacement of Δy = r(1 − cos θ) and a lateral displacement of Δx = r(θ − sin θ), depending on the particular location of each seta, where r is the scrolling radius of the toe pad (i.e. the radius of rolling circle) and θ is the rotation angle of a seta in radians.

Figure 4.

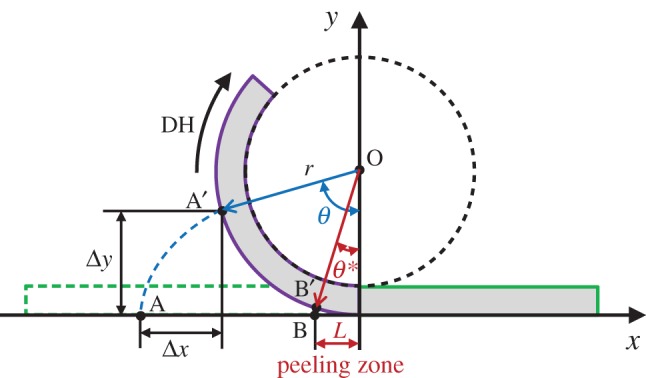
A schematic of the toe pad scrolling motion under DH, which is modelled as a rolling motion of a circle, with a radius r, along a horizontal plane. The trajectory (e.g. from point A to A′) follows the corresponding cycloid curve (e.g. blue-dashed line) depending on the particular location of each seta. Point B′ is the critical separation point of setae with respect to the substrate/wall, which determines the length of a peeling zone, L. θ* is the critical rotation angle that generates the cycloid curve from point B to B′. (Online version in colour.)

It has been measured that a single seta could sustain pull-off forces of approximately 40 µN in the normal direction (90°) and approximately 200 µN in shear (less than 30°), whether the substrate is hydrophobic or hydrophilic [4,25]. For an isolated setal array, detaching strength maintains relatively constant, when the detaching angle is varied from 30° to 90° under a load-drag preloading condition [26]. Such a high adhesion force at the microscale will lead to setal jumping off during toe pad scrolling. This jump-off event is a common phenomenon that has been observed in many other systems such as atomic force microscope pull-off tests for measuring micro-/nano-adhesion [25,27–31] and single carbon nanotube peeling tests [32,33].

Even though individual setae experience a relatively large adhesion force during their jump-off in the detachment, the total peeling force on the whole toe pad is comparatively small relative to that generated in attachment. Using the scrolling model mentioned earlier, at any instance of toe pad scrolling only a fraction of the setae generate adhesion forces that are contributing to the overall peeling force experienced by geckos. This region is defined as a peeling zone possessing a constant length, L, in the x-direction (figure 4), which is determined by the maximum displacement of the setae before jump-off and the scrolling radius r (i.e. L = r × θ*). The adhesion force on individual setae in the peeling zone, F_w–s, can be related to the displacement of each seta in the y-direction, Δy, by the beam theory:

4.1

where subscripts ‘w’ and ‘s’ represent wall and seta, respectively, while l, E and I are the setal length, Young's modulus and the second moment of area, respectively. At the point of setal jump-off, assuming F_w–s = 10 µN, the maximum displacement of individual setae in the y-direction is calculated as Δy_max = 18.6 µm by taking l = 120 µm, E = 2 GPa and diameter of seta d_s = 4.2 µm for calculating I. The averaged toe pad area for a single toe is measured as 24.2 mm² with length of 9.42 mm and width of 2.57 mm, and the scrolling radius is captured as approximately 3 mm in the animal trials. According to the cycloid, taking r = 3 mm and Δy_max = 18.6 µm, we get Δx_max = 0.68 µm (i.e. displacement from point B to B′ in the x-direction; figure 4), and a critical rotation angle θ* = 0.11 for the peeling zone. Therefore, the peeling motion is mostly lifting the setal root up rather than dragging it parallel with respect to the substrate before jump-off, indicating that the experimentally measured vertical pull-off force (e.g. a 90° pulling in Autumn et al. [25]) could be adopted for our approximation. On this basis of calculation, the length of the peeling zone and the force distribution in the peeling zone can be determined by equation (4.1) and the scrolling geometry (i.e. r in figure 4). Taking the values of setal density, 14 400 setae mm⁻² [25], and assuming that setae distribute in a square lattice configuration, we get a setal spacing of approximately 8.3 µm. Integrating the reaction forces on the setae over the peeling zone, we obtain a total peeling force of 4.2 mN, which is three orders of magnitude lower than the shearing force of a single toe at lower angles when clean [34]. Thus, geckos can easily detach their toes through the sequential setal jump-off activated by DH.

Because the sequential setal jump-off can generate high inertial forces, we hypothesize that it contributes to the higher cleaning rate. During the hyperextended peeling, setal arrays on each toe roll up and spread out progressively from the substrate, as schematically shown in figure 5a. The pad scrolling lifts the setal root, whereas the spatulae at the setal tip are adhering to a substrate/wall, or dirt particles, or both. This scrolling motion builds up elastic energy in each contacting seta within the peeling zone and eventually causes it to dynamically jump-off at a critical separation point (i.e. B′ in figure 4; separation front in figure 5a), generating inertial force high enough to dislodge dirt particles. As will be discussed in the following sections, this dynamic self-cleaning mechanism is unique to gecko toe structures.

Figure 5.

Schematics of gecko toe peeling induced by (a) digital hyperextension (DH) from distal to proximal direction without gecko shoe and by (b) limb motion from proximal to distal direction with gecko shoe.

By contrast, when geckos wear the ‘shoes’, DH is disabled during animal walking. Without the help of DH, geckos must lift their limbs to detach toes from the substrate. We observed that this limb motion (LM) results in a proximal-to-distal peeling of the toe pads in a crack growth manner, as schematically shown in figure 5b, which is in the opposite direction to that with DH enabled. The change in peeling mechanism leads to a crowding of the restricted setal arrays ahead of the possible jump-off direction at the separation front (figure 5b). Consequently, the setal jump-off is substantially inhibited, and the static and passive self-cleaning takes over.

It should be clarified that LM or the toe pad scrolling alone can also generate inertial force at the setal tip, but its magnitude is in the order of 100 times lower than that required to remove the particles from setae [23], which is not the dynamic effect proposed and discussed later.

4.2. Dynamic self-cleaning mechanism

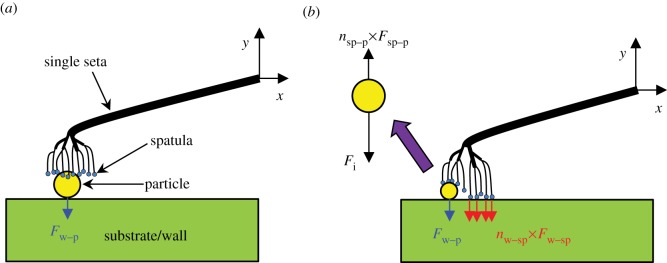
To demonstrate the dynamic self-cleaning mechanism owing to setal jump-off activated by DH, we calculate the inertial force that could separate dirt particles from setae during setal rolling. We first consider two possible configurations when a seta contacts the interface: (i) a seta contacting particles on a substrate/wall while being totally blocked from reaching the substrate/wall (the number of spatulae attaching on the substrate/wall n_w–sp = 0; figure 6a), and (ii) a seta contacting particles on a substrate/wall while being partially or entirely exposed to the substrate/wall (0 < n_w–sp ≤ total number of spatulae within a single seta; figure 6b).

Figure 6.

Single seta detachment during setal rolling: (a) a particle adhering to both the spatular braches of a single seta and substrate/wall, totally blocking the seta from reaching the substrate/wall (n_w–sp = 0), and (b) a particle adhering to some of the spatular branches of a single seta and the substrate/wall, while partially/not blocking the seta from the substrate/wall (0 < n_w–sp ≤ total number of spatulae within a seta). (a,b) configurations, the particles are in contact with the substrate/wall. n_sp–p × F_sp–p = F_s–p; n_w–sp × F_w–sp = F_w–s, where subscripts ‘sp’, ‘p’, ‘s’ and ‘w’ refer to spatula, particle, seta and wall, respectively.

A single seta is modelled as a cantilever beam with length l, diameter d_s and mass m_s. For the first configuration (figure 6a), when the adhesion force between the seta and particle, F_s–p, is smaller than that between the wall and particle, F_w–p, (F_s–p < F_w–p), the particle will stay on the wall while being separated from the seta upon setal retraction. This self-cleaning mechanism is static and passive, based on an energetic disequilibrium, and has been proposed as the primary basis for gecko self-cleaning [23]. In the case of F_s–p > F_w–p, the particle will separate from the wall but still adhere to the seta at a critical point. The sudden release of the seta along with the attached particle will generate inertial force F_i on both the setal tip and the particle. According to the beam theory, maximum acceleration of the setal tip can be determined as

4.2

where y_max is the bending displacement at the setal tip and f is the natural frequency. With y_max = F_w–pl³/3EI, and 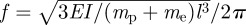, where EI is the bending stiffness of seta and m_e = 33m_s/140 is the effective mass of seta [35], we have a_max = F_w–p/(m_p + 33m_s/140). The maximum inertial force acting on the particle is then described as

4.3

From equation (4.3) we have F_i < F_w–p < F_s–p, which implies that as long as the seta is being pulled off the wall, the particle will stay on the setal tip and self-cleaning will never happen. Therefore, self-cleaning is governed by the static and passive mechanism when setae are being totally blocked by dirt particles from target surfaces.

The setae of Tokay geckos each contain approximately 1000 spatulae and each spatula generates about 10 nN adhesion force on glass [4,36]. The inertial force that a particle experiences at setal retraction (i.e. setal jump-off event) will be significantly greater if a fraction of spatulae adhere to the glass wall (n_w–sp > 0), as in the case of second configuration (figure 6b). Here, we designate the attractive force between the wall and seta as F_w–s, and the inertial force becomes

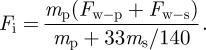4.4

Hence, the inertial force, F_i, increases with increasing F_w–s for a given particle.

To quantitatively determine the inertial force as a function of particle size, we first derive the interaction force between the wall and particle, F_w–p, by taking the derivative of the interaction energy [37], as

4.5

where D denotes the distance between the wall and particle, H_w–p is the Hamaker constant for wall–particle interactions and R_p is the radius of the particle. There is a cut-off gap distance, D = D_w–p, representing the effective separation between the wall and particle, at which maximum attractive force is estimated [37]. Second, F_w–s is determined by assuming that a number of spatular branches within a single seta adhere to the glass wall (i.e. F_w–s = n_w–sp × F_w–sp), each of which generates 10 nN adhesion force [36]. Combining equations (4.4) and (4.5), we plot the force ratio F_i/F_w–p as a function of particle radius, R_p, in figure 7, with different numbers of exposed spatulae to the wall (n_w–sp = 0, 100 and 200).

Figure 7.

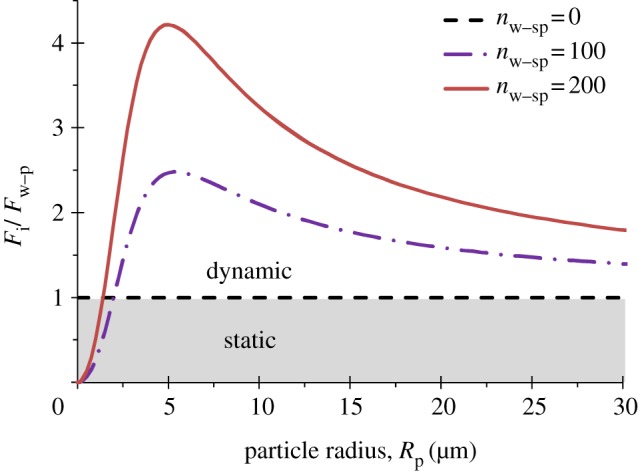
The ratio F_i/F_w–p as a function of particle radius R_p for a number of spatular branches within a single seta adhering to the wall (n_w–sp = 0, 100 and 200). Each spatula is assumed to generate an adhesion force F_w–sp = 10 nN if contacting the wall. (Online version in colour.)

In the calculation, a density of ρ_p = 2.65 g cm⁻³ is used for spherical silica particles to calculate m_p, and d_s = 4.2 µm, l = 120 µm and density of seta ρ_s = 1.36 g cm⁻³ to calculate m_s in equation (4.4). H_w–p = 6 × 10⁻²⁰ J and D_w–p = 0.3 nm are taken as the wall–particle interaction parameters in equation (4.5) [37]. Our results show that even when only 10 per cent of spatula attach on the wall (i.e. n_w–sp = 100), the ratio of F_i/F_w–p is in the range of 1.5–2.5 for particle size R_p ranging from 2.5 to 25 µm (figure 7), which is the size distribution of silica particles used in the animal trials. This suggests that the dynamic effect can overcome substantially higher adhesion force between the seta and particle, F_s–p, than that in the static self-cleaning mechanism. As more dirt particles are removed by each step, the fraction of spatulae exposed to the wall becomes larger (i.e. n_w–sp increases with step), and consequently the dynamic effect is more effective.

As seen in figure 7, the inertial force is quite low for small particles (e.g. R_p < 1.5 µm). However, for such small particles, it is likely that each particle adheres only to a few or a single spatula [23]. We have estimated interaction force between a single spatula and a small particle, F_sp–p, assuming that the spatula tip is round with radius R_sp, and taking the derivative of the interaction energy [37], as

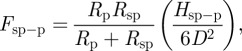4.6

where D is the distance between the spatula and particle, D_sp–p is the cut-off gap distance at which the attractive force, F_sp–p reaches a maximum value and H_sp–p is the Hamaker constant for spatula–particle interaction. We assume that H_sp–p ≈ H_w–p and D_sp–p ≈ D_w–p, which are reasonable for most materials systems [37]. Dividing equation (4.6) by equation (4.5) yields force ratio as

4.7

According to equation (4.7), in the case of single spatula attaching to a small particle, the force between the wall and particle is always larger than that between the spatula and particle, F_w–p > F_sp–p, which suggests that a small particle adhering to a single spatula could always be removed through the static self-cleaning mechanism if the particle contacts the wall.

It is possible that the particles adhering to a seta do not contact the wall at all. In this situation, F_w–p = 0 as shown in figure 6, indicating that the static self-cleaning mechanism becomes ineffective. However, the particles are not blocking the seta to reach the target surface. The spatulae on the same seta are more probably adhering to the wall (i.e. n_w–sp > 0 or F_w–s > 0) comparing with the configurations shown in figure 6. With more exposed spatular branches to the wall, the particles ought to experience a larger inertia to separate themselves from the seta during setal retraction. Using the same formula as equation (4.4), we calculated the inertial force on a particle that only adheres to a seta being pulled away from a wall (figure 8). The inertial force, F_i, generated at the setal jump-off event increases linearly with the wall-seta interaction force, F_w–s, for different particle sizes (figure 8a). The higher the adhesion force, F_w–s, the larger the dynamic effect becomes. Figure 8b shows the inertial force, F_i, as a function of particle radius, R_p, for given numbers of spatulae within the seta adhering to the wall. As the particle size increases, the inertial force, F_i, rapidly increases at first but levels off beyond R_p = 5 µm. However, as the particle radius increases to the size comparable to setal spacing (approx. 8 µm), it is more likely that the particle contacts the substrate. Therefore, the self-cleaning mechanism may change to the static or the dynamic one mentioned earlier in figure 6. For substantially larger particles, gravitational force overrides the surface phenomena, and geckos are not able to pick them up. In our experiment, we have observed that larger particles are more likely to be deposited onto the glass surface compared to smaller particles after one step (figure 3d). In general, if the inertial force defeats the adhesion force between the seta and particle (F_i > F_s–p), then the particle will be dislodged at the jump-off event. For example, if F_w–s = 400 nN (assuming n_w–sp = 40), a 2.5-µm-radius silica microsphere (m_p = 1.7 × 10⁻¹³ kg) adhering only to the seta is acted on by an inertial force F_i = 100 nN, one order of magnitude higher than the force of a single spatula (approx. 10 nN) [36]. This suggests that a particle can be efficiently removed by inertia even if it adheres to multiple spatulae, in this case up to 10.

Figure 8.

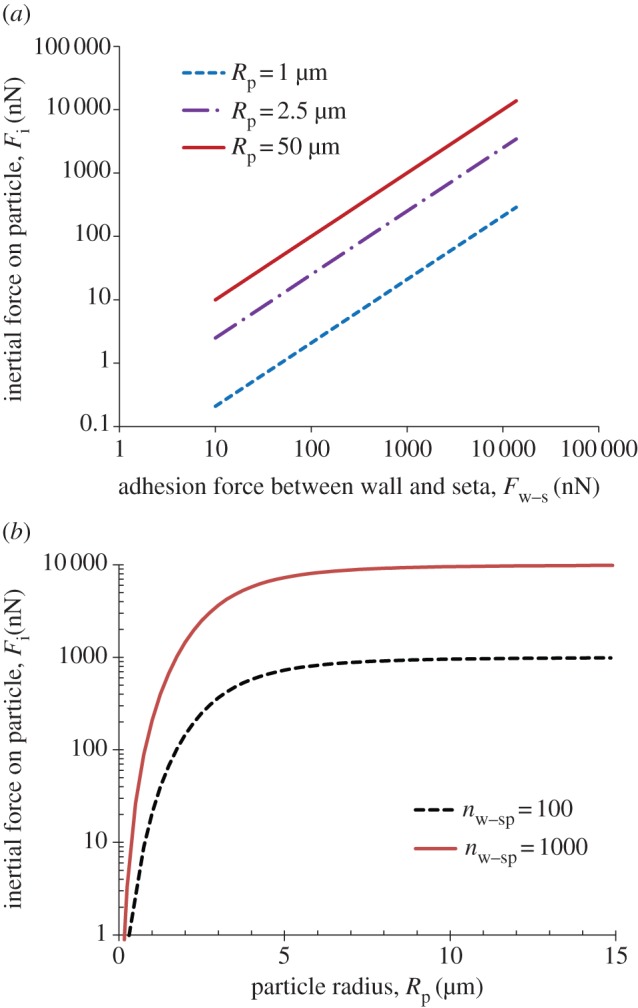
Inertial force, F_i, on particle adhering only to seta, versus (a) the adhering force between the wall and seta, F_w–s, and (b) radius of particle, R_p. F_w–s = n_w–sp × F_w–sp = n_w–sp × 10 nN. (Online version in colour.)

4.3. Effect of digital hyperextension on dynamic self-cleaning

The earlier-mentioned analysis suggests the dynamic self-cleaning mechanism is effective only when setae experience jump-off. The combination of the hierarchical fibrillar structure of gecko toe pads and the distal-to-proximal peeling motion induced by DH at detachment is crucial for achieving this dynamic effect at the micro–nano interface.

Strong frictional adhesion is generated when geckos place their foot and drag proximally, maintaining the angle lower than a critical value: approximately 25.5°, approximately 24.6° and approximately 30.0° for a single toe, isolated setal array and single seta, respectively [38]. A crowding model was proposed to calculate the minimum angle prior to tetrads/setae coming into contact with one another under significant loading [39]. In fact, the smaller the angle is, the more crowded the setal arrays become. A minimum angle of approximately 12.6° was proposed at the point of maximum crowding. Thus, setal arrays in an attachment state are highly crowded.

In our animal trials, geckos were allowed to walk either freely (with DH) or their toes were inhibited from scrolling (without DH), as schematically shown in figure 5. With restricted toes, the geckos are still able to take steps and walk but cannot scroll their toes. In this case, gecko toes peel in the direction from proximal to distal, solely influenced by LM in each step (figure 5b). During this proximal-to-distal peeling, the displacement of setal roots at the separation front is in a direction between vertical and distal (i.e. an angle larger than 90°). On the basis of detachment measurements of isolated setal arrays in various linear directions [26], the setal jump-off will be significantly damped or prohibited. Therefore, the proximal-to-distal peeling would lead only to a minimum-to-zero dynamic effect, and a maximal static self-cleaning. More importantly, because of the asymmetric geometry of angled setal arrays, the crowded region (i.e. densely packed setae in the attachment state) is located ahead of the possible jump-off direction (figure 5b). With limited space in the jump-off direction, the possibility of setal jump-off is further eliminated. Such confined setal arrays are very similar to those used by Hansen & Autumn [23]. In their experiment, no peeling in either direction was performed. After pressed engaging, the setal arrays were simply sheared off the glass wall in each force measurement. As a result, the important phenomenon of dynamic self-cleaning was not observed. The restricted setal arrays and manipulated toes correspond to the static and passive self-cleaning, which accounts for 40–50% of the total recovery (figure 2).

The scenario is profoundly changed when DH is enabled (figure 5a). The distal-to-proximal peeling of flexible toes under DH promotes setal jump-off in three aspects. First, displacement of the setal roots at the separation front is in a direction between vertical and proximal (i.e. an angle smaller than 90°). Thus, the elastic energy pre-stored in the setal shafts could not return to the interface but is instead frictionally dissipated [26] or contributes to the jump-off through higher seta adhesion force. Second, the crowded region is located behind the jump-off direction. Setae can easily separate from one another during toe scrolling and retreat independently from the substrate/wall (figure 5a). Finally, with DH, gecko toes could be substantially curved into a hyperextended position. The setal angles, originally approximately 45°, are significantly increased beyond the separation front (i.e. peeled-off region; figure 5a). Peeled-off setae are progressively spread out after the sequential jump-off event, leaving larger spaces for the consecutive dynamic retraction at the propagating separation front. All these aspects work together, activating the dynamic self-cleaning that can overcome much higher adhering force on the particles compared with the static mechanism. As a result, the rate and extent of self-cleaning can be significantly increased, which is supported by our experimental observations (figure 2).

Our analysis and model suggest that DH significantly enhances the self-cleaning performance of the gecko adhesive system, which raises at least two questions worthy of further study. First, what role did self-cleaning effectiveness play in the evolution of the best-characterized components of the adhesive system such as setal morphology (e.g. setal size, curvature, density, etc.)? In general, studies have largely focused on interpreting design and function by analysing static attachment and release of individual or isolated patches of setae, even though setae operate as part of an integrated locomotor system [40]. More studies, which incorporate whole organism performance trials, should help us identify and test specific hypotheses about the origins and significance of features such as DH, not just to self-cleaning [41], but to adhesive locomotion in general. Second, how effective is active self-cleaning owing to DH in other fibrillar adhesive systems such as those that were independently evolved in lizards belonging to the genus Anolis in the Polychrotidae? Anolis lizards use DH, but the direction of ‘roll-off’ is opposite to that seen in geckos, and the process of ‘roll-off’ is driven by changes in the angle of the limb as it moves through a step cycle rather than by hypertrophied muscles in the toes [42].

There are some synthetic dry adhesives with self-cleaning capability. Stiff polymer fibrillar adhesives, for example, show self-cleaning properties with gold microspheres (radius ≤ 2.5 μm), as samples recovered 25–33% of the original shear adhesion force after 30 simulated steps [43]. Synthetic micro-patterned carbon nanotube-based gecko tapes regained 60 per cent of the shear stress when the tape was dusted and cleaned by water [44]. These synthetic dry adhesives show either lotus effect or similar contact self-cleaning rate as gecko toe pads without DH. The relatively low recovery rate in both isolated natural and synthetic adhesives is attributed to the static and passive self-cleaning. As demonstrated in the present work, a superior self-cleaning rate can be achieved by introducing a dynamic self-cleaning mechanism in biomimetic structures, which provides a new route for the design of highly reuseable and reliable dry adhesives.

5. Conclusions

We have demonstrated that geckos walking naturally and using DH exhibit a self-cleaning rate that is considerably higher than previously observed rates based on passive mechanisms with isolated elements of the toe pad hierarchy. When DH was disabled, the extent of self-cleaning levelled off at 40–50% even after taking eight steps. Whereas, a twofold increase in self-cleaning rate was observed with DH enabled, returning the feet nearly to their original state in only four steps. More rapid self-cleaning and the observation that gecko toes remain clean and functional for long periods of time in non-dust-free environments suggest a dynamic self-cleaning mechanism that efficiently removes dirt particles during animal locomotion. Because of the nature of the adhesion force, asymmetric geometry and animal triggered distal-to-proximal peeling via DH, the rotating setae suddenly release from the attached substrate, generating acceleration high enough to dislodge dirt particles from the toe pads. While some dirt can be removed statically, the dynamic self-cleaning adds another dimension to remove the particles that more strongly adhere to the setae. The fine design of gecko toe pad structures by nature perfectly combines dynamic self-cleaning with attachment/detachment, making gecko feet sticky yet clean.