Nanoscale characterization of the biomechanical hardening of bovine zona pellucida

Abstract

The zona pellucida (ZP) is an extracellular membrane surrounding mammalian oocytes. The so-called zona hardening plays a key role in fertilization process, as it blocks polyspermy, which may also be caused by an increase in the mechanical stiffness of the ZP membrane. However, structural reorganization mechanisms leading to ZP's biomechanical hardening are not fully understood yet. Furthermore, a correct estimate of the elastic properties of the ZP is still lacking. Therefore, the aim of the present study was to investigate the biomechanical behaviour of ZP membranes extracted from mature and fertilized bovine oocytes to better understand the mechanisms involved in the structural reorganization of the ZP that may lead to the biomechanical hardening of the ZP. For that purpose, a hybrid procedure is developed by combining atomic force microscopy nanoindentation measurements, nonlinear finite element analysis and nonlinear optimization. The proposed approach allows us to determine the biomechanical properties of the ZP more realistically than the classical analysis based on Hertz's contact theory, as it accounts for the nonlinearity of finite indentation process, hyperelastic behaviour and material heterogeneity. Experimental results show the presence of significant biomechanical hardening induced by the fertilization process. By comparing various hyperelastic constitutive models, it is found that the Arruda–Boyce eight-chain model best describes the biomechanical response of the ZP. Fertilization leads to an increase in the degree of heterogeneity of membrane elastic properties. The Young modulus changes sharply within a superficial layer whose thickness is related to the characteristic distance between cross-links in the ZP filamentous network. These findings support the hypothesis that biomechanical hardening of bovine ZP is caused by an increase in the number of inter-filaments cross-links whose density should be higher in the ZP inner side.

1. Introduction

The zona pellucida (ZP) is the extracellular coat that surrounds mammalian oocytes, which plays a crucial role in oogenesis, fertilization and preimplantation development [1–3]. The ZP regulates the binding of sperm to ovulated eggs through species-specific sperm receptors activated during fertilization, induces bound sperm to undergo cellular exocytosis, participates in the blocking of polyspermy after fertilization and protects early embryos that traverse the female reproductive tract.

The ZP is mainly composed of sulphated glycoproteins with some species-specific differences. The most extensively studied ZP is that derived from mice mammalian cells, which is composed of three proteins: ZP1, ZP2 and ZP3 [4–6]. Four ZP glycoproteins are instead present in the human oocyte [7]. Five glycoproteins were identified in the bovine egg ZP [8]. Each glycoprotein has a specific function, and all glycoproteins are assembled into long fibrils, forming a three-dimensional network.

Following sperm fusion with the oocyte, cortical granules (a special organelle in eggs) release their contents on the perivitalline space in an event termed ‘cortical reaction’ [9,10]. The exudate of the cortical granules alters the properties of the ZP and cause the ZP to become refractory to sperm binding and penetration [11,12]. This ‘zona hardening’ process after fertilization [4,13–17] involves inactivation of sperm receptors and an increased ZP resistance to dissolution by a variety of agents including heat, proteases, reducing agents and low PH.

Authors usually refer to ‘zona hardening’ not in the sense of a change in physical properties such as the mechanical stiffness of ZP membrane. However, significant variations of the elastic properties of the ZP caused by the fertilization process were found for various species [18–25]. This indicates that penetration of other spermatozoa into fertilized eggs can also be blocked by an increase in the mechanical stiffness (i.e. biomechanical hardening) of a ZP membrane.

However, the characteristics of the zona hardening process may differ for various animal species [18]. For example, for pigs and cows, there is a high incidence of polyspermy in the case of in vitro fertilization (IVF) [26,27]; this was explained with an unvaried ZP resistance to proteolysis after fertilization or with the lack of exposure of oocytes, directly removed from the ovary, to oviduct-specific glycoprotein–heparin complexes that contribute to mask sperm binding sites. However, the lack of biochemical hardening is not coupled with a lack of biomechanical hardening, which may still occur: in fact, a substantial increase in the mechanical stiffness of the bovine ZP membrane after IVF was recently observed [23,28]. Another open question is the extent of the reaction propagation across the thickness of the ZP: in fact, an incomplete or delayed zona reaction was suggested as the major cause of polyspermy in pigs [29,30].

In this paper, biomechanical properties of ZP membranes extracted from mature and fertilized bovine oocytes are investigated with atomic force microscopy (AFM) nanoindentation measurements. Probing the mechanical behaviour of cells and biotissues at the nano- and microscale requires sophisticated experimental techniques such as atomic force spectroscopy (AFS), optical tweezing [31,32], magnetic twisting cytometry [33,34], spherical indentation [35], micropipette aspiration [36,37], etc. [38]. In particular, AFM [39–41] is well suited for nanoscale investigations on biological membranes because of its ability to image and probe very small samples in physiological conditions reproduced in vitro [42–44].

In the present study, both the inner and outer sides of the ZP extracted from the fertilized oocyte are mechanically characterized to analyse in detail the propagation of the zona reaction through the thickness of the ZP membrane. It is possible to evaluate the biomechanical properties of the ZP outer layer and the inner layer, separately, as AFS allows the sample to be indented for a few hundreds of nanometres, hence much less than the 10 μm total thickness of the ZP membrane.

Traditional analyses of AFM indentation data rely on inappropriate application of classical Hertz's contact theory [45–48], based on many simplifying assumptions such as linearly elastic materials, infinitesimal strains, infinite thickness and dimensions of the sample (i.e. infinite elastic half-space), small contact area, perfectly spherical indenter, etc. However, none of these assumptions is likely to be valid when a biological membrane is indented with an AFM (see, the discussion provided in Liu [49]). In fact, most biological materials exhibit highly nonlinear constitutive behaviour, AFM probes produce large deformations in the indentation process and the half-space assumption cannot be adapted to thin biological membranes.

Previous studies used finite element models (FEMs) to properly simulate AFM indentation curves and to evaluate the effects of indentation depth, tip geometry and material nonlinearity on the finite indentation response [50–52]. The proposed approach allows us to describe the biomechanical behaviour of cells with hyperelastic constitutive relationships and to extract values of the elastic properties of the specimen with the aid of finite element analysis [53–55].

In this study, a powerful hybrid procedure is developed by combining experimental measurements, finite element analysis and nonlinear optimization algorithms developed so as to analyse AFM nanoindentation data. The hybrid methodology provides a more realistic description of the biomechanical behaviour of the ZP membrane and a more reliable derivation of ZP elastic properties than the classical analysis based on Hertz's theory and other formulations based on linear elasticity. We attempted to find the hyperelastic constitutive model that better describes the biomechanical behaviour of a ZP membrane and to analyse changes in constitutive behaviour and distribution of the material properties induced by the structural rearrangement of the ZP after fertilization. The proposed approach is completely general because the optimizer can automatically find material parameters that best fit the experimental data. Results are taken as a starting point to formulate hypotheses on the mechanisms of the structural reorganization of the ZP leading to biomechanical hardening.

2. Description of the hybrid procedure

2.1. Preparation of samples and experimental measurements with atomic force microscopy

Ovaries were obtained from cows and heifers at a local abattoir and were kept in a saline solution at 37°C before being transported to the laboratory within 2 h of slaughter. Cumulus–egg complexes (COCs) were isolated from sliced ovaries and were placed in Petri dishes and washed several times in phosphate-buffered saline. Only COCs with an intact unexpanded cumulus oophorus and evenly granulated cytoplasm were chosen for experiments. The selected COCs were washed three times in oocyte collection medium, a tissue culture medium 199 (TCM-199) supplemented with 10 per cent (w/v) heat-treated foetal bovine serum. Oocytes were matured to metaphase II in maturation medium, a TCM-199 buffered with bicarbonate and supplemented with 10 per cent (w/v) heat-treated foetal bovine serum and 0.1 IU ml⁻¹ follicle-stimulating hormone and 10 IU ml⁻¹ luteinizing hormone, at 39°C for 22–24 h at 5 per cent CO₂ in air. After in vitro maturation, a fraction of the completely denuded oocytes were placed on glass slides and routinely stained with a working solution of lacmoid. Cumulus expansion and first polar body expulsion were considered as the signs of the occurrence of oocyte maturation. Commercial frozen semen was used for fertilization procedures. Motile sperm separation was carried out by using the Percoll gradient technique. Sperm concentration was determined with a haemocytometer. After 22–24 h of maturation, COCs were washed three times in Hepes synthetic oviduct fluid (H-SOF) medium and placed in four-well culture dishes containing pre-equilibrated fertilization medium (TALP-IVF) supplemented with heparin (1.2 g ml⁻¹). Spermatozoa were then added at a final concentration of 1 × 10⁶ cells ml⁻¹ in 300 l medium per well containing a maximum of 20 COCs. IVF was accomplished by co-incubating oocytes and sperm cells for 20 h at 39°C at 5 per cent CO₂ in air. The male and female pronuclei and the second polar body expulsion were considered to be signs of fertilization. In order to evaluate the ZP of matured and in vitro fertilized oocytes, COCs were denuded by vortexing for 3 min and washed three times in H-SOF medium. Thereafter, the ZP of denuded oocytes were isolated by aspirating cells in a narrow-bore pipette. The isolated ZP was mounted on polylysine-treated slides and heated on a warming plate for 5 min. The ZP was placed on the glass slide with the outer surface facing upwards, and, in the case of fertilized oocyte, both with the outer and the inner surface facing upwards. Samples were stained with methylene blue and stored at room temperature until observation [56].

Nanomechanical measurements on the ZP were carried out using an SPMagic SX atomic force microscope (Elbatech, Italy). Samples, laid on glass coverslips, were maintained in an aqueous environment (Dulbecco's phosphate-buffered saline) at a constant temperature of 37°C. The AFM probe is an ultrasharp silicon nitride cantilever of calibrated force constant k = 0.06 N m⁻¹, with tip radius of 10 nm (MikroMash, USA). From the SEM image of the tip, the half-opening angle of tip apex was accurately determined as α = 20°.

Nanoindentation was performed by lowering the AFM tip onto the ZP surface at a preset rate of 3 μm s⁻¹, comparable to the typical velocity of spermatozoa observed during IVF [57]. Following contact, the AFM tip exerts a force F = kΔ against the ZP, which is proportional to the cantilever deflection (Δ), and which is recorded for each position (Z) taken by the piezoelectric translator. The indentation (δ) of the ZP membrane hence is δ = (Z − Δ). In this study, the force–indentation function F(δ) was determined with a Matlab routine coded ad hoc by the present authors. In order to obtain statistically significant results, force–indentation curves were recorded at 50 different points of each analysed sample and were repeated on three different oocytes.

2.2. Modelling of nanoindentation on the zona pellucida membrane: finite element analysis

Nanoindentation experiments conducted on the ZP membrane were simulated with the commercial finite element software Abaqus v. 6.7 (Dassault Systèmes, France). For that purpose, an axisymmetric FE model was developed: the model includes a rigid blunt-conical indenter (tip radius of 10 nm and half-open angle of 20°) pressing against a soft layer adherent to a rigid substrate. The Young modulus of the silicon nitride AFM tip is 300 GPa. The ZP membrane was modelled as an incompressible hyperelastic slab with 60 μm diameter and 10 μm thickness.

Figure 1 shows the FEM with the rigid indenter and the ZP membrane: the typical deformation field corresponding to 200 nm indentation is presented. The mesh of the membrane included 69 716 four-node bilinear hybrid CAX4H elements with constant pressure and 70 562 nodes. The hybrid pressure-displacement formulation of CAX4H allowed incompressible behaviour to be modelled. The mesh was properly refined in the contact region between the AFM tip and ZP membrane: the element size of 0.06 nm allowed a good compromise between the convergence of nonlinear analysis and the computation time.

Figure 1.

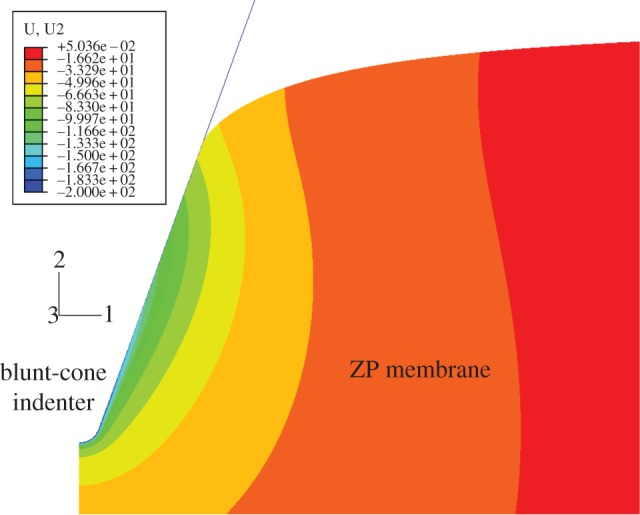
Finite element model simulating the AFM nanoindentation process and typical deformation field for 200-nm indentation.

The penetration of the indenter was simulated by progressively increasing the value of force applied to the AFM tip in the vertical direction: the load transferred by the rigid blunt-conical tip to the ZP membrane generates a state of compression in the soft material of ZP slab. The bottom and the side of the slab are fixed in space. The rigid blunt-cone and the axis of symmetry of the slab are permitted to move only in the vertical direction. Finite element analysis accounted for geometrical nonlinearity (i.e. large deformations), and the automatic time-stepping option was selected to facilitate convergence of nonlinear analysis. The contact between the indenter and ZP membrane was assumed to be frictionless. The ‘hard contact’ (i.e. no force is exchanged before surfaces come in contact) option available in Abaqus was selected.

Frictionless contact was assumed because of the lack of experimental data on the friction coefficient between the AFM tip and bovine ZP. Generally speaking, the actual contact behaviour is somewhere between unconstrained sliding and fully constrained adhesion [50]. In the present case, because the indentation depth is small compared with specimen thickness (only 200 nm versus 10 μm, i.e. 2%) friction/adhesion as well as substrate effects are negligible. In fact, the influence of friction in the extraction of elastic properties becomes significant if the indentation depth reaches half of sample thickness, while substrate effects become important when the ratio of indentation depth to thickness is larger than 10% (see, Costa & Yin [50]).

2.3. Material properties: hyperelastic constitutive models

Three different hyperelastic models were considered in this study to describe the structural behaviour of the ZP membrane in the mature oocyte and after fertilization: (i) two-parameter Mooney–Rivlin (MR); (ii) neo-Hookean (NH); (iii) Arruda–Boyce (AB) eight-chain model.

The two-parameter MR constitutive law [58,59] is a very classical phenomenological model described by the following strain energy density function:

2.1

where C₁₀ and C₀₁ are the MR constants input into Abaqus as material properties. Strain invariants are defined, respectively, as 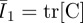and 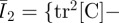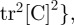where [C] is the Cauchy–Green strain tensor. The Young modulus is

2.2

The NH model [60,61] was selected as it is based on statistical thermodynamics of cross-linked polymer chains. Although this model is not phenomenological, it can however be derived from the two-parameter MR model by setting C₀₁ = 0. Consequently, only one material parameter must be input into Abaqus. The Young modulus is

2.3

The AB model [62] was previously used to describe the mechanical behaviour of biospecimens, including filamentous collagen networks [63,64] and monolayers of endothelial cells [53]. This model relies on statistical mechanics of a material with a cubic representative volume element containing eight chains along diagonal directions. The strain-hardening behaviour of an incompressible material is predicted by using two constants: the shear modulus μ_eight-chain and the distensibility λ_L. The strain energy function is expressed as (2.4)

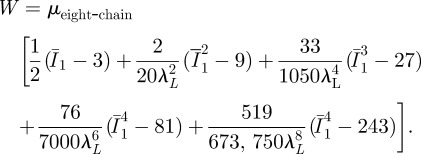2.4

The AB model is activated in Abaqus by inputting the values of μ_eight-chain and λ_L as material parameters. The Young modulus is

2.5

2.4. Extraction of elastic parameters: formulation of the inverse problem

In order to extract more realistic hyperelastic properties of the ZP membrane from the earlier-described FE model, which accounts for the nonlinearity of the finite indentation process and material nonlinearity, a hybrid procedure combining experimental measurements, FE analysis and nonlinear optimization was used. Displacement values measured experimentally are compared with the corresponding results of FE analysis. This leads to formulation of an optimization problem, including the unknown material properties as design variables. The optimization problem describing the inverse problem of material characterization can be stated as follows:

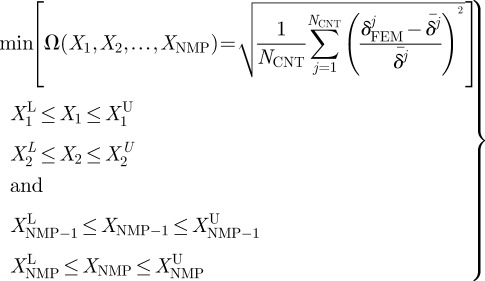2.6

where Ω is the error function to be minimized. The design vector X(X₁,X₂, … ,X_NMP) includes the NMP unknown material properties to be determined that can vary between the lower and upper bounds 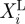and 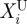(i = 1, … NMP).

In equation (2.6), δ_FEM^j and 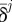, respectively, are the displacement values for the jth load step computed with FE analysis and those measured experimentally with AFM. The number of control locations N_CNT is equal to the number of load steps executed to complete nonlinear FE analysis. Nanoindentation values measured experimentally can be taken as target values in the identification problem because AFM measurements do not require any a priori knowledge of material properties. Conversely, the ‘correct material properties’ (i.e. actual material properties) must be input into the FE model to obtain the force–indentation curve matching the F–δ curve determined experimentally. The suitability of the optimization-based hybrid process for mechanical characterization problems of highly nonlinear materials and heterogeneous biological structures is well-documented in literature [65–67].

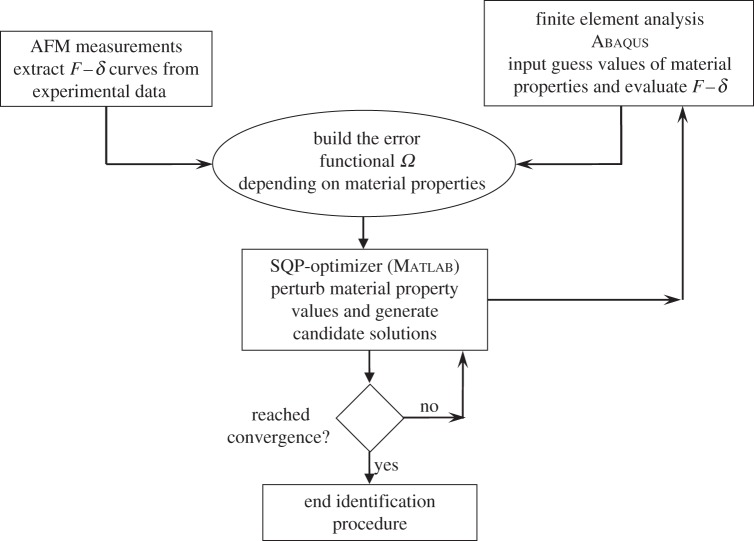
The inverse problem (2.6) was solved with the powerful sequential quadratic programming (SQP) [68] optimization routine implemented in Matlab v. 7.0. The finite element solver of Abaqus was interfaced with the SQP optimization routine of matlab, which processed the results of the FE analysis, compared the computed F–δ curves with experimental data, computed the error function Ω and perturbed material parameters for the subsequent design cycles. The flowchart of the identification process is shown in figure 2.

Figure 2.

Flowchart of the hybrid identification procedure.

Bounds of design variables were set as follows: 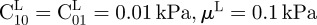and 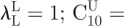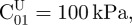μ^U = 1000 kPa and 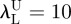. For each sample and each constitutive model, optimization runs were started from five different sets of material properties randomly generated. This multi-start optimization strategy, together with the large range of variability chosen for material parameters, allowed us to cover the whole search space and increased the probability of finding the global optimum. Serial optimization runs were carried out for each test case to avoid premature convergence. This process ended as soon as relative variations of error functional |(Ω_K − Ω_K−1)/Ω_{K − 1}| and design vector ||X_K − X_K−1||/||X_{K − 1}|| between the last two serial runs became smaller than 0.0001.

3. Results

3.1. Preliminary analysis of atomic force microscopy data with the modified Hertzian model

A preliminary evaluation of elastic properties of ZP membranes extracted from mature and fertilized oocytes was carried out by analysing indentation curves with the modified Hertzian model developed in [47,48] for the conical indenter:

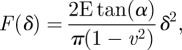where the Poisson ratio was set at 0.5 to account for material incompressibility.

The indentation range of 0–100 nm was analysed, as in this range the infinitesimal strain model assumption can still be considered reasonably valid. In fact, experimental data for all ZP specimens were always fitted by the modified Hertzian model with correlation coefficient r² ≥ 0.95. By analysing experimental data recorded in 50 different points of each sample, the following mean values of the Young modulus were derived: (i) E_MAT = (18.5 ± 1.58) kPa for the ZP extracted from mature oocyte; (ii) E_{FERT_INT} = (145.45 ± 14.06) kPa for the inner layer of the ZP extracted from fertilized oocyte; (iii) E_{FERT_OUT} = (123.51 ± 12.74) kPa for the outer layer of the ZP extracted from fertilized oocyte. The standard deviation on the Young modulus hence is always less than 10 per cent of the average value. The ZP of the fertilized oocytes shows a significant mechanical hardening with respect to the ZP of the mature oocytes.

3.2. Mechanical properties of the zona pellucida membrane extracted with the hybrid procedure

In order to gain a deeper understanding of the biomechanical hardening process that takes place in the ZP membrane after fertilization, a larger indentation depth (0−200 nm) was considered and force–displacement curves were then analysed with the hybrid procedure described in §2. In the 0−200 nm range, the simplified Hertzian model was no longer adequate to describe AFM measurements. In fact, the correlation coefficient r² of Hertzian fitting dropped to 0.85 for the 0−200 nm indentation range while it was always higher than 0.95 for the 0−100 nm indentation range. The hybrid methodology for analysing AFM data proposed in this study provides instead a more reliable derivation of the elastic properties of the sample.

For each sample (i.e. mature ZP, inner and outer layers of fertilized ZP), the experimental curve taken as the target in the optimization process was the average of F–δ curves recorded in 50 different points of the specimen. The standard deviation of experimental data with respect to average F–δ curves taken as the target in the optimization process was about 15 per cent.

Three different constitutive models (NH, MR, AB) were considered for the membrane. A heterogeneous distribution of elastic properties through the thickness of the ZP was hypothesized. In particular, the membrane was divided into two layers of thicknesses, respectively, d₁ and d₂, while the Young modulus was hypothesized to change linearly within both layers, respectively, from E₀ to E₁ and from E₁ to E₂. In the hybrid characterization procedure, the material parameters ‘optimized’ by Abaqus were hence elastic constants and layers' thicknesses; d₁ and d₂ could vary over the entire thickness of the membrane with the unique constraint d₁ < d₂. The corresponding Abaqus FEM including the heterogeneous region composed of two layers is shown in figure 3.

Figure 3.

Abaqus finite element model of the indented ZP, including a heterogeneous distribution of elastic properties across membrane thickness: two layers with linearly variable elastic properties are considered.

A heterogeneous distribution of material properties was also considered by Roduit et al. [69], who modelled the cell as a homogeneous material containing inclusions of stiffer material. While Roduit's discrete model allowed us to distinguish only structures of different stiffness buried in the sample, the present model can find the optimal distribution of material properties that best matches experimental evidence.

Figure 4 compares force–indentation curves acquired experimentally for the ZP of mature oocytes (figure 4a) and the outer layer of the ZP of fertilized oocytes (figure 4b) with the corresponding numerical F–δ curves ‘optimized’ by Abaqus, including different constitutive laws (MR, NH, AB). The quality of fitting between experimental data and FE results was again evaluated by means of the correlation coefficient r². For all ZP samples investigated in this study, table 1 lists elastic properties and r² values corresponding to each hyperelastic model. Data reported in table 1 are the values averaged over the five optimization runs carried out for each sample and constitutive model starting from a random combination of material property values. Remarkably, the standard deviation on material parameters found via optimization was always less than 0.5 per cent, and the correlation coefficient r² changed at most by the third significant digit. This demonstrates the robustness of the hybrid approach to biomechanical identification of the cell membranes used in this research.

Figure 4.

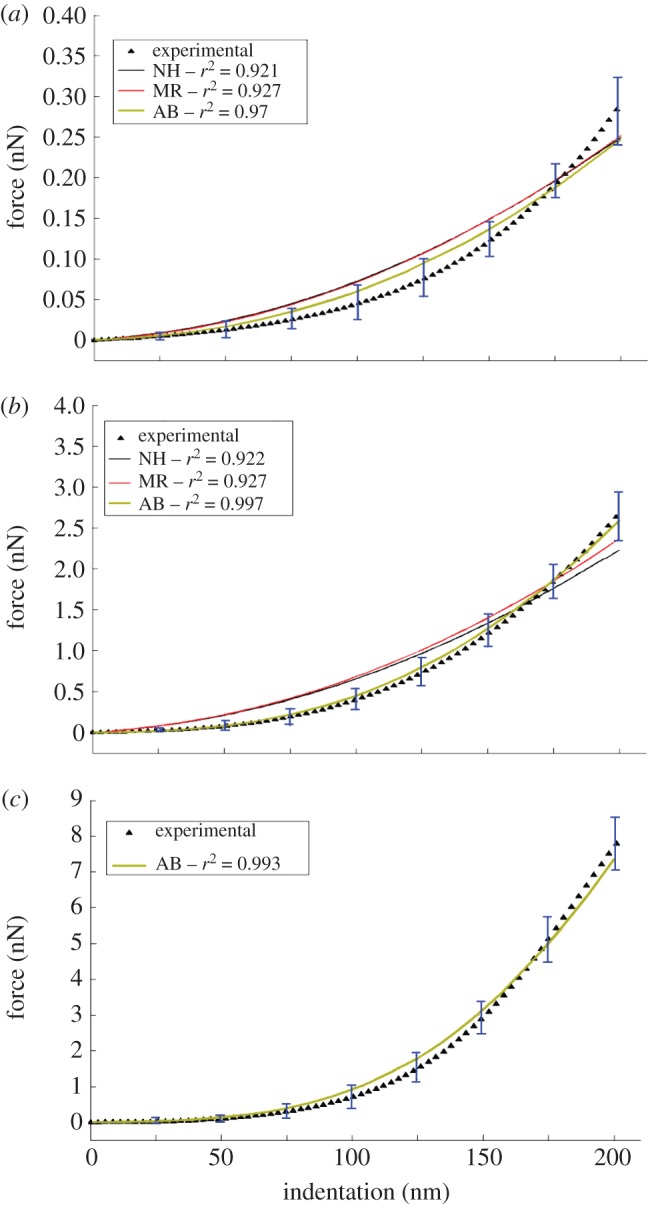
Force–indentation curves acquired experimentally and corresponding numerical curves obtained with the hybrid identification procedure: (a) mature oocyte's ZP; (b) fertilized oocyte's ZP outer layer; (c) fertilized oocyte's ZP inner layer (the figure shows only the results obtained for the Arruda–Boyce eight-chain model).

Table 1.

Biomechanical properties and characteristic layers thicknesses of the zona pellucida isolated from mature and fertilized oocytes. Poisson ratio is set equal to 0.5 to simulate material incompressibility. Values listed in the table were obtained by taking the F–δ curves averaged over AFM measurements carried out on each sample as the target. The standard deviation of material parameters determined from the different optimization runs carried out for each sample and each constitutive model is much smaller than the statistical dispersion of AFM experimental data.

	d1 (nm)	elastic parameters (kPa)	Young's modulus E (kPa)	d2 (nm)	elastic parameters (kPa)	Young's modulus E (kPa)	r2
mature ZP
neo-Hookean	from 0 to 100	C10 : 2.42 → 2.49	14.52 → 14.94	from 100 to 199	C10 : 2.49 → 3.91	14.94 → 23.46	0.921
Mooney–Rivlin		C10 : 2.03 → 2.08	12.97 → 13.28		C10 : 2.08 → 3.29	13.28 → 21.01	0.927
		C01 : 0.131 → 0.134			C01 : 0.134 → 0.211
Arruda–Boyce		μ :2.43 → 2.49	7.29 → 7.47		μ :2.49 → 3.91	7.47 → 11.73	0.970
		λL = 1.61			λL = 1.61
fertilized ZP: outer layer
neo-Hookean	from 0 to 96	C10 : 2.34 → 23.23	14.04 → 139.38	from 96 to 198	C10 : 23.23 → 54.84	139.38 → 329.04	0.922
Mooney–Rivlin		C10 : 2.34 → 23.23	14.19 → 140.88		C10 : 23.23 → 54.73	140.88 → 331.85	0.927
		C01 : 0.025 → 0.25			C01 : 0.25 → 0.579
Arruda–Boyce		μ :2.42 → 24.2	7.26 → 72.6		μ :24.2 → 56.6	72.6 → 169.8	0.997
		λL = 1.61			λL = 1.61
fertilized ZP: inner layer
Arruda–Boyce	from 0 to 97	μ : 2.41 → 38	7.23 → 114	from 97 to 198	μ : 38 → 200	114 → 600	0.993
		λL = 1.56			λL = 1.56

Values of material properties listed in table 1 are indeed representative of the differences in mechanical behaviour existing between the ZP of mature oocytes and the outer and inner layer of the ZP of fertilized oocytes. In fact, relative variations of elastic properties were much larger than standard deviations of experimental data with respect to average F–δ curves taken as the target in the identification process.

The sensitivity of the optimized designs listed in table 1 to perturbations of material properties was also analysed. For that purpose, all optimized values of C₁₀, C₀₁, μ and λ_L were reduced or increased by 10 per cent (i.e. each perturbation was at least 20 times as large as the largest deviation on material properties observed in serial optimization runs) and new FE analyses were run to evaluate the variation of correlation coefficient r² between experimental data and numerical results. Because r² dropped to, 0.88 for MR and NH models and 0.93 for the AB model, respectively, it can be concluded that the data reported in table 1 are the true solution of the identification problem (2.6) and hence are indicative of the relative performance of constitutive models.

Table 1 shows that the best fit of experimental data is provided by the AB model for both the mature ZP (r² = 0.970) and fertilized ZP's outer layer (r² = 0.997). Furthermore, figure 4 shows that force–displacement curves ‘optimized’ via FE analysis always fall within standard deviations of experimental data only in the case of the AB model. This is consistent with the nature of the AB model, which was originally developed to simulate the mechanical behaviour of a polymer chain network and hence is highly suited for describing structural response of filamentous/fibrous biostructures such as ZP. As expected, the MR and NH models produced practically the same results: the NH model is a simplification of the MR model and the structural response is more sensitive to C₁₀ than C₀₁. For this reason, the F–δ curve acquired for fertilized ZP's inner layer, which is much sharper than its counterpart for fertilized ZP's outer layer, was analysed only with the AB model (figure 4c).

Although it may be argued that the AB model includes two independent parameters, the shear modulus μ and the distensibility λ_L, while the MR and NH models actually depend only on the shear modulus μ, which results from the combination of hyperelastic coefficients C₁₀ and C₀₁ (respectively, as μ_MR = 2(C₁₀ + C₀₁) and μ_NH = 2C₁₀), it should be noted that the amount of design freedom included in the optimization process was indeed the same for all the hyperelastic models considered in this study. In fact, optimization results listed in table 1 indicate that the shear modulus varied much more than distensibility: from 2.43 to 3.91 kPa (i.e. by about 61%) for mature ZP; from 2.42 to 56.6 kPa (i.e. by more than 23 times) for the outer layer of fertilized ZP; from 2.41 to 200 kPa (i.e. by about 83 times) for the inner layer of fertilized ZP. Conversely, distensibility changed by less than 5 per cent (i.e. between 1.56 and 1.61). Therefore, the hyperelastic behaviour of the ZP membrane was always driven mainly by shear modulus: that is, by only one elastic parameter regardless of the constitutive model considered in numerical simulations.

The AB model is the most appropriate hyperelastic constitutive model to describe biomechanical behaviour of the ZP surrounding both mature and fertilized oocytes. While it is well known that the oocyte fertilization process is associated with reorganization of ZP structure (see, [70,71] for the human ZP, and [28] for the bovine ZP), it appears that modifications of ZP structure did not result in any variation of constitutive behaviour between mature and fertilized ZPs.

Data reported in table 1 reveal a significantly different level of heterogeneity in biomechanical properties through ZP thickness. Figure 5 shows the corresponding variation of the Young modulus through indentation depth for the three ZP membranes analysed. In the mature oocyte's ZP, the Young modulus changes from E₀ = 7.29 kPa to E₁ = 11.73 kPa within a layer of total thickness d_tot = 199 nm; the variation is marginal in the layer close to external surface (i.e. across the first layer of thickness d₁ = 100 nm) and takes place mainly in the second layer of thickness d₂ = 99 nm.

Figure 5.

Variation of the Young modulus ‘optimized’ by Abaqus through indentation depth.

In the outer side of fertilized oocyte's ZP, the Young modulus increases quasi-linearly from E₀ = 7.26 kPa to E₁ = 169.8 kPa within a layer of thickness d_TOT = 198 nm; there is only a small deviation at d₁ = 96 nm with the local value E = 72.6 kPa, slightly smaller than the value 81.4 kPa, which would correspond to the purely linear variation through d_TOT. In the inner side of the ZP of the fertilized oocyte, there is instead a sharp bilinear gradient of the Young modulus through the total depth of 198 nm: in fact, E varies from E₀ = 7.23 kPa to E₁ = 114 kPa within the layer of thickness d₁ = 97 nm and then rises to E₂ = 600 kPa in the adjacent layer of thickness d₂ = 101 nm. In the case of the ZP of the fertilized oocyte, the gradient of the Young modulus is hence 40 times steeper than for the mature ZP.

4. Discussion

The aim of this research was to investigate the biomechanical properties of the ZP membrane surrounding mature and fertilized bovine oocytes. For that purpose, a hybrid identification procedure was developed by combining nanoindentation measurements carried out with AFM, nonlinear finite element simulations and nonlinear optimization. The new approach is much more general, reliable and accurate than classical analysis based on Hertz's contact theory as it can account for large deformations induced by the AFM probe and nonlinear constitutive behaviour of the ZP (this was supposed to be hyperelastic and the two-parameter MR, NH and AB eight-chain models were compared). Furthermore, it can deal with heterogeneity in the spatial distribution of the hyperelastic properties of the ZP.

The hybrid procedure assessed the local biomechanical behaviour of the ZP membrane in great detail. This is a considerable step forward with respect to the current literature. In fact, analytical models used to process loading force data gathered with MEMS multi-axial sensors [18], closed-form expressions based on structural dynamics of linearly elastic bodies developed to analyse resonance frequency shifts versus displacement curves measured with micro-tactile sensors [19–21] or elastic theory of layered shells applied to the analysis of force–displacement curves obtained from micropipette aspiration experiments [24,25], etc., allowed only average elastic properties of the ZP to be determined.

In order to corroborate the results, the following factors were considered. First, the elastic properties ‘optimized’ for the different ZP layers must be consistent with ‘global’ properties describing the bulk mechanical behaviour of the whole ZP membrane. Second, values of the elastic properties could be sensitive to modelling choices such as the number of layers included in the FE model as well as to the actual radius of curvature and rotation of the AFM tip. Third, because the ZP membrane surrounding the oocyte has an intrinsic curvature, as it is spread out on a rigid substrate during AFM experiments, residual stresses can arise within the membrane that could affect the estimation of its mechanical properties.

The overall mechanical response of the ZP was evaluated by considering a ‘composite membrane’ including five layers. The values of the shear modulus and distensibility determined via optimization (table 1) were assigned to the two layers located near the outer/inner sides of the ZP. Material properties of the intermediate layer were assumed to change linearly from the outer side to the inner side of the ZP membrane. The 200 nm indentation depth was simulated for the composite layered structure including optimized material properties. The bulk modulus was computed at each node lying on the symmetry axis of FE model as the ratio between hydrostatic stress and volumetric strain. The value of the Young modulus averaged over the control path nodes of the fertilized ZP membrane was approximately 22 kPa, which is fully consistent with stiffness values (about 25 kPa) measured by Murayama et al. [19] for the bovine ZP.

The amount of design freedom entailed by the optimization process when multi-layer models are used may depend on the number of layers included in the FE model. For this reason, a three-layer AB model (layers' thicknesses d₁, d₂ and d₃ and the corresponding elastic properties were included as design variables) was implemented for mature and fertilized ZPs by adding one layer to the FE model shown in figure 3. Remarkably, the intermediate layer thickness d₂ found by Abaqus was always very small (approx. 2 nm), and values of mechanical properties found in correspondence of each layer were in good agreement with those obtained with the two-layer model. This proves that the proposed two-layer model is not simply a mathematical artifice to match experimental data and numerical simulations but actually reproduced the real behaviour of the investigated specimens.

The geometry of the AFM tip specified by the manufacturer was checked with SEM inspections. Furthermore, it was checked whether AFM measurements induced any change in tip geometry: for that purpose, SEM images of the AFM tip were recorded after nanoindentation tests conducted on each sample. Because the tip radius remained practically the same, the nominal radius of curvature of 10 nm set in the FE model is actually representative of the whole AFM test. A sensitivity analysis on the effect of variations of AFM tip radius was however conducted by changing the tip radius within the level of resolution of the electron microscope: in particular, the tip radius was set as 5, 8, 10, 12 or 15 nm. This was performed for both mature and fertilized ZP membrane models. Remarkably, mechanical properties (i.e. the hyperelastic model parameters optimized by Abaqus and the bulk modulus averaged over the nodes of the axis of symmetry of the FE model) extracted with the proposed approach never changed by more than 5 per cent.

The rotation of the AFM tip was also not found to be significant. In fact, for the 200 nm indentation depth considered in this study, tip rotation is only 1.06 × 10⁻⁴ rad. The resulting lateral displacement of the tip is about 10⁻³ nm, four orders of magnitude smaller than the contact arc length between the indenter and ZP membrane.

The effect of residual stresses on the estimation of ZP elastic properties was evaluated by including in FE analysis the pre-deformations representing the actual curvature of the membrane surrounding the oocyte. Distributions of elastic properties obtained via optimization for both mature and fertilized ZPs were found to be rather insensitive to residual stresses. Further details on this question are given in the electronic supplementary material.

In view of the previous discussion, the results presented in this study appear to be realistic. The main findings of the study conducted on the bovine ZPs and their biomechanical/biophysical implications can be summarized as follows:

• — the average value of the Young modulus of the ZP membrane increases considerably after fertilization; therefore, the expected biomechanical hardening of the ZP actually occurs. This result is fully consistent with the data reported in literature for bovine and other species' ZPs [18–25];

• — biomechanical hardening associated with the structural reorganization of the ZP after fertilization does not imply any change in constitutive behaviour with respect to mature ZP. The AB eight-chain hyperelastic model always simulated the mechanical behaviour of ZP much better than the NH and MR models for fertilized as well as mature oocytes;

• — the ZP membrane presents a heterogeneous distribution of elastic properties. Biomechanical heterogeneity increased considerably after fertilization. Because in the case of fertilized ZPs, the gradient of the Young modulus is 40 times steeper than for mature ZPs, biomechanical heterogeneity in mature ZPs should not be considered very significant; and

• — the mature oocyte's ZP and the most superficial layers of fertilized ZP's outer and inner sides have the same value of the Young modulus (E ∼ 7.26 kPa).

Besides modifications of structure and morphology induced in the ZP by the fertilization process, extensively analysed in literature with electron microscopy [70,71,28], this study demonstrated that ZP's structural reorganization also yields a different distribution of elastic properties: in fact, biomechanical properties become much more heterogeneous after oocyte fertilization. While mechanical stiffness of the very external layers of fertilized ZP surface is not affected by the fertilization process (E_{FERT_INT} = 7.26 kPa and E_{FERT_OUT} = 7.23 kPa versus E_MAT = 7.29 kPa), structural modifications of the ZP producing significant variations of biomechanical properties seem to always occur across the thickness of the membrane at a characteristic distance of approximately 100 nm from the membrane surface (see table 1 and figure 5).

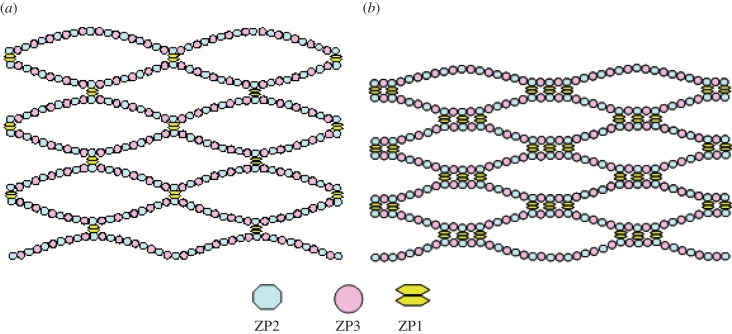
The model of mouse ZP structure proposed by Wassarman [5] is useful to correctly interpret experimental evidence gathered in this study. Wassarman's model, derived from ultrastructural observations, is still the only detailed representation of ZP structure available in the literature. The ZP has a filamentous structure and, in the case of mice, it is composed by three sulphated glycoproteins: ZP1, ZP2 and ZP3. The ZP filaments are constructed of repeating ZP2−ZP3 units and are cross-linked by ZP1 so as to form a three-dimensional array of interconnected filaments (see the schematic in figure 6). Each ZP2−ZP3 dimer has an estimated length of 14 ÷ 17 nm [4,5] and, for the stoichiometric ratio of ZP1 : ZP2−ZP3 of 1 : 5, the mean distance between ZP1 attachment sites on each filament is approximately 75 ÷ 85 nm [6].

Figure 6.

(a) Schematic of the model of zona pellucida filamentous structure hypothesized by Wassarman [5]; (b) increase in number of inter-filament cross-links after fertilization as hypothesized by Green [6].

The higher stiffness of the ZP after fertilization was hypothesized by Green [6] to result from an increase in the number of inter-filament cross-links. In this way, filaments and their junctions become more resistant to extension and bending. The small amount of proteins released from cortical granules during the cortical reaction appears to be approximately enough for the task of binding filaments localized mainly in the inner part of the ZP [6]. Therefore, the density of cross-links should be higher in the inner part of ZP and gradually decreases towards the outer part. Evolution towards an equilibrium structure of the ZP requires that the newly formed analogous-to-ZP1 cross-links should aggregate in close proximity to existing ZP1 cross-linked sites. This clustering process makes the distance between ZP1 sites increase to 100 nm or more. A representation of the ZP network after fertilization is shown in figure 6b.

The characteristic distance of approximately 100 nm found by FE analysis where elastic properties change significantly may be correlated with the spacing between two ZP1 cross-link clusters. Should it be true that fertilization causes the number of ZP1 cross-links to increase, nanoindentation would reveal the ZP's biomechanical hardening in a depth range depending on the characteristic distance between two ZP1 clusters. Because the chosen indentation range was 0–200 nm, AFM measurements were sensitive enough to detect any local hardening eventually induced by cross-links clustering. In support of this statement, it is interesting to note that in mature ZP, biomechanical heterogeneity could not be considered significant even over the entire indentation range of 200 nm. Therefore, the very large gradient of the Young modulus observed for the inner layer of fertilized ZP (i.e. 592.8 kPa) with respect to the corresponding gradient found for the outer layer (i.e. 162.5 kPa) can indeed be explained with the presence of more ZP1 cross-links per mass unity following the zona reaction, in agreement with the work of Green [6].

Although the full structure of the bovine ZP still remains unknown, it is not unreasonable to suppose that a similar mechanism of cross-linking may take place in the filamentous network after fertilization.

5. Conclusion

Mechanical properties of ZP membranes isolated from mature and fertilized bovine oocytes were investigated in great detail with a novel hybrid procedure combining AFM nanoindentation measurements, nonlinear FE analysis and nonlinear optimization. The proposed approach was completely general as it could automatically find the distribution of material properties that best matches experimental data.

As expected, the fertilization process produces a significant biomechanical hardening of the ZP membrane. After fertilization, the ZP's elastic properties become highly heterogeneous but structural reorganization does not entail changes in constitutive behaviour. The study confirms the hypothesis that hardening is due to the increase of the number of inter-filaments cross-links within the ZP, whose density is expected to be higher in the ZP inner side. In fact, the ZP's stiffness was found to change sharply at a depth of 100 nm, which can actually be correlated to the distance between two cross-link clusters of the ZP filamentous network.

In summary, the proposed methodology is a robust and efficient framework for mechanical characterization of cell membranes that can contribute to clarifying fundamental issues of cell biomechanics. Specifically, the full understanding of zona hardening mechanisms, together with a correct estimation of ZP biomechanical properties, will allow fertilization protocols to be optimized.