Models of collective cell behaviour with crowding effects: comparing lattice-based and lattice-free approaches

Abstract

Individual-based models describing the migration and proliferation of a population of cells frequently restrict the cells to a predefined lattice. An implicit assumption of this type of lattice-based model is that a proliferative population will always eventually fill the lattice. Here, we develop a new lattice-free individual-based model that incorporates cell-to-cell crowding effects. We also derive approximate mean-field descriptions for the lattice-free model in two special cases motivated by commonly used experimental set-ups. Lattice-free simulation results are compared with these mean-field descriptions and with a corresponding lattice-based model. Data from a proliferation experiment are used to estimate the parameters for the new model, including the cell proliferation rate, showing that the model fits the data well. An important aspect of the lattice-free model is that the confluent cell density is not predefined, as with lattice-based models, but an emergent model property. As a consequence of the more realistic, irregular configuration of cells in the lattice-free model, the population growth rate is much slower at high cell densities and the population cannot reach the same confluent density as an equivalent lattice-based model.

1. Introduction

Discrete models are often used to study collective cell migration [1–5] and collective cell growth processes [6–12]. These models produce detailed snapshots and movie-based data that are easy to compare with experimental images and time-lapse data [13]. There are two key classes of random walk model that have been used to represent collective cell migration and growth.

Lattice-based random walk models typically represent the spatial domain as a one-, two- or three-dimensional regular lattice, with lattice spacing Δ. Cell motility events are usually represented by nearest-neighbour transitions, and cell proliferation events by placing new agents on the lattice. Computationally, the evolution of the system can be represented by a discrete time-stepping mechanism, in which, during each time step of duration τ, each agent has problem-specific probabilities of moving and of proliferating [13–18]. Alternatively, the evolution of the system can be represented by a continuous-time framework in which the waiting time for a particular event to occur is sampled from some problem-specific distribution [3,19,20].

Classical lattice-based random walks are non-interacting [1,19], meaning that each motility and proliferation event is independent of the state of the system. For example, an agent can move to a target site that is already occupied or a proliferation event can deposit a daughter agent at the same lattice site as the parent agent. These simple mechanisms do not incorporate any form of agent-to-agent interactions since multiple agents can reside on the same lattice site. Therefore, non-interacting models are relevant only for problems where the cell density is so low that cell-to-cell contacts and crowding effects are unimportant.

Many relevant applications of collective cell migration and proliferation involve situations with high cell densities and many cell-to-cell contacts [21–23]. Contact effects, such as contact inhibition of migration [24] and contact inhibition of proliferation [21], can play a major role in determining the behaviour of cell populations. In such situations, the effects of cell-to-cell crowding are often observed experimentally [22]. These observations have motivated the development of interacting random walk models that incorporate crowding effects to replicate contact inhibition of migration and contact inhibition of proliferation. Interacting lattice-based random walk models, also known as exclusion processes [25], allow each lattice site to be occupied by, at most, a single agent. The lattice spacing Δ is thought of as being equivalent to the cell diameter [26]. Interacting lattice-based random walks can be simulated in the same way as a non-interacting random walk, except that individual movement and proliferation probabilities now depend on the state of the system. For example, a motility event that would place an agent on an occupied site would be aborted. These aborted events are a simple way of representing crowding effects in the system [16,20,26]. Interacting lattice-based random walk models have been used to represent many processes in cell biology, including cancer cell migration [16,27], wound healing [8,28] and embryonic development [13].

Recently, research has begun to focus on deriving mean-field (continuum limit) descriptions of lattice-based interacting random walk models. The mean-field description most frequently takes the form of a partial differential equation (PDE) for an agent density. The ability to represent mathematically both the individual-level details and the population-level description of the random walk process is important for two key reasons. First, many experimental observations reflect both individual-level and population-level data for the same system [29]. Second, knowing the continuum-limit PDE for the random walk process enables the use of a range of mathematical tools (e.g. travelling wave analysis and similarity solutions). These can often give greater insight into the collective behaviour than is possible with computational simulations of the individual-based model alone. For example, Liggett [25] showed that an unbiased interacting motility mechanism can be described by the linear diffusion equation; Deroulers et al. [16] showed that agent-to-agent contact effects can lead to a nonlinear diffusion equation; Simpson et al. [12] showed that combining proliferation mechanisms with motility leads to a nonlinear reaction–diffusion PDE that is a generalization of the Fisher–Kolmogorov equation [30,31].

Lattice-free random walk models represent agent motility and proliferation on a continuous domain [32,33] and are more realistic than lattice-based models. Lattice-free models allow the direction of movement to be a continuous variable, rather than restricting agents to a discrete set of directions corresponding to nearest-neighbour lattice sites. This is more consistent with observations of cell migration and proliferation, in which individual cell movements and proliferation events are not restricted to a lattice [18,34]. In two dimensions, this means that each agent is allowed to move in any direction 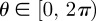. Circular distributions are used to draw random angles for either the direction of movement or the turning angle at each step of a two-dimensional random walk [3,33]. Lattice-free models have been used extensively in studies of molecular motion [35]. Most applications of lattice-free models to processes in cell biology have been non-interacting, which means that each discrete motility and proliferation event is independent of the state of the system and crowding effects are neglected [32,33,35]. In order for lattice-free models to be used for high-density applications in cell biology, crowding mechanisms must be introduced into the lattice-free framework.

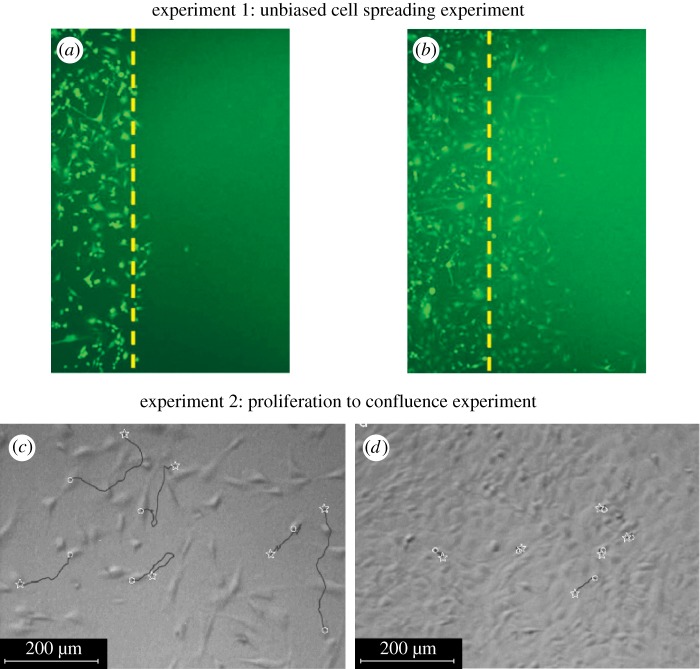
The aim of this work is to compare lattice-based and lattice-free interacting random walk models of cell migration and proliferation. To achieve this, we introduce both a lattice-based and a lattice-free model and apply them to two standard experiments used in cell biology. The first experiment, shown in figure 1a,b, is a scratch assay experiment that involves placing a population of cells on a two-dimensional substrate and then scratching away part of the population to reveal a sharp interface between the occupied region and the cell-free region. The motility of the cell population is characterized by measurements of the rate at which the population spreads into the scratched region. To characterize cell motility only, scratch experiments are often conducted over short time scales (approx. 1 day) for which cell proliferation is minimal [27]. The second experiment we will consider, shown in figure 1c,d, involves placing a sparse population of cells uniformly on a two-dimensional substrate. The cells then migrate and proliferate and the total number of cells in the population increases until the population eventually becomes confluent [22]. This kind of proliferation experiment is usually conducted over longer time scales (approx. 5–7 days) to give the cells the opportunity to proliferate many times during the course of the experiment. The data shown in figure 1c,d illustrate the key role of crowding effects: when the cell density is relatively low (figure 1c), the cell trajectories recorded are quite long, whereas when the cell density is higher (figure 1d), the cell trajectories are much shorter. These observations indicate the importance of contact inhibition of migration [24] in this experiment. Similarly, growth rate data from the experiments in figure 1c,d indicate that the population growth rate decreases as the density increases [22]. This implies that contact inhibition of proliferation is also important for these cells.

Figure 1.

Two canonical cell biology experiments. (a,b) Two snapshots of an unbiased scratch assay in which a dense population of motile cells is placed on a two-dimensional substrate and a portion of the population (to the right of the dashed line) is scratched away (reprinted with permission from the American Physical Society, Khain et al. [27]). After the scratch has been made, the rate at which the cells move along the lateral coordinate into the scratched region is measured. These experimental images correspond to U87 glioma cells with a cell diameter of 20 µm and the amount of time that elapsed between snapshots (a) and (b) is 24 h [27]. (c,d) Two snapshots of a cell proliferation assay using mouse fibroblasts (reprinted from Chemical Engineering Science, Tremel et al. [22], with permission from Elsevier). In these experiments, a sparse population of cells is initially uniformly distributed in a culture system and then allowed to proliferate so that the population grows and eventually becomes confluent. The amount of time that elapsed between snapshots (c) and (d) is approximately 50 h [22]. (Online version in colour.)

Here, we develop a new individual-based lattice-free model for a population of motile and proliferative cells with crowding effects. Bruna & Chapman [2] previously developed a model of hard sphere diffusion allowing for crowding effects. However, our approach differs from this and from other previous lattice-free models [35,36] as we allow agent proliferation (and agent-to-agent interactions are handled in a different way from hard sphere models [2]). We compare simulations of the lattice-free model in the experimental scenarios described above with simulations of a comparable lattice-based model and with experimental data. A variety of lattice types has been used in previous lattice-based modelling, including hexagonal or irregular lattices [37–39]. However, we focus on a square lattice as a basis for comparison with the lattice-free model as this is the most commonly used lattice in cell-based applications [13–15,18,19]. Where possible, we derive mean-field descriptions of the lattice-free model and compare these with averaged simulation results. Our work highlights important similarities and differences between the lattice-based and lattice-free approaches and demonstrates key challenges in deriving mean-field descriptions for interacting lattice-free models.

2. Two-dimensional lattice-based interacting random walk model

2.1. Discrete model

We use a two-dimensional square lattice with spacing Δ. Each site is indexed (i, j) where i, 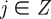, and each site has position 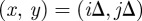. In any one realization of the discrete model, the occupancy of site (i, j) is 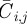, with 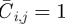for an occupied site and 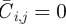for a vacant site.

If there are N(t) agents on the lattice, during the next time step of duration τ, N(t) agents are selected independently at random, one at a time. When chosen, an agent attempts to move with probability 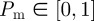. We consider the simplest form of motility in which the target site is chosen at random without any directional bias. For example, a motile agent at (x, y) will attempt to step to eithe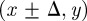r or 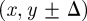, each with equal probability 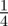. Since biological cells cannot occupy the same position in space, motility events that would place an agent on an occupied site are aborted.

Once the N(t) motility events are attempted, another N(t) agents are selected independently at random, one at a time. When selected, an agent attempts to proliferate with probability 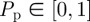. In general, N(t) increases during each time step for 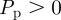, and this computational approach is appropriate for small values of 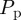, where the increase in N(t) per time step is small. Here, we consider the most straightforward proliferation mechanism in which a proliferative agent at (x, y) attempts to deposit a daughter agent in one of 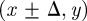or 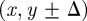with equal probability 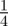. Any attempted proliferation events that would place a daughter agent onto an occupied site are aborted.

This lattice-based model is the same as that of Simpson et al. [12] and is called an exclusion process since no two agents can occupy the same lattice site. All lattice-based simulations are dimensionless in the sense that we set 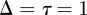, and we note that the simulation results can be rescaled using appropriate length and time scales for any particular application.

2.2. Mean-field model: a single non-proliferative agent

For a single non-proliferative agent, the lattice-based model reduces to a nearest-neighbour random walk in which crowding effects are absent. Standard arguments relate the stochastic motility to a diffusion process in an appropriate limit [40]. Since the motion of a single agent is unbiased, it is straightforward to show that the mean displacement per step is zero. An expression for the mean-squared displacement (MSD) can be derived by considering the x and y components of the displacement in the ith step,

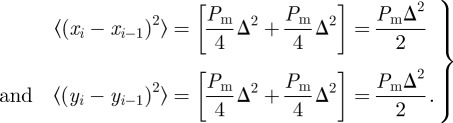2.1

Hence the total MSD per computational time step is 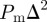and the MSD per unit time is 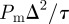. Holding 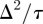constant and letting Δ and τ tend to zero jointly, the probability density function for the position of the single agent satisfies the two-dimensional linear diffusion equation with diffusivity given by [40]

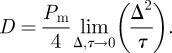2.2

2.3. Mean-field model: a population of interacting proliferative agents

To connect the discrete mechanism for a population of interacting agents with a mean-field model, we average the occupancy of site (i, j) over many statistically identical realizations to obtain 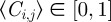. After averaging, we form a discrete conservation statement describing 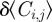, which is the change in average occupancy of site (i, j) during the time interval from time t to time t + τ. The discrete conservation equation encodes all of the processes occurring in the discrete simulations. In this case, we have

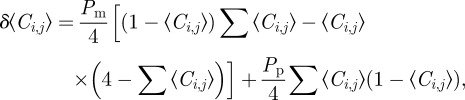2.3

where we define

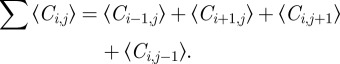2.4

The positive terms on the right-hand side of equation (2.3) represent events that place an agent at site (i, j) (either by movement or by proliferation), while the negative terms represent events that remove agents from site (i, j) (which can only occur by movement). Note that all terms on the right-hand side of equation (2.3) are proportional to terms such as 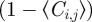. This reflects the fact that potential motility and proliferation events are only successful if the target site is vacant.

To obtain the mean-field equation for the discrete conservation statement, all terms in equation (2.3) are expanded in a Taylor series about site (i, j). Dividing the resulting expression by τ and taking the limit as 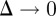and 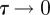, with 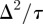held constant, gives the following PDE for C(x, y, t) [3]:

2.5

where the diffusivity is given by equation (2.2) and the growth rate λ by

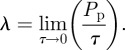2.6

To obtain a well-defined continuum limit requires that 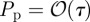so that λ remains finite in the limit  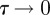[3,12,40].

3. Two-dimensional lattice-free interacting random walk model

3.1. Discrete model

Here, we develop a new individual-based model for cell migration and proliferation that is free from lattice constraints but incorporates crowding effects. Agents can occupy any location in two-dimensional continuous space, provided there is sufficient room to do so. The position of the centre of the ith agent is denoted 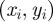for 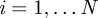. As with the lattice-based model, N(t) agents are selected independently at each time step and, when selected, attempt to move with probability 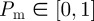. We consider the simplest possible motility mechanism: the agent attempts to move a fixed distance Δ in a randomly chosen direction 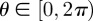. For the purposes of incorporating crowding (exclusion) effects, we assume that each agent is a circle of diameter Δ. These assumptions about the step length and agent diameter mean that the lattice-free model can be easily compared with the lattice-based model. However, we note that it would be straightforward to relax these assumptions and allow the step length, for example, to be drawn from some probability distribution [3]. To enforce exclusion effects, any movement attempt in which the agent's attempted path

passes within a distance Δ of another agent's position is aborted.

Once the N(t) motility events have been attempted, another N(t) agents are selected independently and attempt to proliferate with probability 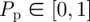. The agent attempts to divide into two daughter agents, separated by distance Δ along an axis of randomly chosen direction 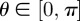. The proliferation attempt is aborted if the path connecting the daughter agents' target positions,

passes within a distance Δ of another agent's position. Figure 2 illustrates the motility and proliferation mechanisms of the lattice-free individual-based model.

Figure 2.

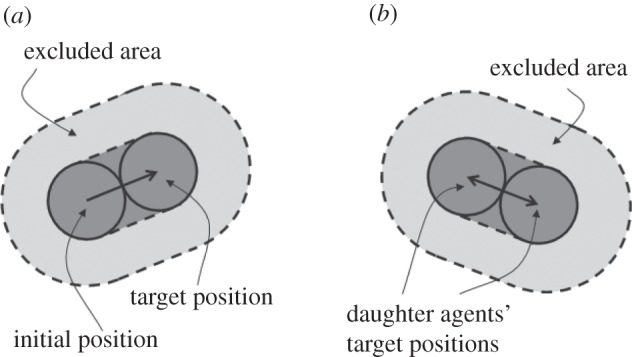
Schematic of the lattice-free model. (a) An attempted motility event. (b) An attempted proliferation event. In each case, the event will be aborted if there is another agent that overlaps the dark grey area or, equivalently, if there is another agent whose centre lies in the light grey area, referred to as the excluded area.

The lattice-free proliferation mechanism is similar to the lattice-based mechanism: in both models, the parent agent and daughter agents are separated by a distance of Δ immediately after a proliferation event. The lattice-free proliferation mechanism differs slightly from the lattice-based mechanism since the parent agent in the lattice-free model moves a distance Δ/2 during a successful proliferation event, whereas the parent agent in the lattice-based model does not move.

There are other subtle differences between the lattice-based and lattice-free models in terms of the mechanism for aborting potential migration and proliferation events. In the lattice-based model, the only condition that determines whether an event is successful is the occupancy of the target site. In the lattice-free model, even if the target location is vacant, an event will be aborted if the path from the initial to the target location is obstructed by another agent.

3.2. Mean-field model: a single non-proliferative agent

For a single, non-proliferative agent, the lattice-free model reduces to a lattice-free random walk without agent-to-agent interactions [3]. As in the lattice-based model, the motion of a single agent is unbiased and so the mean displacement per step is zero. An expression for the MSD can be derived by considering the x and y components of the displacement in the ith step,

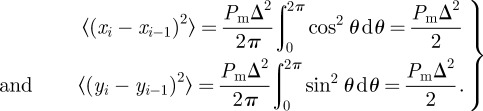3.1

This is the same as in the lattice-based case (equations (2.1)). Hence, the MSD per unit time is 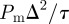, and the probability density function for the position of the agent satisfies the two-dimensional linear diffusion equation [40], with the same diffusivity (2.2) as for the lattice-based model.

3.2.1. Mean-field model: a population of interacting non-proliferative agents

We consider a special initial condition for a population of non-proliferative agents where the distribution of agents within the domain is, on average, independent of the vertical location. This corresponds to the scratch experiment in figure 1a,b. Under these conditions, the two-dimensional motion can be quantified in terms of the horizontal coordinate only [12,27,41].

To derive a mean-field description, we divide the domain into vertical strips, each with width Δ, and associate each agent with the strip that contains the agent's centre (figure 3). Let 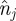represent the total number of agents in strip j and 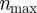the maximum number of agents that can be placed within any strip. We now develop a conservation statement for the relative agent density 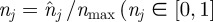), analogous to equation (2.3) for the lattice-based model. The change in 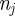during a time interval of duration τ is equal to the change in density associated with events that move agents into strip j (from strips 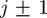) minus the change in density associated with events that move agents out of strip j (into strips 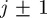). To account for crowding effects, we assume that the probability of an agent successfully entering strip j is proportional to the available space, 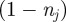, in that strip. Hence

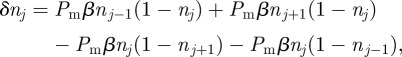3.2

where β is the probability that an attempted movement would take an agent in strip j to strip j + 1 (which by symmetry is the same as the probability that the attempted movement would take the agent to strip j − 1). Incorporating β into the conservation statement allows for the fact that not all successful motility events change the value of n_j. For example, one of the highlighted trajectories in figure 3 would reduce n_j and increase 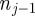, whereas the other would leave n_j unchanged.

Figure 3.

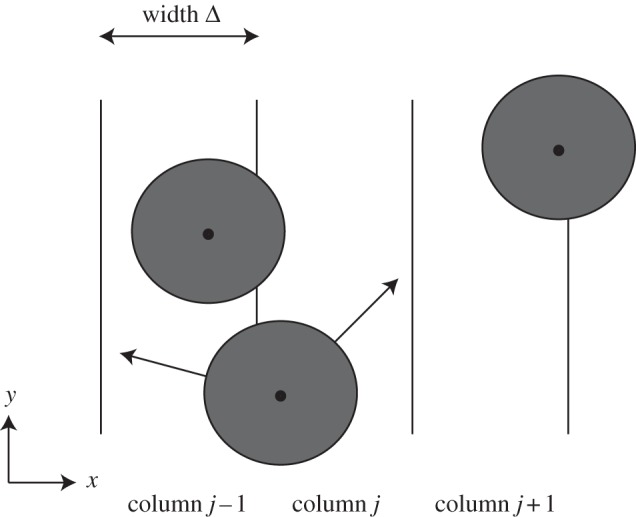
Schematic used to derive the mean-field model for the lattice-free motility mechanism in the special case where the initial distribution of agents within the domain is, on average, independent of the vertical location. We divide the domain into vertical strips, each of width Δ, and associate each agent with the strip that contains the centre of that agent. For example, the middle agent overlaps strips j − 1 and j, but it is associated with strip j since the centre of the agent lies in strip j.

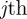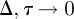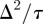As with the lattice-based discrete conservation statement, the nonlinear terms in equation (3.2) vanish. Identifying the discrete occupancy of the column, n_j, with a continuous function C(x, t) and taking the usual limit with held constant leads to the one-dimensional linear diffusion equation for the vertically averaged density C(x, t),

3.3

with

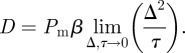3.4

The key result here is that the spatial distribution of agents in the lattice-free model evolves according to a linear diffusion equation. To be consistent with the diffusivity in equation (2.2) for a single non-proliferative agent, we must have 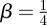. We will confirm this by comparing averaged simulation data with the solution of equation (3.3) in §4.

3.2.2. Mean-field model: a homogeneous population of interacting proliferative agents

We now consider a special initial condition in which the distribution of agents within the domain is, on average, independent of position. This corresponds to the experimental set-up in figure 1c,d. In this special case, the state of the system can be described by a spatially invariant density function, 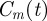, representing the spatially averaged density of agents within the domain [6,12]. To develop a mathematical model for 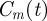, we suppose that the number of agents at time t is N(t) and let 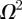be the total area of the domain. We now estimate the probability that a particular proliferation attempt will be successful. This requires that there are no other agents within a certain area, A, surrounding the agent attempting to proliferate. If p_i is the probability that the centre of agent i is not in A, given that agents 1 to i − 1 are not in A, then we have

3.5

where E_i is the proportion of the total area excluded by the first i agents. The probability 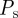that a proliferation attempt will be successful is then the probability that the centres of all N(t) agents lie outside A,

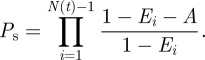3.6

Each agent excludes an area 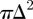although the area excluded by different agents can overlap (figure 4). Hence, we may write a recurrence relation for E_i

3.7

where 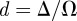and q_i is the expected proportion of agent i's excluded area that overlaps with the area already excluded by the first i−1 agents. The expected overlap, q_i, depends on short-range correlations in agent locations arising from the restriction that no two agents can be closer than a distance Δ apart. To make progress, we make the simplifying assumption that q_i is equal to the proportion of the total area that is already excluded by the first i−1 agents so that 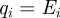. Given that 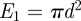, the recurrence relation for E_i can then be solved to give

3.8

Figure 4.

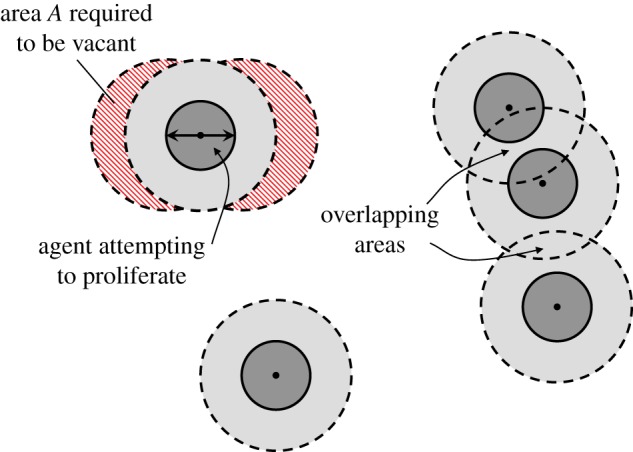
An attempted proliferation event. In order for the proliferation attempt to be successful, there must be no agents whose centres are in the hatched area A. In this example, there are a total of five agents and the area excluded by these agents, E₅, corresponds to the sum of the light and dark grey areas. If there were a sixth agent, the probability that its centre would lie outside A would be given by equation (3.5), 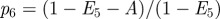, which is the white area divided by the sum of the white and hatched areas. (Online version in colour.)

For consistency with the lattice-based case, we define the spatially averaged agent density C_m(t) to be 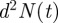, so C_m(t) = 1 is the same density as a fully occupied lattice of spacing Δ. Provided that the domain size is large 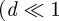), we can treat the spatially averaged agent density as a continuous variable. Combining equations (3.6)–(3.8) gives

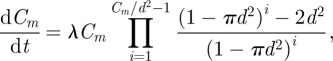3.9

where, as before, .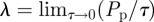

It is worth noting that the agent density cannot exceed the optimal hexagonal arrangement of circles in the plane, which imposes an upper bound of 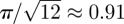on the proportion of area that can be occupied. Since, in our notation, an agent density of C_m(t) = 1 corresponds to circles on a regular square lattice (area coverage π/4), the upper bound on C_m(t) is 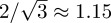. Equation (3.9) cannot, therefore, be accurate at high densities because its equilibrium increases without bound as the domain size tends to infinity 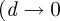). Nevertheless, equation (3.9) may provide a reasonable description of the population growth at low-to-moderate agent densities. We will assess this by comparing numerical solutions of equation (3.9) with simulation results in §4.2.

4. Results

We now compare averaged simulation data with the solutions of the appropriate mean-field models for the two scenarios illustrated in figure 1.

4.1. Non-proliferative simulations

To mimic a scratch assay geometry (figure 1a,b), we consider two-dimensional cell motion with an initial condition in which the distribution of agents within the domain is, on average, independent of the vertical location. Unlike the scratch assay in figure 1a,b, where the initial population is adjacent to the left boundary and spreads unidirectionally, we consider an initial population of agents in the centre of the domain, so that we will observe bidirectional spreading. To achieve this, we initialize the simulations with a fixed average agent density 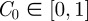in the region 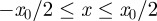and no agents outside this region. In the lattice-based simulations, initially each lattice site in the region 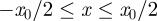is occupied with probability C₀, independent of the other lattice sites (figure 5a). In the lattice-free model, agents are placed at random within the region 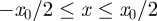so that all agents are located a distance at least Δ from all other agents (figure 6a).

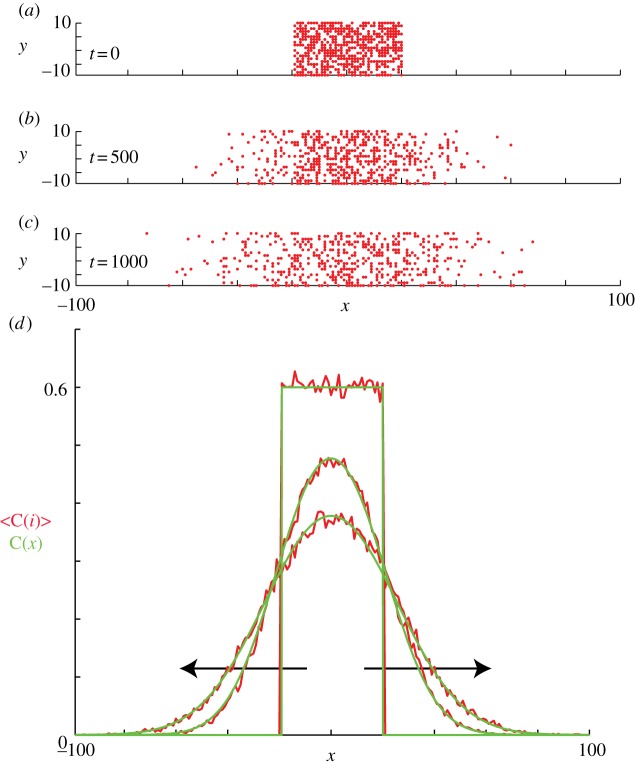
Figure 5.

Non-proliferative simulations of the lattice-based model with 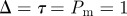and 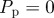. Agents are initially placed at randomly chosen lattice sites in the region 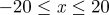and the initial average agent density within this region is C₀ = 0.6. Discrete snapshots in (a–c) show agent locations t = 0, 500 and 1000. Simulation data in (d), averaged over 100 identically prepared realizations, show stochastic density profiles (red) superimposed on the solution of the appropriate continuum model (green), given by equation (4.1) with 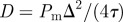. The arrows show the direction of increasing t. (Online version in colour.)

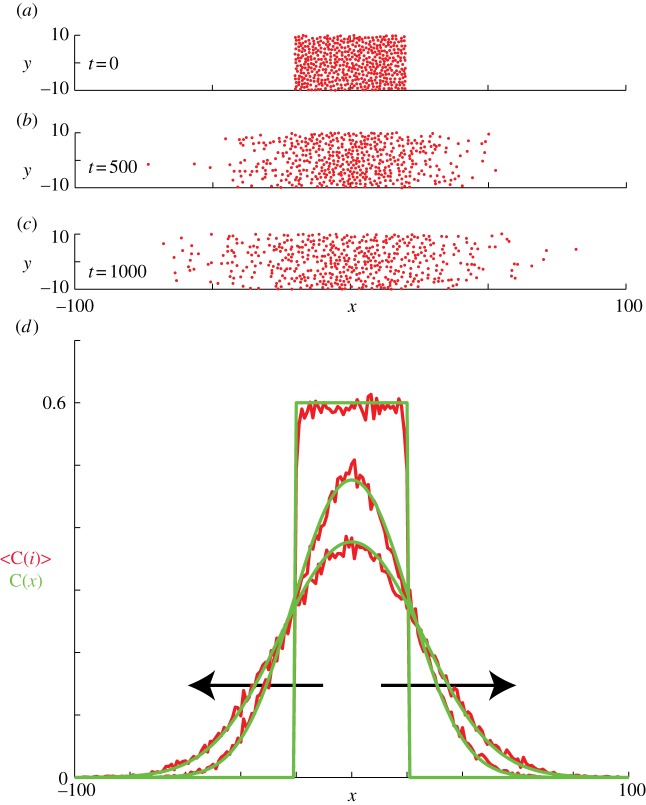
Figure 6.

Non-proliferative simulations of the lattice-free model with 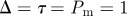and 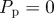. Agents are initially placed at random in the region 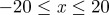and the initial average agent density within this region is C₀ = 0.6. Discrete snapshots in (a–c) show agent locations t = 0, 500 and 1000. Simulation data in (d), averaged over 100 identically prepared realizations, show stochastic density profiles (red) superimposed on the solution of the appropriate continuum model (green), given by equation (4.1) with 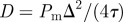. The arrows show the direction of increasing t. (Online version in colour.)

For all simulations, we impose periodic boundary conditions on all boundaries. However, our results are insensitive to the boundary conditions applied to the vertical boundaries because we only perform simulations for relatively short periods of time so that the agents never reach the vertical boundaries. Under these conditions, the appropriate solution of equation (3.3), on 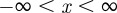, is [42]

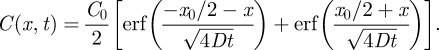4.1

Results in figure 5a–c show snapshots from a single realization of the lattice-based model with an initial density of C₀ = 0.6 and x₀ = 40. Results in figure 5d show the column density of agents, further averaged over 100 identically prepared realizations, compared with equation (4.1) with 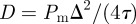. As expected, the averaged simulation data are accurately predicted by the linear diffusion equation [43].

We now investigate corresponding simulations for the lattice-free model. Agent density profiles are obtained in the same way as in the lattice-based model, by averaging the number of agents in vertical strips of width Δ (figure 3) across an ensemble of 100 identically prepared realizations. Figure 6a–c shows snapshots from a single realization of the lattice-free model. We also plot equation (4.1) and find that the solution of the linear diffusion equation matches the discrete data very well. This comparison confirms the validity of the conservation argument in §3.2.1.

The results shown in figures 5 and 6 are for an initial density of C₀ = 0.6. Starting the simulations with a lower initial density results in an equally good match with the mean-field diffusion equation. Initial conditions with are not readily achievable in the lattice-free model; the reasons for this will be discussed in the following section.

The key objective in performing scratch assays (figure 1a,b) is to describe the motility of cells, which is usually done by measuring the rate at which the leading edge of the population moves after the scratch has been made [21,28]. Mathematical models are applied to scratch assays to quantify the cell motility rate so that predictions about the migration of the cells can be made under different conditions, such as a scratch assay performed for a different amount of time or in a different geometry, e.g. a circular scratch. One way to quantify cell motility using the lattice-free model is to perform repeated simulations of the discrete model to characterize the mean rate of advance of the leading edge. This could then be used to calibrate the value of 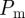to match experimental data [27]. Instead, our mean-field approach shows that the average behaviour of the lattice-free model is given by equation (3.3). This allows us to quantify cell motility in terms of the diffusivity D, without the need for repeated computational simulations. Once an estimate of D has been made using experimental observations, predictions can be made about the migration of the cells under different conditions [44].

4.2. Proliferative simulations

We now consider simulations of a proliferation assay analogous to the experimental set-up shown in figure 1c,d. Simulations are initialized with a low density of agents, distributed randomly throughout the domain. The biological time scale for cell proliferation is much greater than the time scale for cell motility [12,41], so we assume that the proliferation probability is much smaller than the movement probability 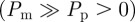. One important consequence of this separation of time scales is that the spatial distribution of agents remains approximately homogeneous: C(x, y, t) = C_m (t) [6,12].

For the lattice-based mean-field model, a homogeneous distribution means that the spatial gradients in equation (2.5) vanish so that we have

4.2

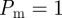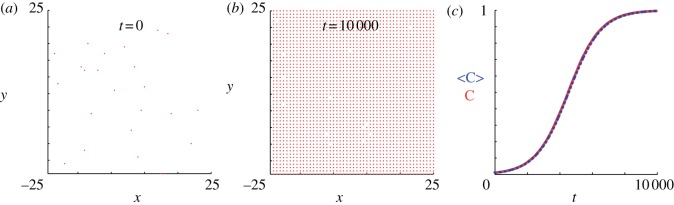
Recent work has shown that, for typical values of the cell diffusivity (10⁻⁶ mm² s⁻¹) [21,45], cell diameter (20 µm) [27] and cell doubling time (18–20 h) [21,44], the appropriate parameters in the discrete model are and 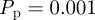 [12]. With these parameters, figure 7a,b shows snapshots from a realization of the lattice-based model. After a sufficient period of time, the lattice becomes fully occupied. To quantify the growth in agent numbers, we record the spatially averaged agent density 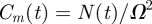, where N(t) is the total number of agents and 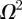is the area of the domain. Figure 7 shows the simulation data for C_m(t) together with the logistic growth curve predicted by equation (4.2), which matches the simulation data very closely.

Figure 7.

Simulations of the lattice-based model with proliferation, 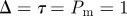and 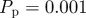. Agents are initially distributed at random and the initial agent density is C₀ = 0.01. Here, we compare simulation data (dashed) and the solution of the mean-field equation (4.2) (solid). (Online version in colour.)

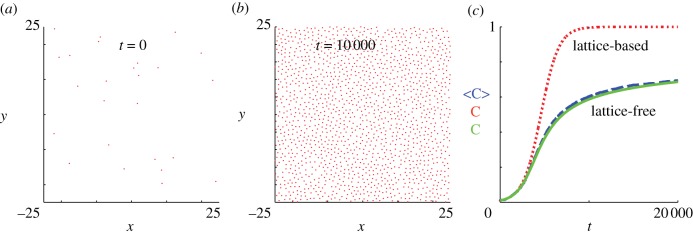
Equivalent simulation results for the lattice-free model are shown in figure 8. In the early stages of the experiment (up to approximately t = 2000), the population growth curve in figure 8c is very close to the lattice-based result. This reflects the fact that, in the absence of significant agent-to-agent crowding effects, the lattice-based and lattice-free models behave similarly. However, at later times, the agent density in the lattice-free model grows much more slowly and does not reach C_m(t) = 1 (the density of a fully occupied lattice), even after the much longer simulation time of t = 20 000. This reduced growth rate is a consequence of the irregular, though more realistic, arrangement of the agents in the lattice-free model (compare figure 7b with figure 8b). Even at moderate densities, this irregular arrangement means that the probability of a successful proliferation event is greatly reduced. In contrast, even at very high densities approaching C_m(t) = 1, a vacant lattice site will always become occupied eventually via a proliferating agent at one of the nearest-neighbour sites.

Figure 8.

Simulations of the lattice-free model with proliferation, 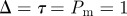and 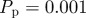. Agents are initially distributed at random and the initial agent density is C₀ = 0.01. Here, we compare simulation data (dashed) and the solution of the approximate mean-field equation (3.9) (solid). Also shown for comparison is the solution of the logistic equation (4.2) describing the corresponding lattice-based model (dotted). (Online version in colour.)

Also shown in figure 8c is the numerical solution of the mean-field equation (3.9) (see appendix A for details of the solution method), which matches the lattice-free simulation data well. This shows that, despite the simplifying assumptions made to arrive at equation (3.9), this mean-field model encompasses the key processes in the lattice-free proliferation model. In particular, equation (3.9) captures the long tail as the population grows more slowly at higher densities.

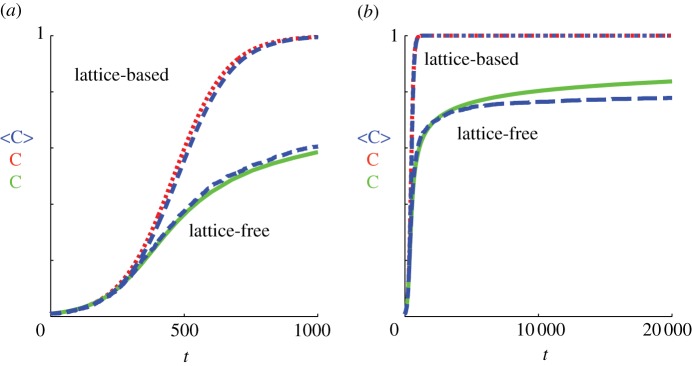
Although we have demonstrated a good match between individual-based simulations and mean-field models for the biologically relevant parameter values 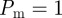and 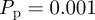in figures 7 and 8, it is well known that the accuracy of the lattice-based mean-field model decreases as the proliferation rate 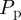increases [6,8,12]. This is due to the formation of clusters, as daughter agents are deposited near parent agents more rapidly [27], which means that the assumption of a spatially homogeneous population is no longer valid. To test the behaviour of the models under these conditions, we compare simulation data and mean-field results for both models when 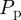is increased by a factor of 10 to 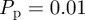(figure 9). The lattice-based simulations reach confluence approximately 10 times faster than in figure 7, but still match the logistic growth curve well. The lattice-free model again grows more slowly than the lattice-based model, with a very long tail. The match between the lattice-free simulations and mean-field model, equation (3.9), is good up to a density of approximately C_m(t) = 0.7. Above this density, the individual-based simulations grow more slowly than predicted by equation (3.9). This is consistent with the observation in §3.2.2 that equation (3.9) is not expected to be accurate at high densities.

Figure 9.

Results from both models with more rapid proliferation, 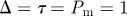and 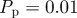. Agents are initially distributed at random and the initial agent density is C₀ = 0.01. Here, we compare simulation data (dashed) and the solution of the relevant mean-field equations for both the lattice-based (dotted) and lattice-free (solid) models. (a) Shows a close up of (b) for earlier times (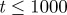). (Online version in colour.)

5. Comparing lattice-based and lattice-free models with experimental data

The results in §4.2 reveal a key difference between the lattice-based and lattice-free models. In the lattice-based model, the lattice rapidly becomes fully occupied and no further proliferation is possible. The lattice-free population grows much more slowly at moderate to high densities and it is likely that it will never reach the same confluent density as the lattice-based model. This is an advantage of the lattice-free model because the population carrying capacity, rather than being determined by an artificially imposed lattice, is an emergent outcome of the model. There are also qualitative differences between the models in that the lattice-based confluent population is always perfectly aligned on the underlying lattice, whereas the lattice-free model predicts a more random distribution of agents. We note that the lattice-free arrangement (figure 8b) is visually a much better representation of experimental results (figure 1d) than the lattice-based arrangement (figure 7b).

We now ask whether these differences would lead us to make different predictions about an experimental system if we applied the two models to the same experimental data. To explore this issue, we fit the mean-field models, equations (3.9) and (4.2), to data from a proliferation experiment [22]. The first 40 h of data correspond to a settling phase during which there was no significant change in density; similar to Tremel et al. [22], we ignore these data and instead use the post-settling data only. Using a standard curve-fitting algorithm (Matlab lsqcurvefit, which uses the trust-region-reflective optimization algorithm [46]), we calibrated λ, Δ and C(0) in equations (3.9) and (4.2) to produce a least-squares fit to the experimental data. The data and fitted model growth curves are shown in figure 10 and the fitted parameter values and least-squares residuals are given in table 1. Note that the data and results in this section are dimensional; dimensionless density C(t) is related to dimensional density 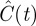via .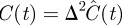

Figure 10.

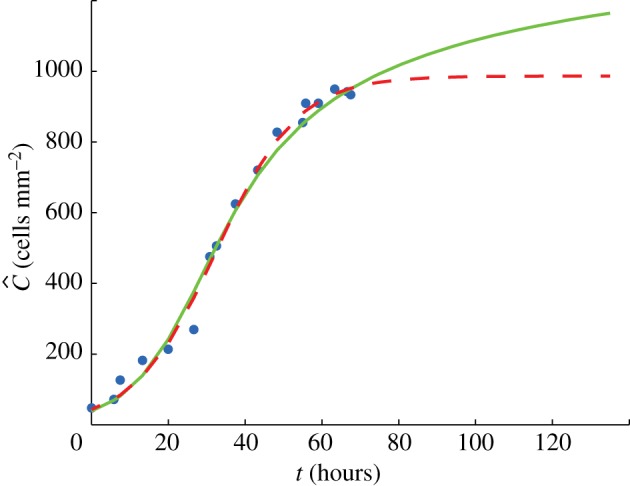
Average cell density against time: data from the experiment of Tremel et al. [22] (points); growth curve predicted by the lattice-free model (solid); growth curve predicted by the lattice-based model (dashed). Model parameters, shown in table 1, were fitted using a least-squares method (Matlab lsqcurvefit) to provide the best match to the data. Note that the first 40 h of the Tremel et al. [22] data, corresponding to the initial settling phase, were neglected and are not shown here; in the graph, t = 0 corresponds to the beginning of the growth phase. (Online version in colour.)

Table 1.

Results of fitting the lattice-free and lattice-based mean-field models (equations (3.9) and (4.2), respectively) to experimental data from a proliferation assay [22]. The three parameters shown in the table were adjusted to obtain a least-squares fit of each model to the data. The final column shows the square root of the sum of squared residuals for each model. The density values shown in the table are in units of cells mm⁻²; these dimensional densities 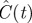can be converted to dimensionless density C(t) via .

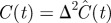	cell diameter Δ	initial density	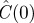proliferation rate λ	least-squares residual
lattice-based model	0.032 mm	43 cells mm−2	0.095 h−1	124 cells mm−2
lattice-free model	0.024 mm	38 cells mm−2	0.105 h−1	153 cells mm−2

The lattice-based model fits slightly better (lower residual) than the lattice-free model, but the difference in fit is relatively small and figure 10 shows that both models produce a reasonable match to the data. The lattice-based model predicts a cell diameter of 32 µm and the lattice-free model predicts a cell diameter of 24 µm. The cells are packed more loosely in the lattice-free model so, in order to achieve a given density, it predicts a smaller cell size than the lattice-based model. Nevertheless, both values are consistent with experimental observations showing that the typical fibroblast cell diameter is in the range 20–30 µm (figure 1a,b) [22]. The lattice-free model estimates a proliferation rate λ that is approximately 10 per cent higher than the lattice-based model. This is intuitively reasonable since more proliferation events are aborted in the lattice-free model than in the lattice-based model, so the lattice-free model requires a higher rate of attempted proliferation events to give a comparable observed proliferation rate.

The most significant difference between the lattice-based and lattice-free models again lies in the predicted long-term behaviour of the population. Although both models have reached similar densities (approx. 950 cells mm⁻²) by t = 70 h, the lattice-based model is at 96 per cent of its maximum density (which is 987 cells mm⁻²), whereas the lattice-free model is only at 53 per cent of the density corresponding to a fully occupied lattice of spacing Δ (which is 1786 cells mm⁻²). The lattice-based model, therefore, predicts that there will be minimal growth beyond t = 70 h, whereas the lattice-free model predicts that significant growth will occur beyond t = 70 h (figure 10), with a slow approach to carrying capacity. Unfortunately, Tremel et al. [22] do not report any data beyond t = 70 h, so it is difficult to draw any conclusions about which of the two models best represents long-term experimental data.

6. Discussion

We have developed a new, discrete model for migration and proliferation of a population of cells in a monolayer. In contrast to the majority of previous discrete models, this model is lattice-free, meaning that there is no restriction on cells to occupy points on a predefined, artificial lattice. This results in a much more realistic configuration of cells (for example, compare figure 7b with figure 8b).

Freeing cells from lattice constraints has some surprising consequences for the population-level predictions of the model. Most notably, it is impossible for the population to reach the maximum density that would be predicted by an equivalent lattice-based model. This is because the cells are not perfectly aligned, but are arranged in a more spatially random configuration. Thus, the available space is used less efficiently and, as the average density increases, it becomes increasingly unlikely that a cell will have the space required to divide into two daughter cells. Some models have used a non-square lattice [16,37,38] to enable a more realistic spatial configuration of cells. However, this approach still has the disadvantage that the carrying capacity of the population is predetermined by the arbitrary choice of lattice.

The mean-field descriptions of the lattice-free model developed in this paper make simplifying assumptions about the spatial structure of the population. This has enabled us to develop practical tools that can predict average population-level behaviour. An important goal for future work is a more rigorous derivation of the continuum limit of the lattice-free model, for example, by using a spatial moment dynamics approach [6,43,47]. Nevertheless, we have shown that population-level behaviour can be predicted in two special cases. First, in the case in which there is no proliferation, the population is well described by the linear diffusion equation. Second, in the case in which the population is spatially homogeneous, the average agent density may be approximated by an ordinary differential equation. This equation predicts lower densities and a slower approach to carrying capacity than the logistic growth equation, which is the equivalent mean-field description for the lattice-based model.

We compared the predictions of the lattice-free model with experimental data from a proliferation assay [22]. Fitting the model parameters to the data gives a fit that is comparable to that of the logistic equation and predicts a similar (though slightly higher) proliferation rate. However, the lattice-based model predicts that the population has reached confluence at 70 h and there will be no further growth. The lattice-free model predicts that the population will continue to grow beyond 70 h, though at a much reduced rate. The significance of this difference is difficult to assess using published data since most proliferation experiments are aimed at measuring the growth rate and hence focus on the early stages of the growth curve rather than the later stages when the population is approaching confluence.

Simulations of the lattice-free model are more computationally intensive than the lattice-based model. This is because, under the simulation method implemented, each attempted movement or proliferation event requires the location of all other agents in the population to be checked, so simulation time is proportional to N(t)². In contrast, the lattice-based model only requires the status of the four nearest-neighbour lattice sites to be checked, so simulation time is proportional to N(t). In practice, this restricts the size of population that can be simulated under the lattice-free model. An important goal for the future is to develop more efficient simulation algorithms, for instance, by indexing which agents are in a given region of the domain at a given point in time. This will enable spatially variable processes to be studied; for example, invasion waves of proliferating cells [44] in the lattice-free framework.

The migration aspect of our lattice-free model is similar to models of hard sphere suspensions [2,36]. The main difference between these previous approaches and our lattice-free model is that our model includes cell proliferation. Another difference is that hard sphere models often assume elastic collisions [36] or only check that the target site for a movement event is vacant [48]. This mechanism would allow agents to ‘leapfrog’ over other agents, which is not biologically realistic [49]. An important aspect of our model is that an agent can only complete an attempted move if the entire path from its initial to its target location is clear of other agents.

Using a lattice-free framework enhances the realism of the model by removing artificial constraints on the cells' spatial distribution. Nevertheless, the model still makes several simplifying assumptions. For instance, the cells are treated as incompressible circles, whereas in reality cells are not circular and can deform in shape to accommodate neighbouring cells. A cell attempting to move or to proliferate is assumed to select a direction at random and, if it encounters another cell in that direction, the attempt is aborted completely. In reality, cells may exhibit some global directional bias, for example, owing to chemotaxis [17,19] or local persistence. A cell may also adjust its direction or step length in order to complete a movement or proliferation event. These extensions will be addressed in future work.

In this paper, we have focused on the simplest possible lattice-free model to enable direct comparison with a lattice-based equivalent. Removing lattice constraints is a necessary prerequisite for tackling complex, inherently non-lattice effects, such as shape deformation and directional persistence.

Appendix A. Method of numerical solution of ordinary differential equations

The lattice-free mean-field equation (3.9) for a homogeneous, proliferating population of cells was solved in Matlab v. 7.10 using the ode45 function. This function implements the Dormand–Prince version of the Runge–Kutta formulae, which uses fourth- and fifth-order approximations in an adaptive step size routine [50].

To ensure that our numerical results are reproducible, we also used a standard fourth-order Runge–Kutta method with a fixed step size 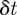. Using 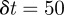or 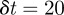gave solutions that are indistinguishable from the results presented in figures 8–10.

For equation (3.9) to be well defined, the upper limit 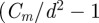) for the index i in the iterated product must be an integer. We solved equation (3.9) in two ways: (i) by rounding 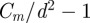to the nearest integer and (ii) by taking the integer part of 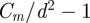(i.e. reducing it to the nearest smaller integer). As a result of either of these procedures, the rate of population increase, 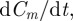is discontinuous in C_m, implying that the solution C_m(t) is non-smooth. However, when the domain is large relative to the agent diameter, we have 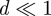ensuring that the discontinuities are small in magnitude and the solution appears smooth over the time scale of interest. For the domain size used in figures 8–10, d = 0.02, and we found that the two rounding methods described above produce identical results.