The value of reputation

Abstract

Reputation plays a central role in human societies. Empirical and theoretical work indicates that a good reputation is valuable in that it increases one's expected payoff in the future. Here, we explore a game that couples a repeated Prisoner's Dilemma (PD), in which participants can earn and can benefit from a good reputation, with a market in which reputation can be bought and sold. This game allows us to investigate how the trading of reputation affects cooperation in the PD, and how participants assess the value of having a good reputation. We find that depending on how the game is set up, trading can have a positive or a negative effect on the overall frequency of cooperation. Moreover, we show that the more valuable a good reputation is in the PD, the higher the price at which it is traded in the market. Our findings have important implications for the use of reputation systems in practice.

1. Introduction

Reputation is a piece of public information that summarizes how a person behaves towards others. Individuals often invest substantial resources to maintain a good reputation. These costs are incurred because having a good reputation is valuable: empirical and theoretical studies from evolutionary game theory and economics indicate that having a good reputation increases one's expected payoff in future interactions with others [1–6]. Therefore, reputation can incentivize cooperative behaviour, i.e. behaviour that is individually costly, but socially beneficial. This function of reputation has been formalized in the framework of indirect reciprocal altruism [4,7–12]. Within this framework, one can quantify the theoretical value of having a good reputation [4]. Here, we examine a game where reputation can be earned in a repeated Prisoner's Dilemma (PD), but can also be bought and sold on a market. This game allows us to investigate how the trading of reputation affects the level of cooperation in the PD, and how people assess the material value of reputation.

In our experiments, players engage in a series of two-player PD games with different partners. In each round, players are randomly paired, and simultaneously choose between cooperation (C) and defection (D). Cooperation decreases one's payoff by a cost c, but increases the other player's payoff by a benefit b (b > c; we use b = 30 and c = 10). Defection has no effect on either payoff. Previous experiments exploring reputation in repeated PDs and related games [6,13–17] have established that giving information about a co-player's decision history promotes cooperation; and giving more information can lead to higher frequencies of cooperation [16]. In these experiments, it is typically left to the participants to assess a partner's reputation based on past history of play, and to then choose an action accordingly. With such a set-up, it is ambiguous how subjects are using the reputational information, and it is therefore impossible to calculate a well-defined theoretical value of a good reputation.

We resolve this ambiguity by assigning each player an explicit reputation that is either ‘good’ or ‘bad’. The assignment depends on the player's behaviour in the previous round and is based on an assignment rule that is known to all players. Our choice of assignment rule is based on the seminal theoretical work of Ohtsuki & Iwasa [4,18,19]. To establish and maintain cooperation, assignment rules must take into account a player's action within the context of both the player's own reputation and the partner's reputation. We use two specific assignment rules that are derived from the social norm ‘standing’ (figure 1). ‘Standing’ assigns a good reputation to players that cooperate, except when a player in good reputation meets a player in bad reputation [8]. Here, the good player must defect to maintain good reputation. This social norm prescribes withholding cooperation from bad players, and thereby creates an incentive to maintain a good reputation.

Figure 1.

Assessment rules for the reputation systems used in our experiments. C and D stand for cooperation and defection, G and B for a good and bad reputation. Assessment rules determine the reputation based on the last action of a player, her own reputation and the opponents' reputation. Eight of such third-order assessment rules, named the ‘leading eight’, have been demonstrated in theory to sustain a high level of cooperation [4]. The leading eight share a number of properties: When playing with a player in good reputation, cooperation results in a good reputation, while defection results in a bad reputation; and a player in good reputation can defect against a player in bad reputation without losing the good reputation. They differ in the way how an interaction between two bad players is evaluated, and how cooperation of a good player towards a bad player is evaluated. In our experiment, we use a reputation system referred to as ‘standing’ (reputation system 1). This system assigns a good reputation to players that cooperate, except when a player in good reputation meets a player in bad reputation. In this case, the good player must defect to stay in good reputation. We also use an alternative system (reputation system 2) that differs from the first system in how interactions between two bad players are evaluated. The maxim of this system could be expressed as ‘Cooperate with those in good reputation, and refuse to cooperate with those in bad reputation. Then, and only then, your reputation will be good.’

To introduce trading, players are given the opportunity to change their reputation in trading rounds before and after each PD. Players in bad reputation can buy a good reputation and players in good reputation can sell their reputation, at a price set by the market. Trading is facilitated by a market maker that always allows players to buy or sell reputation and converges towards stable prices when the supply of reputation meets the demand. The game is investigated in experiments with stochastic end and in finite-length games. We particularly focus on the impact of trading on the levels of cooperation, and on the relation between the price and the theoretical value of having a good reputation. Theoretical properties of the game are described in the electronic supplementary material.

2. Results

2.1. Experiments with stochastic end

We first perform an experiment to demonstrate the effectiveness of a reputation system without trading. Participants repeatedly play PD games with different players. When choosing their action in the PD, the only information they have about their partner is the partner's reputation. After each interaction, the reputation of all players is updated according to the ‘standing’ assessment rule (see reputation system 1 in figure 1). We use a game with stochastic end to eliminate ‘end-game effects’ that arise in finite-length games [20,21] and can prevent cooperative strategies from being successful: subjects are informed that after each round, another PD with a new partner will be played with a probability of 95 per cent; otherwise the experiment ends. For such a rule, the expected number of additional PD games that will be played before the experiment ends does not depend on how many round have already been played. Further details on our experimental setting are given in §4 and the electronic supplementary material.

We observe that cooperation emerges and is maintained at a high frequency of roughly 80 per cent over the course of the experiment (figure 2a). Thus, most participants are in good reputation (figure 2b). The frequency of cooperation is below 100 per cent both because players occasionally make a move that is probably erroneous (players in good reputation, for instance, occasionally cooperate with players in bad reputation), and because there is a small fraction of players that unconditionally opt for defection. The strategies used by the participants largely follow theoretical expectations (see the electronic supplementary material). In a control experiment, where no reputation information of the co-player is provided, cooperation starts at intermediate levels, but quickly drops to an average frequency below 20 per cent (figure 2a). These findings are in line with previous experiments on reputation and indirect reciprocity [6,13–17] and show that information regarding the opponent's reputation as given in our experiments can maintain high levels of cooperation.

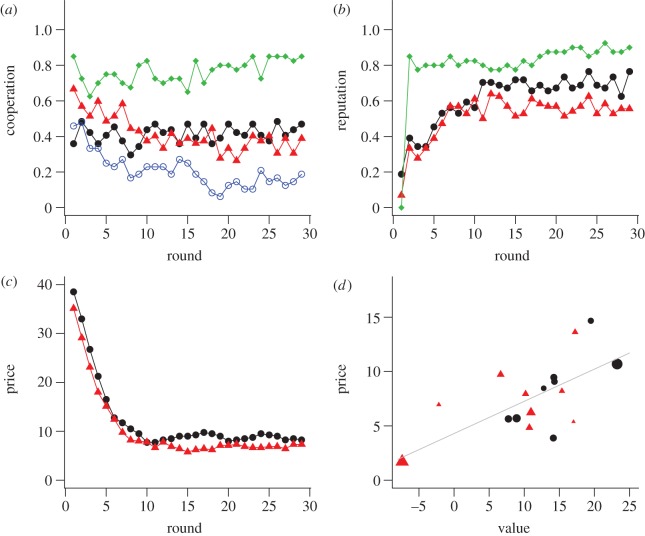
Figure 2.

(a,b) Dynamics of cooperation and reputation over the course of the experiments. The experiment for reputation system 1 without trading is shown in green, the control without any reputational information in blue. Reputation system 1 with trading is shown in red, and the alternative system with trading is shown in black. Cooperation is highest in the absence of trading, and lowest in the control without reputational information. In the presence of trading, the frequency of cooperation stabilizes at about 40% for both reputation systems. The participants in our experiments start with a bad reputation, but quickly establish a high frequency of good reputation. (c) Market prices for a good reputation. A market maker is used to facilitate trading and adjusts the prices depending on supply and demand. The market maker price for obtaining a good reputation is initially set to 40. Prices drop rapidly as participants at the beginning of the experiment often sell their reputation in order to exploit the initial overpricing. After about 10 rounds, the prices equilibrate. The price dynamics and the trading volume are similar for both reputation systems. (d) Average market prices for a good reputation versus theoretical value. For each group, average prices and theoretical values for a good reputation are calculated from the strategies and prices observed after round 10, when prices tend to be stable. In the electronic supplementary material, section 5 it is described in detail how the theoretical values are calculated. The size of the symbols scales with the number of trades made in a group. Note that the value of having a good reputation can even become negative when participants preferentially cooperate with players in bad reputation, as is observed in two experiments (see the electronic supplementary material). We observe a strong positive correlation between price and value. This suggests that the participants are capable of responding correctly to the value of a good reputation.

We next perform a set of experiments in which participants can trade reputation in trading rounds that occur between each PD round. In the trading rounds, participants have the opportunity to buy or sell their good reputation in a market. To provide sufficient liquidity, we use a simple market maker that allows participants to buy or sell at any point in time during the trading round without having an immediate counter-party among the other participants: players in bad reputation are offered to pay a price X to change their reputation to ‘good’; while players in good reputation can receive X − Δ for changing their reputation from ‘good’ to ‘bad’. Whenever a participate sells her good reputation to the market maker, the price decreases from X to X − Δ; and when reputation is bought, the price increases from X to X + Δ. We use a step size of Δ = 2, and an initial price of X = 40. Such a high initial price allows us to investigate whether prices move towards an equilibrium. (If we instead used a starting price close to equilibrium, convergence could not be demonstrated as easily.) The market maker, therefore, requires a number of trades to converge towards stable prices, and thus a high trading activity is important for the markets to accurately reflecting the value of a good reputation in the PD.

We observe frequent trading in this setting. Participants traded their reputation on average 7.5 times over the course of an experiment; and thus, per group of eight players there were on average 90 trades (median 69; range from 42 to 195). Average prices stabilized rapidly within the first 10 rounds (figure 2c), as did the average level of cooperation and the fraction of participants in good reputation (figure 2a,b). The level of cooperation in this setting is lower than in the setting without trading (logistic regression at the level of the cooperation decision, clustered on group to account for the non-independence of observations from subjects in the same group; coefficient = −1.5, p < 0.001), but higher than in the control setting without any reputational information (coefficient = 1.0, p = 0.004; figure 2 and §4). Thus, while cooperation can be maintained in the presence of a market for reputation, as is predicted by theory (see the electronic supplementary material), trading has an adverse effect on cooperation levels. Reasons for such an adverse effect are discussed below.

There is substantial variance in the emerging price and in the level of cooperation between different groups of participants. This between-group variance in pricing and behaviour allows us to assess whether there is a relation between the prices at which a good reputation is traded in the market and the theoretical value it has in the PD. This theoretical value depends on the behaviour of the participants in the PD and on the specific assessment rules used in the reputation system; details about how the theoretical value is estimated are given in the electronic supplementary material, §5. In essence, the more likely participants within a group are to preferentially cooperate with partners in good reputation, the more valuable a good reputation is, and the higher the price is expected to equilibrate in the market. In line with this expectation, we find a positive correlation between price and value (nine groups, linear regression, coefficient = 0.27, R² = 0.49, p = 0.037). Average within-group prices and theoretical values are shown in figure 2d, and details on the statistical analysis are given in §4.

To test whether the relationship between price and value is robust, we also examine a second, modified reputation system. In our first reputation system, two players in a ‘bad’ reputation must cooperate with each other to earn a good reputation. We now use a second system where two ‘bad’ players must defect against each other to earn a good reputation (figure 1). Like the first reputation system, the modified system belongs to the set that can theoretically establish and maintain cooperation [4]. However, the change in the assessment implies different optimal strategies and different theoretical price estimates (see the electronic supplementary material). In line with the modified assessment rule, participants do display different strategies in this alternative reputation system (see the electronic supplementary material). The trading frequency was similar to what we observe for the first reputation system (median 109 trades per group of 12; range from 77 to 190), and despite the different reputation system and behaviour, we again observe a positive correlation between price and theoretical value (eight groups, linear regression, coefficient = 0.42, R² = 0.51, p = 0.046; figure 2d and §4). Taking the results from both reputation systems together, there is strong evidence for a positive relationship between market price and the theoretical value of a good reputation (17 groups, linear regression, coefficient = 0.30, R² = 0.50, p = 0.0014). One potential interpretation of this finding is that participants have an understanding of the monetary value of reputation: in the PD, they gain experience regarding the value of a good reputation over time, and this experience then influences their trading behaviour. Therefore, in groups where the value of a good reputation is higher, the participants trade a good reputation for a higher price. However, we also observe persistent under-pricing in the second half of the experiment, which might indicate an imperfect understanding of the absolute value of a good reputation. Potential reasons for this under-pricing are discussed further below.

2.2. Fixed-length games

While in the game with stochastic end, trading has an adverse impact on the frequency of cooperation, there may also be situations in which trading reputation can actually promote cooperation. One such example is a fixed-length setting where participants enter, interact for a finite number of rounds and then exit the game. Without trading, there is no mechanism in place to incentivize cooperation in the last round, and thus defection is payoff maximizing. Together with the resulting ‘backwards induction’, one would expect that reputation systems are relatively ineffective in such situations [20,21]. If, however, reputations can be traded, ‘end game’ effects might be overcome: a good reputation is valuable even after the final round if it can later be sold. (Such a mechanism requires that new participants enter the game each round as old participants leave, or an external, ‘benevolent’ market maker that offers a positive price even after the last round; see the electronic supplementary material for a theoretical analysis.) For example, business owners who intend to retire might be more inclined to provide a high-quality service if they can subsequently sell their business, because a business in good reputation will obtain a better price than a business in bad reputation [1].

To investigate experimentally whether trading can indeed be beneficial for reputation systems, we set up experiments with a fixed number of interactions for each participant (we use four interactions in our experiments; for further details of the experimental set-up, see §4 and electronic supplementary material). Participants enter and leave the reputation system at different points of time, thus giving rise to a long sequence of interactions. In striking contrast to our earlier results with stochastically repeated games, we observe that adding reputation trading leads to significantly more cooperation in this fixed-length setting (logistic regression clustered on group, coefficient = 0.38, p < 0.001, figure 3 and §4). Thus, a market for reputation can promote cooperation by mitigating problems arising from end-game effects.

Figure 3.

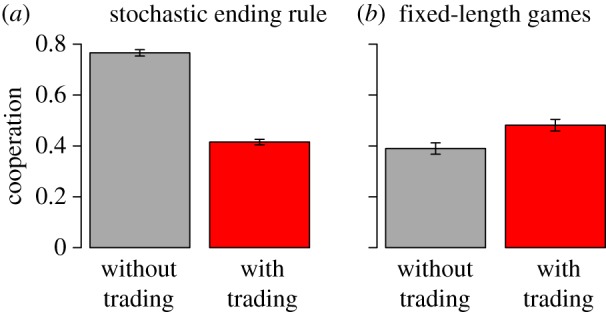
Trading of reputation decreases cooperation in games with stochastic end but increases cooperation in fixed-length games. (a) When interacting in short, fixed-length series of Prisoner's Dilemmas, the trading of reputation can increase the frequency of cooperation. (b) This is a stark contrast to the games with a stochastic end of experiment. Thus, the trading of reputation can help overcoming problems arising from ‘end-game’ effects in fixed-length games. Error bars indicate standard error of the mean, clustered on group to account for non-independence of observations from within one group.

3. Discussion

Our experiments show that the trading of reputation can have a negative or positive impact on the level of cooperation, depending on the details of the setting. In settings with stochastic end, the level of cooperation in the experiments with trading is substantially lower than in the experiments without trading. Such an effect is not expected from our theoretical analysis that shows that cooperative equilibria exist in both games with and without trading. Several factors might contribute to the adverse effects of trading. First, in games with trading, participants might have a lower intrinsic motivation to cooperate. A similar motivational ‘crowding out’ effect is observed in many real-life situations: people may be less cooperative when receiving direct monetary compensation rather than more implicit intrinsic rewards [22–25]. ‘Crowding out’ has empirically been demonstrated in the context of blood donations [25], trust in economic experiments [26] and tardiness of child pickups at a daycare centre [24]. Second, when reputation can be traded, it might be perceived as a less reliable marker for the cooperativeness of a player, which in turn may undermine the reputation system and lead to an ‘informational’ crowding out. A third reason is that when reputation is mispriced in the market, defection is subsidized. If reputation is over-priced, as is the case at the beginning of our experiments, participants have a strong incentive to sell their good reputation. This increases the number of participants in a bad reputation, and thereby subsequently decreases the level of cooperation. Similarly, under-pricing also subsidizes defection, because participants can profit by defecting in the PD and then re-buying a good reputation (see the electronic supplementary material). Interestingly, we observe under-pricing in many of the groups towards the end of our experiment. The reasons for this under-pricing are unclear. Potential factors that might contribute include risk aversion (participants might prefer a guaranteed payoff from the market over an uncertain payoff from the PD), an incorrect perception of the continuation probability of the game towards the end of the experiment, and a hesitancy to trade owing to the mechanisms similar to those behind the no-trade theorem [27]. Exploring these issues further is an important area for future study.

While trading reputation is harmful in settings with stochastic end, our experiments and theoretical analyses suggest that trading can also be beneficial for the functioning of a reputation system, as, for example, in fixed-length games where new players keep entering as old players are leaving, or where a suitable market maker is moderating the trading. Thus, our results can provide guidance for designing and improving reputation systems, particularly in the context of the Internet. Consider, for example, the system used by an online marketplace such as eBay to evaluate sellers. In such a reputation system, a seller who knows he will exit the market soon has little incentive to invest into providing a satisfactory service; while a new seller without a history of transactions is likely to initially make less profitable trades [5]. The trading of reputation could help in both cases: It maintains incentives to be cooperative for sellers that intend to leave, and at the same time helps new sellers get into profitable business. Another context where the trading of reputation is likely to be beneficial involves ‘strict’ reputation systems. In these systems, one can only gain a good reputation through an interaction with a reputable counter-party. Two individuals with bad reputation can never gain a good reputation from interacting with each other. Such strict reputation systems have a substantial advantage: they prevent non-cooperative individuals from ‘gaming the system’ by granting each other a good reputation. However, they face a challenge when starting off: If players begin with a bad reputation, then it is very difficult to subsequently establish a high frequency of players with good reputation, and thus it is difficult to reach a high level of cooperation. The trading of reputation may help to jump-start such a strict system. Further theoretical and experimental analysis is required to investigate such a mechanism.

For most people, earning and maintaining a good reputation seems to provide an intrinsic, instinctively satisfying motivation to do good [28–30]. But a good reputation also comes with explicit material value, which might explain why our emotions around reputation have emerged in the context of biological and cultural evolution. This explicit material value is of relevance in many real world economic situations. Credit and driving history can be seen as a part of ones reputation: a good reputation in the appropriate context gives access to less expensive credit and insurance. The opportunity to buy and sell brands and entire companies illustrates that in the corporate world, reputation can be seen as a tradable asset. But even for individuals, mechanisms exist to exchange resources for reputation. Non-anonymous donations to reputable charitable organizations may be seen as a way to polish ones reputation. And there is even some indication that in the context of marriage, resources can be exchanged for reputation, as, for example, when wealthy commoners marry nobility [31]. Our experiments suggest that people are capable of assessing the explicit material value of having a good reputation, even though the persistent under-pricing indicates an imperfect assessment. This capability has fascinating consequences. It provides us, for example, with the capacity to forego social norms and put our reputation at risk when the individual benefits are sufficiently large.

4. Material and methods

4.1. Participants

Participants were Boston area students recruited by the HBS CLER laboratory, and received a performance-independent fee of USD 10 in addition to the payments earned in the experiment. Written informed consent was obtained from all participants, and the experiments were approved by Harvard University CUHS (F16154-101). During the experiments, which were conducted at the HDSL laboratory, the participants were seated in cubicles and interacted with each others via computer. For implementing the experiments, z-Tree [32] was used. Each participant had an account with an initial endowment of 100 monetary units, equivalent to USD 2. Units were added and subtracted from the account depending on the payoffs earned in the PD interactions and on the trades preformed during trading rounds. We used six different settings: reputation system 1 (‘standing’) with stochastic ending rule and no trading (S1, five groups, 40 participants); reputation system 1 with stochastic ending rule and trading (S1T, nine groups, 72 participants); reputation system 2 with stochastic ending rule and trading (S2T, eight groups, 64 participants); a control with stochastic end and no reputational information (SC, six groups, 48 participants); reputation system 1 with a fixed number of interactions and no trading (F1); and reputation system 1 with a fixed number of interactions and trading (F1T, 10 groups in cross-design with setting F1, 120 participants).

4.2. Games with stochastic ending (S1, S1T, S2T, SC)

The participants interacted repeatedly within groups of eight. In each round, participants were assigned into random pairs and interacted in a simultaneous PD: Both players have the choice between two options, A and B. The payoff for a player choosing option A is 20 if the other player chooses option A; and −10 if the other player chooses option B. The payoff for a player choosing option B is 30 if the other player chooses option A, and 0 if the other player chooses option B. This corresponds to a PD with c = 10 and b = 30. Each player has a reputation that is either ‘Good’ or ‘Bad’. When interacting in the PD, players know their own and their opponents' reputation, except in setting SC where no reputational information is provided. They are not, however, provided with identifiers and so cannot track each other across interactions, except by the reputational information we assign. The initial reputation of all players was set to ‘Bad’. Reputation was updated depending on a player's choice, the player's own reputation and the opponents' reputation. The assignment rules are shown in figure 1, and were known to the participants. After each round, the player's own choice, the other player's choice, the resulting payoff and the updated reputation were displayed. Players were informed that after each round, there was a 95 per cent chance that there was another interaction, and 5 per cent chance that the experiment ends. We used the same randomization in all our experiments, which ensured that all experiments had the same length (29 rounds). A screenshot of the interface for the PD game is shown in the electronic supplementary material. In the settings with trading (S1T, S2T), participants could trade their reputation in a trading round before the first PD interaction and after each interaction. Participants in ‘bad’ reputation could buy a ‘good’ reputation for price X. Participants in ‘good’ reputation could change their reputation to ‘bad’ and receive X – Δ monetary units added to their account. Whenever a participant bought/sold a ‘good’ reputation, the price X was increased/decreased by Δ. A screenshot of the trading interface is shown in electronic supplementary material, section 1. The initial price was set to X = 40, the step size was set to Δ = 2.

4.3. Fixed-length games (F1, F1T)

In the fixed-length game, participants interacted within groups of 12. Each participant interacted in exactly four consecutive rounds with different players. Payoffs and interface were the same as in the setting with stochastic ending rule. Participants entered and left the experiment at different times such that there were nine consecutive trading rounds for each group. An example run is shown in the electronic supplementary material. To avoid a long period of equilibration in this relatively short sequence of PDs, the initial price in the setting with trading was set to 20. Because the fixed-length games were shorter than the games with stochastic end, we could use a cross design for the fixed-length games. Half of the groups started in the setting without trading (F1) and then completed the setting with trading (F1T); while the other half completed the experiments in reverse order.

4.4. Statistical analysis: prices versus value

For each group, we calculate the value of having a good reputation as described in electronic supplementary material, §5, and the average price at which reputation is traded from the data after round 10, at which point behaviour and prices become stable. Because the market maker requires a number of trades to initially converge towards equilibrium prices and requires trading to follow changes in the value of a good reputation, we expect that in groups with many trades, prices are closer to equilibrium. Thus, when analysing the relation between prices and value, we weight the observation from each group by the square root of the number of trades in the group. Using a linear regression between price and value, we find a positive relation between price and value for the standing reputation system (nine groups, coefficient = 0.27, R² = 0.49, p = 0.037), for modified standing (eight groups, coefficient = 0.42, R² = 0.51, p = 0.046), and for the combined data (17 groups, coefficient = 0.30, R² = 0.50, p = 0.0014).

4.5. Statistical analysis: trading and the frequency of cooperation

We use logistic regressions for comparing the level of cooperation depending of whether trading is possible or not, and for comparing the level of cooperation in the setting with trading with the level of cooperation in the absence of reputational information. Our analysis considers each individual decision (0 = D, 1 = C), and clusters at the level of the group to account for the non-independence of observations from within each group. For the games with stochastic end, we observe a strong negative impact of trading (coefficient = −1.5, p < 0.001), but a larger frequency of cooperation in the setting with trading compared with the control without reputational information (coefficient = 1.0, p = 0.004). For the games with fixed length, we used a cross design, where half the groups started in the setting without trading, and then did the setting with trading, while half the groups did the reverse order. We observe a positive relation between trading and cooperation (coefficient = 0.37, p = 0.004, AIC = 1310.6; when including order effects: 0.38, p = 0.004, AIC = 1301.0). When including an interaction between order and the presence of trading, the trading effect loses statistical significance (0.22, p = 0.24, AIC = 1301.4), but the interaction is not significant and the AIC score favours the model without interaction. We also tested if the frequency of trading depends on whether it is introduced early or late, and found no significant effect (Welch two-sample t-test, means are 15.2 and 14.4, t = 0.31, p = 0.76).