RNA-PAIRS: RNA probabilistic assignment of imino resonance shifts

Abstract

The significant biological role of RNA has further highlighted the need for improving the accuracy, efficiency and the reach of methods for investigating RNA structure and function. Nuclear magnetic resonance (NMR) spectroscopy is vital to furthering the goals of RNA structural biology because of its distinctive capabilities. However, the dispersion pattern in the NMR spectra of RNA makes automated resonance assignment, a key step in NMR investigation of biomolecules, remarkably challenging. Herein we present RNA Probabilistic Assignment of Imino Resonance Shifts (RNA-PAIRS), a method for the automated assignment of RNA imino resonances with synchronized verification and correction of predicted secondary structure. RNA-PAIRS represents an advance in modeling the assignment paradigm because it seeds the probabilistic network for assignment with experimental NMR data, and predicted RNA secondary structure, simultaneously and from the start. Subsequently, RNA-PAIRS sets in motion a dynamic network that reverberates between predictions and experimental evidence in order to reconcile and rectify resonance assignments and secondary structure information. The procedure is halted when assignments and base-parings are deemed to be most consistent with observed crosspeaks. The current implementation of RNA-PAIRS uses an initial peak list derived from proton-nitrogen heteronuclear multiple quantum correlation (¹H–¹⁵N 2D HMQC) and proton–proton nuclear Overhauser enhancement spectroscopy (¹H–¹H 2D NOESY) experiments. We have evaluated the performance of RNA-PAIRS by using it to analyze NMR datasets from 26 previously studied RNAs, including a 111-nucleotide complex. For moderately sized RNA molecules, and over a range of comparatively complex structural motifs, the average assignment accuracy exceeds 90%, while the average base pair prediction accuracy exceeded 93%. RNA-PAIRS yielded accurate assignments and base pairings consistent with imino resonances for a majority of the NMR resonances, even when the initial predictions are only modestly accurate. RNA-PAIRS is available as a public web-server at http://pine.nmrfam.wisc.edu/RNA/.

Introduction

RNA plays many important roles in gene expression, and RNA molecules show great promise as drug targets, therapeutic agents, and catalysts or recognition units for use in a variety of biochemical and biomedical applications. The quest for comprehensive information about structure–function relationships via high throughput structure elucidation has thus far focused on protein structures (Fox et al. 2008). Despite the biological abundance and functional importance of RNA, its structure determination has lagged behind that of proteins. For example, at the time of this writing, the Protein Data Bank contained>69,000 3-dimensional coordinate sets for proteins but fewer than 2,100 for RNA molecules. This may be due in part to the fact that nucleic acids can be challenging targets for crystallization. Moreover, the hydrogen bond mediated base pairing that is central to RNA structure may become ambiguous at lower X-ray resolutions. The complementary method of nuclear magnetic resonance (NMR) spectroscopy does not require crystallization (Davis et al. 2005; Miyazaki et al. 2010; Nozinovic et al. 2010; Wang et al. 2010). NMR provides direct observation of atomic connectivity information, including hydrogen-bonded protons. However, efficient and automated approaches to address key RNA structure determination steps remain to be developed. In the resonance assignment step, a key first step in NMR of RNA biomolecules, the dispersion pattern in the NMR spectra of RNA makes automation remarkably challenging. In contrast to proteins (Bahrami et al. 2009), there are currently no methods for automated resonance assignment of RNA.

The structural characteristics of RNA are dominated by the highly stable and regular A-form helix (Wang et al. 2010). RNA secondary structures can be predicted with approximately 73% accuracy by dynamic programming algorithms for the free-energy minimization of empirically derived, sequence-dependent nearest-neighbor thermodynamic parameters (Turner rules) (Dimitrov and Zuker 2004; Mathews et al. 2004; Mathews and Turner 2006; Xia et al. 1998). The accuracy of predictions can be pragmatically reduced by the tendency for RNA sequences to include unpaired bulge-, internal-, or hairpin-loop regions for which no fine-tuned thermodynamic parameters are yet available—although some attempts at estimation have been made (Ding and Lawrence 2003; Dirks et al. 2004; Hart et al. 2008; Rivas and Eddy 1999). For the pseudoknot motif (Giedroc and Cornish 2009; Theimer et al. 2005), which involves base pairs between distant loops in a sequence with intervening helical stems, the computational formulation leads to an NP-complete problem. Comparative sequence analysis has the potential for identifying probable secondary structures from sequence conservation and compensatory mutations that maintain base pairing (Gutell et al. 2002). However, the number of sequences required for comparison is proportional to sequence length, and the influence of variable tertiary and quaternary interactions on sequence conservation across species is largely unknown or ignored. Nevertheless, RNA secondary structure plays an important role in dictating the resultant tertiary fold, and its accurate determination serves as an important first step in using NMR to determine the three-dimensional structures of RNA molecules.

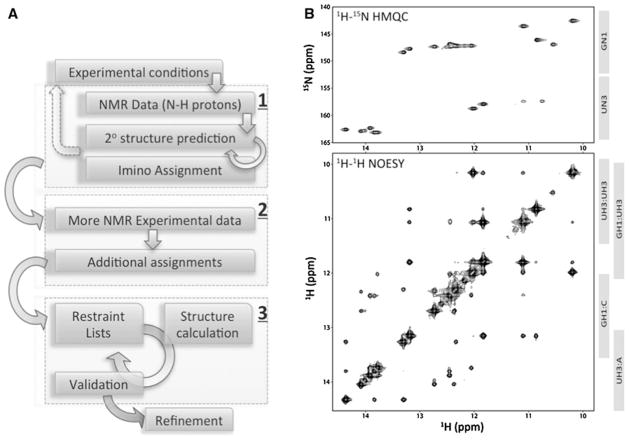
A key initial step in the analysis of RNA NMR data entails the labeling of atoms with resonance frequencies obtained from the NMR experiment—the so-called resonance assignment step. Whereas computational methods for the prediction of RNA secondary structure from primary structure have advanced considerably, similar methods for automating the interpretation of NMR data to obtain resonance assignments, confirm secondary structure predictions, and derive tertiary structure restraints in a robust manner have yet to be developed (Fig. 1a). Current methods for the assignment of NMR resonances of RNA rely almost exclusively on the manual, time-intensive interpretation of through-space (<6 Å) nuclear Overhauser enhancement spectroscopy (NOESY) experiments, which result in ambiguous connectivity information. The more straightforward triple resonance experiments employed in the assignment of protein backbone resonances (Eghbalnia et al. 2005a; Güntert 2009; Stratmann et al. 2010) cannot be relied upon for RNA due to its very different chemistry—for example, intrinsically small scalar couplings across the phosphodiester bond. Additionally, RNA molecules do not offer the NMR chemical shift dispersion found in proteins.

Fig. 1.

a Standard steps for solving RNA structures using NMR. The process can be conceptually divided into three main steps: 1 imino proton assignments and secondary structure validation, 2 full resonance assignment and restraint list construction, 3 structure calculation. The vast majority of work in these steps requires manual intervention—although some automation support is available for structure calculation and refinement. Circular arrows indicate some of the possible steps for iterative refinement while the dotted arrow suggests the potential need for construct modifications. Imino regions of 2D NOESY and HMQC NMR spectra are often highly informative for step 1. b Two types of NMR spectra containing information relevant for assigning NMR signals for imino protons and nitrogens in an RNA molecule (BMRB ID 17921)

We present here a method for the automated assignment of RNA imino resonances with synchronized verification and correction of predicted secondary structure. The approach, named RNA-PAIRS (RNA Probabilistic Assignment of Imino Resonance Shifts), uses predictive information about RNA secondary structure to compensate for potentially incorrect base pairings that can bias the interpretation of data. The resulting secondary structure constraints serve as anchor points for the automated probabilistic assignment of RNA NMR spectra. Through the analysis of experimental data, we demonstrate that a priori predictions of secondary structure are sufficient for accurate resonance assignments and secondary structure modeling with simple RNA structures. RNA-PAIRS, which is freely available from a web server, offers a robust first step toward automating the current time-intensive and potentially error-prone manual approaches to imino proton assignments and secondary structure determination. Our discussion addresses challenges that remain to be addressed in future refinements and extensions to our algorithm.

Methods

Overall approach

The assignment of imino proton signals and the experimental determination of secondary structure are fundamental to RNA structural studies by NMR (Fig. 1a—box 1). Our strategy, which is guided by experience in the field of RNA NMR spectroscopy, achieves robustness by combining specific knowledge regarding structure–function relationships of RNA chemical shifts and their connectivities with knowledge about structural motifs. For example, when reliable a priori information about secondary structure is available, RNA resonance assignments can be guided by through-space sequential “walks” that connect 2D ¹H–¹H NOESY crosspeaks. The imino protons (H1 of guanosine, H3 of uridine) are centrally located in the canonical (Watson–Crick) base pairs of RNA (GC and AU), as well as in the common GU or UU wobble pairs. Hydrogen bonding prevents the imino protons from rapidly exchanging with solvent, and results in a shift to higher frequency of 10–15 ppm. Observation of a NOESY cros-speak between two imino resonances involved in Watson–Crick base pairs indicates a stacking between the two base pairs (Fig. 1b). A crosspeak “walk” among series of adjacent base pairs provides evidence for the secondary structure. Fortuitously, imino proton signals are well separated (at higher frequency) from those of other atom types in RNA. In addition, the H1 and H3 proton signals from GC and AU base pairs fall in partially separated regions (Fig. 1b), and the imino resonances from GU or UU wobble base pairs are distinguishable by the presence of an unusually intense NOE crosspeak arising from the close juxtaposition (<2 Å) of imino protons from these residues. Residue types can be corroborated by the characteristic resonance dispersion of imino nitrogens, as observed in 2D ¹H–¹⁵N heteronuclear multiple quantum coherence (HMQC) experiments. Finally, the 2D HNN-COSY experiment directly correlates the NMR signals from nitrogen atoms involved in base pair hydrogen bonding.

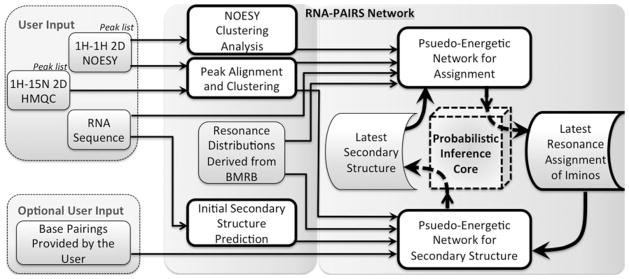
The RNA-PAIRS algorithm starts with an initial secondary structure model. This model can be determined by RNA-PAIRS software, which generates it by an adaptation of free energy minimization algorithms (Xia et al. 1998), or the user can bypass this step and supply a secondary structure model as an input. Next, RNA-PAIRS derives probabilistic assignments of imino proton NMR signals based on the latest available secondary structure prediction and the NMR spectra peak lists. The probabilistic resonance assignments derived from this step are then used to update the probabilities for the current secondary structure. The algorithm proceeds to a subsequent round of deriving probabilistic assignments from the newly estimated secondary structure. The iteration continues until convergence is achieved to a final consistent set of probabilistic imino assignments and RNA secondary structure (Fig. 2).

Fig. 2.

Design of RNA-PAIRS network is presented in block form. Blocks with heavier dark outlines represent the more complex portions of the algorithm—both in terms of computational complexity as well as algorithm design. The box for “user input” identifies the current peak list input for the software, which will be extended to include other experimental data. The direction of the arrows identifies the “flow of logic” in the software. The rightmost box (that intersects “curved” arrows) is the portion of the software where probabilities are updated using the “back and forth” (reverberating) iteration

Initial secondary structure prediction estimate from sequence

RNA secondary structure prediction is a mature field and several tools are available (Zuker 2003; Hofacker 2003; Gruber et al. 2008; Andronescu et al. 2003; Knudsen and Hein 2003; Sato et al. 2009; Ying et al. 2004; Clote 2005). In RNA-PAIRS, because the ultimate prediction of secondary structure is strongly influenced by experimental data, our aim in establishing an initial secondary structure prediction is to obtain a broad range of possible secondary structures as “starting points”. The starting secondary structure pool for the algorithm has to satisfy the competing goals of: (a) lowering the likelihood of missing a potential pairing, and (b) not producing an unwieldy and unreliable pool of secondary structures. To achieve these goals, we build on existing approaches by incorporating two observations that motivate our construction. It has been recently demonstrated that the structural effect of certain localized mutations in RNA can be well represented by a power-law distribution that is sharply centered at a specific secondary structure state (Stich et al. 2010). Earlier work has shown that, among RNAs with the same length and compositional frequency, the native sequence is the more stable form (Le et al. 1990). More colloquially, RNA sequences change during evolution, but RNA structures, including RNA secondary structures, are generally conserved strongly (power-law distribution) in order to preserve function. We use these observations to test the stability of the predicted secondary structure by artificially introducing specific mutations in the sequence and re-predicting the secondary structure of the mutated sequence. The impact of mutations on the predicted secondary structure is used to assign probabilities (scores) to indicate the stability of base pairs potential diversity of base pairings.

In the minimum free energy landscape, base paired nucleotides provide a strong stabilizing force in RNA secondary structure formation. We would envisage that sequence mutations in regions sufficiently far from predicted base paired nucleotides are therefore less likely to lead to secondary structure changes. However, if the (computational) energy landscape near the predicted minimum is rugged, or mutations in loops cause large (destabilizing) energetic changes, then changes to predicted secondary structure are likely to occur. By restricting our computational mutations to the internal sections of larger loops (>2 nt away from base paired nucleotides), the energetic impact of the latter condition is likely to be diminished because larger loops (>5 nt) have near constant energy contributions of the order 6 kcal/mole (Zuker; Hofacker); which for most typical loops does not increase significantly with the length of the loop beyond 6 nt. Therefore, in a pool of randomly mutated sequences, a significant portion should yield relatively small energetic changes—small energy perturbations. Recalculating the secondary structure in the “energy-perturbed” state can provide insight into the (computational) energy landscape regarding stability of the prediction results. Our implementation in RNA-PAIRS generates a large pool of random mutations and uses the ensemble average as an initial estimate of probabilities for the first stage of our algorithm. We use the nearest-neighbor thermodynamic model to predict the minimum free-energy secondary structure of the given RNA sequence to “seed” the population. Next, a population is generated by mutating internal segments of large loops (at least two nucleotides away from location of predicted secondary structures) while retaining compositional frequency. The resulting pool of secondary structures is weighted by the Jaccard distance, and the resulting weighted connectivity matrix is reported as the probability of pairing. Our experience in practice suggests that this approach generates a sufficiently diverse pool of possible pairings.

Formally, given a nucleotide sequence s, we posit that the probability of entries in the connectivity matrix A (a weighted adjacency matrix) is represented by:

$$P(A\mid S)\propto exp\left(\sum _i{w}_i{A}_i(s,A)\right)$$ (1)

where w_i is the weight obtained from the Jaccard distance for the ith loop mutation arrangement, A_i is the secondary structure connectivity matrix predicted for the ith mutation rearrangement (described above) by using the thermodynamic model, and the exponential function is applied to the individual entries of the matrix. For generation of random derangements we use an algorithm that relies on the Mersenne Twister and Ziff’s GFSR4 algorithms, and for deterministic secondary structure prediction we use the RNAfold algorithm (Matlab 2010).

Probabilistic assignment of imino-protons

We describe our approach in the context of the most typical setting where the assignment of RNA NMR resonances relies on 2D HMQC (or HSQC) and 2D NOESY spectra. A required initial stage in RNA-PAIRS is the automatic alignment of peak lists across spectra in two distinct steps. In addition to mostly systematic shifts, we have observed that, compared to proteins, RNA ¹H chemical shifts are more prone to non-systematic shifts across NMR experiments. RNA-PAIRS detects and adjusts a systematic shift across spectra (arising, for example, from referencing problems) by applying a local gradient search algorithm to find an approximate offset that yields the highest correlation between distinctly detectable peaks across spectra. The cost function for optimal selection is the sum of the Euclidean distances of the peaks with the constraint that a match is not allowed if the distance of the cluster and the peak is higher than the maximum shift allowed (this value has been heuristically set to 0.1 ppm). Non-systematic shifts present an essential challenge considering that they may be caused by experimental conditions, sample variations, or overlapped peaks in crowded spectral regions.

The alignment and interpretation of peaks in RNA spectra and the presence of non-systematic shifts requires a novel approach. Unlike 3D protein NMR spectra, where the N–H chemical shift plane provides a convenient 2D basis for aligning shifts across experiments, a basis for aligning RNA chemical shifts across 2D spectra is not easily available. RNA-PAIRS addresses this challenge through the notion of correspondence—by allowing sets of peaks to be related to each other. The idea is implemented by applying an adaptive k-means clustering algorithm (Macqueen 1967) to all ¹H resonances observed in NOESY spectra. The clustering algorithm is followed next by the Hungarian bipartite matching algorithm (Kuhn 1955) in order to find the optimal pairing between NOESY peak clusters and ¹⁵N-HMQC peaks. The clustering approach is further integrated into the iterative process and is dynamically updated as assignment probabilities evolve. Therefore, the number and membership of clusters is a function of the number of ¹⁵N-HMQC peaks, the number of nucleotides in the RNA assembly, the number of base pairs determined in the last iteration of the secondary structure algorithm, and the number of NOESY peaks in each cluster. In order to maintain consistency, each cluster must contain a minimum number of peaks, and if chemical shifts from NOESY clusters remain unmatched in the corresponding HMQC data, a pseudo ¹⁵N-HMQC peaks with unknown nitrogen shift will be generated. If an HMQC peak cannot be matched to peaks in a NOESY spectrum, the algorithm assumes the absence of a hydrogen bond for the given peak.

To derive assignments, RNA-PAIRS applies a pseudo-energetic model that is derived in analogy to Gibbs measures (Georgii 1988) in biophysics and statistical mechanics. In our pseudo-energetic model, probabilistic variables are the assignment candidates (imino-proton chemical shifts derived from ¹⁵N-HMQC and NOESY spectra)—in analogy to particles in a statistical mechanical model. The imino protons in the RNA sequence define the possible assignment of variables—in analogy to particle states. The probability of each configuration of assignments s is given by the Boltzmann distribution:

$$p_s=\frac{1}{Z}{e}^{-\beta E_s}Z=\sum _s{e}^{-\beta E_s}$$

where β resembles the thermodynamic variable (determined empirically), and Z is the partition function. E_S, the energy (cost) of microstate (assignment configuration) s, is the sum of individual and interaction potentials:

$$E_s=\sum _i{U}_i(\lambda ({\nu }_i))+\sum _{i,j}{U}_{ij}(\lambda ({\nu }_i),\lambda ({\nu }_j))$$ (2)

where λ(v_i) represents the state (assignment choices) of probabilistic variable v_i, U_i represents the individual potentials, and U_ij pair-wise interaction potentials.

Individual potentials are derived from statistical analysis of chemical shifts. RNA chemical shifts deposited in BMRB (Ulrich et al. 2008) have been utilized for the generation of empirical probability distribution functions for each nucleotide in multiple base pairing states. The assignment candidates are scored in accordance with the latest base pairing state derived from the secondary structure. The same set of empirical distributions generated from BMRB data also are used for the purpose of updating the predicted secondary structure for the target RNA after the latest assignment probabilities in each iteration.

The versatility of interaction potentials makes them suitable for taking into account evidence from NOESY crosspeaks, as well as evidence for conformational and assignment constraints. For example, because multiple assignment candidates are unlikely to simultaneously be associated to the same nucleotide, the interaction potential for such an occurrence is set to a large value. In general, the intricate task of modeling the pseudo-energy potential terms is guided carefully by the subtleties of RNA nucleotide interactions. In our design, NOESY constraints are the most essential term in the assignment process. Typically, the three dimensional structure of RNA dictates whether a NOESY crosspeak should be observed or not. In the absence of tertiary structure, the probability of observing a NOESY crosspeak can be estimated by considering the sequence and the secondary structure of the RNA. A non-diagonal peak in the imino region of an NOE spectrum represents either adjacent nucleotides, base paired nucleotides, or adjacent based-paired nucleotides. The last category corresponds to an NOE between nucleotides A and B, where A is based-paired with a nucleotide adjacent to B. In considering a peak observed at (ω1, ω2), any configuration s that assigns ω1 and ω2 to adjacent, based-paired, or adjacent based-paired nucleotides will be allocated a lower energy (higher probability) compared to other configurations. The precise weights are adjusted according to a combination of the latest secondary structure probability values and probability estimates for observing NOE peaks in various base pairing configurations.

Assignment of NOE peaks in RNA often faces the challenge of spectral overlap. The presence of regular structures, such as an A-form helix, increases the likelihood of overlap by more intense neighboring crosspeaks that may hinder detection of a crosspeak between two resonances. Therefore, we carefully account for the interaction of terms involving constraints on the regular structure and NOESY crosspeaks. Intense NOESY diagonal peaks can also readily obscure crosspeaks between resonances with similar chemical shifts, obfuscating an otherwise detectable spatial proximity from analysis. This condition is addressed by using a neighborhood clustering approach to relate common crosspeaks between resonances (see (Palla et al. 2005) for a discussion of r-neighborhood clustering). One valuable feature of this analysis is its ability to identify potentially missing crosspeaks from comparison of other shared and unshared crosspeaks between two proton resonances. In addition, this analysis enables us to heuristically relate the Euclidean distance between base pairs with the empirical probability of observing NOESY crosspeak for various base pair configurations. The result is a more accurate NOE potential term in (2).

An important characteristic of our probabilistic model is the flexibility gained by allowing an ensemble of solutions. Rather than seeking a single deterministic solution, which would necessitate the identification of the one configuration that minimizes the total energy, we determine marginal probabilities for every probabilistic variable. We use current marginal probabilities to condition the next iteration until stationary probabilities are achieved. The model relies on the implementation of “belief propagation” algorithms that have been studied in graphical models (Smyth 1997; Yedidia et al. 2005). Those algorithms can rapidly derive the exact marginals when the underlying graph G(V,E) is a tree and has no loops. V is the set of vertices (assignment candidates) and E is the set of edges where there is an edge between every pair of assignment candidates with a pair-wise potential. For loopy graphs, as in our model, the convergence of marginals is not guaranteed (Tatikonda 2002), and the convergence depends on the complexity of the graph and the consistency of the potentials, which is normally governed by the quality of data.

Update probabilities for secondary structure based on Imino-proton assignments

Free energy minimizations based on thermodynamic ideas, and more generally probabilistic approaches, have proven to be effective in predicting secondary structures of RNA from primary sequence (Doshi et al. 2004; Juan and Wilson 1999; Mathews 2004; Mathews et al. 2004; Mathews et al. 1999). This step provides a key extension to our probabilistic paradigm by adding competing and counterbalancing “pseudo energy” terms to represent the evidence obtained from NMR data. An additional term, as well as reevaluation of interaction rules defined earlier (2), restates the energy (cost) of microstate (base pairing configuration) s as follows:

$$E_s=\sum _i{U}_i(\gamma ({\rho }_i))+\sum _{i,j}{U}_{ij}(\gamma ({\rho }_i),\gamma ({\rho }_j))+\sum _{i,j,k}{U}_{\mathit{ijk}}(\gamma ({\rho }_i),\gamma ({\rho }_j),\gamma ({\rho }_k))$$ (3)

The probabilistic variable ρ_i represents nucleotide i, and γ(ρ_i) represents its base pair choice. The allowed base pairs in the initial phase of RNA-PAIRS consist of the most common base pairs A–U, G–C, G–U, A–G, and U–U (Nagaswamy et al. 2002). Evidence provided by experimental data in other stages of RNA-PAIRS allows for the expansion of the “allowed list to less common base pairs, for example G–G base pairs”. Base pair candidates consist of these nucleotide pairings, plus the X-N, where N designates an additional choice for any nucleotide X as being “not base paired”. The energy terms in RNA-PAIRS can be conceptually classified into five categories:

1. Thermodynamic and free energy potentials: these potentials have been estimated from thermodynamic parameters and nearest-neighbor model analysis for RNA structure determination (Xia et al. 1998). The estimates have been implemented in the form of pairwise potential terms.

2. NMR chemical shift evidence: imino proton and nitrogen chemical shifts exhibit different patterns depending on the base pairing status of the nucleotide. As mentioned earlier we have generated empirical probability distribution functions for each nucleotide in multiple base pairing states. Given the latest status of chemical shift assignment and by applying the Bayes rule, RNA-PAIRS derives the probability of each base pairing state and converts it to first-order potential terms in (3) by utilizing the Boltzmann distribution.

3. NOE evidence: non-diagonal NOE peaks are evidence of adjacent, base paired, or adjacent base paired nucleotides. This form of NMR evidence has been added to our energy model as pairwise pseudo-energy potentials. Given the latest probabilistic assignment of NOE peaks, the base paired and neighboring base paired candidates are separated, and their potential terms are added accordingly. These potentials were derived from our study of the frequency of observation of NOE peaks for various base pairing configurations.

4. Secondary structure constraints: these terms in the energy function are designed to make certain configurations significantly less likely. Examples of these configurations include a stem loop that has less than three base pairs, or “twisted” base pairing, where (i, j) is one base pair index, (k, l) is another base pair index, and we have the additional conditions: i > k, l < j, |i − k| <4, |l − j| < 4. A further constraint is to exclude any configuration in which a nucleotide i chooses nucleotide j as its base pair nucleotide while j chooses a nucleotide other than i. The implementation of constraints takes the form of pairwise as well as triplet-wise potentials with “infinite” energy for any “excluded” configuration.

5. Initial secondary structure prediction: any initial secondary structure prediction provided by the user (optional) is converted to pseudo-energy first order potentials according to the Boltzmann distribution model.

Key computational extensions to promote robust convergence

The computational inference network for RNA-PAIRS utilizes key extensions that are unique to our model. Examination of (2) and (3) reveals that the reverberation steps use asymmetric weights. The novel asymmetric approach enables stronger influence of experimental data, while allowing for strong accumulated derived evidence to be dominant when necessary. Unique to our computational approach is the addition of a combinatorial marginal evaluation step. Ordinarily, in order to derive the marginals, RNA-PAIRS uses a multistep iterative approach that utilizes dynamic graph topology, energy rescaling at each iteration step, and a variation of the basic belief propagation algorithm (Huang and Darwiche 1996). After each iteration step involving secondary structure determination and the assignment process, some probabilistic variables and their marginals may reach an effective “fixed state”—one in which the predicted probabilities change only within a small threshold. This “fixed state” is intuitively interpreted to mean that these variables have reached a state of reduced complexity and that the system is one step closer to the “ground state”—representing a fully consistent outcome. In the case of RNA assignments, the absence of sharp pseudo-energy differences that can separate assignment configurations causes the belief propagation algorithm to show non-convergent behavior in certain instances. This behavior can be detected by running the iteration a few cycles past the algorithmic stationary state and checking for a drift or switch in probability values. At the same time, running the iteration longer pinpoints the areas of probability drift or instability. The use of dynamic topology in the course of the first iteration round is not sufficient to address this impediment because the appearance of non-convergence is likely to become prominent after topology has stabilized. To address this challenge, we consider additional modifications to the topology based on a posteriori results. Since we are able to detect unstable assignment regions, we select sufficiently large portions of non-convergence regions (while remaining within computationally tractable bounds), and perform combinatorial computation. In contrast to belief propagation, which is an approximation and is not guaranteed to converge, our combinatorial approach is exact. Subsequently, after performing exact computation, we eliminate conditional dependencies with “near zero” probability values from the full graph by removing the corresponding edges—thereby modifying the topology of the graph based on exact local computations. Our results show that the topological modifications provide excellent improvements in accuracy and convergence, and are therefore key to the successful assignment results.

Validation of RNA-PAIRS

Several sources of RNA NMR data were utilized (Table 1) in the development and validation of the RNA-PAIRS algorithm. We had access to experimental NMR data sets from three previously published RNA structures (Table 1A). We also obtained data sets from several current projects at the National Magnetic Resonance Facility at Madison (Table 1B), allowing for the unique opportunity to interact with researchers intimately familiar with these RNAs. An additional 20 data sets were derived by using PDB and BMRB data sources (Table 1C). One subset of the additional data combined information in the PDB files (structure data) with BMRB data (assigned chemical shifts) to reconstruct peak lists (Table 1C—noted “R”) (21). In our peaklist reconstructions, NOESY crosspeaks were predicted for inter-proton distance measurements of <5.5 Å, and HMQC crosspeaks predicted for imino protons involved in base pairing. A second subset was obtained by simulating peak lists from PDB coordinates in the absence of assigned chemical shifts (Table 1C—noted “S”). For this subset, proton and nitrogen chemical shift predictions were made based on statistical distributions available from the BMRB (21) and heuristic effects from base pairing and neighboring residue identity (Cromsigt et al. 2001; Fürtig et al. 2003). The latter subset enabled us to test several larger RNAs, or more complex structural motifs that would have otherwise been unavailable. For all reconstructed peaklists, spurious peaks were added, random chemical shift variability was introduced, and random peaks were removed in order to approximate errors observed in real data. Assignments and secondary structure predictions were evaluated against known results, whenever available, or crosschecked against human expert assignments. All final results were corroborated with spectra, when available.

Table 1.

Data used for validation of RNA-PAIRS represent a sample of RNA molecules, fold topologies, and length (residues)

RNA Name	Residues	Source description	# Structures	Notes	References
(A.) Data sets from previously published structures
2KF0	24	U6 snRNA internal stem-loop	10	H, B, W, R	Huppler et al. 2002
1XHP	32	U6 snRNA extended internal stem-loop	10	H, B, W, R	Sashital et al. 2004
2JTP	34	SIV frameshift stem-loop	20	H, I, W, R	Marcheschi et al. 2007
(B.) Data sets from currently unpublished structures
17901	30	U6 snRNA 5′ stem-loop	0	H, W, R	B1
17921	47	GAGA tetraloop receptor variant	0	H, B, W, R	B2
17961	111	U2/U6 snRNA complex	0	M, B, I, W, R	B3
(C.) Simulated data sets from structures deposited in PDB
1FHK	14	16S rRNA 690-loop	15	H, W, S	Morosyuk et al. 2001
2KOC	14	UUCG tetraloop	20	H, W, R	Nozinovic et al. 2010
1Z30	18	Bovine enterovirus 1 cloverleaf 1 D-loop	15	H, W, R	Ihle et al. 2005
2O33	20	U2 snRNA stem I	20	H, W, S	Sashital et al. 2007
2RPT	20	Thymidylate synthase binding site	10	H, I, W, S	Tavares et al. 2009
1PJY	22	HIV-1 frameshift inducing stem-loop	20	H, W, R	Staple and Butcher 2003
2QH2	24	Telomerase RNA CR7 domain	20	H, B, W, R	Theimer et al. 2007
2L5Z	26	A730 loop of the neurospora VS ribozyme	21	H, B, W, R	Desjardins et al. 2011
1A3 M	27	16S rRNA A-site	20	H, I, W, S	Fourmy et al. 1998
1YG4	28	ScYLV RNA pseudoknot	1	P, B, W, R	Cornish et al. 2005
2JWV	29	High affinity anti-NFkB RNA Aptamer	10	H, I, W, R	Reiter et al. 2008
2K5Z	29	Duck HBV apical stem-loop	10	H, B, I, W, S	Ampt et al. 2009
2K63	29	Group II intron 5′-splice site	20	H, W, R	Kruschel and Sigel 2009
1LDZ	30	Lead-dependent ribozyme	25	H, I, W, R	Hoogstraten et al. 1998
1NA2	30	Telomerase RNA p2b hairpin	18	H, W, R	Theimer et al. 2003
2L3E	35	P2a-J2a/b-P2b of human telomerase RNA	20	H, I, W, R	Zhang et al. 2010
2L1V	36	5′ UTR preQ1 riboswitch	20	P, B, I, W, R	Kang et al. 2009
1YMO	47	5′ hTR telomerase pseudoknot	20	P, B, W, R	Theimer et al. 2005
1P5O	77	HCV IRES domain II	12	H, B, I, W, S	Lukavsky et al. 2003
1S9S	101	Moloney murine leukemia virus core	20	M, B, I, W, S	D’Souza et al. 2004

Notes identify structural features (H: hairpin, M: multiple hairpin domains, P: pseudoknot, B: bulge loops, I: internal loops, W: wobble base-pairs), and sources (R: experimentally observed chemical shifts, S: simulated chemical shifts).

^#Structures is the count of NMR models. References are provided in the last column. References B1, B2, and B3 identify BRMB entry IDs 17901, 17921, and 17961, respectively. For data sets with published structures, the secondary structures (the sum of base pairings: Watson–Crick, mismatch or wobble), and their motifs (notes in Tables 1, 2, 3), were determined by identifying potential inter-base hydrogen bonds by distance and angle of donor and acceptor heavy atoms

The final test data set comprised 26 peaklist pairs (NOESY and HMQC) for RNAs ranging in size from 14 to 111 residues. The motifs represented included A-form helices, pseudoknots, hairpin-, bulge- and internal-loops, metal binding sites, and many different examples of base pairing and stacking. Also represented were large, multi-domain structures such as 1S9S (D’Souza et al. 2004) and BMRB ID 17961. Test data sets were submitted to the web server (http://pine.nmrfam.wisc.edu/RNA/). Imino resonance assignment probability and secondary structure results were returned via e-mail. Assignment probabilities were crosschecked against original manual assignments and, whenever possible, corroborated with real spectra.

Results

The performance of RNA-PAIRS for the imino proton assignment and secondary structure determination for the case of six experimental RNA data sets and thirteen data sets reconstructed from experimentally determined chemical shifts are summarized in Table 2. Additionally, visual presentation of the results for experimental data sets has been presented in the Supplementary Information (Figure S1). The seven simulated data sets from predicted chemical shifts are presented separately in Table 3. An advantage of the probabilistic assignment in RNA-PAIRS is the additional reporting of possible alternative assignments in addition to reporting the assignment results based on the choice with maximum probability. We also report the assignment accuracy when only the top three reported candidate assignments are considered. For moderately sized RNA molecules (i.e., <40 nucleotides), the percentage of correct assignments is typically high—as is the number of correct base pairing predictions. Aside from the size of the RNA or number of imino protons considered, resonance overlap in the peak lists contributed to degeneracy among potential assignment probabilities, thereby hindering unique assignments. RNA-PAIRS’s ability to select multiple assignments and score them in the output report is advantageous because a correct unique assignment in the absence of additional data is likely to be unattainable in this case.

Table 2.

RNA-PAIRS Assignment and Secondary Structure Accuracy

RNA name	Residues	Observable iminos	% Unassigned	% Correct best choice	% Correct assignment in top 3	% Correct base-pair	Time (s)	Notes
(A.) Data sets from previously published structures
2KF0	24	9	0	100	100	92	38.16	H, B, W
1XHP	32	13	0	100	100	88	11.12	H, B, W
2JTP	34	14	0	79	93	100	54.13	H, I, W
(B.) Data sets from currently unpublished structures
17901	30	12	0	100	100	100	7.1	H, W
17921	47	24	0	71	79	100	67.8	H, B, W
17961	111	23	0	35	61	96	782.3	M, B, I, W
(C.) Simulated data sets from deposited structures
2KOC	14	7	0	100	100	86	10.1	H, W
1Z30	18	8	0	100	100	100	9	H, W
1PJY	22	9	0	100	100	91	24.1	H, W
2QH2	24	10	0	90	100	92	21.3	H, B, W, U
2L5Z	26	10	0	90	100	100	19.6	H, B, W, U
1YG4	28	8	25	38	88	24	40.8	P, B, W
2K63	29	10	0	100	100	100	30.9	H, W
2JWV	29	8	0	88	100	79	32.1	H, I, W
1NA2	30	14	0	86	86	87	34.2	H, W
1LDZ	30	11	0	100	100	93	39.7	H, I, W
2L3E	35	13	0	92	100	89	57.2	H, I, W, U
2L1V	36	7	0	86	86	45	42.7	P, B, I, W
1YMO	47	20	0	20	40	81	235.2	P, B, W, U

Notes indicate structural and data set features (H = hairpin, M = multiple hairpin domains, B = bulge loops, I = internal loops, W = wobble base-pairs, U = unusual chemical shifts observed). 17901, 17921, and 17961 are BMRB IDs for deposited chemical shifts. The BMRB entries referenced are currently in the BMRB release queue. They are expected to become publicly available shortly

Table 3.

RNA-PAIRS assignment and secondary structure accuracy for simulated chemical shifts

RNA name	Residues	Observable iminos	% Unassigned	% Correct best choice	% Correct assignment in top 3	% Correct base-pair	Time (s)	Notes
1FHK	14	6	0	100	100	100	12.8	H, W
2O33	20	8	0	100	100	100	17.7	H, W
2RPT	20	7	0	100	100	100	21.6	H, I, W
2KD8	22	11	0	100	100	100	21.6	H, W
1A3 M	27	11	0	100	100	93	34.6	H, I, W
2K5Z	29	14	0	100	100	100	34.5	H, B, I, W
1P5O	77	28	0	46	76	86	342.8	H, B, I, W
1S9S	101	43	2	23	49	65	914.9	M, B, I, W

Notes indicate structural and data set features as in Table 2

The results obtained for real data sets were in good agreement with those from simulated data sets (compare Tables 2A, B with Tables 2C, 3), with a few notable exceptions. Close inspection of NOESY spectra from 2JTP and BMRB ID 17921 revealed two imino resonances in each that could reasonably be assigned to alternate connectivities. Our simulated data sets did not incorporate a scenario that generated ambiguous resonances, but the observation suggests that RNA-PAIRS properly addressed an equivocal assignment. This supposition is supported by the increased accuracy of similar RNA data sets from simulation. The unusual imino chemical shifts in the 2QH2, 2L5Z and 2L3E data sets (Table 2C), despite being outside the chemical shift distributions considered by our algorithm, were ultimately assigned with 100% accuracy because of our focus on connectivity networks rather than chemical shifts. The lack of outlier chemical shifts for the subset of simulated data sets shown in Table 3, for which chemical shifts were predicted from the same distributions used by our algorithm, promoted higher accuracies for comparable RNAs. However, Table 3 makes apparent the limits of the current form of our algorithm in relation to the number of residues in the RNA, a trend seen across all data sets.

The incorporation of the results from our peak list clustering analysis provided additional evidence for the determination of assignment pseudo-energies, resulting in fewer ambiguities and larger assignment probabilities for most data sets. For one data set in particular, 2KF0 (Table 2A), the assignment probabilities of two imino protons with similar chemical shifts, on physically adjacent residues, were dramatically improved. Further analysis revealed that the prediction (with high likelihood) of a missing crosspeak (overlapped by intense diagonal peaks) between the two imino protons was a key source for the improvement. For another real data set, BMRB ID 17961 (Table 2B), one of our most challenging given its size and complexity, inclusion of peak list clustering improved accuracies for “Best Choice” from 13 to 35%, and “Top Three Choices” from 13 to 61%. Moreover, the time required to complete the assignment algorithm with clustering was reduced by more than 75%; indicating less ambiguity was introduced into the probabilistic engine.

The percentage of correctly predicted base pairs in the secondary structure does not show discernable correlations with either the size of the molecule or number of observed imino protons. Secondary structure prediction accuracies were largely unaffected by false input secondary structures. In the case of RNAs 2KF0 and 1XHP, for which the assignment percentage exceeded the correct base pair percentage, AC wobble pairs played a key role. The absence of imino proton involvement in these base pairs left RNA-PAIRS with little useful experimental evidence for corroborating or adjusting base pairing predictions—a consistent and expected behavior. The presence of uncommon base pairs in the hairpin loops of RNAs 2KOC and 1PJY may explain why the chemical shifts did not provide strong corroboration for “base pairing”. Overall, the observations indicate that RNA-PAIRS can successfully validate and correct secondary structure in a manner that is consistent with input NMR peaklists.

The most favorable results were obtained for RNAs with a single hairpin secondary structure (Table 1). The largest hairpin, 1P5O, showed modest assignment accuracy, despite containing multiple internal bulges and loops. Two structures that involved multiple hairpins folding within the same RNA strand, 1S9S and BMR17961, were less accurately assigned. The larger size of these RNA molecules and the potential of additional resonance overlap is partly responsible for lowered accuracies, but our analysis indicates that the competing folds generated from the initial prediction of secondary structure also play an important role.

We evaluated the assignment of pseudoknot structures by including three data sets, 1YG4, 1YMO, and 2L1V. The abundance of canonical base pairings and stacking in the 2L1V pseudoknot structure provided for good accuracy in assignment—albeit with lower secondary structure confidence. The results obtained for 1YG4 and 1YMO showed low assignment accuracy, with correct assignments coming mostly from helical regions involving Watson–Crick pairings. Detailed knowledge about pairing in pseudoknots improves the results, suggesting that the current form of the secondary structure prediction algorithm in RNA-PAIRS must be improved further to account for non-helical tertiary interactions and for more than one pairing interaction for each residue.

The completion time for the RNA-PAIRS automated assignment algorithm ranges from seconds to minutes (Tables 2, 3). These timings were obtained when running the algorithm on a Dell Optiplex 755 desktop computer with an Intel Core2 Duo processor running at 2.33 GHz, and 4 GB of RAM memory. Faster completion times were achieved when data sets were submitted to our multi-processor web-server, although variable rates of Internet traffic and e-mail server updates accounted the majority of total time between submission and return of results. Nonetheless, these times represent a reduction in the hours or days currently required for RNA imino proton resonance assignment.

RNA-PAIRS is available for public use through a fully automated web-server at http://pine.nmrfam.wisc.edu/RNA/. The server accepts ¹H, ¹⁵N-HMQC (or HSQC) and NOESY peak lists and the sequence of the RNA, and provides the complete probabilistic assignment of imino protons and the secondary structure of the RNA in a process that normally takes less than a minute. The server is fully automated, and no manual intervention or parameter setting is required.

Discussion

Protein structure determination by NMR has benefited from a variety of automated software tools (Shen et al. 2009; Shen and Bax 2010; Berjanskii et al. 2009; Bahrami et al. 2009; Eghbalnia et al. 2005b), but robust NMR chemical shift assignment tools have yet to be developed for RNA. We have implemented a method, as yet unknown in the literature, for the automated assignment of RNA imino protons and validation of secondary structure from NMR data sets. RNA-PAIRS has been successfully deployed as a web-based computational platform available for public use. Ideally, it is valuable to validate results on as large of a data set as possible since additional data sets will help refine our pseudo-energy model and NOESY cluster analysis. Future submissions to the already active web-server and subsequent user feedback will provide an excellent source to guide the refinement of our algorithms, the improvement of prediction accuracies, and our planned extensions.

We broadened our understanding of the precise role of experimental observations and chemical shift dispersion in RNA data sets, by performing controlled tests through the use of simulated NOESY and HMQC peaklists from RNA structures deposited in the PDB. Given the dearth of RNA NMR data in repositories such as the BMRB, this approach proved useful in allowing us to consider larger RNAs and more structural motifs. Several relatively small, simple hairpins were also simulated for better comparison with experimental data sets. In our simulations we noted that NOE connectivity plays a dominant role for RNA resonance assignments—unlike in proteins where the precise chemical shifts of nuclei play a more important role in backbone assignments. Comparison of the similar results for the real and simulated data sets from experimentally determined chemical shifts (Table 2A, B vs. C, respectively) validated our premise regarding the importance of NOE connectivity data. The lower performance observed in cases of poorly predicted secondary structure further confirmed the usefulness of our strategy of initiating assignments with a priori predictions of secondary structure. Simulation of data sets also has allowed us to identify several unique motifs with unusual chemical shifts that can be profiled and incorporated into future versions of our method.

Our novel attempt at NOESY peaklist clustering analysis has, as described, led to considerable improvements in our automated assignment algorithm. Given that this analysis is based upon heuristic rules derived from knowledge of RNA structure and our validation data sets, it is expected that our algorithm will be refined and further improved with more data sets submitted to our web server from the RNA structure community. Beyond this, our clustering analysis has yielded more subtle insights into data structure networks that have the potential to refine methods for protein automated assignment and biomolecular structure calculation/validation, and are currently being investigated.

With RNA-PAIRS we plan to solicit and build an expanded library of real data sets in order to help develop specific enhancements and to guide future developments in the field. Specifically, we foresee including the ability to recognize (possibly predict) an expanded array of non-Watson–Crick base pairs (including G–G) and their geometries, tertiary base pairing, such as in pseudoknots, kissing loops and dimers, and to include the ability to parse data from multiple RNA chains. The incorporation of a secondary structure partition function should enhance our method with the ability to consider and identify alternative conformations supported by competing NOESY connectivities. With additional NMR experimental data, for example, from submissions to our web services, we expect to establish a better knowledgebase for hydrogen bonding patterns of non-W–C pairs. Moreover, the HNN-COSY experiment can be incorporated in order to provides the nitrogen chemical shifts of the imino hydrogen-bond accepting residues. This can be used to identify the paired residues according to known nitrogen chemical shift distributions. Residual dipolar coupling (RDC) values for imino proton-nitrogen pairs have been shown to follow a periodic trend in A-form helices (Walsh and Wang, J Mag Reson 2005, 152–162), and could be incorporated into our algorithm as additional sequential, pairing and structural evidence. While additional data sets provide richer information, it is useful to allow the ¹H–¹⁵N HMQC peak list, and other heteronuclear experiments, to be optional inputs in order to retain flexibility—for example, to avoid the cost of synthesis for isotopically labeled RNA.

RNA-PAIRS is a first step in our broader effort to automate the full assignment and structure determination of RNA molecules by NMR. As complements of new algorithms and methods are implemented, we expect to see additional reductions in the disparity between automated assignment methods for proteins and RNA. The imino atom assignments and corroborated secondary structure obtained from RNA-PAIRS analysis are a primary requisite for further interpretation of NMR data for helical and non-helical regions alike. Our planned enhancements to RNA-PAIRS, along with additional steps incorporating non-exchangeable NMR data sets, are expected to improve and expedite the process of RNA assignment and structure determination.