Novel Method for Probing the Specificity Binding Profile of Ligands: Applications to HIV Protease

Abstract

A detailed understanding of factors influencing the binding specificity of a ligand to a set of desirable targets and undesirable decoys is a key step in the design of potent and selective therapeutics. We have developed a general method for optimizing binding specificity in ligand–receptor complexes based on the theory of electrostatic charge optimization. This methodology can be used to tune the binding of a ligand to a panel of potential targets and decoys, along the continuum from narrow binding to only one partner to broad binding to the entire panel. Using HIV-1 protease as a model system, we probe specificity in three distinct ways. First, we probe interactions that could make the promiscuous protease inhibitor pepstatin more selective toward HIV-1 protease. Next, we study clinically approved HIV-1 protease inhibitors and probe ways to broaden the binding profiles toward both wild-type HIV-1 protease and drug-resistant mutants. Finally, we study a conformational ensemble of wild-type HIV-1 protease to “design in” broad specificity to known drugs before resistance mutations arise. The results from this conformational ensemble were similar to those from the drug-resistant ensemble, suggesting the use of a conformational wild-type ensemble as a tool to develop escape-mutant resistant inhibitors.

Introduction

With the wealth of information arising from genome science and systems biology, it is becoming increasingly clear that the environment in which biological targets exist is complex and filled with a diversity of molecules, each with the potential to make multiple competing interactions with other molecules in the system [1, 2, 3]. An understanding of how chemical and physical principles guide molecules to interact narrowly (selectively) with a single target, or broadly (promiscuously) with a set of binding partners is fundamental to our basic knowledge of biochemistry. Moreover, for the practical purpose of developing pharmacological agents to function in complex biological environments, the advancement of methodology that can properly account for and “design in” desired narrow and broad binding specificity is crucial.

The preferential binding of a ligand to a single target molecule relative to a set of undesirable decoys we term narrow specificity. A common motivation to pursue narrow specificity in drug development is to avoid side-effect inducing interactions with undesired partners. For example, targeting proteins in the kinase family has been a long sought-after goal in drug design because these enzymes play key roles in the regulation of biochemical pathways [4]. However, behavior resulting from kinase inhibition can be unpredictable and can cause multiple undesirable side effects due to cross-reactivity with other kinases having similar binding sites, given that they all bind ATP for their biological activity [5].

In addition to the ability to design highly selective molecules, there are a number of biological applications in which the development of broad-specificity ligands is the goal. For example, in combating the evolution of drug-resistant mutations, it may be desirable to create a molecule that binds tightly to the wild-type target and to escape mutants, thereby creating a “wall of defense” around the target [6]. Drug resistant targets are becoming more prevalent with increased therapeutic administration and can now be found in many strains of bacteria [7], viruses [8, 9, 10], and cancer cells [11, 12], which makes the design of broad specificity inhibitors an attractive area of research. Another example of the need to design for broad specificity is when targeting a redundant biological network. In many cases the inhibition of a single target is not sufficient to achieve a desired outcome due to multiple pathways that a given reaction may follow [13, 14]. Finally, broad specificity could be used to bind an ensemble of states of a receptor, such as when the target exists in various phosphorylation states or different local pH environments [6, 15, 16]. While broad specificity could be achieved with multiple therapeutic agents, it might be advantageous to use a single inhibitor for a variety of physiological and practical reasons.

A number of computational approaches have been used to address specificity. For narrow specificity, negative design is often used, which involves explicit consideration of undesired decoy partners. For example, Sarkar et al. developed variants of granulocyte colony stimulation factor (GCSF) with a narrowed pH dependent binding to a receptor, which led to altered trafficking behavior [17]. To address broad specificity, efforts have been made to perform multiple sequential computations on a set of targets (i.e., serial docking) to detect ligands that bind well across the target ensemble [18, 19]. One could also address narrow specificity with a similar protocol, looking only for molecules that bind tightly to the desired targets and not to the decoys. Beyond small molecule studies, similar specificity considerations have been addressed in protein design, which have resulted in some success [20, 21].

In this work we adopt the specificity framework developed by Kangas and Tidor [22] that is an extension of the electrostatic charge optimization methodology described previously [23, 24, 25]. Electrostatic charge optimization has been applied successfully in the analysis and design of a number of systems, including protein–ligand [26, 27], protein–protein [28], and antibody–antigen [29] binding complexes. The specificity objective function used for optimization of a ligand to a given panel of binding targets and decoys is defined by:

$$\mathit{Sp}={\mathit{Min}}_{d\widehat{I}D}\left[{\mathit{DG}}^o(d;l)\right]-{\mathit{Max}}_{C\widehat{I}T}\left\{{\mathit{Min}}_{t\widehat{I}C}\left[{\mathit{DG}}^o(t;l)\right]\right\}\frac{\mathit{water}}{}$$ (1)

Where Sp is the specificity of a ligand (l) for a panel of desirable targets (T) consisting of classes (C) with one or more targets (t) in each class. Individual decoy structures (d) are contained within the set of all decoys (D). ΔG^o(x;l)is the binding free energy for the complex between ligand (l) and receptor (x), with x being either a target (t) or decoy (d).

ΔG can be formulated as an expression with the ligand partial atomic charges as variables so that the value of Sp can be optimized with respect to the ligand charges (see Methods for more detail). Equation 1 is particularly useful because it represents a single equation that can be used to optimize either broad or narrow specificity given an arbitrary set of desired targets and undesired decoys. To achieve narrow specificity, the function maximizes the free energy gap between the target class with the least favorable binding free energy and the decoy with the most favorable binding free energy. For broad specificity in the case of no decoys, we minimize the binding free energy to the “worst-of-best target” (the energy of the worst target class, where the energy of a class is defined by the tightest binding member of the class). When multiple targets and decoys are included simultaneously in the optimization, the objective function is a balance between the desired broad specificity to the targets of interest versus the desired narrow specificity against the decoys.

In this work, we have chosen the protease of HIV-1 as a model system to study both narrow and broad binding specificity. Protease activity is required for the maturation of budding virions into infectious HIV particles, and inhibition can lead to a less potent virus [30]. Structure-based design efforts have been successful in developing inhibitors of HIV protease [31], yet the currently approved inhibitors each have drawbacks, including negative side effects that can be attributed in part to the fact that most aspartyl proteases have similar active sites due to their common requirement to bind peptide substrates [32]. In fact, early leads for HIV protease inhibitors were generated from existing aspartyl protease inhibitors, such as pepstatin [33, 34, 35], suggesting that the promiscuous nature of early HIV-1 protease inhibitors may have been a result of the process by which they were discovered. On the other hand, the highly variable replication process of the HIV virus has rendered current clinical inhibitors susceptible to viral resistance [10, 36, 37], which would call for more promiscuous inhibitors that could inhibit both the wild type and mutant forms of the enzyme [38].

A number of computational strategies have been employed toward the inhibition of both wild-type and escape mutant HIV-1 proteases, including molecular dynamics [39, 40, 41], docking [42], and analysis of free energy contributions from active site residues [43]. In this work we use the specificity optimization methodology to identify interactions that can contribute to altered specificity. In addition to probing ligand atoms and their interactions, we also assess the extent to which specificity-optimized charges can be mimicked with chemical substitutions to evaluate whether electrostatic optimization may be a good “handle” by which binding specificity can be affected. This final step is particularly important because any chemical substitution will alter non-electrostatic contributions to binding such as van der Waals and internal energies in addition to the electrostatics. The results show that electrostatic specificity optimization may be a useful tool to guide the design of inhibitors with improved specificity profiles.

Results and Discussion

The focus of this paper is to examine the function that electrostatic interactions can play in modulating binding specificity. Three distinct specificity scenarios are analyzed. First, narrow specificity is explored with the promiscuous aspartyl protease inhibitor pepstatin in complex with HIV-1 protease, pepsin, and cathepsin D. Second, a panel of unselected (“wild-type”) and drug-resistant HIV-1 proteases is examined using clinically approved protease inhibitors in an attempt to identify ways of broadening the specificity of these molecules by optimizing interactions with both wild-type and mutant HIV-1 proteases. Finally, a panel consisting of wild-type HIV-1 protease structures in multiple conformations is studied using the HIV-1 protease inhibitor TMC-114 (darunavir) in order to evaluate the effects of structural fluctuations of the binding site on ligand binding specificity.

Narrowing Specificity of Pepstatin Interacting with Three Aspartyl Proteases

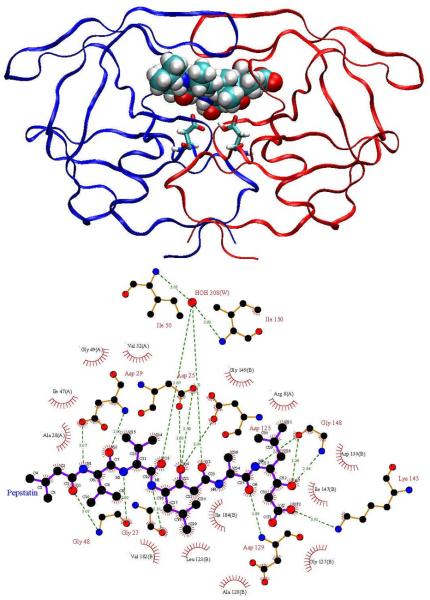
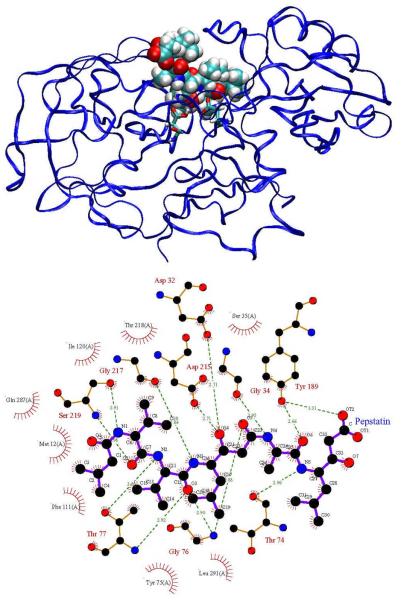
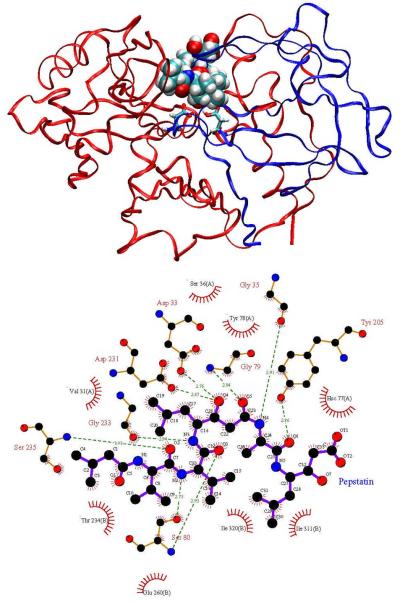
Here we analyze the broad-spectrum aspartyl protease inhibitor pepstatin binding to HIV-1 protease and two other aspartyl proteases, human pepsin and human cathepsin D. The goal is to understand better how pepstatin achieves broad specificity to the proteases and to use it as a probe to study mechanisms for narrowing binding specificity. Aspartyl proteases share several common structural features, which have been described in detail in other works [32, 44]. Pepsin and cathepsin D have high sequence similarity and correspondence between active site residues [44]. HIV-1 protease, however, is a homo-dimer that is significantly smaller in size (198 residues per homo-dimer compared to 327 in pepsin and 342 in cathepsin D) and has much more coverage of the active site by the flaps. Pepstatin inhibits pepsin [45] and cathepsin D [46] in the picomolar range, while it is a weaker HIV-1 protease inhibitor [47]. However, acetyl pepstatin, which truncates the three N-terminal carbons of pepstatin, inhibits HIV-1 protease with a K_i of approximately 20 pM [48]. Figures 1, 2, and 3 show pictorial comparisons of the three aspartyl proteases in complex with pepstatin.

Figure 1.

HIV-1 protease in complex with pepstatin. Top: Ribbon representation of HIV-1 protease colored by chain, pepstatin shown in van der Waals spheres, and the catalytic aspartates shown in licorice. Bottom: LigPlot [78] representation of the HIV protease active site. Hydrogen bonds shown with green dotted lines and van der Waals contacts are shown by red hatched circles. The following two figures show the decoys used in this study, human pepsin and human cathepsin D.

Figure 2.

Human pepsin complexed with pepstatin. Refer to Figure 1 for description.

Figure 3.

Human cathepsin D complexed with pepstatin. Refer to Figure 1 for description.

Optimization

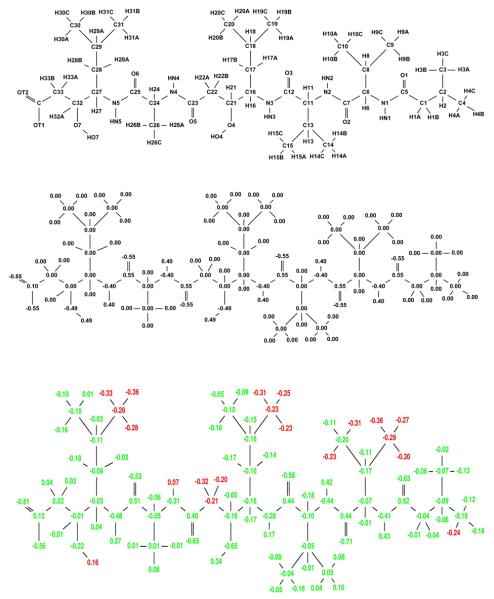
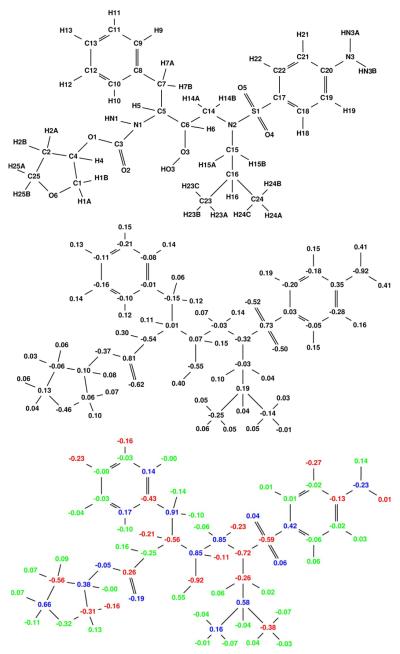
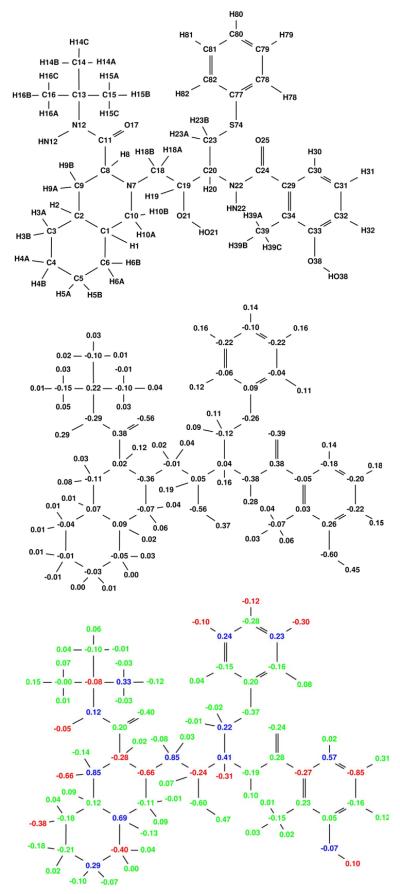
Using Equation 1 with HIV-1 protease as the single target and two decoys (human pepsin and human cathepsin D), the partial atomic charges of pepstatin were optimized to maximize the narrow specificity toward HIV-1 protease. The resulting specificity-optimized partial atomic charge distribution for pepstatin is shown in Figure 4. Most atoms in the optimized charge distribution change by a relatively small amount (shown as green atoms), especially along the pepstatin backbone. The N4 amide shows a significantly reduced dipole magnitude. A number of the pepstatin methyl groups accumulate a negative charge. Some hydrogen atoms accumulate a negative charge, such as those attached to C22. Finally, the O7 hydroxyl shows a substantial decrease in the magnitude of both the oxygen and hydrogen charges. Atom perturbations to mimic chemical functional groups were introduced and the energies associated with these are shown in Table 1.

Figure 4.

Narrow specificity-optimized charges of pepstatin. Top: Pepstatin atom names used in this study. Middle: Starting pepstatin charges are shown in black. Bottom: Optimized charges are shown with coloring such that red denotes charges that became more negative by at least a value l, where l=0.2e+0.2|q| and q is the initial charge of that atom. Blue charges are those that became more positive by at least l and green color represents atoms that changed by less than the tolerance l. The following figures follow this same convention.

Table 1.

Binding energetics for perturbed pepstatin charge distributions based on the narrow specificity-optimized charge distribution. The column heading “Analog” represents the particular functional group change the charge perturbation is modeling. Negative values for the change in binding free energy of each complex is favorable while for specificity a positive value is favorable. Specificity values ΔSp are calculated as the difference between the lowest-energy decoy (pepsin or cathepsin D) and the target (HIV-1 protease) relative to the initial pepstatin charge distribution and are in units of kcal/mol.

Atoms	Analog	$\Delta \Delta G_{\mathit{es}}^{\mathit{HIV}}$	$\Delta {\Delta }_{\mathit{es}}^{\mathit{pep}\sin }$	$\Delta \Delta G_{\mathit{es}}^{\mathit{cath}.D}$	Δ Sp
Stabilize target and destabilize decoys
C4=−0.25 H4(A,B,C)=−0.25	${\mathrm{CH}}_3\to {\mathrm{CO}}_2^{-}$	−2.24	4.85	12.94	7.08
N4= 0.00 HN4= 0.00	NH→CH2	−0.21	0.85	0.86	1.06
C22= 0.30 H22A=−0.30	H→F	−0.13	0.42	1.01	0.55
C22= 0.30 H22B=−0.30	H→F	0.52	0.51	0.63	−0.01
C28= 0.30 H28B=−0.30	H→F	−0.13	0.80	0.01	0.14
Stabilize target (preferentially) and decoys
C32= 0.55 O7=−0.55 HO7=0.00	COH→CO	−3.19	−0.12	−0.88	2.31
O7= 0.00 HO7=0.00	OH→CH3	−1.56	−0.08	−0.93	0.63
C16= 0.30 H16A=−0.30	H→F	−0.48	0.16	−0.25	0.23
Destabilize decoys (preferentially) and target
C9=−0.25 H9(A,B,C)=−0.25	${\mathrm{CH}}_3\to {\mathrm{CO}}_2^{-}$	4.79	24.16	19.01	14.21
C10=−0.25 H10(A,B,C)=−0.25	${\mathrm{CH}}_3\to {\mathrm{CO}}_2^{-}$	0.55	13.52	6.71	6.17
C19=−0.25 H19(A,B,C)=−0.25	${\mathrm{CH}}_3\to {\mathrm{CO}}_2^{-}$	10.54	18.78	20.33	8.24
C31=−0.25 H31(A,B,C)=−0.25	${\mathrm{CH}}_3\to {\mathrm{CO}}_2^{-}$	2.85	13.12	13.20	10.27
C11=0.30 H11=−0.3	H→F	0.48	1.50	2.02	1.04
N3=0.00 HN3=0.00	NH→CH2	0.02	0.91	1.46	0.89

Analysis of optimized charges

The first group in Table 1 includes cases in which narrow specificity is gained through stabilization of the target complex and destabilization of the decoy complexes. A negative charge at the C4 carbon on the N-terminus of pepstatin lead to the largest potential gain in electrostatic specificity (7.1 kcal/mol). In both pepsin and cathepsin D, the C4 group is in a non-polar pocket where a charged group would pay a significant desolvation penalty upon binding without having favorable interactions to compensate. In HIV-1 protease, C4 is near positively charged residues (Arg8 and Lys45) that could interact favorably with the proposed negative ligand charge. Interestingly, the carboxylate group on the pepstatin C-terminus interacts with Lys45 on the opposite side of the 2-fold symmetric HIV-1 protease active site, showing that a salt bridge interaction such as the one proposed here is plausible.

Other specificity-improving modifications can be supported by structural analysis. For example, a reversed dipole associated with H22A enhances specificity by 0.6 kcal/mol. H22A is oriented toward a hydrogen of the buried water molecule in HIV-1 protease. In contrast, the pepsin and cathepsin D complexes position H22A in a non-polar pocket and therefore would incur a greater desolvation penalty with an increased dipole magnitude on the perturbed C22–H22A dipole, while not having any polar residues on the receptor with which to interact. The neutralization of the N4–HN4 dipole results in a computed specificity gain of 1.1 kcal/mol through stabilization of HIV-1 protease by 0.2 kcal/mol and destabilization of both pepsin and cathepsin D by approximately 0.9 kcal/mol. While the hydrogen bond made by HN4 in both pepsin and cathepsin D is of a good length (2.0 Å), the distance in the HIV-1 protease complex is not as good (2.4 Å). This is an interesting case because the enhancement in binding affinity to HIV-1 protease comes by eliminating an unfavorable hydrogen bond where the desolvation free energy outweighs the interaction energy.

The O7 hydroxyl of pepstatin is an example where targets and decoys are both stabilized, with the target being more stabilized. Neutralization leads to a 0.6 kcal/mol gain in specificity. Further perturbation to reverse the dipole direction leads to an even larger gain in specificity (2.3 kcal/mol). Again, this specificity gain can be understood through a detailed structural analysis. In the HIV-1 protease structure, the pepstatin O7 hydroxyl hydrogen is closer to the backbone N–H hydrogen for Gly48 than to the carbonyl oxygen of that same residue (1.7 Å vs. 2.0 Å). In the natural peptide substrate, one would expect a carbonyl in place of the pepstatin O7 hydroxyl to make a β-sheet interaction with the Gly48 N–H, as can be seen in the complexes with peptide substrates bound to a crystal structure with a peptide bound to an inactivated HIV protease [49]. In the pepsin and cathepsin D complexes there is a lack of direct interactions with the O7 hydroxyl, as this region is more solvent-exposed due to the less complete coverage of the active site by the flaps (see Figures 1, 2, and 3).

Finally, specificity can be gained as a result of destabilization to all enzymes, with more destabilization of the decoys relative to the target. The most extreme cases of this involve the introduction of a net charge at buried sites in the complex, which is unfavorable for all complexes. Introduction of a negative charge at the methyl groups of C9, C10, C19, and C31 yields computed specificity gains of 14.2, 6.2, 8.2, and 10.3 kcal/mol, respectively. While these changes produce large specificity gains, they may not be desirable in practice because of the drop in affinity to the target. Only the C10 perturbation results in a reduction of predicted K_i of less than 100-fold. More practical specificity enhancements can come from changes to dipoles that produce smaller gains in specificity but also less loss in target affinity. A C11–H11 dipole modification to a C–F-like charge distribution leads to a computed enhancement in specificity of 1.0 kcal/mol. In this case all three enzymes incur an unfavorable desolvation penalty; however, in cathepsin D and pepsin there are also unfavorable interactions with the hydroxyl of Thr218 (cathepsin D) and Thr234 (pepsin) and the backbone carbonyls of Gly217 (cathepsin D) and Gly233 (pepsin).

Chemical modifications

To assess the feasibility of finding chemical group substitutions whose overall electrostatic and non-electrostatic effect improves narrow specificity, we built chemical changes and evaluated them computationally (Table 2). This is important because any chemical change involves alterations in the internal geometry of the ligand (bond lengths, angles, and torsions) and non-bonded interactions (van der Waals interactions) in addition to the electrostatics. Because one aim of this study is to conserve the shape of pepstatin in order to minimize the non-electrostatic effects of the changes, some charge compromises were made in the modifications. For example, whereas a negative charge at the C4 group would be ideal, such a chemical group is not available. Instead, we chose to replace the C2 isopropyl group with a carboxylate, thus conserving the number of heavy atoms and roughly the geometry; however, this modification also adds negative charge around the C3 atoms, which is not computed to be as favorable as compared to a negative charge at the C4 site alone. Such compromises are often necessary when moving from a theoretical charge space to a specific instance realized with chemical functional groups. Chemical functional group changes with improved computed specificity include an isopropyl to carboxylate (C2, C8, and C18), a hydroxyl to methyl or carbonyl (O7), and C–H dipole reversals (H11F, H16F, and H22F).

Table 2.

Energetics of chemically-modified pepstatin interacting with the target and decoy receptors. Energies expressed as $\Delta \Delta G_{\mathrm{x}}^{\mathrm{i}}$, where i is either HIV protease, pepsin, or cathepsin D and x represents the change in either the electrostatic or total binding free energy between the modified and unmodified pepstatin. Negative values for the binding affinity (ΔΔGes) are favorable while for specificity (ΔSp) a positive value represents preferential stabilization of HIV-1 protease.

Chemical Change	Δ Δ GHIV		$\Delta {\Delta }_{\mathit{es}}^{\mathit{pep}\sin }$		$\Delta \Delta G_{\mathit{es}}^{\mathit{cath}.D}$		Δ Sp
	Δ Δ Ges	Δ Δ Gtot	Δ Δ Ges	Δ Δ Gtot	Δ Δ Ges	Δ Δ Gtot	Δ Spes	Δ Sptot
$\mathrm{C}2\to {\mathrm{CO}}_2^{-}$	0.30	2.10	5.35	6.16	10.72	8.15	5.05	4.06
H22A→F	−0.20	−2.95	0.54	0.36	0.96	1.63	0.74	4.22
O7→CH3	−2.02	−1.59	0.71	−0.78	−0.96	−1.25	1.07	0.34
C32:O7→CO	−4.50	−7.48	−0.51	−1.82	−0.40	−4.94	3.99	2.54
H16→F	−0.88	3.27	0.20	6.82	−0.74	7.70	0.14	3.55
$\mathrm{C}8\to {\mathrm{CO}}_2^{-}$	3.56	6.26	16.36	19.23	8.83	10.41	5.27	4.15
$\mathrm{C}29\to {\mathrm{CO}}_2^{-}$	4.99	6.00	5.87	5.75	10.49	10.38	0.88	−0.25
$\mathrm{C}18\to {\mathrm{CO}}_2^{-}$	13.21	14.43	15.37	19.60	12.74	15.43	−0.47	0.99
H11→F	−0.03	3.85	2.06	5.26	1.30	8.91	1.33	1.41

Determinants of pepstatin's broad binding specificity

To evaluate the electrostatic characteristics that promote promiscuous binding, we performed two additional specificity optimizations with either pepsin or cathepsin D as the target. In regions with similar electrostatic potential for all three receptors, there will be little charge variation in any of the optimizations. On the other hand, in regions with different potentials, the ligand atom charges will vary in at least one optimization. Looking for atoms in which the charges change least across all three optimizations helps reveal sites contributing to broad specificity. The highest concentration of atoms with relatively small charge changes is on either side of the O4 hydroxyl, which interacts with the catalytic aspartates (data not shown). This might be expected, given that proteases act on substrates with a common polypeptide backbone and make similar interactions in this region. It also validates the ability of this methodology to detect similarities in the electrostatic potential and convey that information in an intuitive form.

Broadening Specificity of Therapeutic HIV Protease Inhibitors Toward Binding Escape Mutants

Here we examine the potential for broadening the binding profile of several HIV-1 protease inhibitors to a target panel containing wild-type HIV-1 protease and two drug-resistant variants, V82A (1X) and I63P/V82T/I84V (3X) [50, 51, 52]. The set of ligands includes amprenavir, indinavir, nelfinavir, ritonavir, and saquinavir, as well as the more recently approved inhibitor tipranavir, which is less sensitive to these common mutations [53]. Experimentally, the 1X and 3X mutants reduce K_i values of the inhibitors in the range of 4- to 160-fold [54, 55]. The values reported below are relative changes in specificity (ΔSp) from this starting state and therefore do not depend on the absolute differences in binding free energies.

Optimization

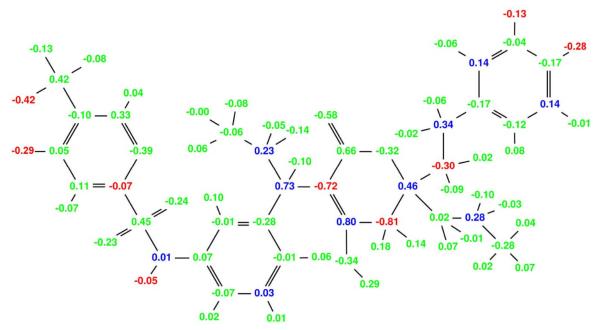
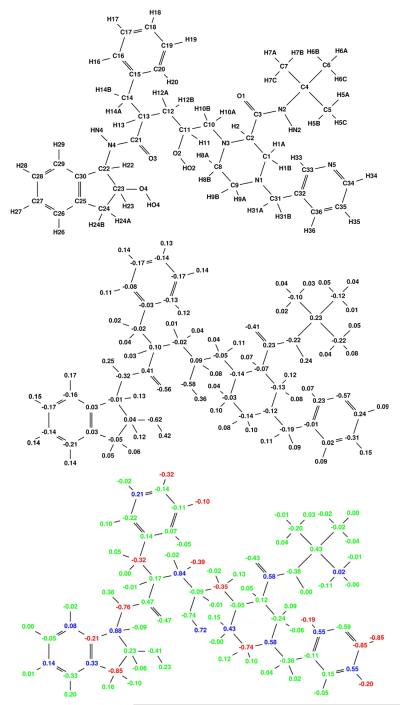
The specificity-optimized partial atomic charges for each of the six ligands are shown in Figures 5 through 10. A majority of the optimized charges vary by only a small amount, indicating that many parts of the inhibitors are well optimized for broad specificity within the three-target ensemble. Tipranavir, which is the least susceptible to resistance from these mutations, shows the least amount of computed gain in electrostatic specificity. As in the pepstatin studies above, we first perturb the starting inhibitor charges with guidance from the specificity optimization and then computationally make chemical functional group modifications based on the top perturbations. Table 3 shows total specificity and binding affinities to the three HIV-1 protease targets for each inhibitor with the top perturbations. The changes range from dipole modifications with an enhanced specificity of almost 1.0 kcal/mol to changes in monopole that have more significant effects of over 2.0 kcal/mol.

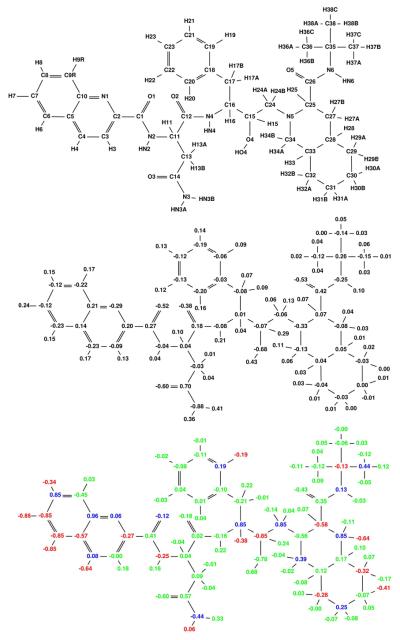
Figure 5.

Broad specificity-optimized charges for amprenavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net specificity gain is computed to be 9.3 kcal/mol for this charge distribution.

Table 3.

Free energies of perturbed charges binding to the wild-type (WT), single V82A mutant (1X), and the I63P/V82T/I84V triple mutant (3X). All atoms of the template inhibitors are fixed at their initial values other than the charges noted. The column labeled “Analog” represents the chemical functional group that is being modeled by the perturbation. Specificity values (ΔSp) are computed as the change in electrostatic binding free energy from the starting charges to the worst-of-best target (see Methods).

Atoms	Analog	$\Delta \Delta G_{\mathit{es}}^{\mathit{WT}}$	$\Delta \Delta G_{\mathit{es}}^{1X}$	$\Delta \Delta G_{\mathit{es}}^{3X}$	Δ Sp
Amprenavir
C5=0.32 H5=−0.20	H→F	−0.89	−0.67	−0.74	0.67
C13=0.27 H13=−0.25	H→F	−0.25	−0.34	−0.25	0.25
C11=0.24 H11=−0.30	H→F	−0.47	−0.48	−0.23	0.23
C21=0.20 H21=−0.23	H→F	−0.28	−0.29	−0.23	0.23
C6=0.40 H6=−0.20	H→F	0.26	−0.20	−0.31	0.20
Indinavir
H34=−0.91	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−3.91	−2.02	−2.79	2.02
C12=0.27 H12B=−0.25	H→F	−0.89	−0.68	−0.51	0.51
C18=0.25 H18=−0.25	H→F	−0.31	−0.38	−0.34	0.34
N2=0.00 H2=0.00	NH→CH2	−0.52	−0.32	−0.24	0.24
C19=0.23 H19=−0.25	H→F	−0.06	−0.23	−0.31	0.23
C34=0.45 H34=−0.11	H→F	−0.21	−0.29	−0.23	0.23
C35=0.43 H35=−0.12	H→F	−0.34	−0.20	−0.24	0.20
Nelfinavir
H9A=−0.92	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−1.14	2.01	0.83	0.83
C20=0.35 H20=−0.15	H→F	−0.58	−1.17	−0.90	0.90
N12=0.00 HN12=0.00	NH→CH2	−0.73	−0.87	−0.95	0.87
O38=−0.08 HO38=−0.08	NH2→CH3	−1.74	−0.68	−0.47	0.47
C80=0.30 H80=−0.25	H→F	−0.31	−0.26	−0.32	0.26
C9=0.20 H9A=−0.22	H→F	−0.13	−0.28	−0.22	0.22
Ritonavir
H86A=−0.97	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−3.39	−2.34	−3.12	2.34
H90B=−0.95	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−3.98	−3.10	−2.28	2.28
C12=0.41 H12=−0.20	H→F	−0.81	−0.88	−0.93	0.88
C15=0.40 H15=−0.20	H→F	−1.19	−0.64	−0.71	0.64
N5=−0.05 C1=−0.05 C4=−0.05	N→CH	−1.16	−0.82	−0.54	0.54
C75=0.28 H75B=−0.25	H→F	−0.12	−0.34	−0.31	0.31
C4=0.54 H4=−0.20	H→F	−0.05	−0.31	−0.20	0.20
C33=0.26 H33=−0.25	H→F	−0.18	−0.21	−0.29	0.21
Saquinavir
H6=−0.85	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−3.83	−3.91	−2.44	2.44
H7=−0.85	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−3.59	−3.31	−2.16	2.16
H4=−0.83	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−2.38	−1.93	−1.46	1.46
C16=0.30 H16=−0.25	H→F	−0.50	−0.70	−0.59	0.59
N1=0.00 C2=0.06 C10=0.06	N→CH	−0.29	−0.31	−0.35	0.31
C27=0.20 H27A=−0.25	H→F	0.10	−0.28	−0.22	0.22
C8=0.22 H8=−0.20	H→F	−0.10	−0.21	−0.25	0.21
C4=0.20 H4=−0.26	H→F	0.01	−0.17	−0.31	0.17
C30=0.20 H30A=−0.20	H→F	−0.16	−0.15	−0.23	0.15
N3=−0.10 HN3A=0.00 HN3B=0.00	NH2→CH3	−0.73	−0.42	0.02	−0.02
H8=−0.88	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−1.04	−0.80	1.66	−1.66
Tipranavir
H37=−0.84	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−1.68	−1.03	−1.21	1.03
N28=−0.20 HN28=0.00	NH→CH2	−1.45	−1.07	−1.03	1.03
C38=0.26 H38=−0.20	H→F	−0.09	−0.25	−0.30	0.25
F42=−1.15	$\mathrm{H}\to {\mathrm{CO}}_2^{-}$	−1.32	−2.30	−0.24	0.24
C39=0.15 F40=0.10	F→H	−0.54	−0.41	−0.22	0.22
C37=0.28 H37=−0.20	H→F	−0.04	−0.19	−0.27	0.19
C17=0.28 H17=−0.25	H→F	−0.12	−0.17	−0.13	0.13

Monopole perturbations

The charge optimizations consistently find the tuning of interactions with Arg8 and Lys45 as a way to improve broad specificity. This can be accomplished from either end of the ligands due to the 2-fold symmetry of HIV-1 protease. Four of the six ligands show broadened computed specificity of this type (amprenavir and nelfinavir are exceptions). For example, the H34 atom of indinavir is in close proximity to Arg8 (3–4 Å) and is mostly solvent exposed. This proximity is maintained across the entire target ensemble and thus introducing a negative formal charge at this atom center leads to improved electrostatic interactions with Arg8 while paying only a minor desolvation penalty upon binding. The result is a net computed gain in specificity of 2.0 kcal/mol. The F42 and H37 atoms of tipranavir accumulate significant negative charge through optimization. A negative formal charge placed on H37 results in a 1.0 kcal/mol gain in specificity whereas F42 results in a gain of 0.2 kcal/mol. While F42 is located closer than H37 to Arg8, it is also significantly more buried by the receptor and therefore pays a more substantial desolvation penalty upon introduction of a formal charge. This again illustrates the subtle balance between interaction and desolvation effects that is difficult to judge visually or with algorithms that do not take solvation effects into account. Ritonavir and saquinavir show similar effects.

Dipole perturbations

The majority of large specificity gains from dipole perturbations come from atoms close to the buried water molecule (H5 of amprenavir, H12B of indinavir, H20 of nelfinavir, both H12 and H15 of ritonavir, and H16 of saquinavir). Table 3 shows the specificity changes that result from these perturbations. Maximal specificity improvements range from 0.6 to 0.9 kcal/mol for dipole perturbations of these atoms. Each of these hydrogen atoms is oriented toward the hydrogen atoms of the buried water molecule. In the tipranavir complex this water is displaced upon binding and thus a similar specificity gain is not observed.

Charge neutralizations

Finally, some sites are determined to be over-charged across the target ensemble, and thus neutralization leads to broadened specificity. For example, neutralization of the N12–HN12 group of nelfinavir leads to enhanced computed specificity of 0.9 kcal/mol by reducing an unfavorable desolvation penalty that is not adequately offset by favorable electrostatic interactions. Structurally, this group does not make hydrogen-bonding interactions, yet is still partially desolvated by the enzyme upon binding. A similar but less pronounced situation is seen in indinavir, where neutralization of the N2–H2 dipole leads to a computed 0.2 kcal/mol enhancement of specificity. Other neutralization sites leading to enhanced specificity are seen on ritonavir, saquinavir, and tipranavir. In each case the buried polar atoms are making either poor or no hydrogen bonding interactions.

Chemical modifications

Three primary chemical modifications were used to reproduce the electrostatic changes above: addition of a carboxylate group (change in monopole); the replacement of hydrogen with fluorine (dipole reversal); and the modification of an amide or hydroxyl to a methylene or methyl (neutralization). The optimizations show no sites in which a net positive charge is preferred as a monopole change. Table 4 shows the changes in affinity to each target as well as the net change in specificity upon computational modification. As opposed to the narrow specificity study on pepstatin, all changes to a negatively charged group result in a loss of specificity because the electrostatic interaction energy is not sufficient to offset the large desolvation penalty.

Table 4.

Free energies (in kcal/mol) of chemically-modified inhibitors interacting with the 3-class target ensemble. All energies are calculated as differences from the initial inhibitor binding energy.

Chemical Change	$\Delta \Delta G_{\mathit{es}}^{\mathit{WT}}$		$\Delta \Delta G_{\mathit{es}}^{1X}$		$\Delta \Delta G_{\mathit{es}}^{3X}$		Δ Sp
	Δ Δ Ges	Δ Δ Gtot	Δ Δ Ges	Δ Δ Gtot	Δ Δ Ges	Δ Δ Gtot	Δ Δ Ges	Δ Δ Gtot
Amprenavir
H21→F	−1.03	−1.77	0.34	−0.39	0.18	−0.39	−0.34	0.39
H11→F	−0.93	−1.50	0.49	−0.31	−0.28	−0.60	−0.49	0.31
H5→F	−1.03	3.07	−0.71	1.47	−0.23	2.83	0.23	−3.07
Indinavir
H18→F	−1.14	−1.75	−0.41	−0.68	−0.31	−0.74	0.31	0.68
H35→F	−1.19	−1.74	−0.03	−0.58	−0.04	−0.65	0.03	0.58
H34→F	−0.97	−1.38	0.00	−0.23	0.01	−0.24	−0.01	0.23
N2→CH2	−0.41	−0.42	−0.58	−0.17	−0.59	−0.38	0.58	0.17
H12B→F	−0.51	1.41	−0.31	0.46	−0.23	1.12	0.23	−1.12
$\mathrm{H}34\to {\mathrm{CO}}_2^{-}$	2.95	8.14	3.56	8.63	2.38	7.10	−3.56	−8.63
Nelfinavir
H80→F	−1.86	−2.35	−1.10	−1.31	−0.77	−1.28	0.77	1.28
H9A→F	−1.49	−0.42	−0.97	0.22	−0.46	−0.87	0.46	−0.22
N12→CH2	−0.81	2.01	−1.03	1.84	−0.96	2.69	0.96	−2.69
$\mathrm{H}9\mathrm{A}\to {\mathrm{CO}}_2^{-}$	1.72	−0.62	5.71	4.66	5.57	2.44	−5.71	−4.66
Ritonavir
H4→F	−2.65	−1.74	−0.13	−0.69	−0.22	−0.72	0.13	0.69
H33→F	−1.30	−1.94	−0.11	−0.70	−0.13	−0.65	0.11	0.65
H12→F	−2.09	−3.19	−2.57	−0.62	−1.64	−0.40	1.64	0.40
H75B→F	−1.80	−1.38	−0.68	−0.49	−1.24	−0.31	0.68	0.31
N5→CH3	−1.42	0.41	−1.32	0.68	−1.39	0.83	1.32	−0.83
H15→F	−2.86	2.01	−1.06	0.99	0.01	0.87	−0.01	−1.01
$\mathrm{C}86\to {\mathrm{CO}}_2^{-}$	2.16	3.89	2.30	4.74	4.46	7.07	−4.46	−7.07
$\mathrm{C}90\to {\mathrm{CO}}_2^{-}$	1.13	3.60	3.22	3.35	8.76	7.75	−8.76	−7.75
Saquinavir
H27A→F	−1.44	−0.39	−0.60	−0.76	−0.16	−0.69	0.16	0.69
N3→CH3	−0.19	−0.58	−0.28	−0.61	−0.32	−0.77	0.28	0.61
H8→F	−1.84	−1.77	−0.09	−0.43	−0.06	−0.76	0.06	0.43
H30A→F	−1.65	−0.19	−0.25	−0.80	−0.16	−0.31	0.16	0.31
H4→F	−1.93	−1.38	−0.40	−0.27	−0.15	−0.38	0.15	0.27
H16→F	−1.64	1.72	−4.70	−0.58	−0.65	1.46	0.65	−1.72
N1→CH2	−0.74	2.31	−0.86	2.01	−1.03	2.63	0.86	−2.01
$\mathrm{C}8\to {\mathrm{CO}}_2^{-}$	3.32	3.41	4.56	5.13	5.75	4.61	−5.75	−5.13
$\mathrm{C}7\to {\mathrm{CO}}_2^{-}$	1.55	3.76	2.25	5.23	3.50	4.56	−3.50	−5.23
$\mathrm{C}6\to {\mathrm{CO}}_2^{-}$	1.15	6.40	2.44	6.47	3.22	5.78	−3.22	−6.32
$\mathrm{C}4\to {\mathrm{CO}}_2^{-}$	1.19	6.41	2.53	6.67	3.85	5.66	−3.85	−6.47
Tipranavir
H37→F	−1.06	−1.54	−0.44	−0.70	−0.50	−1.14	0.44	0.70
F40→H	−0.30	−0.94	0.04	−0.57	−0.17	−0.97	−0.04	0.57
H17→F	−0.54	−1.22	−0.19	−0.94	−0.10	−0.32	0.10	0.32
$\mathrm{C}37\to {\mathrm{CO}}_2^{-}$	1.16	−0.54	3.88	2.84	3.05	1.20	−3.88	−2.84
$\mathrm{F}42\to {\mathrm{CO}}_2^{-}$	0.84	3.34	3.31	3.96	2.04	3.11	−3.31	−3.96

The largest electrostatic specificity gains arise from dipole reversals on buried atoms interacting with the bound water molecule, with gains in specificity ranging from 0.2 kcal/mol (amprenavir H5) to 1.6 kcal/mol (ritonavir H12F). However, because of the buried nature of the active site and the rigid receptor model employed here, in many of these cases there is not sufficient room for the fluorine atom, which has both a greater bond length and van der Waals radius than hydrogen by approximately 0.3 Å each. The computed clashes could potentially be alleviated by accounting for receptor induced-fit effects [56] that were not explored here. Maximum total specificity gains for each inhibitor range from 0.4 kcal/mol (amprenavir H21 and saquinavir H8) to 1.3 kcal/mol (nelfinavir H80). Most of the favorable specificity changes come from atoms around the periphery of the active site that gain favorable interactions with Arg8 while allowing the additional size and bond length associated with fluorine to fit. In other cases, such as the H4F mutation on ritonavir that is more solvent exposed, computed gains in electrostatic specificity are further supplemented by favorable van der Waals interactions, thus leading to a total specificity gain of 0.7 kcal/mol.

Dipole modifications made by changing polar atoms to methyl or methylene groups can create a change in hybridization from sp² to sp³, which affects the geometry of the attached groups. While the change in hybridization is accounted for in our protocol by allowing the ligand to minimize after the modification, in many cases the change in hybridization is too great to be accommodated without significant clashes between the ligand and protein. For example, the greatest electrostatic gain is from the N5 modification of ritonavir that yields 1.3 kcal/mol in enhanced computed electrostatic specificity, yet creates unfavorable van der Waals interactions with the receptors, resulting in a net 0.8 kcal/mol unfavorable specificity change. The largest gain in total specificity is from a change of the N3 amide of saquinavir to a methyl group, which has a computed enhancement of 0.6 kcal/mol due to both favorable electrostatic and non-polar terms.

Additional target classes

To address the question of how more target classes could affect the specificity optimization, we performed two broad specificity calculations with an additional mutant class added to the target ensemble. In one study we added the D30N mutant to the nelfinavir ensemble. The D30N mutation is found mostly in response to nelfinavir treatment and shows little cross-resistance to other protease inhibitors [57]. The primary difference in the specificity-optimized charges upon adding the D30N mutant is seen at the C15–H15 dipole, which is near the D30N mutation. For the second case we included the G48V/L90M mutant as an additional class to the saquinavir target ensemble. The G48V/L90M mutation has been shown to be associated with saquinavir resistance and an increased K_i of over 400-fold relative to the wild type protease [58]. The G48V mutation is in the flap region of the enzyme and the L90M mutation is one shell removed from the active site. The primary difference upon adding the G48V/L90M mutation is to the C16–H16 dipole (0.9 kcal/mol specificity gain upon reversing this dipole). These atoms are not directly interacting with residue 48 but are close to the buried water that is interacting with the flaps. Overall, the addition of a target class resulted in small changes close to the site of mutation but the overall specificity-optimized charge distribution was not changed substantially (data not shown).

Wild-Type Ensemble

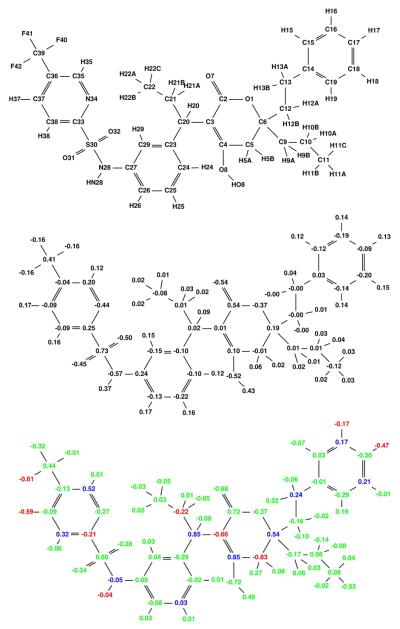
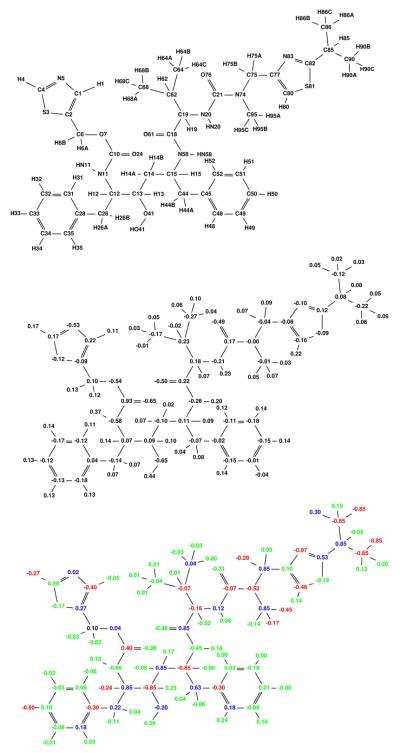
An important question that arises in specificity design is whether one can use information from the wild-type protein to make predictions on potential mutant structures. It has been proposed that targeting a conformational ensemble of wild-type structures can serve as a surrogate for an actual mutant ensemble [6, 59]. To test this hypothesis we performed a broad specificity optimization of tipranavir to a target ensemble that included six wild-type HIV-1 protease receptors with different active site conformations. By placing each target conformation within a separate class, we ensured that a broad specificity optimization would result in a charge distribution computed to bind tightly to each receptor conformation. The resulting broad specificity-optimized charges for tipranavir are shown in Figure 11. It is useful to compare the partial atomic charges to those in Figure 10, in which the ensemble is comprised of the wild-type protease and actual escape mutants. The similarity of the partial atomic charge distributions strongly supports the concept that targeting a wild-type structural ensemble could be a valid approach for designing against potential drug-resistance mutations.

Figure 11.

Broad specificity-optimized charges for tipranavir binding to a target ensemble comprised of six classes, each containing different conformational states of the wild-type HIV protease. The optimized charge distribution is similar to the explicit mutant charge distribution in (Figure 10).

Figure 10.

Broad specificity-optimized charges for tipranavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net specificity gain is computed to be 7.6 kcal/mol for this charge distribution.

Conclusions

The ability to explicitly account for binding specificity between a set of target and decoy proteins is an important step in the drug discovery and optimization process. Early considerations of specificity should lead to drugs with more desirable binding profiles. For narrow specificity, the methods used here identify regions of differing binding potentials, sometimes subtle, between target and decoy. For broad specificity, the methods identify interactions that enhance binding across the entire target ensemble. While not explicitly considered in this work, this method can also simultaneously optimize specificity of a ligand to an ensemble containing both targets and decoys. This real-world scenario allows for broad binding to a panel of desired targets while minimizing potential side effects from interactions with undesirable decoys.

A typical challenge of any de novo optimization method is validating the predictions. This is especially difficult to address in cases where an experimental lab of chemists is not available to synthesize and test new compounds. For the work presented here, we feel that the consistent agreement between the predictions and the detailed structural analysis provides strong validation of the method. Furthermore, the specificity optimization function is rigorous in its formulation and the ability to make valid predictions depends primarily on the accuracy of the force field and implicit solvation method to estimate relative binding free energies. Approximate binding free energy methods such as MM-PBSA and MM-GBSA have proven to be useful in predicting trends in binding energies for a congeneric series of ligands [60, 61, 62]. The binding free energy used in Equation 1 is the electrostatic component of the MM-PBSA binding energy and therefore should be valid for estimating the changes in energy associated with the predictions made in this work.

The similarity in broad specificity results between the studies on the ensemble with explicit escape mutants and those in the conformational wild-type ensemble show that, at least for this case, a conformational ensemble can capture some of the important properties associated with an ensemble containing resistance mutants. This is encouraging for broad specificity work in general because structural variants of a wild-type target are often easier to generate than isolating escape mutants and therefore would allow the drug design process to begin accounting for potential escape mutants or multiple reaction pathways at an earlier stage. While we used a wild-type target ensemble obtained from multiple crystal structures of HIV-1 protease bound to various inhibitors, ensembles generated by other means, such as molecular dynamics, Monte Carlo, normal modes, or other tools that generate conformational ensembles can be used within the methodology described here. It should also be noted that an affinity charge optimization performed on a single target structure did not yield results as similar to the mutant ensemble as did the conformational ensemble (data not shown), further emphasizing the need to explicitly consider specificity in the design process.

In general, adding more receptors into the target class can only make obtaining specificity more difficult because as more potential interaction partners are present, the chemical space in which a ligand can exist to best satisfy interactions with all targets becomes smaller. Similarly, as more decoys exist there becomes a greater chance that they will have similar physical characteristics to the targets of interest and thus designing for narrow specificity also becomes more difficult. In this work we have studied up to four target classes with up to 6 conformational variants in each class and two decoy classes; however, in principle there is no limit to the number of targets, classes, or decoys that can be used with this methodology.

While we have not explicitly taken into consideration many important drug molecule properties, such as those that affect ADMET, the specificity framework described here is capable of incorporating certain ligand properties into the optimization in the form of constraints. For example, adding constraints related to the dipole or ligand solvation energy is currently possible and could be used to simultaneously optimize specificity and logP. Protein flexibility is another important consideration that was only partially considered in this work through the use of multiple crystal structures. Accounting for induced-fit effects is most important when decoys are involved because unfavorable interactions could be partially eliminated through structural relaxation of the decoy. In the case when only broad specificity is being considered (no decoys), accounting for protein flexibility does not present a significant problem because receptor relaxation leads to improved binding energies and therefore predicted enhancements to broad specificity should only get better. Future work to more fully include receptor flexibility and ligand-induced conformational changes will be valuable in increasing the accuracy and general applicability of the method.

Methods

Theoretical Background

We have constructed a matrix formulation of the binding energies for the reaction

$$L+R\iff C$$ (2)

where L and R are the ligand and receptor, respectively, and C is the complex. The electrostatic free energy (ΔG_es) associated with this reaction can be expressed as:

$$\Delta G_{\mathit{es}}={{\overrightarrow{Q}}_l}^{†}\mathbf{L}{\overrightarrow{Q}}_l+{{\overrightarrow{Q}}_r}^{†}\mathbf{C}{\overrightarrow{Q}}_l+{{\overrightarrow{Q}}_r}^{†}\mathbf{R}{\overrightarrow{Q}}_r$$ (3)

where Q⃗_i and Q⃗_r are the ligand and receptor charge vectors, respectively, L is the ligand desolvation matrix, R is the receptor desolvation matrix, and C is the solvent screened interaction matrix between the ligand and receptor. The vector Q⃗_i is of length corresponding to the number of ligand atoms (n) whereas L is an n×n matrix that contains the information about changes in energetics within the ligand upon binding. The matrix C has dimensions n×m, where m is the number of receptor atoms, and has elements corresponding to the bound-state solvent-screened interaction potential between the ligand and the receptor. The term Q⃗_r^†RQ⃗_r is a constant for each ligand–receptor complex because the receptor has fixed partial atomic charges (constant Q⃗_r) and the receptor shape does not change upon charge optimization (constant R). While we have chosen to use the vector Q⃗_i to represent charges at the ligand atom centers, it is possible to place basis points anywhere within the shape defined by the ligand surface [23, 24].

A specificity objective for optimization based on the above framework can be defined as [22]:

$$\mathit{Sp}=-\frac{1}{\beta }\ln \left\{\left[\underset{d\in D}{\Sigma }{e}^{-\beta \Delta G^o(d;l)}\right]\left[\underset{C\in T}{\Sigma }{\left(\underset{t\in C}{\Sigma }{e}^{-\beta \Delta G^o(t;l)}\right)}^{-1}\right]\right\}$$ (4)

where β is $\frac{1}{k_{B}T}$, k_B is the Boltzmann constant, and T is the absolute temperature used to tune the behavior of the function. The first term in square brackets of Equation 4 takes account of each decoy (d) within the set of all decoys (D); the second set of square brackets takes account of the targets, where C represents a class of receptors within the whole set of targets T and t is an individual target molecule within a particular class C. When there are no decoys and only a single target within a single class, this reduces to an equation for the free energy of binding of a single ligand–receptor pair, as expected.

The term in the first square brackets in Equation 4 represents decoy binding and the term in second square brackets represents target binding. The decoy term is a simple Boltzmann sum over standard state decoy binding free energies. The second square-bracketed term includes an inner Boltzmann sum of the standard state binding free energies of the targets within a class. In the outer summation, the reciprocal of each of these terms is added, thus selecting the Boltzmann-weighted contributions from the weakest-binding target class.

In this work, we use the low temperature limit of Equation 4, in which only the tightest-binding decoy is retained from the first square-bracketed term. In the second square-bracketed term, only the worst-of-best target (the energy of the worst target class, where the energy of a class is defined by the tightest binding member of the class) is retained:

$$\mathit{Sp}={\mathit{Min}}_d\left[\Delta G^o(d;l)\right]-{\mathit{Max}}_{C\in T}\left\{{\mathit{Min}}_{t\in C}\left[\Delta G^o(t;l)\right]\right\}$$ (5)

For practical applications this is a desirable formulation, because the objective function maximizes the energetic gap between the binding affinity for the worst-of-best target and the tightest binding decoy. In the case that no decoys are present, the function reduces to a form in which the binding free energy of the worst-of-best target is minimized. Finally, in the case with only a single target within a single class, the formula reduces to an affinity optimization to the target [25, 28].

To solve Equation 5, we use the numerical solver package gams [63] implementing the conopt2 algorithm [64]. This algorithm is based on the generalized reduced gradient (GRG) algorithm with modifications to allow for efficient solving of large systems. Modifications to the original GRG formulations include the use of sparse matrix techniques, dynamical convergence feasibility tolerances, and the reusing of Jacobians when possible. Locally written code provides an interface that allows for the specificity optimizations to be performed with constraints on any charge-related property, such as the net charge, dipole, or the RMS charge deviation from the original partial atomic charges.

Choice of Structural Ensemble

The choice of structural ensembles was made based on biological relevance of the receptors and the quality of the structural information available. All structures were obtained from the RCSB Protein Data Bank (PDB; www.rcsb.org/pdb) [65].

Narrow specificity

For the narrow specificity optimizations, we chose the protease from the HIV-1 NY5 strain (PDB identifier 5HVP) as a target and the human aspartyl proteases pepsin (1PSO) and cathepsin D (1LYB) as decoys. Both pepsin and cathepsin D enzymes have the pepstatin inhibitor bound. HIV-1 protease is instead bound to acetyl pepstatin, which is identical to pepstatin except at the N-terminus where the isovaleryl group is truncated before the final three carbon atoms. In order to create a system in which there was a one-to-one correspondence between basis points in these three systems (a necessary step under the current specificity framework), we built the additional methyl groups onto the acetyl pepstatin molecule in the HIV-1 protease site and performed a rotamer search on the built atoms to determine the low-energy conformations. Geometry minimizations were performed on the best rotamers to select the low-energy conformation.

Broad specificity

The explicit escape mutant ensemble was comprised of the wild-type protease (1FGC), the V82A mutant (1ODX) and the triple mutant I63P/V82T/I84V (1K6V). Initial binding free energies were normalized such that binding to the mutant complexes was 1.0 kcal/mol higher than to wild type. Additional calculations were performed by adding the D30N mutant (1FFI) as a nelfinavir target and the G48V/L90M mutant (1FB7) as a saquinavir target. Initial binding free energies were normalized such that binding of nelfinavir to the D30N mutant and saquinavir to the G48V/L90M mutant were 2.0 kcal/mol higher than to wild type.

Wild-type ensemble

A structural ensemble of wild-type HIV-1 protease structures was used to obtain conformational variation in the active site. The PDB identifiers for these targets are 1G2K, 1HVH, 1HWR, 2BPV, and 2BPY. Both occupancies in the 1HVH structure were kept and treated as distinct targets to add additional structural diversity into the ensemble, resulting in a total of six classes. Initial binding free energies were normalized to be equivalent among all members of this wild-type ensemble.

Ligand Docked Conformation

In the narrow specificity studies with pepstatin, the bound complexes were taken directly from the PDB structures. In the broad specificity studies, multiple ligand bound state conformations were generated in order to populate each class with multiple targets. First, all HIV-1 protease structures were aligned using an RMSD fit of the Cα atoms to the wild-type 1FGC structure. Ligands were placed based on known crystal structure coordinates; 1HPV, 1HSG, 1OHR, 1HXW, 1C6Z, and 1D4S for amprenavir, indinavir, nelfinavir, ritonavir, saquinavir, and tipranavir, respectively. This gave us confidence in the binding mode and allowed us to avoid variations associated with docking. The aligned ligands were minimized for 100 steps in the context of each target using varying dielectric constants (ε= 1, 2, 4, 1r, 2r, and 4r) in order to generate six complexes within each target class. The receptor atoms were held fixed throughout the procedure. The resulting ensembles maintained the same hydrogen-bonding characteristics as seen in the crystal structures from which they were obtained.

Structure Preparation

The charmm molecular modeling package [66] was used with the CHARMm all-atom parameter set [67] for molecular mechanics calculations. For HIV-1 protease structures, water molecules and ions were removed except for the single buried active site water molecule making interactions with the backbone amide of Ile50 [68]. For the tipranavir calculations, this water was removed because it is not present in the native tipranavir 1D4S crystal structure. In the pepsin structure, water residue numbers 8, 17, and 46 were retained while in the cathepsin D structure waters 1, 2, 3, 5, and 118 were retained. These water molecules are either completely buried within the protein with no solvent accessible surface area or make at least 2 hydrogen bonding interactions with pepstatin.

The hbuild [69] facility of charmm was used to add all hydrogen atoms using a dielectric constant of ε=1. Distance cutoffs for electrostatic or van der Waals interactions were not applied. One of the catalytic aspartates was protonated at the position in which the hydrogen was shared between the catalytic diad. Rotameric states of all histidine, asparagine, and glutamine side chains were checked to ensure the appropriate hydrogen-bonding pattern.

Continuum Electrostatics Calculations

Electrostatic binding free energies were calculated using the continuum electrostatic model with a molecular dielectric of ε=4 and a solvent dielectric of ε=80. The molecular surface was used to define the solvent boundary with a solvent probe radius of 1.4 Å to define the surface [70]. A salt concentration of 0.145 mM and a 2.0 Å ion-excluding Stern layer were used [71]. A locally modified version of the delphi software package [72, 73] was used to solve the linearized Poisson–Boltzmann equation. Averages of the potentials were taken over ten translations on a grid with density 3.8 grids/Å centered on the charged atoms.

The parse parameter set [74] was used for peptide atoms. For non-peptide-like ligands (all except pepstatin) standard parameters were not available. Geometry optimizations were performed using Gaussian98 [75] at the RHF level of theory with the 6-31G* basis set and atom-based partial atomic charges were obtained using a 2-stage RESP fit [76]. Parameters for the molecular mechanics calculations described above were obtained by using the closest CHARMm atom types.

Charge Optimization

Equation 5 was solved using locally written and commercially available software. The free energy ΔG is defined by Equation 3, as described above. Typical optimizations were performed with constraints on each atomic charge q_i such that |q_i|≥0.85e to keep the charges within chemically reasonable limits. Due to the nonlinear nature of Equation 5 and the possibility for multiple extrema, a numerical solver was needed for the optimizations. We performed the optimizations using the gams software package [63] and the conopt2 solver [64]. Two specificity optimizations were performed in each case with initial charges used to seed the solver coming from either the affinity-optimized charges or all zero charges. All optimizations converged to the same answer, providing assurance that the global optimum was obtained. As a further test, optimizations of a few systems were run using the baron algorithm [77] in gams, which is a branch-and-bound procedure that is guaranteed to reach the global solution. In each case this procedure converged to the same solution as the conopt2 solver.

In the case of narrow specificity optimizations with decoys, any dimension within the decoy energy-charge space that is steeper than that of the target will result in an unbounded optimum specificity. We added an additional constraint into the optimizations to eliminate unbounded solutions such that the RMSD of the charge remain below a specified value.

$$\lambda =\sqrt[]{\frac{{\Sigma }_{i\in N}{(q_i-q_i^o)}^2}{N}}$$ (6)

The sum is taken over each charge q_i in the set of N atoms. This constraint on the RMSD of the charge forces the optimization to perturb the charges in the direction that can gain the most specificity for the given change in the RMSD charge. We found that a constraint of 0.01eλ≤λ0.1e worked well in all optimizations.

Modeling Mutations

Modifications to the starting ligand structures were built using charmm with parameters as described above. Torsion angles of the new group were sampled at 60° followed by 100 steps of adapted-basis Newton–Rhapson (ABNR) minimization of the new atoms with the rest of the protein and ligand atoms fixed. Then, minimization of the entire ligand was performed with the receptor fixed. The minimum energy structure from this procedure was used for continuum electrostatic calculations. The same procedure was repeated on the wild-type structures to ensure an equal reference point. For fluorination, the hydrogen atom to be replaced was mutated to a fluorine atom and the bond length was allowed to minimize to convergence. In the case that a clash ensued with the protein, the ligand was allowed to minimize to convergence with the receptor fixed.

Free energies of binding were computed using an MM-PBSA approach, adding the solvation free energies to the in vacuo interaction energies (internal plus van der Waals). The non-polar component of the solvation energy was computed using the solvent accessible surface area and the relationship:

$$\Delta G_{SA}=\mathit{ax}+b$$ (7)

where a=5.2 cal/Ų, b=920 cal, and x is the calculated solvent accessible surface area using a 1.4-Šprobe radius [74].

Figure 6.

Broad specificity-optimized charges for indinavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net computed specificity gain is computed to be 11.8 kcal/mol for this charge distribution.

Figure 7.

Broad specificity-optimized charges for nelfinavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net specificity gain is computed to be 8.7 kcal/mol for this charge distribution.

Figure 8.

Broad specificity-optimized charges for ritonavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net specificity gain is computed to be 17.0 kcal/mol for this charge distribution.

Figure 9.

Broad specificity-optimized charges for saquinavir binding to a target ensemble comprised of three classes: wild-type, V82A mutant (1X), and I63P/V82T/I84V mutant (3X). Colors are as described in Figure 4. The net specificity gain is computed to be 15.1 kcal/mol for this charge distribution.