Open Quantum Dynamics Calculations with the Hierarchy Equations of Motion on Parallel Computers

Abstract

Calculating the evolution of an open quantum system, i.e., a system in contact with a thermal environment, has presented a theoretical and computational challenge for many years. With the advent of supercomputers containing large amounts of memory and many processors, the computational challenge posed by the previously intractable theoretical models can now be addressed. The hierarchy equations of motion present one such model and offer a powerful method that remained under-utilized so far due to its considerable computational expense. By exploiting concurrent processing on parallel computers the hierarchy equations of motion can be applied to biological-scale systems. Herein we introduce the quantum dynamics software PHI, that solves the hierarchical equations of motion. We describe the integrator employed by PHI and demonstrate PHI’s scaling and efficiency running on large parallel computers by applying the software to the calculation of inter-complex excitation transfer between the light harvesting complexes 1 and 2 of purple photosynthetic bacteria, a 50 pigment system.

1 Introduction

Quantum dynamics plays a major role in many biological processes.^1–4 To model such processes one has to account for the environment in which they occur, that is, one where thermal noise at an ambient temperature is present. Although many methods have been developed that account to some degree for the interaction between a quantum system and a thermal environment,^4–16 they typically involve limitations in regard to the relative interaction strengths found within a system and between the system and environment, or make approximations regarding the quantum nature of the system, or neglect non-Markovian effects. Such limitations and approximations are often permissible for a particular system and then the respective methods yield valuable insight, but they do not apply in general.

Purple bacteria are one of the simplest photosynthetic life forms, capable, through efficient light harvesting, of living in photon-poor environments.¹⁷ The primary pigment-protein complexes found in purple bacteria, light harvesting complex 2 (LH2), light harvesting complex 1 (LH1) and the reaction center (RC), have evolved to rapidly transfer excitation energy across many tens of nanometers and convert it, before the energy is lost through fluorescence or internal conversion, to a more stable form resulting in over 90% light-harvesting efficiency.^18,19 This remarkable efficiency due to rapid excitation transfer has been the subject of many experimental^20–29 and theoretical^30–37 investigations. It has been shown that excitation transfer benefits not only from quantum coherence,^38–40 but also from environmental noise.^40–47 In order to model excitation dynamics in purple bacteria, one has to take into account the strong interactions not only between the excited states themselves, but also with their surrounding environment.^34,48–54

There are only a few quantum dynamics methods for computation of open quantum system density matrices that take into account arbitrary intra-system and system-environment interactions, include non-Markovian effects, and make no assumptions about the quantum nature of the dynamics. ^55–61 The hierarchy equations of motion (HEOM) of Tanimura and Kubo,⁵⁸ which employ a hierarchy of auxiliary density matrices to account for non-Markovian dynamics without resorting to perturbative approximations,^58–71 is one of the earliest open quantum system descriptions and remains the only one applicable to large systems.^34–36,71 Although the HEOM are computationally expensive, typically requiring many gigabytes (GBs) of computer memory and many days of computation time, their application to large systems has been possible by exploiting GPUs⁷² and highly parallel computers.^34–36 The GPU-HEOM implementation⁷² yields tremendous improvement in computation time, but is severely limited to small (less than 10 pigments) systems by the small amount of memory available with current generation GPUs. By performing the HEOM integration on multi-processor CPUs, the system size is limited by the much larger main computer memory instead of GPU memory, allowing much larger systems to be modeled as shown here.

Implementing the HEOM on a multi-processor computer is, however, difficult due to the highly connected nature of the auxiliary density matrices. To achieve peak performance, the communication between processing elements needs to be minimized through a partitioning scheme that assigns each matrix in the hierarchy to a different processor. Additional improvements to calculation time can also be achieved by employing adaptive integration methods: either by adaptively filtering the number of auxiliary matrixes or by adaptively adjusting the integration step size.

Besides an application to large photosynthetic systems, such as those found in cyanobacteria, plants and artificial light harvesting,^73–77 the HEOM method is applicable to a wide range of other quantum systems. Indeed, any process that can be described by a set of N discrete quantum states in contact with a bosonic environment can be modeled.⁶¹

In the following section we present the partitioning scheme and integration methods used to implement the HEOM, as well as performance benchmarks of our parallel hierarchy integrator PHI¹.

2 Methods

Many systems can be modeled with an effective Hamiltonian^78–80 that describes the subset of relevant states |n〉, with energies E_n and interactions V_nm, written as

$$H_0={\displaystyle \sum _n^N{E}_n|n\rangle \langle n|+}{\displaystyle \sum _{n,m}^N{V}_{nm}|n\rangle \langle m|.}$$ (1)

At present PHI accounts only for Hermitian effective Hamiltonian operators, and thereby assumes a single excitation subspace. Systems such as those in a biological context are embedded in a T = 300 K thermal environment. Such environment can be modeled as an infinite set of harmonic oscillators¹¹

$$H_B={\displaystyle \sum _{\xi }\left[\frac{p_{\xi }^2}{2m_{\xi }}+\frac{m_{\xi }{\omega }_{\xi }^2{q}_{\xi }^2}{2}\right]}.$$ (2)

The thermal bath is coupled to the states |n〉 through the system-bath interaction term

$$H_{SB}={\displaystyle \sum _a^M{\widehat{F}}_a{u}_a,}$$ (3)

where u_a = ∑_ξc_aξq_ξ with c_aξ being the coupling strength of vibrational mode ξ to the system via operator F̂_a. In the case that each state |n〉 is independently coupled to the environment holds M = N and F̂_a=|a〉 〈a|, where |a〉 denotes one of the states |n〉 arising in Eq. (1). The system-bath coupling introduces a shift in the minimum energy positions of the bath coordinates q_ξ, which can be countered by the renormalization term

$$H_{REN}={\displaystyle \sum _{ab}^M{\widehat{F}}_a{\widehat{F}}_b}{\displaystyle \sum _{\xi }\frac{c_{a\xi }{c}_{b\xi }}{2m_{\xi }{\omega }_{\xi }^2}.}$$ (4)

In the case of system-bath coupling that is independent for each state |n〉, the renormalization term reduces to $H_{REN}={\displaystyle {\sum }_a^N|a\rangle \langle a|}{\lambda }_a$, where ${\lambda }_a={\mathrm{\Sigma }}_{\xi }{c}_{a\xi }^2/2m_{\xi }{\omega }_{\xi }^2$ is the bath reorganization energy. The total Hamiltonian is thus given by H_T = H_S+H_B+H_SB, where H_S =H₀+H_REN is the renormalized system Hamiltonian.

The bath degrees of freedom are not of interest and, thus, are traced out of the dynamics to calculate the bath averaged density matrix evolution as

$$\widehat{\rho }(t)={\text{tr}}_B\left\{\int e^{-i{ℒ}_{T}t/\overline{h}}\widehat{\rho }(0)\otimes e^{-\beta H_B}dt\right\}{\text{/tr}}_B\{e^{-\beta H_B}\}={\langle 𝒰(t)\rangle }_B\widehat{\rho }(0),$$ (5)

where β = 1/k_bT. Eq. (5) corresponds to the so-called factorized initial condition that does not include initial correlations between system and environment. Although initial correlations between system and environment would not be present in the case of instantaneous photo-excitation,⁶¹ they can be included when modeling other processes using the HEOM.^59,65 Once the thermal average is performed, the influence of the environment enters only through the bath correlation functions given by,⁴

$$C_{ab}(t)={\langle u_a(t)u_b(0)\rangle }_B=\frac{1}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }d\omega J_{ab}(\omega )\frac{e^{-i\omega t}}{1-e^{-\beta \overline{h}\omega }},}$$ (6)

where the spectral density J_ab(ω) is given by

$$J_{ab}(\omega )=\frac{\pi }{2}{\displaystyle \sum _{\xi }\frac{c_{a\xi }{c}_{b\xi }}{m_{\xi }{\omega }_{\xi }}\delta (\omega -{\omega }_{\xi })}.$$ (7)

As the coupling of environmental fluctuations to off-diagonal components in the system Hamiltonian are typically smaller than the coupling to diagonal components, i.e. |C_ab| ≪ |C_aa|, they are usually ignored.⁵⁴ In the present work only diagonal coupling to the environment is accounted for.

Currently only a few methods^{55–58,60,61} offer numerically tractable equations of motion for the solution, Eq. (5), for system sizes as they arise in the case of pigment systems of photosynthetic light harvesting. The hierarchy equations of motion^{58–63,66,67,69,71,81} (HEOM) is computationally expensive, but nevertheless furnishes an attractive method due to its applicability across a broad range of interaction scenarios.^{34–36,66,69,72,80–86}

Correlation functions

The HEOM arise by exploiting bath correlation functions C_ab(t) described by sums of exponentially decaying terms.⁵⁸ The HEOM work particularly well when the spectral density arising in Eq. (6) and Eq. (7) can be expressed as a so-called Drude spectral density,⁴ given by

$$J_a(\omega )=2{\lambda }_a\frac{\omega {\gamma }_a}{({\omega }^2+{\gamma }_a^2)},$$ (8)

where λ_a = ∫(J_a(ω)/πω)dω is the bath reorganization energy that determines the system-bath interaction strength, and 1/γ_a is the bath response time. The Drude spectral density describes over-damped harmonic oscillator modes ξ. The correlation function associated with the Drude spectral density is⁶⁹

$$C_a(t)={\displaystyle \sum _{k=0}^{\infty }{c}_{ak}\text{exp}}(-{\nu }_{ak}t),$$ (9)

where ν_a0 = γ_a, ν_ak≥1 = 2πk/βh̄ are the Matsubara frequencies⁶⁴ and the coefficients c_ak are

$$c_{a0}={\gamma }_a{\lambda }_a[\cot (\beta \overline{h}{\gamma }_a/2)-i]$$ (10)

$$c_{ak\ge 1}=\frac{4{\lambda }_a{\gamma }_a}{\beta \overline{h}}\frac{{\nu }_{ak}}{{\nu }_{ak}^2-{\gamma }_a^2}.$$ (11)

The summation to infinity in Eq. (9) needs to be truncated at a finite level, which is achieved by exploiting that beyond some finite K, ν_aK exp(− ν_aKt) ≈ δ(t).⁶⁰

The expansion of the correlation function using Matsubara frequencies, Eq. (9) and (11), is not the only possible expansion, and recent work has shown that alternative expansions can yield better results for low cut-offs K.^87,88

In principle one can also employ correlation functions for under-damped harmonic oscillators, namely ones of the form C(t) = cexp(−γt) cos(Ωt), to derive the HEOM,^89–91 thus enabling the use of arbitrary, multi-peaked spectral densities through, e.g., a Meier-Tannor decomposition.⁹² The Lorentzian peaks in such spectral densities, however, lead to many more terms in the HEOM which are only valid to second-order in system-bath coupling, such that in practice only Drude spectral densities are employed.^90,91 At present, PHI treats spectral densities consisting of single or sums of Drude spectral densities.

Hierarchy equations of motion

In deriving the HEOM each exponential term in Eq. (9) leads to the introduction of a set of operators, ρ̂n, called auxiliary density matrices (ADMs).⁶¹ The ρ̂n are indexed by a vector n = (n₁₀, …, n_1K, …, n_M0, …, n_MK). The equations of motion, which couple the ADMs in a hierarchical structure, are^34,35,61,71

$${\dot{\widehat{\rho }}}_n=-\frac{i}{\overline{h}}[{\widehat{H}}_{s,}{\widehat{\rho }}_n]-{\displaystyle \sum _{a=1}^M{\displaystyle \sum _{k=0}^K{n}_{ak}{\nu }_{ak}{\widehat{\rho }}_n-}{\displaystyle \sum _{a=1}^M\left(\frac{2{\lambda }_a}{\beta {\overline{h}}^2{\gamma }_a}-{\displaystyle \sum _{k=0}^K\frac{c_{ak}}{\overline{h}{\nu }_{ak}}}\right)[{\widehat{F}}_a,[{\widehat{F}}_a,{\widehat{\rho }}_n]]-i{\displaystyle \sum _{a=1}^M\left[{\widehat{F}}_a,{\displaystyle \sum _{k=0}^K{\widehat{\rho }}_{n_{ak}^{+}}}\right]-\frac{i}{\overline{h}}}{\displaystyle \sum _{a=1}^M{\displaystyle \sum _{k=0}^K{n}_{ak}\left(c_{ak}{\widehat{F}}_a{\widehat{\rho }}_{n_{ak}^{-}}-{\widehat{\rho }}_{n_{ak}^{-}}{\widehat{F}}_a{c}_{ak}^{*}\right)}}}}.$$ (12)

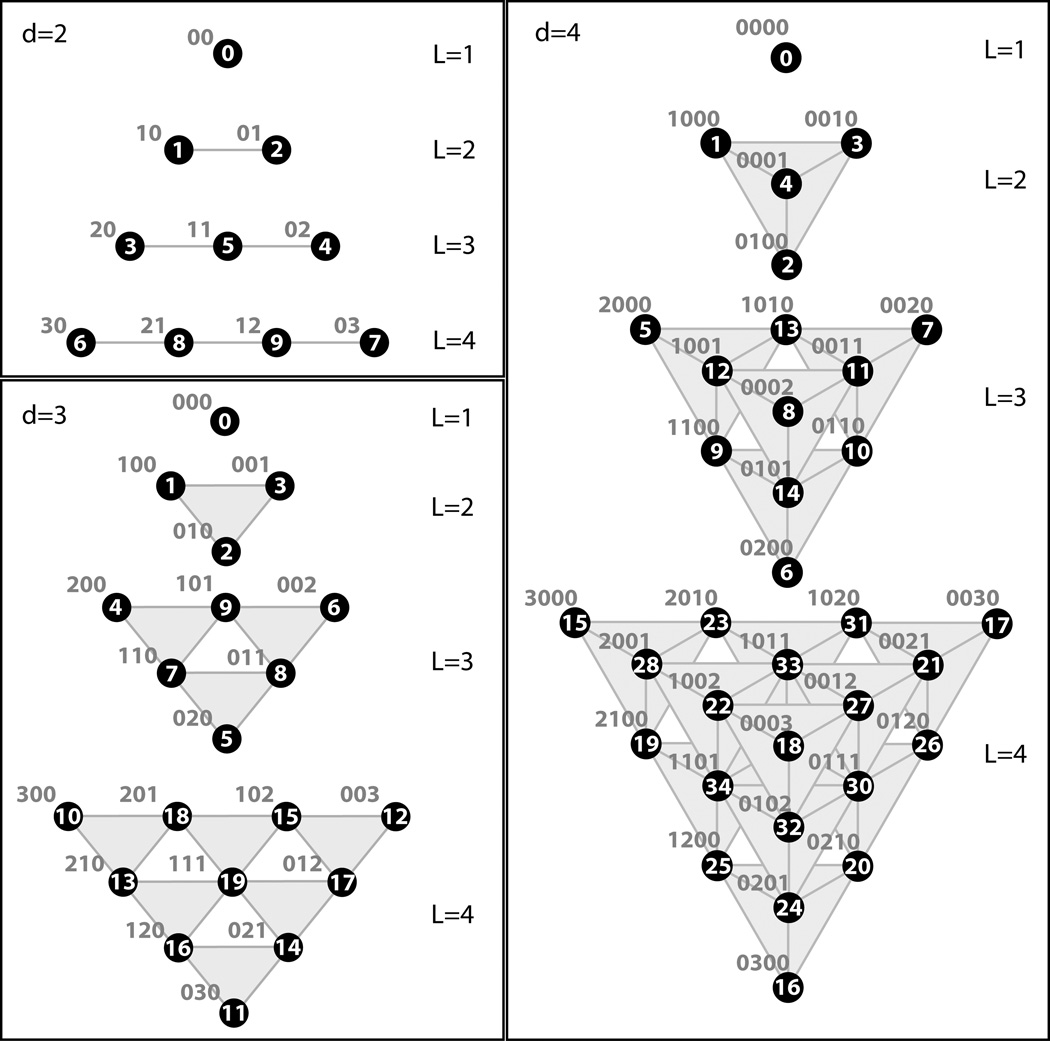
Each ADM with index n is coupled to ADMs with indices ${\mathbf{n}}_{ak}^{\pm }=(n_{10},\dots ,n_{ak}\pm 1,\dots ,n_{MK})$. As there are no negative indices n_ak arising in the derivation of the HEOM,⁶⁷ any ADM with a negative value for any n_ak is set to zero.. The system density matrix ρ̂ is the density matrix with index vector n = 0. Each density matrix in the hierarchy is assigned to a hierarchy level $L={\displaystyle {\sum }_{a=1}^M{\displaystyle {\sum }_{k=0}^K{n}_{ak}}}$. The coupling of the HEOM leads to a structure that can be visualized as a Pascal’s d−simplex, where d = M(K+1). Example hierarchies for d = 2, 3 and 4 are shown Figure 1.

Figure 1.

The first 4 hierarchy levels of Pascal’s d−simplices for d = M(K +1) = 2, 3, and 4. Each circle corresponds to a single ADM with the corresponding index vectors n shown in blue text. The numbering inside the circles corresponds to the scheme described in the hierarchy generation algorithm in Listing 1. The shaded regions indicate which ADMs are at the same level. Connectivity of the ADMs to those in the levels above and below is not shown.

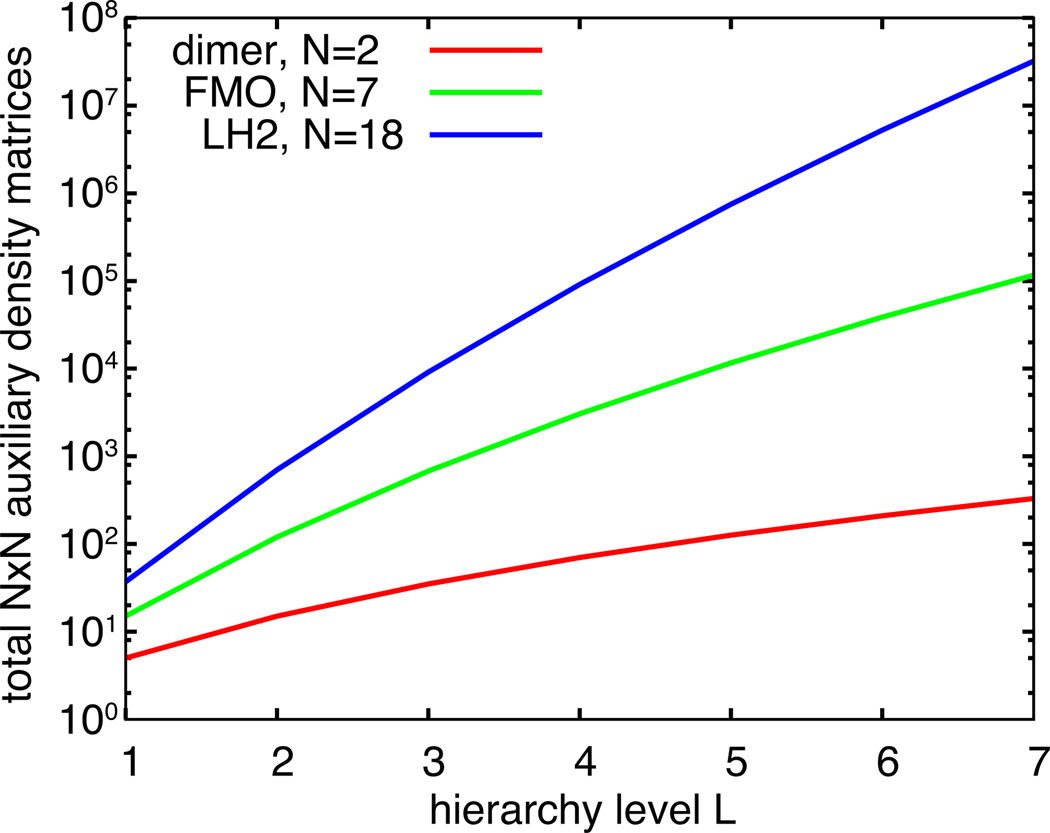
The number of matrices rapidly increase with hierarchy level L (Figure 2) and, in principle, is infinite. The ADMs account for the non-Markovian extent of the dynamics, meaning that more ADMs are needed to capture dynamics with greater non-Markovian character. Due to this behavior, however, a natural truncation L_T can be chosen such that L_T min_ak (ν_ak) ≫ ω_max, where ω_max is the maximum oscillation frequency in the system, without compromising the dynamics.⁶¹ Employing such truncation is often unfeasible due to computational limitations and, thus, convergence needs to be checked for each system to arrive at feasible values of L_T.

Figure 2.

Total number of ADMs with increasing hierarchy level L for a pigment dimer, for the Fenna-Mathews-Olson (FMO) complex⁸⁰ and for light-harvesting complex 2 (LH2).³⁴

Having chosen a truncation level L_T , the manner in which the HEOM is cut-off must also be specified. There are two ways to truncate the HEOM, either with so-called time non-local (TNL) truncation that sets all ADMs in levels L_T or greater to zero,⁶⁰ or with so-called time-local (TL) truncation that employs the Markovian approximation for ADMs in level L_T.⁹³ In case of the Markovian approximation it is assumed that for all ADMs with L = L_T −1

$${\displaystyle \sum _{k=0}^K{\widehat{\rho }}_{{\mathbf{n}}_{ak}^{+}}\approx -i\left({\widehat{Q}}_a^K(t){\rho }_{\mathbf{n}}-{\rho }_{\mathbf{n}}{\widehat{Q}}_a^K{(t)}^{†}\right),}$$ (13)

where

$${\widehat{Q}}_a^K(t)={\displaystyle {\int }_0^t\left({\displaystyle \sum _{k=0}^K{c}_{ak}\text{exp}}(-{\nu }_{ak}\tau )\right)}\text{exp}\left(-\frac{i}{\overline{h}}{H}_S\tau \right){\widehat{F}}_a\text{exp}\left(\frac{i}{\overline{h}}{H}_S\tau \right)d\tau .$$ (14)

It has been shown that TNL truncation produces spurious peaks in absorption spectra^66,71 and, thus, TL truncation should be employed whenever possible.

3 Numerical integration of HEOM

The HEOM present a significant computational challenge for all systems but one, a two state system. Within single pigment-protein complexes in photosynthetic systems, pigment numbers lie typically between 6 and 90, depending on species and growth conditions.¹⁷ To overcome the issues of poor scaling with system size and truncation (Figure 2), and because of the highly coupled nature of the equations, the HEOM need to be implemented computationally in the most efficient manner. This section describes the implementation of the HEOM in the parallel hierarchy integration software PHI capable of calculating excitation dynamics for systems containing up to 60 pigments at permissible truncation levels.³⁶

Adaptive integration

Since the HEOM describes thermally averaged time evolution, the ADMs will exponentially approach, in the absence of an external driving field, a steady-state. Any initial state of the system will relax to a steady state, leading during the relaxation to increasingly smaller changes in time of the elements of each ADM.

Shi et al.⁶⁹ proposed a rescaling of the ADMs that permits an automatic removal of the ADMs while integrating the HEOM. During integration, the ADMs are adaptively removed when their maximum absolute value is less than a defined filter accuracy δ_F. This filtering greatly reduces the memory requirements for integrating the HEOM for moderate-sized systems,^69,72 but can lead to artifacts with choices of δ_F values that are too large.

By employing the same rescaling of the ADMs as employed by Shi et al.⁶⁹ one can exploit the damped dynamics by integrating the HEOM with an adaptive timestep. Among the many adaptive integration methods, the Runga-Kutta-Fehlberg (RKF45) method⁹⁴ stands out as most practical as it is a 5th order integration algorithm that does not require the re-calculation of a timestep with a different step size in order to evaluate the integration error. The method, instead, re-uses the interim Runga-Kutta steps to also compute a 4th order integration step; at the end of a single timestep, the 4th order timestep calculation is compared with the 5th order timestep calculation and the step is kept or discarded according to a tolerance δ_I and the stepsize is increased or reduced accordingly.

Adaptive integration by the RKF45 algorithm requires 6 evaluations of the equations of motion, compared to 4 evaluations when using Runga-Kutta 4 (RK4) fixed timestep integration. The additional computation per RK45 step compared to a RK4 step, however, typically results in an order of magnitude decrease in the number of integration steps compared to RK4 with an overall reduction in total computation time. Rapid initial dynamics as well as long-time relaxation to the steady-state are both covered efficiently, with an overall short calculation time and a pre-defined integration error tolerance.

Adaptive timestep integration, however, cannot typically be used in conjunction with the adaptive ADM filtering method of Shi et al. as the latter introduces artifacts in the time evolution of the ADMs that result in the adaptive integration method taking smaller time-steps than without the automatic filtering. As will be shown in Results below, suitable choices of δ_F and δ_I values still result in speed-up within an acceptable error.

Partitioning

Central to efficient integration of the HEOM is the use of parallel computing. Unfortunately, large numbers of processors linked in computer clusters (i.e., in distributed memory computers) with a low network bandwidth cannot be used since the HEOM, particularly for systems of many pigments, are extremely coupled, and require a high bandwidth for inter-processor communication. This communication cost can, however, be managed by employing multiple threads running on a multi-processor, shared memory computer.

In principle it is relatively straightforward to assign P processing threads (where each thread is an independently executing process able to communicate with other threads and access the same shared memory) to a set of ADMs. Integration then proceeds by computing and applying the integration updates from the HEOM in parallel, pausing between each step to synchronize data between the P threads. The communication overhead due to the highly coupled nature of the HEOM means that even with modern symmetric multi-processing (SMP) hardware, however, the ADMs need to be well partitioned to avoid memory contention and maximize use of memory bandwidth available to each processor.

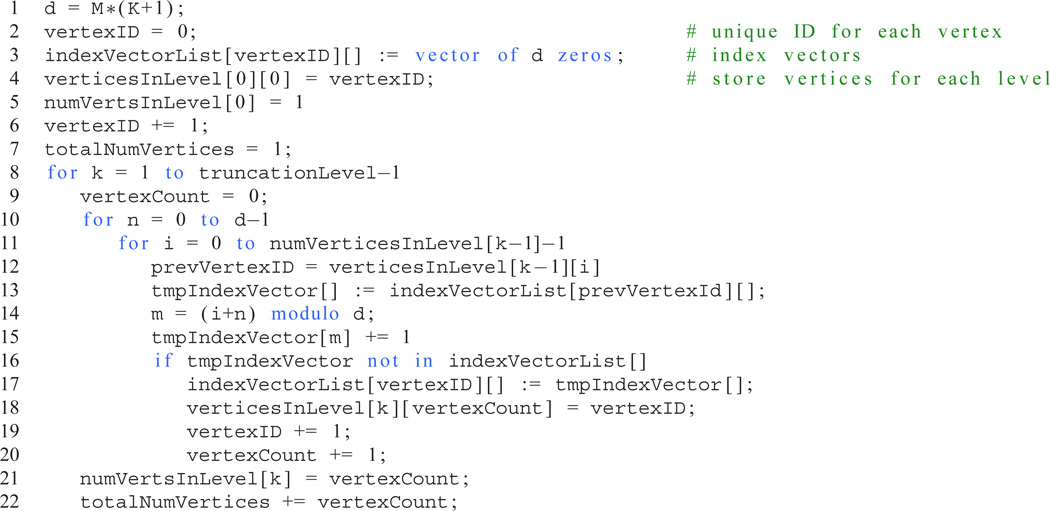
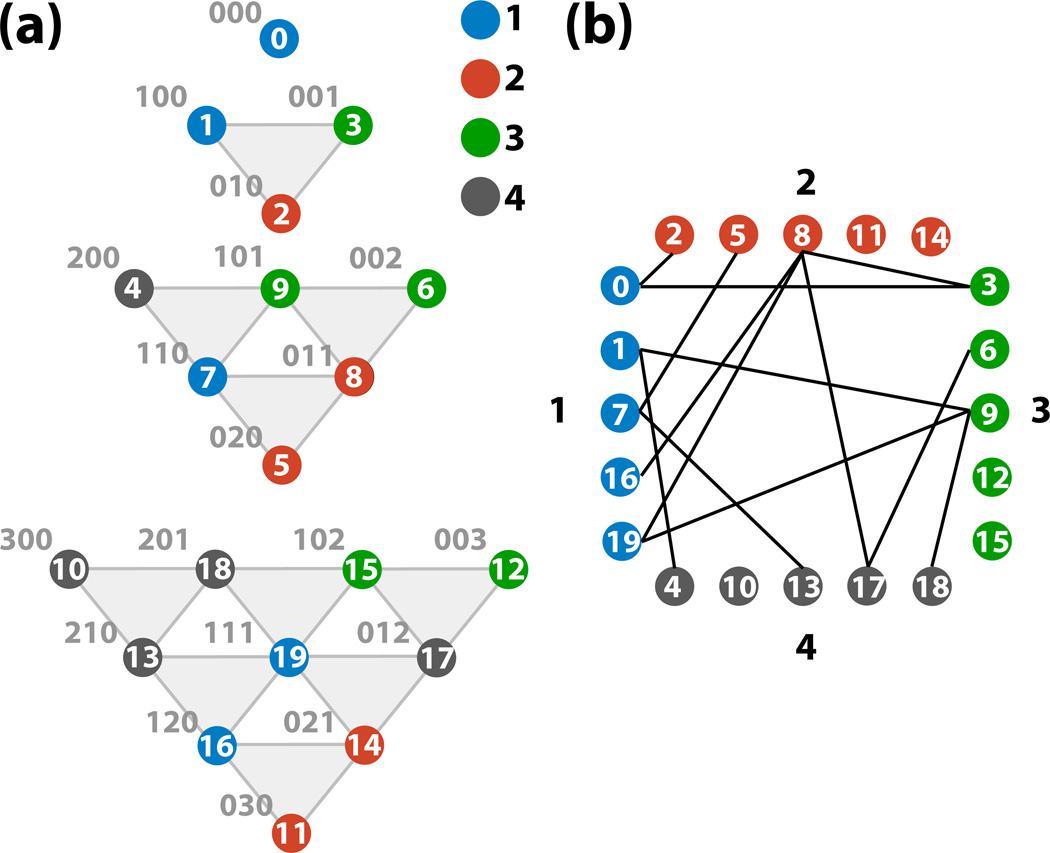
An algorithm for generating the index vectors n of the ADMs and, thus, the vertices of the associated Pascal’s d-simplex, is given in Listing 1. The partitioning algorithm (Listing 2) employs the numbering scheme in Listing 1 to assign each vertex to a set such that the number of inter-set edges is minimimal whilst ensuring that each set contains almost the same number of vertices. An example of the partitioning of a hierarchy of ADMs associated with a Pascal’s 3-simplex is shown in Figure 3. The partitioning algorithm presented here reduces the inter-set connections compared to either block- or cyclic-partitioning schemes often employed in parallel programming. Assigning each set to a separate thread and, crucially, instructing each thread to allocate the memory required to store the ADMs in its set, reduces inter-processor memory contention and dramatically improves the performance of the parallel HEOM integration software PHI.

Listing 1.

Pseudo-code to generate index vectors n for any Pascal’s d-simplex, where d = M(K+1) for the HEOM, up to a specified truncation level. Scalar assignment operations are indicated by “=”; vector assignment operations are indicated by “:=”.

Listing 2.

Algorithm to partition the vertices of a Pascal’s d-simplex into P sets, minimizing inter-set connections while ensuring the numbers of vertices in each set differ by at most 1. The algorithm employs the results of the index vector generation code in Listing 1. Scalar assignment operations indicated using “=”; vector assignment operations indicated using “:=”; the “==” operator indicates a test for equality.

Figure 3.

Partitioning of a Pascal’s 3-simplex into four sets. The partitioning (a) results in each subset containing 5 vertices, with (b) 13 edges crossing between subsets.

4 Results

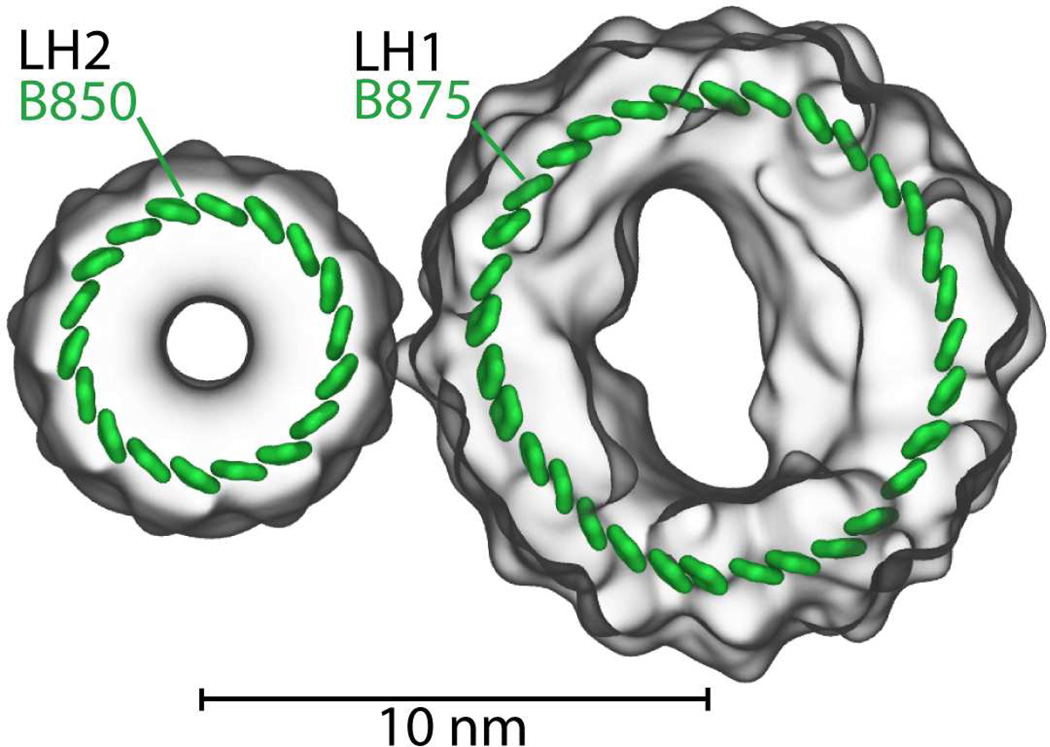
Excitation dynamics is a key process in photosynthetic light harvesting. Excitation needs to be transferred over many nanometers for light energy to be utilized by the cell. Since the excitation life time is rather short, namely only 1 ns, transfer needs to be fast to be efficient. In purple photosynthetic bacteria, such as Rps. molischianum, the needed efficiency is achieved by placing pigment molecules into ring-like structures as shown in Figure 4 and transferring excitation between the ring-like structures. Light energy typically absorbed by light harvesting complex 2 (LH2, B850 ring)³² is passed by inter-complex excitation transfer to light-harvesting complex 1 (LH1, B875 ring)⁹⁵ prior to charge separation at the photosynthetic reaction center.¹⁷ The close packing arrangements and pigment orientations in the ring-like structures result in quantum coherence that enhances excitation transfer between the rings.³⁹

Figure 4.

Pigment-protein complexes light harvesting complex 2 (LH2) and light harvesting complex 1 (LH1). Shown are the 18 pigments forming the B850 ring of LH2 and the 32 pigments forming the B875 ring of LH1.^32,95

We present here the effects of employing different HEOM integration parameters and methods. First, we examine the effect of adaptive timestep integration for a pigment dimer and for an 18-pigment ring, the so-called B850 ring in LH2.³² Second, we employ the B850 ring as a model system to investigate the parallel performance of PHI. Finally, the transfer of excitation between the two ring-structures, the B850 ring and the 32-pigment B875 ring in LH1⁹⁵ (shown in Figure 4), is computed.

Effect of integration timestep and method

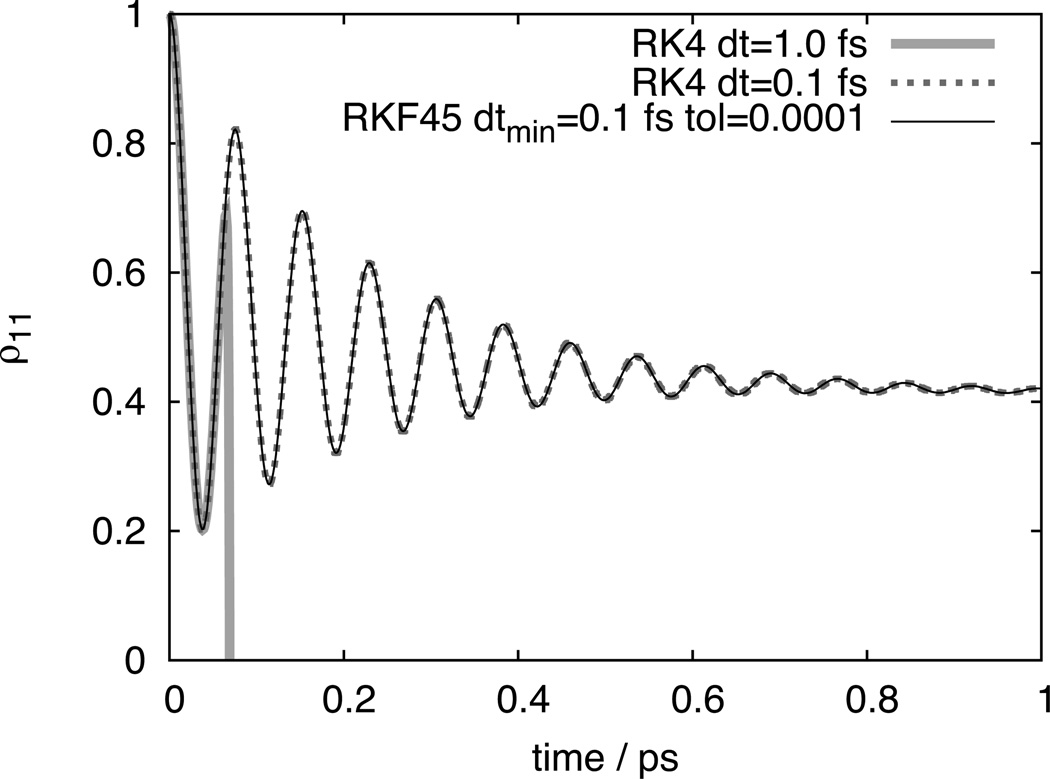
Below, results are presented to demonstrate the effect of fixed and and adaptive timesteps on integration speed and accuracy. First, a model dimer system is employed to highlight the importance of choosing an appropriate timestep. The dimer is specified by HS = ΔEσ̂ _z+Vσ̂_x, where ΔE = 100 cm⁻¹, V = 200 cm⁻¹, reorganization energies are λ₁ = λ₂ = 50 cm⁻¹, and response frequencies are γ₁ = γ₂ = 1/(0.1 ps); σ̂_z and σ̂_x are Pauli matrices.¹⁵ As can be seen from Figure 5, using too large a timestep can rapidly cause integration errors. Fortunately, in such a simple system such gross errors are easy to detect and rectify. For larger systems, however, finding the optimum timestep can be time-consuming. By employing the RKF45 adaptive timestep integration method (see Methods) such effort can be avoided and it becomes much easier to achieve greatly improved performance.

Figure 5.

Comparison of HEOM integration schemes. Integration on 4 processors (CPU cores) took 0.23 minutes for Runga-Kutta 4 integration using 0.1 fs timesteps, and 0.03 minutes using Runga-Kutta-Fehlberg 4/5 adaptive integration with a minimum timestep of 0.1 fs and a tolerance of 0.0001.

Effect of integration timestep and method

To examine the accuracy and speed of different integration options we consider the case of light excitation of one of the primary absorbing states of the B850 ring of pigments in light harvesting complex 2 (LH2). The excitation dynamics of the 18-pigment B850 ring was previously characterized³⁴ and calculations are repeated here to investigate the effect of different integration methods. The resulting exciton dynamics is shown in Figure 6 for the reference calculation; Table 1 presents the accuracy and computation time of adaptive and non-adaptive integration methods. One can clearly discern that the Shi et al. adaptive filtering dramatically reduces computation time in the case of Runga-Kutta 4 (RK4) integration. Excellent performance can also be achieved using RKF45 adaptive timestep integration, with typically shorter calculation times and improved accuracy than needed for the other methods listed. Both adaptive methods can be combined for optimal performance as long as the RKF45 tolerance is larger than the ADM filter accuracy, i.e., for δ_I > δ_F; otherwise longer computation times result. In general, optimal RK4 timestep and ADM filter accuracy both depend on system parameters and, thus, require time-consuming benchmark calculations. Employing RKF45 adaptive timestep integration yields significant performance gains without prior benchmarks.

Figure 6.

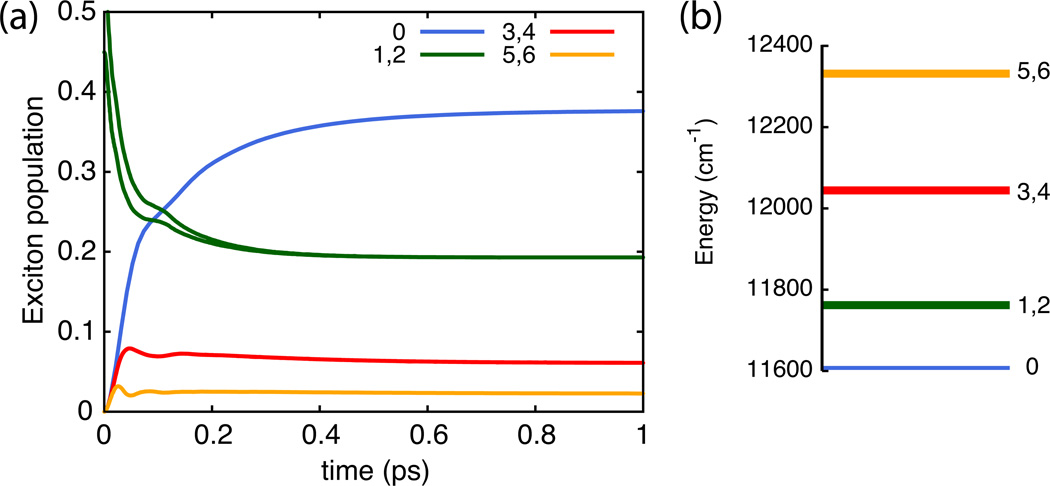
Exciton dynamics of the seven lowest-energy exciton states of the B850 ring in LH2 with the initial state given by a super-position of the degenerate 850 nm exciton states 1 and 2. Populations are shown in (a) and energies of associated states in (b).

Table 1.

Accuracy and performance of different integration methods for calculating excitation dynamics of the B850 pigments of LH2 with parameters and truncation as given in Ref. 34.

integration method	ADM filter†δF	integration tolerance‡δI	integration stepsize (fs)	average error║	calculation time (min)
RK4			0.1	0	920
RK4			1.0	2.0×10−7	91.8
RK4			2.0	5.4×10−7	46.0
RK4	10−6		1.0	2.0×10−7	83.9
RK4	10−6		2.0	5.5×10−7	42.1
RK4	10−4		1.0	7.8×10−6	43.4
RK4	10−4		2.0	1.1×10−5	25.7
RK4	10−2		1.0	2.7×10−3	34.5
RK4	10−2		2.0	2.9×10−3	21.9
RKF45		10−6	1.0→7.5	6.1×10−7	35.6
RKF45		10−4	1.0→7.4	8.2×10−7	33.3
RKF45		10−2	1.0→8.1	1.2×10−6	33.1
RKF45	10−6	10−6	1.0→2.0	3.3×10−7	66.1
RKF45	10−6	10−4	1.0→4.6	6.7×10−7	34.1
RKF45	10−6	10−2	1.0→8.1	9.9×10−7	33.0
RKF45	10−4	10−6	0.6→1.2	7.8×10−6	71.0
RKF45	10−4	10−4	1.0→2.4	1.1×10−5	34.4
RKF45	10−4	10−2	1.0→4.6	1.5×10−5	24.1
RKF45	10−2	10−6	0.3→1.2	2.0×10−3	93.2
RKF45	10−2	10−4	0.7→2.4	2.8×10−3	50.9
RKF45	10−2	10−2	1.0→3.8	3.3×10−3	27.9

^†filter constant for Shi et al. adaptive ADM filtering.⁶⁹

^‡integration tolerance for Runga-Kutta-Fehlberg 4/5 adaptive integration.⁹⁴

^║$\mathit{\text{error}}={(N^2{N}_t)}^{-1}{\displaystyle {\sum }_n^{N_t}{\displaystyle {\sum }_{i,j}^N\left|{\rho }_{ij}(t_n)-{\rho }_{ij}^{ref}(t_n)\right|}}$ is the average absolute error in each element of the system density matrix per timestep.

Parallel performance

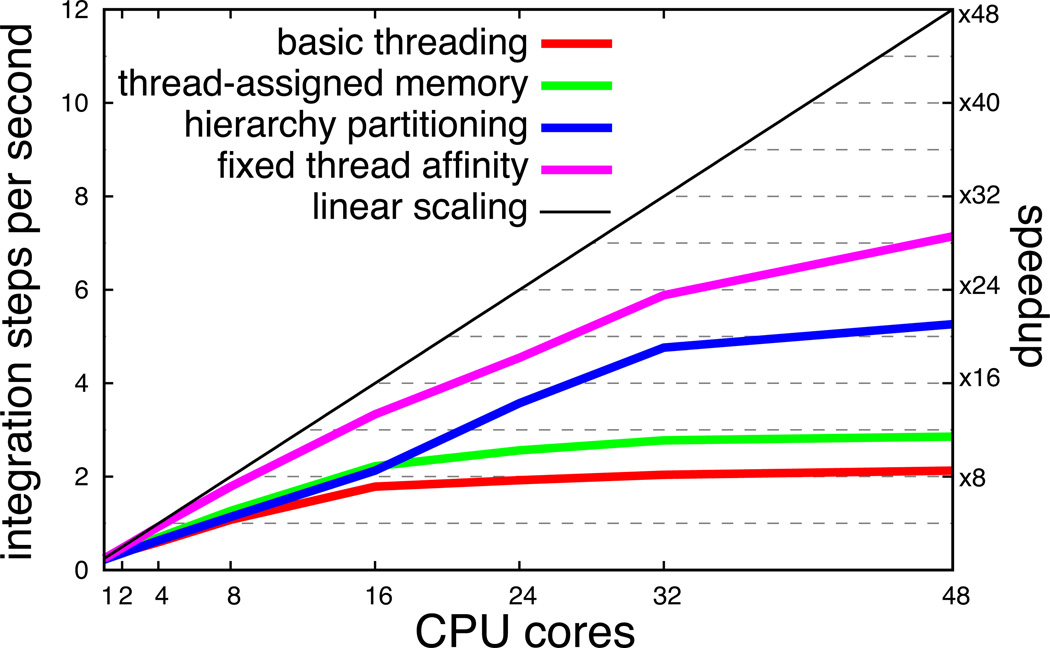
Key to employing the HEOM to calculate excitation dynamics in large pigment systems is scalability to many processors. With efficient scaling, the size of problem that can be treated depends only on the size of the computer available and is not limited by the speed of a single processor. To endow PHI with optimal scaling capabilities, three steps were taken: (1) memory assignment was changed from being initially assigned to a single large block to being assigned to separate smaller blocks, one for each integration thread; (2) the partitioning of the ADMs was done satisfying minimum inter-thread communication; (3) each thread was assigned to a specific processor. The effect of the three steps, shown in Figure 7, is a greater than 3-fold reduction in calculation time when employing 48-cores, and a significantly better scaling compared to cyclic decomposition, a simple and obvious choice, but not an optimal one.

Figure 7.

Parallel scaling of PHI on a 48-core AMD Magny-Cours shared-memory computer running Linux. The system employed for benchmarking is the set of 18 pigments in the B850 ring of LH2 with L_T = 4 and K = 1. Note that increasing the number of Matsubara frequencies K results in a dramatic reduction in performance of PHI. “Basic partitioning” refers to a cyclic partitioning of ADMs and the memory for all ADMs being assigned to a consecutive block; “thread-assigned memory” refers to instructing each thread to perform memory assignment for its set of ADMs in the cycling partitioning scheme; “hierarchy partitioning” refers to employing the partitioning described in Listings 1 and 2 and using thread-assigned memory; “fixed thread affinity” refers to employing the partitioning scheme in Listings 1 and 2, using thread-assigned memory and instructing the operating system’s thread scheduler to affix each thread to a particular processor such that no thread migration occurs.

A significant boost in parallel performance is thus gained from the hierarchical partitioning scheme detailed in Listings 1 and 2. The performance saturation seen around 48 cores in Figure 7 indicates that inter-processor communication is still a bottleneck and any scheme to reduce this bottleneck will result in further performance improvement. The rapid bandwidth saturation, arising even with the high-bandwidth processor-memory bus (42 GB/sec for the AMD Magny-Cours CPU), suggests that parallel performance on a distributed memory computer is relatively poor.

Excitation transfer between LH2 and LH1

With the improvements in scalability and calculation time for integration of the HEOM described above, one can model excitation transfer between two large pigment-protein complexes, LH2 and LH1 (Figure 4).

In the photosynthetic light harvesting apparatus of purple bacteria most excitation transfer steps occur between the 18-pigment B850 ring in LH2 and the 32-pigment B875 ring in LH1.^18,19,32 In order to describe this transfer one needs to account for N = 50 pigments. Modeling a system of this size is not possible a with single-processor implementation of the HEOM, but requires PHI running on a parallel computer.

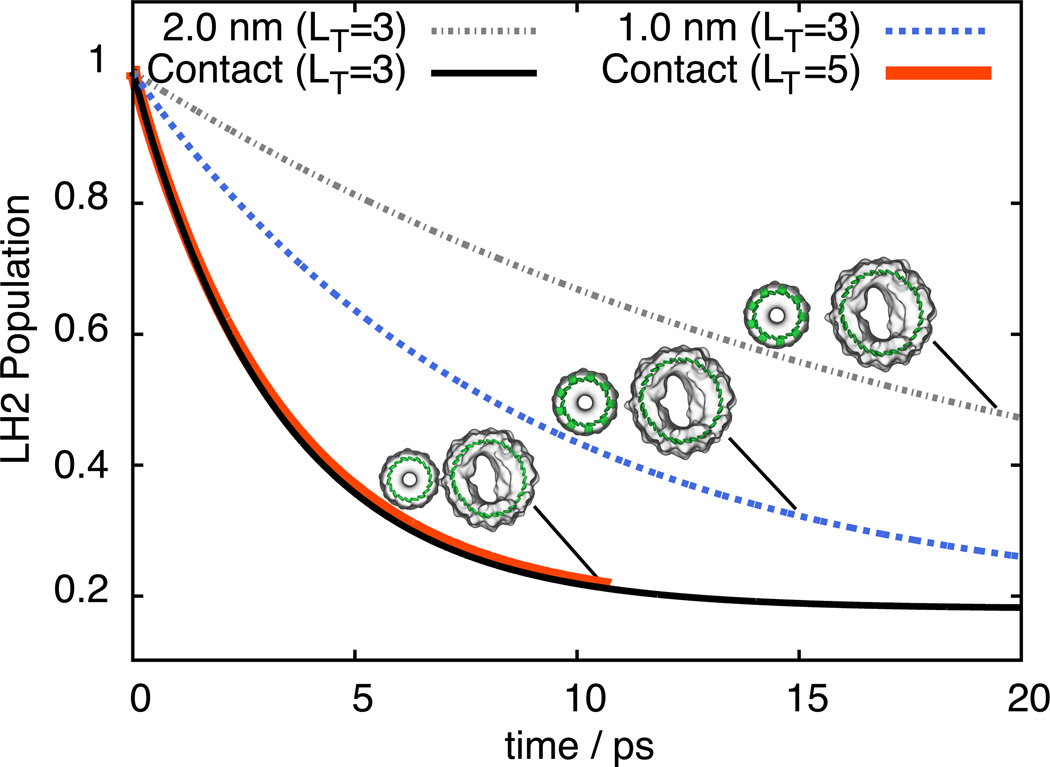
The parameters describing the B850 and B875 Hamiltonians are taken from Ref. 48, with bath parameters λn = λ = 180 cm⁻¹ and 1/γn = 1/γ = 100 fs, a choice that had been shown to reproduce experimental spectra.⁵⁴ The population of an initially excited LH2 complex is shown in Figure 8 for different truncations and inter-complex separation distances. The results show that TL truncation with a cut-off of L_T = 3 yields a population decay close to that of an L_T = 5 cut-off. The lower truncation requires 50 MB of memory to store the hierarchy of ADMs and 415 MB of memory for RKF45 integration; the higher truncation requires, however, 12 GB of memory to store the hierarchy of ADMs and 96 GB of memory for RKF45 integration.

Figure 8.

Total excited state population of LH2 reflecting inter-complex excitation transfer from LH2 to LH1 at different protein (LH2) - protein (LH1) edge-edge separations.

The excitation transfer time can be calculated by fitting a simple kinetic model

$$\frac{d{P}_{B850}}{dt}=-\frac{P_{B850}}{{\tau }_{B850\to B875}}+\frac{1-P_{B850}}{{\tau }_{B875\to B850}}$$ (15)

describing excitation transfer between B850 and B875 BChl rings (Figure 8). In our calculations we assumed three separations between the proteins LH1 and LH2 holding the B875 and B850 BChl rings, respectively, namely, edge-edge separations of 2 nm, 1 nm, and 0 nm (contact). In case of contact, transfer times (summarized in Table 2) are τ_B850→B875 = 5.3 ps and τ_B875→B850 = 9.2 ps; inter-protein separations of 1 nm and 2 nm result in 260% and 590% longer transfer times, respectively.

Table 2.

Excitation transfer times between the B850 pigments in LH2 and the B875 pigments in LH1.

Hierarchy Truncation	Inter-protein distance (nm)	τB850→B875 (ps)	τB875→B850 (ps)
LT = 5	0.0	4.1	18.4
LT = 3	0.0	4.0	18.1
LT = 3	1.0	10.4	46.7
LT = 3	2.0	23.6	105

5 Conclusion

The hierarchy equations of motion (HEOM) employ a highly coupled set of density matrices to calculate the noise-averaged time evolution of a quantum system coupled to a thermal environment. The large number of matrices required to model multi-pigment systems using the HEOM has restricted the method to systems with only very few pigments. By employing adaptive numerical integration methods (hierarchy filtering of Shi et al.⁶⁹ and adaptive timestep integration⁹⁴) and a novel hierarchy partitioning scheme, efficient scaling has been realized. The software implementation available in the program PHI can be run on parallel computers allowing the HEOM to be solved for pigment numbers as large as found in biological systems. The performance of PHI has been demonstrated here by investigating the accuracy of the adaptive integration methods and by applying PHI to model excitation transfer in a fifty pigment system, namely the 18-BChl B850 ring in light harvesting complex 2 (LH2) and 32-BChl B875 ring in light harvesting complex 1 (LH1) of purple photosynthetic bacteria. It was shown that excitation transfer between LH2 and LH1 practically occurs as a Poisson process, i.e., an incoherent hopping process, described by a single exponential decay of excited state population. The excitation transfer times for LH2→LH1 and LH1→LH2 were calculated for direct protein-protein contact, as well as for protein-protein separations of 1 nm and 2 nm. Resulting transfer rates compare well with observations²³ and generalized Förster theory results;⁷⁸ the latter agreement should be considered an a posteriori justification of generalized Förster theory.

The efficient parallel implementation of the HEOM makes it possible to model even larger light harvesting systems than studied here such as photosystem 1 and photosystem 2 in cyanobacteria and plants,^73,74 as well as conjugated polymers⁷⁶ and pigment dendrimers⁷⁷ used in artificial light harvesting. The current implementation of the HEOM would also benefit the calculation of exact quantum dynamics in Wigner space, recently shown to also be computationally challenging due to large memory requirements,⁹⁶ and is a promising future feature of PHI. Additionally, the general applicability of the HEOM lets PHI to be used for investigations of other open quantum systems such as charge transfer reactions,⁹⁰ e.g., in DNA⁹⁷ and in the photosynthetic reaction center,⁹⁸ or coherently coupled spin systems such as those employed in quantum computing.^99–101