Extended Fujita Approach to the Molecular Weight Distribution of Polysaccharides and other Polymeric Systems

Abstract

In 1962 H. Fujita (Mathematical Theory of Sedimentation Analysis, Academic Press, New York, pp. 182–192) examined the possibility of transforming a quasi-continuous distribution g(s) of sedimentation coefficient s into a distribution f(M) of molecular weight M for linear polymers using the relation f(M) = g(s).(ds/dM) and showed that this could be done if information about the relation between s and M is available from other sources. Fujita provided the transformation based on the scaling relation s = κM^0.5, where κ is taken as a constant for that particular polymer and the exponent 0.5 essentially corresponds to a randomly coiled polymer under ideal conditions. This method was successfully applied to mucus glycoproteins (S.E. Harding, Adv. Carbohyd. Chem. Biochem. 47 (1989), 345–381). We now describe an extension of the method to general conformation types via the scaling relation s = κM^b, where b = 0.4–0.5 for a coil, ~0.15–0.2 for a rod and ~0.67 for a sphere. We give examples of distributions f(M) vs M obtained for polysaccharides from SEDFIT derived least squares g(s) vs s profiles (P. Schuck, Biophys. J. 78 (2000) 1606–1619) and the analytical derivative for ds/dM performed with Microcal ORIGIN. We also describe a more direct route from a direct numerical solution of the integral equation describing the molecular weight distribution problem. Both routes give identical distributions although the latter offers the advantage of being incorporated completely within SEDFIT. The method currently assumes that solutions behave ideally: sedimentation velocity has the major advantage over sedimentation equilibrium in that concentrations less than 0.2 mg/ml can be employed, and for many systems non-ideality effects can be reasonably ignored. For large, non-globular polymer systems, diffusive contributions are also likely to be small.

1. Introduction

Nearly five decades ago Fujita [1] provided the means for converting distributions of sedimentation coefficient to distributions of molecular weight for polydisperse systems with a quasi-continuous distribution of molecular weight. Besides synthetic polymers, natural polymers exhibiting polydisperse distributions include polysaccharides, nucleic acids and many other types of glycoconjugate such as mucin glycoproteins. Knowledge of molecular weight distribution is important - for example in the case of polysaccharides their performance in food materials as gelling and thickening agents is closely related to their molecular weight distribution, and in biopharmaceuticals their performance as excipients and hydrogels, and indeed their safety as vaccines is closely related to their molecular weight distributions. The original Fujita method provided only for the analysis of polymers possessing a random coil conformation. We now describe the extension of the method to other conformations and take advantage of improved and rapid ways of defining distributions of sedimentation coefficient from analytical ultracentrifuge experiments.

1.1. Background: molecular weight determination for polydisperse systems

The last two decades have seen a number of significant advances in the methodology for evaluating molecular weight distributions of polydisperse macromolecular systems in solution. These advances have centred around the coupling of chromatographic or membrane based fractionation procedures with a multi-angle laser light scattering photometer. Ever since the first application of SEC-MALLs (size exclusion chromatography coupled to multi-angle light scattering [2]) to polysaccharides [3,4] and to mucus glycoproteins [5,6] it has become, when applicable, the method of choice for the determination of molecular weight distributions of polymer systems. Although SEC columns have an upper limit of separation, the dynamic range can be increased by using an alternative separation strategy of field flow fractionation (FFF) in FFF – MALLs where the columns are replaced by a separation membrane [7]. One other major difficulty however has been that of non-inertness of such columns or membranes [7a], and for cases where anomalous column or membrane interactions are suspected, procedures based on the analytical ultracentrifuge – which requires no separation media but relies on the inherent fractionation of a centrifugal field – can be used. Before we describe the extension of the Fujita approach based on sedimentation velocity we will briefly review some current approaches based on sedimentation equilibrium in the analytical ultracentrifuge. Sedimentation equilibrium offers the advantage that the optical records for solutions of polymer at sedimentation equilibrium are an absolute function of molecular weight without requiring assumptions or corrections to allow for ambiguities caused by conformation – but used by itself, suffers from poor resolution of components, and is based around the measurement of average molecular weights [8,9]. Nonetheless the ratios of the different averages can be used to describe a distribution.

1.2. M_w, M_z and M_z/M_w analysis from sedimentation equilibrium

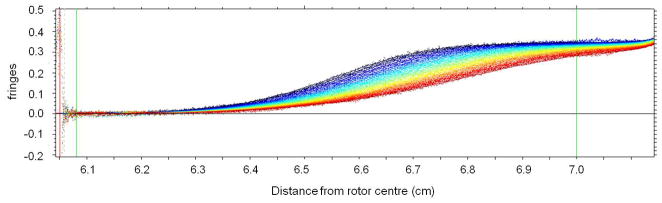
Figure 1 shows the optical record (registered using the Rayleigh Interfence system) of a polymer system – a bronchial mucin glycoprotein at sedimentation equilibrium in the analytical ultracentrifuge: each of the curved fringes represents a plot of concentration of polymer relative to the meniscus. Provided the meniscus concentration can be determined the actual concentration as a function of radial position r in the ultracentrifuge cell can be defined and various manipulations of the fundamental equation of sedimentation equilibrium can be used to obtain the weight average molecular weight M_w for the distribution. A popular method for the analysis of monodisperse and interacting paucidisperse systems is the SEDPHAT approach, which fits Boltzmann exponential corresponding to each species to multiple data sets from different rotor speeds and loading concentrations, and embeds various forms of mass conservation constraints, signal constraints, and mass action law [11]. The possibility to formulate a priori such a finite, discrete model of the distribution, leads to a well-conditioned global model which can be fitted to the available data and extrapolated to the cell base. Although this approach has also been extended to quasi-continuous distributions through the use of additional regularization constraints [11], the analysis of intrinsically continuous distributions with unknown shape and molecular weight range poses a more difficult problem. In particular, for polymer systems with a broad distribution of molecular weight – such as the mucin in Figure 1 - a major problem is in registering the concentration across the entire range from the air/solution meniscus to the cell base, particularly if the fringes are showing strong upward curvature near the base (even though there is still a finite slope at the meniscus) and/or the radial position of the base is poorly defined. For such systems an operational point average molecular weight known as M*(r) has proved useful which allows for a more robust evaluation of M_w,app for the distribution [12, 13, 14] using the identity M*(r→r_b) = M_w,app, the apparent weight average molecular weight for the whole distribution (from the meniscus r=r_a to the base r_b). Subsequent correction for thermodynamic non-ideality then yields M_w. Other procedures which miss or ignore the contribution from material near the cell base will always lead to an underestimate for M_w,app and hence M_w for polydisperse systems.

Figure 1.

Sedimentation equilibrium of a polydisperse polymer system: Rayleigh interference fringes for a bronchial mucus glycoprotein (BM-GRE, M_w ~ 6.0×10⁶ g/mol). A loading concentration of ~0.2 mg/ml in a Beckman Model E analytical ultracentrifuge (rotor speed 1967rpm) and a cell of 30mm optical path length was used. The direction of sedimentation is from left to right. Note the very steep rising fringes at the cell base and yet there is still a finite curvature at the air-solution meniscus [10].

The Schlieren optical system on the older generation analytical ultracentrifuges such as the Model E (Beckman Instruments, Palo Alto), MOM (Hungarian Optical Works, Budapest or Centriscan (MSE, Crawley, UK) permitted also the evaluation of the (apparent) z-average or M_z,app for the distribution. Although this system is not available on the XL-I analytical ultracentrifuge it is nonetheless still possible to estimate M_z,app from mathematical manipulations of the relations describing the distributions of solute recorded by Rayleigh Interference optics [15]. M_w,app and M_z,app differ from the actual molecular weights M_w or M_z because of the effects of thermodynamic non-ideality (see 16 & refs therein.). If the concentration, c is sufficiently low then M_w,app ~ M_w and M_z,app ~ M_z, otherwise measurement of M_w,app or M_z,app at several concentrations and extrapolation (of 1/M_w,app or 1/M_z,app) to c=0 is required.

A major drawback with regards measurement of M_w (or M_z) of polymer systems by sedimentation equilibrium has been the restriction to an optical path length limit of no more than 12mm in cells used in the XL-I analytical ultracentrifuge (compared with 30mm in the older Model E analytical ultracentrifuges). This has meant that a minimum concentration of ~ 0.5 mg/ml has been required (compared with the former 0.2 mg/ml) to ensure a sufficient Rayleigh fringe increment between r_a and r_b to facilitate a measurable M. This requirement has had serious resonances for polymeric systems. Whereas at 0.2 mg/ml M_w ~ M_w,app has been a reasonable approximation for many polysaccharides and mucins for example, the same approximation can lead to serious underestimates of M_w at 0.5 mg/ml [16]. However the availability now of longer ~20mm path length cells by Nanolytics Ltd. (Potsdam, Germany), has meant that measurements as low as 0.3 mg/ml are possible and for most systems that is acceptable – by “acceptable” we mean underestimates of no more than 10% (see Table 1). For other systems an extrapolation to c=0 is mandatory.

Table 1.

Comparative non-ideality of polysaccharides for a loading concentrations of 0.3 mg/ml (adapted from ref [10] and references therein)

	10−6×M	104×B	BM ml/g	a1+2BMc	a underestimate (%) of M
Pullulan P5	0.0053	10.3	5.5	1.003	0
Pullulan P50	0.047	5.5	25.9	1.015	2
Xanthan (fraction)	0.36	2.4	86	1.053	5
β-glucan	0.17	6.1	104	1.063	6
Dextran T500	0.42	3.4	143	1.086	9
Pullulan P800	0.76	2.3	175	1.105	10
Chitosan (Protan 203)	0.44	5.1	224	1.135	14
Pullulan P1200	1.24	2.2	273	1.164	16
Mucin glyco-protein CFPHIb	2.0	1.5	300	1.180	18
Pectin (citrus fraction)	0.045	50.0	450	1.270	27
Scleroglucan	5.7	0.50	570	1.342	34
Alginate	0.35	29.0	1015	1.609	61

^aBased on the lowest possible concentration in a 20mm centrepiece (~0.3 mg/ml)

^bfrom the bronchial secretion of a patient with Cystic Fibrosis

Once M_z and M_w have been defined and non-ideality has been adequately catered for then the ratio of the measured M_z and M_w can be used to define the polydispersity of a distribution. Furthermore these ratios can be related to the width or standard deviation of a distribution (whatever form this may take, e.g. log-normal, Schulz) – the weight average σ_w or number average σ_n using the Herdan relations [17, 15], and Table 2 gives three examples.

Table 2.

Estimates of M_w, M_z and σ_w from sedimentation equilibrium

Sample	Mw (kDa)	Mz (kDa)	Mz/Mw	σw (kDa)
a Alginate (Manucol DM)	136	115	1.18	50
Glycoconjugate ASA_Z	215	315	1.5	150
b Glycoconjugate ASA_Z	240	375	1.6	190

^afrom Ref [16];

^bfrom SEC-MALS for comparison

$$\frac{{\sigma }_w}{M_w}={\left[\left(\frac{M_z}{M_w}\right)-1\right]}^{1/2}\frac{{\sigma }_n}{M_n}={\left[\left(\frac{M_w}{M_n}\right)-1\right]}^{1/2}$$ (1)

A special case is a log-normal distribution defined (using the notation of Fujita [1]) by

$$f(M)=\frac{exp(-{\beta }^2/4)}{M_0{(\pi )}^{1/2}}exp\left\{-\frac{{[ln(M/M_0)]}^2}{{\beta }^2}\right\}$$ (2)

a relation which assumes Gaussian form when f(M) is plotted against ln (M/M_o), with M_o the maximum value of M occurring and β/√2 the standard deviation of the logarithmic plot, related to σ_w by

$$\beta /\surd 2={\{ln{({\sigma }_{\text{w}}/{\text{M}}_{\text{w}})}^2+1\}}^{1/2}.$$ (3)

For such log-normal distributions, succesive average molecular weights are given by

$${\text{M}}_{\text{n}}=exp{\{\beta /2\}}^2;{\text{M}}_{\text{w}}={\text{M}}_{\text{w}}/{\text{M}}_{\text{o}}exp(3/4){\beta }^2\text{and}{\text{M}}_{\text{z}}={\text{M}}_{\text{o}}exp(5/4){\beta }^2$$ (4)

and so

$${\text{M}}_{\text{w}}/{\text{M}}_{\text{n}}={\text{M}}_{\text{z}}/{\text{M}}_{\text{w}}=exp\{{\beta }^2/2\}$$ (5)

So it is possible to estimate also M_n for a log-normal distribution if M_z and M_w are known (n.b. this is not the case for a Schulz or most probable distribution [p296 of ref. 1]).

N.B. σ_w or σ_n should not be confused with the notation used by some authors for reduced molecular weight moments (differing from the convention established by Rinde in 1928 [18]).

1.3. Off-line calibration of size exclusion chromatography by sedimentation equilibrium

Perhaps the simplest procedure for defining a molecular weight distribution – although this loses the special feature of analytical ultracentrifugation as a method free of columns or membranes – is to use sedimentation equilibrium in conjunction with preparative size exclusion chromatography (SEC) [19, 20, 21]. Fractions of relatively narrow (elution volume) band width are isolated from the eluate and their M_w values evaluated by low speed sedimentation equilibrium in the usual way: the SEC columns can thereby be “self-calibrated” and elution volume values converted into corresponding molecular weights – a distribution can therefore be defined and in a way which avoids the problem of using inappropriate standards. This method was described in 1988 and applied to alginate [19], and subsequently dextrans and pectins [20, 21] – with the latter excellent agreement with a comparative off-line SEC-light scattering procedure was observed [21]. With the optical path length restrictions of the XL-I compared to the Model E as mentioned above this approach has fallen into disuse over the last two decades, although the ability to run 7×20mm path length cells simultaneously in a multi-hole rotor now renders this method as an attractive alternative to procedures using SEC-MALS.

However a much more convenient alternative is now possible based on sedimentation velocity (Figure 2) rather than sedimentation equilibrium, and takes into account the huge advances in software over the last decade in the way that sedimentation coefficient distributions can be described: and at much lower concentrations than required for sedimentation equilibrium.

Figure 2.

Sedimentation velocity of a polydisperse polymer system: A subset of radial displacement profiles displayed in SEDFIT obtained from Rayleigh interference fringes (scanned every 2 min) for a low methoxy pectin (M_w ~ 380,000 g/mol). A loading concentration of 0.15 mg/ml in a Beckman XL-I analytical ultracentrifuge (rotor speed 45000 rpm) and a cell of 12mm optical path length was used. The direction of sedimentation is from left to right.

2. Fujita method: f(M) vs M distribution from sedimentation velocity data for polymers with a random coil conformation

In 1962 Fujita [pp182–192 of ref 1] had examined the possibility of transforming a (differential) distribution g(s) of sedimentation coefficient s into a (differential) distribution f(M) of molecular weight M for linear polymers and concluded that the sedimentation velocity determination of g(s) allows the evaluation of the molecular weight distribution f(M) versus M of a given material if information about the relation between s and M is available from other sources. g(s) is defined as the population (weight fraction) of species with a sedimentation coefficient between s and s+ds and f(M) is defined as the population (weight fraction) of species with a molecular weight between M and dM. Historically, g(s) profiles could be defined using procedures based on conversion of concentration gradient (Schlieren) optical records by Rinde [18] and later Bridgman [22]. Essentially the transformation from g(s) versus s is simple and is as follows [1]:

$$\text{g}(\text{s})\text{ds}=\text{f}(\text{M})\text{dM}$$ (6)

and so

$$\text{f}(\text{M})=\text{g}(\text{s})·(\text{ds}/\text{dM})$$ (7)

In Fujita [1] the sedimentation coefficient s was given for the case of random coils

$$\text{s}={\kappa }_{\text{s}}{\text{M}}^{0.5}$$ (8)

where the pre-exponential factor κ_s is taken as a constant for that particular polymer under a defined set of conditions and the exponent 0.5 corresponds to a randomly coiled polymer under theta solvent or “pseudo-ideal” conditions (i.e. conditions where exclusion volume effects are matched by associative effects – see e.g. ref [22a]). The differential is then

$$\text{ds}/\text{dM}={{\kappa }_{\text{s}}}^2/2\text{s}$$ (9)

Fujita [1] provided distributions for polystyrene samples in cyclohexane based on sedimentation data of McCormick et al [23], and these are reproduced in Figure 3.

Figure 3.

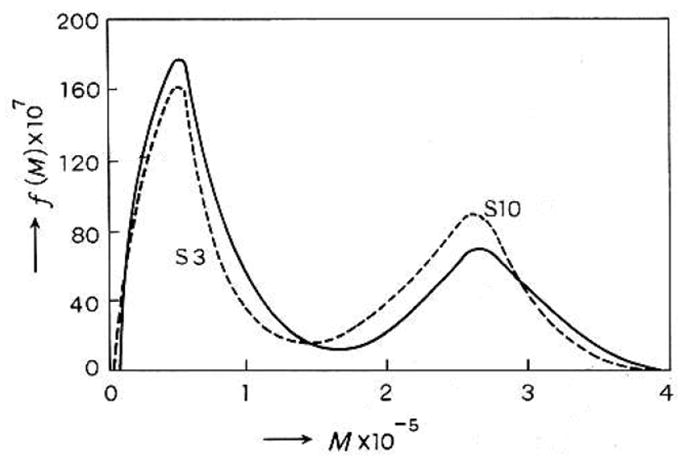
Fujita’s plot [1] of sedimentation coefficient distribution for a 50:50 mixture of two polystyrene samples S3 and S10 in cyclohexane obtained using Eqs. (7–12). The dashed line represents the predicted distribution for the mixture based on the individually obtained distributions for S3 and S10. [Permission being sort from Elsevier].

The method was later applied to biological materials – mucin glycoproteins – by Harding [24] based on data of Pain [25]. Using a sedimentation coefficient distribution for pig gastric mucin [29] and the assumption of a random coil conformation under ideal conditions (b=0.5), and a known pair of values for s and M, namely an s value of 33 × 10⁻¹³s is approximately equivalent to a molecular weight of 2.5 million it was possible to perform the transformation to obtain the equivalent molecular weight distribution. The form of the distribution was shown also to be similar to that of the distribution of contour lengths estimated from electron microscopy studies on this polymer [26, 27]. In a later publication Bernhard and Oppermann [28] used data from the XL-A ultracentrifuge to estimate a molecular weight distribution for 4-chlorophenyl cellulose-tricarbinate with the calibration made using molecular weights obtained using the MSTAR procedure [12–14]. Although those researchers did not transform the y-axis via Eqs. (7) and (9) reasonable agreement with calibrated SEC (cf Section 1.3 above) was still obtained.

These methods have been based on the assumption that diffusion broadening to the width of the apparent g(s) vs s distributions have been negligible.

3. Extended Fujita method: f(M) vs M distribution from sedimentation velocity data for general conformation types

A straightforward extension of the Fujita method is possible based on use of the general scaling relation (see, for example ref 29)

$$s={\kappa }_{\text{s}}{\text{M}}^{\text{b}}$$ (10)

where b = 0.4–0.5 for a coil, ~0.15–0.2 for a rod and ~0.67 for a sphere [18,27], and hence

$$\text{ds}/\text{dM}=\text{b}·{{\kappa }_{\text{s}}}^{1/\text{b}}·{\text{s}}^{(\text{b}-1)/\text{b}}$$ (11)

For b=0.5 Eq. (11) reduces to Fujita’s formula (Eq.9).

To do the transformation the conformation type or b needs to be known under the particular solvent conditions and at least one pair of s-M values is needed to define the κ_s from Eq. 10. Furthermore the method applies to the infinite dilution or non-ideality free sedimentation coefficient distribution, so is only valid for values of s (or a distribution of s values) extrapolated to zero concentration or s values measured at low enough concentrations where non-ideality effects are small. This is indeed possible since sedimentation coefficients can be measured at much lower concentrations than those needed for a sedimentation equilibrium experiment. With 12mm path length cells it is possible to get reliable measurements at 0.1 mg/ml and below – the new 20mm path length cells allow us now to go to even lower concentrations: at such concentrations non-ideality may not be an issue. In the unlikely event that non-ideality effects are still suspected then the determination should be repeated at different loading concentrations.

4. Modern implementation

One approach is to first of all generate a differential sedimentation coefficient distribution g(s) versus s. The current generation of XL-I analytical ultracentrifuges do not have the concentration gradient or “Schlieren” optical system so the methodology as outlined by Rinde [18] and Bridgeman [22] is not directly applicable. The last decade however has seen the development of accurate and reliable numerical solutions of the fundamental equation describing the concentration (as registered by Rayleigh interference or uv-absorption optics) versus radial displacement and time and have been implemented in the SEDFIT software [30–35]. For single solute and paucidisperse systems the c(s)/c(M) family of models in SEDFIT also provides a reliable means for correcting for the contribution of diffusion broadening to the apparent width of a peak by taking into account the relationship between the sedimentation coefficient and diffusion coefficient. Initially, this was introduced for compact macromolecules such as folded proteins, for which b ~ 0.67 can be fixed and the pre-exponential factor κ_s in Eq. (10) is related to the translational frictional ratio (a measure of the asymmetry of the particle): for these systems a weighted average frictional ratio can be floated in the data analysis (or specified if this is known from other measurements) and accurate“diffusion” corrected sedimentation coefficient distributions or c(s) versus s profiles can be described, which may be transformed to approximate molecular weight distributions using the best-fit κ_s and b.

For polydisperse systems representation of the distribution of frictional ratios by a single parameter as represented in the standard c(s) vs s procedure is not so applicable. The extension of this approach to general two-dimensional size-and-shape distributions is possible, but often not sufficiently defined by the experimental data [33]. However, a g(s) (i.e. uncorrected for diffusion) versus s profile can still be reliably defined (implemented as a model termed ls-g*(s) in SEDFIT, to indicate its origin in least-squares fitting of the sedimentation boundaries). Furthermore for large polymeric systems diffusion effects are likely to be small and so g(s) profiles will give a good representation of the distribution.

Once the sedimentation coefficient distribution has been defined the transformation can be implemented by exporting the sedimentation coefficient distribution data to, for example Microcal ORIGIN and applying the transformation and differentiation for f(M) vs M analytically (Eqs. 10 & 11). Values for b and κ_s have to be supplied by the researcher: this can be done by specifying the b and κ_s value directly. For many polymers and biopolymers these values are available for specified solvent conditions in the Polymer Handbook [33a] and do not have to be determined. If the conformation type is not known then the limits of plausible values of b should be attempted which would give a measure of the uncertainty of the distribution. κ_s can be specified provided at least one pair of s-M values is known: we suggest for example a combination from the weighted average sedimentation coefficient from the distribution combined with a sedimentation equilibrium or SEC-MALLs evaluation of M. If b (or κ_s) are not known a priori, these should be pre-determined using set of samples of known molecular weight and linear regression applied to a plot of

$$logs=log{\kappa }_s+\mathit{b}logM$$ (12)

An alternative and more convenient approach is to build the transformation within the SEDFIT algorithm itself: in the latter case the differentiation is done numerically without any loss in accuracy.

5. Direct SEDFIT implementation

The first step is identification of the parameters in the scaling law linking sedimentation coefficient, s, and molecular weight, M above (Eqs 10 & 12). SEDFIT can read an ASCII file containing rows of (s, M) pairs, tab or space-delimited, and estimate b_S by linear regression from the slope of a plot of log s = log κ_s + b logM.

The distribution f(M) vs M can then be defined by solving the integral equation

$$a(r,t)=\int f(M){\chi }_1(s(M),D(M),r,t)dM+b(r)+\beta (t)$$ (13)

where a(r,t) denotes the experimental data as a function of radius r and time t, f(M) the unknown molecular weight distribution, χ₁ (s(M), D(M), r, t) the Lamm equation solution at unit loading concentration of a species with sedimentation coefficient s and diffusion coefficient D, and b(r) and β(t) are systematic baseline noise contributions [31]: b(r) is not to be confused with the power law exponent b in Eqs. s (10–12). To solve this equation numerically, the range of possible molecular weight values is discretized into typically 100–200 values, for each M-value the corresponding s-value and D-value is determined via Eq. (13) and the Svedberg equation [36]

$$M(1-\overline{v}\rho )=\frac{\mathit{sRT}}{D}$$ (14)

(with v̄ the partial specific volume, ρ the solvent density, R the gas constant and T the absolute temperature), and finite element solutions of the ideal Lamm equation are calculated with the adaptive grid algorithm [32]. This leads to an algebraic problem that can be solved with standard tools [33]. For simplicity, since diffusion coefficients are expected to be very small for large polymers, and the experimental times are comparatively short due to their high sedimentation coefficient, Lamm equation solutions may be calculated with D = 0, leading essentially to a variant of the ls-g*(s) method [34].

It should be noted that Eq. (13) is expressed directly as a differential molecular weight distribution and normalized as such, which eliminates renormalization with differentials ds/dM otherwise required when the problem is expressed as a differential sedimentation coefficient distribution. Since Eq. (13) is a mathematically ill-posed problem, regularization however is an important requirement for its solution [33]. Since the application of this extended Fujita approach is envisioned for polymers with essentially continuous molecular weight distribution (as opposed, for example, to the discrete molecular weights of most proteins), and therefore Tikhonov-Phillips regularization [35] is to be preferred over maximum entropy algorithms which perform better for discrete distributions. In order to generate sufficient information in the experimental data, it is necessary to include into the analysis representative scans spanning the entire sedimentation process from the initial depletion near the meniscus at early times until the trailing edge of the sedimentation boundary has merged into the region of optical artifacts in the bottom region at later times. In contrast to methods like dc/dt, no subset selection is necessary, and no limit for the steepness of the boundaries applies (other than those from artifact-free detection).

6. Examples

We now briefly illustrate application of the “extended Fujita” approach to a range of polydisperse biopolymer systems. We have chosen two neutral polysaccharides (glucomannan and pullulan), three polyanionic polysaccharides of wide ranging molecular weight (pectin, alginate and xanthan), one polycationic polysaccharide (chitosan), a glycopolypeptide (from a mucin), and finally a large glycoconjugate vaccine, the latter molecule with a molecular weight distribution well beyond the range possible with SEC-MALLs.

6.1. Konjac glucomannan (KGM)

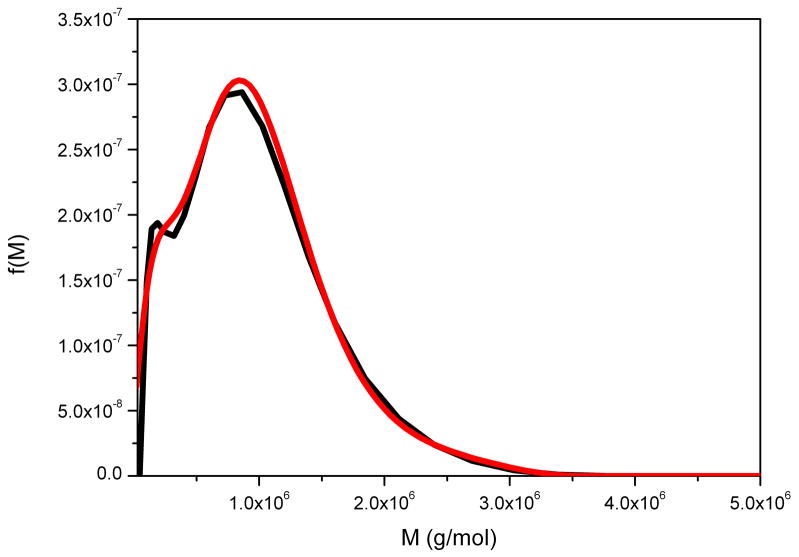
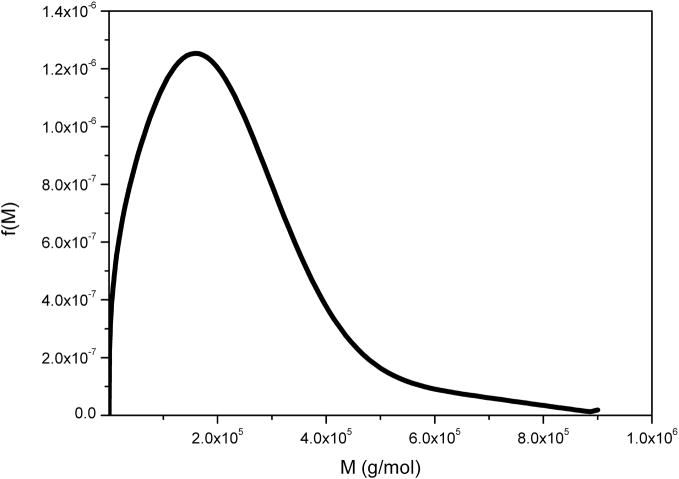
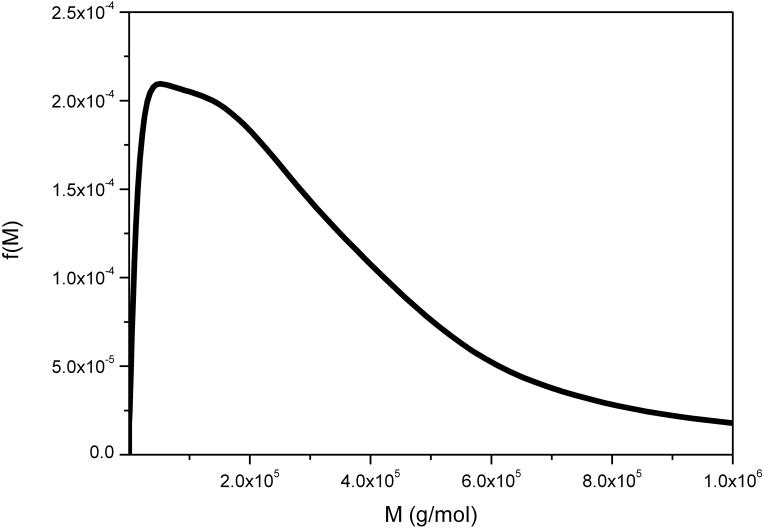
This is a neutral heteropolysaccharide extracted from the tubers of Amorphophallas konjac and is an important dietary fibre and food thickening ingredient, whose function is closely related to its molecular weight distribution – difficult to measure using SEC-MALLs because of anomalous reactions with column material [37]. Figure 4 compares the distributions obtained from g(s) vs s and the derivative of Eq. (11) performed analytically to give f(M) vs M, with the distribution determined directly using SEDFIT. The two distributions are ~ identical. The small difference in the resolution of a subpopulation at ~ 15 kg/mol can be attributed to differences in the regularization level of fitting the sedimentation data. That the partial peak disappears in the current f(M) analysis indicates that this features is not essential in order to explain the experimental data within the noise of data acquisition.

Figure 4.

Molecular weight distribution, f(M) vs M, for konjac glucomannan obtained from the ls-g(s) versus distribution and analytical derivative (black line) and direct or full numerical (red line) procedures. Loading concentration c_o ~ 0.25 mg/ml. κ_s = 0.044 and b = 0.32. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 840000 g/mol.

6.2. Pullulan

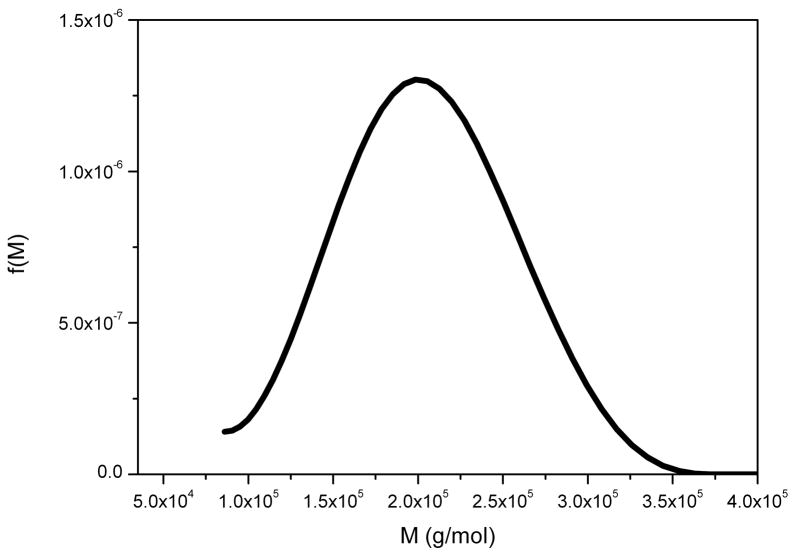
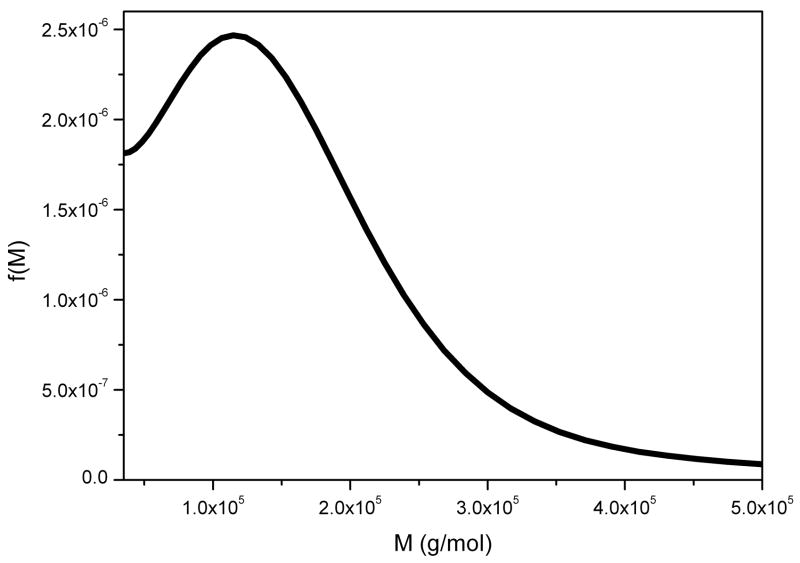
This is an α(1–6)-linked microbial glucan – another neutral polysaccharide - and is used commercially in the formulation of pharmaceutical capsules and is commonly used as a “standard” polysaccharide for calibrating columns etc. as it can be obtained in narrow molecular weight fractions and behaves like a random coil in solution [38]. Figure 5 shows the f(M) vs M distribution obtained for P200 pullulan (a standard pullulan where the “200” stands for the weight average molar mass in kg/mol).

Figure 5.

Molecular weight distribution f(M) vs M for pullulan P200. Loading concentration c_o ~ 0.1 mg/ml. κ_s = 0.025 and b = 0.46. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 197000 g/mol.

6.3. Pectin

Pectin is a family of complex polyuronide-based and highly polyanionic structural polysaccharides and its molecular size and the conformation and flexibility of a pectin molecule is important to the functional properties in the plant cell wall and also significantly affects their commercial use in the food and biomedical industries [39]. Pectins vary in their degree of methyl esterification (DE) > 50 % are classified as high methoxyl (HM) pectins (Fig. 6a) and consequently low methoxyl (LM) pectins (Fig. 6b) have a DE < 50 %, although the two classes appear to have similar conformational characteristics [40]).

Figure 6.

Molecular weight distributions f(M) versus M for (a) high methoxyl pectin and (b) low methoxy pectin. Samples were centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M sodium chloride. For both cases, κ_s = 0.017 and b = 0.39.

(a) Loading concentration c_o ~ 0.20 mg/ml. M_w = 150 000 (g/mol)

(b) Loading concentration c_o ~ 0.15 mg/ml. M_w = 230 000 g/mol.

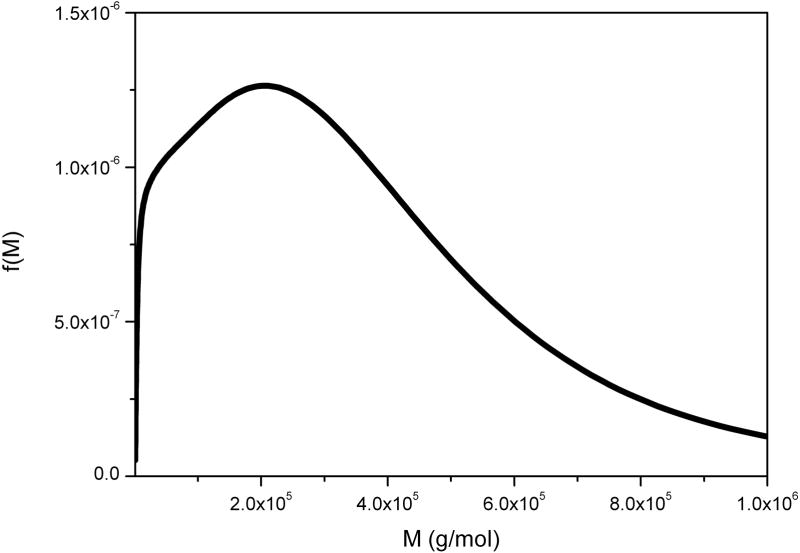
6.4. Alginate

Alginates are another family of polyanionic polyuronide polysaccharides from brown seaweeds and bacteria like Pseudomonas aeroginosa containing β(1–4)-linked D-mannuronic acid (M) and α(1–4)-linked L-guluronic acid (G) residues. Their conformational flexibility depends critically on the M:G ratio and the distribution of the residues. They are used widely in the food, pharmaceutical and printing industries, where many of their applications are dependent on not only their flexibility but on their molecular weight distributions. The alginates secreted by P. aeroginosa in the bronchial tract also contribute to the problems encountered in Cystic Fibrosis. Figure 7 shows the molecular weight distribution for an alginate extracted from the brown seaweed Laminaria digitata.

Figure 7.

Molecular weight distribution f(M) vs M for a commercial alginate. Loading concentration c_o ~ 0.2 mg/ml. κ_s = 0.052 and b = 0.33. Sample was centrifuged at 45 000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 140 000 g/mol. NB. The limit for reliable sedimentation coefficient values is >0.5S.

6.5. Xanthan

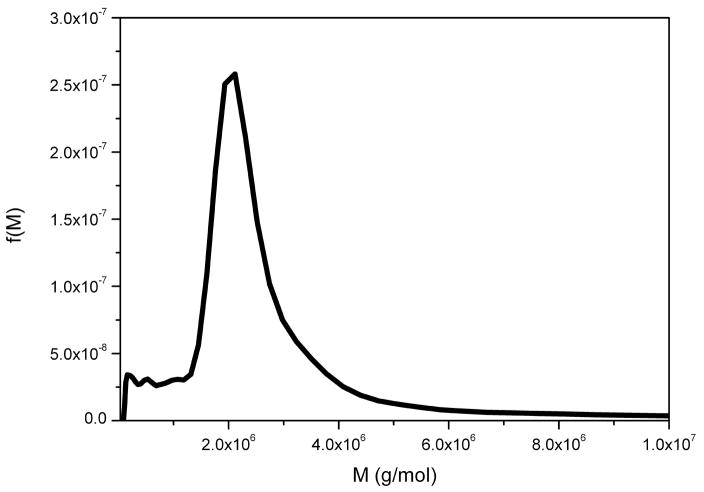
Xanthan is the large molecular weight extracellular and polyanionic polysaccharide from Xanthomonas campestris [40] It has a β(1–4)-D-glucopyranose backbone with side chains of (3-1)-α-linked D-mannopyranose-(2-1)-β-D-glucuronic acid-(4-1)-β-D-mannopyranose on alternating residues. Xanthan is widely used in the food industry as a thickener and stabiliser and is also widely used in the oil industry. Figure 8 shows the molecular weight distribution of an xanthan preparation obtained using the extended Fujita approach.

Figure 8.

Molecular weight distribution f(M) vs M for xanthan. Loading concentration c_o ~ 0.2 mg/ml in 0.1 M pH 6.8 phosphate buffer. κ_s = 0.197 and b = 0.26. Rotor speed = 45000 rpm at a temperature of 20.0 °C. M_w = 2.6 × 10⁶ g/mol.

6.6. Chitosan

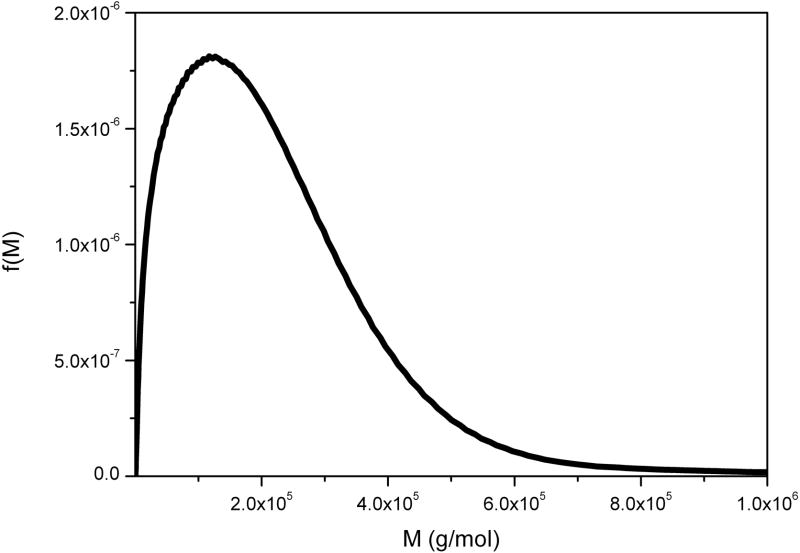
Chitosan is the generic name for a family of strongly polycationic (when solubilised) derivatives of poly-N-acetyl-D-glucosamine (chitin) extracted from the shells of crustaceans or from the mycelia of fungi and due to being in a unique position as the only “natural” polycationic polymer chitosan and its derivatives have received a great deal of attention from, for example, the food, cosmetic and pharmaceutical industries [41]. Because of its cationic nature, characterisation of its molecular weight has proven difficult with SEC-MALLs because of anomalous binding to column materials. Its characterisation by our method is by contrast relatively straightforward (Figure 9).

Figure 9.

Molecular weight distribution f(M) vs M for chitosan of degree of acetylation ~20%. Loading concentration c_o ~ 0.25 mg/ml in 0.2 M pH 4.3 acetate buffer. κ_s = 0.10 and b = 0.24. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C. M_w = 210 000 g/mol. NB. The distributions shown extend to higher molar masses.

6.7. Glycopolypeptide from a mucin

Mucins are the major macromolecular component of mucus – natures natural lubricant - and have molecular weights from ~ 400,000–20×10⁶ g/mol [24]. They have a polypeptide backbone with branches of sugar chains (ranging from 3–30 residues) O-linked via serine or threonine residues along the chain. Figure 10 shows the molecular weight distribution for a glycopolypeptide preparation from human gastric mucin.

Figure 10.

Molecular weight distribution, f(M) vs M for a mucin glycopeptides HMG Hug from human gastric mucin. Loading concentration c_o ~ 0.3 mg/ml in 0.1 M pH 6.8 phosphate buffer. κ_s = 0.008 and b = 0.50. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C. NB The distributions shown extend to higher molar masses.

6.8. Glycoconjugate vaccine

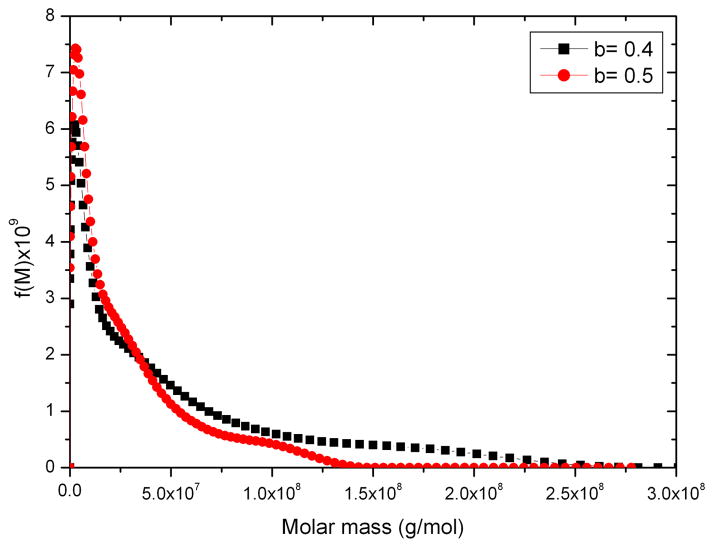
Finally Figure 11 shows the molecular weight distribution for a very large glycoconjugate vaccine, too large to analyse by SEC-MALLs [16]. In this case there was some uncertainty in the value of the power law coefficient so two values were chosen to indicate the possible spread range for the distribution: as can be seen the differences do not lead to greatly different distributions.

Figure 11.

Molecular weight distribution for a large glycoconjugate construct of a protein and bacterial polysaccharide. Loading concentration c_o ~ 0.3 mg/ml in 0.1 M pH 6.8 phosphate buffer.. The distributions for two different selections of the power law coefficient b are shown. The sample was centrifuged at 7000 rpm at a temperature of 20.0°C.

7. Conclusions and Perspectives

The SEDFIT software now with the extended Fujita algorithm is now freely available for download from sedfitsedphat.nibib.nih.gov/software. This complements the molecular weight distributions c(M) that have been widely applied for the study of paucidisperse systems, in particular, interacting and non-interacting proteins [42, 43]. The method currently assumes ideal conditions but the low concentrations – 0.2 mg/ml and below that are required renders this complication negligible for most systems. Indeed, the provision of the new 20mm optical path lengths – an extension of ~70% on what was previously possible with the XL-I ultracentrifuge means that the lowest concentration can be proportionally lower. This is fortunate as extrapolation of a distribution to zero concentration to eliminate non-ideality effects would be an extremely difficult but nonetheless useful challenge for future research. The method currently also assumes that translational diffusion effects are also negligible. Again – and fortunately – the types of macromolecule the method is primarily intended for – large, polydisperse and linear/asymmetric molecules with high degrees of solvation – are very slow diffusing and hence the contributions to the width of the f(M) vs M distributions will be accordingly small. For example the translational diffusion coefficient for xanthan is some 20× less than that for lysozyme.

The method does need calibrating for the particular conformational system. The conformation coefficient b and pre-exponential factor κ_s need to be previously known. κ_s can be defined by a known s-M pair, from sedimentation velocity and sedimentation equilibrium experiments or SEC-MALLs respectively. If sedimentation equilibrium is used to obtain M, using for example MSTAR, advantage can again be taken of the large 20mm optical path length cells. If b is also not known then 3 or 4 pairs of s-M values are needed and the parameters determined using Eq. (12) is required. The software provides for a weight-average conformation coefficient b to be extracted by linear regression from the experimental data, in analogy to the weighted-average frictional ratio for folded proteins, but this is applicable only for relatively small polymers that show significant diffusion during the sedimentation experiment. Calibration with a scaling law is essential since the description of the sedimentation data with a two-dimensional size-and-shape distribution [44] will lead to ill-defined results, especially in the absence of significant diffusion from large macromolecules (this is similar to studies of large nanoparticles) [33].

Experimentally, care has to be expressed in filling the cells – menisci in solvent and solution channels need to be carefully matched, otherwise necessitating extended models accounting for co-solvent re-distribution [45]. The scans to be included in the analysis should comprise representatively the entire sedimentation process, from the beginning of depletion near the meniscus from the sedimentation of the fastest species at early times up to the virtual complete sedimentation of the smallest species from the radial observation window. This ensures that a very wide range of sedimentation coefficients can be accurately described in a single experiment, typically spanning a 100 fold to 1000 fold range. This also improves accuracy and resolution by allowing optimal discrimination of the sedimenting signal from the systematic baseline signal profiles [31] and thereby lowers the detection limit, in principle, to signals less than 0.1 fringes. Solvent densities and partial specific volumes are required as with any ultracentrifuge experiment, and particular attention is required for copolymer systems.

The method should be seen very much as complementary or companion approach to SEC-MALLs, providing an alternative and rapid means for molecular weight determination particularly for cases where SEC-MALLs fails. Certainly in cases where column or membrane interactions are suspected and also where very large macromolecular systems are being analysed – such as the glycoconjugate vaccine materials – the sedimentation velocity method should become the method of choice.