Virtual Mastoidectomy Performance Evaluation through Multi-Volume Analysis

Abstract

Purpose

Development of a visualization system that provides surgical instructors with a method to compare the results of many virtual surgeries (n > 100).

Methods

A masked distance field models the overlap between expert and resident results. Multiple volume displays are used side-by-side with a 2D point display.

Results

Performance characteristics were examined by comparing the results of specific residents with those of experts and the entire class.

Conclusions

The software provides a promising approach for comparing performance between large groups of residents learning mastoidectomy techniques.

1 Introduction

The creation of more realistic and effective surgical simulation is an ongoing and active area of research. A often overlooked component of a successful simulation suite is the analysis of the output of those surgical simulations. This type of technology is especially needed during the use of a simulation by many residents during a training course where many volumes can be recorded. Tools are needed to examine the performance over time of individual residents as well as the performance of the class in general. Our application is the analysis of datasets acquired from a mastoidectomy simulator involving virtually drilling on a volumetric bone. In the surgery, bone is carefully removed from the temporal bone region of the skull using a drill in order to access the middle and inner ear. The anatomy data used in the simulator is acquired using CT scans obtained from cadavers. Using a haptic 3D joystick as a virtual surgical drill, users remove portions of the bone on the computer to expose underlying structures, as in actual surgery. This simulation system trains residents on the psychomotor and cognitive skills necessary to perform in the operating room.

The traditional curriculum for mastoidectomy surgery consists of expert surgeons commenting on the performance of a resident performing the procedure on a cadaver or artificial bone. With the use of a computer simulation, data on performance from an entire group of residents can be evaluated and compared. The computer simulation removes variability inherent in different temporal bones used by different trainees as well as potentially eliminating the subjective biases of the expert observer by allowing for objective, algorithmic assessment. The application detailed in this article provides a way to compare the output of one of these standardized virtually drilled bones to others and presents a unified view of these resident examinations. It also allows for the automated graphical analysis of multiple volume data files facilitating the comparison of performance of surgical skill as well as the uniform analysis and application of descriptive metrics previously defined [18] for objective comparison across trainees and compared to expert performance. We hypothesize that with further development and testing, such applications can provide both formative and summative assessment of skill with a reduced burden on expert surgeons, allowing them to devote more time to other matters.

This application utilizes the output of these simulations (virtual bones that have been partially drilled away on the computer) and organizes them for comparative analysis and qualitative visualization. Through a multi-institutional study, 80 residents were asked to perform a virtual mastoidectomy on a temporal bone before and after a training class. Some of the residents declined to provide data after the class, so we have 80 pre-test mastoidectomy performances and 50 post-test performances: 130 volumes total.

To create a system that allows meaningful exploration of a multi-volume dataset, we create distance field representations of volumes created by experts performing the simulation. Our task presents some aspects that are different from many other multi-volume dataset studies. For instance, we are not concerned with registration issues, since all the volumes are modified from the same original volume in the simulation. Also, we are not concerned with segmentation or the creation of an atlas. Our focus is on the problem of finding distance measures between volumes that reflect the differences between expert and resident performances from the virtual surgery. The distance field representation captures shape information of the expert simulation example that is used to construct a distance measure between the expert and resident data.

After performing a masking operation on the distance fields based on a resident volume, we compute histogram distances to extract features that represent the amount of overlap between the two volumes. We use these and other features to construct a feature vector. Dimensionality reduction techniques are used to display a 2D plot of the vectors from the whole dataset. We link the 2D plot of volumes to individual volume rendering windows so that the data space of the multi-volume dataset can be explored interactively. The contribution of this article is both the novel shape comparison based on masked distance fields and the interactive application that utilizes this and other volume comparison techniques to visualize a multi-volume dataset.

2 Previous Work

Multifield visualization is a topic of high interest, but most work considers only a small number of fields. Woodring and Shen [19] show a method to compare volumes using set operators and a tree to composite multiple volumes into one display. This works well for four or even eight volumes, but applying it to a global view of our dataset is infeasible. We do build on their approach for our individual volume displays. However, the problem of visualizing a large dataset of multiple, related volumetric images has not been widely studied. Joshi et al. [9] used distance features to place brain imaging data into a three-dimensional space for exploration, with a corresponding distance grid to aid in an overview of the space. However, displaying the separate brain volumes in a shared three-dimensional space creates occlusion problems and does not allow for the easy visual comparison of multiple volumes. In addition, they were forced to display only isosurfaces of the brains because of the difficulties of rendering 500 volumes simultaneously. Parallel coordinates have been used for an overview component of a visualization for a 4D anatomical motion database, as described by Keefe et al. [10]

We use a method inspired by Bruckner and Möller [1] to generate features for our volumes. In that work, the authors generate a distance field for each isosurface value. They compute a histogram of that distance field and, using that, find a mutual-information histogram distance measure between each pair of isosurface values. Our use of distance fields is inspired by their work, but we use different processing methods on those fields. We generate a distance field for each expert volume and expert-derived volume and use a masking approach to compare histograms. They use a similarity map to display one value per pair of isosurface values while we generate a high-dimensional feature vector using a variety of distance measures. They use a mutual information-based histogram distance measure while we employ an earth-movers distance. We share with them the requirement of having a pre-processing step, where generating distance fields of volumetric data and computing either mutual information or earth-movers distance is performed. We compare our distance measure to theirs.

Our shape analysis of the volumes used in our application is based on a binary mask: a voxel is either occupied or not. The task of extracting a binary mask from volumetric datasets has been widely studied and many methods, from isovalue choice to much more complex manual, automatic, and semi-automatic approaches, have been used. [6, 20] Mahfouz et al. [13] looked at geometrical measures to create feature vectors on medical volumes. That work used a dataset of 228 computed tomography (CT) volumes of human knees, and they were able to classify the sex of the individual by a 45 length feature vector generated by the voxels of the patellae. They considered individual measures, such as moments, rather than measures based on the difference between voxels in individual volumes.

3 Methods

3.1 Definitions

Our goal is to create a visualization system to evaluate student performance on a volumetric surgical simulator. During the simulation, material is removed from the original virtual bone. This procedure defines a region that is a subset of the original bone. Instructors who wish to examine the performance of a particular resident will want to compare the region drilled by the resident to regions drilled in other situations: by experts, by other students, or even by the same student at a different time. This paper describes a system by which instructors can review a large number of these surgical simulation performances and evaluate the quality of the drilling results. The system consists of two main parts:

1. Extraction of features that quantify the overlap of space between the resident drilled regions and the expert drilled regions. Intuitively, higher overlap of these regions is an indicator of good surgical technique by the resident, while a low overlap indicates poor technique. We employ an approach based on the distance field of the expert drilled regions to quantify this overlap, as explained below.

2. Interactive visualization that displays the position of expert and resident volumes in the feature-space defined by the features of each volume, but also allows direct viewing of the comparison between expected and actual performance of the resident bone via volume rendering.

We convert each volume in our dataset into a cavity representation before any other processing is performed. We are using the set of voxels that were removed by drilling as our definition of the final product from each resident. In other words, the set of voxels that are inside the cavity drilled away by the user are used as the volume in this analysis. The empty space is treated as positive space during analysis. A student who does not drill at all during the simulation will produce an empty cavity volume as the result. This is a key point to remember in the following sections. All of the data volumes are considered binary volumes for processing, although we use numerical values of the original opacity of the bone in our rendering.

Our dataset consists of two disjoint subsets. The smaller subset contains volumes that are from surgical performances by known experts; we call this the reference set. The remaining volumes in the set have been obtained from surgical residents who have unknown competency in the procedure. We call this set the test set. We use 130 test volumes and four reference volumes to demonstrate the utility of our system.

3.2 Composite reference volumes

To account for the variation in performance in experts, we compare the entire set of reference volumes with our test volumes. We create two composite volumes to describe this set: ALL and ANY. A voxel in volume ALL is occupied if and only if the correpsonding voxel is occupied in all reference volumes. Similarly, a voxel in volume ANY is occupied if and only if any correpsonding voxels in the reference volumes are occupied. So, where R is the set of reference volumes:

$$\text{ALL}=\underset{V\in R}{\cap }V,\text{ANY}=\underset{V\in R}{\cup }V.$$ (1)

The ANY and ALL volumes will be referred to as composite reference volumes, since they are formed by an operation on all the volumes in the reference set. These composite volumes designate the maximal and minimal boundaries of the reference set. In our application, the portion of the bone that is removed is the portion that is considered for scoring the performance of each user. Therefore, the ALL volume represents where it is mandatory for a user to remove bone from the skull, since all of the experts removed bone in those areas. Similarly, the ANY volume represents regions where a user is allowed to remove bone from the skull, since at least one expert removed bone in those areas.

3.3 Feature vectors

As stated in Sec. 3.1, one of our goals is the definition of a feature that gives a similarity measure between two volumes. There are, of course, a wide variety of features that have been used in the literature for various types of volume visualization and analysis. We are using a distance field-based histogram similarity feature rather than texture- [2] or size-based [3] measures for two reasons: (1) all of the volumes in our dataset are pre-registered, since they were constructed by modifying the same base volume and (2) a large proportion of each volume are unchanged from user to user. We use a distance field to represent shape of our objects. This technique is a common step for non-linear registration techniques [7,14] as well as shape skeletonization algorithms [5,12].

The distance field representation of the volume is a scalar field where each point has a value equal to the shortest distance to the boundary of the volume. We use a signed Euclidean distance field. Let d be the Euclidean distance to the boundary; voxels outside of the boundary of the object will have a value of −d, while voxels inside the boundary will have a value of d. A signed distance field is computed for all of the volumes in the reference set, as well as the ALL and ANY composite volumes. In Fig. 1, (c) shows a signed distance field generated from (a). Teal and green pixels show negative values of the distance field, while blue pixels are positive values.

Fig. 1.

A 2D example of our technique. A distance field (c) is computed based on the reference data boundary (a). Test data boundaries (b) are used as a mask over this distance field (creating (d)) and the reference data is used as a mask as well (creating (e)). The histograms of the two masked distance fields are calculated (producing (g) and (e)) These histograms are compared using the methods detailed in Sec. 3.3.

The signed distance field representation is a tool for describing the shape of the volume, but we need a function that characterizes the differences between the test data items and those in the reference set. Histogram comparison is often used for this purpose. However, since we expect the shapes between the reference and test datasets to be fairly close, direct histogram comparison between the two distance fields would reveal very little. In order to magnify the shape difference between the two volumes, we define a masking operation to retrieve only the part of the part of the reference volume distance field that is overlapping the test volume. For every pair of reference volume R and test volume T, we define M_R,T as a volume that includes the values from the distance field of R only where the voxels from T are occupied. Fig. 1(d) shows the result of this masking operation in 2D. Only the values in the distance field of the reference volume that correspond with occupied voxels in the mask set are kept, all others are discarded.

After this masking operation, which excludes the regions of the reference volume distance field that do not overlap the region of the test volume, we calculate a histogram of M_R,T. Since we are concerned with binary volumes that have a large amount of overlapping voxels, the following procedure will produce features characterizing the area that the test volume occupies but the reference volume does not, as well as characterizing the area in which the test volume fails to occupy the reference volume area. We also compute M_R,R, which is the reference volume distance field excluding all regions outside the reference volume. This will be used later to compare with M_R,T.

3.3.1 Histogram distances

We create two signatures for every combination of test volume and expert volume. A histogram of M_R,T is obtained. We divide this histogram into halves: one where the distance field is negative (H_out) and one where it is zero or positive (H_in). Based on these two histograms, we calculate a distance between a given reference volume and all test volumes.

Next, we must define functions in terms of the histograms to quantify the difference between the reference and test volumes. We will refer to the scoring function as ω, with ω_in evaluating the inside portion of the distance field (H_in) and ω_out evaluating the outside portion (H_out). This is a better approach in our case than full histogram matching since H_out of M_R,R (where R is the reference volume) will consist entirely of zero-valued bins (See Fig 1(h)).

We employ the Earth Mover’s Distance (EMD) to compare the inside (positive) portions of the two histograms:

$${\omega }_{\text{in}}(A_{\text{in}},B_{\text{in}})=\mathit{EMD}(A_{\text{in}},B_{\text{in}}),$$ (2)

where A is the histogram of the distance field (computed from the reference volume) masked by the test volume (M_R,T ) and B is the histogram of the same distance field masked by the reference volume (M_R,R). The EMD operation is appropriate since the purpose of ω is to evaluate the difference between the shape of the region occupied by both the reference and test datasets and negative bins of the histogram represent space outside that region.

As shown in Fig. 1, the histogram for the reference example has no entries for outside distances, since the mask is the same as the distance field generation object. Therefore, using a similar approach as in Eq. 2 to measure the distance for outside histograms will not work, since there are no negative values in the expert histogram. The EMD for the negative values is equivalent to simply summing the total number of pixels contained in all bins in the histogram:

$$\mathit{EMD}(A_{\text{out}},B_{\text{out}})=\alpha \sum _{i\in \mathit{bins}}{r}_i$$ (3)

where α is the constant weight defined as the penalty for creating or destroying a unit of “earth” in the EMD. Using this definition for ω_out would effectively “flatten” the distance-based signature into a simple counting of voxels. Since this flattening of the signature is an undesirable result for our similarity feature, we use the method described below to find an appropriate distance feature that quantifies the region outside the original expert bone.

Virtual mastoidectomies are performed using a 3D joystick. As in the actual surgery, this produces small variations around the edges of the drilled region. However, variation is unlikely in a region far away from voxels that the user intended to drill. Therefore, we chose to penalize voxels where the magnitude (absolute value) of the expert distance field is large. The large magnitude represents a significant distance from the expected boundary, so these voxels are less likely to be modified by the user by chance. Errors in voxels that have a smaller magnitude of the expert distance field should be penalized as well, but not as much. We use a weighted sum that depends on the value of the bin. The larger the distance from the boundary of the expert that the bin represents, the larger the effect that bin should have on the total distance value. We adopt a function

$${\omega }_{\text{out}}(A_{\text{out}})=\frac{{\sum }_{i=1}^n{(n-i)}^s\ast A_{\text{out}}[i]}{{\sum }_{i=1}^n{i}^s},$$ (4)

as a distance measure. In this function, n represents the number of bins in the histogram A_out, while s is a parameter that controls how fast the penalty increases. We use a value of 1.2 for s. A_out[i] represents the ith bin of the histogram.

We compare the test volumes to the ALL, ANY, and individual reference volumes in order to generate features. All features together comprise a vector of length 12: the ω_in and ω_out values for the ALL and ANY volumes and the four reference volumes.

3.3.2 Other features

We compared our feature vector to two other methods derived from previous work in order to acertain the effectiveness of these features in terms of mastoidectomy evaluation. The quality of these features will be addressed in Sec. 5.

Features were generated a method from Sanchez-Cruz and Bribiesca [15]. In this method, distances are calculated between two volumes using their non-overlapping sets. For a pair of volumes, A, where A is from the reference set, and B, where B is from the test set, we calculate the set of voxels A – B and B – A. We then find the solution to the transportation problem [11] which assigns these sets to each other with the smallest distance between corresponding elements. Unassigned elements, in the case of unequal set sizes, are given as a penalty. The volume sets needed to be down-sampled to a third of their original sizes due to the large memory and computation requirements of this method. As with the previous method, we generate a distance feature for each combination of a test volume with the ALL and ANY composite volumes along with four reference volumes, giving us six features for each volume.

Features were also generated using a variant of the method described by Bruckner and Möller [1]. Their method uses the mutual information between two distance fields as a distance measure. We use the normalized mutual information as suggested in their work. For each test volume, this generates six features, since we are finding the mutual information between the test volume and all four reference volumes and the ALL and ANY composite volumes.

3.4 Multi-volume dataset viewer

Even with defined similarity features between volumes, a way to interact with the data space is needed. Our solution is a visualization program with two displays. On one side is a grid of volume viewing panels and on the other is a 2D scatterplot. This follows the general framework of modern visualization for large datasets: examination of small-scale and individual data points using a set of tools and the linking of those examination to a large-scale dataset overview.

Due to the large number of volumes in the dataset, we provide an overview of the data space to users which is a more efficient way to browse the virtual mastoidectomies than a flat list. We append all the features from the distance field histogram method (Sec. 3.3) into a high-dimensional feature vector that encodes shape-based distance information between each volume and the composite or individual reference volumes. We map these feature vectors into a two-dimensional space. We give the user the choice between two projection methods, principal component analysis (PCA) and locally-linear embedding (LLE). We can also append the features from Sec. 3.3.2 or any other features desired into this vector. We discuss the effects of using the features from Sec. 3.3.2 in Sec. 5.1.

Since we wish to compare a small number of reference volumes to a large number of test volumes, techniques like PCA and LLE is well suited to the task. For comparing all pair-wise distances in a set, techniques like self-organizing maps [8] and multidimensional scaling are appropriate. We are not comparing all pair-wise distances, so we do not use these techniques.

3.5 Comparative rendering

The second main component of the visualization framework is a set of volume visualization windows using small multiples [17]. Only four multiples are displayed, since the user needs to resolve detail in the volume image. However, given a large pixel display, higher number of multiples could be displayed. While using configurations that had more windows but at a smaller size, users complained about the amount of zooming necessary to view details of the volumes.

Joshi et al. [9], describe a multi-volume visualization technique that displays all volumes in the same shared 3D space. However, this hinders detailed comparision. In our application, we link the cameras of all the multiple volume display windows. This allows for meaningful comparisons between the two objects and avoids the problem of having to fly around objects to view them. As a metaphor, the shared 3D space approach can be thought of as walking around a museum, comparing objects in fixed locations, while our approach can be thought of as putting objects on a table in front of you. Another drawback of the shared 3D space approach is that of occlusion due to overlapping. While we have overlapping items in the 2D scatterplot display, our volumes are viewed separately and never overlap.

We use a six item classification in our volume visualization display. Recall that we have constructed ANY and ALL composite volumes by combining all the volumes in the reference set. The combination of these two volumes define three regions as shown in Table 1. Each test volume defines a binary division of the space as well, which gives us six combinations: Unobserved, Optional, and Consensus regions that are inside the test volume region and those that are outside the test volume region. Given these six classes, we can define colors to control display of the regions. These colors are user editable, although only some combinations make sense. This is discussed in Sec. 4.

Table 1.

Four combinations of the ANY and ALL regions result in three meaningful values. These values are used for voxels outside and inside the user-drilled area, giving six regions of bone.

ALL	ANY	Interpretation
0	0	Unobserved: No expert modified that region
0	1	Optional: Some experts modified that region
1	0	(Meaningless, does not occur)
1	1	Consensus: All experts modified that region

4 Interaction

We use a brushing and linking approach to facilitate the exploration of the dataset. By clicking and dragging individual points in the scatterplot display into the volume windows, the existing volume on that volume display is replaced by the selected point. This allows users to arbitrarily select volumes of interest. These can be either near or far from each other in the volume data space and investigate the shape differences between the different volumes.

The camera is locked between the different volume displays. Unlocked cameras provide flexibility, but users felt that since the volumes are pre-registered to each other, the ability to view different parts of different volumes at the same time was unnecessary and potentially confusing.

Each volume has metadata associated with it: the institution at which the resident is located, the year of experience of the resident and whether the performance was a post-test (performed after training) or a pre-test (performed before training). This metadata is incorporated into the scatterplot display by coloring the glyphs used to represent each volume. In Fig. 2, the scatterplot display displays pre-test volumes (those that were virtually drilled before training) in green and post-test ones (those virtually drilled after training) in red. The expert volumes are displayed in blue for reference. Selection of which metadata property controls the coloring is controlled by the user. In Fig. 3, the glyph color encodes the institution at which that user is studying.

Fig. 2.

Proximity in the scatterplot relates to commonality between volumes. The two volumes displayed with the green and yellow triangle show incorrect over-drilling, as seen by the large amounts of red in the corresponding volume display. The red and blue triangles show results closer to the experts’. Blue circles on the scatterplot represent expert volumes, while green circles represent pre-training resident results and red circles represent post-training resident results. Arrows connect the same user’s pre- and post- results, if available. See Sec. 4 for more detail.

Fig. 3.

This image shows the inverse cavity rendering, where the bone that has been drilled away in the simulation is rendered as solid. Blue color shows the consensus areas that have been drilled, while bright green shows areas where drilling is considered optional. The semitransparent teal color designates regions that are considered consensus areas for drilling based on the expert data, but was not drilled by the user. Red indicates over-drilling errors. The scatterplot display in this example is color coded for institution: each different color is a different institution. The scatterplot here uses LLE for layout.

We use an arrow glyph to show the temporal progression between two volumes. We asked users to provide a sample volume before and after going through a training session. As shown in Figs. 2 and 3, many arrows are displayed which connect two data points. The arrow goes from the data point that represents a virtual mastoidectomy performed before training to a data point representing a post-training virtual mastoidectomy. The display of these arrows can be toggled by the user.

The features incorporated into the feature vector which is used for the scatterplot display can also be changed by the user. Four sets are available: the distance field histogram metric for the individual test volumes, the same metric on the composite volumes, and the two metrics described in Sec. 3.3.2. We discuss the effects of the selections on the point display in Sec. 5.1.

5 Discussion

The volume visualization portion of the display benefits a great deal from the composite volumes defined in Sec. 3.2. As shown in Fig. 4, the boundaries between the ANY and ALL volumes can be a very effective visual indicator of correctness. Orange-colored voxels can be drilled or not; they belong to the ANY set but not the ALL set. Green-colored voxels belong to the ALL set and designate areas that should be drilled away. The colors and opacities of the different classes of voxels, as listed in Tab. 1, can be given arbitrary colors and opacities, depending on the visualization effect desired. In Fig. 3, the removed voxels are shown with high opacity. Surrounding the removed voxels is a low-opacity teal region which contains voxels that should have been removed but were not. This display mode presents an easier way for users to examine errors in drilling which occur deep in the bone cavity. The display mode in Figs. 3 and 4 has high opacity only for the bone left as solid, which is a more natural visualization for experts and residents and is preferred as a orienting display mode for the users.

Fig. 4.

Comparison of good and poor mastoidectomy performances using one of the volumetric display modes. In a good mastoidectomy, most of the green volume should be removed, since green represents consensus areas where all experts removed bone (the ALL volume). Red areas are those that were not drilled away by any expert but were removed by that particular resident.

The manual interaction between the reduced dimensionality data space and the individual volume rendering displays is key to the utility of this software. Due to the nature of dimensionality reduction, the resulting scatterplot may not have axes that have simple meanings related to clinical performance. In our case, while surgeons explored the dataset, useful facts come to light that can help to evaluate the residents who use the simulator. In Fig. 2, two volumes from the upper right of the scatterplot and two from the lower left have been selected. The selected volumes are indicated on the scatterplot by triangles, with the color of the triangle matching the color of the triangle on the upper left corner of each volume display. On the corresponding volume displays, the similarities between the data items that are in close proximity are apparent. The items on the lower left of the scatter plot (the upper left and lower left volumes in the volume display) have large areas of red voxels. These correspond to voxels that no experts drilled away but were removed by the user. This, in turn, corresponds to an error in performing the mastoidectomy procedure. Data items in this lower left area of the scatterplot show similar behavior. The other two items displayed have good performance, showing little of the red and removing much of the green, consensus portion of the bone, which all expert examples removed.

Occlusion can be an issue in scatterplot displays. A slight offset of the position of the point (jitter) has been used to avoid occlusion in displays which have categorical or integer values [16], but this technique can be misleading for continuous data like ours. Other approaches include filtering, transparency to see overlapped points, and distortion to separate the points [4]. We employ a transparency-based solution for the occlusion issues. Overlapping points can be easily recognized, and when items are dragged over to a volume display window, a menu pops up allowing the user to choose from any item near the mouse cursor when the drag operation was initiated. We found this to be sufficient for the amount of occlusion in our current dataset. Different techniques might need to be employed if the number of data points doubles.

In addition to the software being used by instructors to gauge the performance of the class as a whole and find students who are doing very well or very poorly, the software could be used as a self examination by each individual resident. We demonstrate a preliminary version of this with our arrow glyph. This tracks the progress from post-instruction to pre-instruction. We plan that after deployment of the simulator many more time-stamped samples of each resident’s surgical performances will be acquired, and from that we can construct a trend line. This can be plotted that in the data-space view, along with the locations of expert performances. This will let the resident know if he or she is progressing and improving the quality of procedural technique.

5.1 Effects of different feature vectors

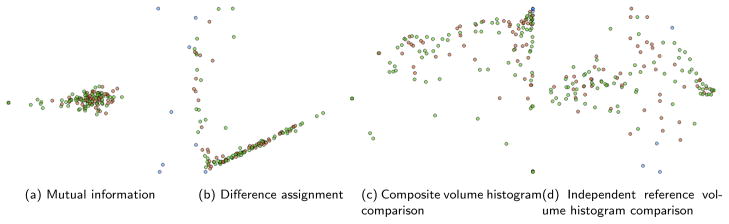
The selection of the features that are included in the feature vector can dramatically change the scatterplot display. Fig. 5 shows the examples from selecting one of the feature sets described earlier as the only constituent. of the feature vector. The software allows us to compare the masked distance field approach described in Sec. 3.3 with features from other works, as described in Sec. 3.3.2.

Fig. 5.

Comparison of scatterplots generated from various feature vectors.

The Mutual Information feature is shown in Fig. 5(a). This shows a continuum of bad examples (the left) and good examples (on the right). However, items that are bad because of over-drilling and items that are bad because of under-drilling appear in a similar location. This makes it difficult to understand nuances of student performance at a glance. The difference assignment feature, as described by Sanchez-Cruz [15], performs even more poorly than the Mutual Information feature for this application. As shown in Fig. 5(b), most of the data items are forced along a single line. Manual exploration of this space determined very little useful information contained in this feature. It may be useful in other types of data, but is not good for evaluating the quality of mastoidectomies.

We found that the composite volume histogram comparison feature produced the most intuitive dataspace for investigating the overall performance of residents. With this feature (shown in Fig. 5(c)), the expert reference volumes are clustered in the upper right corner of the 2D space. Data points near this corner tend to have good performance characteristics: most of the consensus area is drilled away and little over-drilling occurs. Data points in the bottom right tend to be under-drilled. In the bottom right corner are volumes that were not drilled on at all. The data points in the upper left are items where substantial over-drilling occurred but a large portion of the consensus area was drilled as well. These volumes represent residents who removed all that was needed to complete the procedure, but were too aggressive and went too deep into the bone. Finally, the lower left corner is sparsely populated, but consists of those users who made major over-drilling mistakes but did not drill away the areas necessary to complete the surgery. These users probably have more substantial misunderstandings of the mastoid anatomy than the other groups, or they had problems using the simulator.

Based on the interactions of expert surgeons with the software, we discovered some interesting properties of the multi-visualization dataset. This section discusses these properties. An experienced otologic surgeon graded the pre-test bones using the “Post. canal wall thinned” metric. This metric has been previously shown to be relevant to general performance for mastoidectomies: an expert looks at the results of a mastoidectomy, either virtual or on cadaver bone, and determines if the Post. wall of the external auditory canal is thinned properly. Grading was done on a 1 through 5 scale. We mapped the results to our scatterplot, as shown in Fig. 6. Low scores were assigned red colors, while high scores were assigned green colors, with pale yellow representing a score of 3. Good scores clustered around the middle of the plot, while items in the far bottom left and right corners of the plot tended to have low scores. This follows from our previous analysis: the lower left corner contains examples that have substantial over-drilling errors and those in the lower right corner did not drill enough. The two red dots in the middle were an anomaly, so more investigation was done. The examples from those particular users were considered good by the experts, but they did remove much more of the Post. canal wall than is allowed.

Fig. 6.

Scatterplot display of pre-test items, graded by experts using the “Post. wall thinned” metric. Green shows good performance, while red shows bad performance. The scatterplot layout here uses the composite and individual expert histogram matching features.

In addition, flaws in the grading system used by experts for evaluating virtual mastoidectomies presented themselves via interaction with the software. After coloring by a composite score given by experts, some anomalous high scores were shown in the lower left corner of the plot. By dragging these data items on the scatterplot to the volume rendering window, we identified the problem. The mastoidectomies in question were done well, but only after the users had performed extraneous drilling on the side of the bone. This indicates a failure to orient the bone properly before starting the procedure. However, the portion of the bone drilled incorrectly was to the rear of the virtual specimen and the metrics used for scoring do not take that part into account. This shows an important problem with defining metrics for scoring this type of procedure: failure to include a case for errors that are unusual. Overall, the experts feel that this tool is a useful overview of the volumes and a convenient way to browse the dataset, but further research must be done on procedure-specific metrics for it to be a completely automated scoring system for mastoidectomies.

5.2 Implementation notes and future work

We used logarithmic histograms (log(1.0 + x) for each bin quantity x) in our calculations, as we found it achieved better results than a linear histogram. This may be data dependent, and for other types of datasets linear histograms might produce good results.

Some experimentation was done with a gradient-based rendering technique in which colors would change smoothly based on the value of the expert distance fields. However, during testing, users complained that the color gradients were confusing and obscured the boundaries between the sections described in Tab. 1. We feel that future experimentation with non-photorealistic rendering techniques for the volume displays would be fruitful.

6 Conclusion

We have described a system for viewing the similarities and differences of a multi-volume dataset consisting of results from a mastoidectomy surgery simulator. This system allows users to compare resident performance to expert performance using similarity measures based on histograms of the distance fields of the expert results. The analysis of the multi-volume dataset includes the construction of two composite volumes defining the observed range of the expert volumes. The application provides a solid starting point for the investigation of any similar multi-volume datasets.