Evidence of widespread selection on standing variation in Europe at height-associated SNPs

Abstract

Strong signatures of positive selection at newly arising genetic variants are well-documented in humans^1–8, but this form of selection may not be widespread in recent human evolution⁹. Because many human traits are highly polygenic and partly determined by common, ancient genetic variation, an alternative model for rapid genetic adaptation has been proposed: weak selection acting on many pre-existing (standing) genetic variants, or polygenic adaptation^10–12. By studying height, a classic polygenic trait, we demonstrate the first human signature of widespread selection on standing variation. We show that frequencies of alleles associated with increased height, both at known loci and genome-wide, are systematically elevated in Northern Europeans compared with Southern Europeans (p<4.3×10⁻⁴). This pattern mirrors intra-European height differences and is not confounded by ancestry or other ascertainment biases. The systematic frequency differences are consistent with the presence of widespread weak selection (selection coefficients ~10⁻³–10⁻⁵ per allele) rather than genetic drift alone (p<10⁻¹⁵).

Recent positive selection on newly arising alleles produces a strong genetic signature: a long haplotype of unexpectedly high frequency¹³. In contrast, weak polygenic selection on standing variation acts on multiple haplotypes simultaneously^14–16. As a result, the effects of polygenic adaptation on patterns of variation are generally modest and spread across many haplotypes at any one locus. To overcome these difficulties, we implemented an approach that combines evidence for selection across many loci. Specifically, we examined the single nucleotide polymorphisms (SNPs) tested in genome-wide association (GWAS) studies to identify which of the two alleles at each SNP is associated with increased trait values (“trait-increasing allele”), and then tested these trait-increasing alleles as a group for systematic, directional differences in allele frequencies between populations. Under polygenic selection, we expect that the trait-increasing alleles will tend to have greater frequencies in the population with higher trait values, compared to the population with lower trait values^10,17.

We propose that adult height in Europe might provide an example of polygenic adaptation in humans. Northern Europeans are typically taller than Southern Europeans (Supplemental Table 1), and although nongenetic factors can produce phenotypic differences between groups^18,19, we suspected that the height differences between these closely-related populations might be partially explained by genetic differences due to widespread selection on standing variation. We tested this hypothesis using recent GWAS data for height generated by the Genetic Investigation of ANthropometric Traits (GIANT) consortium²⁰ and Northern- and Southern-European allele frequency estimates based on two separate datasets, MIGen²¹ and POPRES²². In this case, we expect the height-increasing allele at height-associated loci to be more frequent in Northern- than in Southern-European populations.

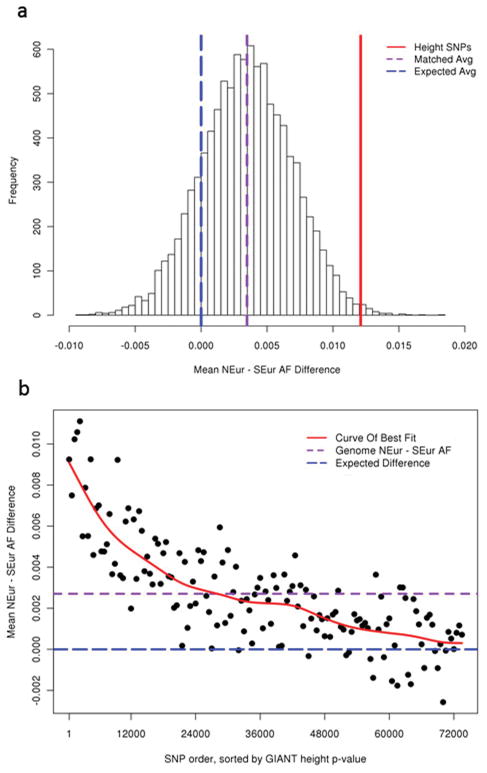
We first compared the Northern- and Southern-European allele frequencies of 139 variants that are known to be associated with height at genome-wide significance²⁰ and were directly genotyped in the MIGen study. We used 257 U.S. individuals of Northern-European ancestry and 254 Spanish individuals from MIGen as the Northern- and Southern-European populations, respectively (Supplementary Note and Supplementary Figure 1). We found that the height-increasing alleles are more likely to have higher frequencies in Northern than in Southern Europeans (85 out of 139, sign test p = 0.011; mean frequency difference = 0.012, t-test p = 4.3×10⁻⁴; Table 1). This result was robust when compared to 10,000 sets of SNPs drawn at random from the genome, matched on a per-SNP basis to the known height SNPs by the average Northern- and Southern-European allele frequencies (p = 0.0056 for mean frequency difference; Figure 1a; Online Methods). We observed similar results in an independent dataset, POPRES (Table 1, Supplementary Table 2 and Supplementary Figure 2a). Thus, the group of height-increasing alleles at known associated variants is more common in Northern than in Southern Europe, indicating that the phenotypic difference between these two populations is at least partly due to genetic factors.

Table 1.

Comparisons of the mean AF difference and the maximum likelihood estimate of s in pairwise combinations of populations across Europe

Populations	Comparison	Sample size (N)	Mean AF difference	t-test p-value	s (w=sβ)	LRT p-value (w=sβ vs. drift)	s (w=sβ)	LRT p-value (w=sβ vs. drift)
					T = 20		T = 500
U.S. vs. Spain (MIGen)	N vs S	257, 254	0.0079	9.67E–16	0.138	9.57E–16	0.0055	9.65E–16
Sweden vs. Spain (MIGen)	N vs S	58, 58	0.0094	1.47E–07	0.183	5.48E–08	0.00728	5.44E–08
UK vs. Italy (POPRES)	N vs S	208, 208	0.016	1.06E–33	0.264	2.99E–35	0.0105	3.24E–35
UK vs. Portugal (POPRES)	N vs S	125, 125	0.012	1.72E–20	0.207	4.91E–18	0.00824	4.98E–18
UK vs. Switzerland (French) (POPRES)	N vs C	208, 208	0.0044	5.18E–07	0.0757	1.52E–05	0.00302	1.52E–05
Switzerland (French) vs. Italy (POPRES)	C vs S	208, 208	0.011	1.73E–25	0.188	1.32E–22	0.00746	1.36E–22
Switzerland (French) vs. Portugal (POPRES)	C vs S	125, 125	0.0081	1.86E–12	0.139	1.07E–09	0.00554	1.08E–09

Each population is categorized as Northern (N), Central (C), or Southern (S) European. Results shown are for the set of ~1,400 independent SNPs (see main text and Supplemental Methods for exact numbers in each comparison), comparing the mean allele frequency difference between the more Northern population and the more Southern population, as well as the maximum likelihood estimate of the selection coefficients under a model in which the coefficients are proportional to the estimated effects on height (w = s*β, where β is the estimated increase in height per allele, in standard deviations). The p-values shown for the mean allele frequency difference are assessed by t-test. The p-values for the estimates of s are assessed by likelihood ratio test (LRT), comparing a model of drift alone vs. a model of drift plus selection. Though too recent to be the realistic time frames for historical divergence (T, in generations) between the Northern- and Southern-European populations, results for T = 20 and 500 were included to account for the likely bi-directional migration between European populations, which would decrease the apparent time of divergence between the two populations. Note that our analysis is actually estimating the product of T and s. Because our estimates of T and s cannot be decoupled, the LRT statistics and p values are nearly identical across ranges of T (see Supplemental Tables 4–10 for more detailed results across a full range of T). Accordingly, we are not estimating T but are instead estimating s under a range of values for T that are likely to span the actual (unknown) value of

Figure 1. Mean allele frequency difference of height SNPs, matched SNPs and genome-wide SNPs between Northern- and Southern-European populations.

a, Mean frequency difference of the height-increasing alleles from 139 known height SNPs in MIGen (solid red line) are compared against that of 10,000 sets of randomly-drawn SNPs, with each set matched by average Northern- and Southern-European allele frequencies to the known height SNPs on a per-SNP basis. Shown in purple is the mean value across the 10,000 sets of matched SNPs, and in blue is the expected mean difference for the sets of matched SNPs (x=0). b, Mean frequency difference of the height-increasing allele for sets of 500 independent (r² < 0.1) SNPs across the genome. SNPs were sorted by GIANT height association p-value. Shown in red is the curve of best fit, in purple the genome-wide mean frequency difference, and in blue the expected mean difference (y=0). U.S. individuals of Northern-European ancestry and Spanish individuals from the MIGen dataset were used. NEur, Northern European. SEur, Southern European. AF, allele frequency.

We noted that the randomly matched SNPs used as a control in this analysis also showed a subtle trend towards the height-increasing allele being more common in Northern than Southern Europeans (mean frequency difference across 10,000 matched SNP sets = 0.0035; Figure 1a). In fact, throughout much of the genome, the predicted height-increasing alleles are more likely to have higher frequency in Northern than Southern Europeans (Figure 1b and Supplementary Figure 2b). This observation suggested that, beyond the 180 known loci²⁰, many additional height-associated SNPs in the genome may reach genome-wide significance in GWAS studies as power is improved (consistent with previous modeling^20,23), and that the height-increasing alleles at these variants may further contribute to the height difference between these populations.

While there appears to be a genome-wide trend for the height-increasing allele to be the Northern-predominant allele (i.e., the allele that is more common in Northern than in Southern Europeans), we must also considered confounding by ancestry as a possible explanation for this observation^24–27. The GIANT consortium took multiple steps to control for ancestry²⁰, but if these steps were not completely effective, then SNPs with an allele frequency difference between Northern and Southern Europeans would tend to be spuriously associated with height, with the Northern-predominant allele appearing to be a height-increasing allele.

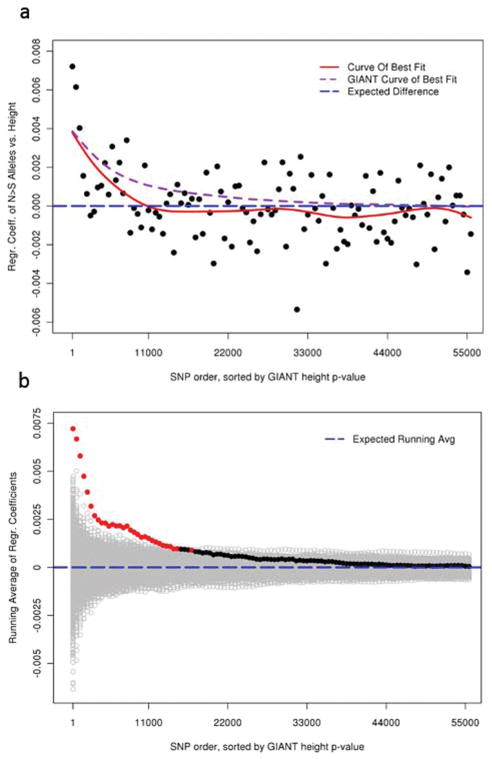
We therefore estimated the effect sizes for the Northern-predominant alleles on height in a family-based cohort (the Framingham Heart Study), using a sibship-based regression analysis that is immune to stratification (see Online Methods), and compared these estimates with those from GIANT. We observed that, for the most strongly associated ~1,400 SNPs, the estimated effects of the Northern-predominant alleles on height are indistinguishable between the sibship-based test and the GIANT data set (paired t-test p = 0.36; Supplementary Figure 3). For the remaining SNPs, the average estimates of effect size from the family-based analysis fall towards zero slightly faster than the GIANT estimates (Figure 2a; Supplementary Figure 4a). This faster decrease could be due to low power in the smaller family-based sample and/or residual stratification in the remaining GIANT data, although there is clearly a signal of true association beyond these ~1,400 SNPs (Figures 2a, 2b; Supplementary Figures 4a, 4b). To ensure that our conclusions are not confounded by stratification, we therefore focus our subsequent analyses on this set of ~1,400 independent SNPs. The allele frequency of these ~1,400 height-increasing alleles is significantly higher in Northern than in Southern Europeans, including multiple comparisons within MIGen and within POPRES (all t-test p < 1.5×10⁻⁷; Table 1). We also found that the frequencies in a central European population (Swiss-French from POPRES) fall between those of the Northern- and Southern-European POPRES populations (Table 1). Thus, the observation that many height-increasing alleles are more common in Northern than in Southern Europeans is not explained by stratification. Rather, consistent with selection, the data suggest a small but systematic increase in frequency of height-increasing alleles in Northern Europe and/or a decrease in frequency in Southern Europe.

Figure 2. Within-family analyses of height and the Northern-predominant alleles across the genome.

Ordered by GIANT height association p-values, height was regressed against the number of Northern-predominant alleles for each SNP, using data from a total of 4,819 individuals in 1,761 sibships. Height and allele counts were both normalized within sibships. a, The average regression coefficients in groups of 500 SNPs are plotted on the y-axis. The SNP ranks are plotted on the x-axis. The red line is the curve of best fit; purple dashed line is the directly comparable curve of best fit for the GIANT effect sizes; blue dashed line is y=0. b, The running averages of the regression coefficients were plotted on the y-axis (red and black filled circles). The running averages of regression coefficients from 1,000 analyses where phenotypes were permuted within sibships are also shown (grey open circles). Observed data points are colored black if they are less extreme than 0.01% of the permuted values. The blue dashed line is y=0.

Finally, we asked whether this systematic change in frequency of height-increasing alleles could be explained by genetic drift or, alternatively, if the data are more consistent with a model that also incorporates selection (Online Methods). In the absence of selection, the expected difference in allele frequency has a mean of 0 and a variance of p(1−p)(2 × F_ST + 1/N₁ + 1/N₂), where p is the estimated ancestral allele frequency, F_ST is estimated using the genome-wide data, and N_i are the population sample sizes²⁸. The expected effect of selection on allele frequency differences is estimated as:

$$\mathrm{\Delta }{\text{AF}}_{\text{Sel}}\approx T\times \left(\frac{{wp}^2+wp+p}{1+2wp}-p\right)$$

where T is the number of generations of differential selection, and w is the selective pressure per allele per generation (Online Methods). We used a likelihood ratio test (LRT) to compare models incorporating selection and drift to a model of drift alone; using simulations (Supplementary Note), we verified that the LRT gave expected results under the null model of drift alone (Supplementary Figures 5, 6), in models incorporating both drift and selection (Supplementary Table 3), and is robust to the choice of ancestral allele frequency, p (data not shown).

By calculating the combined likelihood of the frequency data at the ~1,400 independent SNPs under each of the different models, we found that models incorporating both selection and drift were more consistent with the data than models of drift alone, with LRT p-values ~10⁻¹⁶ over a range of values of T (Table 1, Supplementary Tables 4–10; see Supplementary Tables 11 and 12 for results using a larger genome-wide set SNPs). Given typical effect sizes of height-associated variants, which are generally 10⁻² to 10⁻³ standard deviations or smaller (1 standard deviation ≈ 6.5 cm), we estimate that, in a model where selection is proportional to effect size, the typical selective pressure on individual height-associated variants would be ~10⁻³ to 10⁻⁵ per allele per generation. Thus, the data are much more consistent with the presence of widespread weak selection on standing variation than with a model of drift alone.

We also addressed several other factors that could confound our results. First, we considered whether demographic biases in GIANT could have produced our results. Because GIANT consists largely of individuals of Northern-European ancestry, the consortium could have greater power to identify height-associated variants whose frequencies are closer to 0.5 in Northern Europeans. However, when we reordered the GIANT GWAS results based on discovery power in Southern Europeans (Supplementary Note), our results were essentially unchanged (Supplementary Table 2, Supplementary Figures 7, 8). Second, the height SNPs were limited to SNPs contained in HapMap, which itself ascertained SNPs in part by sequencing in Northern- but not Southern-European samples. This ascertainment bias could in theory influence the Northern- and Southern-European minor allele frequency distributions in HapMap SNPs, and hence the height-associated SNPs. However, the minor allele frequency distribution of the ~1,400 height-associated SNPs is indistinguishable between Northern and Southern Europeans (Kolmagoroff-Smirnov p = 0.996). Furthermore, we showed through simulations using an even more biased scheme of SNP ascertainment based on 1000 Genomes²⁹ that such bias does not account for our results (Supplementary Note). Importantly, our results show a directional rather than overall shift in allele frequencies, so ascertainment biases in GIANT or HapMap would only be potentially relevant if height-increasing alleles were systematically biased towards being the major or minor allele. However, there is no statistically significant bias in either the known height-increasing alleles (70/138 major alleles in Northern Europeans, 71/139 major alleles in Southern Europeans) nor the expanded set of ~1,400 SNPs (752/1,434 major alleles in Northern Europeans, 740/1,436 major alleles in Southern Europeans; all p >0.05). Thus, our results cannot be explained by having ascertained height-associated SNPs largely in Northern Europeans.

Another important potential bias is that we studied a phenotype (height) and pair of populations (Northern and Southern Europeans) where the phenotype was known to differ between the populations. As discussed by Orr¹⁷, once we selected a phenotype known to be differentiated, it may not be surprising to observe more height-increasing alleles in the taller population. To test whether height in Northern and Southern Europeans could simply be an extreme example of a neutrally evolving trait, we simulated 10,000 neutrally evolving traits that have the same genetic architecture as height (Supplementary Note). We estimate that we would have had to ascertain height in Northern and Southern Europeans from more than 10¹⁶ neutrally evolving trait/population pairs to obtain the level of differentiation we observed in the actual data (Supplementary Figure 9), suggesting our observations are not simply the extreme end of neutrally evolving traits but rather reflect the effects of selection.

In summary, we have provided an empirical example of widespread weak selection on standing variation. We observed genetic differences using multiple populations across Europe, thereby showing that the adult height differences across Europe are not due entirely to environmental differences, but rather are at least partly genetic differences arising from selection. Height differences across populations outside of Europe may also be genetic in origin, but potential nongenetic factors such as differences in timing of secular trends mean that this inference would need to be tested directly with genetic data in additional populations. By aggregating evidence of directionally consistent intra-European frequency differences over many individual height-increasing alleles, none of which individually has a clear signal of selection, we could observe a combined signature of widespread weak selection. However, we were not able to distinguish whether this differential weak selection (either positive or negative) favored increased height in Northern Europe and/or decreased height in Southern Europe. One intriguing possibility is that sexual selection or assortative mating (sexual selection for partners with similar height percentiles) fueled the selective process. It also remains possible that selection is not acting on height per se, but acted on a phenotype closely correlated with height or on a combination of phenotypes that includes height.

Our analysis is practicable because many variants have been reproducibly associated with height, and also suggests that many more loci with small effects on height remain to be identified. As more genome-wide association data become available for human traits or diseases, this approach can be used to search for other examples of human polygenic adaptation, including traits or diseases associated with climate or other environmental variables that vary across otherwise closely related populations^8,30,31.

Online Methods

Study Cohorts

We used a GWAS dataset for height, generated from the GIANT consortium²⁰, as our source for per SNP association statistics. The intra-European allele frequencies were obtained from MIGen²¹ and POPRES²². Family-based analyses were conducted using the Framingham Heart Study (FHS)³². Please see Supplementary Note for a detailed description these cohorts.

Defining classes of height-associated SNPs for sign tests and mean allele frequency difference analyses

The height-increasing allele was defined as the allele that is associated with increased height in the GIANT dataset. The GIANT dataset however contained imputed genotypes. We were concerned that imputation using the HapMap CEU panel as the reference panel would bias our analyses, which focus on intra-European differences. Therefore, we only examined SNPs directly genotyped in MIGen or POPRES for our analysis. In order to determine if the allele frequency of the height-increasing alleles are systematically increased or decreased in either the Northern- or Southern-European populations, we compared the Northern- and Southern-European allele frequencies for three different classes of SNPs in our analyses: (1) the 180 known height-associated SNPs identified by GIANT²⁰; (2) sets of frequency-matched SNPs to the height-associated SNPs; and (3) sets of independent SNPs genome-wide. A fourth class of SNPs consisting of ~1,400 independent SNPs most strongly associated with height, for which the effect size estimates are similar between GIANT and a family-based analysis, was also defined and used for much of the later analyses presented in the manuscript (see definitions and descriptions below). Intra-European differences in allele frequencies were assessed using sign tests, which tested whether the proportion of SNPs with the height-increasing allele was significantly more common in Northern vs. Southern Europeans compared with a 50/50 expectation, and paired t-tests, which tested whether the mean Northern-European to Southern-European allele frequency differences were significantly different from zero. The analyses were performed using R-2.11.

For the 180 known height-associated SNPs, the allele frequency for only 139 and 109 SNPs were analyzed in MIGen and POPRES, respectively, due to our restriction of using only directly genotyped SNPs. These groups of SNPs include 55 and 30 height SNPs that were directly genotyped, and 84 and 79 proxies that were in high LD (r²≥0.8 in CEU) with an original height SNP, in MIGen and POPRES, respectively. In the case that multiple proxy SNPs were available in CEU, we selected the SNP with the lowest p-value for height association in GIANT. Our analysis showed similar patterns in the directly genotyped SNPs and proxies, and mean allele frequency differences remained significant for both subsets of SNPs (Supplementary Table 13).

For the sets of matched SNPs, randomly drawn SNPs were matched to the height-associated SNPs on ancestral European allele frequency (estimated as the average allele frequency of Northern- and Southern-European populations). The genome-wide data used had been pruned by clumping SNPs in high LD (r²≥0.8) into a single cluster so to avoid drawing highly correlated SNPs. Clumping was done by first randomly choosing a SNP as the index SNP, then clustering all SNPs within 0.5 Mb of the index SNP that had a pairwise r²≥0.8 based on HapMap phase 2 CEU data. In total 10,000 sets of matched SNPs were generated.

For the set of independent SNPs genome-wide, we calculated the mean Northern- to Southern-European allele frequency differences of the predicted height-increasing alleles in successive groups of 500 independent variants, sorted by their GIANT height association p-value starting from the most strongly associated SNP. Here, SNPs were clumped using the method described above but with an r² threshold of ≥ 0.1 to ensure that each clump of SNPs is nearly or completely independent from each other. In total, 73,657 SNPs and 54,542 SNPs genome-wide were used from the MIGen and POPRES datasets, respectively, to estimate Northern- and Southern-European allele frequency. Curves of best fit were determined using a smooth splined approach with spar parameter equal to 0.75 in R-2.11.

Within-sibship association test of Northern-predominant alleles and increased height

For each SNP, the allele that is more common in Northern Europe than in Southern Europe is defined as the Northern-predominant allele. To test whether Northern-predominant alleles are associated with increased height in a family-based test that is immune to stratification, we conducted a within-sibship test using data from the family-based Framingham Heart Study. The number of SNPs genotyped in FHS and used in these analyses (after clumping to remove correlated SNPs) was 55,927 and 52,680 for the MIGen and POPRES allele frequency data sets, respectively. For each individual within a sibship and for each independent SNP (r² < 0.1), we designated the genotype as the number of Northern-predominant alleles carried by that individual. Missing genotypes were skipped and treated as neither a Northern- or Southern-predominant allele. We then adjusted the genotype at each SNP within each sibship by subtracting from the observed number of Northern-predominant alleles the average number of Northern-predominant alleles for that SNP in that sibship. Similarly, we adjusted the age- and sex-corrected height values within each sibship by subtracting the sibship mean. Then, across all individuals (each adjusted by the means in his/her own sibship), we regressed the sibship-adjusted height values against the sibship-adjusted genotypes, producing a pure family-based test immune to stratification. The family-based effect size estimates (i.e., the regression coefficients) were compared with the effect sizes estimated by the GIANT consortium. We note that FHS was one of the cohorts included in the GIANT meta-analysis. We therefore removed the FHS results from the GIANT data and repeated the GIANT meta-analysis in order to generate new GIANT estimates that are completely independent of our family-based test.

From this comparison, we identified a set of ~1,400 most strongly associated and clearly independent SNPs for which the effect sizes are similar in GIANT and in our family-based test. This latter SNP set was determined by first clumping the above-mentioned genome-wide datasets according to the GIANT height association p-value, using an r²≥0.1. The top 5,000 SNPs from this list were then further pruned by requiring that no two SNPs occupy the same 1Mb window, preferentially keeping SNPs more strongly associated with height. This yielded 1,437 SNPs in the MIGen dataset and 1,429 in the POPRES dataset. These SNPs have comparable effect sizes between our FHS within-sibship regression coefficients and GIANT effect sizes (p = 0.36 and 0.89 for MIGen and POPRES, respectively, by paired t-test; Supplementary Figure 3). Thus, the height effect size estimates for this set of ~1,400 SNPs are not inflated by stratification. In our subsequent analyses, we use these sets of ~1,400 SNPs, as well as the genome-wide data from which the ~1,400 SNPs were selected.

For within-sibship analyses using genome-wide sets of SNPs, running averages of regression coefficients were also determined by successively calculating regression coefficients for each group of 500 SNPs and then calculating a running average of all regression coefficients up to and including that group of SNPs. To determine the significance of these running averages, simulations were conducted by randomly redistributing the height values within each sibship 1,000 times, and calculating the regression coefficients and running averages for each simulation. The observed running average regression coefficients were considered significant if none of the simulations had as large a running average regression coefficient at that point in the genome as the observed values.

Modeling genetic drift and selection

To calculate the relative likelihoods that the observed Northern- and Southern-European allele frequency data for height-increasing alleles is consistent with a model with genetic drift alone or with models that incorporate selection, we used a likelihood ratio test, and modeled drift according to the methods outlined in Ayodo et al.²⁸

To model the effects of drift alone, the allele frequency difference between two populations was estimated as a random normal variable with mean 0 and variance equal to p(1−p)(c + 1/N₁ + 1/N₂), where p is the ancestral allele frequency (the average of the two populations), c is a genetic drift parameter equal to 2 × F_ST, where F_ST is determined using the genome-wide data (F_ST = 0.0019 for MIGen and 0.0031 for POPRES), and N₁ and N₂ are total chromosome counts for each of our two populations. c was estimated using the strictly clumped datasets described above. For each SNP, the negative log likelihoods of observing the Northern-European Southern-European allele frequency difference was calculated using R, and summed over all independent SNPs (r² < 0.1) genome-wide or in groups of 500 independent SNPs sorted by GIANT height association p-value.

To model the effect of drift and selection on the observed Northern-European Southern-European allele frequency differences, we first estimated the expected amount of allele frequency differences that could be attributed to selection using the following equation (see section 4.1 for derivation):

$$\mathrm{\Delta }{\text{AF}}_{\text{Sel}}\approx T\times \left(\frac{{wp}^2+wp+p}{1+2wp}-p\right)$$

where p is the ancestral allele frequency (estimated as the average of Northern- and Southern-European allele frequencies), T is the number of generations since the two populations have split, and w is the selective pressure experienced by the population under different models of ongoing selection. Additional details regarding our modeling can be found in Supplementary Note.

Ruling out potential ascertainment biases

A number of additional biases could have influenced our results, including ascertainment bias due to GIANT cohort collection, HapMap SNP ascertainment, and our choice for phenotype. Please refer to the Supplementary Note for a detailed description of analyses demonstrating that these potential ascertainment biases of our study design did not influence our results.