Compass magnetoreception in birds arising from photo-induced radical pairs in rotationally disordered cryptochromes

Abstract

According to the radical pair model, the magnetic compass sense of migratory birds relies on photochemical transformations in the eye to detect the direction of the geomagnetic field. Magnetically sensitive radical pairs are thought to be generated in cryptochrome proteins contained in magnetoreceptor cells in the retina. A prerequisite of the current model is for some degree of rotational ordering of both the cryptochromes within the cells and of the cells within the retina so that the directional responses of individual molecules do not average to zero. Here, it is argued that anisotropic distributions of radical pairs can be generated by the photoselection effects that arise from the directionality of the light entering the eye. Light-induced rotational order among the transient radical pairs rather than intrinsic ordering of their molecular precursors is seen as the fundamental condition for a magnetoreceptor cell to exhibit an anisotropic response. A theoretical analysis shows that a viable compass magnetoreceptor could result from randomly oriented cryptochromes contained in randomly oriented cells distributed around the retina.

1. Introduction

A variety of evidence has accumulated over the last decade in support of the proposal [1] that birds use magnetically sensitive, light-dependent chemical reactions in the eye to detect the direction of the Earth's magnetic field (reviewed in [2–6]). The inspiration for this compass mechanism came from behavioural experiments on captive birds [7–10] and the fact that photochemical reactions of radical pairs in vitro can be influenced by applied magnetic fields (reviewed in [11–14]). Largely ignored for 20 years, this hypothesis was revived in 2000 when it was proposed [15] that the required chemistry could be hosted by molecules of the photo-active protein cryptochrome [16] contained in specialized magnetoreceptor cells in the retina. Ritz et al. [15] suggested that photo-excitation of the fully oxidized form of the flavin adenine dinucleotide (FAD) cofactor in cryptochrome, followed by electron transfer along a chain of three tryptophan residues (the ‘Trp triad’) would give a magnetically sensitive radical pair comprising the semi-reduced FAD radical and a Trp radical. A magnetic compass detector could result from anisotropic interconversion of the singlet and triplet states of this radical pair when combined with appropriate spin-selective reactivity [15]. Although there is some doubt about the exact identity of the radical pair [17–19], most of the experimental and theoretical studies over the last decade seem to support the involvement of cryptochrome [17,20–37].

The essential features of the current model [15] are as follows. (i) Multiple, identical magnetoreceptor cells are distributed around the retina. (ii) Each cell contains multiple, identical receptors (i.e. cryptochrome molecules). (iii) The overall response of a cell, summed over the receptors within it, depends on its orientation with respect to the geomagnetic field vector. (iv) The response of an individual receptor depends on its orientation within the cell. (v) Receptor and cellular motion is assumed to be slow enough to be negligible. A direct consequence of (iii) and (iv) is that the receptors should not be randomly oriented in the cells, and the cells should not be randomly oriented within the retina. Complete rotational disorder would result in individual cells producing no directional information and/or different cells having uncorrelated directional responses. At both receptor and cellular levels, there could be no magnetic compass without some degree of ordering [15].

Ritz et al. [15] imagined perfect ordering of both the receptors and the magnetoreceptor cells. Every receptor within a cell was imagined to have exactly the same orientation with respect to a cell-fixed axis system, and the cells were assumed to be ordered within the retina. If, for example, the magnetoreceptor cells had approximate cylindrical symmetry they might be aligned with their symmetry axes normal to the retina, in the same manner as the rod and cone visual receptor cells. A consequence of any such alignment would be that cells in different positions in the retina, and consequently different orientations with respect to the geomagnetic field vector, would have correlated magnetic responses from which the bird could in principle extract a compass bearing [4]. However, perfect crystal-like ordering of receptors and cells is not essential. As argued recently in three independent theoretical studies [32,38,39], a certain amount of static rotational disorder could be tolerated. However, an absolute requirement of the model is that there must be some rotational order, at both receptor and cellular levels.

Cryptochromes, the only molecules under consideration as potential radical pair magnetoreceptors, are small globular water-soluble proteins that are not expected to dissolve and align in membranes as does, for example, the visual receptor rhodopsin in the stacked membrane discs in the rod and cone cells. It has been suggested that the necessary degree of ordering could arise by attachment to cytoskeletal filaments or to ordered membrane proteins [32,40]. Niessner et al. [35] have recently reported the localization of cryptochrome 1a in bands along the membrane discs of the outer segments of ultraviolet/violet cones in the retinas of European robins and domestic chickens. Although association with such ordered structures suggests that the cryptochrome molecules could themselves be aligned, this has yet to be demonstrated. Nor is it known yet whether these particular cryptochromes have a magnetoreceptive function. The lack of an established molecular alignment mechanism has been cited as a major stumbling block of the cryptochrome radical pair hypothesis [41].

An unspoken assumption of the current model is that the absorption of light that leads to the formation of magnetically sensitive radical pairs is isotropic. That is, it is implicitly assumed that magnetoreceptor molecules absorb photons with equal probability, irrespective of their orientation with respect to the direction of propagation of the incident light. This is unlikely to be true and once this assumption is relaxed, it can be seen that even a totally disordered array of static receptor molecules could give rise to a signal that varies with both the location of the cell in the retina and the orientation of the bird's eye with respect to the geomagnetic field vector. The basis of this effect is known as photoselection [42].

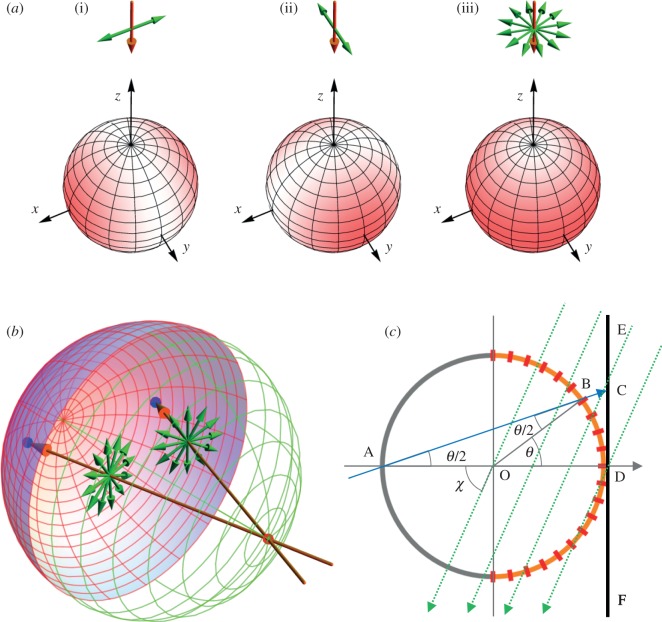
The absorption of light by molecules is intrinsically anisotropic. The probability that a molecule is excited by a photon is determined by the relative orientation of two vectors. One is the transition dipole of the electronic transition, μ, whose direction is fixed within the molecule and determined by its electronic structure. The other is the electric vector, e, of the incident light that lies in the plane perpendicular to the direction of light-propagation. If the light is unpolarized, e has no preferred direction in that plane. The probability that a photon is absorbed is proportional to cos²Ω, where Ω is the angle between the two vectors. Thus, the probability of absorption is zero for molecules oriented such that μ is perpendicular to e and at a maximum for orientations in which μ is parallel to e. Because the electric vector is confined to the plane perpendicular to the propagation direction, the absorption of light is necessarily anisotropic (figure 1a). This photoselection effect is most commonly encountered using plane-polarized light [42,43], but it clearly also operates when the light is not polarized. This is the case considered here: anisotropic absorption arises simply and solely from the fact that e is perpendicular to the direction in which the light propagates.

Figure 1.

Photoselection effects in a model eye. (a) Selective excitation of a subset of disordered molecules by an exciting light beam. The colour density (red) on each sphere indicates the probability that molecules oriented in those directions are excited by a beam of light (brown arrows) directed along the z-axis. In (i) and (ii), the light is polarized with the electric vector (green arrows) aligned along the x- and y-axis, respectively. In (iii), the light is unpolarized, and all orientations of the electric vector in the xy-plane are equally likely. In all three cases, molecules whose transition dipoles lie along the light propagation direction (the z-axis) are not excited at all. (b) Two unpolarized rays of light (brown), each with representative electric vectors (green), are shown entering the eye through the pupil (red spot) and striking the retina (pink/blue hemispherical shell) at different positions (blue spots). For unpolarized light, all orientations of the electric vectors in the plane perpendicular to the propagation direction are equally likely. The extent to which receptors in the retina are photo-excited depends on the direction of their transition dipoles with respect to the incoming light. (c) Model of the eye (based on fig. 5 of [15]) showing a vertical cross section through the centre, O, of a spherical eyeball. The pupil is at A and the retina is the (orange) hemispherical shell on the right-hand side of the figure. A representative ray of light (blue) enters the eye at A and strikes the retina at B. The position of B is specified by θ, the angle between the retina normal, OB, and the z-axis, which is directed along AOD. The angle between the direction of light propagation, AB, and the z-axis is θ/2. Magnetoreceptor cells (red rectangles) are distributed around the retina (−90° ≤ θ ≤ + 90°). A two-dimensional image of the retina is obtained by projecting the light vector AB onto a plane (EF) perpendicular to the z-axis and immediately behind the eye. The image of B is at C. The electric vector of the light ray lies in the plane perpendicular to ABC. The lines of flux of the geomagnetic field (inclination angle χ) are indicated by sloping dotted arrows (green).

To see more clearly how photoselection with unpolarized light could allow randomly oriented cryptochromes to act as a magnetic direction sensor, we imagine, for simplicity, the retina to be a hemispherical shell illuminated by light emanating from a point source (the pupil) positioned at the opposing pole. As indicated in figure 1b, the electric vectors of incoming photons are roughly tangential to the retina at the point of ‘impact’. Receptor molecules oriented with their μ-vectors normal to the retina surface therefore have a lower probability of absorbing light than those whose μ-vectors lie in the plane of the retina. Thus, light absorption leads to a non-uniform orientational distribution of photo-excited molecules and hence of the radical pairs formed from them, even though the absorbing molecules have no rotational order. Light-induced rotational ordering of the transient radical pairs rather than intrinsic ordering of their molecular precursors may therefore be seen as the fundamental condition for a magnetoreceptor cell to exhibit an anisotropic response. We emphasize that this phenomenon does not require the light to be polarized. However, if it is, either naturally, as a result of the scattering of sunlight in the sky [44,45], or because of polarizing elements within the eye, then the photoselection effect is likely to be enhanced.

In the following pages, we explore the magnetoreceptive properties of photoselected distributions of radical pair orientations and argue that a viable magnetic compass could be based on arrays of immobile but completely disordered cryptochromes.

2. Theory

Following Ritz et al. [15], we model the bird's eye as a sphere with the retina covering a hemispherical section of its inner surface (figure 1c). The eye is imagined to operate as a pinhole camera, with the pupil (i.e. the pinhole) being at the spherical pole directly opposite the centre of the retina. Rays of light are assumed to enter the eye and to strike the retina at a position determined simply by their direction, without refraction or scattering. Identical receptor cells are assumed to be distributed throughout the retina. No assumption is made about the mechanism of signal transduction other than that the intrinsic sensitivity of the cells is independent of their location. Although clearly a crude simplification of the potential reality, this model captures the essential physics.

The point of departure from Ritz et al. [15] is that we no longer require the receptors (cryptochromes) within each cell to be mutually aligned. However, in order to compare the range of possible responses with and without photoselection, and with and without receptor alignment, we allow for the possibility of perfect ordering. We assume throughout that molecular motions are slow enough that they may be ignored. The following paragraphs sketch the method used to calculate the effects of photoselection on a radical pair magnetoreceptor; full details can be found in the electronic supplementary material.

We assume that the probability of radical pair formation from a molecule with a given orientation in a cell at a given position in the retina is proportional to the probability that that molecule absorbs a photon. This quantity, denoted p, is calculated from the relative directions of the molecular transition dipole, μ, and the electric vector of the light, e. For unpolarized light, p is averaged over the allowed directions of the electric vector to give 〈p〉. To model the magnetic field effect on an individual radical pair, we follow previous practice [20,46] and define Φ_S as the fractional yield of the reaction product formed from the singlet state of the radical pair. These two quantities—the probability of radical pair formation and the singlet yield per radical pair—are combined to give the yield of the singlet reaction product:

2.1

We refer to S as the ‘signal’ and the reaction product as the signalling state. In the absence of photoselection effects, that is for isotropic illumination, 〈p〉 = 1 and S = Φ_S. For randomly oriented receptor molecules, S is averaged appropriately. When the light is polarized, 〈p〉 is replaced by p.

In some of the simulations presented below, we use a simplified version of Φ_S, denoted :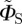

2.2

in which ξ defines the direction of the magnetic field vector with respect to the molecular axis system. This form of Φ_S is obtained by (i) ignoring the isotropic magnetic field effect (which contains no directional information), (ii) omitting all but the first (i.e. simplest) term in a potentially infinite series of anisotropic components, and (iii) dropping a numerical factor (because we do not attempt here to model absolute magnetic field effects or their dependence on the strength of the magnetic field). Note that 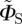, unlike Φ_S, is not restricted to values in the range (0, 1). When 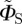is used, the anisotropic signal is calculated as 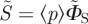or 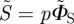. As in Ritz et al. [15], we assume that S (or 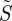) represents the yield of the signalling state and that its dependence on the direction of the magnetic field supplies the directional information required for the compass sense.

3. Results

3.1. Model calculations

To illustrate the features of photoselection most clearly, we use the simplest physically reasonable form of the anisotropic component of the reaction yield, equation (2.2), to calculate the ‘signal’ 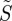from cells at different positions within the retina (equation (2.1)). As described above, 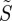is calculated from the probability that the light incident on a cell excites a receptor molecule within it multiplied by the probability that the radical pair so formed reacts to form the signalling state; the product is then averaged over all the orientations of the receptor molecules in the cell.

First, we consider the signals from cells at different locations around the retina, with the eye in a fixed orientation with respect to the magnetic field vector (figure 2). The anisotropic signal 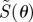, with photoselection effects included, is plotted as a function of θ, the position of the cell in the retina when the transition dipole μ is parallel either to the molecular z-axis (figure 2a) or to the molecular y-axis (figure 2b). (The molecular z-axis is the symmetry axis of the magnetic response.) Also shown are the corresponding signals without photoselection, i.e. with isotropic absorption of light (figure 2c). Signals for these three conditions are compared for completely disordered receptors and for perfectly ordered receptors aligned in each of three orthogonal directions within the cell.

Figure 2.

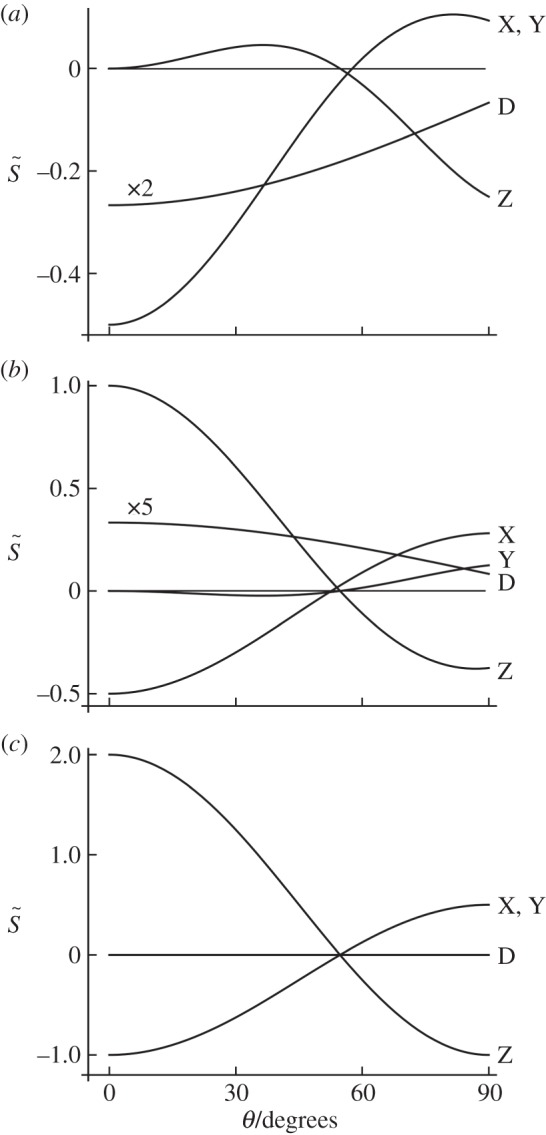
Calculated signal anisotropies 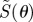for cells at different positions θ (defined in figure 1c) in the retina (with ϕ = 0). The model eye ‘looks’ directly along the magnetic field vector (χ = 0). The transition dipole μ is (a) parallel to the molecular z-axis or (b) parallel to the molecular y-axis; photoselection effects are included in both cases. In (c), the photo-excitation of the receptors is isotropic (so that the direction of μ within the molecule is irrelevant). D: cells in which the receptor molecules are completely disordered. X, Y and Z: cells in which the receptor molecules are perfectly ordered with their z-axes being parallel, respectively, to the cell x-axis, y-axis or z-axis. The calculations were performed for unpolarized light. Note that the vertical scales of the three graphs differ. The lines (D) for completely disordered receptors in (a) and (b) have been scaled vertically by factors or 2 and 5, respectively. Analytical expressions for 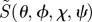are given in the electronic supplementary material, tables S1–S3.

As expected, 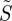is only equal to zero for isotropically illuminated, completely disordered receptors (line D in figure 2c). In all other cases, 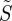varies with θ. Not surprisingly, the signals are generally stronger when the receptors are perfectly ordered and/or excited uniformly irrespective of their orientation than when they are completely disordered and/or excited photoselectively. In all cases, except isotropic illumination of totally disordered receptors, the calculated signals are in principle suitable as the basis of a magnetic compass.

The variation of with cell location can be visualized more comprehensively by projecting the retina onto a plane placed immediately behind the eyeball (as indicated in figure 1c) to obtain ‘visual modulation patterns’ with the same format as in Ritz et al. [15]. Figure 3 shows such projections for an eye looking horizontally towards magnetic north in the northern hemisphere in a geomagnetic field with inclination χ = 66°. The different panels show the variation of 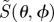with and without photoselection, when the transition dipole is parallel to either the molecular z- or y-axis, and for perfectly ordered and completely disordered receptors. All of the simulated signals are anisotropic and all vary with position in the retina. All could in principle form the basis of a compass sensor. As before, the variation in 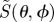is generally smaller for randomly ordered than for perfectly ordered receptors, and smaller with photoselection than without.

Figure 3.

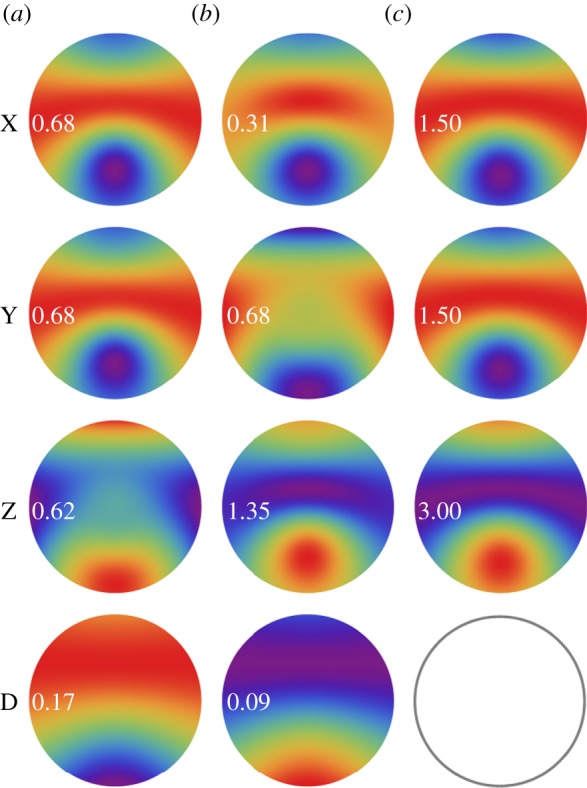
Calculated signal anisotropies 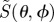for cells at different positions (θ, ϕ) in the retina presented as visual modulation patterns. The model eye ‘looks’ horizontally towards magnetic north in the northern hemisphere in a magnetic field of inclination χ = 66°. The transition dipole μ is (a) parallel to the molecular z-axis or (b) parallel to the molecular y-axis; photoselection effects are included in both cases. In (c), the photo-excitation of the receptors is isotropic. The first (X), second (Y) and third (Z) rows represent perfectly ordered receptor molecules with their z-axes parallel to, respectively, the cell x-axis, y-axis and z-axis. The final row (D) represents 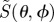for cells in which the receptor molecules are completely disordered. 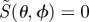for isotropically excited disordered receptors (bottom right). The calculations were performed for unpolarized light. In each case, the number in white represents the difference, 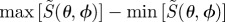, and the colours run from red (maximum) through the spectrum to violet (minimum). θ varies from zero at the centre of each pattern to 90° at the edge. ϕ increases anticlockwise from zero on the right, to 90° at the top, 180° on the left, and 270° at the bottom. Analytical expressions for 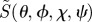are given in the electronic supplementary material, tables S1–S3.

Figure 4 shows visual modulation patterns for an eye looking horizontally in different directions in a magnetic field with inclination χ = 66°. The receptors are completely disordered, and the transition moment is parallel to the molecular y-axis. Photoselection effects are included. The general forms of these patterns are qualitatively similar to those presented by Ritz et al. for perfectly ordered receptors and for isotropic illumination [15]. Once again, we see that photoselection can give rise to usable compass information, even though there is no alignment among the light-absorbing molecules.

Figure 4.

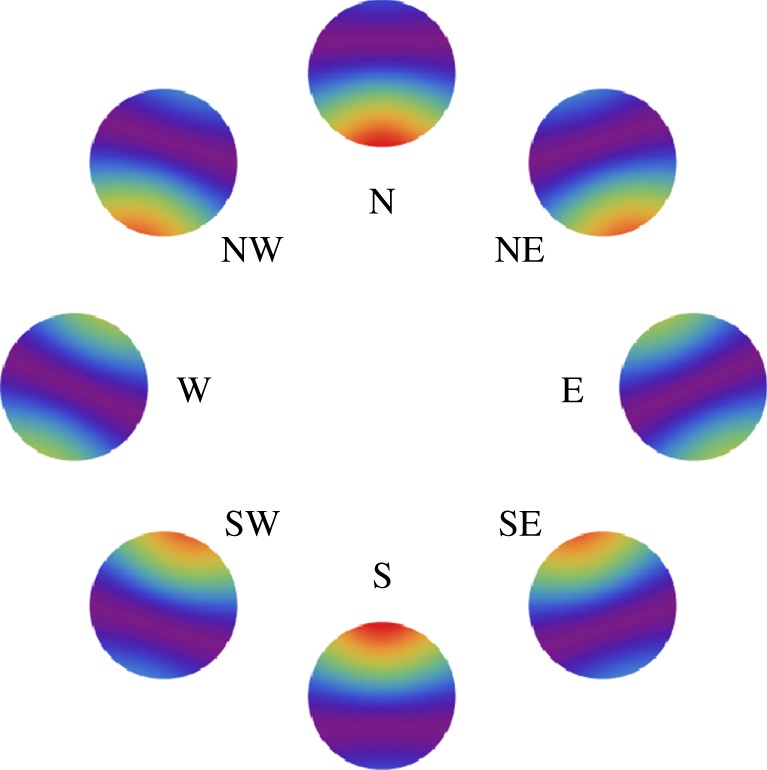
Calculated signal anisotropies 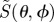for cells at different positions (θ, ϕ) in the retina presented as visual modulation patterns. The model eye ‘looks’ horizontally towards different compass points as indicated, in a magnetic field of inclination χ = 66°. The transition dipole μ is parallel to the molecular y-axis and photoselection effects are included. The receptor molecules are completely disordered and the calculations were performed for unpolarized light. The colour scheme is as described for figure 3. All eight patterns have the same scaling, with .

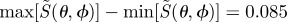3.2. Cryptochrome-based radical pairs

We now move from model magnetoreceptor systems to more realistic radical pairs, based on cryptochrome photochemistry. Behavioural experiments, in which the magnetic orientation of European robins was tested in the presence of weak radiofrequency magnetic fields [17], suggest that the magnetically sensitive radical pair comprises a cryptochrome-bound radical derived from the FAD cofactor paired with a radical in which the electron spin has no significant hyperfine couplings to magnetic nuclei (e.g. ¹H and ¹⁴N). We denote this radical 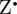. Figure 5a shows the structure of the neutral, protonated 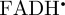radical with representations of the ¹H and ¹⁴N hyperfine tensors. The nuclei with the largest anisotropic hyperfine interactions are the two nitrogens in the central ring of the tricyclic isoalloxazine ring system (N5 and N10) and the proton (H5) attached to N5. The ¹⁴N tensors are almost axial, parallel to one another, and perpendicular to the plane of the ring system. Figure 5a also defines a molecular axis system (x, y, z) in which x is the N5–N10 direction, y is the long axis of the flavin and z is normal to the plane of the ring system. The symmetry axes of the hyperfine tensors of N5 and N10 lie close to the molecular z-axis.

Figure 5.

(a) Structure of the flavin adenine dinucleotide radical (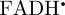) showing the approximate direction of the transition dipole μ of the fully oxidized FAD molecule (dashed purple line; in the xy-plane, making an angle of 15° with the y-axis) and the anisotropic ¹H and ¹⁴N hyperfine interactions. The size and shape of the polar plots represent the hyperfine tensors of the labelled nuclear spins. (b) and (c) are polar plots of the anisotropic parts of the fractional yield of the reaction product formed from the singlet state of the radical pair (Φ_S) for (b) [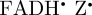] and (c) [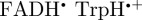]. The colours run from red (maximum positive signal) through the spectrum to blue (maximum negative signal). Further details of the simulations and the hyperfine tensors are given in the electronic supplementary material.

We begin by simulating the magnetic field-dependent reaction yield of the [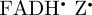] radical pair. Figure 5b shows the anisotropic part of Φ_S, calculated as described in [20,27,47], using hyperfine coupling data for 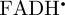(see the electronic supplementary material, [48]). The initial state of the spin system was taken to be pure singlet [26,33,49], the magnetic field strength was set at 50 μT (approximately the geomagnetic field in northern Europe) and the lifetime of the radical pair (1 μs) is close to that expected [2] to give the optimum magnetic sensitivity for an in vivo magnetoreceptor. As 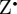is magnetically isotropic, the relative orientation of the radicals is immaterial. The two radicals were assumed not to interact magnetically.

The anisotropic part of the reaction product yield for [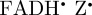] (figure 5b) has a high degree of rotational symmetry around the molecular z-axis. Previous simulations of cryptochrome-based radical pairs showed that the anisotropy of Φ_S is dominated by the hyperfine tensors of N5 and N10 [20]. The same clearly applies to figure 5b in which the symmetry of the two nitrogen hyperfine interactions is directly reflected in the symmetry of Φ_S. Decomposition of figure 5b into its spherical harmonic components (see the electronic supplementary material) shows that Φ_S is overwhelmingly dominated by the 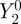component (see the electronic supplementary material, equation S8), which is proportional to 3 cos²ξ − 1, where ξ is the angle between the magnetic field vector and the molecular z-axis (equation (2.2)). Thus, the form of the reaction yield anisotropy expected for [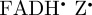] is essentially identical to the simplified reaction yield anisotropy, 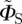, used in the model calculations, the results of which are shown in figures 2–4.

Although a [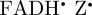] radical pair (or its deprotonated form [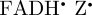]) is consistent with the robin experiments [17], it may be that there is some other explanation for the observed effects of radiofrequency fields on the birds' ability to orient magnetically. We have therefore also simulated the anisotropic part of Φ_S for a 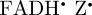radical paired with the radical cation of the terminal tryptophan residue of the Trp-triad in cryptochrome, 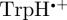. The calculations for [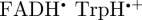] were performed under the same conditions as those for [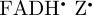]. The hyperfine coupling data for 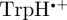are given in the electronic supplementary material, and the relative orientation of the two radicals was taken from the crystal structure of Drosophila melanogaster cryptochrome (Protein Data Bank accession code 3TVS [50]).

Inclusion of some of the 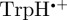hyperfine interactions reduces the symmetry of Φ_S compared with the [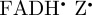] case (figure 5c). Spherical harmonic decomposition (included in the electronic supplementary material) shows that the dominant contributors to Φ_S are the terms 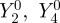and 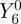, all of which are cylindrically symmetric around the molecular z-axis. Although the form of Φ_S for [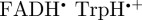] is more complex than that predicted for [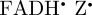], there remains a degree of cylindrical symmetry around the z-axis because the N5 and N10 hyperfine tensors are still the major determinants of the anisotropic signal.

The other factor that must be considered for a radical pair magnetoreceptor is the direction of the transition dipole of the light absorber. For both the radical pairs considered above, the relevant absorption band is that of the fully oxidized state of the FAD, centred at 450 nm. Experimental and theoretical studies of the electronic states of fully oxidized flavins [51,52] concur that the transition dipole of this band lies in the plane of the flavin ring system, rotated by about 15° from the molecular y-axis (dashed purple line in figure 5a).

To summarize, the magnetic field effect (Φ_S) expected for cryptochrome-based radical pairs has either near-perfect ([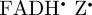]) or approximate ([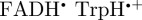]) symmetry around the molecular z-axis. The transition dipole lies in the xy-plane, roughly parallel to the molecular y-axis of the FAD chromophores. Figures 2b, 3b and 4 therefore provide an excellent impression of magnetic compass sensing by [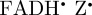] and a good guide for [].

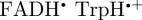3.3. Polarized light

Finally, we turn briefly to the effects of polarized light. It is clear that polarization is irrelevant in the original model of Ritz et al. in which the absorbing molecules are assumed to be excited isotropically. The simulations in figures 2–4 were performed with unpolarized light; however, photoselection effects are expected to be more pronounced for excitation with polarized light because of the greater orientation-selection possible when the electric vector of the light has a preferred direction in the plane perpendicular to the propagation direction (figure 1a). Figure 6 shows the variation of 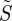for disordered receptors in a cell at the position in the retina diametrically opposite the pupil (θ = 0), as a function of the orientation of the model eye with respect to the magnetic field direction (χ,ψ), for (a) unpolarized light, and light polarized along (b) the retina x-axis (ɛ = 0) or (c) the retina y-axis (ɛ = π/2) (see the electronic supplementary material, equation S3). In all three cases, the behaviour of an FAD-based radical pair was modelled by taking the transition dipole μ to be parallel to the molecular y-axis and using equation (2.2) for the anisotropic part of the magnetic field effect. As anticipated, the dependence on the magnetic field direction is stronger when the light is polarized and depends on the direction of the polarization axis. Although, the enhanced photoselection effects afforded by polarized light have the potential to boost the signal obtainable from completely disordered receptors, we stress that polarization is not essential. As indicated in figures 2–4, photoselection with unpolarized light is in principle sufficient for a magnetic compass.

Figure 6.

Calculated signal anisotropies for a cell containing completely disordered receptors positioned at the centre of the retina (θ = 0, point D in figure 1c) with the model eye ‘looking’ in different directions (χ,ψ) with respect to the magnetic field vector. (a) unpolarized light; (b) polarized light, ɛ = 0 (electric vector parallel to the retina x-axis); (c) polarized light, ɛ = π/2 (electric vector parallel to the retina y-axis). The transition dipole μ is parallel to the molecular y-axis; photoselection effects are included in all three cases. Analytical expressions for are given in the electronic supplementary material, tables S4 and S5.

4. Discussion

The main conclusion here is that photoselection effects can in principle allow a radical pair photo-reaction to act as a magnetic direction sensor even though the receptor molecules have no rotational order and the light is unpolarized. The sensitivity of such a compass is less than the optimum performance of one composed of perfectly ordered receptors. It is lower still when compared with isotropic excitation of perfectly ordered receptors, although it is difficult to see how light entering the eye via the pupil could illuminate a static receptor molecule in the retina with the same probability from all directions. The sensitivity penalty associated with complete receptor disorder is less severe when the comparison is with imperfectly ordered receptor molecules and/or when the cells are not perfectly aligned with respect to the retina [32,38,39] (as assumed in Ritz et al. [15]). Nevertheless, it is important to ask whether a magneto-sensor based on disordered cryptochromes would be sufficiently sensitive to be viable. We believe that this question is unanswerable at present. So little is known about the signal transduction mechanisms that the primary detection sensitivity is currently a matter of speculation [53]. It is true that one can estimate the number of cryptochrome molecules needed in the eye to achieve a given angular resolution for the compass [20,32,39,54], but the results are heavily model-dependent, requiring many simplifying assumptions. Similar problems are encountered when estimating the compass accuracy from behavioural studies. The observation that radiofrequency fields that are some 30 000 times weaker than the geomagnetic field are able to disrupt the magnetic orientation of European robins [17] could be taken to suggest an exquisite level of magnetic sensitivity, one that might easily accommodate the lower efficiency associated with completely disordered cryptochromes.

If one accepts that rotational ordering of cryptochromes is not a prerequisite for compass performance, then at least some of the objections to the radical pair hypothesis fall away. The proteins would then no longer need to be anchored to aligned structures such as cytoskeletal filaments or membrane proteins and could be contained within cells that have no preferred orientation in the retina. However, the requirement identified by Lau et al. [38] still remains: rotational motion must be constrained. Unless the average time the molecule takes to rotate through approximately 90° is longer than about a quarter of the radical pair lifetime, the magnetic field effect is very likely to be strongly attenuated. As argued in Lau et al. [38], for a molecule that has the size of cryptochrome, this would require the rotational diffusion to be only 10 times slower than in pure water. Such a modest degree of immobilization could be achieved in a number of ways without requiring specific interactions with aligned cellular structures.