Turnover of fibrillar collagen in soft biological tissue with application to the expansion of abdominal aortic aneurysms

Abstract

A better understanding of the inherent properties of vascular tissue to adapt to its mechanical environment is crucial to improve the predictability of biomechanical simulations. Fibrillar collagen in the vascular wall plays a central role in tissue adaptation owing to its relatively short lifetime. Pathological alterations of collagen turnover may fail to result in homeostasis and could be responsible for abdominal aortic aneurysm (AAA) growth at later stages of the disease. For this reason our previously reported multiscale constitutive framework (Martufi, G. & Gasser, T. C. 2011 J. Biomech. 44, 2544–2550 (doi:10.1016/j.jbiomech.2011.07.015)) has been enriched by a collagen turnover model. Specifically, the framework's collagen fibril level allowed a sound integration of vascular wall biology, and the impact of collagen turnover on the macroscopic properties of AAAs was studied. To this end, model parameters were taken from the literature and/or estimated from clinical follow-up data of AAAs (on average 50.7 mm-large). Likewise, the in vivo stretch of the AAA wall was set, such that 10 per cent of collagen fibres were engaged. Results showed that the stretch spectrum, at which collagen fibrils are deposed, is the most influential parameter, i.e. it determines whether the vascular geometry grows, shrinks or remains stable over time. Most importantly, collagen turnover also had a remarkable impact on the macroscopic stress field. It avoided high stress gradients across the vessel wall, thus predicted a physiologically reasonable stress field. Although the constitutive model could be successfully calibrated to match the growth of small AAAs, a rigorous validation against experimental data is crucial to further explore the model's descriptive and predictive capabilities.

1. Introduction

Abdominal aortic aneurysms (AAAs) are defined as local and permanent dilatations of the infrarenal aorta that are frequently observed in the elderly male population. AAAs can grow into shapes that are prone to rupture, which are lethal in up to 90 per cent [1] of all cases. A rupture risk assessment is central to the management of AAA patients, and accurate rupture risk assessments could reduce the related mortality rate without unnecessarily increasing the rate of AAA repair interventions. Growth rate and wall strength of AAAs are thought to be linked [2–5], such that a reliable growth predictor would reinforce an AAA rupture risk assessment, i.e. give a better-graded indication for elective repair.

Describing the growth of aneurysms is an active field of research, and models for abdominal aortic [6–9] and cerebral [10–14] aneurysms have been reported. Although these models are able to predict some clinical observations, they still require significant development to be launched clinically, i.e. to predict patient–individual aneurysm rupture in a clinical setting.

AAAs are the result of irreversible pathological remodelling of the extracellular matrix (ECM) [15]. ECMs provide an essential mechanical environment to which vascular tissue is continuously exposed, and mainly contain elastin, collagen and proteoglycans (PGs) [16]. While elastin is a stable protein having a half-life of tens of years [17], collagen is normally in a continual state of deposition and degradation [18]. Specifically, vascular collagen has a normal half-life of 60–70 days [19], which decreases by up to 10-fold in the case of disease and injury [20]. Moreover, elastin decreases significantly [21] and fragments [22] through the aneurysmatic expansion of the aorta.

Collagen fibrils are regarded as one basic building block of ECMs and give mechanical strength, stiffness and toughness to the vasculature. Collagen fibrils are locally secreted by fibroblasts and assembled into organized suprafibrillar structures that, to a large extent, determine the macroscopic mechanical behaviour [23]. Consequently, understanding the development of hierarchical collagen structures is crucial to understanding the mechanical properties of the vascular wall.

It is well accepted that the collagen structure develops under the action of mechanical loading and eventually leads to mechanically optimized structures. Physiological maintenance of these structures relies on a delicate (coupled) balance between continual degradation and synthesis of collagen. The maintenance of fibrillar collagen is realized by fibroblast cells, i.e. by synthesis of new collagen and degradation by metalloproteinases (MMPs) of existing collagen [24]. Mature fibroblasts perceive changes in the mechanical strains/stresses and adjust their expression and synthesis of collagen molecules in order to account for the changes in their micro-mechanical environment. While an alteration of collagen turnover is essential in response to injury [24–28], a malfunction of collagen turnover could fail to result in homeostasis and determine AAAs disease [29]. Specifically, at later stages of aneurysm disease, collagen synthesis is insufficient to counteract higher mechanical wall stress [29]. Consequently, the structural integrity of the wall is not ensured, such that wall strength decreases and the risk for AAA rupture increases proportionally.

The present work introduces a novel growth model for AAAs, where their expansion is a direct consequence of the pathological remodelling of fibrillar collagen. Collagen fibrils are thought to be assembled into collagen fibres that, in turn, define the tissue's macroscopic properties [30–33]. This multi-scale view allowed us to integrate vascular wall biology within the constitutive framework and led to robust and fast finite element (FE) implementation. The model was calibrated to the growth of AAAs that were followed-up with computer tomography–angiography (CT–A).

In contrast to earlier models [6,7,9,11–14], the present description does not constrain the collagen fibres to develop along certain orientations, and the predicted collagen organizations were in good agreement with our histological study of the AAA wall [34].

2. Methods

2.1. Passive constitutive response

The wall of later stage aneurysms shows a negligible amount [21] of fragmented [22] elastin, as well as a severe decrease in smooth muscle cells [35]. Consequently, the AAA wall was regarded as a fibrous collagenous tissue, where collagen fibres reinforced an otherwise isotropic matrix material. At low strains, collagen fibres are (mechanically) inactive, and the non-collagenous (matrix) material determines the vascular wall's properties. The matrix material was described by the (classical) isotropic neoHookean strain energy function ψ_nH = c(I₁ − 3), where c > 0 was a stress-like material parameter, i.e. twice the referential shear stiffness, and I₁ = J^−2/3F^TF : I denoted a strain invariant [36].

An orientation density function ρ(N) = ρ(−N) defined the alignment of the collagen fibres with respect to their referential orientations N (with |N| = 1) [37]. For simplicity, the passive wall response was modelled with an isotropic collagen orientation density (ρ(N) = ρ₀), which adjusted over time according to the local stretch field (see §2.2).

Collagen fibres were assembled from bundles of collagen fibrils with different undulations, following a virtually linear stress–strain law [33]. The classic ‘shear-lag’ theory [38,39] was adopted, and shear forces were thought to be distributed all along the length of the collagen fibril in order to support inter-fibrilar load transition. Specifically, small PGs such as decorin bind non-covalently but specifically to the collagen fibril at about 60 nm intervals [40]. The PG-based cross-linking was supported by numerous experimental studies showing that PGs play a direct role in inter-fibril load sharing [40–46], and this has also been verified through theoretical investigations [47–49]. However, it was also noted that the biomechanical role of PGs is discussed controversially, and some data indicate minimal, if any, PG contribution to tensile properties of the tissue [47,50,51].

The undulation of collagen fibrils, within a collagen fibre, was determined by a triangular probability density function (PDF). Specifically, the triangular PDF defined the relative amount of engaged collagen fibrils in response to the stretch λ that was applied to the collagen fibre [33]. Consequently, the limits λ_min and λ_max of the triangular PDF denoted fibre stretches, at which the first and last collagen fibrils engaged, i.e. straightened out. Assuming an incompressible collagen fibre, these assumptions yielded piece-wise analytical expressions for the collagen fibre's Cauchy stress [33]

2.1

with Δλ = λ_max−λ_min and and k denoting the stiffness of the collagen fibril proteoglycan-complexes. Finally, an affine deformation between the continuum and the collagen fibre was considered, i.e. λ = |FN|.

2.2. Collagen turnover model

Collagen turnover in the vascular wall is accomplished by fibroblast cells that are spread throughout the collagen network. Apart from continuously producing and degrading collagen fibrils, fibroblasts are thought to sense the state of stress or strain and even pre-stretch collagen fibrils prior to deposition. Specifically, a biomechanical mode for collagen turnover has to fulfil three tasks:

• — Detail what quantity stimulates collagen turnover, i.e. define the sensing mechanism.

• — Quantify how the stimulus is translated into degradation and production of collagen.

• — Detail how matured collagen is removed and how newly formed collagen is integrated into the existing collagen structure.

2.2.1. Sensing mechanism

We considered fibroblasts being connected to collagen fibrils, which in turn allowed them to sense the collagen fibre stretch λ. At a certain λ, those fibroblast cells that are connected to active collagen fibrils will experience a mechanical stimulus, whereas those that are connected to undulated fibrils cannot feel any stretch (figure 1a). Consequently, a stretch-based model [6,7,12–14] that allowed a gradual sensing of the collagen fibre stretch was considered.

Figure 1.

The hierarchical structure of a collagen fibre built-up of statistically distributed collagen fibrils that are interlinked by proteoglycan (PG) bridges and populated by fibroblast cells. (a) Homeostatic condition at 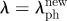that leads to (b) Supra-physiological stretched condition at that leads to .

In a normal vessel wall, only about 6 or 7 per cent of collagen fibrils are engaged at physiological deformation [52,53]. Unfortunately, such data do not exist for the AAA wall and, motivated by the higher stress, we assumed that 10 per cent of collagen fibrils were engaged in the AAA wall. On the basis of triangular PDF, the density of engaged collagen fibrils was related to the distribution parameters according to for λ_min ≤ λ ≤ Δλ/2. Consequently, the physiological stretch could be expressed through with denoting the density of engaged collagen fibrils at the physiological deformation, i.e. 10 per cent. Similarly, we introduced the homeostatic collagen fibre stretch

2.2

In order to reach this stretch, the newly formed collagen fibrils had to be deposited with and Here, and denote the lower undulation limit, the higher undulation limit and the width of the triangular PDF that defines the collagen that was deposited. At homeostasis and physiological loading, the collagen stretch will tend to and a suitable optimality condition reads

2.3

where ζ(N) serves as the mechanical stimulus. For ζ > 1, the existing collagen is stretched higher than the newly formed collagen, such that in total, more collagen is required to reach homeostasis. In that case, collagen turnover needs to be amplified in order to increase the total collagen density in the tissue. Similarly, for ζ < 1, collagen turnover needs to slow down to reach homeostasis through a net loss of collagen. It is emphasized that ζ depends on the orientation through the collagen orientation vector N, and similar collagen-stretch-based stimuli have been proposed earlier in the literature [6,7,12–14]. In contrast, other stimuli such as stress [8–11] and the ratio between systolic and diastolic stretches [54] have also been suggested.

2.2.2. Collagen degradation and production rates

It was assumed that collagen degraded isotropically according to

2.4

where η defines the time-scale of the degradation process and ρ is the total collagen density. Equation (2.4) is independent from the orientation N and the local strain, such that degrading collagen is purely time-based; i.e. as soon as collagen matures, it is removed.

The proposed collagen production was based on the idea that fibroblasts will produce collagen in an effort to maintain a homeostatic environment. Consequently, for a particular direction N, the production of collagen fibrils was related to the stimulus ζ(N) and reads

2.5

Here, denotes the maximum collagen production rate, which aimed at modelling the limited capability of fibroblasts to produce collagen fibrils [55]. According to equation (2.5), the collagen production along the referential direction N is proportional to the mechanical stimulus ζ(N), but it cannot exceed the maximum rate According to equations (2.4) and (2.5), the net production of collagen vanishes at homeostatic conditions , i.e. Likewise, the model agrees with the observation that mechanical stretching of collagen fibrils protect them from enzymatic degradation by MMPs [56].

2.2.3. Collagen fibril disintegration and integration

Collagen fibrils disintegrate from the existing collagen structure without changing their undulation characteristics; i.e. the collagen density ρ is reduced, but the limits λ_min and λ_max of the triangular PDF that determine the fibril undulation spectrum remain unchanged. In contrast, newly formed collagen fibrils are integrated at a certain distribution of pre-stretches. The idea of integrating pre-stretched collagen has been used in the past [57] and is supported by the observation that fibroblasts have the ability to contract the surrounding ECM [17]. Likewise, fibroblasts are observed to direct the formation of groups of short collagen fibrils that appear to connect fibroblast cells [58].

The deformation of a newly formed collagen fibril is demonstrated in figure 2, where we defined a local intermediate configuration Ω_{st i} at which the individual ith collagen fibril was straight but did not carry any load, i.e. it was stress-free. The individual ith collagen fibril was thought to be integrated (cross-linked) in the current (deformed) configuration Ω at a certain stretch that was measured relative to its hypothetical intermediate configuration Ω_{st i}. Consequently, the straightening stretch was required to straighten this collagen fibril relative to the reference (undeformed) configuration Ω₀, where λ = |FN| denotes the total macroscopic stretch in direction of the fibril. Similar to the passive model, collagen fibrils were considered in a statistical sense, and the undulation of the newly formed collagen fibrils followed a triangular PDF having the limits and Finally, and as demonstrated later, adding the newly formed collagen to the already existing one, can be regarded as a continuous update of the PDF that represents the collagen fibril distribution.

Figure 2.

Finite strain kinematics of the collagenous tissue. The ith newly formed collagen fibril maps from the reference configuration Ω₀ through its intermediate configuration Ω_{st i} into the current configuration Ω.

2.2.4. Updating of the collagen fibril distribution

The cumulative collagen distribution X was defined by adding the newly formed collagen distribution to the already existing collagen distribution . For convenience, the mean E(X) = (λ_max + λ_min)/2 and variance var(X) = (λ_max − λ_min)²/24 of the triangular PDF were introduced, such that the cumulative triangular distribution was given by

2.6

Here, the weighted mean and the weighted variance decomposition were applied, and denotes the relative amount of newly formed collagen. In addition, the abbreviations

and

were used.

Consequently, the distribution X was defined through equation (2.6) as soon as and and dξ⁺ of the newly formed collagen were given. In vivo collagen fibrils are deposited on top of the cyclically stretched vascular wall, such that differently oriented collagen fibrils might have different and Unfortunately, no related experimental data are available, and we simply used orientation-independent undulation limits throughout this study.

Solving the set of equations (2.6) for and of the cumulative distribution of collagen fibrils gives

2.7

with 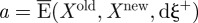and

Finally, it is noted that equation (2.7) only held for small differences between and , such that collagen turnover that was close only to the homeostatic condition could be described within this statistical framework.

2.3. Numerical implementation

The proposed multiscale model for vascular tissue was implemented in FE software (FEAP v. 8.2, University of California at Berkeley, CA, USA) at the Gauss point level of a Q1P0 mixed Finite Element [59] formulation. To this end, a quasi-incompressible implementation was followed, and the volumetric energy contribution ψ_vol = κ(J − 1)² was added to the constitutive description. The volumetric stiffness κ was adjusted at each time step such that the volume ratio J → 1 with J = det F. Consequently, the macroscopic Cauchy stress was additively decomposed and reads

2.8

where σ_vol is the volumetric stress contribution, and and are contributions that arose from the matrix material and the collagen reinforcement, respectively. The superimposed bar indicates isochoric stress quantities, and σ_vol and are detailed elsewhere [60]. The macroscopic stress 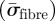that arose from the collagen fibres was computed by integration over all fibres, i.e. over all directions. This contribution is detailed in §2.3.1.

2.3.1. Microfibre model

Following the pioneering work of Lanir [30], the macroscopic stress contribution from the collagen fibres was computed by integration over the solid angle ω, i.e. by a spherical integration over the unit sphere, and reads

2.9

This integral was numerically approximated by a spherical design [31,61], i.e. where l_int denotes the total number of integration points. Details regarding the numerical implementations are given in table 1. It is noted that the applied two-scale simulation required considerable memory demands owing to storing the microstructural data (λ_min, λ_max and ρ) at each Gauss point.

Table 1.

Numerical implementation of the collagen-related contributions of the multiscale vascular tissue model. The Cauchy stress and the spatial stiffness at the Gauss point of a finite element were computed. The microstructure was represented by the collagen orientation density ρ and the undulation limits λ_min and λ_max, which were stored in the history vector.

3. Results

In this section, the application of the introduced constitutive framework is demonstrated. Specifically, the interplay between collagen structure and wall stress, as well as the applicability to investigate realistic (clinically relevant) problems is shown. Passive constitutive properties were taken from the literature, and turnover properties were estimated from clinical follow-up data of 30 small AAAs, i.e. having maximum diameters smaller than 55 mm. To this end, the expansion of the aneurysms between two consecutive CT–A scans was measured, and patient-specific mean arterial pressures (MAPs = 1/3 systolic + 2/3 diastolic blood pressure) were computed from the patient charts. The data analysis revealed a maximum outer diameter of 50.7 (s.d. 5.05) mm, MAP of 103 (s.d. 10.44) mmHg (13.73 (s.d. 1.39) kPa) and an average growth rate of 2.9 (s.d. 5.6) mm yr⁻¹. Structural FE simulations (A4research, VASCOPS GmbH, Austria) of these cases showed a circumferential strain and Cauchy stress in the aneurysmatic sac of 6 (s.d. 1.13) per cent and 106 (s.d. 48.76) kPa, respectively.

3.1. Parameter estimation

The material parameters c,k and the structural parameters λ_min, λ_max defines the passive (time-independent) constitutive response. Previously reported parameters [33] that capture the mean population properties of the AAA wall [62], were used in the present study. Similarly, the width of the triangular PDF that defined the newly formed collagen was estimated from [33,34] and set to Δλ^new = 0.24.

The turnover parameter η that defined the time scale for homeostatic collagen turnover was set to two months, i.e. the half-life of vascular collagen [19]. In contrast, no applicable data to estimate the turnover parameters and are reported in the literature, and these parameters were estimated from the response of a numerical relaxation test and the expansion of an AAA tube model.

3.2. Relaxation test

Because the spectrum of the collagen deposition stretch was assumed to be constant, was also constant, and the mechanical stimulus through equation (2.3) for a relaxation test, i.e. where the macroscopic stretch λ is fixed, is time-independent. Without constraining the collagen production rate (i.e. ), collagen would be constantly produced, such that the stress increases continuously until infinity. Consequently, we used such a relaxation test to define the limit of the collagen production rate [63]. To this end, a strain of 6 per cent was applied and a steady-state target stress of 106 kPa was reached with Here, sr stands for steradian and denotes the unit of the solid angle. The undulation parameters and were used, where §3.3 motivates this choice.

3.3. Abdominal aortic aneurysm tube model

The AAA tube model was loaded with a pressure of 13.73 kPa, and had an outer diameter and wall thickness of 50.7 mm and 2 mm, respectively. Symmetry conditions were applied and 300 hexahedral finite elements represented a quarter of the model (figure 5). Bending effects from non-homogeneous stress across the wall were captured by five finite elements across the thickness. The limit of the collagen production was fixed at By setting the undulation of the newly formed collagen to and the tube model showed homeostasis, i.e. its diameter neither grew nor shrank over time (see dashed line in figure 3). Here, homeostasis is understood as a purely hypothetical condition, because the AAA is known to grow, i.e. to continuously change its tissue constitution over time.

Figure 5.

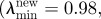
Maximum principal Cauchy stress computed with the abdominal aortic aneurysm (AAA) tube model. (a) Prediction that neglected collagen turnover (passive model). (b) Prediction that accounted for collagen turnover and used parameters ( ) leading to homeostasis. (c) Prediction that accounted for collagen turnover and used parameters ) that matched the growth of small AAAs.

Figure 3.

Evolution of the abdominal aortic aneurysm (AAA) tube model over time with respect to different undulations of the newly formed collagen fibrils. The maximum collagen production rate was set to The width of the triangular probability density function (PDF) was fixed at Δλ^new = 0.24, while the lower undulation limit was changed.

In addition to the homeostatic solution, the implications of a step-change in were investigated (figure 3). Increasing the undulation of collagen fibrils, i.e. decreasing their pre-stretch at deposition, triggered continuous growth while the AAA tube model shrank when depositing the newly formed collagen fibrils at a lower undulation. Finally, the AAA tube model matched the average expansion of small AAAs for and i.e. the diameter increased by 2.9 mm yr⁻¹ (see the black solid line in figures 3 and 4).

Figure 4.

Calibration of the abdominal aortic aneurysm (AAA) tube model (thick line) with respect to clinical follow-up data (thin lines) of small AAAs.

Owing to its highly nonlinear character, the passive constitutive model predicted a strong stress gradient across the wall thickness (figure 5a). Such a stress gradient is considered to be non-physiological and, among other constitutive refinements, residual strains in the load-free configuration are able to smooth the stress across the wall thickness. Activating collagen turnover and ) on the top of the passive formulation redistributed the stress in the collagen fibres. Consequently, at homeostatic conditions, the stress across the wall was almost uniform (figure 5b). Depositing newly formed collagen at a higher undulation ( and ) caused not only continuous growth of the tube but also failed to reach homeostasis, leading to a weak stress gradient across the wall (figure 5c).

3.4. Organ-level analysis

3.4.1. Modelling assumptions

The aneurysm geometry between the renal arteries and 1.5 cm distal the aortic bifurcation was segmented from routinely taken CT–A data (A4research). In order to provide an artefact-insensitive and user-independent reconstruction, deformable (active) contour models were applied [64]. A single finite element across the wall thickness was used, and in total, 6209 hexahedral elements represented the AAA. A constant wall thickness of 2 mm was prescribed, and the influence of the intra-luminal thrombus was disregarded. The model was loaded by 100 mmHg (13.33 kPa) MAP and fixed at the bottom and top slices (nodal degrees of freedom were locked). Finally, no contact with surrounding organs that could have influenced the expansion of the aneurysm was considered.

3.4.2. Problem-solving and numerical predictions

Passive response. The stress field without collagen turnover, i.e. with the passive constitutive description, was computed first. To this end, the pressure loading was incremented and the quasi-static solution was computed using a direct solver (FEAP v. 8.2, University of California at Berkeley). We neither observed numerical instabilities nor required any kind of numerical regularization. In line with the results from alternative passive AAA wall models [65], the macroscopic stress was complex distributed over the wall and showed regions of stress concentrations (figure 6a).

Figure 6.

Stress and shape development of a patient-specific abdominal aortic aneurysm (AAA) model. (a–c) Maximum principal Cauchy stress in a patient-specific AAA model. (a) Maximum principal Cauchy stress prediction that neglected collagen turnover (passive model). (b) Maximum principal Cauchy stress prediction that accounted for collagen turnover and used parameters ) leading to homeostasis (dashed line). (c) Maximum principal Cauchy stress prediction after one year collagen turnover with parameters ( ) that matched the growth of small AAAs. (d) AAA shape difference between the homeostatic solution (b) (dashed line) and the prediction after 1-year growth (solid line; c).

Homeostatic conditions. On top of the passive prediction, collagen turnover was activated ( ), such that the AAA geometry remained stable over time. This homogenized the wall stress distribution (compare figure 6a,b) and shifted the initially isotropic collagen distribution to a locally orthotropic distribution (figure 7a,b). Consequently, collagen adapted [66] until the optimal microstructure configuration was reached and the macroscopic stress converged to the homeostatic solution.

Figure 7.

Numerically predicted collagen distribution in the abdominal aortic aneurysm (AAA) wall. The view is perpendicular to the wall and taken at the site of peak wall stress (PWS). (a) Isotropic distribution used by the mode that neglected collagen turnover (passive model). (b) Predicted distribution at homeostasis. (c) Predicted distribution after 10 years' growth.

Abdominal aortic aneurysm growth. On top of the homeostatic prediction, collagen undulation parameters were changed ( ), such that the AAA enlarged over time (figure 6). While the macroscopic stress did not change considerably (figure 6c), the collagen distribution in the wall was altered with respect to its initial configuration (figure 7). Finally, figure 6d illustrates the AAA shape development for 1-year growth.

To carry higher wall stress, more collagen was required, such that collagen turnover (production and degradation ) rates peaked at the site of peak wall stress. Owing to the fibroblast's limited capability to produce collagen, the collagen production was no longer able to compensate for the increasing wall stress. Consequently, AAA growth was amplified and the risk for rupture increased, i.e. wall stress increased considerably over time (figure 8).

Figure 8.

Development of the maximum principal Cauchy stress in the abdominal aortic aneurysm (AAA) wall after 2, 5 and 10 years. Simulation used parameters (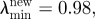 ) that matched the growth of small AAAs over a period of about one year.

4. Discussion

Biological tissues respond to their mechanical environment and predictions based on passive constitutive models, i.e. suppressing tissue remodelling and growth can only cover a limited time period. Vascular tissue develops at its in vivo loading state, which induces residual strains in its (hypothetical) load-free configuration, i.e. in the setting that typically serves as a reference for computations. Predicting realistic physiological stress states with passive constitutive models requires residual strains in the load-free configuration, which, for complex geometries, are unfortunately unknown. Consequently, the key for improving biomechanical models is to understand the tissue's inherent property to adapt to mechanical environments, and in that respect, computational simulations can be potentially helpful. Specifically, multiscale models allow considering biological process at the microscale that, in turn, define the development of the vascular wall's macroscopic mechanical properties.

The present work enriched our previously reported multiscale constitutive model [33] by considering collagen turnover. Specifically, the model's collagen fibril level provided an interface to integrate the vascular wall biology and to study the impact of collagen turnover on the macroscopic properties of AAAs. The applied concept aimed at reflecting the mechanics of later stage AAAs, i.e. where the impact of elastin and smooth muscle cells can be neglected. However, such a modelling approach does not reflect aneurysm formation, where the interaction between elastin, collagen and smooth muscle cells should be particularly considered [9,11,67]. That explains also the manifold overestimation of growth of the non-aneurysmal regions as it was predicted by our model.

Most importantly, the results indicated a remarkable impact of collagen turnover: it avoided high stress gradients across the vessel that is thought to be non-physiological. Likewise, the deposition of collagen fibrils at certain stretch defined homeostatic conditions and vascular geometry remained stable over time. In contrast, depositing collagen fibrils at a higher undulation limit triggered continuous growth, where the expansion rate of small AAAs was used for parameter identification.

Finally, setting an upper boundary for the collagen production rate (constraint collagen turnover) destabilized the equilibrium of collagen turnover and amplified growth. The observation that collagen cross-linking increased in the aneurysmatic aortic wall justified limiting the collagen production. Specifically, increased collagen cross-linking suggested that at a certain stage the synthesis of collagen was reduced, while existing collagen continued to be cross-linked [68,69]. By limiting the collagen production in our model, the mechanical stimulus was deactivated and the collagen synthesis could no longer support a net increase of collagen. Considering the rapidity of collagen remodelling, this circumstance could quickly lead to aneurysm rupture [29]. Note that the final common pathway of aneurysm progression involves proteolytic activity, and collagen degradation is a prerequisite for aneurysm rupture [70].

The undulation limits and of the newly formed collagen as well as the maximum collagen production rate were key parameters in our model. The experimental identification of these parameters was not straightforward and, when only considering macroscopic observations, not unique either. Specifically, increasing the undulation limits and lowering the maximum collagen production both led to an increased AAA growth rate. The definition of experimental protocols that would allow the unique identification of these parameters remains to be addressed in future studies.

Collagen undulation is a microstructural parameter that is directly related to the load transmission from the ECM to fibroblast cells. Consequently, we proposed that alteration of the distribution of collagen undulation is the main contributor to control AAA expansion rate. Through the histomechanical collagen fibre model, the distribution of collagen undulation is directly related to the stress–stretch property of the collagen fibre. Consequently, our mechanical stimulus could be formulated as the strain-based equation (2.3), i.e. very similar to earlier models [6,7,12–14]. With the help of the histomechanical relation equation (2.1), the mechanical stimulus could also be formulated in stress space that leads to a stress-based stimulus, which has also been suggested in the literature [8–11].

One key assumption in our model (similar to model [14]) was linking the collagen turnover rate to the amount of existing collagen, i.e. through the collagen density ρ in the rate equations. This assumption implied that the fibroblast–collagen ratio remained constant, and, to the authors' knowledge, no sound experimental evidence for that has been reported in the literature. Similarly, we assumed a constant pre-stretch of newly formed collagen without sound experimental evidence.

Apart from the macroscopic consequences of collagen turnover, it shifted the initially isotropic collagen orientation density into a locally orthotropic distribution. This corresponds well with our histological study of the AAA wall [34].

Most interestingly, AAAs do not always enlarge. Sometimes, they might remain stable or even shrink over time [71]. While the present collagen turnover model is basically able to predict shrinking, i.e. when placing the newly formed collagen fibrils at lower undulation limits, no portion of the investigated AAA in this study shrank over time.

Although collagen turns over on top of a pulsating vascular wall, our collagen turnover model considered average rather than pulsating mechanical quantities. Specifically, the differences in strain pulsations in circumferential and axial directions may influence the undulation characteristics of collagen fibrils, i.e. collagen fibrils aligned with circumferential directions and axial directions may differ. This difference has also been found by fitting the passive model to biaxial AAA data [34]. Consequently, relating the width of the undulation spectrum (i.e. the parameter Δλ^new) of collagen fibrils to the physiological strain pulsation might improve the present model.

Certainly, a change in collagen density will affect the thickness of the vessel wall. To the authors' best knowledge, no related experimental data have been reported in the literature and, for simplicity, the incompressibility assumption was used in the present study. However, for larger growth, this assumption leads to an unrealistically thin wall. It is also noted that approaches that predict the wall thickness based on the homeostasis assumption have been reported in the literature [72]. Although an intra-luminal thrombus is known to be an important solid structure [73] that increases the predictability of AAA models [74], it was disregarded in the present study. Besides the intra-luminal thrombus's direct solid mechanical impact, it must also be seen as a dynamic structure that develops in time. Consequently, a clinically relevant AAA growth model should also account for the flow [75] of blood through the aneurysm and its coagulation process [76] to thrombus formation. Similarly, possible contact with surrounding organs was not considered through our AAA model. Naturally, the present growth model could be improved by considering the intra-luminal thrombus and possible contact of the AAA, especially with the spine. Finally, although the model was able to successfully capture the enlargement of small AAAs, a rigorous validation against experimental data would be crucial to evaluate its descriptive and predictive capabilities.