Effects of worker size on the dynamics of fire ant tunnel construction

Abstract

Social insects work together to complete tasks. However, different individuals within a colony may vary in task proficiency. We investigated if fire ant (Solenopsis invicta) worker body size influenced the ability to construct tunnels—a key component of subterranean nests. We monitored excavation by worker groups in a substrate of small wetted glass particles in quasi-two-dimensional arenas. Morphological and network features of the tunnel system were measured. Total tunnel area did not differ significantly between groups of large and small workers, although the tunnel area of control sized workers was significantly larger than that of large workers. Moreover, large workers created wider but shorter tunnels, with slower growth rate of tunnel number. However, edge–vertex scaling and degree distribution of the tunnel network were similar across all treatments. In all cases, the amount of excavated material was correlated with the number of active workers. Our study reveals that morphological features of excavated tunnels show modest variation when constructed by workers of varying sizes, but topological features associated with the tunnel network are conserved. These results suggest that important behavioural aspects of tunnel construction—and thus nest building—are similar among morphologically distinct members of fire ant societies.

1. Introduction

The remarkable success of social organisms is due in part to their ability to share and divide colony-level tasks among individuals [1]. For example, most social insects (ants, social bees, social wasps and termites) cooperate to construct nests [2]. Social insect nests are thought to have been critical to the evolution of sociality [3]. Nests serve to protect the colony from predation and exposure to the elements, while providing a location with homeostatic features [4] for rearing the young and safely storing food [1,5,6]. In addition to providing protection from the elements and predators, the architecture of the nest organizes the colony and influences the frequency and type of social interactions that occur. These interactions facilitate information transfer and worker recruitment and are important to the colony's daily function [7–11]. Thus, the efficient construction and maintenance of a nest is fundamental to the success of many social insects.

Many ants construct subterranean nests which consist of underground tunnels and chambers formed through the excavation of soil [1]. Nests are often initiated by newly mated queens [1,12] and are later cared for by the worker population. Nest construction and repair is an essential task that colonies must face throughout their life. For instance, ant species that remain in the same nest must continuously expand to accommodate colony growth while ants that relocate must construct new nests [1,13–16].

The basic mechanics of tunnel construction are similar among ant species [17]: workers loosen a soil pellet from the tunnel face with their forelimbs and mandibles and then carry the pellet in their mandibles to the surface where it is deposited in a pile (see figure 1 and electronic supplementary material, videos S1–S3). Groups of ants that collectively excavate ultimately form a network of interconnected tunnels and chambers [18,19] that is thought to facilitate traffic flow, food and brood storage, and gas and temperature regulation [1,5,6]. The formation of this tunnel network is a self-organized process in which workers operate according to excavation rules which may differ across species or even across worker castes [7,11,19–22].

Figure 1.

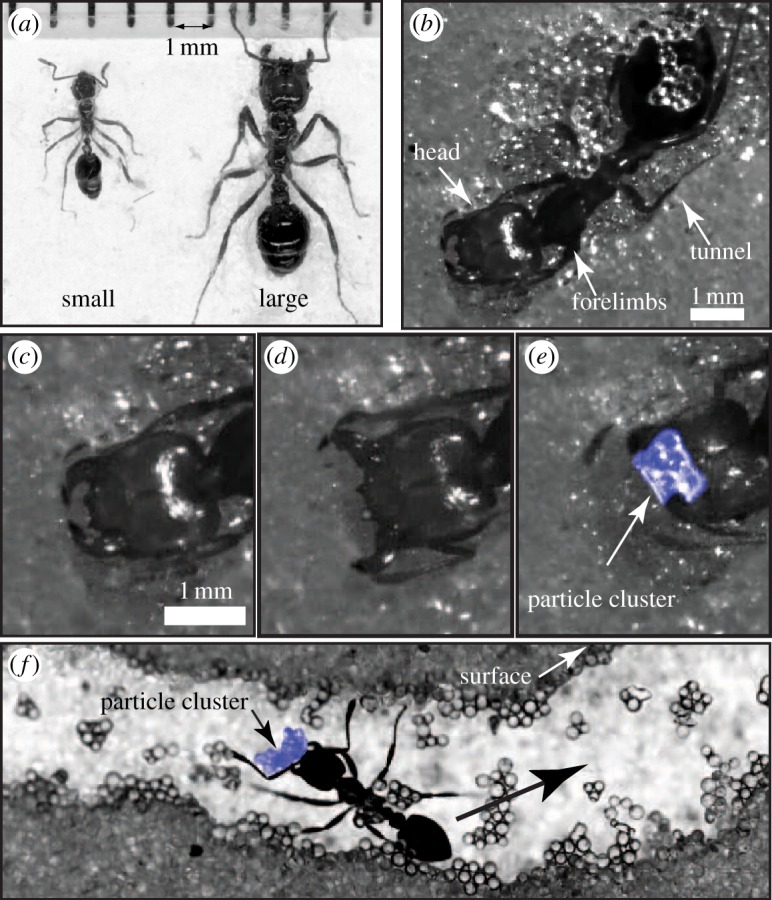
Solenopsis invicta workers digging tunnels. (a) Comparison of size difference between small and large workers. (b) Ventral view of a tunnelling worker. (c–e) The mechanics of tunnel excavation involve loosening, carrying and transporting substrate (0.25 ± 0.04 mm diameter wetted glass particles) from the tunnel face to the surface (see electronic supplementary material for videos). Excavated material is loosened and manipulated using the mandibles. (f) Excavated material is held in the mandibles and carried to the surface (direction designated by black arrow). (Online version in colour.)

The excavation behaviours of social insects and the dynamics of tunnel network formation have been studied extensively through laboratory experiment [18,23–28]. Environmental factors such as soil granularity and cohesiveness influence the morphology and orientation of tunnels [23,24,29] while the excavation dynamics (digging rate, network growth rate) are a function of group size [25,30] and worker age [11].

Morphological features of the ant could also play a role in digging proficiency and thus the ability to construct a nest. For example, worker body size is an important trait that affects colony function and is believed to be under evolutionary selective pressures. Moreover, variation in body size (polymorphism) in social insects can influence the likelihood and effectiveness of performing certain colony tasks such as the rearing of brood or foraging for food [31–35]. Since mandible width correlates with body size [36] and since tunnel excavation involves the use of mandibles to loosen and carry soil to the surface, a natural hypothesis is that body size correlates with digging proficiency. However, the relationship of ant size and tunnelling performance has not been investigated.

The red imported fire ant (Solenopsis invicta) is an excellent species to examine the role of worker size on tunnel construction. First, worker size in S. invicta is influenced by genetic and environmental factors [36–38], and workers display considerable variation in size. For example, worker head width varies continuously over a nearly threefold range (figure 1a). Second, the large subterranean nests constructed by S. invicta can house hundreds to hundreds of thousands of colony members and are among the most complex structures made by ants [19]. Fire ant nests have a characteristic structure which can be divided into three components: (i) a surface mound densely filled with tunnels, (ii) subsurface tunnels directly below the mound that extend downwards up to 1.5 m deep and connect to larger horizontal chambers, and (iii) shallow (1–10 cm deep) foraging tunnels which radiate horizontally away from the mound and can be upwards of 50 m in total length [10,39–41]. Finally, S. invicta is an invasive species and thus, in addition to constructing nests in their native range of the Amazon Basin of South America, S. invicta build nests within the diverse array of soil types found in the southern USA (such as clay, dry and wet sand) [10].

In this paper, we investigate the role of worker body size on tunnel excavation in S. invicta. We visualize tunnel network growth and ant digging behaviour by teams of S. invicta workers of varying body size in quasi-two-dimensional, vertical, digging arenas, similar to those previously used in studies of ant tunnel construction [18,23,25,27,28]. Based on the expectation that increased mandible size allows ants to carry larger loads [35], we hypothesize that larger ants should outperform smaller ants during tunnel excavation. Morphological and topological analysis of the growing tunnel network reveals that workers of all size exhibit similar digging proficiency. We show quantitatively how worker size influences (i) the rate of tunnel growth, (ii) the morphology of excavated tunnels, and (iii) the topology of the tunnel network.

2. Methods

2.1. Ants

Five mature S. invicta colonies (denoted as colonies A–E) were collected during the summer and autumn of 2008 and 2009 from roadsides outside of Atlanta, GA, USA. Colony members were separated from the soil in the laboratory using the water drip method [42]. Colonies were then housed in plastic bins that contained an enclosed nest area made from Petri dishes and an open foraging arena. Colonies were provided ad libitum water and insects as food.

Digging experiments were carried out with three treatments of worker size: small workers, large workers and control workers. Large and small workers from each colony were isolated using a sieving process in which ants migrated downwards, away from a light source, through a series of sieves with decreasing mesh size. Small workers were collected from the bottom sieve (bounding mesh size = 0.71 mm), and large workers were collected from the top sieve (bounding mesh size = 1 mm). Control workers, which represented a random sample of workers from the focal colony, were collected from the remaining worker groups, having gone through the same sieving process as the large and small worker treatments. The body size distribution of mature S. invicta colonies is skewed such that a majority of the colony are smaller workers [10], and thus the control groups comprised a relatively large number of small workers with a few larger workers.

Approximately 150 workers of a given size class were then separated using the wet mass of 25 individuals from each treatment as a gauge of the relationship between worker mass and worker number (wet mass of 25 individuals: small 14.56 ± 1.53 mg, large 56.73 ± 9.34 mg and control 29.34 ± 9.18 mg). Groups of ants were momentarily sedated by placing the confinement chamber on top of an ice bath for 30 s after which they were transferred to the digging arena. As in previous digging experiments, queen and brood were not present during experiments [25–29]. Brood items were explicitly excluded because large and small S. invicta workers display different behaviours in their presence [10].

Digging trials were conducted on groups of workers drawn from the five colonies (A–E). Each trial spanned 3 days. Eight digging trials (an octet) were prepared on a single date. Octets always included a combination of large, small and control worker groups from a given colony. Colonies A, B, C were used to supply worker groups for octets on two or more occasions while worker groups from colonies D and E were each used in only a single octet. Between the varied treatments and test dates, 71 digging trials were performed in total with a breakdown of 24 large worker treatments (A = 5, B = 5, C = 8, D = 3, E = 3), 23 small worker treatments (A = 6, B = 6, C = 7, D = 2, E = 2) and 24 control treatments (A = 7, B = 3, C = 8, D = 3, E = 3).

2.2. Digging arenas

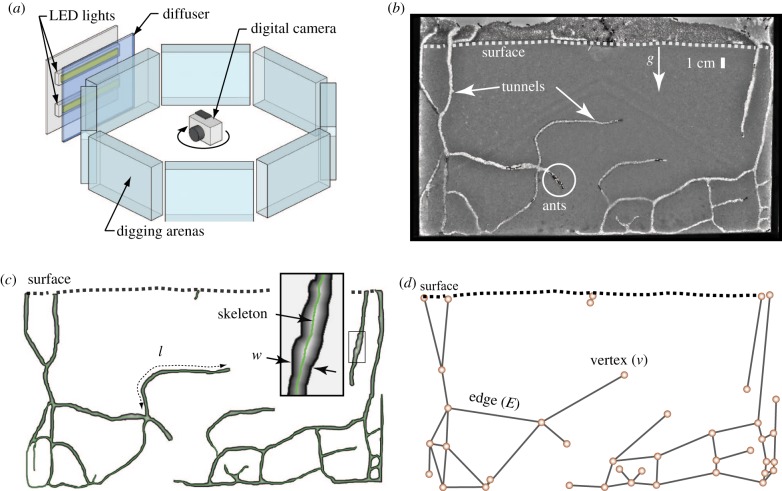
We studied excavation in the laboratory so that we could isolate and test for the effects of ant size on tunnelling proficiency. As in other studies, quasi-two-dimensional digging arenas were used to enable visualization of ant behaviour and tunnel growth simultaneously [23,25–30,43]. Vertically oriented arenas were created from two sheets of glass separated by a steel spacer, forming a 27 × 34 × 0.3 cm digging chamber (figure 2). Similar to previous studies [23,24,28], we used approximately spherical, wetted 0.25 ± 0.04 mm diameter glass particles as a digging substrate. The arenas were initially filled with dry particles to a height of approximately 20 cm, leaving a 7 cm gap at the top of the arena. Particles were then wetted with 100 ml of water which was allowed to drain through the digging arena (and out the porous bottom) prior to the introduction of the ants. Water is important for the stability of tunnels [23], and it is known that expansion of S. invicta nests in Nature typically occurs after rainfall [10]. The substrate was not intended to mimic the natural soils of the S. invicta habitat, which vary widely in water content and particle size distribution. Instead, the medium was chosen to control the digging substrate properties (cohesiveness, granularity) and produce reproducible excavation conditions among replicate experiments. We note, however, that this substrate is similar in particle size and wetness to sandy soils in which fire ant nests in Nature can be found [10].

Figure 2.

Overview of the experimental set-up and digging arena. (a) Time lapse images were collected from eight arenas simultaneously using a rotating camera. (b) Quasi-two-dimensional digging arenas were filled with a substrate of wetted 0.25 ± 0.04 mm diameter glass particles. Tunnels extend downwards vertically from the surface and branch subsurface forming a connected network of paths. Excavated material was deposited by the ants in a loosely packed pile on the surface. (c) Tunnel networks were represented as binary image masks. (d) The network representation considers tunnels as edges and the branch and endpoints as vertices. (Online version in colour.)

Eight digging arenas arranged on an octagonal frame with a digital camera in the centre were simultaneously used during experiments (see figure 2 and electronic supplementary material, appendix S4). Digging experiments were performed in a dark room. The camera was pointed at each arena in turn by a stepper motor controlled by LabVIEW (National Instruments, Austin, TX, USA). Images of the arenas were captured every 5 min, illuminating a backlight momentarily behind each arena during image capture.

2.3. Analysis

Tunnel images from 12 h increments were used to create a black-and-white image mask of the tunnels in Adobe Photoshop (figure 2b,c). Image masks were imported into Matlab and tunnel morphology and network topology were measured (see electronic supplementary material, appendix S4, for details). Morphological measurements included total projected tunnel area, A, total path length of tunnels, L, and tunnel width, W. Furthermore the path length of tunnel segments between branch points, l, was recorded. Network measurements included the number of edges, E, and vertices, v (figure 2d), along with the degree of each vertex, k, defined as the number of edges converging at the focal vertex.

All statistics were calculated using JMP (SAS software, Cary, NC, USA) or Matlab (Mathworks, Natick, MA, USA). Statistical tests for differences among treatments were computed using an ANOVA considering treatment as a fixed effect, colony as a random effect and date (octet) nested within colony as a random effect. Tukey's HSD was used to determine differences among treatments. We used linear and nonlinear regression to determine fit parameters where necessary. We used ANCOVA to test if linear slopes differed among treatments and ANOVA to test for differences in y-intercepts. We used the method of Motulsky & Ransnas [44] to estimate nonlinear regression fit parameters (see electronic supplementary material, appendix S4, for details). All results are presented as the least-squares mean ± s.e. of the measurement.

3. Results

Upon introduction into the arena, workers in all S. invicta treatments began digging within 2–4 h. We estimated that only 20–30% of the workers in the groups participated in the digging process at any one time; the remaining workers aggregated on the arena wall above the digging substrate. Tunnels were initiated at the surface and extended downwards for all treatments. Observations of fire ant workers at the tunnel face indicate that ants excavated and manipulated the digging substrate using their mandibles as well as their forelimbs (figure 1; electronic supplementary material, video S1) as has been described for many other ant species [17]. After approximately 24 h, lateral tunnel branches were created off the main tunnels. As the lateral tunnels grew in length, they often recombined with previously created tunnels forming new tunnel junctions and paths through the network. Tunnels were excavated through the successive trips of workers from the tunnel face to the surface and the excavated material was deposited in large piles on the surface (see electronic supplementary material, videos S2 and S3).

3.1. Tunnel area, length and width

We characterized the shape and size of the tunnel networks created by different treatments. The total size of the tunnel network was measured by the two-dimensional projected area. Since tunnel networks can grow in size through both the widening and lengthening of tunnels, we also measured the length and width of tunnel segments.

The final area after 72 h, A, significantly differed among size treatments (figure 3b and table 1; F_2,60 = 5.34, p = 0.007). There was no significant difference in A between large and small (p = 0.344) and control and small (p = 0.168) workers; however, the control groups produced larger area tunnel networks than the large treatments (p = 0.005). Worker size had a significant effect on the final length of tunnels, L (table 1; F_2,60 = 13.520, p < 0.0001). The tunnels of the large treatments were significantly shorter in total tunnel length than those of the small (p = 0.010) and control group (p < 0.0001) treatments. However, the total tunnel length between the small and control treatments was not significantly different (p = 0.095).

Figure 3.

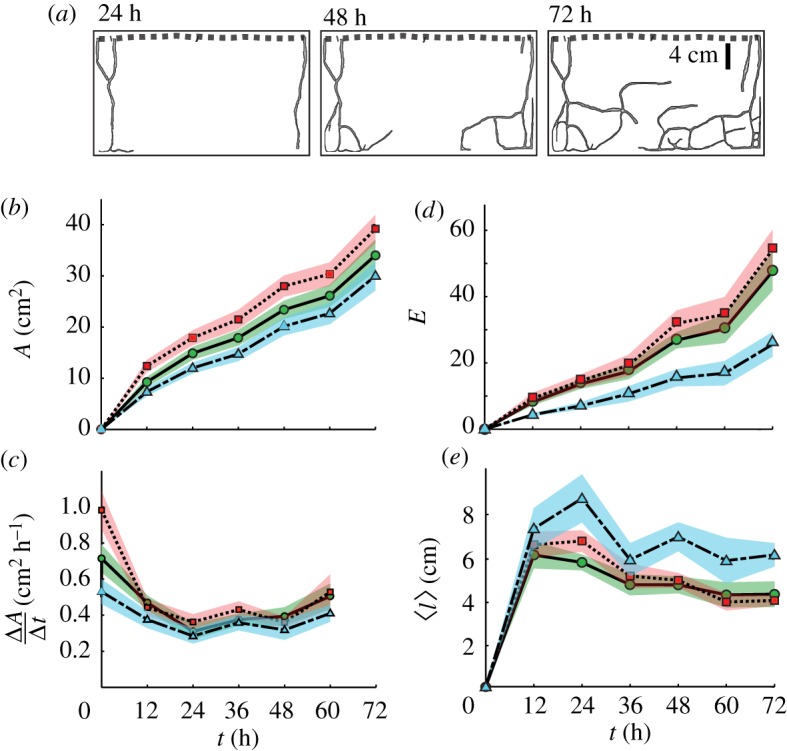
Digging dynamics of S. invicta worker groups in quasi-two-dimensional arenas. (a) Image masks showing tunnel network growth as a function of time. (b) Tunnel area (A) versus time for small, control and large ants (solid line, dashed line and dot–dash line, respectively). Shaded areas are ± s.e. (c) Digging rate (ΔA/Δt) versus time. (d) The number of edges (E) in the tunnel network increased in time. (e) The mean path length, 〈l〉, between vertices in the network decreased in time after 12 h. (Online version in colour.)

Table 1.

Mean (±s.d.) values of S. invicta tunnel network structure, topology and activity among three treatments composed of groups of small, large and control workers after 72 h of digging. Area is the total excavated area. Length is the total length of tunnels and width is the mean tunnel width. The probability distribution function of the tunnel widths was fitted by a lognormal function, where w is the local tunnel width and μ and σ are fit parameters. The tunnel network consisted of edges representing tunnels and vertices representing tunnel junctions. A connected component is a self-contained network in which all vertices are accessible from the other. The number of surface entrances and connected components did not differ among treatments. N_12h is the number of subsurface ants at 12 h and 〈N〉 is the average number of subsurface diggers over the duration of the test.

	treatment	small	large	control
	replicates	23	24	24
spatial	area (cm2)	34.03 ± 14.75	29.99 ± 13.72	39.18 ± 13.84
	length (cm)	159.17 ± 61.73	119.17 ± 51.07	186.04 ± 70.28
	width (cm)	0.22 ± 0.04	0.26 ± 0.07	0.22 ± 0.05
	μ (lognormal fit parameters)	−1.35 ± 0.05	−1.07 ± 0.03	−1.27 ± 0.05
	σ (lognormal fit parameters)	0.40 ± 0.06	0.37 ± 0.02	0.38 ± 0.04
	mode[P(width)] (cm)	0.22	0.3	0.24
network	vertices	50.70 ± 34.54	25.65 ± 19.20	61.44 ± 39.76
	edges	49.78 ± 31.03	27.83 ± 17.61	58.72 ± 34.98
	connected components	5.13 ± 3.40	4.70 ± 2.65	5.24 ± 3.72
	surface entrances	7.13 ± 4.32	5.91 ± 3.30	7.56 ± 4.55
activity	N12h	5.00 ± 4.72	4.52 ± 3.38	9.76 ± 7.30
	〈N〉	8.46 ± 6.49	7.01 ± 4.59	10.96 ± 6.74

The growth rate in the first 12 h was significantly influenced by treatment (figure 3c; F_2,60 = 8.336, p = 0.0006). The control group outperformed the large workers (p = 0.0004) but the difference in initial growth rate between the control and small worker groups was not significant (p = 0.078). Furthermore, the difference in initial digging rate between the large and small worker groups was not significant (p = 0.161).

For all treatments, the average tunnel width, W, was approximately constant in time indicating that tunnels grew in area primarily through lengthening and not widening (figure 4a). Tunnel width was significantly affected by worker size (figure 5; F_2,60 = 16.167, p < 0.0001) and groups of large workers created the widest tunnels, which were significantly wider than both the control (p = 0.0002) and small treatment (p < 0.0001) tunnels. The small worker and control groups created tunnels which were not significantly different in width (p = 0.522). The probability distribution of the local width, w, evaluated along the centre of tunnels was fit by a lognormal function 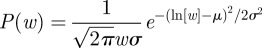for all treatments where μ and σ are fit parameters (figure 4b; R² > 0.98 for all treatment fits; see table 1 for μ and σ).

Figure 4.

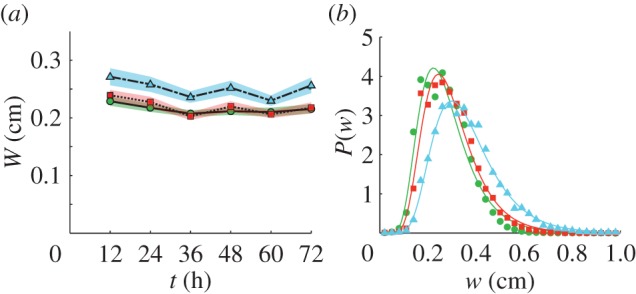
Tunnel width. (a) The mean width, W, of the tunnels versus time for small, control and large ants (solid line, dashed line and dot–dash line, respectively). Shaded areas are ± s.e. (b) The probability distribution of local tunnel width, P(w), is fitted by a lognormal function (described in the text) with parameters given in table 1. (Online version in colour.)

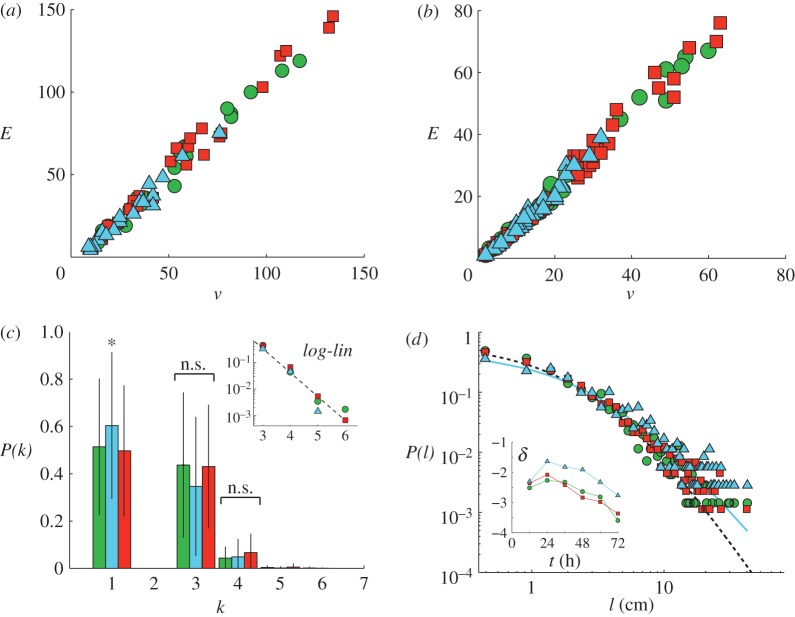
Figure 5.

Tunnel network properties. (a) Edge–vertex relationships for small, control and large treatments (green circles, red squares and blue triangles, respectively) were linear for the entire network. (b) Edge–vertex relationship of individual connected components. (c) Distribution of vertex degree. Small, large, and control treatments from left to right respectively. The asterisk (*) symbol denotes a statistically significant effect of treatment and n.s. indicates no treatment effect. (d) The probability distribution of path lengths was fitted by an extended power law (see text). Small and control treatment fits are given by the dashed line and the large treatment fit is given by the solid line. The inset shows the time dependence of the extended power law exponent δ. (Online version in colour.)

3.2. Tunnel network properties

We measured the network topology to understand how the connectivity of the tunnel networks varied among worker treatments. Junctions where tunnels terminated or came together are called vertices and the tunnel sections that connected these vertices are called edges [45]. The analysis included counting the number of edges and vertices and examining the functional relationship between the two. We also counted the number of edges emanating from a vertex; this is defined as the vertex degree. Lastly, the path length, l, is defined as the distance an ant must walk to traverse an edge.

The number of edges in the network, E, grew throughout each test (figure 3d). In the final network, E was significantly affected by treatment (F_2,60 = 11.001, p < 0.0001). Although E in the small and control treatments did not differ significantly (p = 0.436), E for the large treatment was significantly less than E for both small (p = 0.005) and control treatments (p < 0.0001). The relationship between the total number of vertices and total number of edges composing the network was linear, E = βv, with slope β = 1.04 ± 0.01 independent of treatment (figure 5a; ANCOVA parameters for slope difference, F_2,70 = 0.356, p = 0.702).

Tunnel networks were often composed of several connected components—each of which were independently connected sections of the tunnel network that did not merge below the surface (see figure 2b). The edge to vertex relationship for the connected components was linear with slope independent of treatment and slightly larger than that of the entire network (β = 1.13 ± 0.01; ANCOVA parameters for slope difference, F_1,351 = 0.003, p = 0.957). Treatment did not significantly affect the size of the largest connected component, measured as the number of edges in the connected component normalized by the total number of edges (figure 5b; F_2,60 = 1.194, p = 0.312). The largest connected component with respect to the total network size was, on average, v_conn/v = 0.56 ± 0.21, with a value of 1 representing a completely connected network and a value near 0 representing many unconnected components.

The vertex degree probability distribution, P(k), significantly differed among the three treatments for the k = 1 vertices only (figure 5c; F_2,60 = 9.565, p = 0.0002). Vertices with k = 1 comprised tunnel ends and surface entrances. Networks created by large worker groups were composed of slightly more degree 1 vertices than the small (p = 0.005) and the control (p = 0.0003) treatments. Differences between treatments for k > 1 were not significant (k = 3, F_2,60 = 0.521, p = 0.597; k = 4, F_2,60 = 1.167, p = 0.319). The tail of the degree distribution was linear on semi-log axes for all three treatments, indicating a possible exponential decay of P(k) at large k (inset figure 5c). Furthermore, the number of surface vertices (entrances) did not significantly differ between treatments (table 1; F_2,60 = 1.134, p = 0.328).

The probability distribution of path lengths was fitted by an extended power law function, P(l) = Q(l + l₀)^δ, for all treatments (figure 5d). The constant was constrained Q = −(δ + 1)(l₀)^[−(δ+1)] owing to the normalization condition of the probability distribution 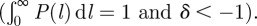The fit parameters for P(l) between the control and small worker treatments did not differ significantly (small versus pooled, F_48,44 = 0.659, p = 0.920; control versus pooled, F_46,46 = 1.577, p = 0.063). However, the large worker treatment did significantly differ from the pooled small-control data (F_54,92 = 2.469, p < 0.0001). The fit exponent, δ, represents the probability of finding longer tunnels in the network, and a decrease in δ corresponds to a decrease in this probability (figure 5d). Thus, over time, all tunnel networks experienced a ‘shortening’ effect in which the path length between vertices decreased. This was also observed in the mean path length (figure 3d), which decreased over time.

We compared P(l) for the small and control networks at 48 h and the large networks at 72 h and found that they did not significantly differ (small versus pooled, F_103,43 = 1.414, p = 0.101; control versus pooled, F_99,47 = 1.058, p = 0.423; large versus pooled, F_94,52 = 0.843, p = 0.766). Thus, the exponent δ(t) was similar in shape for all treatments but the large worker treatments lagged behind the smaller and control worker treatments in time by roughly 12–24 h. A similar time lag of the large treatment network was also observed in the number of edges (figure 3d) and tunnel length. This indicates that topological features of large treatment networks were similar to the other treatments but grew at a slower rate.

3.3. Subsurface workers during digging trials

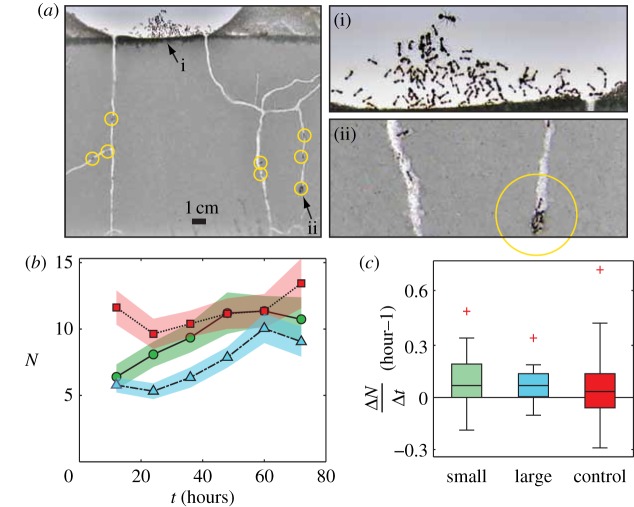
We measured the number of workers below the surface in the images at 12 h increments during tunnel excavation (figure 6). The number of workers subsurface after 12 h differed significantly among the treatments (F_2,60 = 12.6195, p < 0.0001). The control treatments outnumbered the small (p = 0.0002) and large (p = 0.0002) treatments in quantity of subsurface workers (F_2,60 = 12.6195, p < 0.0001). However, the number of subsurface workers did not differ significantly between large and small treatments (p = 0.9996). In contrast, after 72 h of digging, the number of ants subsurface was not significantly different among treatments (F_2,60 = 2.4576, p < 0.0942). Linear regression indicated that the number of subsurface ants increased over time for all treatments (small: R² = 0.07, N = 138, test against zero slope, F_1,136 = 9.768, p = 0.002; control: R² = 0.03, N = 150, test against zero slope, F_1,148 = 4.77, p = 0.03; large: R² = 0.15, N = 138, test against zero slope, F_1,136 = 24.16, p < 0.0001).

Figure 6.

Worker activity during tunnel construction. (a) Workers in an arena were typically found either (i) clustered togther above the surface of the digging substrate or (ii) subsurface engaged in digging activities. (b) The number of ants subsurface (N) as a function of time (solid line, dashed line and dot–dash line, respectively). Shaded areas are ± s.e. (c) The mean time rate of change of N (ΔN/Δt) for the three treatments. (Online version in colour.)

To determine how worker activity affected digging performance, we computed the mean number of subsurface workers 〈N〉 (over the 3 day tests). The mean number of workers subsurface during the digging tests was linearly correlated with the final tunnel area, A = α〈N〉 (α = 3.62 ± 0.13 cm², R² = 0.3), with α independent of treatment (ANCOVA test for difference in slope among treatments; F_2,64 = 1.210, p = 0.305; figure 7).

Figure 7.

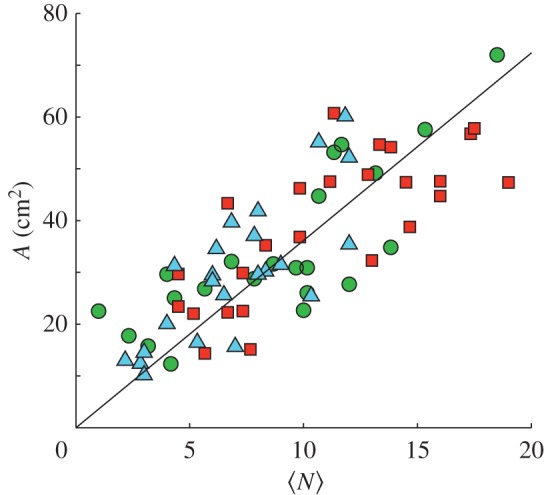
Tunnel area versus subsurface workers. Tunnel area (A) after 72 h was positively correlated with the time average number of ants 〈N〉 found subsurface over the same period (A = α〈N〉; α = 3.62). The slope, α, did not differ among the three treatments. Small, control and large treatments are represented by the green circles, red squares and blue triangles, respectively. (Online version in colour.)

4. Discussion

Our results indicate that, despite a factor of three in fire ant body size, excavation rate was insensitive to size. However, the control treatments (containing a mixture of approx. 70% small and 30% large ants) significantly outperformed the large treatments. We now discuss the morphological, topological and behavioural differences exhibited by the three treatments during tunnelling trials.

4.1. Tunnel area, length and width

Groups of large and small workers excavated tunnel networks which did not differ significantly in total tunnel area (figure 3). This indicates that worker size does not have an effect on digging proficiency and S. invicta workers of all sizes are capable of excavating or repairing tunnels. This lack of difference in the areal rate of tunnel growth between the large and small workers is surprising given the differences in body size. In addition to larger mandible width in larger ants, a scaling argument that considers both metabolic energy consumption [46] and stride frequency versus body mass predicts that the average walking speed of an ant increases as (body mass)^1/4. Experiments across 24 ant species are consistent with this scaling [47]. Thus, although larger S. invicta workers might walk faster and carry larger loads, the observation that their digging performance is comparable to that of small workers suggests that behavioural factors in addition to body size are likely to be important in determining excavation rate.

We observed slight morphological differences in tunnel shape between the large and small treatments. Larger workers built wider and, thus, shorter tunnels than small workers. The tunnel width, however, was only 20 per cent wider in the tunnels of the large workers when compared with the small and control treatments (figure 4). This was also surprising given that the head width of large workers is approximately three times that of the small and control treatments.

Control groups significantly outperformed large worker treatments from the same colony, excavating tunnels of approximately 35 per cent greater final area. The proximate cause of this difference was that the initial growth rate of the control treatments was nearly twice that of the large treatments, and thus control treatments took an early lead in tunnel growth and maintained it for the duration of the experiment (figure 3b). After 24 h the digging rate was similar among all treatments. We posit that the high initial digging rate of the control treatments was due to the large number of digging ants observed in the initial 12 h (figure 6). It is noteworthy that tunnel shape did not significantly differ between the control and small treatments. This may be due to the fact that natural body size distribution of S. invicta colonies is skewed such that smaller workers of head width less than 0.75 mm account for 70 per cent of the colony [35,48].

4.2. Worker activity

Final tunnel area and length were positively correlated with the number of ants observed below the surface over the duration of the experiment (figure 7). The slope of the best fit line to these data was independent of treatment. These observations suggest an explanation for the variance in final tunnel area—larger tunnel networks were created when more workers participated in the digging process. Such a relationship has also been observed in a field study [11]. The independence of slope also indicates that individual ants excavate at approximately the same rate. From the best fit slope, we estimated that the upper limit digging rate for a single S. invicta worker was 0.05 cm² h⁻¹ independent of worker size. The excavation rate we observed for S. invicta workers was similar to rates observed for other ant species in similar laboratory experiments (Messor sancta, 0.024 cm² h⁻¹ [7]; Lasius niger, 0.027 cm² h⁻¹ [28]) and field study (Pogonomyrmex badius, 0.0156 cm² h⁻¹ [11]). We note that our estimate is an upper bound of the digging rate because we probably underestimated the number of digging workers in our measurement.

It is unclear why relatively few ants (20–30%) participated in excavation in our experiments. A previous study of laboratory colonies of S. invicta reported that workers were active for only 10 out of every 30 min [49], which is consistent with our observations of inactivity [19]. However, traffic and overcrowding at the tunnelling site may also be important in determining the number of workers that participate in digging. Studies of worker flow on foraging trails [50–52] and within artificial nests have shown that traffic dynamics are important in organizing worker movement [53] and determining tunnel size and branch locations [54,55]. Furthermore, the diameters of foraging tunnels in S. invicta nests in Nature decrease away from the nest, which may reflect a decrease in worker traffic at these distances [41]. Thus, the constraints imposed by locomotion within confined and crowded environments, including traffic and multi-ant interactions could be important in ant nest construction and warrant future study.

4.3. Tunnel network topology

Several topological properties such as edge-to-vertex ratio and degree distribution of the tunnel networks did not depend on worker size. The number of edges increased linearly with the number of vertices, with a slope slightly greater than 1 for both the whole network and the connected components. In a previous study of tunnel networks of the ant Messor sancta, the edge–vertex relationship followed a power law (E ∼ V^1.31) [43]. We hypothesize that the difference in edge–vertex relationship between M. sancta and S. invicta reflects the different excavation rules individual ants follow during tunnel construction.

The network topology of all three treatments was similar when rate effects were removed. The rate of tunnel lengthening by the large treatments lagged behind that of the small and control groups, and after 72 h the large worker networks contained approximately the same number of edges as in the small and control worker networks 12–24 h earlier. This slower growth rate of the larger worker tunnels resulted in slower overall network edge–vertex growth in the large treatment networks. When this time delay was accounted for, the differences in the edge number and path length distribution, P(l), vanished among the three treatments. It is likely that large workers exhibited this time lag because of a slower initial worker recruitment leading to slower tunnel growth. The invariance of the tunnel networks among the three treatments when properly rescaled by the different tunnel growth rates suggests similar excavation behaviours among fire ant workers of all sizes.

5. Conclusion

Our study revealed that S. invicta workers of all body sizes constructed subsurface tunnel networks with comparable spatial and topological features. The distribution functions characterizing the tunnel morphology were similar across treatments, and the topological network measures were conserved across worker size as well. The control group created the largest, most complex nests, largely a result of more rapid initial digging. Thus, our results provide support to the hypothesis of adaptive demography such that the worker size distribution of a colony is tuned to optimize ‘success’, of which tunnel construction is a critical aspect. In our system, the natural (control) distribution of worker sizes within nests was most effective at tunnelling, while the behavioural programmes directing tunnel construction were similar across workers of different sizes. We also found that a large percentage of the worker population was inactive at any time during digging experiments. Consequently, nest size was regulated by the fraction of workers in the group that participated in digging.

While our study focused on digging in a controlled substrate composed of slightly wet glass particles, we note that fire ants are found in a diverse array of terrains and soil types, and it is known that the nest properties are dependent upon the soil properties [10]. For instance, in fire ant nests in Nature, the above-surface nest mounds created from cohesive soils like clay are substantially larger than mounds created from sandy soils [10]. It is likely that the soil properties determine the stability and size of these structures; for instance, the cohesive soils are held together through interparticle capillary forces or van der Waals forces and thus soil particles strongly cohere [23]. Such observations indicate that further study is required to elucidate the factors important to tunnel excavation in varied soil types.

Finally, the division of labour among worker groups in social insect colonies is a complex process, and understanding the behavioural rules that govern task allocation is important to understanding the biology of social insects. The division of labour and problem-solving abilities of social insects has already led to significant technological advances such as ant colony optimization algorithms [56]. Therefore, detailed understanding of the tunnel navigation and cooperative excavation abilities exhibited by social insects may provide principles for the development of autonomous subterranean robot teams. Such autonomous systems could work together [57] to excavate or navigate in subterranean environments like those found in disaster sites or after earthquakes [58]. The development of robotic excavators may shed light on the important constraints of cooperative tunnel excavation, and thus provide further information about the challenges that tunnelling ants must overcome.