Embodied linearity of speed control in Drosophila melanogaster

Abstract

Fruitflies regulate flight speed by adjusting their body angle. To understand how low-level posture control serves an overall linear visual speed control strategy, we visually induced free-flight acceleration responses in a wind tunnel and measured the body kinematics using high-speed videography. Subsequently, we reverse engineered the transfer function mapping body pitch angle onto flight speed. A linear model is able to reproduce the behavioural data with good accuracy. Our results show that linearity in speed control is realized already at the level of body posture-mediated speed control and is therefore embodied at the level of the complex aerodynamic mechanisms of body and wings. Together with previous results, this study reveals the existence of a linear hierarchical control strategy, which can provide relevant control principles for biomimetic implementations, such as autonomous flying micro air vehicles.

1. Introduction

Fruitflies, like many other insects, control their ground speed from the visually perceived motion of objects passing by (optic flow) (for reviews, see [1,2]). Because these reflexive speed responses are highly stereotyped and easily elicited in freely flying insects, they have served as a powerful behavioural paradigm to study the underlying sensorimotor mechanisms for many decades (mosquitoes [3]; honey bees [4,5]; flies [6–9]). More recently, the visuomotor control mechanisms underlying flight speed responses were studied in fruitflies using a real-time controlled virtual reality (VR) environment termed TrackFly [8]. By presenting flies with short bouts of regressive (back-to-front) moving patterns, the backward drift an insect might visually perceive when hit by a gust of wind was simulated to elicit compensatory forward acceleration responses. These were shown to depend directly on the velocity (measured in metres per second) of the moving patterns according to an amazingly simple proportional control law [9] (likewise for lift responses see [10,11]).

The underlying physiological mechanisms that lead up to these simple control laws are complex and remain only partly understood. The principal mechanism by which a fly accelerates is to pitch its body nose down to point the flight force more forward [12,13], not unlike a helicopter. These changes in pitch are brought about by subtle changes of the wing stroke pattern, suitable to modulate pitch torque [14]. While tethered studies revealed a constant angle between the stroke-averaged flight force and the body [15], the free-flight situation manifests itself as somewhat more complex. First, the aerodynamic forces generated by the flapping wings depend on their motion relative to the surrounding air and therefore on flight speed. Second, active control of the direction of the stroke-averaged aerodynamic force vector, as recently explored in free-flight studies [16], may play an additional role.

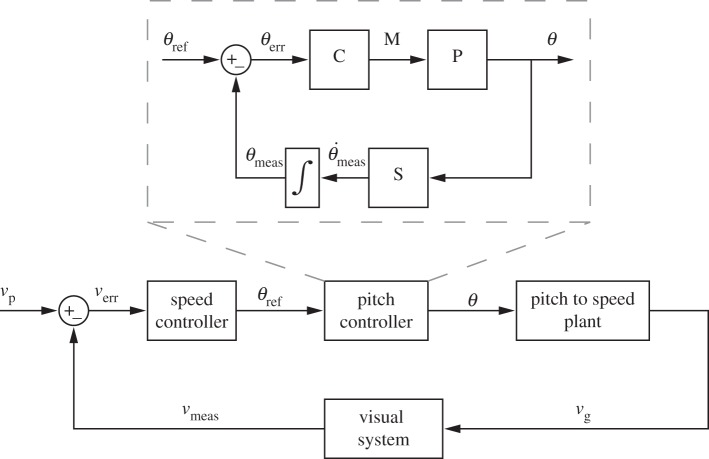
The important role of body pitch for the control of flight speed implies the involvement of a second sensory modality, namely mechanosensory feedback from the halteres, which sense the angular velocity of the body from the resulting Coriolis forces acting on them [17,18]. Taken together, the speed control system can be conceptualized as two nested feedback control loops (figure 1). An outer speed control loop compares a set point retinal slip speed (the ‘preferred’ retinal slip speed [6]) with current visual input and generates as output a body pitch angle. It represents the set point pitch angle of an inner pitch control loop, which controls the body pitch angle—and hence flight speed—based on haltere signals (and possibly additional visual [19] cues).

Figure 1.

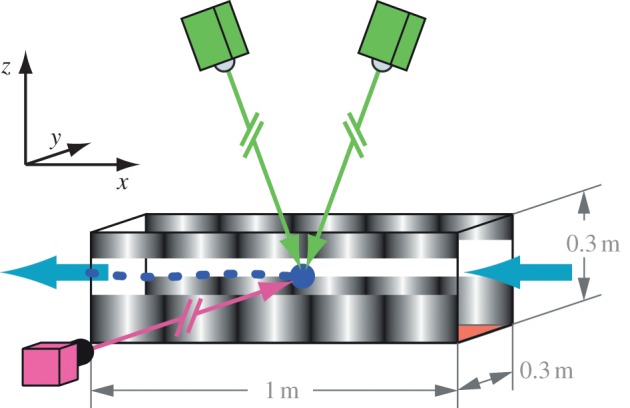
Hierarchical flight speed control scheme. An outer visual loop sets the desired pitch angle (θ_ref) according to the error between the preferred speed v_p and the measured ground speed v_g. In the inner pitch control loop (inset), the pitch controller C sets the pitch angle θ to the desired value θ_ref by producing a torque M around the pitch axis. P represents the plant for pitch rotation. The sensor S, representing the halteres and the visual system, measures the rotational speed 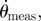which is then integrated to get the measured pitch angle θ_meas. The pitch angle θ is converted to v_g via the pitch-to-speed plant.

The involvement of two sensory modalities for a stereotyped behavioural response offers a suitable model system to explore functional principles underlying multi-modal flight control mechanisms. It is amenable to a behavioural system identification approach, in which the behaviour is modelled as a feedback controller [9,20–22] and the inner dynamics are subsequently ‘reverse engineered’ [8–11,23]. This method allows abstracting from the underlying complex physiological processes, while still capturing the fundamental high-level sensing and control principles.

Importantly, the identification of control laws requires a quantification of a system's plant properties. In the case of flight speed responses, these represent the dynamics of body pitch changes and how they consequently affect flight speed. While the body pitch rotational dynamics have previously been investigated [24], the pitch-to-speed transfer function has so far not been explored in detail. The relationship between body pitch angle and flight speed has been measured only under steady-state conditions [12,13], which precludes the identification of system dynamics and consequently the description of the time course of speed responses.

Using the TrackFly VR set-up, we reverse engineered the dynamics of pitch-mediated speed control. We used horizontally moving visual patterns to elicit changes in horizontal flight speed of varying strength, whereas the body posture and flight speed co-varied systematically (see example in figure 3a(i–iii)). This approach simplified the system identification due to a reduction of the dimensionality to just 3 d.f.: body pitch angle and motion along the x–z plane. The analysis can be further simplified to 2 d.f. since the accelerations occur horizontally with no significant displacement along the vertical axis.

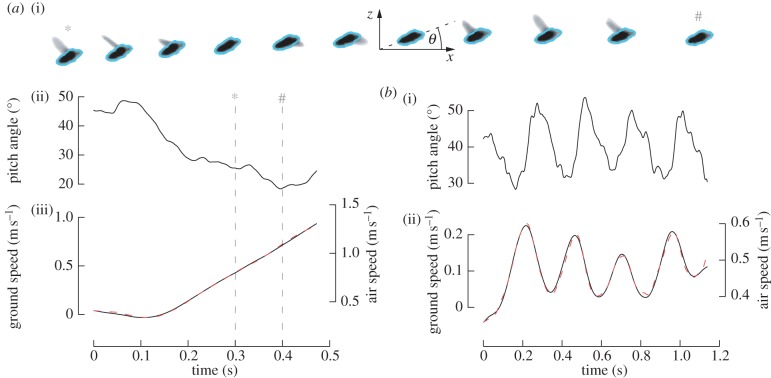
Figure 3.

Behavioural measurements. (a) Speed response. The fly was stimulated with a sine grating that moved regressively at a constant retinal slip speed (SF = 10 m⁻¹, TF = 6 s⁻¹, wind speed WS = 0.37 m s⁻¹). (a(i)) High-speed camera images (down-sampled to 100 fps) filmed 300–400 ms after onset of the motion stimulus. The template matched to measure the pitch angle and position is shown in cyan. (a(ii)) Time course of the measured pitch angle (θ, defined in the inset of (a(i)), low-pass filtered with a zero-phase, fifth-order Butterworth filter with a cut-off frequency of 50 Hz). (a(iii)) Measured ground speed (black solid line) and linear model fitted according to equation (3.1) (red dashed line). (b(i),(ii)) Corresponding data for a sinusoidal modulation of retinal slip speed (SF = 6.67 m⁻¹, TF = 2.9 + 6.5 · sin(2π · 5) s⁻¹, WS = 0.37 m s⁻¹).

We measured the body kinematics of the acceleration manoeuvres using high-speed videography and reverse engineered the transfer function between pitch angle and horizontal flight speed. We show that the pitch-to-speed dynamics are well described by a first-order linear transfer function. The linearity in longitudinal speed control, which has previously been described for the outer, visual control loop [7,9], extends to body posture control and is therefore embodied in the flight motor system of the fly. This linearity results from a combination of body and wing drag, of which the second dominates.

The embodiment of linear control properties provides a key to understand how flies achieve their amazing flight control feats with comparatively limited neural circuitry. Similar hardware tuning in miniature biomimetic micro air vehicles (MAVs) may eventually provide them with supreme flight capabilities under likewise severe size and performance constraints.

2. Methods

2.1. Animals

Fruitflies (Drosophila melanogaster) descending from an initial population of 200 wild caught females were reared on a standard nutritive medium under a 12 L : 12 D cycle at a room temperature of about 24°C. Two-to-five day-old flies were isolated and deprived of food, but not water, for 12–16 h preceding an experiment. Experiments were performed during the first 6 h of subjective day.

2.2. Experimental set-up

The experiments were conducted using TrackFly, a wind tunnel equipped with VR display technology, to which a high-speed camera filming from the side was added (figure 2). As TrackFly has already been described in detail in Fry et al. [8], we provide only an overview of the relevant system's components here.

Figure 2.

Schematic of the wind tunnel working section and filming system. Flies were released at the downwind end of the tunnel (left side in the figure), where they spontaneously elicited upwind flight (air flow is indicated by blue arrows). The three-dimensional position of individual flies was tracked in real time using Trackit 3D (SciTrackS GmbH, Pfaffhausen, Switzerland, cameras shown in green). The position data were used to control the speed of the visual pattern projected onto the side walls, as well as trigger a high-speed (1000 fps) recording of acceleration manoeuvres from the side (camera shown in pink). For further details on the applied methods, see Fry et al. [8].

2.2.1. Wind tunnel

The experiments were performed in an open-circuit, closed-throat wind tunnel (Engineering Laboratory Design, Inc., Lake City, MN, USA). It provided a laminar air flow in a working section built from clear acrylic (1.55 m in length and 0.3 m in height and width). For the present experiments, constant wind speeds of 0.37 and 0.74 m s⁻¹ were used. At the downwind end of the tunnel, a 5 per cent water solution of vinegar was vaporized at a rate of approximately 7.2 mg s⁻¹ to motivate the flies to fly upwind.

2.2.2. Real-time position tracking

Trackit 3D (SciTrackS GmbH, Pfaffhausen, Switzerland [25]), a two camera (green in figure 2) three-dimensional tracking system, was used to track the position of flies in real time (latency: 38 ms) from above against a long wavelength (more than 700 nm) back lighting.

2.2.3. Image rendering and display

Custom programmed software based on the VisionEgg open-source library [26] was used to render visual stimuli consisting of vertically oriented sine gratings. The images were displayed using a 60 Hz flicker-free LCD projector (Sony, VPL-ES1, Tokyo, Japan) onto tracing paper screens attached to the side walls of the tunnel. These screens consisted of two 0.1 m vertically spaced sections (1 × 0.13 m and 1 × 0.07 m for the bottom and top screens, respectively), leaving a 0.1 m vertical slit along the length of the screen.

2.2.4. High-speed recording

To measure the body pitch angle, flies were filmed through these slits from the side using a high-speed camera (Photonfocus, MV-D1024-Trackcam, Lachen, Switzerland, in pink in figure 2). The high-speed camera was equipped with a 1024 × 1024 pixels CMOS image sensor and filmed the centre of the wind tunnel at 1000 frames per second (fps), with an exposure time of 50 µs and a field of view of 22.5 × 10 cm (approx. 14°). The high frame rate was achieved by exploiting the dynamic region of interest functionality of the camera (also see [27]).

2.3. Measurement procedure

The experiments were completely automated and consisted of a pre-test positioning phase and a testing phase. The visual stimuli consisted of horizontally moving vertically oriented sine gratings of different linear spatial frequency (SF) and temporal frequency (TF) (following the notation of Fry et al. [8]).

2.3.1. Positioning phase

Inspired by David's approach [6–8], we induced single flies to fly with near zero ground speed at the downwind end of the working section by automatically varying the horizontal speed of a progressive (front-to-back) moving sine grating (SF = 6.67 m⁻¹) according to the position of the fly in the tunnel. As soon as the fly was induced to hover stably near the predefined starting position, the VR system triggered a test, after which the positioning procedure was resumed.

2.3.2. Testing phase

The high-speed recording was triggered and the fly stimulated with a short presentation (less than or equal to 3 s) of a moving pattern on the side walls of the wind tunnel. The stimuli consisted of open- and closed-loop steps and open-loop sinusoidal oscillations in retinal slip speed. In the open-loop case, the visual loop was artificially opened by continuously adjusting the pattern phase according to the fly's current position along the wind tunnel using the VR software (explained in detail in Fry et al. [8]). Owing to the proportional dependence of acceleration on retinal slip speed [7], this procedure also provided experimental control over the strength of the resulting accelerations. Typically, the fly flew out of the field of view of the high-speed camera long before the maximum testing duration of 3 s was reached, with an average test duration of 0.50 ± 0.17 s (mean and standard deviation).

2.3.3. Body pitch angle and x–z position measurement

We implemented a template matching algorithm to measure the body pitch angle and the x–z position (cyan in figure 3a(i)). The algorithm was able to ignore the wings, which due to the short exposure time were sometimes clearly visible in the acquired images, depending on the stroke angle at which the frame was taken. For each measured trajectory, the template was obtained from an image, in which the wings were not visible. The absolute pitch angle of the template was calculated by extracting the orientation from the central moments of the image.

3. Results

3.1. System identification of the pitch-to-speed plant

We measured a total of 284 flight trajectories, representative examples of which are shown in figure 3 (also see electronic supplementary material, movie S1). In the first example (figure 3a(i–iii)), the fly was stimulated with a constant, regressive retinal pattern speed, to which the fly responded with a roughly constant forward acceleration. In the second example (figure 3b(i–ii)), the fly was stimulated with a horizontally oscillating retinal slip speed, to which it responded with a likewise oscillating flight speed. These responses demonstrate the linear and time invariant properties previously described for speed responses [9–11].

In both examples, the body acceleration is closely correlated with body pitch angle and air speed. The flight speed can be closely fitted by a first-order linear differential equation of the form

3.1

where v_air is the fly's air speed in the x-direction, θ is the fly's body pitch angle and k₀, k₁ and k₂ are free parameters. In the case in which the fly is hovering on the spot, i.e. v_air = 0 and 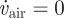, θ evaluates to k₁, which therefore represents the hovering angle. Defining β = k₁ − θ as the nose-down deviation of the pitch angle from the hovering pitch angle, equation (3.1) can be re-written as

3.2

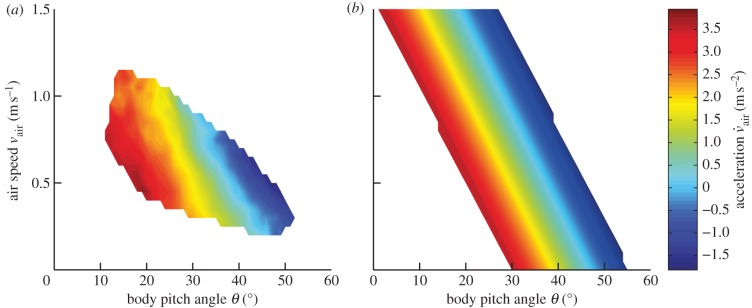
Assuming a constant angle between the stroke-averaged flight force and the body, β approximately describes the fly's stroke plane angle. We fitted the model of equation (3.1) to each flight trajectory using a general nonlinear optimization method (fmincon command, Matlab, The MathWorks Inc., Natick, MA, USA) that minimized the mean quadratic error of prediction with a median R² of 0.997 (see two representative examples in figure 3a(iii) and 3b(ii)). We obtained the following values (median and interquartile range): k₀ = 12.28 [10.78 13.65] m s⁻², k₁ = 0.83 [0.78 0.89] rad and k₂ = 4.03 [3.03 5.22] s⁻¹. k₁ converted to degrees yields a value of 47.5°, which is close to the previously published hovering angle of D. melanogaster of around 45° [14]. The high R² of the fit shows that a simple first-order linear model suitably describes the transfer function between pitch angle and air speed. In other words, a fixed combination of pitch angle and air speed results in a constant acceleration, independent of time. This allowed us to pool all data and calculate the average horizontal acceleration as a function of pitch angle and air speed (figure 4a). As predicted by the linear model, the iso-response curves (representing acceleration responses of varying strength) run diagonally across the air speed–pitch angle parameter space. The flies' acceleration depends linearly on both air speed and pitch angle over the measured parameter range.

Figure 4.

Acceleration responses. (a) Pooled behavioural data. Horizontal acceleration is plotted in colour code as a function of pitch angle and air speed. Grid size is 1° and 0.05 m s⁻¹. The figure represents a total of 284 trials, of which 191 were measured with step stimuli and 93 with sinusoidal stimuli. For each point on the grid, the median horizontal acceleration of each single measured flight trajectory was calculated by selecting the data in which the absolute vertical acceleration was smaller than 0.5 m s⁻² (approx. 5% of the gravitational acceleration g, i.e. approx. 5% of the total vertical force) and the absolute vertical speed was smaller than 0.05 m s⁻¹. The total mean acceleration was then computed by calculating the mean of the median accelerations of the single trajectories. For a point to be valid, the data from at least six different flights were required. (b) Model output. Output of the fitted model based on equation (3.1).

3.2. The effect of damping on the pitch-to-speed linearity

To understand the origin of this linearity, it is useful to consider the aerodynamic effects related to forward flapping flight. As the advance ratio (J, the ratio of body speed and mean wing tip speed) increases, the wings meet an increased air flow on the down stroke, and conversely a reduced air flow during the up stroke. This leads to a damping effect on flight speed: the so-called flapping counter force [24,28–30] (see also [31]). This phenomenon is analogous to the recently described flapping counter torque, a passive moment that develops during turning manoeuvres [32]. These effects are passive in the sense that they do not depend on changes in wing kinematics. Lacking detailed measurements of the wing kinematics, we non-specifically refer to wing damping without excluding the possibility that an active component may also be present.

To estimate wing damping, we first calculated the forward acceleration of a fly expected in the presence of body drag alone 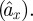To calculate 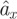, we assumed a constant angle between the stroke-averaged wing force and the body, which leads to the following equation:

3.3

where g is the gravitational acceleration, a_z is the measured vertical acceleration and a_BD and a_BL are the horizontal and vertical accelerations, respectively, owing to body drag. We calculated a_BD and a_BL as a function of the measured air speeds and pitch angles using a model presented by Dickson et al. [22] (see appendix A and electronic supplementary material, figure S1a,b). 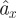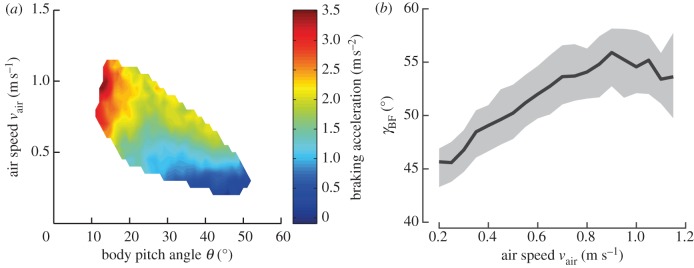From , we subsequently subtracted the actual measured acceleration 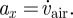The difference in acceleration can be attributed to wing damping (figure 5a). A comparison of the wing damping acceleration (figure 5a) with that due to body drag (see the electronic supplementary material, figure S1a) reveals a significant role of wing damping for speed control. For example, at a typical terminal speed of 0.5 m s⁻¹ and a pitch angle of 38° (approx. corresponding to steady state), wing damping accounts for 88 per cent of the total braking force.

Figure 5.

Effect of wing damping. (a) Braking acceleration owing to wing damping. Acceleration was calculated according equation (3.3), colour coded and plotted as a function of pitch angle θ and air speed v_air. (b) Stroke-averaged force angle in the body frame of reference (γ_BF). γ_BF was calculated as a function of air speed according to equation (3.4). Black line, median γ_BF; shaded area, γ_BF interquartile range.

Wing damping increases monotonically with air speed and decreasing pitch angle (figure 5a). For typical cruising speeds below approximately 0.5 m s⁻¹, wing damping is small and covaries with air speed. At high air speeds, wing damping increases quickly as pitch angles are reduced. This effect is explained by the strongly inclined stroke plane, which is expected to lead to a roughly quadratic dependence of wing damping on air speed. While this effect causes a reduction of the total force, the fly is required to produce sufficient vertical force to offset its body weight. Taken together, it is reasonable to assume that at around θ = 10° the fruitfly reaches its locomotor limits of air speed. Indeed, in the few cases in which we observed flies pitching nose down to less than 10°, they quickly lost altitude, suggesting they were no longer able to produce sufficient lift (data not shown).

The loss of aerodynamic efficiency in the direction of flight can also be expressed in a backward tilting of the stroke-averaged force vector with respect to the body. Based on the measured body kinematics, we were able to calculate the direction of the mean force vector in the body frame of reference as a function of the pitch angle and the air speed, from

3.4

Because γ_BF varied comparatively little with respect to pitch angle (see the electronic supplementary material, figure S1d), we averaged the data and calculated the force angle as a function of the air speed only (figure 5b). We find that γ_BF depends roughly linearly on air speed in the measured range of 0.2–0.9 m s⁻¹, between 46° and 56°. Therefore, within the normal flight speed range of Drosophila (v_air < 0.85 m s⁻¹ [33]), wing damping leads to a backward tilting of γ_BF by 15° s m⁻¹. Above 0.9 m s⁻¹, as the air speed increases γ_BF saturates and decreases again. This is expected because the body pitch angle is low at high air speeds and the differences between the aerodynamic forces during the up- and down-stroke are consequently small.

The combination of a high wing damping and a comparatively low body drag therefore explains the measured linearity in the pitch-to-speed transfer function.

4. Discussion

4.1. Linear strategies for flight speed control

In this study, we performed a detailed behavioural and biomechanical analysis of body pitch-mediated speed control in the fruitfly. In a wind tunnel, we visually induced acceleration responses in freely flying flies, while measuring the time course of body posture and flight speed during the resulting manoeuvre. So far, the relationship between body posture and flight speed has only been measured under steady-state conditions [12,13,15], which allows predicting terminal velocities for given pitch angles. Our analysis of the time courses of pitch-dependent speed manoeuvres extends beyond previous approaches in that it provides a quantitative description of the pitch-to-speed dynamics, i.e. the transfer function of the plant on which the lower level neuromotor controllers act. This approach allowed us to explore the high-level control strategies on the empirical basis of measured flight speed behaviour, without making assumptions about the low-level aerodynamic mechanisms.

The pitch angle to flight speed transfer function is well described with a simple linear model (figure 4b). Together with the previous finding that flight speed depends linearly on pattern slip speed [9], our results lead to the conclusion that the multi-modal flight speed reflex of fruitflies is realized entirely within a linear control scheme. An interesting property of the identified linearity lies in its independence of an absolute reference of the pitch angle. This is because in a linear system, any given change in the sensor input leads to a given characteristic change in the output, which is independent of the absolute sensor reading. In consequence, linear controllers can operate on differential sensory input, without the need for an absolute sensor reading. The linear speed control strategy implies that flies need only to sense changes in pitch angle, i.e. the angular velocity of the pitching body, and not the absolute pitch angle. Such control properties are particularly relevant to animals whose sensory systems are known to signal disturbances more faithfully than absolute quantities [34]. In flies, it is in fact not clear if they can at all sense body orientation in an absolute sense [35,36], while the sensing of rotational velocity by the visual system (for a review, see [37]) and the halteres [17–19] is very evident.

In the nested control loop shown in figure 1, visual and mechanosensory feedback play complementary roles. The visual loop provides the external reference to set the ground speed [6,7,38] with comparably slow response properties [9,11,39]. In contrast, the mechanosensory loop provides extremely fast [18,40,41] proprioceptive feedback to control pitch, which is inherently unstable [30,42]. Additional visual input is also present to control pitch at lower frequencies [19].

As an emergent property of the nested control structure, this system provides an automatic drift compensation mechanism. An error in the pitch integrator, for example, would propagate to the body pitch angle, and next flight speed. This error would be sensed by the visual system and be compensated by adjusting the pitch angle set point.

Similarly, a change of wind speed would simply be compensated by an adjustment of the pitch set point value. This mechanism is likely to be general to flying insects, in which wind speed compensation is ubiquitous (Aedes [3]; Drosophila [6,7]; Apis [43]). Owing to the linearity of the system, the control dynamics around the floating set point remain unaffected.

In conclusion, the linear plant provides the basis for a two-level nested controller requiring only two inputs. (i) Translational optic flow provides a visual reference signal to control the ground speed. (ii) Mechanosensory feedback from the halteres signals the body rotational velocity. Because drift is compensated in the visual feedback loop, the system is robust for imperfect integration at the level of pitch angle computation, as could result, for example, from a leaky integration of the angular velocity. All these beneficial properties of the speed control system depend critically on the linearity of the pitch-to-speed transfer function.

4.2. The importance of wing damping

The identified linear relationship between the body pitch angle and air speed is consistent with previous results obtained in Drosophila hydei under steady-state conditions [13]. The linear dependence of body pitch and flight speed (measured at steady state) was attributed to opposing effects of a squared increase of body drag with air speed and a reduced projected area as the fly pitches nose down to increase flight speed. We instead find that body drag provides little damping compared with the flapping wings (figure 5a,b).

Analogous to the wing damping we measured for the speed responses, the wings of fruitflies provide substantial passive damping during the saccadic turning manoeuvres [24,32,44], while body drag is comparatively insignificant [45]. Lacking detailed wing kinematics, we cannot exclude the possibility that the fly additionally adjusts them at increasing air speeds to maintain the measured linear relationship between body angle and flight speed [16]. Detailed measurements of wing kinematics are therefore required to assess the degree to which the fly actively tunes its linear speed damping. This approach would have to be followed through with a dynamically scaled wing model [46] or computational fluid dynamics [47] to capture the significant unsteady effects that are expected to arise at elevated advance ratios [28]. An analogous approach was taken in a recent study on the hawkmoth Manduca sexta, in which a combination of passive open-loop dynamics and feedback control was revealed [48]. By combining theory, modelling and behavioural studies within an integrative framework further progress can be made in our understanding of insect flight control mechanisms.

4.3. Embodied linearity

Recent behavioural studies have revealed that important visual flight control reflexes are organized within a linear control framework [9,11,49]. Such linearity is likely to have evolved due to selective advantages, such as the ability to operate on differential sensory inputs or to compensate drift efficiently. In the present case, we can show that this linearity emerges already at the level of the myogenic wing actuation mechanism and direct wing control reflexes.

The embodyment of suitable control properties in the low-level physiology may provide a quite general mechanism that provides high robustness and efficiency to demanding neuromotor control problems. These mechanisms may also provide design principles for MAVs, which underlie similarly severe performance constraints as flying insects. These are expected to be applicable also at the much larger scale, at which MAVs are currently being realized. Specifically, the linear damping resulting from flapping wings is related to a turbulent flow regime characteristic for high Reynolds numbers [32], and is therefore expected to apply similarly in larger flapping MAVs. More generally even, the embodiment of linear properties in the low-level actuation mechanisms may represent an important principle in entirely different animal locomotion systems and be relevant to various biorobotic applications.

Appendix A. Body drag estimate

Body drag was calculated as a function of air speed and pitch angle according to a model proposed by Dickson et al. [22]. Parallel (F_P) and normal (F_N) aerodynamic force components with respect to the body long axis are calculated as follows:

A 1

and

A 2

where ρ is the air density, S the body reference area, u_b the incident air velocity vector, δ the angle between the body longitudinal axis and the incident flow, and C_P, C_N the experimentally determined force coefficients. The coefficients are calculated from

A 3

where k_P = 0.6 and k_N = 1.2 in the case of D. melanogaster [22]. The horizontal and vertical components of the aerodynamic force acting on the body can be calculated from

A 4

and

A 5

The body accelerations for drag and lift as a function of the pitch angle and the air speed, calculated according to equations (A 1)–(A 5), are shown in the electronic supplementary material, figure S1a,b.