Perspectives on biomechanical growth and remodeling mechanisms in glaucoma

Abstract

Glaucoma is a blinding diseases in which damage to the axons results in loss of retinal ganglion cells. Experimental evidence indicates that chronic intraocular pressure elevation initiates axonal insult at the level of the lamina cribrosa. The lamina cribrosa is a porous collagen structure through which the axons pass on their path from the retina to the brain. Recent experimental studies revealed the extensive structural changes of the lamina cribrosa and its surrounding tissues during the development and progression of glaucoma. In this perspective paper we review the experimental evidence for growth and remodeling mechanisms in glaucoma including adaptation of tissue anisotropy, tissue thickening/thinning, tissue elongation/shortening and tissue migration. We discuss the existing predictive computational approaches that try to elucidate the potential biomechanical basis of theses growth and remodeling mechanisms and highlight open questions, challenges, and avenues for further development.

1. Introduction

The human eye gives us our sense of sight, allowing us to learn more about the surrounding world than we do with any of the other four senses. The shell-like structure of the eye can be divided into three main layers: the fibrous load bearing layer, the vascular layer, and the neural layer. Each ocular tissue is a collection of cells and extracellular matrix components that perform specialized functions. The extracellular matrix consists of fibers (e.g., collagen fibrils and elastin) and a ground substance (e.g., proteoglycans). The cornea, the sclera, and the lamina cribrosa (LC) make up the fibrous layer, and are principally responsible for the mechanical stiffness of the eye. The optimally organized collagen fibril structure in these connective tissues provides the structural integrity necessary to resist the intraocular pressure (IOP) load and also give the eye the stable shape necessary for focused vision.

Glaucoma is characterized by irreversible loss of vision, and is often associated with chronically elevated intraocular pressure. There are varying levels of individual susceptibility to IOP, although IOP lowering is the only clinical treatment that has been proven to arrest or delay the onset and progression of the disease. Most evidence suggests that glaucomatous damage to the retinal ganglion cells (RGC) is due to RGC axonal insult at the level of the LC (Quigley and Addicks, 1981). The LC is a porous, connective tissue structure through which the RGC axons pass on their path from the retina to the brain, and represents a relatively vulnerable structure in the otherwise robust corneoscleral pressure vessel. The blood supply for the LC and its contained RGC axons is delivered through capillaries contained within the load-bearing LC trabeculae themselves, which directly couples the mechanical and vascular responses of these tissues (Downs et al., 2008). The connective tissues of the LC and its surrounding tissues undergo extensive structural changes during the development and progression of glaucoma. In this paper, we review the experimental evidence that biomechanical growth and remodeling (G&R) mechanisms underlie these structural changes. The G&R mechanisms involved in glaucoma occur at very different length scales (Grytz et al., 2011b), and thus we will attempt to elucidate the relationships between the different G&R mechanisms at each scale.

Computational models have been helpful in investigations of the biomechanical environment of the optic nerve head (ONH), which is comprised of the LC, pre- and retrolaminar neural tissues, and the surrounding peripapillary sclera. These models have been based on linear and nonlinear, isotropic and anisotropic elastic continuum models (Sigal, 2009; Sigal et al., 2005, 2009, 2007; Norman et al., 2011; Ethier et al., 2003; Girard et al., 2011; Roberts et al., 2010a,b, 2009; Downs et al., 2008). These models have been especially useful in increasing our understanding of the impact of eye-specific variations in material and geometric parameters on LC stress and strain, which is thought to relate to an individual’s risk of developing glaucoma. However, models using nonlinear and anisotropic elastic tissue properties alone have been insufficient to explain the extensive structural changes in the LC connective tissues observed during the development and progression of glaucoma. Different homeostatic control mechanisms and G&R stimuli have been suggested to simulate G&R in eye tissues. Most existing computational G&R formulations motivate the G&R process using phenomenological stimuli defined at the macro-scale, such as an imbalance of the tissue stress/strain or retinal blur. Only recently, however, have experimental studies elucidated basic G&R mechanisms of collagen fibrils at the micro-level (Camp et al., 2011; Flynn et al., 2010; Bhole et al., 2009). In the recent past, computational models have been used to simulate the connective tissue’s ability to grow and remodel in response to its biomechanical environment. We review the different homeostatic control mechanisms and G&R stimuli used in existing computational G&R approaches to simulate G&R phenomena seen in the eye and in glaucoma. We also provide perspectives on the G&R mechanisms characteristic to glaucoma, and highlight open questions, challenges, and avenues for further development.

2. Growth and remodeling stimuli and homeostatic control mechanisms

Different G&R stimuli at multiple length scales have been suggested to govern the G&R mechanisms seen in ocular tissues, ranging from the retinal blur at the organ-level in myopia (Wallman and Winawer, 2004) to the collagen fibril stretch at the micro-level (Grytz et al., 2011b). A full understanding regarding G&R triggering and control remains elusive. In general, a homeostatic control mechanism can be defined by one or multiple stimulus functions φ_i, which may depend on several feedback variables γ_j that drive the G&R process in an effort to reach a homeostatic state. Homeostasis or a homeostatic-like state is often defined by means of target values ${\eta }_k^{hom}$ of model variables η_k that evolve during the G&R process. Theses target variables are defined as functions of the stimuli φ_i, which depend on the feedback variable γ_j:

$${\eta }_k\to {\eta }_k^{hom}({\phi }_i({\gamma }_j))\text{with}i,j,k=1,2,\dots$$ (1)

In some cases, the model variables η_k are identical to the feedback variables γ_j and the homeostatic state can be directly defined with respect to the feedback variables

$${\phi }_i({\gamma }_j)\to {\phi }_i({\gamma }_j^{hom})=0\text{with}i,j=1,2,\dots ,$$ (2)

where the stimuli typically vanish at homeostasis. In the following section, we present three homeostatic control mechanisms that have been successfully applied to predict G&R phenomena observed in ocular tissues. The different approaches are based on homeostatic control mechanisms defined at different length scales.

2.1. Homeostatic control mechanism at the organ-level

Wallman and Winawer (2004) gathered extensive experimental evidence that the axial length of the eye is governed to a homeostatic control mechanism guided by visual error signals at the organ-level. During its development, the eye faces the functional challenge of ensuring that its length matches the focal length of its optics. It has been shown that focused vision (the stimuli) guides the scleral expansion or contraction that controls the size of the eye. Artificially induced refractive errors that create a defocused image on the retina leads to G&R in the sclera that alters the size of the eye. Based on these phenomenological observations, Bryant and McDonnell (1998) suggested an optical feedback-controlled stimulus that motivates scleral remodeling as a mechanism for myopic eye elongation. Scleral G&R was motivated by two stimuli representing the retinal blur D_b and the accommodative pathway D_a, where both stimuli were driven by the refractive error in the left E_l and right eyes E_r

$${\phi }_1=D_a(E_l,E_r)\to D_a(0,0)=0,{\phi }_2=D_b(E_l,E_r)\to D_b(0,0)=0.$$ (3)

In the case of a blurry or defocus vision, the scleral tissue was assumed to grow isotropically and become stiffer in an effort to eliminate the induced refractive error $E_l^{hom}=E_r^{hom}=0$. The application of the stimuli (3) demonstrated that the rate of ocular elongation in experimental myopia may be controlled by regulating the rate of soft tissue remodeling in the scleral shell (Bryant and McDonnell, 1998). This phenomenological approach showed that one can predict and investigate G&R phenomena using relatively simple G&R stimuli.

2.2. Homeostatic control mechanism at the tissue-level

Most existing continuum-based G&R formulations for soft tissues are based on homeostatic control mechanisms at the tissue-level. Traditionally, the G&R process is motivated from an imbalance in the local mechanical stress (Taber and Humphrey, 2001; Gleason and Humphrey, 2004; Hariton et al., 2007; Ricken et al., 2007) or strain environment (Driessen et al., 2004; Kuhl et al., 2005; Himpel et al., 2008). Each of these theories have been successfully applied to qualitatively predict the preferred collagen fibril orientation in both soft and hard tissues. Kuhl and Holzapfel (2007) and Driessen et al. (2008) investigated different stress- and strain-based stimuli, both suggesting that the Cauchy stress is a reasonable candidate to drive the remodeling process in cardiovascular tissues. Hariton et al. (2007) suggested that collagen fibrils in cardiovascular tissues are oriented between the directions of the two maximum principal stresses. This hypothesis was adopted by Grytz and Meschke (2010) and Grytz et al. (2011a) to predict the collagen fibril architecture in the cornea, sclera and LC. The proposed stimulus reads

$$\phi ({\tau }_1,{\tau }_2)=\{\begin{array}{ll}{\tau }_2/{\tau }_1\hfill & \text{for}{\tau }_2\ge 0\hfill \\ 0\hfill & \text{for}{\tau }_2<0\hfill \end{array},$$ (4)

where τ₁, τ₂ are the first and the second principal Kirchhoff stresses. In contrast to (3), the phenomenological stimulus (4) does not directly define a homeostatic state. Instead, the stimulus (4) was used to define a presumed optimal target architecture of the collagen fibrils in the eye tissues similar to (1). The collagen fibrils were split into two families and their architecture was represented by two generalized structure tensors H_famα (α = 1, 2). The generalized structure tensors incorporate the structural information of preferred collagen fibril orientations and collagen fibril dispersion. The homeostatic state was defined with respect to an optimal collagen fibril architecture, here represented by means of target values for the two generalized structure tensors ${\mathbf{H}}_{\text{fam}\alpha }^{hom}(\alpha =1,2)$ as functions of the stimulus (4)

$${\mathbf{H}}_{\text{fam}\alpha }\to {\mathbf{H}}_{\text{fam}\alpha }^{hom}(\phi ({\tau }_1,{\tau }_2)).$$ (5)

The homeostatic control mechanism (5) has been used to predict the collagen fibril architecture in the corneoscleral shell (Grytz and Meschke, 2010) and later in the LC and peripapillary sclera (Grytz et al., 2011a). These studies revealed the significant impact of collagen fibril anisotropy in the ONH on the IOP-related mechanical stress and strain environment in the LC. The main results of the latter study and their implications with respect to glaucoma are highlighted in Section 3.2.

Homeostatic control mechanisms similar to (5) have also been used to predict the collagen fibril architecture in several other tissues including the aortic valves and the arterial wall (Driessen et al., 2004, 2008; Kuhl and Holzapfel, 2007; Hariton et al., 2007; Creane et al., 2011). The general applicability of the stimulus (4) to multiple tissue types supports the existence of characteristic homeostatic control mechanisms in connective tissues. However, the stimulus remains a phenomenological approach limited to the application it was designed for: the adaptation of connective tissue anisotropy.

2.3. Homeostatic control mechanisms at the collagen fibril-level

The lack of knowledge of micro-scale remodeling mechanisms and pathways has limited most existing G&R formulations based on phenomenological observations at the organ- or tissue-level as outlined in the previous two subsections. Recent experimental studies, however, have revealed the existence of a homeostatic control mechanism at the collagen fibril level. Camp et al. (2011), Flynn et al. (2010), and Bhole et al. (2009) showed that mechanical strain in the collagen fibrils protects them against enzymatic degradation by matrix metalloproteases. These experimental studies suggest that the strain-based protective mechanism is invoked very abruptly and at very low strain levels and has been hypothesized to be the basis of a smart structural mechanism to achieve load-optimized connective tissue architectures. Foolen et al. (2010) demonstrated that chicken embryo periosteum resides in a homeostatic mechanical state, which is characterized by the “transition stretch”. The “transition stretch” corresponds to portion of the stress–strain curve of the tissue where the toe region ends and the heel region begins. After perturbation of the homeostatic strain state, adaptation of the collagen fibril crimp structure re-established the overall tissue stretch at the previous homeostatic stretch level. As the nonlinear constitutive response of soft tissues is strongly related to the (un-)crimping of collagen fibrils, the findings of Foolen et al. (2010) also point toward the existence of a homeostatic control mechanical at the collagen fibril-level.

We recently proposed a G&R stimulus that embraces these experimental findings, where the elastic stretch λ^fib experienced by the collagen fibril material will stimulate a G&R process in an effort to maintain a homeostatic elastic stretch environment λ^hom at the collagen fibril-level (Grytz et al., 2011b)

$$\phi ({\lambda }^{\text{fib}})={\lambda }^{\text{fib}}-{\lambda }^{hom}\to \phi ({\lambda }^{hom})=0.$$ (6)

The numerical application of the stimulus (6) requires the computation of the collagen fibril stretch λ^fib that calls for a multi-scale approach. In Grytz et al. (2011b), we estimated the collagen fibril stretch using a previously derived microstructurally motivated constitutive formulation (Grytz and Meschke, 2009). The application of (6) demonstrated that a biomechanically driven homeostatic control mechanism can successfully predict the LC thickening observed in early experimental glaucoma (see Section 4.3).

2.4. The importance of homeostatic control mechanisms at lower length scales

As our knowledge evolves and new G&R stimuli at lower length scales are discovered, the general applicability of the stimuli should improve. While stimuli at the organ-level such as (3) have proven their usefulness, they can only be applied to very specific G&R phenomena, such as the refractive error-driven elongation process of the eye. Applicability increases with stimuli defined at the tissue-level such as (4). While the stimulus (4) was also designed to predict one particular G&R phenomenon (the remodeling of the anisotropic collagen fibril architecture) it can be applied across different collagenous tissues. The collagen fibril-based stimulus (6) further generalized applicability, as it can be applied to different collagenous tissues, and also be used to motivate different G&R phenomena. In Section 7 we will show that the collagen fibril-based stimulus (6) can be used to motivate tissue elongation/shortening as well as tissue thickening/thinning. It has been hypothesized that (6) is a key stimulus in the development and adaptation of connective tissue anisotropy (Camp et al., 2011).

3. Tissue anisotropy in the ONH and its adaptation

Collagen fibrils are the main load bearing constituents of the ocular coats and their complex arrangement within the tissue is believed to dictate the anisotropic constitutive response of ocular tissues (Pinsky et al., 2005; Pandolfi and Manganiello, 2006; Girard et al., 2009; Grytz and Meschke, 2010; Grytz et al., 2011a). Therefore, ocular tissue anisotropy is often related to its heterogeneous collagen fibril architecture and adaptation of tissue anisotropy is interpreted as a phenomena that is caused by the reorganization of the collagen fibril architecture. In glaucoma, IOP-related stress and strain environment of the LC is of particular interest as it may directly or indirectly relate to the axononal insult of RGC in glaucoma (Quigley and Anderson, 1976; Minckler et al., 1977; Radius and Anderson, 1979a,b, 1981; Quigley et al., 1981; Quigley and Addicks, 1980; Minckler, 1980; Downs et al., 2008; Sigal et al., 2010b). Hence, this section is focused on tissue anisotropy in the ONH, which includes the LC and surrounding peripapillary sclera.

3.1. Experimental evidence of tissue anisotropy in the ONH

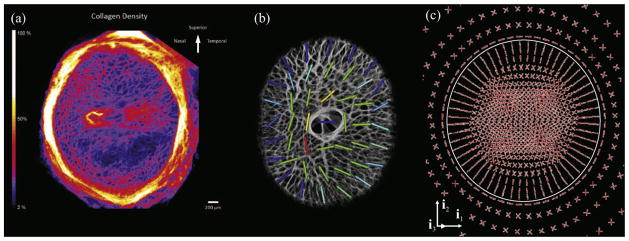
Pioneer work on the heterogeneous collagen fibril architecture in the ONH was done by Quigley et al. (1983) and Quigley and Addicks (1981) (Fig. 1a). The collagen architecture of LC has remained the focus of additional studies (Marshall et al., 1993; Goldbaum et al., 1989; Morrison et al., 1989; Quigley et al., 1991a,b; Hernandez et al., 1987; Thale et al., 1996; Hernandez and Gong, 1996). Earlier studies indicated that the scleral canal was surrounded by a ring of circumferentially oriented collagen fibrils that surround the scleral canal in the peripapillary sclera (Morrison et al., 1989; Goldbaum et al., 1989, Fig. 1b). Recent advances in second harmonic image generation techniques allowed Winkler et al. (2010) to verify the existence of a distinct ring of collagen fibrils surrounding the scleral canal (Fig. 2a). Studies of collagen fiber orientation in the eye using wide-angle X-ray scattering Boote et al. (2010) also reported this ring of collagen fibrils.

Fig. 1.

(a) Electron micrograph of the collagen fibril architecture of the LC, illustrating the complex nature of LC trabeculae size, shape and orientation (reproduced from Quigley and Addicks, 1981). (b) Longitudinal section of the border between optic nerve and choroid and sclera (S), stained for type IV collagen. An axon bundle (solid straight arrows) passes through the LC. Just external to the LC, large sclera-like fibers are circumferentially oriented (open arrow) (reproduced from Goldbaum et al., 1989).

Fig. 2.

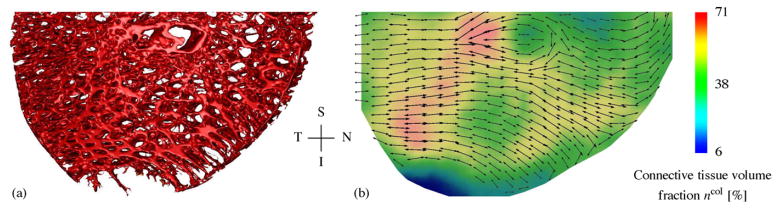
(a) Collagen density map of the human ONH as viewed from the posterior aspect of the eye (reproduced from Winkler et al., 2010). (b) Regional predominant laminar beam orientations obtained from the three-dimensionally reconstructed monkey LC (reproduced from Roberts et al., 2009). (c) Preferred collagen fibril orientations of the LC and peripapillary sclera, predicted in a numerical model by a remodeling algorithm (reproduced from Grytz et al., 2011a).

Light microscopy of histologic sections have shown that the collagen fibril architecture of the LC forms a porous structure through which the RGC axon bundles pass on their path from the retina to the brain (Hernandez et al., 1987; Quigley and Addicks, 1981, Fig. 1a). However, the anisotropic characteristics of the complex three-dimensional architecture in the LC cannot be full appreciated in single section images. Three-dimensional reconstruction of the LC microarchitecture was necessary to quantitatively analyze the local preferred LC beam orientation and connective tissue volume fraction (Roberts et al., 2009, Fig. 2b). Using the mean intercept length (MIL) method Roberts et al. (2009) reported the existence of a preferred radial orientation of collagen fibrils in the periphery of the monkey LC.

3.2. Numerical prediction of the tissue anisotropy in the ONH

The first numerical approach to model the adaptation of tissue anisotropy in the ocular coats was proposed by Grytz and Meschke (2010). Biomechanically induced adaptation of tissue anisotropy was captured by allowing collagen fibrils to be reoriented in response to the IOP-related loading conditions. A numerical approach was used to reorient the collagen fibrils toward an optimal collagen fibril architecture driven by the stress-based stimulus function (4). The model was used to predict the collagen fibril architecture in the corneoscleral shell. The model predicted the existence of the circumferential ring of collagen fibrils at the limbus as measured experimentally (Newton and Meek, 1998; Aghamohammadzadeh et al., 2004) and elucidated its important mechanical function of stabilizing the curvature of the cornea at various IOP levels.

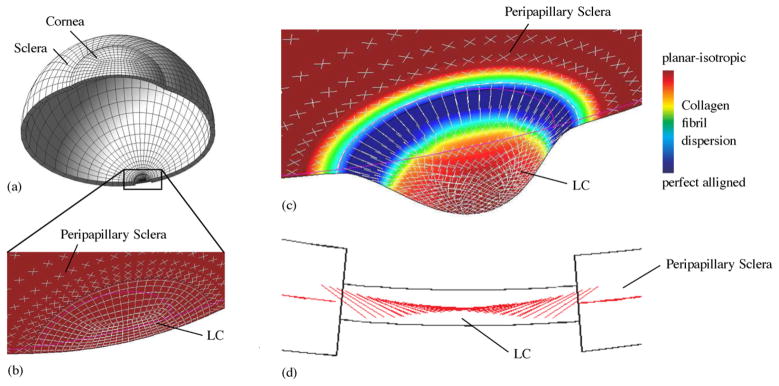
In a follow up study, the same numerical approach was used to investigate the tissue anisotropy in the ONH (Grytz et al., 2011a, Fig. 3), which used a model of the eye that included the peripapillary sclera and LC. The initial collagen fibril architecture was represented by planar isotropic collagen fibril orientations (Fig. 3b). Subjecting the initial model to a normal IOP level (16 mmHg) led to large scleral expansions outside the physiologic range without any LC bending. As the remodeling simulation progressed, a circumferentially aligned ring of collagen fibrils formed around the scleral canal. This ring in the peripapillary sclera was found to shield the LC from IOP-induced membrane forces. The formation of the ring greatly reduced scleral canal expansion but induced significant bending in the LC. Furthermore, the remodeling simulation predicted a preferred radial and out-of-plane orientation of collagen fibrils in the periphery of the LC (Fig. 3c and d). The radially aligned collagen fibrils in the periphery of the LC were found to reduce the bending deformations of the LC and to reinforce the LC against high transverse shear forces.

Fig. 3.

Adaptation of the collagen fibril orientations in the peripapillary sclera and LC. (a) Shell model of the human eye including the PPS and LC subjected to 16 mmHg IOP. (b) The initial collagen fibril architecture represented by planar isotropically dispersed collagen fibrils. (c) The optimal collagen fibril architecture at the homeostatic state of the remodeling simulation. Shown in (b, c) is the 10-fold magnified deformation of the mid-surface of the PPS and LC, collagen fibril dispersion (contour plot) and preferred collagen fibril orientations (white lines). (d) Sagittal section showing the out-of-plane orientation of the preferred collagen fibril orientations in the LC periphery at simulated homeostasis (adapted from Grytz et al., 2011a).

Both numerically predicted morphologies (the peripapillary scleral ring and the radial alignment of collagen fibrils in the periphery of the LC; Fig. 2c) were in good agreement with the experimental findings of Winkler et al. (2010) (Fig. 2a) and Roberts et al. (2009) (Fig. 2b). The existence of radially aligned collagen fibrils in the periphery of the LC was completely unknown at the time the numerical results were obtained. Hence, modern G&R simulation tools are capable of both reproducing specific G&R phenomena and predicting experimentally unknown morphologies. In addition, while the experimental studies were able to observe the characteristic morphologies, their biomechanical manifestations remained unclear until elucidated by modeling studies. The G&R simulation revealed a reasonable biomechanical explanation, namely that the circumpapillary scleral ring of fibrils shields the LC form high membrane forces while the radial trabeculae reinforce the LC against shear forces. Both morphologies have a significant impact on the ONH stress and strain environment, which is thought to be crucial in understanding the pathogenesis of glaucoma.

Previous computational parametric studies and sensitivity analyses showed that eye-specific changes in the material properties and/or geometry might significantly change the mechanical environment of the LC (Sigal, 2009; Sigal et al., 2005, 2007, 2009, 2011; Norman et al., 2011). These studies suggested that natural variations of these parameters might be involved in the eye-specific susceptibility to glaucoma, which occurs across a broad range of IOPs. It was found that the structural stiffness of the sclera significantly impacts the laminar mechanical environment. These studies were based on isotropic, linear constitutive formulations, and the incorporation of tissue anisotropy in the ONH might change our perspective on the most important factors that impact the laminar mechanical environment. In particular, the peripapillary ring of collagen fibrils predicted in the anisotropic model seems to dominate the IOP-related deformation response of the LC (Fig. 3c).

4. Growth and remodeling in early glaucoma

Several structural changes in the eye have been associated with early stages of glaucoma. While in the past it was often believed that material failure or a yield response of the laminar trabeculae may be the source of these structural changes (Burgoyne et al., 2005; Downs et al., 2008; Sigal and Ethier, 2009; Levy and Crapps, 1984; Radius, 1987; Albon et al., 2000; Edwards and Good, 2001; Jonas et al., 2004; Quigley, 2005; Wells et al., 2008; Ren et al., 2009), there is increasing experimental evidence that G&R is a primary mechanism in glaucomatous ONH changes (Downs et al., 2011b; Roberts et al., 2009; Yang et al., 2007, 2010, 2011a).

4.1. Experimental evidence of growth and remodeling in early glaucoma

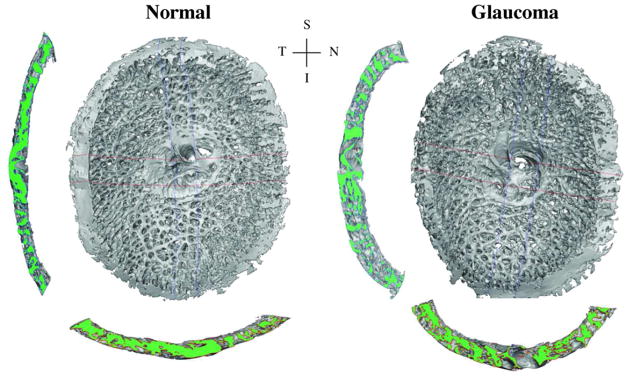
Based on the monkey model of glaucoma, experiments have shown that inducing elevated intraocular pressure (IOP) leads to many of the structural changes in the eye associated with early stages of glaucoma (Figs. 4 and 5). It has been shown that chronic intraocular IOP elevations in monkey eyes result in several structural changes in the LC: (i) overall thickening of the LC (20–61 μm, Yang et al., 2007, 2011a); (ii) permanent posterior LC deformation (25–233 μm, Yang et al., 2007, 2011a); (iii) increase in connective tissue volume (44–82%, Roberts et al., 2009); (iv) increased number of laminar beams through the LC thickness (17–48%, Roberts et al., 2009); (v) outward migration of the posterior lamina insertion point (Yang et al., 2010); and (vi) less pronounced outward migration of the anterior lamina insertion point (Yang et al., 2010). The ONH is populated with astrocytes, microglia, LC cells that are very active and strain sensitive (Hernandez, 2000; Morrison, 2006; O’Brien et al., 1997; Kirwan et al., 2005, 2004; Irnaten et al., 2009). These changes are progressive, occur on a relatively short time scale, and their character indicates that G&R mechanisms are the key driver of the morphogenesis (Downs et al., 2011b). The sclera also changes markedly in early experimental glaucoma, exhibiting significant thinning (Downs et al., 2001, 2002) and changes in material properties (Girard et al., 2011).

Fig. 4.

3D reconstructions of the LC connective tissues of a monkey, with one eye having early experimental glaucoma. Shown are en face views of the 3D LC reconstructions, as well as views of the central vertical (left) and horizontal (below) sections. Note the thicker and deeper cupped lamina in the early glaucoma eye (adapted from Roberts et al., 2009). S—superior, I—inferior, N—nasal, T—temporal.

Fig. 5.

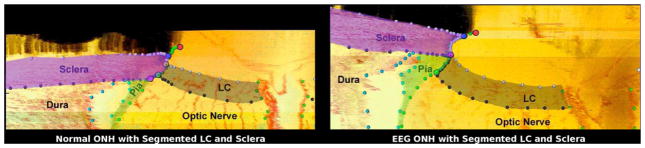
Histologic sections through the ONH with segmented LC and scleral tissues of a monkey, with one eye having early experimental glaucoma (EEG). Note the outward migration of the LC insertion from the sclera into the pia in the early glaucoma eye compared to its contralateral control (adapted from Yang et al., 2010).

Yang et al. (2011b) have observed the outward migration of the LC during the earliest stage of glaucoma in the monkey model of the disease (Fig. 5). Roberts et al. (2009) counted an increased number of laminar beams through the LC thickness in monkey eyes with early glaucoma (Fig. 4) leading to the hypothesis that outward LC migration occurs via the recruitment of retrolaminar tissue into the LC. The LC usually inserts into the sclera in normal monkey and human eyes and spans the scleral canal (Fig. 5). In early experimental glaucoma, chronic IOP elevation led to a migration process that relocating the laminar insertion to a more posterior position within the neural canal that resulted in a partial or complete insertion into the pial sheath of the optic nerve. The pial sheath surrounds the retrolaminar optic nerve and is thought to provide elasticity to the nerve to protect it as the eye moves (Sawaguchi et al., 1994), but it is not part of the fibrous layer of the ocular coats responsible in carrying the IOP-induced pressure load. As a result, the biomechanical environment of the LC and the axons in the ONH is likely to be significantly altered if the LC migrates from a scleral insertion to a pial insertion. While pial insertions have been documented in human eyes (Sigal et al., 2010a), posterior LC migration and retrolaminar tissue recruitment has not yet been shown to be associated with human glaucoma. However, LC migration and retrolaminar tissue recruitment may be crucial in understanding the mechanisms of glaucomatous pathophysiology and individual susceptibility to the disease.

These experimental results show that the LC is a very dynamic structure that is able to grow, remodel and migrate in response to biomechanical stimuli such as chronic exposure to IOP above a homeostatic level.

4.2. Adaptation of anisotropy in the LC and surrounding peripapillary sclera

The anisotropic nature of the ONH is hypothesized to protect the RGC axons from IOP-related biomechanical insult. Tissue anisotropy is also likely to change in response to IOP exposure, although experimental results showing such change are sparse. Yan et al. (2010) reported that anisotropy is significantly different in persons of African descent compared to those of European descent, which could partially explain the biomechanical underpinnings of the significantly greater prevalence of glaucoma in the black population. Roberts et al. (2009) analyzed predominant laminar trabeculae orientations in early experimental glaucoma eyes compared to their contralateral controls in the monkey, but no differences in the predominant orientations were found at this stage of the disease. It may be that adaptation of the anisotropy in glaucoma occurs later in the disease process than the observed changes in laminar thickness, connective tissue volume, and position noted in studies of those same monkey eyes.

Evidence is emerging that focal laminar defects (acquired pits of the optic nerve or APON) are a progressive part of the glaucomatous disease process in some patients (Girkin et al., 2011). These laminar lesions may be created by focal failure of the adjacent laminar trabeculae or the laminar insertions into the sclera or pia, as they are most often seen at the periphery of the LC. In the APON cases where postmortem histologic 3D reconstructions of the LC have been performed, the laminar trabeculae seem to have formed a protective region of tangentially aligned laminar beams around the edges of the lesion through adaptation of the anisotropic connective tissue architecture (Fig. 6).

Fig. 6.

(a) 3D reconstructions of the inferior half of the LC connective tissues of a glaucomatous human eye with laminar disinsertion from the neural canal. (b) The connective tissue volume fraction (contour plot) and the direction and strength of the preferred orientation of the laminar trabeculae (lines with arrow heads) obtained from the 3D reconstructions using the MIL method. Note the focal defect in the inferior periphery of the LC in (a) and the tangentially aligned laminar trabeculae around the edges of the lesion in (b). S—superior, I—inferior, N—nasal, T—temporal.

4.3. Numerical modeling of growth and remodeling in early glaucoma

We recently used a G&R approach to computationally simulate the structural changes of the LC during the earliest stages of glaucoma (Grytz et al., 2011b). In the last decade, many computational formulations have been developed to model finite growth of soft tissues (Epstein and Maugin, 2000; Lubarda and Hoger, 2002; Göktepe et al., 2010; Himpel et al., 2005; Klisch et al., 2003; Kuhl et al., 2007). Ambrosi et al. (2011) summarized the recent advances in computational modeling of biological growth and remodeling. While existing numerical models are well established to simulate finite growth of soft tissues based on the kinematic growth of finite elements, these methods are insufficient to simulate tissue recruitment and tissue migration. These G&R mechanisms are believed to be key components of the G&R process of the LC during the earliest stages of glaucoma (Roberts et al., 2009; Yang et al., 2010; Downs et al., 2011b). Recently, Schmid et al. (in press) proposed a mixture-based growth formulation, wherein the growth process is consistently introduced at both the kinematic and constitutive levels. We modified this approach in Grytz et al. (2011b) to account for tissue recruitment and tissue migration as seen in early experimental glaucoma.

The G&R approach proposed in Grytz et al. (2011b) is based on the homeostatic control mechanism at the collagen fibril-level discussed in Section 2.3. Tissue G&R was captured by two simultaneous mechanisms at the micro-scale: (i) tissue remodeling was assumed to occur through the adaptation of the collagen fibril residual stretch λ_R; and (ii) tissue growth was assumed to occur through a change in collagen fibril synthesis and degradation rates. Both mechanisms were assumed to occur simultaneously in an effort to reach a homeostatic stretch at the collagen fibril-level as defined by the stimulus (6).

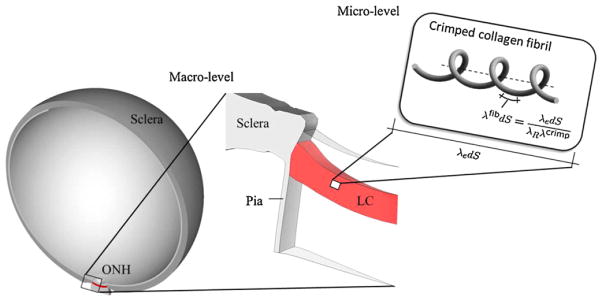
In a previous study based on a multi-scale approach (see Fig. 7) the collagen fibril stretch λ^fib was found in Grytz et al. (2011b) to differ from the tissue stretch λ_e due to collagen fibril crimping λ^crimp and the existence of a residual stretch λ_R

Fig. 7.

Diagram of the multi-scale approach proposed in Grytz et al. (2011b). Shown is from left to right: the human eye model (adapted from Sigal, 2009), the ONH region including the LC at the macro-level, and the crimped collagen fibril at the micro-level. The macro-level problem is solved by using the finite element method, where the micro-level problem is incorporated through the constitutive formulation suggested by Grytz and Meschke (2009). The absolute elastic stretch experienced by the collagen fibril material λ^fib differs from the stretch experienced by the bulk tissue material λ_e due to residual stretch λ_R and collagen fibril crimping λ^crimp.

$${\lambda }^{\text{fib}}=\frac{{\lambda }_e}{{\lambda }_R{\lambda }^{\text{crimp}}}.$$ (7)

To simulate tissue remodeling, the evolution of the residual stretch was assumed to be a linear function of the collagen fibril-level stimulus (6)

$${\stackrel{.}{\lambda }}_R={\stackrel{.}{\lambda }}_R(\phi )=\frac{\phi }{{\tau }_R},$$ (8)

where τ_R relates to the remodeling time needed to achieve homeostasis. From the relationship (7), one can discern that the adaptation of the residual stretch λ_R impacts the tissue stretch λ_e as well as the collagen fibril stretch λ^fib and its crimping response λ^crimp. Consequently, the adaptation of λ_R can lead to tissue elongation/shortening at the macro-scale through the interaction with λ_e and to a changing collagen fibril crimp geometry at the micro-scale through λ^crimp depending on the tissue boundary conditions.

To simulate tissue growth, the collagen fibril mass was assumed to change within the tissue (Grytz et al., 2011b). The change in collagen fibril mass was modeled using a simple evolution equation for the growth Jacobian $J_g^{\text{col}}$ that represents the ratio of the volume occupied by collagen fibrils at the final (grown) ${\text{d}V}_g^{\text{col}}$ and initial configuration ${\text{d}V}_0^{\text{col}}$

$${\stackrel{.}{J}}_g^{\text{col}}={\stackrel{.}{J}}_g^{\text{col}}(\phi )=\frac{\text{d}}{\text{d}t}\left(\frac{{\text{d}V}_g^{\text{col}}}{{\text{d}V}_0^{\text{col}}}\right)=k^{\text{col}}\phi .$$ (9)

The weighting function k^col was used to control the growth rate and to constrain the volumetric growth between maximal and minimal volume change limits. The use of a growth Jacobian allowed for a simple translation from the change in collagen fibril mass to the change in bulk tissue volume based on the mixture theory similar to the approach by Schmid et al. (in press). The change in bulk tissue volume was then used to simulate the kinematic tissue thickening or thinning using a transversely isotropic growth tensor F_g based on a multiplicative split of the deformation gradient into elastic and growth components as initially suggested by Rodriguez et al. (1994).

To simulate tissue recruitment and migration, we assumed that the turnover rate of collagen fibrils can change in the LC and the pre- and retrolaminar tissues (Grytz et al., 2011b). Furthermore, the LC was defined as neural canal tissues with a high collagen fibril content (collagen fibril volume fraction of 10% or more). Accordingly, collagen fibril mass in the LC can be reduced until the tissue is no longer considered as being part of the LC. Conversely, collagen fibril mass in the pre- or retrolaminar tissues can be increased beyond the inclusion threshold and as such met the definition of having been recruited into the LC. The spacial redistribution of collagen mass allows the simulation of tissue migration across finite element borders at the macro-scale, which underscores the importance of the mixture theory in modeling tissue migration and tissue recruitment.

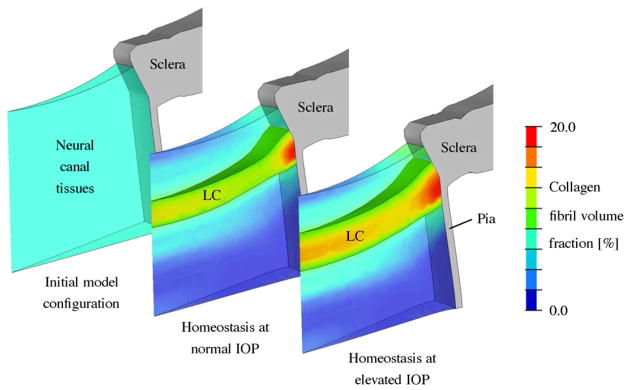
The proposed G&R algorithm was applied to a generic finite element model of the human ONH with uniform initial collagen content throughout the tissues within the neural canal (Fig. 8). The model was able to achieve homeostasis at normal (15 mmHg) and elevated IOP (25 mmHg). At normal IOP, the G&R algorithm created a LC-like structure that spanned the scleral canal and hence this result provides evidence to support the biomechanical need for a LC in humans. To maintain homeostasis at elevated IOP, the simulation significantly thickened the LC (~40%). This thickening principally occurred through a local increase in collagen fibril mass in the pre- and retrolaminar tissues and the recruitment of adjacent neural canal tissues into the LC. This tissue recruitment led to the inward and outward migration of the anterior and posterior LC insertion points, respectively. The adaptation of the residual stretch played a minor role in achieving homeostasis in the simulation. Consequently, the key G&R mechanism seen in the early glaucoma simulation was the significant thickening of the LC due to the recruitment of the neural canal tissues, which is in good agreement with the experimental evidence (Roberts et al., 2009; Yang et al., 2011b). Winkler et al. (2010) showed that the collagen density is gradually changing through the depth of the neural canal with a steep increase at the level of the LC, where the collagen content is between 10% and 29%. The data presented by Roberts et al. (2009) indicate that connective tissue volume fraction in the monkey LC is between 12% and 45%, which includes the laminar capillary volume, cells, and non-fibrillar extracellular matrix components. These experimental findings underlie the importance of the mixture theory for numerically modeling the neural canal tissues. The numerical G&R simulation presented in Fig. 8 predicted a gradually changing distribution of collagen through the depth of the neural canal, which agrees with the available experimental evidence. A rather arbitrary threshold of 10% collagen volume fraction was used to identify and visualize the LC in the simulation. However, the main results of the G&R analysis hold regardless of the threshold value chosen as long as the chosen threshold is reasonable. In essence, the boundaries of the LC will move as the collagen fibril density threshold value is changed, but the development of an LC and the elevated-IOP induced thickening will remain.

Fig. 8.

G&R simulation of the LC thickening seen in early experimental glaucoma. The collagen fibril volume fraction in the neural canal tissues is shown for the initial configuration and the modeled homeostatic configuration at normal (15 mmHg) and elevated IOPs (25 mmHg). Neural canal tissues with a collagen fibril density of 10% or more were defined to represent the LC. The simulation starts with an initial homogeneous collagen fibril density (6%) throughout the neural canal tissues without presupposing the existence of a LC. After reaching model homeostasis at normal IOP (15 mmHg), the model predicted the existence of a LC-like structure spanning the scleral canal of similar dimensions, shape and location of the normal LC in vivo. To regain model homeostasis after IOP elevation to 25 mmHg, the model predicted the significant thickening of the LC due to local increase in collagen fibril density in the pre- and retrolaminar tissues and the recruitment of these tissues into the LC. The borders of the LC insertion into the surrounding sclera also migrated as the LC thickened (Grytz et al., 2011b).

5. Growth and remodeling in advanced glaucoma

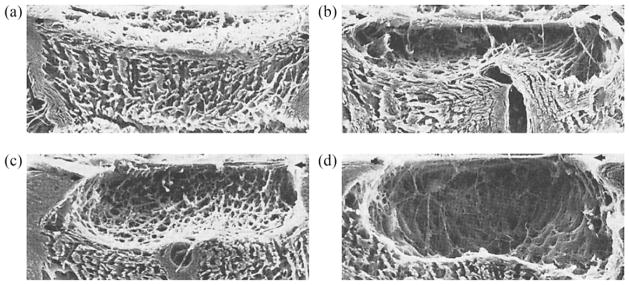
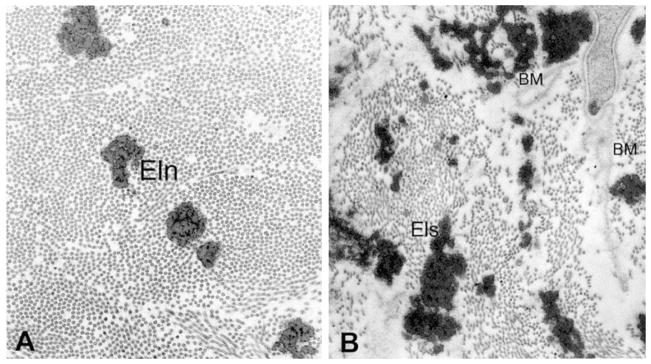
Experimental evidence has demonstrated that the LC thickens, migrates posteriorly, and adds trabeculae through its thickness with minor to moderate loss of RGC axons very early in the disease process. In contrast, the typical end-stage glaucomatous ONH exhibits profound degeneration of RGC mass paralleled by profound excavation, thinning, and scarring of the LC beneath the scleral canal rim (Quigley, 2011; Quigley et al., 1983, Fig. 9). This is a progressive process that has not been well described in humans because cadaver eyes used in research rarely exhibit clinically documented and identifiable early forms of glaucoma. The general process of LC remodeling has been previously proposed but is not well described or understood (see Fig. 4 in Burgoyne and Downs, 2008). A recent review of the literature has identified progressive remodeling as the mechanism that is most likely to drive the transformation of a normal LC morphology into that of a blind glaucomatous eye with end-stage, excavated, thinned and scarred LC (Downs et al., 2011b). The significant decrease in collagen fibril density and regularity seen in the extracellular matrix of glaucomatous LCs underscores the importance of investigating G&R mechanisms in glaucoma at different length scales (Hernandez, 2000, Fig. 10).

Fig. 9.

Electron micrographs of the connective tissues of the ONH after trypsin digestion of (a) a normal eye, (b and c) eyes with moderate glaucomatous damage, and (d) a blind glaucomatous eye (reproduced from Quigley et al., 1983).

Fig. 10.

Ultrastructure of the extra cellular matrix in the normal and glaucomatous human LC. (a) Normal extra cellular matrix consists of densely packed collagen fibrils of the same size. Interspersed between the collagen are fibers of elastin (Eln). (b) The extra cellular matrix in the glaucomatous LC exhibits elastotic fibers (Els) of irregular shape and high electron-density. The density of collagen fibrils is markedly decreased particularly. Basement membranes (BM) not associated with cell surfaces are also present (reproduced from Hernandez, 2000).

To date, no computational simulation strategy has been proposed to model the entire growth and remodeling process seen in glaucoma. The profound structural changes of the ONH from normal to end-stage glaucoma present multiple challenges for computational growth and remodeling approaches. Crucial parts of the remodeling process, such as the stimulus that leads to RGC damage and eventual RGC degeneration, are not well understood. Experimental studies have shown that IOP elevation may lead to active transport blockade within RGC axons passing through the LC, which then may lead to RCG death through apoptosis. The numerical simulation of this process would require the coupling of macroscopic effects (~10⁻¹ m), such as IOP, with mechanisms occurring at a very small length scale (~10⁻⁸ m), such as the active transport within RGC axons. The numerical simulation of interacting mechanisms across such a broad range of length scales presents great challenges for future G&R approaches in modeling glaucomatous progression. However, if one disregards the stimulus, the effect of RGC mass loss can be modeled within a G&R approach that is based on the mixture theory such as proposed in Grytz et al. (2011b). In contrast, a simulation strategy has yet to be developed for the tissue scarring and gliosis that occurs after significant RGC loss in the LC.

6. Growth and remodeling in myopia

The understanding of G&R in myopia is important for understanding the glaucomatous remodeling process.

6.1. Experimental evidence of growth and remodeling in myopia

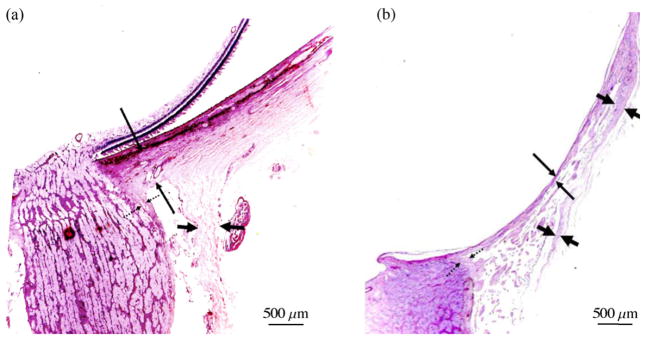
Wallman and Winawer (2004) gathered extensive experimental evidence that the size of the eye can change due to G&R mechanisms guided by visual error signals. Experimentally applied lenses were used to simulate hyperopia and myopia by causing the image focal plane to fall either behind or in front of the retina. Eye elongation compensated for the optical effects of the lenses as seen in various species (chicks, Schaeffel et al., 1988; Irving et al., 1992; rhesus monkeys, Hung et al., 1995; marmosets, Whatham and Judge, 2001; guinea pigs, McFadden et al., 2004; tree shrews McBrien et al., 2000). The axial length of the eye is predominantly altered through growth and remodeling processes that elongate or shorten the sclera in the posterior globe. If, instead of being defocused by a lens, the image on the retina is obscured by a diffuser, the eye elongates and becomes myopic (tree shrew, Sherman et al., 1977; marmoset, Troilo and Judge, 1993; chick, Wallman et al., 1978; rhesus macaque, Wiesel and Raviola, 1977; mice, Schaeffel et al., 2004). Because no images are brought into focus by the excessive ocular elongation, the G&R of the sclera continues as long as vision remains obscure, resulting in eyes whose vitreous chambers are as much as 25% larger than normal (Wallman and Adams, 1987). Recently Jonas et al. (2011) demonstrated the dramatic elongation and thinning of the sclera at the ONH in highly myopic human eyes (Fig. 11). Such dramatic structural changes in the sclera of myopic eyes will impact the stress and strain environment of the LC and likely contributes to the increased glaucoma susceptibility in highly myopic eyes.

Fig. 11.

Histologic section through the ONH of (a) emmetropic and (b) highly myopic glaucomatous eyes (stained by the periodic acid-Schiff method). Long thin arrows: thickness of the peripapillary scleral flange; dotted arrows: pia mater; short thick arrows: dura mater. Note the significant elongation and thinning of the peripapillary sclera in the highly myopic eye (reproduced from Jonas et al., 2011).

6.2. Numerical modeling of growth and remodeling in myopia

Bryant and McDonnell (1998) used an isotropic growth formulation to simulate myopic eye elongation based on an organ-level stimulus (3). The simulated eye elongation was qualitatively similar to the experimental data presented by Norton and Siegwart (1995), suggesting that the proposed growth mechanism for axial elongation of the eye is plausible. Growth based approaches are based on the addition or reduction of tissue mass and volume to allow for tissue elongation or shortening, respectively. However, the mass of the fibrous layer, which is the only layer of the mammalian sclera, is slightly reduced during myopic eye elongation through a reduction in extracellular matrix component synthesis, and an increase in synthesis of enzymes that degrade the extracellular matrix (McBrien and Gentle, 2003).

7. Perspectives on characteristic G&R mechanisms and discussions

G&R phenomena seen in ocular and other soft tissues can be classified by characteristic mechanisms such as (i) adaptation of connective tissue anisotropy, (ii) connective tissue thickening/thinning, (iii) connective tissue elongation/shortening and (iv) connective tissue migration. Perspectives on characteristic mechanisms and the potential role of the LC in glaucoma are discussed in this section.

7.1. Connective tissue thickening/thinning versus connective tissue elongation/shortening

We acknowledge that biological tissues can grow and remodel in every direction. Soft connective tissue G&R phenomena, however, are often classified into tissue thickening/thinning or elongation/shortening because these two phenomena are assumed to have two different etiologies. Tissue elongation/shortening is understood here as the elongation or shortening of a connective tissue in its main tensile loading direction(s) without changing the mass or density of the tissue or of its constituents. Conversely, tissue thickening/thinning is understood here as the thickening or thinning of a connective tissue normal to its main tensile loading direction(s) due to changes in collagen fibril mass.

In Grytz et al. (2011b) we proposed a G&R approach based on two simultaneous mechanisms at the micro-scale: (i) tissue remodeling through the adaptation of the residual stretch of the collagen fibrils; and (ii) tissue growth through a change in collagen fibril mass. At the macro-scale, the fist mechanism leads to tissue elongation/shortening while the latter mechanism leads to thickening/thinning. Therefore, we use this model here to investigate the etiologies of connective tissue thickening/thinning versus elongation/shortening.

Let us imagine two identical collagenous tissue samples. In a first theoretical experiment, both samples are subjected to a constant uniaxial stress overload. In a second theoretical experiment, both samples are subjected to an constant uniaxial stretch overload. In both experiments, the collagen fibrils are stretched beyond their homeostatic state as defined in (6). Each of the two tissue samples can use a different mechanisms to regain homeostasis. One tissue sample can remodel through adapting the residual stretch of its collagen fibrils, while the other can grow through increasing its collagen fibril mass content.

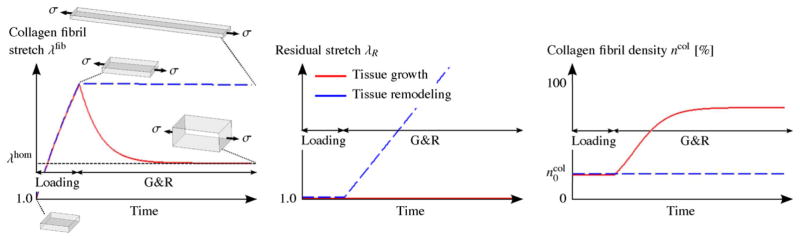
Fig. 12 shows the qualitative G&R evolution of these two tissue samples subjected to the stress-based overload. One can see the unsuccessful effort of the remodeling tissue to recover homeostasis (dashed blue line) as the adaptation of the residual stretch leads to an continuous elongation of the tissue without reducing the collagen fibril stretch. In contrast, the growing tissue (red line) quickly recovers homeostasis by increasing its collagen fibril density. Note that a similar result can be obtained at low tissue stress, leading to a collagen fibril stretch below the homeostatic stretch level. At low tissue stress, the remodeling mechanism would shorten the tissue without recovering homeostasis while the growth mechanism would lead to tissue thinning and homeostasis.

Fig. 12.

Stress-based overload. A constant uniaxial tissue stress σ is applied to two tissue samples such that the collagen fibrils are stretched beyond their homeostatic stretch state λ^hom. The tissues can either grow in thickness direction through increasing the collagen fibril density η^col (red line) or remodel through the adaptation of the residual stretch λ_R (dashed blue line) to overcome the overload and to regain homeostasis at the collagen fibril level. From left to right, shown is the qualitative evolution of the collagen fibril stretch λ^fib, the residual stretch λ_R and the collagen fibril density η^col. The results are based on the G&R algorithm proposed in Grytz et al. (2011b). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

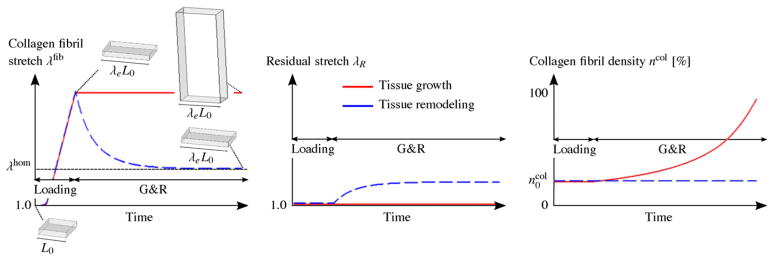
Fig. 13 shows the qualitative G&R evolution of the two tissue samples subjected now to the stretch-based overload. Here the effectiveness of the competing mechanisms flips around. The growth mechanism (red line) continuously increases the collagen fibril density leading to unstoppable tissue thickening without reducing the collagen fibril stretch. In contrast, now the remodeling mechanisms (dashed blue line) serves its usefulness as it quickly recovers homeostasis by adapting the residual stretch. Note that tissue shortening below the homeostatic stretch level leads to a similar result, where the growth mechanism shrinks the tissue without recovering homeostasis while the competing remodeling mechanism recovers homeostasis by adapting the residual stretch. The results of these theoretical experiments suggest that the adaptation of the residual stretch leads to tissue elongation/shortening, which seems to be an effective remodeling mechanism when the tissue is subjected to a stretch-based overload. In contrast, tissue thickening/thinning due to collagen fibril mass increase/decrease seems to be an effective mechanism to regain homeostasis when the tissue is subjected to a stress-based overload.

Fig. 13.

Stretch-based overload. A constant uniaxial tissue stretch λ_e is applied to two tissue samples such that the collagen fibrils are stretched beyond their homeostatic stretch state λ^hom. The tissues can either grow in thickness direction through an increase in the collagen fibril density η^col (red line) or remodel through the adaptation of the residual stretch λ_R (dashed blue line) to overcome the overload and to regain homeostasis at the collagen fibril level. From left to right, the qualitative evolution of the collagen fibril stretch λ^fib, the residual stretch λ_R and the collagen fibril density η^col are shown. The results are based on the G&R algorithm proposed in Grytz et al. (2011b). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

Based on these findings, we expected that the LC thickened in early glaucoma (Section 4) because the eye was subjected to a pressure overload, which results in a stress overload at the LC. In case of myopia, however, the adaptation of the residual stretch might be the underlying mechanism that leads to the scleral elongation seen in highly myopic human eyes.

In addition to the adaptation of the residual stretch, tissue elongation/shortening can also be modeled using a growth-based formulation. Göktepe et al. (2010) used two transversely isotropic growth tensors to either model tissue thickening or tissue elongation in the heart. Tissue elongation was the result of tissue growth in the main tensile loading directions (the in-plane directions) of the heart tissue. Bryant and McDonnell (1998) used an isotropic growth formulation to simulate myopic eye elongation that qualitatively agreed well with experimental data presented by Norton and Siegwart (1995), but in mammalian myopia the tissue mass seems to show little change (McBrien and Gentle, 2003). The dominant mechanism in human myopia remains unknown, but the small change in tissue mass points toward a remodeling mechanism (e.g. through the adaptation of the residual strain state) and not to a growth mechanism. As the residual stretch is closely related to collagen fibril crimp adaptation (7), a multi-scale experiment investigating the scleral elongation as well as a potential adaptation of the collagen fibril crimp similar to the study by Foolen et al. (2010) might reveal the remodeling mechanism underlying human myopia.

7.2. Eye volume overload—a potential mechanism for eye elongation

In Section 7.1 we showed that tissue thickening due to an increase in collagen fibril mass is a suitable growth mechanism to overcome a stress-based overload, while tissue elongation due to residual stretch adaptation is a suitable mechanism to overcome a stretch-based overload. In the eye, these two different etiologies may be related to an IOP-based (stress-based overload) and a volume-based overload (stretch-based overload). Of course, a volume overload of the eye will also cause IOP to increase, but one of the two etiologies might dominate. The in- and outflow facilities of the eye are known to be IOP dependent. Consequently, a constant IOP load can be obtained by IOP-dependent regulation of the fluid production and/or fluid outflow in the eye. Structural changes in trabeculae meshwork may change the IOP-dependent outflow facilities of the eye leading to an IOP overload. This IOP overload may then trigger the growth mechanism leading to LC thickening seen in early glaucoma. Conversely, a pathophysiologic (relatively IOP-independent) fluid production in the eye may lead to a constant fluid overproduction and as such to a volume overload in the eye. A constant volume overload in the eye might then trigger the remodeling mechanism leading to eye elongation such as seen in myopia or pediatric glaucoma. Note that similar G&R etiologies have been suggested to cause eccentric and concentric cardiac growth through sarcomerogenesis in the heart (Göktepe et al., 2010).

7.3. Independent versus dependent remodeling mechanisms leading to residual strains

In several recent studies (Grytz et al., 2011b; Watton et al., 2009a,b; Nagel and Kelly, in press; Machyshyn et al., 2010) the evolution of the residual stretch (or recruitment stretch) was treated like an independent, active remodeling mechanism as discussed in previous subsection. Note that our definition of the residual stretch λ_R is similar to the definition of the recruitment stretch used by Watton et al. (2009a), Watton et al. (2009b), Nagel and Kelly (in press), and Machyshyn et al. (2010). Therefore, the residual stretch can be interpreted as the macroscopic stretch level that the bulk tissue must undergo in the direction of the collagen fibril for it to bear tensile load.

It has also been suggested that the evolution of residual strains is strictly a dependent remodeling mechanism, where residual strains are a natural consequence of continuously synthesized and degraded constituents while the tissue is subjected to external loading (Humphrey and Rajagopal, 2002). Existing numerical approaches based on this hypothesis often define a natural configuration of the continuously renewing constituents (Valentín et al., 2011; Zeinali-Davarani et al., 2011a,b). The assumed natural configuration together with the in vivo strain state of the bulk tissue can then be used to calculate the residual strain state. It remains unclear if the adaptation of the residual strain state is an independent remodeling mechanism in soft tissues or not, but it is likely both. In support of the active mechanism, Foolen et al. (2010) demonstrated that a homeostatic residual strain state was regained upon strain perturbation even without a functioning protein synthesis pathway (protein synthesis was prevented via the addition of cycloheximide to the tissue sample). However, these experimental results were based on chicken embryo periosteum and the remodeling response of mature tissue might be very different.

7.4. Perspectives on connective tissue migration

Tissue thickening/thinning and tissue elongation/shortening have been frequently seen and reported in soft tissues. The phenomenon of soft connective tissue migration has been described less frequently but is no less fascinating. Migration of soft connective tissue is understood here as a G&R phenomena that leads to a relocation of one tissue type relative to its surrounding tissues. The underlying biomechanical mechanisms leading to tissue migration are still unknown. Most existing computational G&R approaches were not designed to simulate this phenomenon, possibly due to its rarity in vivo. In our latest attempt to model G&R during early glaucoma (Grytz et al., 2011b), we proposed a mixture-based G&R approach that allowed us to simulate tissue migration. The model predicted the tissue recruitment to occurs on both the anterior and posterior surfaces of the LC. In contrast, the experimental results showed a predominantly outward migration of the LC. This migration process is not yet well understood, but it may relate to the dynamics of IOP, including low- and high-frequency IOP fluctuations. To investigate the effect of IOP dynamics, ongoing research projects are targeting the continuous IOP telemetry recording in the monkey model of glaucoma (Downs et al., 2011a). Also additional mechanism and stimuli, such as the biological availability of nutrients, enzymes or growth factors, need to be incorporated into the G&R algorithm to capture all aspects of the LC morphologic changes seen in early experimental glaucoma.

In particular, the availability of nutrients and enzymes may impact the synthesis and degradation process of collagen in the LC. As such, they may contribute to the G&R phenomena that lead to the predominant outward migration of LC (Fig. 5) and the focal LC defects (Fig. 6) seen in glaucoma. The computational implementation of G&R stimuli based on the nutrient and enzyme availability in the tissue requires the coupling of mechanical, biological and chemical mechanisms. Ricken et al. (2007) proposed a triphasic model (solid, interstices filled with water containing nutrients) for the phenomenological description of tissue growth for hard and soft tissues. The Theory of Porous Media was used to account for growth based on both the state of mechanical stress and the availability of nutrients for mass exchange. The triphasic model was successfully used to investigate wound healing, stent restinosis occurring after angioplasty, bone remodeling, and topology optimization of organic material (Ricken et al., 2007; Ricken and Bluhm, 2009, 2010). It may prove useful to extend the triphasic concept to include the nutrient and enzyme concentrations in the tissue and to link the model with a microstructural-based growth formulation (Grytz et al., 2011b) to model connective tissue migration and loss in glaucoma.

7.5. The role of the lamina cribrosa

Our recent G&R simulation created a LC-like structure that spanned the scleral canal at normal IOP (Grytz et al., 2011b) even though the initial configuration did not include a LC. As such, the G&R simulation provided evidence in support of the biomechanical need for a LC in humans to provide mechanical support to the neural canal tissues. For a given IOP, larger globes would lead to a higher mechanical loading of the neural canal tissues, and vice-versa. In this case, the G&R algorithm would predict a thicker LC in larger eyes and a thinner LC in smaller eyes. Consequently, smaller eyes such as those in rodents might not require a collagenous LC to resist the IOP-induced stress in the ONH. With respect to glaucoma, the question remains if the LC and its structural changes are the cause or the consequence of RGC axonal loss in glaucoma. Interestingly, rodents do not have a collagenous LC, yet still develop RGC axonal damage at the level of the lamina region due to chronic IOP elevation (Howell et al., 2007).

8. Concluding remarks

The numerical G&R examples reviewed in this paper show that G&R mechanisms and stimuli don’t have to be very complicated before one can predict and investigate G&R phenomena in glaucoma. Computer simulations or other mathematical models have become necessary to inform biomechanics of the ONH in glaucoma and investigate G&R mechanisms as they pertain to the pathophysiology of glaucoma. Without the understanding of biomechanics gained from such simulations, we have little hope in elucidating the physical effects of IOP on the ONH. This review shows that the latest advances in predictive G&R simulations can provide reasonable explanations of G&R phenomena seen in experiments and predict novel findings. The application of computational G&R simulations opens a new perspective for understanding and investigating the causes of glaucoma.

As our knowledge evolves and new G&R stimuli and mechanism at lower length scales are discovered, the numerical implementations become more complex and require the development of physical approaches and microstructure-based formulations. Future success in G&R research will strongly depend on the identification of basic G&R mechanisms and their interactions at different length scales. However, bridging different length scales remains a computational, theoretical and experimental challenge. As our understanding of the different G&R mechanisms in the eye tissues grows, confidence in simulation tools grows, which may lead to patient-specific diagnostic and predictive G&R simulations that translate computational biomechanics to the bedside.