Direct In Situ Determination of the Mechanisms Controlling Nanoparticle Nucleation and Growth

Abstract

Although nanocrystal morphology is controllable using conventional colloidal synthesis, multiple characterization techniques are typically needed to determine key properties like the nucleation rate, induction time, growth rate, and the resulting morphology. Recently, researchers have demonstrated growth of nanocrystals by in situ electron beam reduction, offering direct observations of single nanocrystals and eliminating the need for multiple characterization techniques; however, they found nanocrystal morphologies consistent with two different growth mechanisms for the same electron beam parameters. Here we show that the electron beam current plays a role analogous to the concentration of reducing agent in conventional synthesis, by controlling the growth mechanism and final morphology of silver nanocrystals grown via in situ electron beam reduction. We demonstrate that low beam currents encourage reaction limited growth that yield nanocrystals with faceted structures, while higher beam currents encourage diffusion limited growth that yield spherical nanocrystals. By isolating these two growth regimes, we demonstrate a new level of control over nanocrystal morphology, regulated by the fundamental growth mechanism. We find that the induction threshold dose for nucleation is independent of the beam current, pixel dwell time, and magnification being used. Our results indicate that in situ electron microscopy data can be interpreted by classical models, by allowing simultaneous measurement of nucleation induction times, growth rates, and evolution of nanocrystal morphology. The results suggest that systematic dose experiments should be performed for all future in situ liquid studies to confirm the exact mechanisms underlying observations of nucleation and growth.

Control over the morphology and size of nanocrystals allows for control of their properties, a trait unrivaled by conventional macroscopic materials.^1-5 Nucleation and subsequent growth of nanocrystals from solution are two growth stages that affect the final morphology of the nanomaterial. These phenomena are well described by the classic nucleation theory (CNT)⁶ and the Lifshitz–Slyozov–Wagner (LSW) growth model, respectively.^7-9 The LSW growth model predicts two asymptotic limits for the growth of nanocrystals: diffusion and reaction limited growth.⁹ When diffusion of monomers to the surface of the crystal is the slowest process, the model predicts that crystals will grow by an Ostwald ripening mechanism, in which the radius of a spherical crystal will grow with time as r ~ t^1/3. Yet when the surface reaction limits the growth of the nanocrystal, the model predicts that the radius will grow as r ~ t^1/2. Moreover, the growth mechanism is thought to dictate the morphology of the initial crystalline seed, which will in turn determine the final morphology of the nanocrystal.¹⁰ Diffusion controlled growth typically results in multiply twinned seeds that grow to have polyhedral or near spherical shapes. On the other hand, reaction limited growth results in singly twinned seeds that can grow into anisotropic crystalline plates or bipyramidal crystals.¹⁰

To truly understand the nucleation and growth dynamics of nanocrystals and facilitate comparison with classical models, direct in situ observations of the nucleation and growth steps must be made. In situ electron microscopy has recently shown much promise for directly investigating dynamic processes in liquid at the nanoscale, with applications including nanomaterials,¹¹ biomolecular imaging,^12-14 colloidal science,^15-17 and nanocrystal growth.^18-22 Although this technique has been shown to sometimes suffer from imaging artifacts, many of the adverse conditions can be minimized using simple experimental procedures and ideal microscope parameters, such as scanning transmission electron microscopy (STEM) techniques and relatively low electron doses.²³ A recent review of the topic by de Jonge and Ross details many of the strategies for in situ fluid transmission electron microscopy (TEM) and further applications.²⁴ Notably, Zheng and co-workers demonstrated the first real-time in situ observations of platinum nanoparticle growth using fluid stage TEM.¹⁸ They found that the electron beam induced growth of nanoparticles proceeds by monomer attachment from solution and coalescence of particles, which provided new insight into size focusing during nanoparticle growth. However, the complex chemistry of the precursor and solvent limited the author’s ability to characterize the radiochemical reaction mechanisms responsible for the nanocrystal formation. Similar electron beam induced observations of nanoparticle growth were seen with scanning electron microscopy (SEM),²⁵ scanning transmission electron microscopy (STEM),^{19, 23} and TEM.²¹ Growth of silver nanocrystals onto TiO₂ nanowires within an SEM was shown to occur due to the reduction of silver ions by solvated electrons in solution and electrons generated in the TiO₂.²⁵ However, the particle growth rates and quantitative measures of the reaction rates and kinetic processes were not described for the SEM experiment.

We have previously demonstrated the growth of lead sulfide nanoparticles due to continuous irradiation with a focused STEM probe and also via laser induced decomposition within a Dynamic TEM (DTEM).¹⁹ In that paper, two important observations were reported. First, the STEM experiments showed evidence of lead sulfide nanoparticle growth occurring by both thermodynamic and kinetic mechanisms. Second, the DTEM experiments revealed the first decoupling of the nucleation/growth reaction from the effects caused by exposure to the incident electron beam. These results combined to suggest that there must be a critical threshold for both the induction of nucleation and growth as well as the mechanism of growth dictating final morphology. While the induction threshold for nucleation and growth will likely depend on the solution/sample being imaged, no values have yet been reported and experiments systematically exploring the effects of imaging at, below, or above these thresholds are also lacking.

To study the nucleation and growth mechanisms responsible for morphological control over nanocrystal growth, we grew silver nanocrystals in an in situ fluid stage with an aberration corrected STEM. The incident electron beam was used as both the STEM imaging probe and as the ionizing radiation source to stimulate growth by electron beam reduction. We first identified an imaging condition (threshold electron dose rate) below which no visible growth occurred over a time of minutes. Above this threshold, we measured the induction time for nucleation (i.e. time delay for nucleation to start) while independently varying the electron beam current, pixel dwell time, and magnification. We calculate the corresponding induction threshold doses and show that they are relatively constant while varying these electron beam parameters. From these results, we propose that the underlying reason for the induction threshold dose is that a sufficient amount of electrons must interact with the silver precursor to establish the supersaturation condition necessary for nucleation. Following the nucleation study, we show that growth of nanocrystals is a hindered diffusion limited process at beam currents much larger than the threshold for crystal growth, where various electron beam artifacts affect the growth rate. However, at beam currents near the growth threshold, evidence of reaction limited growth is observed in the faceted morphology of the resultant nanocrystals and their growth trajectories. From these observations, it seems that the beam current is analogous to the concentration of reducing agent in conventional colloidal nanoparticle synthesis.

RESULTS AND DISCUSSION

The radiochemistry of electron beam induced nanoparticle growth

Nanocrystal growth by electron beam reduction can be explained through a radiochemical mechanism, where incident beam electrons (E₀ = 200 keV) radiolyze the water, creating free radicals and aqueous electrons ${\mathrm{e}}_{\mathrm{aq}}^{-}$ that reduce soluble metallic precursors into solid metal atoms, which then aggregate to form nuclei and subsequently grow into nanocrystals.²⁶ Secondary electrons created inside the silicon nitride windows are also thought to be transferred into the fluid to form aqueous electrons.^{23, 27} Radiolysis of water by electrons forms numerous radicals and molecular species, shown in the following reaction.²⁸

$${\mathrm{H}}_2\mathrm{O}\to {\mathrm{e}}_{\mathrm{aq}}^{-},{\mathrm{H}}_3{\mathrm{O}}^{+},{\mathrm{H}}^{•},{\mathrm{H}}_2,{\mathrm{OH}}^{•},{\mathrm{H}}_2{\mathrm{O}}_2$$ (1)

The reduction of metal ions to solid atoms then proceeds by a reduction reaction with hydrogen radicals or aqueous electrons.^{29, 30}

$${\mathrm{M}}_{\mathrm{n}}+{\mathrm{e}}_{\mathrm{aq}}^{-},{\mathrm{H}}^{•}\to {\mathrm{M}}^{\mathrm{n}-1}$$ (2)

Here Mⁿ is a metal ion with a valence of n. Hydroxide radicals have also been shown to oxidize metal ions and atoms to higher valence states, effectively slowing the growth of nanocrystals.²⁶

$${\mathrm{M}}^{\mathrm{n}}+{\mathrm{OH}}^{•}\to {\mathrm{M}}^{\mathrm{n}+1}$$ (3)

Electron beam induced growth of nanocrystals is nearly analogous to conventional chemical reduction of nanocrystals, except for the existence of multiple reducing agents, oxidative species, and electron beam interactions. In fact, oxidative species are often used in conjunction with reducing species to establish reaction limited growth modes in conventional syntheses.³¹ The typical electron beam interactions have been studied for liquid samples; phenomenon such as charging, sputtering, and contamination have been characterized in the context of nanocrystal growth and nanoparticle suspensions, with experimental methods suggested for reducing their effects.²³

The effect of electron beam parameters on the interaction volume

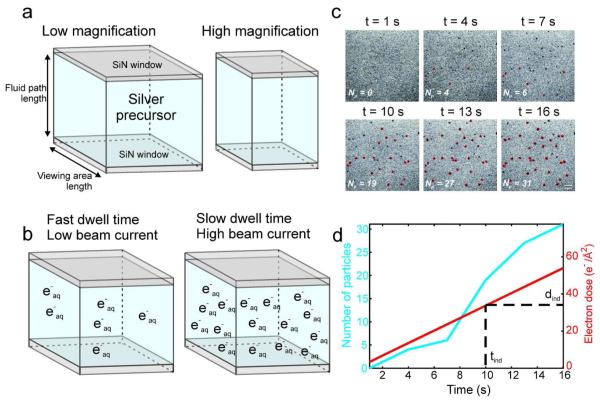
Figure 1 summarizes the experimental setup and the relevant STEM beam parameters, which are the magnification, electron beam current, and pixel dwell time. The magnification is defined by the area the STEM beam is scanned over; lower magnifications correspond to large scan areas, while high magnifications have smaller scan areas. The electron beam current is a measure of the number of electrons impacting the sample per second, while the pixel dwell time is the length of time the STEM probe is held on each pixel in the image during scanning, and therefore defines how fast the electron beam is rastered across the sample. Combining these parameters together, an effective electron dose rate, ḋ, can be defined as the flux of incident electrons through the sample (c.f. Methods for further details).

Figure 1.

(a) Schematic representation of the interaction volume for in situ nanoparticle growth. The interaction volume is dictated by both the viewing area size and the fluid path length. At low nominal magnification the scan area is large, yielding a large interaction volume, while at higher magnification and identical fluid path length the scan area is relatively small, yielding a smaller interaction volume. (b) Schematic representation of the concentration of aqueous electrons in the interaction volume after a single STEM scan, showing the effect of pixel dwell time and beam current on radical production, while holding the interaction volume constant. (c) Time lapsed series of (cropped) BF-STEM images showing nucleation of silver nanocrystals from 1.0 mM AgNO₃. The red outlines indicate particles that are detected by image analysis, while undetected particles are still below the detection threshold. The magnification is M = 100,000x, the frame rate is .33 fps, the dwell time is 5 μs, and the current density if i_e = 40 pA, yielding an electron dose rate of 3.37 electrons/Ų s. The scale bar is 100 nm. (d) The total number of particles (left axis) and the cumulative electron dose (right axis) as a function of time for the images in (c). The vertical dashed line marks the median nucleation induction time, while the horizontal dashed line marks the corresponding median induction dose.

The interaction volume is shown schematically in Figure 1a, and is defined as the viewing area multiplied by the fluid path length. This is the volume that is directly irradiated by the incident beam electrons. Adjusting the STEM beam parameters affects the interaction volume and the radicals produced as seen in Figures 1a & 1b. Increasing the magnification reduces the interaction volume for a fixed fluid path length (Figure 1a). However, Figure 1b demonstrates that increasing the electron beam current or pixel dwell time increases the amount of radicals produced by radiolysis during one STEM scan, but does not change the interaction volume size. This is simply because more incident electrons pass through the interaction volume in a single scan for a larger beam current or dwell time, leading to more ionization scattering events per scan.

Nucleation induction time and dose

Nanocrystal growth does not occur immediately upon irradiation with electrons, but occurs after an initial nucleation induction time, which is defined as the period of time between the achievement of a steady state supersaturation concentration of silver atoms and the detection of nanocrystals:³²

$${\mathrm{t}}_{\mathrm{ind}}={\mathrm{t}}_{\mathrm{i}}+{\mathrm{t}}_{\mathrm{n}}+{\mathrm{t}}_{\mathrm{g}}$$ (4)

Here t_ind is the induction time prior to crystal detection, t_i is the time required to establish a steady state seed population, t_n is the time required for nucleation, and t_g is the time required for a nuclei to grow to a detectable size.⁶ In this case, t_g is the amount of time it takes for a nuclei to grow to a sufficient size that an image analysis algorithm can detect it. The induction time gives important insight into the thermodynamics of crystal nucleation, such as approximation of the nucleation rate, the growth time t_g, and the associated kinetic parameters.³²

Figure 1c shows a time lapsed series of (cropped) BF images of nanoparticles nucleating over time; the number of particles in each frame is shown in the lower left corner. The red outlines mark the particles detected by the image analysis algorithm, while the other particles still remain below the detection threshold. The precursor concentration was 1 millimolar (mM) AgNO_3, the magnification was M = 100,000x, the beam current was 40 pA, and the pixel dwell time was 5 μs, yielding an electron dose rate of 3.37 electrons/Ųs. The induction time for each particle is calculated by taking the difference of the total number of particles in each successive frame. This method yields the number of new particles formed in each frame as a function of time. For instance, in Figure 1c, there are no particles after 1 second of imaging and 4 particles are detected after 4 seconds of imaging; taking the difference in the total number of particles in these successive frames yields 4 particles with an induction time of 4 seconds. This method is repeated for each frame consecutively, forming a distribution of induction times. Because this method assumes that the number of particles is monotonically increasing over the time period of interest, the induction time distribution is only calculated for the initial nucleation period, i.e., from time zero until the maximum number of total particles is reached. Figure 1d shows the number of particles detected as a function of time with the cumulative electron dose overlaid. The vertical dashed line marks the median induction time, calculated from the distribution of induction times. The corresponding median induction threshold dose (horizontal dashed line), d_ind, is then calculated by multiplying the median induction time by the electron dose rate. The induction threshold dose is a general threshold that defines the cumulative electron dose necessary to initiate nucleation and growth of nanocrystals above the detection limit. In this paper we will report the median induction doses instead of the means—the median has its typical statistical definition as the midpoint in the distribution of the data, and is a non-parametric statistical value that does not assume a specific data distribution.

Nanocrystal growth

We used in situ STEM to initiate and directly observe growth of silver nanocrystals from an aqueous silver nitrate precursor. Movies of the nanocrystal nucleation and growth were recorded and analyzed using custom image analysis algorithms, which are described in previous publications.^{22, 23} For improved statistics, we performed the majority of the experiments at low magnification; however, the detection limit was set to ~5 nm (particle diameter) at M = 100,000x by the image analysis algorithm and the microscope resolution. The pixel size at this magnification is 3.13 nm/pixel. By tracking nanocrystal growth in the in situ movies, we directly studied nanocrystal nucleation and growth mechanics. We performed a parametric study on the effects of the STEM beam current, pixel dwell time, and magnification on the nucleation induction time in order to establish the induction threshold dose necessary for nucleation and growth of silver nanocrystals. Following the induction time measurements, we tracked the growth of the nanocrystals as a function of time for different beam currents, and established two distinct growth mechanisms predicted by classical nanocrystal growth theory.

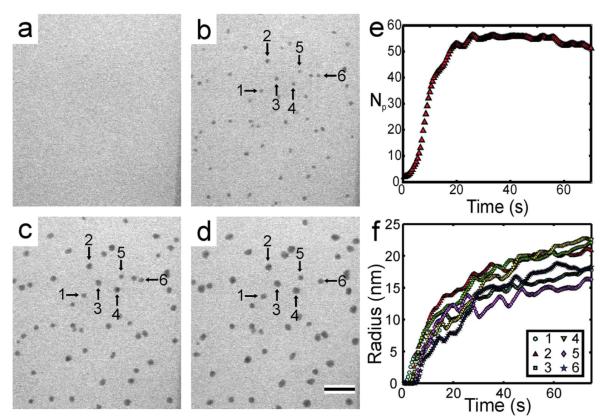
Silver nanocrystal growth was initiated using the STEM beam with variable beam currents, pixel dwell times (i.e. scan speeds), and magnifications (i.e. interaction volumes). Figure 2a-d shows a typical time lapsed series of images of silver nanocrystals growing from 1 mM AgNO₃, at a magnification of M = 100,000x, a beam current of i_e = 40 pA, and a pixel dwell time of 5 μs (c.f. supplementary movie #1 for full movie). The fluid path length was measured to be ~350 nm near the edge of the window (c.f. Methods for details on fluid path length measurement). Only nanocrystals in one focal plane were tracked for their growth with time. The threshold intensity of the image analysis algorithm was adjusted for each experimental movie to yield nanocrystals in the black and white thresholded image that were the same size, by visual inspection, as the corresponding particles in the grayscale STEM image. Even though the threshold was adjusted, the detection limit remained at ~5 nm for M = 100,000x. Figure 2e plots the number of particles as a function of time, while Figure 2f shows the radius as a function of time for 6 nanocrystals marked in Figures 2a-d.

Figure 2.

Time lapsed series of (cropped) BF-STEM images showing growth of silver nanocrystals from 1.0 mM AgNO₃ at t = 0 (a), 15 (b), 45 (c) and 75 s (d). The times are relative to the initial exposure of the area to the electron beam. M = 100,000x and i_e = 40 pA, which corresponded to an electron dose rate of 3.37 electrons/Ųs. The scale bar in (d) is 200 nm. (e) The total number of particles (N_p) as a function of time. The data was filtered with a running average of 5 seconds. (f) Radius as a function of time for the nanocrystals specified with arrows in (b-d). The data was filtered with a running average of 10 seconds.

Nanocrystals did not grow immediately upon irradiation but became visible after a few seconds, as shown in the plot of the number of particles in Figure 2e and the individual growth trajectories in Figure 2f. The rate of nucleation, which is proportional to the slope of N_p in Figure 2e, was small for the initial 2 seconds of irradiation, at this time the majority of the nuclei were below the detection limit of 5 nm. After this initial time period, the rate increased drastically and detection of nuclei proceeded for approximately 20 seconds. Following nucleation, Figure 2f shows that the nanocrystals grew with a non-constant rate, where they grew more rapidly during the first 20 – 30 seconds of irradiation, after which the growth rate slowed significantly. As the nanocrystals grew in radius, their contrast became darker, suggesting that they were growing in 3-dimensions (Figures 2b-d). In this case, growth proceeded by an increase in each individual nanocrystal radius, and coalescence events were not observed. For this experiment, the nanoparticles were thought to grow on the silicon nitride windows as no Brownian motion was observed for any of the particles during growth (c.f. supplementary movie #1). We did not observe any nanoparticle growth in the bulk solution.

Nanocrystal nucleation

Continuously scanning STEM images of silver nanocrystal nucleation were acquired while varying the beam current, pixel dwell time, and magnification. An annular dark field detector (ADF) was used to acquire the images at a frame rate of 1 frame per second. The fluid path length and silicon nitride window thicknesses were held constant for all experiments in the following section at 800 nm and 50 nm, respectively (c.f. Methods for details).

Below a threshold electron dose rate of ḋ_thr = 0.5 electrons/(Ų s) (< 7 pA beam current), nanocrystals were not observed to nucleate and grow in the field of view (above the detection threshold of ~5 nm). We term this quantity the nanocrystal growth threshold. Establishing this condition for in situ nanoparticle growth systems will be important in future studies, as it will allow researchers to separate electron beam induced growth from other important growth modes, such as chemical or electrochemical reduction.

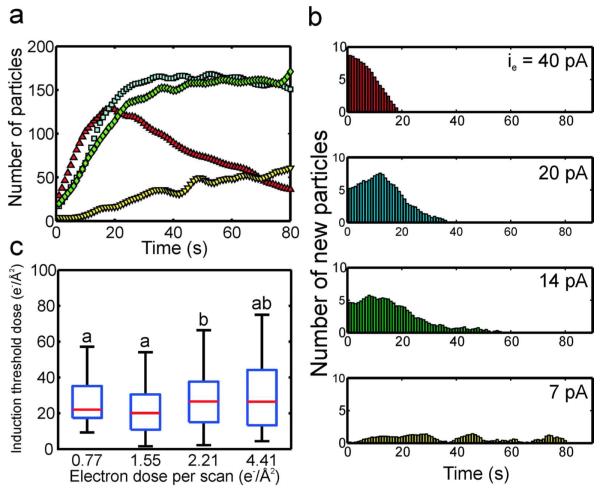
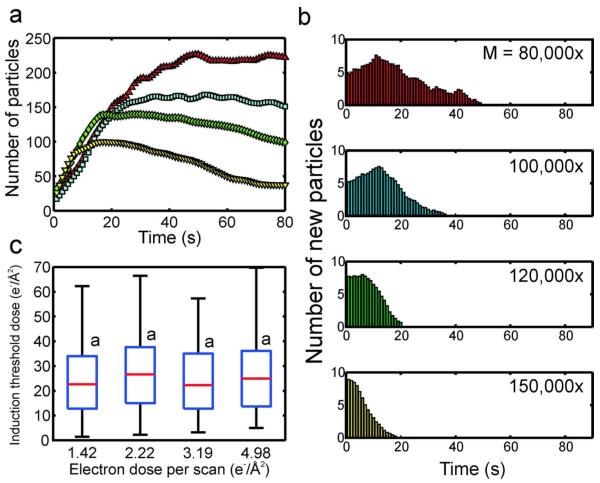
Above ḋ_thr, approximately 50-150 nanocrystals nucleated and grew in the field of view for each beam current. Figure 3a shows the number of nanocrystals detected in the viewing area as a function of time for several different beam currents at a magnification of M = 100,000x and pixel dwell time of 5 μs (scan time of 1.31 s). Supporting movie # 2 shows that the nanocrystals grew attached to the silicon nitride windows, although some nanocrystals moved sporadically during nucleation and growth, either aggregating or moving out of the field of view. For the case of the highest beam current (red triangles, 40 pA), approximately 20% of the nanocrystals were detected after the first second of irradiation, and the number of nanocrystals grew to a maximum at an approximately constant rate in 20 seconds (Figure 3a). After the maximum was reached, the number of nanocrystals declined due to coalescence events¹⁸, aggregation, and repulsion of nanocrystals from the viewing area by electron beam charging.²³ When the beam current was decreased by 50% (blue squares), the number of crystals grew to a maximum after approximately 30 seconds. In this case, after the maximum was reached, the number of nanocrystals remained approximately constant. This suggests that charging effects were likely reduced as the beam current was lowered, which is consistent with previous observations of electron beam charging in in situ fluid experiments.³³ Between the three highest beam currents, the initial rate of nanocrystal nucleation did not change by more than ~20%, suggesting that the beam current did not have a significant effect on the nucleation rate. The low nucleation rate and total number of particles for the 7 pA beam current was partially an artifact of the low signal to noise ratio and image resolution at this beam current, which presented errors in the image analysis algorithm.

Figure 3.

(a) The number of nanocrystals as a function of time for four different beam currents, imaged at M = 100,000x and 5 μs pixel dwell time (red triangle: i_e = 40 pA, blue square: i_e = 20 pA, green diamond: i_e = 14 pA, yellow inverted triangle: i_e = 7 pA). (b) Histograms of the number of new particles as a function of time for each beam current. (c) Box plots of the induction threshold doses as a function of electron dose per scan (c.f. Methods for calculation of electron dose per scan from beam current). On each box, the central mark is the median, the edges of the box are the 25^th (bottom edge) and 75^th percentiles (top edge), and the whiskers extend to the most extreme data points not considered outliers. Values with a similar letter do not differ significantly (Wilcoxon rank sum test, P < 0.01).

Histograms of the number of new particles as a function of time for each beam current are plotted in Figure 3b. The cut-off times for these measurements are given in the supplementary material (c.f. Table S1). For the histograms, the time axis is directly equivalent to the induction time, for example at i_e = 40 pA there were approximately 8 new particles formed after 1 second of imaging, meaning that 8 particles had an induction time of 1 second. The relatively low time resolution of the STEM (0.5 - 4 sec) introduced an inherent amount of error equal to the length of the STEM scan time, because it could not be determined when during this time the particles nucleated, just that they were present after the scan. However, this error is on the order of seconds, which is relatively small in reference to the size of the induction time distributions. Figure 3b shows that at the 40 pA beam current, there was a burst of particles detected following the first STEM scan, after which there was a steady decrease in the number of nanocrystals with subsequently larger induction times, which ended at ~20 seconds. At 20 pA, the peak of the induction time distribution was no longer concentrated on the first STEM scan, but was shifted to the right 10 seconds, and the width of the distribution stretched to ~40 seconds. When the beam current was lowered to 14 pA the width of the distribution was stretched further to ~60 seconds. At the lowest beam current (7 pA) the induction time distribution covered the entire 80 second sampling period. This is due partially to the particularly low resolution at this beam current, which makes particle detection difficult in the image analysis algorithm.

Figure 3c shows box plots of the induction threshold dose distributions as a function of the electron dose per scan, where each box corresponds to a different beam current, with the smallest beam current (7 pA) on the left, increasing to the largest beam current on the right (40 pA). The electron dose per scan is used instead of the beam current to facilitate a comparison of the beam current, magnification, and pixel dwell time results (c.f. Methods for calculation of electron dose per scan). The induction threshold dose is calculated by multiplying the induction times from Figure 3b by the corresponding electron dose rate for that beam current (c.f. Nucleation induction time and dose section for detailed method). Note that, as is customary in box plots, the whiskers are not error bars but represent the extrema of the distribution. The letters above the box plots indicate the induction threshold doses whose distributions and medians do not vary significantly, determined by a Wilcoxon rank sum test with a p-value < 0.01. Although the induction threshold dose distribution of the 2.21 electrons/Ų dose per scan case differed statistically from the distributions at the other beam currents, the medians of all the induction threshold doses did not vary by more than 25%. The average of the four induction threshold doses was 23.8 ± 3.24 electrons/Ų.

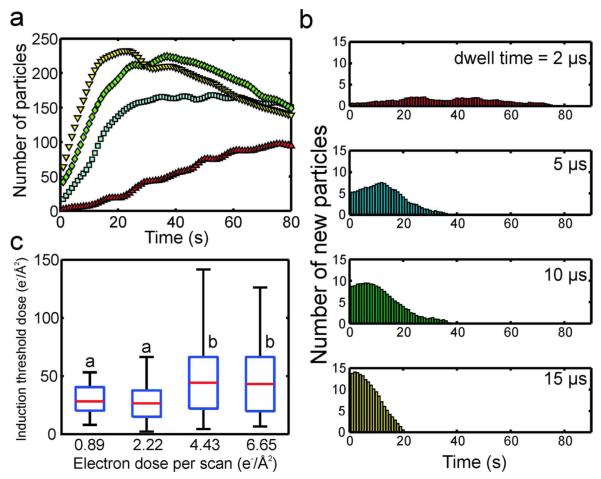
We also varied the electron dose per scan by changing the pixel dwell time (Figure 4) and magnification (Figure 5) independently, while holding all other parameters constant. The pixel dwell time was varied between 2 - 15 μs at a magnification of M = 100,000x and beam current of i_e = 20 pA, where an increased pixel dwell time resulted in a slower scan, and larger amount of electron dose per scan (c.f. Figure 1b). Figure 4a shows that as the pixel dwell time was increased, the number of nanocrystals detected after the first scan increased monotonically, similar to what was observed while increasing the electron dose per scan with the beam current (c.f. Figure 3a). Figure 4b plots the histograms of the number of new particles as a function of time for each dwell time. Again, a similar trend to Figure 3b is observed, where increasing the electron dose per scan decreased the width of the distribution and also moved the maximum towards smaller induction times. Figure 4c shows box plots of the induction threshold doses while varying electron dose per scan with the pixel dwell time, where the average of the four medians was 35.6 ± 9.4 electrons/Ų. In this case, the average is ~30% larger than in Figure 3c, and the standard deviation is 3 times larger—this is due to the 10 and 15 μs induction threshold doses, which have significantly larger medians than the 2 and 5 μs cases. This is likely a result of the error created by the scanning electron beam, which for the larger pixel dwell times, is scanning slowly from top to bottom across the irradiated area. Therefore the induction dose is met more quickly at the top of the image than at the bottom, leading to a larger induction time and dose distribution size. Although experimental error led to a higher average induction threshold dose for the dwell time experiments, order of magnitude agreement is still achieved with the induction threshold doses measured while varying the beam current (c.f. Figure 3c).

Figure 4.

(a) The number of nanocrystals as a function of time for four different pixel dwell times, imaged at M = 100,000x and i_e = 20 pA. The dwell times were 2 (red triangle), 5 (blue square), 10 (green diamond) and 15 μs (yellow inverted triangle). (b) Histograms of the number of new particles as a function of time for each pixel dwell time. (c) Box plots of the induction threshold doses as a function of electron dose per scan (c.f. Methods for calculation of electron dose per scan from pixel dwell time). On each box, the central mark is the median, the edges of the box are the 25^th (bottom edge) and 75^th percentiles (top edge), and the whiskers extend to the most extreme data points not considered outliers. Values with a similar letter do not differ significantly (Wilcoxon rank sum test, P < 0.01).

Figure 5.

(a) The number of nanocrystals as a function of time for four different magnifications, imaged with pixel dwell time of 5 μs and i_e = 20 pA (red triangle: M = 80,000x, blue square: M = 100,000x, green diamond: M = 120,000x, yellow inverted triangle: M = 150,000x). (b) Histograms of the number of new particles as a function of time for each magnification. (c) Box plots of the induction threshold doses as a function of electron dose per scan (c.f. Methods for calculation of electron dose per scan from magnification). On each box, the central mark is the median, the edges of the box are the 25^th (bottom edge) and 75^th percentiles (top edge), and the whiskers extend to the most extreme data points not considered outliers. Values with a similar letter do not differ significantly (Wilcoxon rank sum test, P < 0.01).

Figure 5 shows the induction time and dose results while varying the magnification between M = 80,000 – 150,000x, with a beam current of i_e = 20 pA and a pixel dwell time of 5 μs. Below M = 80,000x, no growth above the detection threshold was observed. As the magnification was increased the electron dose per scan increased because the irradiated area, and interaction volume, decreased in size (c.f. Figure 1a). Figure 5a shows the number of particles detected as a function of time for each of the four magnifications. In contrast to the beam current and dwell time experiments, the number of particles detected after a single scan was approximately the same for each magnification, as were the nanocrystal formation rates. The maximum number of particles detected decreased monotonically as the magnification was increased, because the irradiated area was being decreased while the particle size remained relatively constant between the different magnifications. Figure 5b shows the histograms of the number of new particles formed as a function of time for each magnification. The induction time distributions followed a similar trend to the beam current and dwell time experiments, where the width of the distribution decreased with increased magnification (or electron dose per scan), and the maximum of the distributions shifted to larger times for lower magnifications. The induction threshold doses as a function of electron dose per scan are plotted in Figure 5c for each magnification. In this case all the distributions had statistically similar medians, with an average of 24.1 ± 2.0 electrons/Ų.

We interpret the induction time and dose results in terms of classical nucleation theory, where a supersaturation condition has to be met before nucleation will commence, and subsequent nanocrystal growth depletes the precursor, finally halting nucleation. In this case, the solution must receive enough electrons in a certain amount of time that the concentration of aqueous electrons becomes large enough to reduce enough precursor to meet the supersaturation condition necessary for nucleation. However, we measured a continuous distribution of induction times for each experiment, suggesting that the supersaturation condition was met at different times within the irradiated area. The random nature of nucleation, wherein atoms must collide to create a cluster of critical size to form a nucleus, likely contributed to this distribution of nucleation induction times. The scanning electron beam could in part have led to the distribution of induction times—because the beam was scanning from the top left of the image to the bottom right, the top of the image received electrons before the bottom, inducing nucleation more quickly at the top of the image. As the electron dose per scan was lowered, the rate of precursor reduction was reduced due to the lower concentration of aqueous electrons in the interaction volume (c.f. Figure 1b). This in turn led to longer induction times, and coupled with the effect of the scanning electron beam, to wider induction time distributions (Figure 3b, 4b, and 5b). The rate of nanocrystal formation increased when the pixel dwell time was increased (Figure 4a), however, it did not change significantly when the beam current (Figure 3a) or magnification (Figure 5a) was changed. Further study of the effects of the electron beam parameters on the nucleation rate must be performed to understand this. When the number of nanocrystals leveled out or reached a maximum, nucleation stopped due to depletion of the silver atoms by monomer addition to the nanocrystals present (c.f. Figure 3a).

Using induction time and dose measurements, we were able to indirectly probe the nucleation mechanism for electron beam reduction of silver nanocrystals. By varying the beam current, dwell time, and magnification, we showed that the induction threshold dose was relatively unaffected by these STEM beam parameters. The average of all the induction threshold doses from each experiment (Figures 3c, 4c, 5c) was <d_ind> = 27.8 ± 7.8 electrons/Ų. We take this to be the average cumulative electron dose that the solution must receive to initiate nucleation at the given concentration, window thickness, and fluid path length. Along with the nanocrystal growth threshold discussed earlier, ḋ_thr , the constant induction threshold dose suggests that the only criterion for nucleation is that a certain number of electrons must impact the solution in a maximum amount of time set by ḋ_thr . If the solution receives electrons at a rate slower than ḋ_thr , the concentration of reducing aqueous electrons will be too small to establish supersaturation. However, if the electron dose rate is higher than ḋ_thr , the concentration of aqueous electrons will always become large enough to establish supersaturation, and the only condition necessary for nucleation to occur then is that a cumulative dose of <d_ind> must impact the solution.

The effect of electron beam parameters on nanocrystal morphology

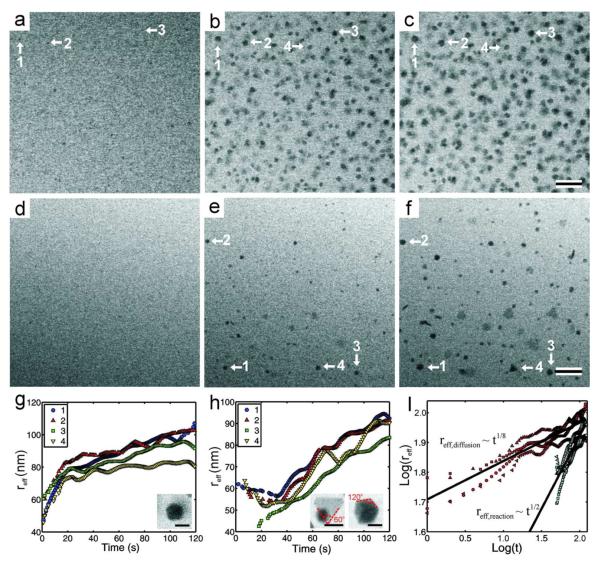
We also observed the nanocrystal growth rate and morphology to change with the beam current. Figure 6 compares nanocrystal growth and morphology at a beam current ~7 times larger than the nanocrystal growth threshold, ḋ_thr , to that at a beam current only ~1.2 times larger than the growth threshold. Figures 6a-c show the growth of nanocrystals at 40 pA (6.7* ḋ_thr) over a time of 120 seconds, while Figures 6d-f show the growth of nanocrystals at 7 pA (1.2* ḋ_thr ) for the same amount of time. We define an effective radius (r_eff), equal to the square root of the area, to facilitate direct comparison between the growth of non-spherical and spherical nanocrystals. Figures 6g and 6h show the effective radius as a function of time at the high and low beam current conditions, respectively, for four nanocrystals marked in the time-lapsed series. Inset in Figures 6g and 6h are higher magnification examples of the nanocrystal morphology observed for each respective growth condition. The high beam current case qualitatively yielded near-spherical nanocrystals while the low beam current case yielded a mixture of near-spherical and faceted nanocrystals. Figure 6i shows the logarithmic relationship between the effective radius and growth time for nanocrystal growth at both beam currents. Power law fits for the growth rates showed that for an average of four nanocrystal growth trajectories, the effective radius grows as t^1/8 with a beam current of 40 pA, and as t^1/2 with a 7 pA beam current.

Figure 6.

(a)-(c) Time series of BF-STEM images taken at t = 0 (a), 60 (b), and 120 s (c), with i_e = 40 pA, M = 100,000x, 5 μs dwell time, resulting in an electron dose rate of 3.37 electrons/(Ųs). (d)-(f) Time series of BF-STEM images taken at t = 0 (d), 60 (e), and 120 s (f), with i_e = 7 pA, M = 100,000x, 5 μs dwell time, resulting in an electron dose rate of 0.59 electrons/(Ųs). The scale bar for both time series is 200 nm. (g) Plot of the effective radius (r_eff) as a function of time for 4 individual nanocrystals indicated in (a)-(c) with arrows. Inset is a higher magnification image showing the near spherical morphology of the resulting nanocrystal, the scale bar is 100 nm. (h) Plot of the effective radius (r_eff) as a function of time for 4 individual nanocrystals indicated in (d)-(f) with arrows. Inset are higher magnification images showing the faceted morphology of the resulting nanocrystals, the scale bars are 100 nm. (i) Logarithmic relationship between the effective radius and time. The red data points correspond to (g) while the blue correspond to (h), the different markers correspond to the individual nanocrystals indicated in the legends of (g) and (h). The black lines are the average power law fits for the 4 different nanocrystals, obtained by linear regression. A 10 point averaging filter was used on (g), (h), and (i) to reduce noise in the data.

Nanocrystal growth at the high beam current condition (Figure 6g) qualitatively followed a diffusion limited process.^{8, 9} In this case there is an abundance of reducing agents, which rapidly reduce the silver precursor at the surface of the growing nanocrystal. Therefore, the nanocrystal growth is limited by how fast the silver precursor can diffuse to the surface of the nanocrystal. The nanocrystal shapes shown in Figures 6a-c and the inset in Figure 6g are near-spherical and their growth trajectories have the shape of a diffusion limited process, where the growth rate was highest at early times where the silver precursor was abundant, but slowed with time as the species were consumed and additional ions diffused to the crystal surface from the bulk solution. However, the power law fit (Figure 6i) shows that the effective radius scaled as t^1/8, almost 3 times smaller than the t^1/3 scaling predicted for the purely diffusion limited case in the LSW model. It is not entirely clear why the power law scaling was depressed, but multiple effects could have caused hindrance of the nanocrystal growth. The high density of nanocrystals in the viewing area may have led to the suppressed growth, as the LSW model assumes a single nanocrystal in free solution. Finally, it was noted that nanocrystals grew on the silicon nitride windows at higher beam currents (c.f. supplementary movie #1), which may also compromise the validity of the LSW model, as this model technically applies to growth of nanocrystals in free solution.

Growth at the low beam current condition (Figure 6h) followed the characteristics of reaction limited growth predicted by the LSW theory. In this case there are not enough reducing agents to rapidly deplete the silver precursor at the surface of the nanocrystals, and the nanocrystal growth is limited by the rate of the surface reduction reaction. Figure 6i shows that the effective radius for these nanocrystals followed a t^1/2 power law, consistent with what is predicted in the LSW model for reaction limited growth. In this case, the reduction and subsequent addition of silver atoms to the nuclei is sufficiently slow that formation of crystalline seeds proceeds by random hexagonal close packing (rhcp).¹⁰ Rhcp typically leads to the formation of twin planes and inclusion of stacking faults in the crystalline seeds, which in turn grow to form bipyramidal crystals and nanoplates, respectively.¹⁰ Additionally, because the surface reaction is the rate limiting step, the precursor silver ions do not react instantly at the nanocrystal surface, and they are able to seek the lowest energy face of the nanocrystal, and induce anisotropic growth of faceted crystals.³⁴ Although we cannot currently acquire ex situ high resolution images of the defects in the nanocrystals, we can deduce the possible morphologies by measuring the edge angles of the nanocrystals in situ. The 60° edge angles on the left inset in Figure 6h, along with the constant BF contrast in the crystal, suggests a trigonal plate morphology, where the particle is of a single crystal orientation. The 120° edge angles in the right inset, along with the varying diffraction contrast, suggests an icosahedral morphology (20-sided polyhedral) or a pentagonal bipyramid (10-sided polyhedral). Included in the supplementary materials (FigureS2) is a higher magnification image of crystalline plates and faceted nanocrystals grown on a different area of the window with identical imaging parameters as Figures 6d-f. The smaller particles in the top right grew while acquiring the image and were not present prior. To our knowledge, this is the first time nanoplate growth has been demonstrated for in situ electron beam induced growth. Refer to the supplementary material for a full movie of nanoplate growth (supplementary movie #3) on a different area of the window. It is interesting to note in this movie that the nanoplates were not all completely attached to the window, but reoriented during growth, and can be seen to have their faces perpendicular to the window surface at times, which makes them appear as rod shapes in the projection image. Perpendicularly oriented nanoplates can also be seen in Figure 6f. It appears that in both cases, one edge of the nanoplate is anchored to the window, and the plate reorients by pivoting on this edge. Reorientation during nanoplate growth further differentiates this growth mode from the diffusion limited mechanism where the crystals grew exclusively attached the silicon nitride windows (c.f. Figure 2 and supplementary movie #1). This suggests that the final particle morphology may also be controlled by how the nanocrystal is anchored to the window surface. However, we have not found an imaging condition that separates nanoplate growth from faceted nanocrystal growth, and future experiments must be performed to determine this growth condition.

CONCLUSION

We have demonstrated controlled growth of silver nanocrystals by electron beam irradiation. Nucleation proceeds by the classical theory, where nuclei are directly observed to form after an initial induction time. We found that varying the current density, pixel dwell time, and magnification caused the nucleation induction time distribution to change but had no systematic effect on the induction threshold dose. From these results we concluded that the only criterion for nucleation is that a threshold number of electrons must hit the sample in a maximum amount of time, set by the nanocrystal growth threshold. If the cumulative electron dose we determined is received in a time longer than this maximum, supersaturation will not be achieved and nucleation will not commence. The approach described here for systematically calculating the induction threshold dose will be important for future in situ electron microscopy experiments, as it provides insight into nucleation mechanisms and is a robust methodology for determining the electron dose conditions necessary for reproducible and controllable nanocrystal growth experiments.

After the induction threshold dose is met, we found that the beam current largely dictates the growth mechanism and final morphology of the nanocrystals in the same way that the concentration of reducing agent does for conventional colloidal synthesis. At beam currents near the growth threshold the nanocrystals grew by a reaction limited mechanism, supported by the t^1/2 scaling of the growth rate and faceted morphology of the nanocrystals. At this growth condition, we showed the first evidence of nanoplate growth by in situ electron beam reduction. At a beam current ~7 times larger than the growth threshold, the nanocrystals grew by a hindered diffusion limited mechanism. We suspect that the depression of growth rate is due to either multi-particle effects or attached growth. These results demonstrate that STEM affords a high level of control over electron beam induced nucleation and growth compared to TEM, through changes in the magnification, beam current, and pixel dwell time.

METHODS

Stock solutions of silver nitrate (AgNO₃, Fisher Scientific) were made by dissolving the salt in deionized (DI) water (Millipore grade: 18.2 MΩ) at concentrations of 0.1 mM and 1 mM. The solutions were stored in non-transparent containers since silver nitrate is light sensitive. We utilized a continuous flow in situ fluid stage (Hummingbird Scientific, USA) equipped with a reusable tip. Prior to sample loading, the stage tip was cleaned with ethanol and DI water, and dried with compressed air. The liquid layer was formed in the fluid stage tip by sandwiching two 2.6 × 2.6 mm square silicon chips (Hummingbird Scientific, USA), with a 50 × 200 μm opening etched from the center. A 50 nm amorphous silicon nitride membrane spanned the opening in the center of the silicon chips to form the electron transparent window. Prior to loading, the windows were oxygen plasma cleaned for 1 minute to remove organic contamination and render the surfaces hydrophilic.²³ The silicon chips had no spacers on them, yet surface roughness and attached residues from processing created the necessary spacing for the fluid layer. This typically resulted in a fluid spacing in the center of the window between 600 – 800 nm, measured using the log-ratio EELS method.^{35, 36} If different conditions are used, it is indicated in the text.

Approximately 1 μL of the stock solution was placed between the silicon nitride windows with a micropipette. The growth experiments were performed in a JEOL 2100F/Cs (S)TEM, operated in continuous capture mode to produce movies of the nanocrystal growth. Stock precursor solution was flowed into the stage tip at a flow rate of 5 μL/min in between each growth trial for ~5 minutes using a syringe pump (Harvard Apparatus, USA), to replenish spent precursor and keep the concentration approximately constant. Bright field (BF) images were recorded with a Gatan CCD detector, with a collection angle of ~5-10 mrad. Annular dark field (ADF) images were recorded with an annular JEOL CCD detector with an inner collection angle of ~70 mrad. Movies were recorded at 1 frame per second regardless of the scan time. The movies were then analyzed following the experiments using custom MATLAB algorithms to track the growth of the nanocrystals with time.

Before inserting the in situ holder into the microscope, the beam current was measured for each microscope spot size (strength of the C1 crossover) using readings from the phosphorescent screen. To calculate the resulting electron dose rate, the beam current was divided by the size of the viewing area.

$$\stackrel{.}{d}=\frac{i_e}{eA}$$ (3)

Here ḋ is the electron dose rate (electrons/Ųs), i_e is the beam current (C/s), e is the elementary charge (C/electron), and A is the area of the STEM scan (Ų), determined by the magnification. The electron dose per scan is then calculated by multiplying ḋ by the pixel dwell time and the number of pixels in the image. The interaction volume size is calculated by multiplying the viewing area by the fluid path length. Further details on sample loading and cleaning, microscope parameters, and image acquisition and analysis are presented in previous publications. ^{19, 22, 23}