Light-dependent changes in outer retinal water diffusion in rats in vivo

Abstract

Purpose

To test the hypothesis that in rats, intraretinal light-dependent changes on diffusion-weighted magnetic resonance imaging (MRI) in vivo are consistent with known retinal layer-specific physiology.

Methods

In male Sprague-Dawley rats, retinal morphology (thickness, extent, surface area, volume) and intraretinal profiles of the apparent diffusion coefficient (ADC, i.e., water mobility) parallel and perpendicular to the optic nerve were measured in vivo using quantitative MRI methods during light and dark stimulation.

Results

The parallel ADC in the posterior half of the avascular, photoreceptor-dominated outer retina was significantly higher in light than dark, and this pattern was reversed (dark>light) in the anterior outer retina. The perpendicular ADC in the posterior outer retina was similar in light and dark, but was significantly higher in dark than light in the anterior outer retina. No light-dark changes in the inner retina were noted.

Conclusions

We identified light-dependent intraretinal diffusion changes that reflected established stimulation-based changes in outer retinal hydration. These findings are expected to motivate future applications of functional diffusion-based MRI in blinding disorders of the outer retina.

Introduction

The rat retina has well defined layers that can be divided into three unique regions: the brain-like inner retina (containing neurons, synapses, glia, and blood vessels); the anterior outer retina (containing neurons, synapses, and glia); and the posterior outer retina (containing a relatively homogenous population of well aligned rod photoreceptors), which is bounded posteriorly by the retinal pigment epithelium (RPE). Adjacent to this region, essential non-neuronal support cells (RPE and Müller glia) regulate, for example, retinal hydration. Using electrodes to detect changes in an extracellular marker, large light-dependent changes in the interphotoreceptor-space volume of the posterior outer retina, and relatively minimal changes in the inner retina, have been well documented in frog and chick retinal preparations ex vivo, and in cat retina in vivo [1-3]. However, because of the small size of the rat eye compared to that of cats, it is not yet known if similar light-dependent patterns also occur in the outer retina of rats in vivo.

In this study, we examined the potential of noninvasive imaging to detect outer retinal hydration changes between light and dark exposure. We took advantage of our recently developed method for microscopically imaging water mobility (i.e., the apparent diffusion coefficient [ADC]) in different retinal layers [4]. The rationale for this approach came from previous work on the brain in which the ADC was found to be exquisitely sensitive to changes in water mobility during a functional challenge [5-12]. Our working hypothesis was that in rats, different retinal layers would demonstrate light-dependent changes on diffusion-weighted magnetic resonance imaging (MRI) in vivo that were consistent with the physiology observed in frog, chick, and cat retinas.

Methods

Animals

Male Sprague-Dawley rats (n=8; age: 5.8±0.2 months (mean±standard error of the mean [SEM]); wt: 544±15 g; Hilltop Labs Animals, Scottdale, PA) were housed and maintained in normal 12 h:12 h light-dark cycling before experimentation, and were treated in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and The Association for Research in Vision and Ophthalmology Statement for the Use of Animals in Ophthalmic and Vision Research. Aside from the light exposure used during the MRI examination, all procedures took place in darkness or dim red light.

Magnetic resonance imaging acquisition

After overnight dark adaptation, rats were anesthetized with urethane (5.35±0.36 ml/kg bodyweight, of a 36% w/v solution in 0.9% saline; Sigma-Aldrich, Milwaukee, WI). Within 5 min of the urethane injection, atropine (2–3 drops 1% atropine sulfate ophthalmic solution; Falcon Pharmaceuticals, Fort Worth, TX) was applied to the left eye to dilate the pupil and ensure maximal dark-light differences during imaging. Full dilation throughout scanning was confirmed in each animal by observing the iris in MRI images (data not shown). A similar amount (2–3 drops) of lidocaine solution (0.6% dissolved in saline, Sigma Aldrich) was also applied to ensure corneal anesthesia. Scanning started after the pupil was fully dilated (1.1±0.1 h post-application). MRI data were acquired on a 7 T system (Clinscan; Bruker ClinScan, Billeric, MA) using a receive-only surface coil (1.0 cm diameter) centered on the left eye. The eye was stimulated with continuous (i.e., nonflickering) white light during half of the scans: one end of a fiber-optic line was attached to a light source (150 W EJA halogen bulb, Mark II Light Source; Prescott’s Inc., Monument, CO), and the other end was placed caudal to the eye to project light at a white piece of paper placed approximately 1 cm from the eye. When the light was on during MRI scans, the eye was exposed to approximately 600 lx (measured outside the magnet with a Traceable Dual-Range Light Meter [Control Company, Friendswood, TX] placed against a 1 cm diameter aperture—measured this way, normal laboratory lighting is approximately 150–300 lx). Aside from the fiber optic light source, all lights in the MRI room were off.

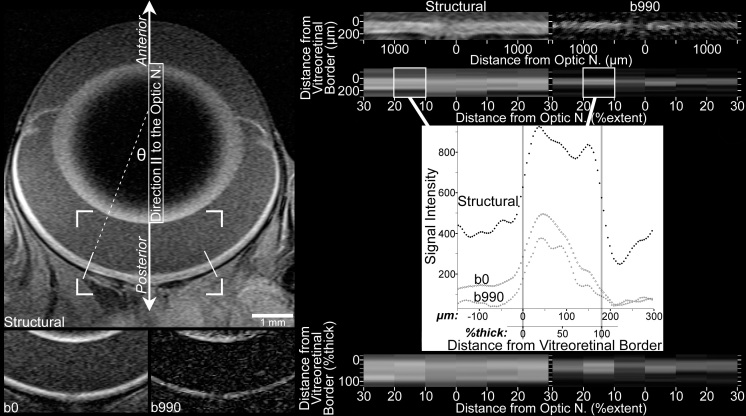
All images were collected as single slices perpendicular to the vitreoretinal border, passing through the optic nerve head and the center of the lens. Collection of structural images (two per lighting condition; spin-echo; repetition time 1,000 ms; echo time 13 ms; acquisition time 3 min 47 s; matrix size 160×320; slice thickness 600 µm; field of view 8 mm×8 mm; for an in-plane resolution of 25 µm [axial; up/down in sample images on the left side of Figure 1] ×50 µm [superior/inferior]) was intermixed with collection of diffusion-weighted images. Note that these relatively high-resolution acquisition parameters limit comparisons with previous studies of retinal ADC in rat [13], mouse [14], and cat [15], which were collected at lower in-plane resolution—resulting in higher apparent signal-to-noise on raw images, but also more partial volume averaging of adjacent retinal layers. Twelve images per lighting condition (24 total) were collected with diffusion weighting: Weighting was applied parallel to the optic nerve (to calculate the ADC parallel to the optic nerve [ADC_║]; Figure 1) in four images—one per b value (250 s/mm², 500 s/mm², 750 s/mm², and 990 s/mm²)—for each lighting condition. Weighting was applied in the two mutually perpendicular directions to the optic nerve (which were later combined to measure the ADC perpendicular to the optic nerve [ADC_┴]) at four b values per direction (250 s/mm², 500 s/mm², 750 s/mm², and 990 s/mm²). These measurements were collected using a diffusion-weighted spin-echo sequence, in which a twice-refocused spin-echo module [16] was inserted to introduce diffusion weightings (repetition time 1,000 ms; echo time 33 ms; acquisition time 3 min 25 s; slice thickness 600 µm; matrix size 288×144; field of view 8 mm×8 mm; resolution 27.8 µm×55.6 µm). In this sequence, each diffusion gradient lobe had the same duration of 4,000 μs, and three refocusing pulses per excitation: two for the diffusion module (0.52 ms in duration) and one for the readout. This produced three echoes: the first in the middle of the diffusion module (13.03 ms from the center of the excitation pulse); the second after the diffusion module but before the third refocusing pulse (at 26.06 ms); and the third at the echo time (33 ms). The same sequence was used to collect four images per lighting condition without diffusion-weighting gradients (b=0). The reproducibility and sensitivity of these imaging parameters was validated in our previous work using an osmotic challenge, and in diabetic rats [4].

Figure 1.

Image processing included linearization of the central retina, followed by spatial normalization according to location along the extent of the retina (‘%extent’) between the optic nerve (at 0%extent) and ciliary body (at 100%extent), and location within the thickness of the retina (%thick) between the vitreoretinal border (at 0%thick) and the retina-choroid border (at 100%thick). Top left: Structural image shows the orientation of the eye relative to the direction parallel to the optic nerve (║) and anterior/posterior orientation. Only the central retina is analyzed, from 10% to 30% of the hemiretinal extent (the distance, measured along the vitreoretinal border, from the optic nerve to the ciliary body). The 30%extent boundaries are indicated by solid white lines angled perpendicular to the vitreoretinal border. Cell structures of interest within the retina include the rod outer segments, which are found in the posterior outer retina and have their long axis oriented radially, relative to the center of the eye (parallel to incident light). Although the curvature of the eye produces measurements of apparent diffusion coefficient parallel to the optic nerve (ADC║) that include structures (e.g., photoreceptors) oriented off-║ by ≤θ, this should have negligible impact on ADC comparisons (see Discussion). Bottom left: Cropped images (the corners of the cropped region are overlaid on the structural image above) collected with b=0 and b=990 s/mm² in the ║ direction. For display purposes, brightness and contrast settings are the same for all b0 and b990_║ images in this figure, but a different pair of brightness and contrast settings is applied to structural images. Due to resampling and averaging steps used to produce the b0 and structural images (see Methods), the b990_║ image best displays the native spatial resolution of diffusion images. Top right: The linearized central retina from the structural and b990_║ images is shown here. Since the vitreoretinal border smoothly follows the curvature of the eye, its location can be determined with accuracy in excess of the native spatial resolution: Using the images on the left, the approximate location of the border is found in several neighboring columns of voxels. A polynomial best fit to these locations specifies the vitreoretinal border. Linearized images are produced by sampling every 4.63 μm along perpendiculars to those high-order polynomials. Data in the linearized images is binned by retinal extent, and averaged within each bin. This spatial averaging improves signal-to-noise before diffusion calculations, and since it is done on linearized images, the critical spatial information—distance from the vitreoretinal border—is well preserved. Mid right (plot): Signal intensity data from the left 10%–20%extent bin is plotted to show the location of vitreoretinal and retina-choroid borders, which are determined in structural data using the half-height approach (i.e., the border is at the halfway point between local minimum and maximum) [20]. The same borders are found in the b0 profile, and are used to align b0 and structural images. As detailed extensively in previous work [4], data collected with b≥0 are then aligned to b0 data using the broad signal peak in the anterior approximately one-half to two-thirds of the retina (visible here from approximately 0 to 100 μm). Bottom right: As previously described [19], after the retinal thickness is calculated by subtracting the vitreoretinal and retina-choroid borders, the data are resampled according to distance from the vitreoretinal border relative to the retinal thickness. Finally, the resampled data (within each %extent bin, one value every 4%thick) from 10%–30%extent on each side of the optic nerve are averaged to produce a single profile, which is used for within- and across-subjects comparisons.

To minimize the potential contribution of light-dark order or stimulus duration, the experiments were performed in the following way. For five rats, we alternated between light and darkness while the order of scans was randomized (e.g., b250_┴,Light, b990_║,Dark, b0_Light, b500_║,Dark, b750_║,Light, b0_Dark, structural_Light, b990_┴,Dark, …). For these rats, uninterrupted exposure to light (or darkness) lasted no more than 3 min 47 s (the acquisition time of a single structural image). For the other three rats, the light and dark of each scan type was paired, but the order was randomized in all other regards (e.g., b250_┴,Dark, b250_┴,Light, b750_║,Light, b750_║,Dark, b0_Dark, b0_Light, b500_║,Dark, b500_║,Light, …). The multiple acquisitions of structural and b0 images were split respectively into two and four light-dark pairs. Thus, for those rats, the sequence of scans contained no more than two light (or two dark) scans in a row, and uninterrupted exposure to light was always less than 7 min 12 s (e.g., structural_Dark, structural_Light, b0_Light, b0_Dark, …; although a 7 min 34 s exposure could have occurred if the two pairs of structural scans were collected one after the other, but, by chance, that specific order of scans did not arise from randomization). No differences were noted between these two acquisition strategies (not shown), and data were combined for further analysis. At the end of scanning, each rat had been exposed to the 600 lx stimulus for a total of 70 min, including a brief period of light exposure (<4 min) during animal setup and coil placement, a single approximately 4 min:4 min light-dark cycle performed immediately before the start of image acquisition, and all periods of light exposure during image acquisition. Light-induced retinal damage—a phenomenon that typically takes several hours of continuous exposure to much more substantial illumination (>1,600 lx [17])—is unlikely with the present stimulus parameters. In a study of intermittent exposure to a 2,000 lx stimulus [18], a cumulative ≥3 h of exposure was necessary to produce even mild retinal damage in Sprague-Dawley male rats raised in cyclical lighting (as in the present study).

Image processing

Because the possibility of light-dependent gross structural changes (e.g., whole-retinal thickness) could not be excluded a priori, each complete set of images per animal per lighting condition was processed separately until statistical comparisons were performed, as will be explained shortly.

Images were exported from Siemens’s Syngo software (after reconstruction to an isotropic matrix: 320×320 for structural images, 288×288 for diffusion images) for additional processing. To facilitate registration, all images were resampled in ImageJ to a 576×576 matrix. Structural images were resampled using bilinear signal interpolation. Diffusion images were resampled without signal interpolation (i.e., each voxel was converted to a 2×2 matrix of voxels with the same signal intensity value as the original). The two structural images (per subject per lighting condition) were registered and averaged to produce a single structural image, and the four b0 images were registered and averaged to produce a single b0 image (per rat per lighting condition).

After image resizing, averaging, and registration steps were complete, the structural image was used to measure gross retinal morphology, as previously detailed [4,19]: the hemiretinal extent, which is the distance between the optic nerve head and ciliary body, was measured along the vitreoretinal border in each hemiretina, then averaged to yield a single measure of retinal extent per animal per lighting condition. The contrast between the retina and vitreous makes this border straightforward to identify in the present T₁-weighted structural images: vitreous T₁ is approximately 3.5 s, and retinal T₁ is approximately 2.0 s (similar to brain gray matter) at this field strength. Polynomial functions fit to the vitreoretinal border were integrated about the central axis of the eye to calculate surface area of the vitreoretinal border, and were also used to linearize the retina (Figure 1). Data from the linearized central retina (between 10% and 30% of hemiretinal extent; abbreviated henceforth as '10%–30%extent') were binned together and used to calculate average profiles of signal intensity as a function of depth into the retina (Figure 1). Profiles from the structural image were used to calculate retinal thickness with the half-height approach, wherein a border is demarked where the profile crosses the midpoint between the local minimum and maximum [19,20]. Thickness was calculated as the distance between the vitreoretinal and retina-choroid borders as defined on the structural image. The choroid, which contains very fast-flowing blood, appears black in the present scans and was readily distinguished from the retina (Figure 1); its location was validated by our previous work using gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA) [21]. Knowing these two boundaries (vitreoretinal and retina-choroid), and confirming that the whole retinal thickness was normal (relative to histology and optical coherence tomography), allowed us to take advantage of the highly ordered and well described layering of the retina to approximate the location of different cell layers. We previously verified that the border between the inner and outer retina can be accurately localized in this way, allowing us to monitor inner versus outer retinal responses to light and darkness using other MRI techniques [22,23].

Thickness data and polynomial functions were combined, as previously described [19], to calculate retinal volume. A second, finer, automated registration step was then applied to the data using variants of the half-height approach. Briefly, the inner half of the retina is easily identified in structural and diffusion-weighted images due to its proximity to the vitreous. It maintains relatively high signal intensities at all diffusion directions for the range of b values used presently, forming a broad peak in signal intensity profiles (Figure 1). Each profile’s inner retinal profile peak is centered on the same location to complete registration, which is checked with visual inspection and some quantitative techniques (see section below on verification of image registration). This registration step was adopted without modification from a previous study [4], and is detailed extensively therein. As with the registration steps used to generate the averaged structural and b0 images, this automated registration was required to compensate for minor involuntary eye movement observed between the start and end of the approximately 2 h scanning period. We note that movement from one image to the next was negligible, consistent with previous measurements under urethane anesthesia [24]. This, combined with interspersed acquisition of dark and light stimulation, precluded full analyses of factors that could conceivably influence involuntary eye movement (e.g., light versus dark exposure, or the history thereof). Finally, all profiles (structural, b0, and diffusion-weighted) were expressed with signal intensity as a percentage of the whole retinal thickness ([%thick]—hereafter, whole-retinal-thickness percentages are thus abbreviated; see, e.g., Figure 1). To avoid partial-volume averaging with nonretinal tissue, areas within 12%thick of the structurally defined vitreoretinal and retina-choroid borders are routinely excluded from statistical comparisons [4,19].

Dark-light comparisons of structural and data collected when the diffusion weighting gradient was set to 0

Paired two-tailed t tests (α=0.05) were used to compare gross retinal morphology (thickness, extent, surface area, volume) in light versus darkness. Structural signal intensity profiles were similarly compared, as were b0 signal intensity profiles, but only results falling below a standard false discovery-rate threshold (q=0.05; 20 tests in each; from 12%–88%thick) were considered significant [25].

Analysis of apparent diffusion coefficient

The tissue apparent diffusion coefficient (ADC) was calculated based on the relationship between signal intensity and b value. Log-transformed signal intensity (symbolized below as some variant of natural logarithm of the signal intensity [ln(S)]) decreases with increasing diffusion gradient strength defined as a “b” value” in an approximately linear fashion. As in previous studies, the slope of the function relating ln(S) and b is the ADC [4,13,14], as shown in Equation 1:

$$\ln ({\text{S}}_{\text{b}})=-\text{b}*\text{ADC}+\ln ({\text{S}}_0)$$

where S_b is the signal intensity when diffusion weighting is applied with a given b value, and S₀ is the signal intensity when b=0.

Multiple data points relating ln(S) to b are collected from each subject and used to calculate the ADC using stimulus- and direction-specific versions of Equation 1. For example Equation 2 and Equation 3:

$${\text{ln(S}}_{\text{b, ||, Light}})=-\text{b}\ast {\text{ADC}}_{\text{||, Light}}+{\text{ln(S}}_{\text{0, Light}})$$

$${\text{ln(S}}_{\text{b, ||, Dark}})=-\text{b}\ast {\text{ADC}}_{\text{||, Dark}}+{\text{ln(S}}_{\text{0, Dark}})$$

To test for light-dependent changes, Equation 2 and Equation 3 are subtracted and simplified to Equation 4:

$${\text{ln(S}}_{\text{b, ||, Dark}}{\text{/S}}_{\text{b, ||, Light}})=-\text{b}\ast (\Delta {\text{ADC}}_{\text{||, Dark - Light}})+{\text{ln(S}}_{\text{0, Dark}}/{\text{S}}_{\text{0, Light}})$$

In an ordinary least-squares (OLS) analysis, linear regression is used to calculate the slope relating the b value to the log-transformed ratio of dark-to-light signal intensity for each subject. A one-sample t test is then used to test whether those slopes—as per Equation 4, the difference between the ADC in dark versus light (i.e., ΔADC)—are, on average, significantly different from zero.

ΔADC is convenient for estimating effect sizes, since Cohen’s d (for ΔADC_{║,Dark-Light}≠0) is given as the mean of subjects’ calculated ΔADC_{║,Dark-Light}s divided by the standard deviation (SD). As part of our analyses of intraretinal ADCs, we offer a brief comparison of these effect sizes (reported as an absolute value of Cohen’s d) when data from all five b values are used, versus using data from only b0 and one other b value. Effect sizes (absolute value of Cohen’s d; |d|) for dark-light differences in ADC_║ and ADC_┴ were calculated for regions of the retina showing significant results. For a region with multiple adjacent positions reaching significance (e.g., at 80%–88%thick), we report |d| as reaching the highest value calculated in that range of positions (e.g., if |d|=1.2, 1.4, and 1.1 at, respectively, 80%thick, 84%thick, and 88%thick, then |d| reached 1.4 in 80%thick–88%thick). We note that OLS-based p values are typically higher than the p values obtained using the generalized estimating equation (GEE) analyses described next. Using these |d| values in power calculations (for instance) may therefore produce conservative results. OLS-based p values can be derived from the |d| values reported in the results section, such that |d|>0.89 demonstrates a two-tailed p<0.05 from an OLS analysis. |d| is calculated using data from all five b values (0, 250, 500, 750, 990)—as used in the analyses of the retinal ADC and shown in Figure 2—and using data from only b0 and another b value (e.g., b0 and b990 only). These effect-size calculations were performed, in part, to provide guidance for future studies, in which total scan time could be reduced by collecting data at fewer b values than used presently.

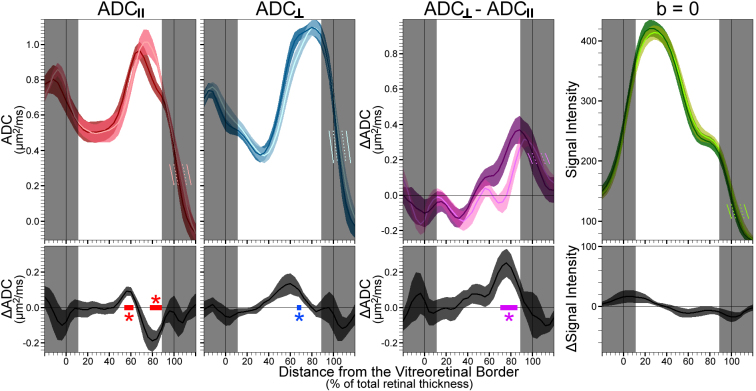
Figure 2.

Summary of light-dependent changes in apparent diffusion coefficient (ADC). Top: The mean(±standard error of the mean [SEM]) ADCs measured parallel to the optic nerve (ADC║) and measured perpendicular to the optic nerve (ADC┴) are shown alongside the difference between those measures (ADC┴-ADC║; to examine diffusion anisotropy) and the signal intensities of b=0 s/mm² images. All ADC data shown here is calculated using all five b values (0–990 s/mm2). Dark (color with darker shade) and light data were compared at each point within 12%–88% thickness (in 4%thick increments). Shaded profile sections near the vitreoretinal and retina-choroid borders (0%thick and 100%thick respectively, marked with vertical lines) were not evaluated because of partial-volume averaging with nonretinal tissue. Light-colored line segments in these shaded areas show the position of the mean light data if purposely misregistered (relative to dark) by ±4%thick (dotted line segment) or ±8%thick (solid line segment). These misregistration steps were used post hoc to evaluate the robustness of dark-light ADC differences to registration errors. Bottom: Dark-light difference plots (grayscale; mean±SEM) show where ADC_║, ADC_┴, and anisotropy (ADC_┴−ADC_║) changed within the retina (*q<0.05). Based on known anatomic borders (Figure 3), we attribute ADC differences at 56%–68%thick to the anterior outer retina, which contains the rod nuclei, and differences at 72%–88%thick to the posterior outer retina, which contains the rod outer segments. In each case of purposeful misregistration by 4%thick, 8%thick, or 12%thick in either direction, dark-light comparisons of both ADC_║ and anisotropy (ADC_┴−ADC_║) yield multiple results with p<0.05 in the outer retina (not pictured). No significant differences in signal intensity were found in b=0 data (bottom right plot; p>0.05 throughout). Note that the posterior one-third of the retina (68%–88%thick) tends to have the lowest signal intensities at b=0, as well as the highest ADCs. For this reason, there is some risk that ADCs are underestimated when the data with the lowest signal (b=990 s/mm²) are used to calculate the ADC. As noted in the results section for assessing signal-to-noise relevant to ADC calculations, the pictured ADCs for the anterior two-thirds of the retina (12%–64%thick) appear accurate, but the ADCs for the posterior one-third of the retina (68%–88%thick) may ultimately be approximately 17% higher than pictured here. Importantly, the pictured dark-light differences remain significant regardless of the analysis strategy.

As we have previously discussed in some detail [4] the OLS procedure described above has some shortcomings for calculating retinal ADC, related, for instance, to its inability to use within-subject variability to refine group average estimates and standard errors. Where possible, we therefore use an extension of the OLS approach—a GEE analysis—which can appropriately account for the repeated measures composing each within-individual relationship into calculations of the across-subjects ADC means and standard errors [26]. We calculated the ADC at different depths into the retina as previously detailed [4], using autoregressive [AR (1)] GEE fits for Equations 1–4. For instance, a GEE fit based on Equation 2 is used to calculate the group mean and standard error values for ADC_║,Light shown in Figure 2, while a GEE fit to Equation 4 is used to calculate the dark-light difference in ADC_║ and to test the null hypothesis that ΔADC_{║,Dark - Light}=(ADC_║,Dark - ADC_║,Light)=0. A similar approach is used to calculate anisotropy of diffusion, which is characterized within the central retina (Figure 1) as the difference in water diffusion perpendicular versus parallel to the direction of the optic nerve (i.e., ADC_┴ - ADC_║). We have previously published detailed procedures for performing these ADC calculations, including samples of relevant R code and illustrations of best-fit lines for the ln(S_b) versus b relationship described in Equation 1 [4].

We used GEE fits of the monoexponential model to test for dark-light differences from 12%thick to 88%thick (at 20 points per profile in 4% increments) in three profiles (ADC_║, ADC_┴, and ADC_┴ - ADC_║). Findings below a standard false discovery-rate threshold (q=0.05; 60 tests) were considered significant.

Verification of image registration

The second registration step, mentioned in the section above on image processing, is critical to properly localizing ADC data within the structurally defined vitreoretinal and retina-choroid borders. That fully automated approach—which yields reproducible outcomes [4]—was applied to the present data. Though visual inspection suggested good postregistration alignment in all cases, we sought to confirm this with the following additional quantitative checks.

As previously described for the present imaging parameters, rapid diffusion in the vitreous causes large signal loss with even modest b values [4]. This produces artifactually low vitreous ADC estimates when all b values are used. However, vitreous signal intensity is above background levels when b=250 s/mm². This allows for a calculation of vitreous ADCs using the OLS-based procedure with only the 0 s/mm² and 250 s/mm² b values (henceforth, ADC_║,0,250 and ADC_┴,0,250). The resulting profile shows high (>2.0 μm²/ms) ADC_0,250s in the vitreous, with an abrupt change to low (typically ≤0.5 μm²/ms) ADC_0,250s in the inner half of the retina (see [4]). The ADC_0,250-defined vitreoretinal border is then determined by the half-height approach described above. Based on our previous use of this method [4], the local minimum in each subject’s four ADC_0,250 profiles (light_║, light_┴, dark_║, and dark_┴) was calculated between 4%thick and 44%thick, and the local maximum between −24%thick and 0%thick. The vitreoretinal borders defined by each ADC_0,250 profile (which are expected to fall near the vitreoretinal border defined by structural images, at 0%thick) were compared across diffusion directions and stimulus conditions using a two-way repeated measures ANOVA (ANOVA; α=0.05) to verify good alignment before the comparisons of light versus dark intraretinal ADCs.

A related approach is used to estimate the location of the retina-choroid border: water movement within the choroid is predominantly in the direction of blood flow, which is parallel to the surface of the eye (i.e., ┴ for the central retinal data considered here). Due to the high water mobility of fast-flowing choroidal blood, diffusion weighting will greatly diminish signal, even at low b values, analogous to the vitreous. Although this produces artifactually low ADCs when all b values are used, high ADC_0,250 values with high anisotropy (i.e., ADC_┴,0,250>ADC_║,0,250) are expected of the choroid. We have previously used the measurement ADC_┴,0,250 - ADC_║,0,250 to localize the choroid in diffusion images, and found reasonable agreement with previous work that used intravascular contrast (gadolinium-based) to highlight the choroid [4,21]. On each subject’s light and dark profiles of ADC_┴,0,250 - ADC_║,0,250, we calculated the local minimum from 66%thick to 96%thick, the local maximum from 64%thick to 128%thick, and the borders of the choroid with the retina and sclera using the half-height approach. To verify good alignment of light and dark ADC data, the location of these borders was compared with a paired two-tailed t test (α=0.05). Based on previous work, the apparent borders of the choroid are expected to fall at approximately 85% and approximately 115%thick [4]. We note that the slight choroidal overlap with the structurally defined retinal borders (i.e., the appearance of choroid at <100%thick) herein is consistent with gadolinium-based measurements [21], and is attributable to several factors, including partial volume averaging.

Although the above analyses confirmed good alignment of ADC data, we also evaluated their robustness to alignment errors: The GEE-based dark-light comparisons described in the section above on analysis of the ADC were repeated after purposely misaligning light and dark ADC data: All dark data were fixed in place, while all light data were shifted by the same amount to either the left or right. Since profiles are reported in 4%thick increments, tests were repeated after shifts of 4%thick, 8%thick, and 12%thick from the original position. Of the retinal regions with significant dark-light differences in the first pass analysis, those that retained differences of p<0.05 after each of the six deliberate misalignments were considered highly robust to alignment errors.

Assessing signal-to-noise relevant to ADC calculations

Accurate ADC measurements require high signal-to-noise ratios (SNRs). At the present high spatial image resolution, SNR is at a premium. To avoid increased intra-individual variability (e.g., pixel-to-pixel), spatial averaging was performed on linearized images—to preserve retinal layer-specific information—before calculating the ADC as described above. Following image processing (Figure 1), results from central retinas (10%–30%extent) were averaged to produce a single profile of signal intensity as a function of depth into the retina (%thick) for each image. Each rat contributed two structural profiles (one for light, one for dark), two b0 profiles (light and dark), and 24 diffusion-weighted profiles (three diffusion directions, four nonzero b values, light and dark) to subsequent analyses. With the present imaging parameters, vitreous signal is indistinguishable from noise for b values of ≥500 s/mm² (present observations; also see [4]). Thus, noise was measured at b values of >500 s/mm² in the profile region occupied by the vitreous. Profile signal intensities (S) at −24%thick were collected from each rat’s b750 and b990 images, and the standard deviation of those values (S_noise,SD) calculated. Next, profile intensities were collected from three positions in the retina—selected because they yielded significant dark-light differences—at 56%–60%thick, 68%thick, and 80%–88%thick. Since the lowest signal intensities (S_tissue,mean) used to calculate retinal ADCs are measured at b990, we use the spatially averaged tissue signal at that b value to calculate signal-to-noise ratios [27]: SNR_tissue=0.655×(S_tissue,mean/S_noise,SD). Some ADC calculations are also performed on the vitreous and choroid (see section on verification of image registration), but only using b0 and b250. For those tissues, SNR_tissue was calculated from the S_tissue,mean of b250 profiles at −24%thick (vitreous) and 104%thick (choroid).

In addition, we checked to see if low SNR resulted in underestimation of ADCs (i.e., the rectified noise floor effect) [27]. To test for this effect, we calculated retinal ADCs using the GEE analysis of all five b values described above, then reran those ADC calculations, omitting the highest b value (990 s/mm²). Similar results obtained from both analyses would indicate that signal at the highest b value was far enough from the noise levels to preserve the linear relationship described by Equation 1—suggesting sufficient SNR for accurate ADC calculation [27]. In cases where retinal ADCs differed when using 0≤b≤990 s/mm² versus 0≤b≤750 s/mm², we retested for dark-light differences using the 0≤b≤750 s/mm² data.

Results

Dark-light comparisons of structural and data collected when the diffusion weighting gradient was set to 0

There were no differences on any measure of gross retinal morphology between light and darkness (p>0.05; Table 1). Central retinal signal intensities were not affected by lighting conditions at any retinal depth in structural images (the lowest p value, P_min, was 0.213 in the inner half of the retina [12%–48%thick] and 0.176 in the outer half of the retina [52%–88%thick]). Similarly, there was no effect of lighting condition on signal intensities in b0 images (Figure 2; P_min was 0.059 in the inner half and 0.141 in the outer half).

Table 1. Gross retinal morphology (values shown as mean±SEM from all (n=8) in rats.

Morphologic metric	Dark	Light	Difference
			(Dark-Light)	P value
Thickness (µm)	189±9	187±9	2±1	0.128
Extent (µm)	5110±52	5110±49	0±31	0.992
Surface area (mm2)	64.92±1.00	65.37±0.98	−0.45±0.68	0.527
Volume (mm3)	10.15±0.37	10.25±0.32	−0.09±0.23	0.699

Analysis of ADC

Regardless of lighting conditions or gradient directions, the intraretinal ADC profiles had relatively lower values in the inner half of the retina (approximately 0.5 μm²/ms) compared to those in the outer half (approximately 1.0 μm²/ms; Figure 1). This pattern reasonably replicates previous observations for retinal layer-specific measurements of the ADC in the rat and reflects the robustness of our registration protocol [4,13]. With light and dark exposure, three distinct patterns in the intraretinal ADC profiles were apparent:

(1) Near the retina-choroid border, the ADC was significantly greater in the light than in the dark, but only in the direction parallel to the optic nerve and long axis of photoreceptors (i.e., ADC_║,Dark<ADC_║,Light; q<0.05 for 80%–88%thick, where P_min=6.13 e-5). This pattern was not seen for diffusion perpendicular to the optic nerve (ADC_┴,Dark≈ADC_┴,Light; P_min>0.05 for 76%–88%thick). Since ADC_║ generally appears lower than ADC_┴ in this part of the retina (Figure 2), ADC_║ and ADC_┴ are more similar in light than darkness. Put differently, anisotropy of diffusion (ADC_┴-ADC_║>0) near the retina-choroid border is greater in darkness than in light (q<0.05 for 72%–84%thick, P_min=1.24 e-3).

(2) Anterior to that, but still in the photoreceptor-dominated outer half of the retina, we found that water diffusion was significantly lower in the light than in the dark, both for parallel (ADC_║,Dark> ADC_║,Light; q<0.05 at 56 and 60%thick, P_min=1.00 e-4) and perpendicular (ADC_┴,Dark> ADC_┴,Light; q<0.05 at 68%thick, P_min=7.76 e-3) directions.

(3) In the inner half of the retina, we found that diffusion was similar in light and darkness, both for parallel (ADC_║,Dark≈ADC_║,Light; P_min>0.05 for 12%–36%thick) and perpendicular (ADC_┴,Dark≈ADC_┴,Light; P_min>0.05 for 12%–48%thick) directions.

When data from all five b values were used in OLS analyses of ADC_║ at 56%–60%thick (based on Equation 4), |d| reached 0.91. Using data from b0 and only one other b value, |d| reached 0.47 (using b0 and b250), 0.91 (b0 and b500), 0.25 (b0 and b750), and 1.39 (b0 and b990) for 56%–60%thick. When data from all five b values were used in OLS analyses of ADC_║ at 80%–88%thick, |d| reached 1.42. Using data from b0 and only one other b value, |d| reached 0.50 (using b0 and b250), 0.31 (b0 and b500), 1.11 (b0 and b750), and 1.04 (b0 and b990) for 80%–88%thick. When data from all five b values were used in OLS analyses of ADC_┴ at 68%thick, |d|=0.92. Using data from b0 and only one other b value, |d|=0.23 (using b0 and b250), 0.57 (b0 and b500), 0.74 (b0 and b750), and 0.78 (b0 and b990) at 68%thick. In short, effect sizes calculated using data from all five b values were usually larger than effect sizes calculated using data from only two b values.

Verification of image registration

Results of the ADC_0,250-based localization of vitreoretinal and retina-choroid borders, which are presented in Table 2, were in good agreement with previous work [4], and suggested reasonable alignment of structural data with diffusion data. The consistency of vitreous ADC_0,250 values with previous work [4,13], as well as a confirmation the significant anisotropy (ADC_┴,0,250>ADC_║,0,250) used to localize the choroid, are also noted in Table 2. Calculated choroidal thicknesses were in reasonable agreement with previous in vivo and ex vivo studies [4,21], and were similar in darkness and light (mean±SEM of 50±6 μm and 46±5 μm, respectively). Importantly, locations of ADC_0,250-based borders were similar (p>0.05) across lighting conditions and diffusion directions, suggesting that the first-pass analysis was free of alignment errors.

Table 2. ADC-based localization of retina/not-retina borders within the structurally-defined %thick scale. Values are shown as mean±SEM separately for dark (bold) and light (italic).

ADC location	Vitreoretinal border			Retina-Choroid border			Choroid-Sclera Border
	Local Max. (vitreous; μm2/ms)	Local Min. (retina; μm2/ms)	Location (%thick)	Local Max. (choroid; μm2/ms)	Local Min. (retina; μm2/ms)	Location (%thick)	Location (%thick)
ADC┴,0,250	2.54±0.12†	0.36±0.04‡	−7.5±1.3**	1.88±0.10*	1.08±0.14a	-	-
	2.22±0.14†	0.34±0.08‡	−2.7±1.9**	2.06±0.10*	1.06±0.12a
ADC║,0,250	2.06±0.22†	0.43±0.07‡	−3.3±2.6**	1.73±0.19*	0.56±0.09a	-	-
	2.18±0.14†	0.40±0.12‡	−2.8±1.8**	1.46±0.14*	0.66±0.11a
ADC┴,0,250 - ADC║,0,250	-	-	-	1.44±0.16	−0.33±0.10	87.5±3.4b	113.9±4.1c
	-	-	-	1.45±0.15	0.02±0.20	83.4±3.5b	108.3±4.0c

† Consistent with the literature value for rat vitreous, 2.3±0.4 μm²/ms [13] Statistically similar value in all four cases (two-way repeated measures ANOVA; F [_1,7] <3.20 and p>0.11 for both main effects and interaction). ‡ Statistically similar value in all four cases (two-way repeated measures ANOVA; F [_1,7] <3.20 and p>0.056 for both main effects and interaction). ** Statistically similar location in all four cases (two-way repeated measures ANOVA; F [_1,7] <0.56 and p>0.47 for both main effects and interaction). * A main effect of direction (┴ > ║; F [_1,7]=9.76, p=0.017), but neither a significant effect of dark versus light nor an interaction (F [_1,7] <3.99 and p>0.085) was found with two-way repeated measures ANOVA. ^aA main effect of direction (┴ > ║; F [_1,7]=9.90, p=0.016), but neither a significant effect of dark versus light nor an interaction (F [_1,7] <0.43 and p>0.53) was found with two-way repeated measures ANOVA. ^bStatistically similar location for light and dark data (p=0.41; paired two-tailed t test). ^cStatistically similar location for light and dark data (p=0.65; paired two-tailed t test).

Following each of the six intentional misalignments of light and dark data—shifting light data anterior or posterior (left or right in Figure 2 plots) by 4%thick, 8%thick, and 12%thick—dark-light differences in ADC_║ were still found in the posterior outer retina (i.e., at least one point between 80%thick and 88%thick reached p<0.05). Dark-light differences in anisotropy (ADC_┴-ADC_║) were similarly robust to misalignment, being present in the outer half of the retina following each of the six intentional misalignments (always at least two points within 52%–88%thick at p<0.05). However, those findings fell outside the 72%–84%thick range (selected based on the significant findings noted in the section on analysis of ADC) when light data were shifted left by 8%thick or 12%thick. For five of the six intentional misalignments (excepting a 4%thick leftward shift of light data) dark-light differences were still found for ADC_║ in the anterior outer retina (at both 56%thick and 60%thick), and for ADC_┴ in the outer retina (at least one point within 52%–88%thick). Taken together, these data strongly support the good alignment of the diffusion data, and that the significant findings in the previous section—particularly for ADC_║ in the posterior outer retina—were robust to some misalignment.

Assessing signal-to-noise relevant to ADC calculations

SNR_tissues were calculated for each subject, and are presented here as the across-subject mean±SEM: In the retina, when b=990 s/mm², SNR_tissues at 56%–60%thick, 68%thick, and 80%–88%thick, respectively, were 13.4±2.2, 10.5±2.0, and 8.4±0.8. In the vitreous (−24%thick) and choroid (104%thick), when b=250 s/mm², SNR_tissues were, respectively, 8.1±1.3 and 9.1±1.3.

We also compared ADCs calculated using 0≤b≤750 s/mm² (i.e., omitting the highest b value data that had the lowest SNR) to the ADCs shown in Figure 2 (calculated with 0≤b≤990 s/mm²). For the anterior two-thirds of the retina, omitting the b=990 s/mm² data had little effect: from 12%thick to 64%thick, the mean ADCs (for ADC_║,Light, ADC_║,Dark, ADC_┴,Light, and ADC_┴,Dark) calculated with 0≤b≤990 s/mm² fell within the 95% confidence interval of those ADCs calculated with 0≤b≤750 s/mm². In this section of the retina, ADCs calculated with 0≤b≤750 s/mm² data were on average 4% higher than those shown in Figure 2—well within the present experimental error—indicating that the SNR was adequate at all five b values. For the posterior one-third of the retina, omitting the b=990 s/mm² data produced an increase in ADC: From 68%thick to 88%thick, at least one of mean ADCs (for ADC_║,Light, ADC_║,Dark, ADC_┴,Light, and ADC_┴,Dark) calculated with 0≤b≤990 s/mm² fell below the 95% confidence interval of those ADCs calculated with 0≤b≤750 s/mm². In this section of the retina, ADCs calculated with 0≤b≤750 s/mm² were on average 17% higher than those shown in Figure 2. Importantly, the apparent underestimation of ADCs in this region (Figure 2) was similar across all four curves (ADC_║ and ADC_┴, in light and dark), meaning that the dark-light differences—the central focus of the present work—remained when analysis was restricted to the 0≤b≤750 s/mm² data: reanalyzing this 68%–88%thick span using only 0≤b≤750 s/mm² data, we again found that ADC_┴,Dark>ADC_┴,Light in the anterior outer retina (though strongest result shifted from 68%thick [see above] to 64%thick, where p=3.05 e-5), and that ADC_║,Dark<ADC_║,Light from 80%–88%thick (P_min=2.72 e-4; data not shown).

Discussion

In this study, robust and spatially specific light-dependent intraretinal ADC changes are demonstrated for the first time. Given the very high-resolution demands of the present in vivo experiments, it was critical to first establish that the results are reproducible. To this end, we previously published a comparison of intraretinal profiles obtained from three separate groups of control rats to assess the consistency of the ADC profiles. In addition, in one group, the ADC was measured twice per animal—shortly after anesthetizing the rats and then again almost 5 h after the start of the first scans, still under urethane anesthesia. Full details are presented elsewhere [4]. We note that in all cases, no significant (p>0.05) differences in ADC profiles were found, and all of the profiles were in reasonable agreement with a previous report on control rats [13]. These considerations strongly support the reproducibility of the present methods for measuring very high spatial resolution ADC intraretinal profiles.

The present study used our previously validated [4] approach for automated registration to compensate for minor involuntary eye movement during the scanning period. This registration is critical to ensuring that data at each b value is well aligned to landmarks in structural images and to avoiding haphazardly mixing data from adjacent retinal layers, which would diminish test-retest and between-group reproducibility of ADC measurements. In the present study, the locations of vitreoretinal and retina-choroid borders were calculated with diffusion-weighted data after it was registered to structural data, then mapped to the structurally defined %thick scale. We found reasonable agreement between those borders and previous work [4,21] again arguing that inter-image pixel displacement is negligible. Importantly, when comparing dark and light data, those analyses revealed no systematic differences in the location of retina-nonretina borders (Table 2). This is consistent with the average profiles presented in Figure 2, where dark and light data are clearly well aligned from approximately 92%–112%thick (near the retina-choroid border). Since the dark-light comparisons were the focus of the present study, we also tested whether intentional misalignment of dark versus light data would alter statistical comparisons. All results were robust to most misalignment steps, and the significant dark-light difference at posterior outer retina was robust to all misalignment steps. In short, extensive testing [4] repeatedly demonstrated the high-quality of our image registration approach, and strongly argues that dark-light differences are not an artifact of inter-image pixel displacement.

The phrase “functional MRI (fMRI)” was, early on in its development, defined as “the ability to detect local signal increase secondary to behavioral tasks” [28]. Over time, this definition came to be equated with hemodynamically based contrasts, particularly BOLD. The combination of “diffusion weighted” with “fMRI,” as in DfMRI, has been used to describe the activity-dependent changes in diffusion-weighted brain signal, but the interpretation of these changes has been difficult: at the spatial resolution available in brain studies, neuronal, glial, and vascular signals are convoluted, and several experimental and theoretical studies have argued for a substantial hemodynamic component to the activity-dependent, diffusion-weighted signals [9,29,30]. We feel that DfMRI does not adequately capture our experimental approach in this work. First, we examined the outer retina, which lacks blood vessels, ensuring minimal contribution of hemodynamic signals. Second, we observed a higher ADC_║ in dark than light for the anterior outer retina, but a lower ADC_║ in dark than light for the posterior outer retina. Since opposite responses occurred over an approximately 100 μm span, the microscopic image resolution we used was critical to fully characterizing activity-dependent diffusion changes in the retina. Thus, in the rest of this discussion, we will refer to our Microscopic Functional Apparent-Diffusion Coefficient imaging of the retina as mfADC.

It is clear that mfADC has great potential for investigating a range of sight-threatening disorders in preclinical models and in the clinic, since it is based on an endogenous contrast mechanism [31]. However, more work is needed to determine feasibility of achieving sufficient spatial resolution in a clinically realistic time frame on a clinical scanner: the total scan time in this initial study, just over 2 h, is impractical for that purpose. Since measurements of ADC_║ appeared more sensitive to retinal dark-light differences than ADC_┴, focusing only on the former may be a sensible approach to reducing total scan time. More work is needed to balance reductions in scan time with, for example, selecting an optimal number and range of b values for measuring the mfADC response. Retinal ADCs reported in the present work, and the corresponding dark-light ADC differences, were calculated with a linear fit to the log-transformed signal intensities from all five available b values (0, 250, 500, 750, and 990 s/mm²; Equations 2–4). Effect-size calculations (of dark versus light) using only b0 and b990 consistently yielded similar results as the effect-size calculations using all five b values, suggesting that in future studies, scan time may be reduced by collecting only these two b values. Although the present use of b values ranging from 0 to 990 s/mm² was enough to detect light-dependent diffusion changes in the avascular outer retina, models linking this finding to the relevant retinal biology will be improved by measuring at more and at higher b values.

In this study, we also looked for possible effects of low SNR on ADC values. Importantly, although some differences were noted using either 0≤b≤750 s/mm² or 0≤b≤990 s/mm² data to calculate ADC, our central finding in this study of dark-light differences remained. Nonetheless, future studies will need to balance the need for good SNR against the number and range of diffusion weightings (b values), scan time, and image resolution. Careful selection of imaging parameters is warranted when studying pathologies associated with elevated ADCs, such as vasogenic edema, since the same diffusion gradients will be more effective than normal at reducing the SNR. In this case, there will be greater risk of underestimating ADCs and therefore possibly reducing sensitivity for disease versus control comparisons. SNR can be improved by reducing image resolution, but at the expense of increasing partial-volume averaging of the retina with adjacent tissue. Alternative imaging sequences (e.g., rapid acquisition with refocused echoes [RARE], half fourier acquisition single shot turbo spin-echo [HASTE], echo planar imaging [EPI]) may allow for improvements in SNR without sacrificing image resolution. We hope that the present findings of robust activity-dependent changes in retinal ADCs will help motivate such further investigations.

Our present analysis examined averaged central retina (10%–30%extent) to improve the SNR. Since the retina has some curvature in the image plane, measurements of retinal diffusion in the║ direction include cell structures in the retina (e.g., photoreceptors) that are oriented off-║ to some degree (by ≤θ in Figure 1). Across subjects, the upper bound (θ; mean±standard deviation of the mean) is 27±3 °, and the average off-║ orientation is 19±2 ° with the 10%–30%extent span of the retina. To gauge the impact of this off-║ alignment, we considered a hypothetical case where ADCs measured with perfect alignment in the ║ and _┴ directions were 1 μm²/ms and 0 μm²/ms. This high-anisotropy hypothetical defines an upper bound on error in ADC_║ measurement caused by off-║ mixing of ║ and _┴ diffusion components. Even with such extreme anisotropy, an ADC_║ measurement of approximately 0.95 μm²/ms [based on cos (19 °)] is expected. Known modest levels of anisotropy for the retina [4,14] will produce correspondingly smaller errors. Furthermore, the small contribution of off-║ components in the central retina of each subject are unlikely to change between light and dark conditions. For these reasons, the influence of slightly off-║ orientations caused by the curvature of the eye were expected to be negligible in the present study.

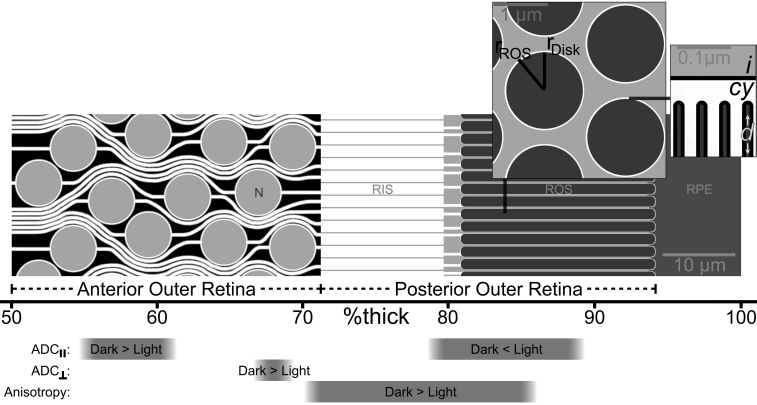
A major finding of this study was that ADC_║ was greater (i.e., relatively more mobile water) in the posterior outer retina in the light than in the dark. Structurally, the outer retina in the rat is avascular, with the posterior half spanning from the posterior border of the Müller glia to the apical RPE. It is occupied almost exclusively by well aligned rod outer segments (ROSs) and the fluid between ROSs (the interphotoreceptor space [IPS] volume). Each ROS is lipid-dense, being filled with a compact stack of well aligned disks—the only type of membrane-bound internal structure found in the ROS. The IPS is free of barriers to diffusion parallel to the long axis of the ROS (e.g., [32]). In contrast, the intracellular space of the ROS is highly membranous. Therein, disks substantially restrict diffusion in the ║ direction—between one-seventh and 1/1,000 the level of free diffusion, based on ex vivo studies (though _┴ diffusion, being parallel to disk surfaces, appears relatively unrestricted) [33-37]. The light-induced increase in posterior outer retinal ADC_║ may therefore reflect increases in IPS water (with unrestricted║ diffusion) relative to intracellular water (with highly restricted ║ diffusion). This pattern is consistent with previous studies, discussed below, which find light-induced increases in IPS volume. We note that the present data are consistent with proportional changes in IPS versus intracellular water content, but not changes in total water content (proton density): In the absence of diffusion-weighting gradients (i.e., structural and b0 images), we found no light-dependent changes in signal. In addition, morphometric parameters—which are sensitive to changes in retinal water content [4]—did not change with lighting condition (Table 1).

Physiologically, photoreceptors are depolarized in darkness, and because this is metabolically costly (see [38] for review) relatively more waste products are produced in darkness than in light [39]. Such waste products, including water and CO₂, are released into the IPS—the interstitial space surrounding the outer segments of the photoreceptors and the apical membrane of the RPE [40]. Dissolved CO₂, in rapid equilibrium with carbonic acid (H₂CO₃), lowers the pH and raises the salt content of the IPS. In turn, ion flux across the apical RPE membrane is stimulated, greatly facilitating removal of IPS waste, presumably to prevent damaging acidification [40-42]. One major consequence of increased RPE pumping in the dark, as revealed by electrode measurements of an extracellular marker, is that the IPS volume is about 17% lower in the dark than in the light [1-3]. This volume change occurs over several seconds, and is maintained during prolonged lighting conditions [1,2]. The present finding that posterior outer retinal ADC_║ is higher in light than darkness is consistent with such proportional increases in IPS volume, and suggests that mfADC may be useful for evaluating the health of the photoreceptor-RPE complex. Future studies can be envisioned that test the effects of different stimulus parameters—including light intensity and duration—on mfADC responses in both healthy and diseased retinas.

Another important observation in this study is that, in the anterior outer retina, the ADC in both directions was greater in the dark than in the light, in contrast to the posterior outer retinal response. Structurally, the anterior outer retina is almost completely composed of a heterogeneous mixture of photoreceptor somas and Müller cell processes, separated by a thin, tortuous, interstitial space [43]. Because of this complex microenvironment, relative to that in the posterior outer retina, straightforward interpretation of the intra- and extracellular contributions to the ADC changes is difficult [44]. There is little information about how anterior outer retinal hydration might change with light and dark conditions, since electrode studies are limited by the diffusion of extracellular tracers (e.g., [2]). One speculative explanation involves glutamate: photoreceptors release more glutamate (the major neurotransmitter in the retina) in the dark than in the light, and glutamate can cause swelling (i.e., presumptive fluid accumulation) of the Müller cell somas [45,46]. This swelling plausibly extends to the Müller cell end-feet in the anterior outer retina. More work is needed to determine the sensitivity of mfADC changes in the anterior outer retina to photoreceptor-Müller cell interactions.

In a narrow region near the border between the anterior and posterior of the outer retina (72%–76%thick), we found significant dark-light differences in the anisotropy of diffusion (ADC_║ - ADC_┴), but it is unclear whether this was due to a change in ADC_║, ADC_┴, or both: dark-light differences for both ADC_║ and ADC_┴ failed to reach significance in that 72%–76%thick range (Figure 2 and Figure 3). Data from this portion of the retina, which we estimate to be occupied by the disk-free inner segments of rod photoreceptors, is difficult to interpret: Given the present whole-retinal thicknesses of approximately 190 μm, and the pixel size in diffusion-weighted images (27.8 μm), each pixel spanned approximately 15%thick. While this is enough to distinguish the significant results at anterior outer retina at 56%–60%thick from the posterior outer retina at 80%–88%thick, the intervening space falls within the range of the partial-volume averaging effects of each. Furthermore, in contrast to water diffusion in rod outer segments, which is well characterized ex vivo [33-37], we are not aware of any ex vivo studies of diffusion in rod inner segments. Future ex vivo studies of this topic, or in vivo mfADC studies collected with higher image resolution (to reduce partial volume averaging), are needed to fully interpret data from the 72%–76%thick region of the retina.

Figure 3.

Locations of significant light-dependent changes in apparent diffusion coefficient (ADC) are shown relative to known outer retinal morphology. Unique light-dependent changes were found for ADCs measured parallel to the optic nerve (ADC║), perpendicular to the optic nerve (ADC┴), and in diffusion anisotropy (i.e., ADC┴ - ADC║). Central retinal rods and associated structures are depicted to scale, based on the well documented layered microstructure of the rat retina, with rod nuclei (N) and rod inner and outer segments (RIS, ROS) anterior to the retinal pigment epithelium (RPE). The rod cytoplasm is shown in white, interstitial space (and rod nuclei) in light gray, and processes from Müller glia in black between rod somas. The dimensions of all structures are illustrated accurately based on the extensive body of literature for the rat retina, including the diameters of rod nuclei [43,53], the connections between rod nuclei and other structures (“rod fiber” in [43]), and the connection between RIS and ROS [43,54]. Note that the dimensions of each cellular element are based on an average of at least two literature sources. For illustrative purposes, the main panel (which shows the ║ direction oriented from left to right) displays all structures centered on same two-dimensional plane. Though this is a fair depiction of RIS and ROS, which are spaced in a regular hexagonal lattice [32,55], the arrangement of rod somas is less orderly, and it is generally not possible to see several neighboring rod nuclei at full diameter in a single histological section. The gray within ROSs is a depiction of the several hundred photopigment-laden disks (approximately 30.5 per μm of ROS length [54-60]) at low magnification, which is clarified in the inserts. Results and landmarks are depicted against the %thick scale used for the mfADC data. Optical coherence tomography images of the rat retina [61-65] demonstrate that the distance from vitreoretinal border to the choroid is approximately 200 μm, with the following divisions: the border between the outer plexiform layer and outer nuclear layer (i.e., the anterior-most position of the photoreceptor nuclei) occurs approximately 101 μm from the vitreoretinal border (i.e., 50%thick); the division between outer nuclear layer and the bacillary layer (posterior outer retina, containing rod inner and outer segments) occurs at approximately 143 μm (72%thick); and the posterior limit of the rod outer segments occurs at approximately 187 μm (94%thick) from the vitreoretinal border, with the remaining space to the choroid (at 100%thick) occupied by RPE. Histological studies of the rat retina are in good agreement with those figures, showing that rod outer segments are approximately 27 μm long, while rod inner segments are approximately two-thirds that length [32,43,53,55,60,66], for a combined approximately 45 μm span for the posterior half of the outer retina. The outer nuclear layer (which we refer to as the anterior outer retina) is approximately 39 μm thick [58-60,66-69], and the distance between the outer nuclear layer and vitreoretinal border is approximately 106 μm [67-69]. Including an approximately 8 μm RPE [68], histological studies therefore describe the anterior outer retina spanning from 53% to 73%thick, and a posterior outer retina from 73% to 96%thick. Left insert (║ into/out of plane): Cross sections show the radii of ROS (r_ROS) and disks contained within (r_Disk), along with the thin rim of cytoplasm that runs the length of the ROS between the disk and ROS membranes. The depiction of ROS and disk radii are based on published electron micrographs, where r_ROS is approximately 0.73 μm [32,43,54,55,57,58] and the difference between r_ROS and r_Disk is approximately 0.03 μm [54-56,60]. The inter-ROS spacing shown here is based on known photoreceptor density: an approximately 10 µm² area is illustrated here, and the literature’s ranges for packing density range from 3.1 to 4.0 rods per 10 µm² [43,59,70]. Right insert (║ left/right): Fine detail of the ROS shows the location of intra-disk (d) cytoplasmic (cy) and interphotoreceptor (i) water between membranes (black lines). The total disk thickness is depicted as equal to the thickness of the between-disk cytoplasmic space, based on available information available for the rat [54-56,60], and the pattern found in several other species [71]. The range of literature values may be due to the sensitivity of ROS disks to fixation method [54,72].

We documented, with mfADC, that inner retinal water diffusion was independent of light. The inner retina consists of an even more complex inventory of cell types and arrangements than the anterior outer retina, which limits a full interpretation. Functionally, the inner retina contains a light-driven pathway, known as the ON pathway, and a dark-driven pathway, known as the OFF pathway [47]. With an approximately equal representation of ON and OFF cells in the inner retina, similar activity has been reported during light or dark conditions [23,48]. The present mfADC results are consistent with the above interpretation, although more studies are needed to determine if changes in inner retinal physiology alter mfADC.

We used previously validated diffusion-weighted imaging methods to measure retinal responses to light versus darkness in vivo. This approach does not rely on exogenous contrast agents, and since it yielded significant functional changes in only the avascular outer retina, is likely independent of hemodynamic-based contrast. Previous investigations used MRI to collect data sensitized to the rate of loss of coherence in an ensemble of spins that include all interactions (including static dephasing; i.e., T₂*), a dominant contributor in the hemodynamically based (BOLD) signals, and reported light-induced functional changes in retinal and choroidal hemodynamics [49,50]. Such changes would not be expected from the present images, collected with a spin-echo sequence (which is largely insensitive to T₂*) in the avascular outer retina. The spatial resolution of this approach surpasses current BOLD and retinal blood-flow fMRI capabilities in rats [20,51]. Based on known morphology and physiology, the mfADC signal in the posterior outer retina is consistent with light-dependent increases in IPS volume [1,2]. Although more work is needed to optimize the data acquisition, future studies may pair mfADC measurements with other high-resolution MRI methods—sensitized, for instance, to ion physiology [22] retinal lipid content [52], or hemodynamics [20,51]—to noninvasively gain a comprehensive understanding of retinal anatomy and physiology. The wide availability of diffusion-weighted MRI suggests that rapid translation of mfADC into a range of clinical and preclinical applications is likely.