Biexciton quantum yield heterogeneities in single CdSe(CdS) core(shell) nanocrystals and its correlation to exciton blinking

Abstract

We explore biexciton (BX) non-radiative recombination processes in single semiconductor nanocrystals (NCs) using confocal fluorescence microscopy and second-order photon intensity correlation. More specifically, we measure the photoluminescence blinking and BX quantum yields (QYs), and study the correlation between these two measurements for single core(shell) CdSe(CdS) nanocrystals (NCs). We find that NCs with a high “on” time fraction are significantly more likely to have a high BX QY than NCs with a low “on” fraction, even though the BX QYs of NCs with a high “on” fraction vary dramatically. The BX QYs of single NCs are also weakly dependent upon excitation wavelength. The weak correlation between exciton “on” fractions and BX QYs suggests that multiple recombination processes are involved in the BX recombination. To explain our results, we propose a model that combines both trapping and an Auger mechanism for BX recombination.

INTRODUCTION

The exciton (X) emission of semiconductor nanocrystals (NCs), also known as quantum dots (QDs), is tunable in wavelength, narrow in linewidth, and high in efficiency. These properties make NCs promising materials for biological imaging^1-4 and light emitting device^5-7 applications. Furthermore, the efficiency of multiexciton (MX) emission in NCs determines whether they can be used as single photon sources^8-11 or in lasing applications^{12, 13}. More specifically, a low MX quantum yield (QY) is desirable for the use of NCs as a single photon source; while for lasing applications, it is ideal that the MX QYs of the NCs are high. Understanding X and MX physics in single NCs will facilitate the design and choice of proper NCs for numerous applications. Such an understanding requires an elucidation of the photo-physics that determines MX QYs.

Exciton emission from single NCs has been extensively studied over the last fifteen years. It is well known that the emission of single NCs switches between a high intensity “on” state and a low intensity “off” state under continuous excitation. This phenomenon is known as “blinking” or fluorescence intermittency.^14-16 Many models involving charging and Auger recombination or trap-assisted recombination have been proposed to explain X blinking.^{15, 17-20} However, MX emission and recombination pathways in single NCs have not been investigated as thoroughly as for Xs.^{21, 22} This is largely due to the low emission QYs and fast non-radiative rates of MXs. Recently, using a CdSe(CdZnS) core(shell) NC sample, we were able to spectrally separate triexciton (TX) emission from the exciton/biexciton (X/BX) emission of single NCs due to the fact that TX emission is blue-shifted from X/BX emission. A blinking phenomenon similar to Xs has been observed in TX emission.²³ As for BXs, their emission largely overlaps with X emission, making it virtually impossible to spectrally separate the two at room temperature. To study the BX emission efficiency of single NCs, Nair et al. developed a method that directly measures the BX QYs of single NCs using photon statistics.²⁴ The method has been applied to measure BX QYs of CdSe(CdZnS) core(shell) NCs²⁴ and CdSe(CdS) core(shell) NCs with varying shell thickness.²⁵ BX non-radiatiave recombination in NCs is usually attributed to an Auger relaxation process.²⁶ In this process, when the BX non-radiatively recombines, a carrier is ejected into a high energy state, and then relaxes back to the band-edge. Since the Auger process is very efficient in NCs, BX QYs of NCs are normally low. Recently, long BX lifetimes (~10 ns) have been observed in ensemble CdSe(CdS) NC samples with a thick CdS shell (> 5.5 nm).²⁷ The slow BX non-radiative recombination rate in these NCs is attributed to suppressed Auger recombination. However, BX QYs of single thick-shell CdSe(CdS) NCs vary dramatically from 0.1 to near unity, which was attributed to a wide variation in Auger rates.²⁵ In addition, exciton emission of individual thick-shell CdSe(CdS) NCs generally shows very few intensity switching events between “on” and “off” states over as long as 50 mins of measurement.^{25, 28} This suppression of blinking was attributed to suppressed photo ionization of the CdSe core by the thick CdS shell.^{25, 28} Meanwhile, a different type of exciton emission behavior was reported for similar thick-shell CdSe(CdS) NCs.²⁹ In those studies, the X PL intensity of single NCs rapidly switches between two emission states. However, the lower intensity state was described as a “grey” state with moderate emission instead of a “dark” state with low emission close to the background level.^{29, 30} The authors proposed that the hole was localized in the core whereas the electron was delocalized over the entire NC, making the Auger recombination less efficient.^{29, 30} Very low BX QYs have also been observed in these NCs. These studies imply that the presence of a thick shell suppresses or reduces X blinking by limiting access to non-radiative pathways for Xs, and/or slows the Auger recombination rates. If the former, the recombination processes of BXs in these thick-shell NCs is not necessarily affected, therefore the BX QYs of the thick-shell NCs should be similar to the BX QYs of normal NCs. If the latter, the non-radiative rates for BXs in the thick-shell NCs should be slow, hence high BX QYs are expected in these NCs. A study that quantifies the relationship between X blinking and BX QYs of single NCs should facilitate a deeper understanding of the BX recombination mechanism.

In this work, we explore the BX recombination process in single NCs by studying the relationship between BX QYs and X “on” fractions (the time fraction that the NC stays in the “on” state), as well as the excitation wavelength dependence of the BX. Biexciton QYs are expected to correlate with X “on” fractions if BX recombination and X blinking events originate from the same process. Specifically, we measure the photoluminescence (PL) intensity time trace and second-order PL intensity correlation (g⁽²⁾(τ)) of single CdSe(CdS) under pulsed excitation of core(shell) NCs with different sizes and emission wavelengths. The CdSe(CdS) NCs are custom synthesized with a shell thickness of 2.25 nm or 2.35 nm (corresponding to 6-7 monolayers (MLs) of CdS^{28, 31}), and they have high ensemble PL QYs (≥80%) and high average “on” fractions (~ 0.9). The X “on” fraction of a single NC is calculated from the PL time trace with a chosen threshold between the “on” and “off” states. The number of excitations per pulse is low (≤ 0.2) and is kept constant for all the single NC experiments. We also verified that in our experiments, the “on” fraction can be used to characterize the blinking behavior of the single NCs at long enough collection time. The BX QY of the same NC is determined from the relative size of the 0-time coincidence feature in its g⁽²⁾(τ) measurement. We observe that for NCs with low “on” fractions, the BX QY is low. However, for NCs with a high “on” fraction, the BX QY varies dramatically from very low (undetectable) to high (~ 0.4 or 0.5). It is significantly more likely for NCs with a high “on” fraction to have a high BX QY. The weak correlation between the “on” fraction and the BX QY indicates that exciton blinking events and biexciton non-radiative recombination do not share the same process. It is, therefore, plausible that multiple processes play a role in the non-radiative recombination of BXs. We propose a model involving both trap-assisted and Auger-like recombination to explain our observations. To further test the model, we compare the BX QYs of single CdSe(CdS) NCs excited at a lower energy corresponding to their second absorption peak and a higher energy which pumps the NC into a quasi-continuum of electronic states. The BX QYs of most NCs are higher when they are excited at lower energy. We speculate that this is because when the NC is excited at higher energy compared to at lower energy, more non-radiative recombination centers or deeper trapping sites are accessible, resulting in a faster non-radiative rate for the BX and a lower BX QY.

EXPERIMENTAL METHODS

The NC samples used in this study are custom-synthesized CdSe(CdS) core(shell) NCs with emission peaks at 593 nm (QD593) and 624 nm (QD624). The photoluminescence (PL) QY of QD593 is 80% and QD624 is 97%, determined by comparison to Rhodamine 610 in ethanol. The shape and size distribution of the NCs was characterized by transmission electron microscopy (TEM) on a JEOL2010 transmission electron microscope (200 kV).

Fig. 1 shows the absorption and PL spectra of QD593 (Fig 1a) and QD624 (Fig 1c). TEM images of QD593 and QD624 are illustrated in Fig 1b and Fig 1d, respectively. The absorption spectra have multiple distinct excitonic features and the emission spectra are quite narrow (FWHM < 30 nm) for both of the samples. TEM measurements demonstrate that the size and shape of the CdSe(CdS) NCs are quite uniform. TEM imaging over large areas of NCs shows an average diameter of 7.5 ± 0.4 nm for NC593 and 9.1 ± 0.4 nm for QD624. The diameter of the CdSe core for QD593 is 3.0 nm and QD624 is 4.4 nm, estimated from the first absorption peak position.³² According to TEM measurements, the shell thickness of QD593 is 2.25 nm while that of QD624 is 2.35 nm.

Figure 1.

Absorption (blue line) and PL (red line) spectra for (a) QD593 and (c) QD624, and TEM images of the corresponding NCs (b) QD593 (d) QD624.

For single NC measurements, the CdSe(CdS) NCs were diluted in a toluene/poly(methyl methacrylate) solution (concentration of 4% by weight) and spun cast onto glass coverslips (Electron Microscopy Sciences). Individual NCs were studied by confocal epifluorescence microscopy using an oil immersion microscope objective (100x, 1.40 NA, Plan Apochromat). The NCs were excited with a pulsed diode laser (PicoQuant) at 414 nm or a pulse-picked supercontinuum laser (NKT Photonics) at their second absorption peak (514 nm for QD593 and 580 nm for QD624). The repetition rate of the lasers is 2.5 MHz. Typical excitation fluences for all the excitation wavelengths are low enough that the average absorbed photons per pulse 〈N〉 is ≤ 0.2 (see Supporting Information for 〈N〉 calculation) and remains constant during the course of the measurements. The emission of single NCs was divided in half using a beam splitter and focused onto two avalanche photodiodes (Perkin-Elmer) in a Hanbury-Brown and Twiss geometry using suitable spectral filters. PL intensity time traces and g⁽²⁾(τ) were simultaneously recorded using pulse counters (National Instruments) and a correlator card (Timeharp 200, PicoQuant). Transient PL spectra of NCs in hexane were obtained by dispersion on a streak camera (Hamamatsu C5680). The excitation source for transient PL studies was the output of an optical parametric amplifier at 410 nm pumped by an amplified Ti:sapphire laser running at 840 Hz. The NC samples were stirred vigorously during the transient PL experiments. All measurements were performed at room temperature.

RESULTS AND DISCUSSION

We simultaneously measure X blinking traces and second-order photon intensity correlation (g⁽²⁾(τ)) of single NCs from both QD593 and QD624 samples. Fig. 2 shows representative blinking traces and g⁽²⁾(τ) data for a single NC from sample QD593 (a and b) and a single NC from sample QD624 (c and d) (more blinking traces are available in Supporting Information). The histograms of the PL intensity distribution in Fig. 2a and 2c reveal well-resolved two-state blinking of the CdSe(CdS) NCs. The dashed line in the histogram indicates the threshold chosen to determine the “on” and “off” states. The threshold level was chosen so that small changes in the threshold value do not affect the determination of “on” and “off” states. The probability of “on” and “off” times of both QD593 and QD624 follow a power-law distribution $P_{\mathit{on}/\mathit{off}}\propto t_{\mathit{on}/\mathit{off}}^{-{\alpha }_{\mathit{on}/\mathit{off}}}$ where α_on = 0.9 for “on” times and α_off = 2.2 for “off” times (see Supporting Information). Note that typically, the value of α is between 1 and 2.^{15, 33} A small α_on indicates a slow decay of the “on” times probability due to many long “on” events. A large α_off shows a fast decay of the “off” time probability because most of the NCs have very short “off” events. The average time that the NC stays in the “on”/ “off” states can be expressed as $\langle t_{\mathit{on}/\mathit{off}}\rangle ={\int }_{t_{\mathit{min}}}^{t_{\mathit{acq}}}t\times P_{\mathit{on}/\mathit{off}}\mathit{dt}/{\int }_{t_{\mathit{min}}}^{t_{\mathit{acq}}}{P}_{\mathit{on}/\mathit{off}}\mathit{dt}$, where t_min is the bin time (50 ms in our study), and t_acq is the total acquisition time. The “on” time fraction can be estimated as 〈t_on〉/(〈t_on〉 + 〈t_off〉) which evolves with t_acq. The calculated evolution of the “on” fraction in time using this equation (see Supporting Information for the plot of “on” fraction evolution over time) shows that the “on” fraction increases rapidly with time and saturates in ~ 150 s. The evolution of the “on” fraction of a collection of randomly selected NCs from sample QD624 from the measured PL blinking traces (see Supporting Information) shows that for most of the NCs, the “on” fraction increases over time quickly as the model predicts, saturating to a constant value or remains relatively constant. Note that the value of α_on/off for individual NCs may vary. We verified that as long as α_on is < 1.0 and α_off is > 2.0, which is the case for the majority of the NCs in our study, small changes in α_on/off slightly changes the value of the “on” fraction, but the evolution of “on” fraction in time follows the same trend and has saturated by ~150 s. Therefore, the “on” fraction measured at a long enough acquisition time (>150 s) is a valid parameter to characterize the blinking behavior of the single NCs. From the blinking time traces we collected, we calculate the time fraction of these NC staying in the “on” state during 150 s of measurement. The distribution of “on” time fraction for 120 NCs in sample QD593 and 92 NCs in sample QD624 is shown in Fig. 3a and 3c, respectively. The average “on” fraction is as high as 90% for QD593 and 93% for QD624.

Figure 2.

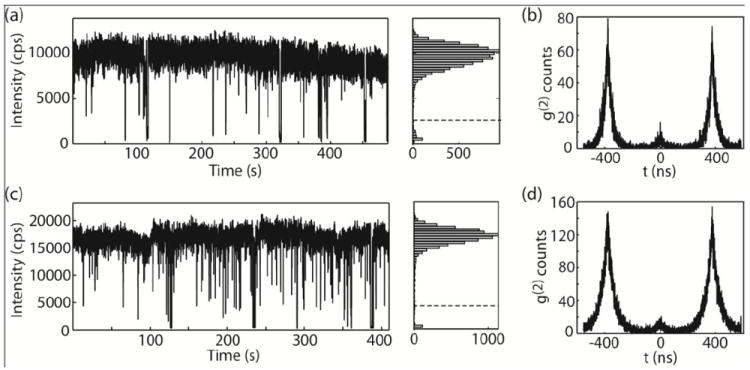
Representative blinking and g⁽²⁾ measurements of single NCs from sample QD593 (a-b) and QD624 (c-d). (a) Representative PL blinking trace of a single NC from sample QD593. Histogram indicating the distribution of intensities observed in the trace. The dashed line indicates the value chosen as the threshold between “on” and “off” states in calculating the “on” time fraction. (b) The g⁽²⁾(τ) measurement of the same NC. (c-d) Blinking (c) and g⁽²⁾(τ) (d) data for a single NC from sample QD624.

Figure 3.

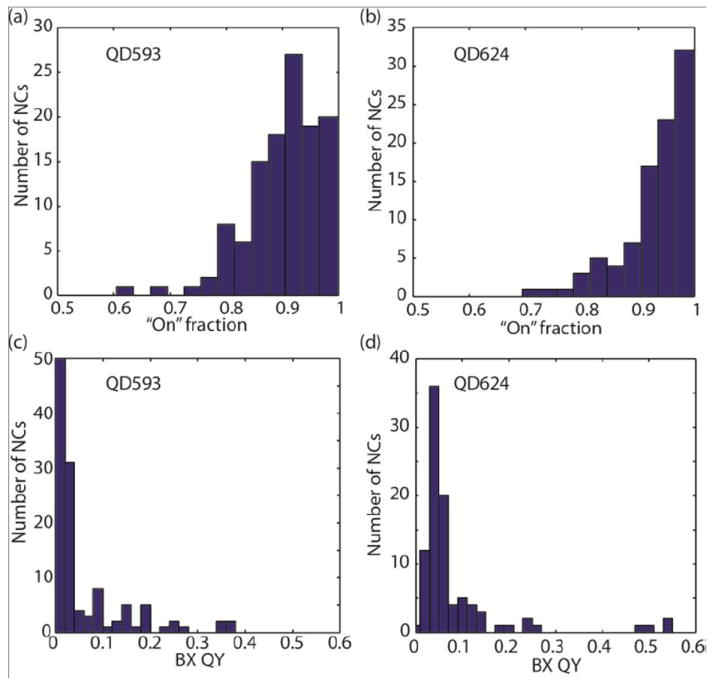
Histograms of the distribution of “on” time fractions and BX QY of the NCs observed in each sample. (a-b) Blinking “on” time fraction distribution for QD593 (a) and QD624 (b). The average “on” time fraction for QD593 is 0.90 with a standard deviation of ± 0.07 while the “on” time fraction for QD624 is 0.93 with a standard deviation of of ± 0.06. (c-d) BX QY distribution for QD593 (c) and QD624 (d). The average BX QY for QD593 is 0.06 while average the “on” time fraction for QD624 is 0.08.

The BX QYs of single NCs are calculated from their g⁽²⁾(τ) function based on the method developed by Nair et. al²⁴ and plotted in Fig. 3b and 3d. Significant variation has been observed in the BX QYs of the NCs used in this study. The BX QYs of QD593 range from undetectable to 0.38 with an average of 0.06, and the BX QYs of QD624 range from 0.01 to 0.55 with an average of 0.08. Note that the variation in BX QYs calculated from repeated g⁽²⁾(τ) measurements on the same single NC is < 0.01. Therefore, the wide distribution of BX QYs is from NC-to-NC variations and not experimental artifacts. Large distributions in BX QYs within one NC sample have also been observed in CdSe(CdZnS) core(shell) NCs²⁴ and CdSe(CdS) core(shell) NCs with greater than 10 CdS MLs.²⁵ As previously discussed, the NC-to-NC variation arises due to the distribution of non-radiative decay rates in BXs.²⁴ Since the NCs are quite uniform in size and shape, the variation is likely caused by defects in the crystal structure, differences in the core-shell interface, or surface abnormalities of each individual NC.²⁶ We also notice that the BX QYs of some of the CdSe(CdS) NCs we studied are very high. In these NCs, either the number of non-radiative recombination pathways for BXs is reduced and/or the non-radiative rates are slower. Meanwhile, the ensemble BX lifetime of QD593 is ~ 170 ps and that of QD624 is ~ 500 ps, similar to the previously reported BX lifetimes of CdSe(CdZnS) and thin shell CdSe(CdS) NCs (see Supporting Information for the ensemble PL decay of the NCs). The short ensemble BX lifetimes suggest that the BX non-radiative decay rates for ensemble NC samples in our study are fast. This is consistent with the low average BX QY of single NCs in our study (0.06 for QD593 and 0.08 for QD624).³⁴

To reveal the relationship between X blinking and BX QY, the “on” fraction and the corresponding BX QY of the same NC is plotted in Fig 4. Fig. 4a shows the “on” fraction versus BX QY for QD593. From the plot, there is a weak correlation between the “on” fraction and BX QY. For the NCs with a small “on” fraction (< 0.8), the BX QY is relatively low (<0.1). For NCs with “on” fraction > 0.8, there is a wide distribution of BX QYs, ranging from very low (undetectable) to as high as 0.38. Since there are much fewer NCs with a low “on” fraction (< 0.8), we calculated the p-value of the data to test its statistical significance. We obtain a p-value of 0.04 with thresholds for “on” fraction of 0.8 and BX QY of 0.1, which means the NCs with an on-fraction > 0.8 are statistically more likely to have a BX QY higher than 0.1. A similar phenomenon is observed for QD624 as shown in Fig 4(b). In the QD624 sample, the BX QYs of the majority of the NCs are < 0.1. For NCs with “on” fraction > 0.9, the BX QYs vary from 0.01 to 0.55. A p-value of 0.09 is obtained with thresholds for “on” fraction of 0.9 and BX QY of 0.2, which means the NCs with an “on” fraction > 0.9 are significantly more likely to have BX QY higher than 0.2. It is worth noting that for NCs with the same “on” fraction, the BX QY varies dramatically. Park et al. also observed that in CdSe(CdS) NCs with thick CdS shells (> 15 monolayers of CdS), the BX QYs of individual NCs vary drastically from < 0.1 to near unity.²⁵ They also showed that X blinking of these thick-shelled NCs is completely suppressed.²⁵ This suggests that even in non-blinking NCs, there is still a wide distribution in BX QYs. The observations indicate that reduced X blinking does not imply high BX QYs.

Figure 4.

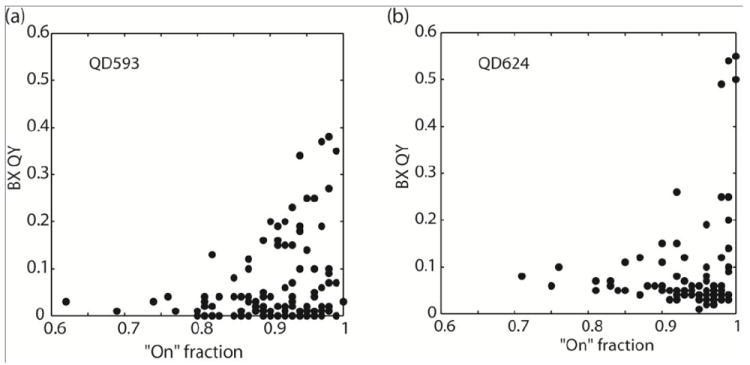
BX QY versus the blinking “on” time fraction of the same NC for samples (a) QD593 (b) QD624.

The weak correlation between “on” fraction and BX QY suggests that suppression of X blinking is a necessary but not sufficient condition to suppress BX non-radiative recombination. It is plausible that the BX non-radiatively recombines through the X non-radiative pathways and some other mechanism. A blinking model that is compatible with our recent studies proposes that X blinking is caused by large variations of the non-radiative relaxation rates due to opening and closing of multiple non-radiative recombination centers (NRCs).¹⁹ In this model, the total non-radiative recombination rate can be expressed as $k_{\mathit{nr}}(t)={\sum }_{i=1}^N{k}_i{\sigma }_i(t)$ where k_i is the non-radiative recombination rate of the ith NRC in the active state and σ_i switches stochastically between 0 (inactive) and 1 (active).¹⁹ k_nr is fast when many NRCs are active and slow when fewer NRCs are available for non-radiative recombination of the exciton.

Another blinking model we discuss here is the multiple charging model recently proposed by Califano.³⁵ According to this model, trapped holes are responsible for the very low QYs observed during “off” blinking events. They propose that the “off” state is caused by a negatively charged X with two delocalized electrons and a hole trapped in a surface state ( $X_s^{-}$) or a neutral BX with two delocalized electrons and its two holes in surface trapping sites (BX_SS). Since the holes are localized on the surface, the core of the NC is left in a multiply charged state. The QYs of both $X_s^{-}$ and BX_SS are lower than that of a normal BX, compatible with our previous experimental findings.²³ It is reasonable to adapt the model and assume that the accessibility of the surface trapping sites affects the probability of forming the “off” state X, in another word, having a blinking event. In this case, the X “on” fraction is dependent upon the access to surface trapping sites. Meanwhile, the theoretical studies in Ref. 35 showed that the Auger rates of a normal BX or a BX with one or two trapped holes (BX_S(S)) are similar, but that the QYs of BX_SS can be much lower than those of the BX depending on how many and how deeply the holes are trapped.³⁵ This indicates that whether the holes are trapped and how deeply they are trapped slows the radiative rates of the BX or BX_SS, without changing the Auger rates. The accessibility to the surface trapping sites determines whether the BX recombination goes through the “hole trapping” step before radiative or Auger recombination.

Here, we adopt the above multiple NRCs and multiple charging models of X blinking and propose a process of BX recombination that involves both trap-assisted process and Auger recombination. The proposed process is illustrated in Fig. 5. In this picture, BX recombines (i) radiatively by emitting a photon; (ii) through trapping process where (ii-a) NRCs serve as non-radiative channels or (ii-b) where surface trapping sites trap the holes and slow the radiative rate of the BX; or (iii) non-radiatively through Auger recombination. According to this model, in NCs with a low “on” fraction, NRCs or surface trapping sites are more easily accessible for Xs. BXs in these NCs also go through the readily available NRCs (Fig 5(ii-a)) or form a BX_SS with a slower radiative rate (Fig 5(ii-b)), or through the Auger mechanism if the Auger rate is much faster than the BX radiative rate. In NCs with a high “on” fraction, either the number of NRCs is reduced or access to NRCs or surface trapping sites is limited. However, BXs can still recombine non-radiatively through the Auger mechanism resulting in a low BX QY. Only when Auger recombination is also suppressed in these NCs will BXs recombine radiatively, leading to a high BX QY. To summarize, the model proposes that the BX recombines non-radiatively through both trap related processes and Auger recombination. Variations in Auger rates then account for the wide distribution of BX QYs when trap-assisted recombination is significantly reduced.

Figure 5.

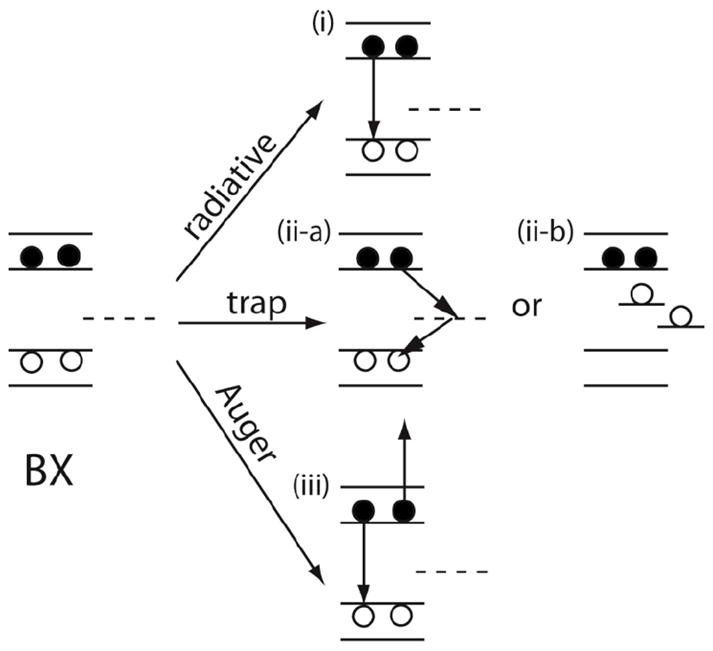
Schematic illustration of biexciton (BX) recombination pathways. The biexciton recombines radiatively by emitting a photon or non-radiatively through non-radiative recombination centers or Auger recombination.

To further understand the BX recombination process in single NCs, we explore the effect of excitation wavelengths on BX QYs. Previously, Knappenberger et. al observed excitation wavelength-dependent “on” time statistics of single NC PL blinking in CdSe(ZnS) core(shell) NCs which they attributed to multiple trap states with a distribution of energies.³⁶ In our study, we excite the NCs into different excitonic states by varying the excitation wavelength and measuring the BX QYs of the same NCs excited at two different wavelengths. To ensure that there is no irreversible effect caused by excitation at one wavelength, the order in which NCs are exposed to different wavelengths is varied. NCs from sample QD593 and QD624 are excited at their second absorption peak (514 nm for QD593 and 580 nm for QD624), which corresponds to the 2S_2/31S_e transition of CdSe nanocrystals.³⁷ The NCs are also excited at 414 nm, where a continuum of electronic transitions in CdSe is accessible.³⁷ Note that the NCs we use are CdSe(CdS) core(shell) NCs, the surface states of the CdS shell will also play a role when the NCs are excited at 414 nm (higher than the band gap energy of bulk CdS (2.42 eV, 513 nm)³⁸).

The BX QYs of single NCs at different excitation wavelengths are shown in Fig. 6. Points along the diagonal of the plot show small difference in the BX QYs of the NC at different excitation wavelengths while points that deviate from the diagonal show relatively big differences in the BX QYs. Fig. 6(a) illustrates the BX QYs of single NCs from QD593 sample excited at 514 nm and 414 nm. From the plot, the BX QYs at 514 nm and 414 nm are correlated. Some NCs have very small or even non-measurable BX QYs (points close to the origin) and therefore show no difference in the BX QYs at different excitation wavelengths. For the majority of the NCs, the BX QY at 514 nm is higher than at 414 nm. Fig. 6b shows the BX QYs of single NCs from QD624 sample excited at 580 nm and 414 nm. We find that 75% of the NCs have a BX QY < 0.1 at 414 nm excitation. For these NCs, most of the points on the plot in Fig 6b fall close to the diagonal, indicating a small or even undistinguishable difference between the BX QYs at 580 nm and 414 nm. For NCs with a BX QY > 0.1, the BX QY depends more strongly on the excitation wavelength, and ~70% of the BX QYs measured are higher at 580 nm than 414 nm excitation. Since g⁽²⁾ measurements give the ratio between BX QY and X QY, we verified that the X QY of the NCs is independent of excitation wavelength by comparing the X decay of the NCs at different excitation wavelengths (see Supporting Information). Therefore, the difference we observed in BX QYs of single NCs excited at different excitation wavelengths is due to changes in the BX recombination dynamics.

Figure 6.

Biexciton QYs for single NCs excited at their second absorption peak versus 414 nm. (a) BX QYs of single NCs excited at 514 nm versus 414 nm for sample QD593. (b) BX QYs of single NCs excited at 580 nm versus 414 nm for sample QD624. The dashed lines are along the diagonal of the plots. Points fall above the dashed lines indicate the BX QY of the NC excited at the second absorption peak is higher than excited at 414 nm.

As discussed previously by Nair et al., the change in BX QY is attributed to the change in the non-radiative decay rate of the BX.²⁴ In this letter, we propose that the BX recombines non-radiatively through either the Auger or trapping mechanisms. Therefore, we discuss the effect of excitation wavelength on the two mechanisms individually. Previous studies demonstrate that when a NC is excited by a photon with energy higher than the band-edge, the exciton quickly relaxes to its band-edge through thermalization processes, the rate of which is much faster than the Auger rate.³⁹ Therefore, the Auger rate of BX recombination should not be affected by which electronic state the NC is excited into. For the multiple NRC model, k_tr is dependent upon the number of available trapping sites. While for the multiple charging model, the QY of BX_SS depends on how deep the holes are trapped. In our experiments, at 414 nm excitation, higher energy trapping sites including CdS surface states are more easily accessed (see schematic illustration in Fig. 7). Therefore, one would expect k_tr at 414 nm excitation to be faster than k_tr at the excitation of the NC’s second absorption peak or the holes are more deeply trapped at 414 nm excitation, leading to a lower BX QY at 414 nm than at 514 nm for QD593 or 580 nm for QD624. Our results suggest this is the case for most NCs. The excitation wavelength has a bigger effect on the NCs with high BX QYs (> 0.1). In these NCs, the trapping process is relatively slow, meaning that there are fewer or shallower trapping sites available than for the NCs with a low BX QY. The change in the number or depth of trapping sites when excited at 414 nm has a relatively bigger effect on the trapping process, which results in a bigger difference in the BX QY, consistent with our observation.

Figure 7.

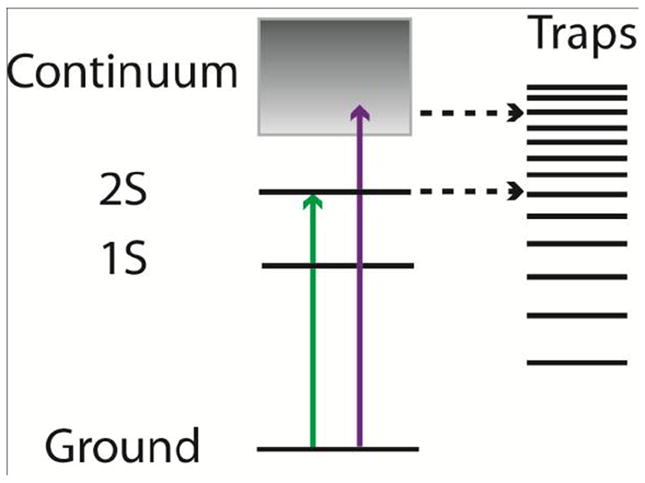
Schematic illustration of the excitation and trapping processes in NCs. Green and purple arrows represent different excitation wavelengths. For the lower energy excitation (green), fewer trap states are accessible compared to higher energy excitation (purple).

CONCLUSIONS

In conclusion, we study BX recombination in single CdSe(CdS) NCs by exploring the relationship between the “on” fraction and BX QYs, and the effect of excitation wavelengths on BX QYs. We observe a weak correlation between “on” fraction and BX QYs. Specifically, low BX QYs were observed in NCs with a low “on” fraction. However, for NCs with a high “on” fraction, the BX QYs vary dramatically from undetectable to as high as ~ 0.4-0.5. Moreover, we found that the BX QYs of single NCs weakly depend on the excitation wavelength. The BX QYs of NCs excited at shorter wavelengths are lower than for excitation at longer wavelengths. We propose a model for BX recombination that involves both Auger and trap-assisted recombination through multiple non-radiative recombination centers or surface trapping sites with a distribution of energies.