Abstract
The conformations and stabilities of the β-hairpin model peptides of Waters1,2 have been experimentally characterized as a function of lysine ε-methylation. These models were developed to explore molecular recognition of known epigenetic recognition motifs. This system offered an opportunity to computationally examine the role of cation-π interactions, desolvation of the ε-methylated ammonium groups, and aromatic/aromatic interactions on the observed differences in NMR spectra. AMOEBA, a second-generation force field4, was chosen as it includes both multipole electrostatics and polarizability thought to be essential to accurately characterize such interactions. Independent parameterization of ε-methylated amines was required from which aqueous solvation free energies were estimated and shown to agree with literature values. Molecular dynamics simulations (100 ns) using the derived parameters with model peptides, such as Ac-R-W-V-W-V-N-G-Orn-K(Me)n -I-L-Q-NH2, where n = 0, 1, 2, or 3, were conducted in explicit solvent. Distances between the centers of the indole rings of the two-tryptophan residues, 2 and 4, and the ε-methylated ammonium group on Lys-9 as well as the distance between the N- and C-termini were monitored to estimate the strength and orientation of the cation-π and aromatic/aromatic interactions. In agreement with the experimental data, the stability of the β-hairpin increased significantly with lysine ε-methylation. The ability of MD simulations to reproduce the observed NOEs for the four peptides was further estimated for the monopole-based force fields, AMBER, CHARMM, and OPLSAA. AMOEBA correctly predicted over 80% of the observed NOEs for all four peptides, while the three-monopole force fields were 40–50% predictive in only two cases and approximately 10% in the other ten examples. Preliminary analysis suggests that the decreased cost of desolvation of the substituted ammonium group significantly compensated for the reduced cation-π interaction resulting from the increased separation due to steric bulk of the ε-methylated amines.
INTRODUCTION
Cation-π interactions play a vital role in biomolecular recognition. Interactions between basic and aromatic side chains have been shown to contribute to folding in natural and de novo designed proteins as well as small structured peptides5–10. Interactions between small molecules and proteins are also mediated by cation-π interactions11–14. Perhaps, the best studied system in which a small molecule, acetylcholine, is selectively hydrolyzed by the enzyme acetylcholinesterase, depends on diffusion of the charged tetramethylammonium group of choline down a long tunnel of aromatic residues to the active site15,16. In one well-studied example of the role of cation-π interactions in protein/protein recognition17, the photoactivated rhodopsin-bound conformation of an undecapeptide was shown to be folded with an almost ideal cation-π interaction18. The ε-nitrogen of lysine was ideally located above the phenyl ring of the phenylalanine and also salt bridged with the C-terminal carboxyl group. As such, this provided a unique experimental system to probe the relative contributions of the cation-π and salt-bridge interactions to the conformational stability19,20. This receptor-bound conformation has recently been independently confirmed by DEER spectroscopy21.
Molecular Recognition in Epigenetics
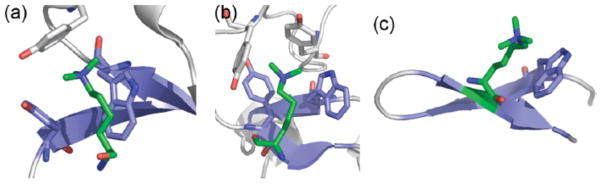
Some protein-protein interactions that control gene expression are recognized by a cation-π interaction between trimethyllysine (KMe3, where methylation is on the ε-amino group) and an aromatic pocket8,22–24. Incorporation of methylated lysine residues at specific locations of the histone tails facilitates recruitment of chromatin remodeling proteins regulating chromatin condensation and gene expression22. Proteins involved in chromatin remodeling, including chromodomains, PHD domains, and Tudor domains, recognize and bind the histone ε-trimethylated lysine with an aromatic cage made up of three or four aromatic rings23,24, for example, KMe3 of histone 3A bound to the aromatic pocket containing two tyrosines and a tryptophan of the HP1 chromodomain (PDB code: 1KNE, Fig. 2a). The stabilizing forces between the ε-methylated lysine and its aromatic binding pocket are driven by cation-π and van der Waals interaction (Figure 1)8,23,24. Model peptides to investigate interactions of methylated lysines were developed by Rieman and Waters based on known biological systems of epigenetic recognition1. In each case of the four model β-hairpin peptides of this study, two of the aromatic residues reside within a β- sheet, forming a cleft for the modified lysine side chains (Fig. 2).
Figure 2.
(a) Structure of the aromatic binding pocket of the HP1 chromodomain bound to a histone peptide containing trimethyllysine (KMe3, green); β-sheet structure is shown in blue (PDB 1KNE). (b) Structure of the aromatic binding pocket of the BPTF PHD domain bound to a histone peptide containing KMe3 (green); β-sheet structure is shown in blue (PDB 2FUU). (c) NMR structure of the β-hairpin peptide WKMe3 indicating the cation-π interaction between Trp and KMe3 (green); β-sheet
Figure 1.
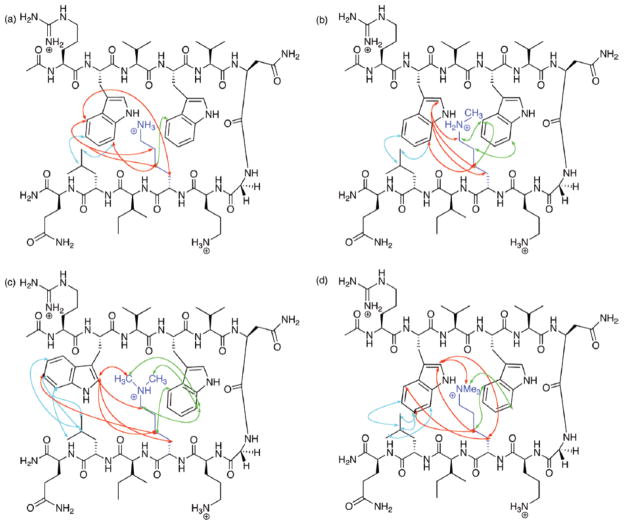
Diagnostic NOEs observed by Rieman and Waters1 in the series of four peptides differing by the degree of lysine-9 ε-N-methylation. Upper left = Lys; Upper right = Lys(Me); Lower left = Lys(Me2); Lower right = Lys(Me3). Red arrows indicate NOEs between Lys(Me)n and Trp2; green arrows indicate NOEs between Lys(Me)n and Trp4; cyan arrows indicate NOEs between Lys(Me)n and Leu11.
Gas-phase models of cation-π interactions
A prototypical example of a cation-π system is a single monoatomic ion interacting with a benzene molecule in the gas phase9. For example, a classic study from Kebarle’s group determined an experimental standard-state interaction enthalpy (ΔH) of −18.3 kcal/mol for the K+-benzene system25 via molecular beam-mass spectrometry methods. Amicangelo and Armentrout26 used threshold collision-induced dissociation (TCID) experiments to obtain ΔH = −17.5 kcal/mol for K+-benzene. Quantum mechanical estimation of this cation-π interaction energy (ΔE) exhibits only a relatively weak dependence on basis set and level of theory. Amunugama and Rodgers27 reported ΔE = −18.5 kcal/mol at MP2/6-311+G(2d,2p), while Feller, et al.28 obtained ΔE = −20.6 kcal/mol and ΔH = −20.1 kcal/mol at CCSD(T)/CBS. Standard fixed charge force field models, such as CHARMM, Amber and OPLS-AA, use ion parameters fit to reproduce liquid phase ion hydration and benzene parameters reasonable for liquid benzene. Due to the neglect of polarization, these parameters underestimate the strength of the K+-benzene interaction. Simple energy minimization yields interaction energies of −9.3 kcal/mol (OPLS-AA), −11.1 kcal/mol (CHARMM22) and −12.6 kcal/mol (Amber ff99). The AMOEBA force field yields an interaction energy of − 20.6 kcal/mol and a corresponding ΔH of −19.4 kcal/mol. In AMOEBA, roughly half of the overall attraction arises from polarization terms. Experimental results for the similar-sized NH4+ ion provide a NH4+-benzene enthalpy of −19.3 kcal/mol29, while AMOEBA dynamics simulation gives ΔH = −19.0 kcal/mol for this system.
Strength of cation-π interactions
The role of cation-π interactions in molecular recognition has been a topic of some controversy. In particular, the relative strength of cation-π interactions compared with salt bridges has produced significant disagreement between theoretical and experimental estimates19. Theoretical studies by Gallivan and Dougherty30 suggested that a cation-π interaction in solvent with a protein-like dielectric (ethyl acetate, ε~5.99) contribute maximally −6.2 kcal/mol to the free energy (ΔG) of the system. By their calculations, the cation-π interaction was relatively insensitive to dielectric since the calculated value in water (ε~78) was only reduced to −5.5 kcal/mol. The value for the salt bridge, however, was −19.7 kcal/mol in ethyl acetate and reduced to −2.2 kcal/mol in water in agreement with Coulomb’s law. Additional gas-phase calculations by Mo et al.31 estimated the intermolecular interaction energy at between −6 and −12 kcal/mol for a series of nonbonded complexes of N-substituted piperidines and substituted monocyclic aromatics and suggested that the interaction had significant polarization and charge-transfer components. The procedure used in both cases, however, compared a charged state for the cation-π interaction with a neutral state for the salt bridge19.
On the other hand, Hunter et al.32,33 estimated the energy of a pyridinium cation-π interaction in chloroform (ε~4–5) at only −2.5 ±0.4 kJ/mol or −0.6 ±0.1 kcal/mol by a chemical double-mutant cycle, in agreement with experimental studies on the modeled system. Bartoli and Roelens34 showed both experimentally and computationally that the counteranion has a dramatic effect on the strength of the interaction in a cation-π interaction in a model lipophilic cyclophane system with a series of tetramethylammonium (TMA) and acetylcholine salts in CDCl3. The charge dispersion on the anion was a major factor in determining the influence of the anion on the strength of the cation-π interaction. An anion with a diffuse negative charge such as picrate yielded a ΔG of approximately −2 kcal/mol for the cation-π interaction in chloroform, but an anion with a more concentrated charge such as acetate limited the ΔG of the interaction to approximately −0.6 kcal/mol in CDCl3.
Experimental estimates of the interaction strength of cation-π interactions
The most thorough experimental estimates of cation-π strengths have come from model peptide studies. Such studies often focus on helix or β-hairpin35 model peptides whose relative stabilities as a function of amino acid sequence can be quantitated. Fernandez-Recio et al.36 studied the interaction between tryptophan and histidine pairs in either the i and i + 3 or i and i +4 positions in an α-helix. Helix stabilization was only seen with Trp/His+ in the i/i + 4 orientation and estimated at -1 kcal/mol. Tsou et al.37 estimated the extent of α-helix stabilization by the interaction between a protonated amine (lysine, ornithine, and diaminobutyric acid) and the phenyl ring of phenylalanine in water as −0.4 kcal/mol, seen only in the Phe-Orn case. Similar studies using a designed β-hairpin to orient the interacting residues measured interaction energies between Phe or Trp and Lys or Arg in diagonal positions on the β-hairpin at between −0.20 and −0.48 kcal/mol38. It has been suggested that observed cation-π interactions are more hydrophobic in nature than electrostatic. Slutsky and Marsh39 used a model coil-coil peptide to estimate the interaction between Arg and Phe/Trp/Tyr. Only the Arg/Phe combination proved more stable than the control, Lys/Glu, and the authors suggested that hydrophobic packing of Arg side-chain methylenes rather than a cation-π interaction was responsible. Other studies by Andrew et al.40 of interactions between Val/Ile and Lys/Arg in the i and i + 4 positions found helix stabilizations between −0.14 and −0.32 kcal/mol. In addition, the nonpolar/polar pairs Ile-Lys, Ile-Arg, and Val-Lys occur in protein helices more often than expected. Phe-Lys, Lys-Phe, Phe-Arg, Arg-Phe, and Tyr-Lys were all stabilizing by −0.10 to −0.18 kcal/mol when placed i, i + 4 on the surface of a helix in aqueous solution. The similarity in the experimental values for helix stabilization between non-aromatic hydrophobic side chains such as Val and Ile and aromatic side chains with Arg and Lys suggest that much of the stabilization energy measured for aromatic residues with Lys/Arg may simply arise from hydrophobic forces rather than cation-π stabilization alone. Tatko and Waters, however, compared6 the interaction of norleucine (Nle) and Lys with Phe, Trp, or Cha (R-cyclohexylalanine) in the diagonal positions of a designed β-hairpin and found that interaction energies between Lys and Phe or Trp were between −0.2 and −0.4 kcal/mol. The interaction energies between Nle and Phe or Trp were slightly less favorable (−0.1 to −0.2 kcal/mol). The NMR and thermal denaturation studies showed that the Lys side chain interacts in a specific manner with Phe or Trp through the polarized Cε, and Nle does not interact in a specific manner with either aromatic side chain. These results indicate that Lys and Nle interact in fundamentally different ways with aromatic residues, arguing that observed cation-π interactions were not predominately hydrophobic in nature.
The debate about the strength of cation-π interactions and their role in protein/peptide folding is ongoing and multifaceted; while there is little doubt about the importance of the cation-π interaction among non-covalent forces, considerable controversy still exists in the literature regarding the relative strengths of such interactions. The large differences in energetics predicted by calculations and the question of the relative strengths of cation-π versus salt-bridge interactions prompted a detailed computational analysis of the best-characterized experimental system of β-hairpins developed by the Waters group1,41–43, one of the most robust for experimentally probing the strength of cation-π interactions. In particular, the papers of Rieman and Waters describing the syntheses and physical-chemical characterization of two different sequences of dodecameric peptides that form β-hairpins differing only in the degree of lysine ε-methylation1,41 (Fig. 1) and another by Hughes et al. describing the impact of shortening the lysine side chain by one or two methylenes for a similar series of ε-N-methylated peptides2 provided excellent biophysical characterizations. This characterization of peptide conformations afforded an excellent opportunity for molecular dynamics simulations in explicit solvent to examine in detail the fundamental basis of differences in stability with direct comparison to precise experimental characterization. One might speculate that the enhanced lipophilicity of the methylated ammonium groups would be counter-balanced by a decrease in the cation-π interaction due to delocalization of the charge and steric repulsion of the N-methyls by the indole rings. In order to computationally characterize these peptides, a second-generation force field AMOEBA was chosen as it includes multipole electrostatics and polarizability4. Limitations of monopole electrostatics in reproducing the geometries of aromatic interactions are well-known44. The AMOEBA force field has been validated by numerous studies comparing calculated structures with high-resolution experimental data4. In particular, the relative solvation free energies of protonated ammonium, methyl ammonium, dimethyl ammonium and trimethyl ammonium were calculated with AMOEBA4 after parameterization in this study and shown to agree with experimental estimates as well as those calculated by Kelley et al. using the SM6 continuum-solvation model (7).
METHODS
Parameterization of methylammonium series
Most of the ε-methylated lysine parameters were transferred from the existing AMOEBA force field for proteins and small organic molecules. The –N-CH3 group related torsion and vdW parameters did not exist in the current parameters and were developed with methylammonium-ion model compounds. The vdW parameters of –NH- atoms in the ε-methylated lysine were adjusted to reproduce the methylammonium ion-water dimer hydrogen bond structure optimized at MP2 level with the 6-311++G(d, p) basis set using Gaussian 09, Revision A.0261. Then the HCNC torsion in ε-methyl-lysine and CCNC torsion parameters in ε-mono-, di-, tri-methyl-lysine residues were fit to the ab initio potential energy surfaces obtained with MP2/6-31G* calculations. The potential surfaces were reproduced by restrained optimization while fixing the specific torsions examined. Torsional parameter fitting was carried out with TINKER TORSFIT program45.
The electrostatic parameters for the ε-methylated lysine dipeptides (lysine capped with N-methylamide and acetyl groups) were derived with Stone’s distributed multipole analysis program GDMA46 and TINKER POLEDIT45. DMA was set to the original setting for calculating multipoles with the fully analytical integrals (set parameter SWITCH in GDMA 2.x to 0). The wave functions were from MP2/6-311G(d, p) calculations. Then the AMOEBA electrostatic potentials around the methylated lysines were validated with the TINKER POTENTIAL program45. Potential grids were 1.0 Å distant from the vdW shell of each atom. There were 5 layers of grids spherically and uniformly distributed around the molecule with a spacing of 0.35 Å between the layers on which comparative electrostatic potentials were calculated (for a more detailed description of current AMOEBA parameterization, see Ren et al.47)
Molecular dynamics simulations
All MD simulations were preformed at the Washington University High-Performance Computing Facility. The group of Prof. Pengyu Ren of the Department of Biomedical Engineering at the University of Texas assisted Mr. Malcolm Tobias and Dr. Xiange Zheng in installing their version (PMEMD) of AMOEBA4 on the IBM supercomputer cluster. The β-hairpin systems were solvated with water, and neutralized with Na+ and Cl− counter-ions. The fully solvated systems contained between 7460–7661 atoms depending on the degree of methylation. The MD simulations were undertaken with periodic boundary conditions using both the NAMD version 2.6b148 and PMEMD49 simulation package. Particle-mesh Ewald (PME)50 was used to account for long-range electrostatics interactions.
PMEMD is the parallel version of AMBER49 module Sander; a customized version of PMEMD from Prof. Pengyu Ren’s group at the University of Texas, which incorporated the multipole, polarizable force field AMOEBA4, was utilized in this work. Each system was prepared in the following steps before the production MD run: 1) minimization to 0.1 Debye with a restraint of 500.0 kcal/mol/Å2 applied to the protein; 2) minimization to 0.01 Debye with a restraint of 100.0 kcal/mol/Å2 applied to the protein; 3) minimization to 0.01 Debye with restraint removed; 4) heating from 0 to 300 K for 50 ps and equilibration for 25 ps with protein restrained by 2.0 kcal/mol/Å2; 5) equilibration for 200 ps with restraint removed. Subsequently, The MD simulations were performed for 100 ns with a 1fs time step, and trajectories were saved every 20 ps. A non-bonded cutoff of 12 Å was applied in the PMEMD simulations.
MD Simulations using NAMD
To determine the utility of multipole electrostatics and polarization, simulations were also performed with the NAMD program using several monopole, non-polarizable force field, including the CHARMM22 Proteins51, AMBER49, and OPLS52. Each system was solvated with a 12 Å water box using the TIP3P water model53 and neutralized with an ionic strength of 40 mM NaCl. The parameters and settings used in all simulations with different force fields were as follows: 1), the isothermal-adiabatic ensemble (NPT) at 1 atm pressure, using the Nosé-Hoover Langevin piston54 with a decay period of 200 fs (damping timescale of 100 fs for heating and equilibration phases and 500 fs for production phase); 2), a bond-interactions calculation frequency of 2 fs, short-range electrostatics and van der Waals-interactions frequency of 2 fs, with 10.0 Å as cutoff and 8.5 Å as smooth switching; 3), long-range computing frequency of 4 fs, with PME grid points at least 1 Å in all directions, and 4), rigidBonds applied to constrain all bonds between hydrogens and heavy atoms. Minimization, heating and equilibration were performed prior to the MD run in order to eliminate steric clashes, minimize water-protein interactions, and stabilize the solvated systems. A time step of 1 fs was used in minimization while 2 fs in heating and equilibration. Other parameters utilized in these steps include: 1), minimization of the system for 6 ps with backbone atoms fixed followed by another 6 ps with the constraints removed; 2), heating the system from 0 to 300 K in 75 K intervals, each for 16 ps; with restraints applied on C-alpha atoms; 3), equilibrating the system for 80 ps with C-alpha atoms restrained followed by another 600 ps with all restraints removed. The MD simulations were then resumed as production runs for 100 ns.
Force-field preparation and parameterization of non-standard residues
Parameterization methodology of the methylated lysine residues for the AMOEBA force field is described in detail below. In simulations using the NAMD package, three types of force field were used: AMBER, CHARMM, and OPLSAA. In the CHARMM force field, the parameters of non-standard residues were transferred from similar atom types of the lysine residue in the same force field. With the AMBER force field, the two input files required by NAMD - the topology/parameter file (.prmtop) and initial coordinate file (.inpcrd) – as well as the parameters of non-standard residues, were prepared using the xleap module and the leaprc.ff10 force field of AMBER 1155. The CHARMM-format OPLS-AA force field of standard residues was obtained from Mackerell’s charmm tarball (http://mackerell.umaryland.edu/CHARMM_ff_params.html) that was included in the c35b2 and c36a2 release of the CHARMM program and derived from the Jorgensen’s original OPLS force field52. The OPLS-AA parameters for non-standard residues were implemented manually: their RESP charges were derived from QM calculations performed for the AMOEBA parameters, and valence and vdW parameters transferred to similar atom types of the regular lysine residue in the CHARMM force field.
Analyses of MD simulations
The primary source for experimental validation was the NMR experimental NOE studies monitoring the stability of the β-hairpin structure with the cation-π and aromatic/aromatic interactions between the two indole rings (Trp-2 and Trp-4) and the ε-methylated ammonium groups of Lys-9 that were essential. For this reason, the distances between the α-carbons of the C- and N-terminal residues of the peptide were monitored as well as distances between the protonated nitrogen of Lys(Me)n, where n = 0 to 3 and the centers of mass of the two indole rings of Trp-2 and Trp-4. In addition, the MD simulations were evaluated with regards to their ability to predict the diagnostics NOEs for the four model peptides reported by Rieman and Waters1 (Fig. 1).
RESULTS AND DISCUSSION
MD simulations of the ε-methylated-lysine series of β-hairpin models of Waters1,2 have been conducted with multiple force fields in explicit solvent. The use of AMOEBA was essential since it includes both multipole electrostatic and polarizability that were crucial in reproducing the physics of electrostatic in the cation–π and aromatic/aromatic interactions. One possible limitation in this study was the length of the MD simulations achieved to adequately sample conformational transitions. Because of the enhanced complexity of energetic interactions with the AMOEBA multipole potentials compared with those using simpler monopole electrostatics, AMOEBA requires significantly longer computational times for the same simulation.
AMOEBA Force-Field Parameterization
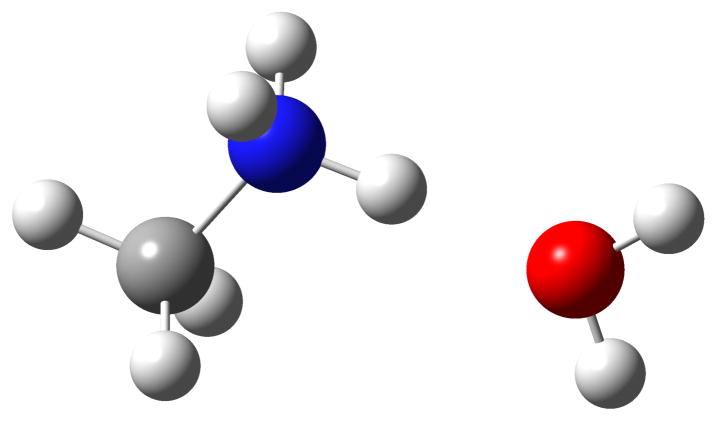
The first priority was AMOEBA parameterization of the ε-methylated amines of lysine. We used mono- through tetramethylammonium ions to model the ε-methylated lysines for parameterizing necessary vdW and valence parameters. The vdW parameterization results for the N and the polar H atoms in methylammonium are shown in Table 1. The model compound here was methylammonium ion. It interacted with water at the N-H side. The hydrogen bond energy is for the dimer with N-H---O hydrogen bond (Fig. 3).
Table 1.
Methylammonium Ion --- Water Dimer Results after adjusting N and HN vdW Parameters.
| QM (MP2/6-311++G** opt., MP2/aug-cc-pVTZ single point with BSSE) | AMOEBA | |
|---|---|---|
| N(MeAm+)-O(water) | 2.75 Angstrom | 2.78 Angstrom |
| C(MeAm+)-O(water) | 3.50 Angstrom | 3.53 Angstrom |
| Intermolecular Energy | −18.30 kcal/mol (after BSSE) −18.92 kcal/mol (before BSSE) |
−18.74 kcal/mol |
Figure 3.
Methylammonium Ion -Water Dimer.
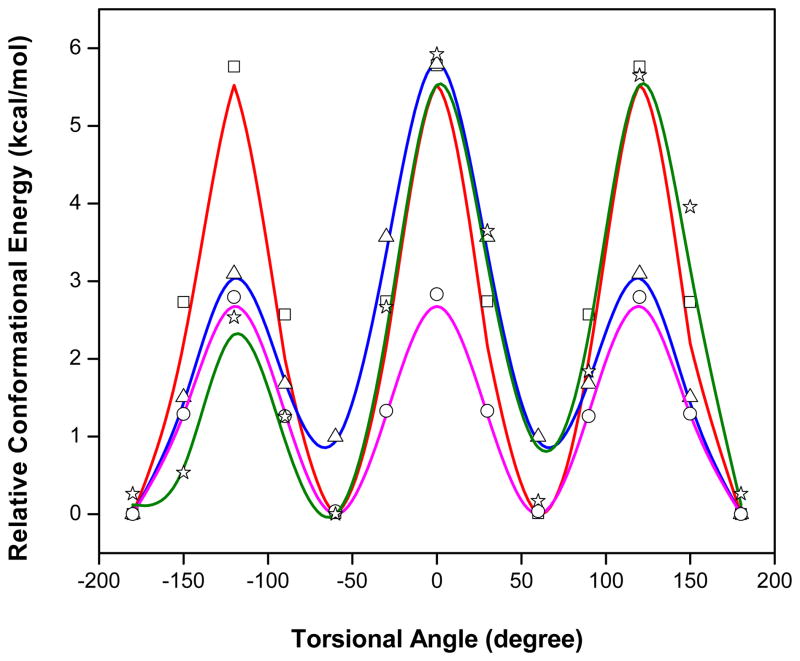
AMOEBA gave excellent agreement with the QM results for both structure and energetics. The necessary torsional fitting shown in Figure 4. Lys(Me) was represented by a dimethylammonium ion, Lys(Me2) was represented by the trimethylammonium ion, and Lys(Me3) was represented by the tetramethylammonium ion.
Figure 4.
Torsional parameters for methylated ammoniums. Lines = QM potential-energy plots. Symbols = AMOEBA energies for the corresponding conformations. C-N-CH torsion in dimethylammonium, RMSD = 0.07 kcal/mol; (blue line, triangle): CCNC torsion in dimethylammonium, RMSD = 0.13 kcal/mol; (green line, star): CCNC torsion in trimethylammonium, RMSD = 0.39 kcal/mol; (red line, square): CCNC in tetramethylammonium, RMSD = 0.40 kcal/mol (pink line, circle).
Based on Figure 4, the AMOEBA torsional potentials agreed with the QM results. C-N-C-H torsion in dimethylammonium, RMSD = 0.07 kcal/mol; (blue line, triangle): CCNC torsion in dimethylammonium, RMSD = 0.13 kcal/mol; (green line, star): CCNC torsion in trimethylammonium, RMSD = 0.39 kcal/mo; (red line, (pink line, circle). square): CCNC in tetramethylammonium, RMSD = 0.40 kcal/mol. All the RMSDs were 0.4 kcal/mol or less. This insured reliable dynamic torsional sampling during the MD simulations.
AMOEBA has recently been used to study the solvation of chloride ion56 and Zn(II)57. AMOEBA parameters for the substituted ammonium ions were first used to predict their solvation free energies. Fortunately, experimental solvation free energies for these compounds had been carefully collected by the Truhlar group3 for the series with the exception of tetramethylammonium. They also did the implicit SCRF-solvation calculation for these compounds with their SM6 model. These data provided an independent method to validate (Table 2) the AMOEBA parameters derived from quantum mechanics and distributed multipole analysis58.
Table 2.
Calculated Hydration Free Energy (kcal/mol) of Methylated Ammoniums Using AMOEBA Parameters Versus Experimental Values3
| AMOEBA | Kelley et al.3 | |||
|---|---|---|---|---|
| Absolute | Relative | Absolute* | Relative | |
| NH4+ | −73.429 | 0.0 | 180.7 | 0.0 |
| CH3NH3+ | −64.325 | 9.1 | 189.5 | 8.8 |
| (CH3)2NH2+ | −56.394 | 17.0 | 197.3 | 17.4 |
| (CH3)3NH+ | −49.336 | 24.1 | 204.8 | 24.1 |
| (CH3)4N+ | −43.215 | 30.2 | N/A | |
Absolute* = scaled relative to the solvation of a proton
As mentioned in the Method Section, the electrostatic parameters were derived directly from the QM-calculated wave functions of the ε-methylated lysine dipeptides. The potential validation results are shown in Table 3. They show an excellent reproduction of the potentials around the molecules with the newly parameterized AMOEBA force field.
Table 3.
Electrostatic Potential Validation Results for ε-Methylated Lysines
| Number of Potential Grids | Average Potential (kcal/mol/grid) | RMS (kcal/mol) | ||
|---|---|---|---|---|
| QM | AMOEBA | |||
| Lys(Me) | 22808 | 51.76 | 51.82 | 0.48 |
| Lys(Me2) | 23617 | 51.07 | 51.11 | 0.72 |
| Lys(Me3) | 24278 | 50.40 | 50.48 | 0.55 |
Parameterization of ε-methylated lysines for monopole force fields
A comparison of the ability of AMOEBA with three monopole force fields (AMBER, CHARMM and OPLS) utilizing monopole electrostatics without polarizability to predict the observed NOEs for the four peptides required similar care in parameterization of the ε-methylated lysines for the monopole force fields. The CHARMM, AMBER, and OPLS parameter charges were obtained from RESP fitting to B3LYP/cc-pVTZ potential. Torsions were validated with MP2/6-31g* potential surface (the same as for AMOEBA). The parameters and methodology used in their derivation for AMBER, CHARMM and OPLSAA parameters are available for further examination (see Supplemental Material).
In order to determine whether the lengths of the MD simulations were sufficient for adequate conformational sampling, two 100-ns MD simulations from different starting NMR conformations were run for both AMOEBA and CHARMM for all four peptide hairpins. Examination of the distribution of distances cover by the two simulations gave confidence that 100-ns MD simulations gave adequate coverage of conformational space (data not shown). Comparison of distance-distribution plots for all MD simulations were consistent with adequate sampling. In addition, visual inspection of MD runs showed significant exploration of conformational space.
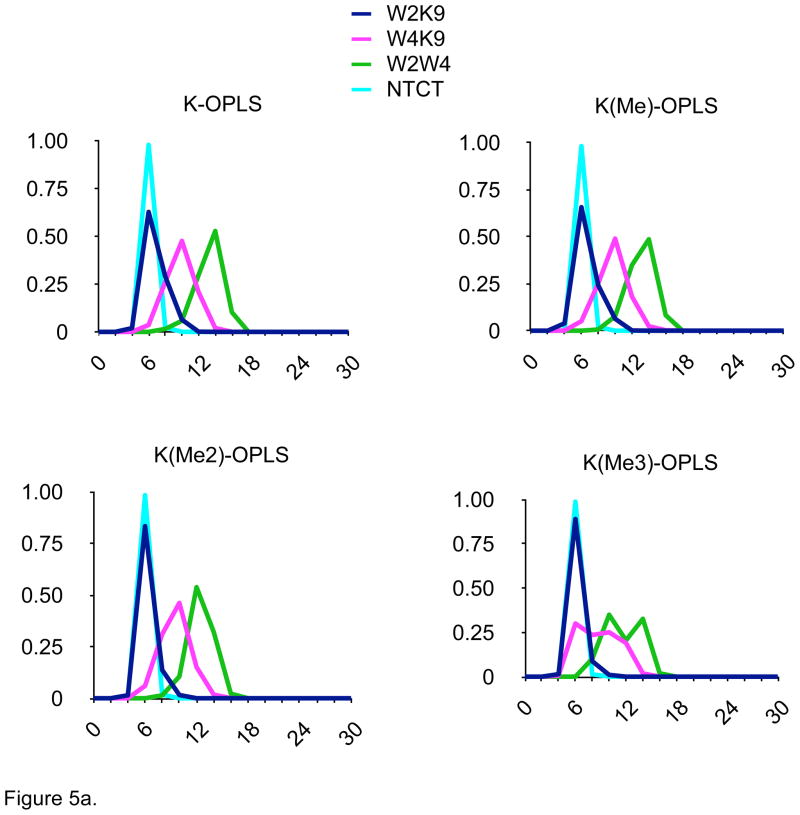
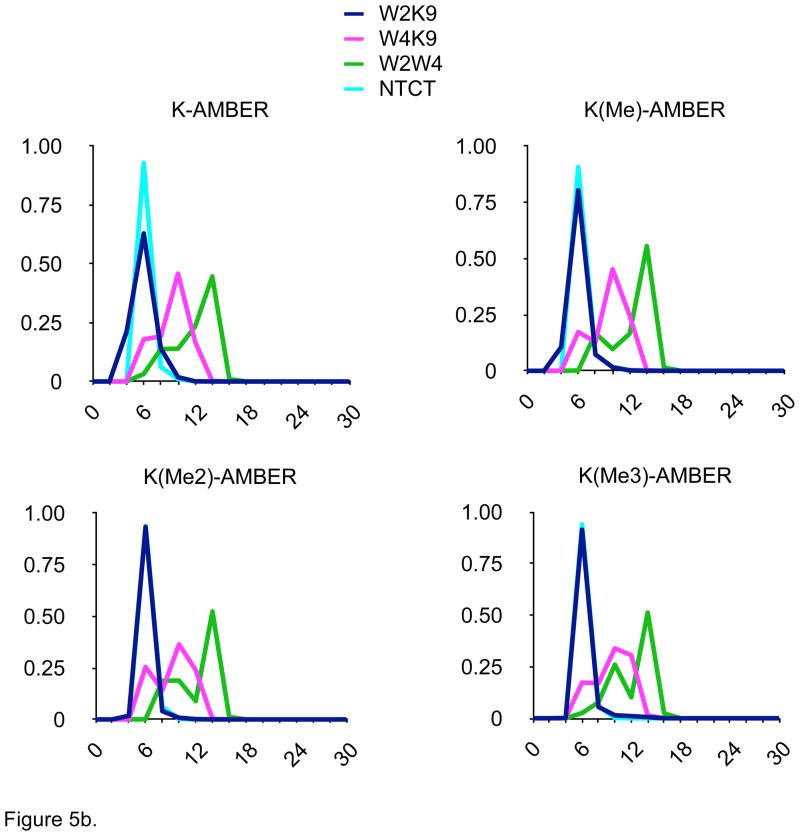
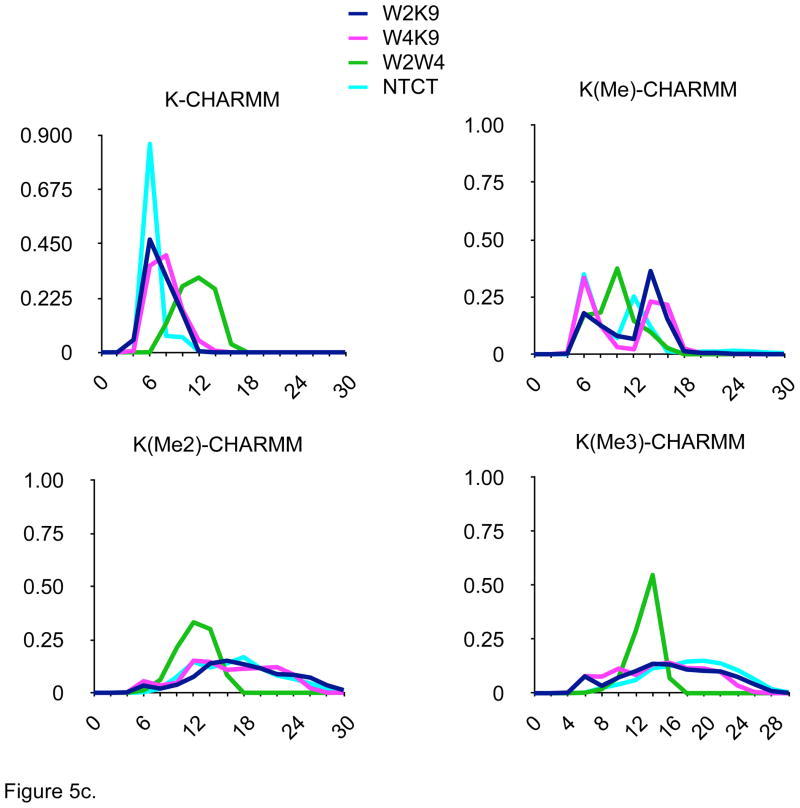
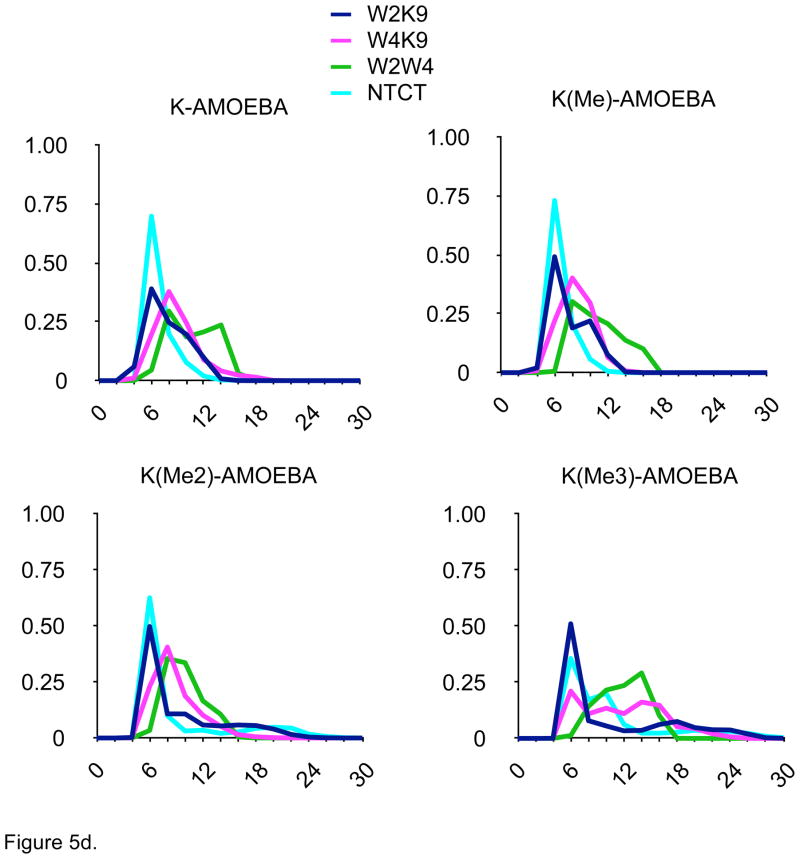
Other conformational parameters, such as N- to C-terminal carbon-alpha distances, indoles to ε-ammonium distance as well as location of turn residues, strand register, and interstrand hydrogen bonding (data not shown), were also monitored. The distance distributions determined for the four-hairpin models were quite distinct in the AMOEBA simulations (Fig. 5d) and different from the other monopole force fields (Fig. 5a–5c), but consistent with the different patterns of NOEs determined experimentally by Rieman and Waters1 (Fig. 1). In contrast, the distance distributions seen with the monopole force fields were dramatically different, especially as Lys-9 was methylated (Figs. 5b–5d). In particular, the proximity of the Lys-ε-amino group to the indole rings, especially the W2/K9 distance, was preserved across the series of methylated hairpins in the AMOEBA simulations. Increased methylation did destabilize the hairpin to some extent as estimated by changes in the distributions of N-C distances (Fig. 5d); the decreased cost of desolvation of the ε-methylated Lys-9 ammonium group would appear to significantly compensate hairpin stability for the reduced cation-π interaction resulting from the increased distance due to the steric bulk of the ε-methylated amines.
Figure 5.
Distance distributions for 100 nsec MD simulations in explicit solvent of four model β-hairpin peptides with four different force fields. W2K9 = distance between indole of Trp-2 and ε-amine of Lys-9; W2K9 = distance between indole of Trp-4 and ε-amine of Lys-9; W2W4 = distance between indoles of Trp-2 and Trp-4; NTCT = distance between carbon alphas of N- and C-terminal amino acids. Ordinate = relative percentage (%), Axis = Distance between residues (Å).
Figure 5a. Data from MD simulation with OPLSaa force field.
Figure 5b. Data from MD simulation with AMBER force field.
Figure 5c. Data from MD simulation with CHARMM force field.
Figure 5d. Data from MD simulation with AMOEBA force field.
One significant issue was the dramatic difference in distance distributions seen between the MD results for each of the three-monopole force fields. This would seem to indicate that the balance between specific intermolecular interactions has been parameterized differently for AMBER, CHARMM and OPLS to attempt to overcome limitations in the monopole approximation. These differences may help to explain the observations that the different monopole force fields favor different secondary structures.
Comparison with NMR Data
The question remaining was validation of the MD results with the experimental measurements. We analyzed differences in the MD simulations of the four peptides to determine if the NOE patterns observed by Rieman and Waters1 (Fig. 1) were consistent with the conformational ensembles observed by MD. The NOE patterns observed between the indole rings and the ε-amine of the lysine side chains (Fig. 1) seemed most diagnostic of differences in peptide dynamics and the resulting conformational ensembles as a function of lysine ε-methylation. One must realize, however, that the NOE patterns result from ensemble averages, and do not represent any unique conformer(s).
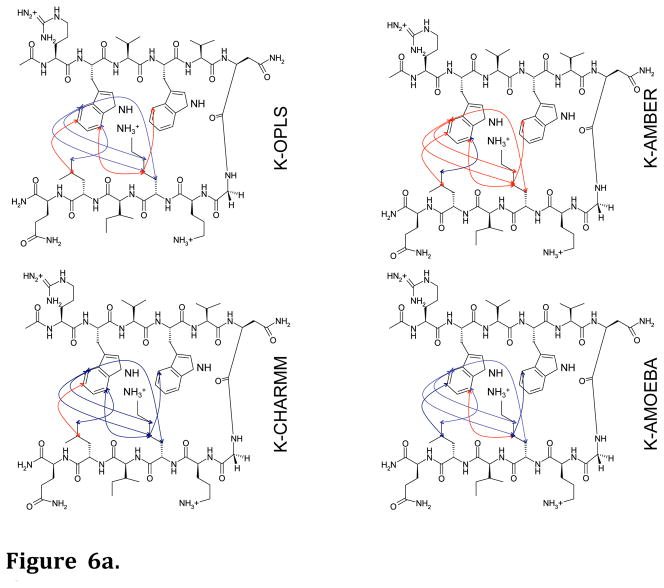
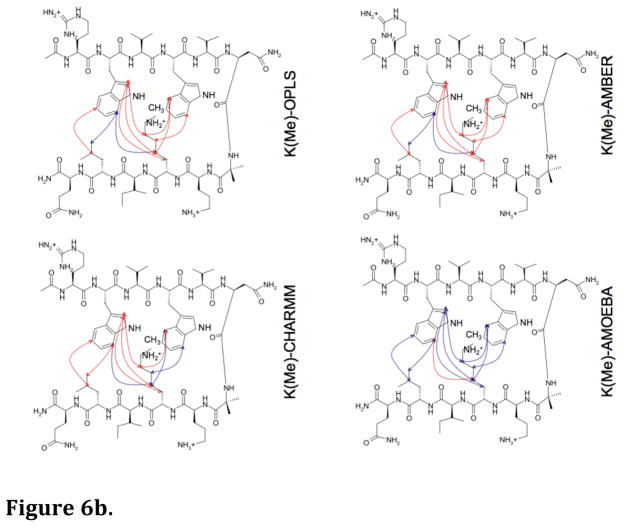
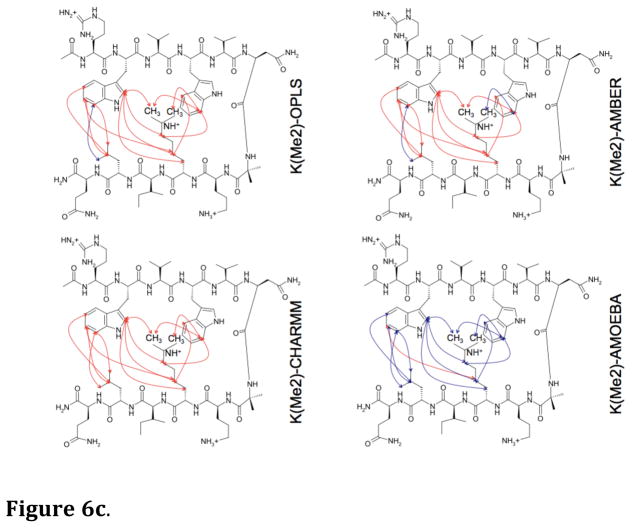
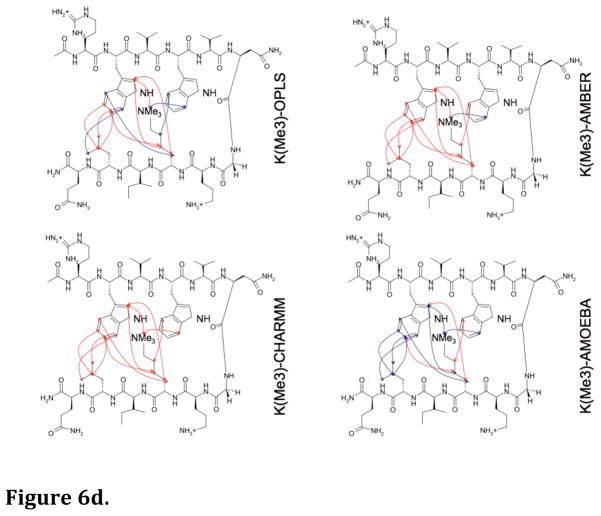
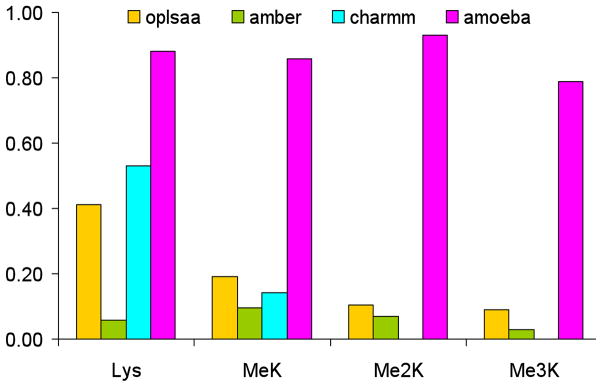
Long MD simulations (100 ns) in water were performed for each hairpin model with the four force fields. From the MD simulations, the predicted NOEs were estimated by weighting interatomic proton positions by 1/r6 in accord with previous approaches59,60. The predictability of the observed NOEs by each of the four force fields for each of the four hairpin peptides is shown in Figures 6a–6d. It is apparent that AMOEBA generates a conformational ensemble during the MD simulations that, to a first approximation, resembles that observed experimentally regardless of the amount of lysine ε-methylation (Fig. 7). The monopole force fields do not, presumably due to their inability to reproduce the complex electrostatics of aromatic interactions. What is even more perplexing is the lack of convergence of the different monopole force fields in their predictions (Fig. 6a–6d, Fig. 7, Suppl. Fig. 1a–1d). This again suggests that the parameters developed for each monopole force field may have chosen different weightings of intermolecular forces. Supplemental Figures 1a–1d show the overlap between NOEs predicted by the four different force fields (including NOEs predicted and not observed) and the experimentally measured NOEs for the four model hairpin peptides. Again, the variance in prediction by the three-monopole force fields is consistent with fundamental differences in parameter weights between them.
Figure 6.
Figure 6a. Diagnostic NOEs predicted by MD simulations for the Lys-9 peptide. Blue lines = correctly predicted NOEs; red lines = experimental NOEs that were not predicted.
Figure 6b. Diagnostic NOEs predicted by MD simulations for the Lys(Me)-containing peptide. Blue lines = correctly predicted NOEs; red lines = experimental NOEs that were not predicted.
Figure 6c. Diagnostic NOEs predicted by MD simulations on the hairpin peptide containing Lys(Me2). Blue lines = correctly predicted NOEs; red lines = experimental NOEs that were not predicted.
Figure 6d. Diagnostic NOEs predicted by MD simulations for the Lys(Me3)-containing peptide. Blue lines = correctly predicted NOEs; red lines = experimental NOEs that were not predicted.
Figure 7.
Summary of the percentage of experimentally observed NOEs for the four model b-hairpin peptides predicted by 100 nsec MD simulation in explicit solvent by the four force fields compared.
Conclusions
The agreement between predicted and observed NOEs for these four β-hairpin model peptides, where the dynamics of systems with aromatic/aromatic and cation-π interactions are crucial, requires both an accurate force field as well as adequate conformational sampling. The inability of the three force fields using monopole electrostatics in common use raises serious questions regarding any conclusions from molecular simulations where dynamics are crucial. In particular, molecular modeling studies of one recognition motifs of epigenetics, ε-methylated lysines, can be studied with second-generation force fields that consider multipole electrostatics and polarizability. While the agreement between the NOEs predicted by the MD simulations with AMOEBA are impressive and demonstrate the necessity for more complex electrostatics in dealing with aromatic/aromatic and cation-π interactions, the lack of complete agreement raises a question. Is this an indication of a need for further improvement in the parameterization of AMOEBA, or simply minor experimental error in the NMR experiments. In order to address this question, the four peptides will be resynthesized, and additional NMR experiments will be performed to provide further relaxation data for validation.
Supplementary Material
Supplemental Figure 1. Comparison of Experimental (dark blue) NOEs with predicted NOEs from 100 nsec MD simulations in explicit solvent.
Supplemental Figure 1b. Data for Lys(Me)-9 hairpin model.
Supplemental Figure 1c. Data for Lys(Me2)-9 hairpin model.
Supplemental Figure 1d. Data for Lys(Me3)-9 hairpin model.
Acknowledgments
XZ and GRM acknowledge support by contract HDTRA1-08-C-0015 from the Department of Defense. CW and JWP acknowledge support from NSF (CHE-0535675) and NIH (R01-GM6955302). Discussions with Prof. Marcey L. Waters of the Department of Chemistry at the University of North Carolina, whose lab developed the model hairpin peptide system and measured the experimental NOEs, were extremely helpful.
Footnotes
Supporting Information Available: ε-Methylated lysine parameters for the AMOEBA, OPLS-AA and Amber force fields in TINKER format are available online. This information is available free of charge via the internet at http://pubs.acs.org.
References
- 1.Riemen AJ, Waters ML. Biochemistry. 2009;48:1525. doi: 10.1021/bi801706k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hughes RM, Benshoff ML, Waters ML. Chemistry. 2007;13:5753. doi: 10.1002/chem.200601753. [DOI] [PubMed] [Google Scholar]
- 3.Kelly CP, Cramer CJ, Truhlar DG. J Phys Chem B. 2006;110:16066. doi: 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
- 4.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Jr, Head-Gordon M, Clark GN, Johnson ME, Head-Gordon T. J Phys Chem B. 2010;114:2549. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tatko CD, Waters ML. Protein Sci. 2003;12:2443. doi: 10.1110/ps.03284003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tatko CD, Waters ML. J Am Chem Soc. 2004;126:7. doi: 10.1021/ja038258n. [DOI] [PubMed] [Google Scholar]
- 7.Hughes RM, Waters ML. J Am Chem Soc. 2005;127:6518. doi: 10.1021/ja0507259. [DOI] [PubMed] [Google Scholar]
- 8.Hughes RM, Wiggins KR, Khorasanizadeh S, Waters ML. Proc Natl Acad Sci U S A. 2007;104:11184. doi: 10.1073/pnas.0610850104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ma JC, Dougherty DA. Chem Rev. 1997;97:1303. doi: 10.1021/cr9603744. [DOI] [PubMed] [Google Scholar]
- 10.Gallivan JP, Dougherty DA. Proc Natl Acad Sci USA. 1999;96:9459. doi: 10.1073/pnas.96.17.9459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Scharer K, Morgenthaler M, Paulini R, Obst-Sander U, Banner DW, Schlatter D, Benz J, Stihle M, Diederich F. Angew Chem, Int Ed. 2005;44:4400. doi: 10.1002/anie.200500883. [DOI] [PubMed] [Google Scholar]
- 12.Kearney PC, Mizoue LS, Kumpf RA, Forman JE, McCurdy AE, Dougherty DA. J Am Chem Soc. 1993;115:9907. [Google Scholar]
- 13.McCurdy A, Dougherty DA. J Am Chem Soc. 1992;114:10314. [Google Scholar]
- 14.Dai QH, Tommos C, Fuentes EJ, Blomberg MR, Dutton PL, Wand AJ. J Am Chem Soc. 2002;124:10952. doi: 10.1021/ja0264201. [DOI] [PubMed] [Google Scholar]
- 15.Bourne Y, Radic Z, Sulzenbacher G, Kim E, Taylor P, Marchot P. J Biol Chem. 2006;281:29256. doi: 10.1074/jbc.M603018200. [DOI] [PubMed] [Google Scholar]
- 16.Dvir H, Silman I, Harel M, Rosenberry TL, Sussman JL. Chem Biol Interact. 2010;187:10. doi: 10.1016/j.cbi.2010.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Crowley PB, Golovin A. Proteins. 2005;59:231. doi: 10.1002/prot.20417. [DOI] [PubMed] [Google Scholar]
- 18.Kisselev OG, Kao J, Ponder JW, Fann YC, Gautam N, Marshall GR. Proc Natl Acad Sci USA. 1998;95:4270. doi: 10.1073/pnas.95.8.4270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Anderson MA, Ogbay B, Arimoto R, Sha W, Kisselev OG, Cistola DP, Marshall GR. J Am Chem Soc. 2006;128:7531. doi: 10.1021/ja058513z. [DOI] [PubMed] [Google Scholar]
- 20.Anderson MA, Ogbay B, Kisselev OG, Cistola DP, Marshall GR. Chem Biol Drug Des. 2006;68:295. doi: 10.1111/j.1747-0285.2006.00460.x. [DOI] [PubMed] [Google Scholar]
- 21.Van Eps N, Anderson LL, Kisselev OG, Baranski TJ, Hubbell WL, Marshall GR. Biochemistry. 2010;49:6877. doi: 10.1021/bi100846c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Martin C, Zhang Y. Nat Rev Mol Cell Biol. 2005;6:838. doi: 10.1038/nrm1761. [DOI] [PubMed] [Google Scholar]
- 23.Jacobs SA, Khorasanizadeh S. Science. 2002;295:2080. doi: 10.1126/science.1069473. [DOI] [PubMed] [Google Scholar]
- 24.Li H, Ilin S, Wang W, Duncan EM, Wysocka J, Allis CD, Patel DJ. Nature. 2006;442:91. doi: 10.1038/nature04802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sunner J, Nishizawa K, Kebarle P. J Phys Chem. 1981;85:1814. [Google Scholar]
- 26.Amicangelo JC, Armentrout PB. J Phys Chem A. 2000;104:11420. [Google Scholar]
- 27.Amunugama R, Rodgers MT. J Phys Chem A. 2002;106:5529. [Google Scholar]
- 28.Feller D. Chem Phys Lett. 2000;322:543. [Google Scholar]
- 29.Deakyne CA, Meot-Ner M. J Am Chem Soc. 1985;107:474. [Google Scholar]
- 30.Gallivan JP, Dougherty DA. J Am Chem Soc. 2000;122:870. [Google Scholar]
- 31.Mo Y, Subramanian G, Gao J, Ferguson DM. J Am Chem Soc. 2002;124:4832. doi: 10.1021/ja0174433. [DOI] [PubMed] [Google Scholar]
- 32.Hunter CA, Low CM, Rotger C, Vinter JG, Zonta C. Proc Natl Acad Sci USA. 2002;99:4873. doi: 10.1073/pnas.072647899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hunter CA, Low CM, Rotger C, Vinter JG, Zonta C. Chem Commun (Camb) 2003:834. doi: 10.1039/b300693j. [DOI] [PubMed] [Google Scholar]
- 34.Bartoli S, Roelens S. J Am Chem Soc. 2002;124:8307. doi: 10.1021/ja025884w. [DOI] [PubMed] [Google Scholar]
- 35.Stotz CE, Topp EM. J Pharm Sci. 2004;93:2881. doi: 10.1002/jps.20188. [DOI] [PubMed] [Google Scholar]
- 36.Fernandez-Recio J, Vazquez A, Civera C, Sevilla P, Sancho J. J Mol Biol. 1997;267:184. doi: 10.1006/jmbi.1996.0831. [DOI] [PubMed] [Google Scholar]
- 37.Tsou LK, Tatko CD, Waters ML. J Am Chem Soc. 2002;124:14917. doi: 10.1021/ja026721a. [DOI] [PubMed] [Google Scholar]
- 38.Tatko CD, Waters ML. Protein Sci. 2003;12:2443. doi: 10.1110/ps.03284003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Slutsky MM, Marsh EN. Protein Sci. 2004;13:2244. doi: 10.1110/ps.04702104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Andrew CD, Bhattacharjee S, Kokkoni N, Hirst JD, Jones GR, Doig AJ. J Am Chem Soc. 2002;124:12706. doi: 10.1021/ja027629h. [DOI] [PubMed] [Google Scholar]
- 41.Riemen AJ, Waters ML. J Am Chem Soc. 2010;132:9007. doi: 10.1021/ja101079z. [DOI] [PubMed] [Google Scholar]
- 42.Riemen AJ, Waters ML. J Am Chem Soc. 2009;131:14081. doi: 10.1021/ja9047575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hughes RM, Waters ML. Curr Opin Struct Biol. 2006;16:514. doi: 10.1016/j.sbi.2006.06.008. [DOI] [PubMed] [Google Scholar]
- 44.Chessari G, Hunter CA, Low CM, Packer MJ, Vinter JG, Zonta C. Chemistry. 2002;8:2860. doi: 10.1002/1521-3765(20020703)8:13<2860::AID-CHEM2860>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 45.Ponder JW. TINKER. 6.1.01. Departmet of Chemistry, Washington University; St. Louis, MO: 2012. Revision on June 29. [Google Scholar]
- 46.Stone AJ. J Chem Theory Comput. 2005;1:1128–1132. doi: 10.1021/ct050190+. [DOI] [PubMed] [Google Scholar]
- 47.Ren P, Wu C, Ponder JW. J Chem Theory Comput. 2011;7:3143. doi: 10.1021/ct200304d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J Comput Chem. 2005;26:1781. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Case DA, Darden TA, Cheatham TEI, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Pearlman DA, Crowley M, Walker RC, Zhang W, Wang B, Hayik S, Roitberg A, Seabra G, Wong KF, Paesani F, Wu X, Brozell S, Tsui V, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Beroza P, Mathews DH, Schafmeister C, Ross WS, Kollman PA. University of California; San Francisco: 2006. [Google Scholar]
- 50.Darden T, York D, Pedersen L. J Chem Phys. 1993;98:10089. [Google Scholar]
- 51.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczer K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J Phys Chem B. 1998:3586. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 52.Jorgensen WL, Maxwell DS, Tirado-Rives J. J Am Chem Soc y. 1996;118:11225. [Google Scholar]
- 53.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983:926. [Google Scholar]
- 54.Evans DJ, Holian BL. J Chem Phys. 1985;83:4069. [Google Scholar]
- 55.Case DA, Darden TA, Cheatham TEI, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Wang B, Hayik S, Roitberg A, Seabra G, Kolossavai I, Wong KF, Paesani F, Vanicek J, Liu J, Wu X, Brozell S, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh M-J, Cui G, Roe RD, Mathews DH, Seetin MG, Sagui C, Babin V, Luchko T, Gusarov S, Kavelenko A, Kollman PA. AMBER University of California; San Francisco: 2010. [Google Scholar]
- 56.Zhao Z, Rogers DM, Beck TL. J Chem Phys. 2010;132:014502. doi: 10.1063/1.3283900. [DOI] [PubMed] [Google Scholar]
- 57.Wu JC, Piquemal JP, Chaudret R, Reinhardt P, Ren P. J Chem Theory Comput. 2010;6:2059. doi: 10.1021/ct100091j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stone AJ. J Chem Theory Comput. 2005;1:1128. doi: 10.1021/ct050190+. [DOI] [PubMed] [Google Scholar]
- 59.Peter C, Daura X, van Gunsteren WF. J Biomol NMR. 2001;20:297. doi: 10.1023/a:1011241030461. [DOI] [PubMed] [Google Scholar]
- 60.Gattin Z, Schwartz J, Mathad RI, Jaun B, van Gunsteren WF. Chemistry. 2009;15:6389. doi: 10.1002/chem.200802523. [DOI] [PubMed] [Google Scholar]
- 61.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09, Revision A.02. Gaussian, Inc; Wallingford CT: 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figure 1. Comparison of Experimental (dark blue) NOEs with predicted NOEs from 100 nsec MD simulations in explicit solvent.
Supplemental Figure 1b. Data for Lys(Me)-9 hairpin model.
Supplemental Figure 1c. Data for Lys(Me2)-9 hairpin model.
Supplemental Figure 1d. Data for Lys(Me3)-9 hairpin model.