Three Mechanisms for the Calcium Alleviation of Mineral Toxicities

Abstract

Ca²⁺ in rooting medium is essential for root elongation, even in the absence of added toxicants. In the presence of rhizotoxic levels of Al³⁺, H⁺, or Na⁺ (or other cationic toxicants), supplementation of the medium with higher levels of Ca²⁺ alleviates growth inhibition. Experiments to determine the mechanisms of alleviation entailed measurements of root elongation in wheat (Triticum aestivum L. cv Scout 66) seedlings in controlled medium. A Gouy-Chapman-Stern model was used to compute the electrical potentials and the activities of ions at the root-cell plasma membrane surfaces. Analysis of root elongation relative to the computed surface activities of ions revealed three separate mechanisms of Ca²⁺ alleviation. Mechanism I is the displacement of cell-surface toxicant by the Ca²⁺-induced reduction in cell-surface negativity. Mechanism II is the restoration of Ca²⁺ at the cell surface if the surface Ca²⁺ has been reduced by the toxicant to growth-limiting levels. Mechanism III is the collective ameliorative effect of Ca²⁺ beyond mechanisms I and II, and may involve Ca²⁺-toxicant interactions at the cell surface other than the displacement interactions of mechanisms I and II. Mechanism I operated in the alleviation of all of the tested toxicities; mechanism II was generally a minor component of alleviation; and mechanism III was toxicant specific and operated strongly in the alleviation of Na⁺ toxicity, moderately in the alleviation of H⁺ toxicity, and not at all in the alleviation of Al³⁺ toxicity.

Ca²⁺ in rooting medium is essential for root elongation, even in the absence of added toxicants (Hanson, 1984; present study). In the presence of rhizotoxic levels of Al³⁺, H⁺, or Na⁺ (or other cationic toxicants), supplementation of the medium with higher levels of Ca²⁺ alleviates growth inhibition (LaHaye and Epstein, 1969; Hanson, 1984; Kinraide and Parker, 1987; Yan et al., 1992; Yermiyahu et al., 1997a; present study). Several separate mechanisms for Ca²⁺ alleviation of mineral toxicity have been proposed. A commonly proposed, or at least implied, mechanism is the restoration of toxicant-displaced Ca²⁺ (LaHaye and Epstein, 1969; Hanson, 1984; Cramer et al., 1985; Lynch et al., 1987; Shortle and Smith, 1988; Schulze, 1989; Läuchli, 1990; Rengel, 1992; Yan et al., 1992; Yermiyahu et al., 1997a). The present investigation attempts to identify the mechanisms by which Ca²⁺ alleviates mineral rhizotoxicity and to determine the relative importance of these mechanisms.

Several previous investigations have demonstrated the importance of ψ₀ in root-mineral interactions (Wagatsuma and Akiba, 1989; Suhayda et al., 1990; Kinraide, 1994; Yermiyahu et al., 1997a). Because PM surfaces are usually negatively charged (Wagatsuma and Akiba, 1989), the ion concentrations at root PM surfaces can differ significantly from the concentrations in the rooting medium. Treatments that reduce PM surface negativity, such as increases in the ionic strength or decreases in the pH of the rooting medium, reduce the effectiveness of cationic toxicants and increase the effectiveness of at least one anionic toxicant (Kinraide, 1994). Presumably, the effectiveness of ionic nutrients and ameliorants such as Ca²⁺ are similarly modified.

Because of the importance of ψ₀, a model for its computation has been developed specifically for root cells of the experimental subject, an Al-sensitive wheat cultivar (Triticum aestivum L. cv Scout 66) (Yermiyahu et al., 1997b). Although developed specifically for cv Scout 66 on the basis of ion sorption, the model appears to be suitable for the estimation of ψ₀ (or values that are at least proportional to ψ₀) for plants in general. This model has been refined to improve its compatibility with published ζ potentials from diverse plant sources (Kinraide et al., 1998).

Knowledge of ψ₀ allows the computation of {I^Ζ}₀. Use of {I^Ζ}₀ rather than ion activities in the bulk-phase rooting medium ({I^Ζ}_∞) has enabled the separate analysis of three mechanisms for the Ca²⁺ alleviation of mineral rhizotoxicity.

MATERIALS AND METHODS

Growth Experiments

Root elongation in response to combinations of toxic and nontoxic minerals was assessed by the cultivation of 2-d-old seedlings of an Al-sensitive wheat cultivar (Triticum aestivum L. cv Scout 66) in aerated solutions at 25°C in the dark for 2 d according to methods described previously (Kinraide, 1997). The composition of specific solutions will be presented with the results of the experiments.

Computation of Ion Activities at the PM Surface

{I^Ζ}₀ was computed from {I^Ζ}_∞ and ψ₀ after the latter was computed with a Gouy-Chapman-Stern model that was developed specifically for cv Scout 66 (Yermiyahu et al., 1997b) and then refined to improve its compatibility with published ζ potentials from diverse plant sources (Kinraide et al., 1998). A diskette with a computer program for the Gouy-Chapman-Stern model, together with a manual for its use, may be obtained from the author.

Analysis of Root Elongation

Root elongation will be expressed in several ways. RL is the mean length of roots from a solution in which the two longest roots from each of five seedlings were measured. RRL_C is defined as 100(RL_T − RL_S)/(RL_C − RL_S), where RL_T is the RL in the presence of toxicant, RL_C is the RL in the corresponding toxicant-free control (or low-toxicant control in the case of H⁺), and RL_S is the RL in the presence of toxicant sufficient to maximize its growth-inhibitory effects (RL_S is nearly equal to RL at the time of seedling transfer to the test solutions). In each particular experiment RL_S is a single value, but each RL_T has its corresponding RL_C.

RRL_C is problematical because of an implication that the difference in RL_T and RL_C is attributable solely to toxicant. In Al³⁺ toxicity, for example, an Al-bearing solution and its Al-free control may be at an equally low pH, but it is not true that the two solutions impose similar H⁺ stresses. H⁺ stress is higher in the control solutions because Al³⁺ displaces H⁺ from the PM surface (Kinraide, 1997). Consequently, another designation for root elongation in response to toxicants is defined here. RRL_max is defined as 100(RL_T − RL_S)/(RL_max − RL_S), where RL_max is RL in toxicant-free, Ca²⁺-sufficient solutions. In this formulation RL_max is a single value within each experiment.

When growth is plotted against measures of toxicant intensity, such as {T}₀, the resulting curves are often downwardly sigmoidal and can be expressed by a Weibull equation that has been used previously to describe growth responses to toxicants (Kinraide, 1997; Yermiyahu et al., 1997a). If growth is limited only by {T}₀, then:

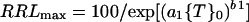1

where a₁ and b₁ are coefficients that can be evaluated by regression analysis. a₁ increases with the strength of the toxicant (when {T}₀ = 1/a₁, RRL_max = 36.8, irrespective of b₁); b₁ is a shape factor that confers sigmoidality when its value is greater than 1. Higher values of b₁ yield higher negative slopes at {T}₀ = 1/a₁, and lower values of b₁ yield higher negative slopes at {T}₀ = 0.

If {Ca²⁺}₀ is limiting (because of toxicant displacement of Ca²⁺ from the PM surface or for some other reason), the addition of Ca²⁺ may enhance growth, and plots of growth versus {Ca²⁺}₀ may be upwardly sigmoidal. If growth is limited only by {Ca²⁺}₀ insufficiency, then:

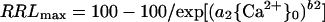2

In Equation 1, RRL_max progresses from 100 toward 0 as toxicant increases, and in Equation 2, RRL_max progresses from 0 toward 100 as Ca²⁺ increases. Neither progression is necessarily sigmoidal because b₁ or b₂ may be less than 1. If the responses to {T}₀ and {Ca²⁺}₀ are independent, then the joint effect of the two are multiplicative and:

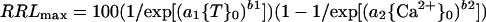3

It is possible that toxicant and Ca²⁺ interact at the PM (e.g. by channel blockade), in which case Equation 3 is inadequate. A possible way to express interaction would be to incorporate a dependence on Ca²⁺ into the coefficient for the toxicant. Thus, a₁ could be written:

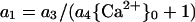4

so that a₁ decreases as {Ca²⁺}₀ increases. Just as Ca²⁺ may be an antagonist of toxicant action, so may the toxicant be an antagonist of Ca²⁺ action. Thus, a₂ could be written as a₂ = a₅/(a₆{T}₀ + 1), but in anticipation of the results, no value statistically significantly different from 0 was ever observed for a₆.

It is acknowledged here that Equations 1 through 4 are not mechanistically derived, and the coefficients have no special physiological meaning. However, they can serve to quantify both toxicant strengths and Ca²⁺-toxicant interactions, as demonstrated later. Although the coefficients may seem numerous, they are the minimal number for the required shapes, two for each sigmoidal curve plus an additional coefficient for each interaction.

Replication and Statistics

To compile data from a sufficient range of values for each of the variables, data were pooled from growth experiments performed under similar conditions. Not every experiment added to the pool was replicated, but considerable overlap among treatment variables occurred among experiments. An attempt was made to minimize intercorrelations among independent variables within a pool (data are presented below). A statistics program (SYSTAT, version 6, Systat, Evanston, IL) was used for multiple, nonlinear regression analyses. All values for coefficients presented in Results are significantly different from 0 (95% confidence intervals do not encompass 0).

RESULTS

Ca²⁺ Alleviation of Al³⁺ Toxicity

Ca²⁺ alleviates Al³⁺ toxicity, but recent studies indicate that, ordinarily, the alleviation is not caused by the restoration of Al³⁺-inhibited Ca²⁺ uptake (Ryan et al., 1994) or by the restoration of Al³⁺-displaced cell-surface Ca²⁺ (Kinraide et al., 1994; Ryan et al., 1997). Ca²⁺ and other cations are ameliorative in the following order: Tris(ethylenediamine)cobalt³⁺ > Ca²⁺ ≈ Mg²⁺ ≈ Sr²⁺ > Na⁺ ≈ K⁺ (Kinraide and Parker, 1987; Kinraide et al., 1992, 1994; Ryan et al., 1994, 1997). Thus, it was concluded that Ca²⁺ and other cations relieve Al³⁺ toxicity solely by the displacement of Al³⁺ from the cell surface by electrostatic effects, i.e. by the reduction of cell-surface negativity and the consequent reduction of {Al³⁺}₀. Alleviation of toxicity by the electrostatic displacement of toxicant will be referred to as mechanism I. The use of {T}₀ instead of {T}_∞ in Equation 1 is an attempt to express that mechanism quantitatively.

If mechanism I is the sole means by which Ca²⁺ relieves Al³⁺ toxicity, then Equation 1 will describe adequately root elongation, and an attempt to evaluate Equation 3 will lead to nonsignificant values for a₂ and b₂, as has been observed for all data published previously (analyses not presented). Nevertheless, Al³⁺ does displace Ca²⁺ from cell or PM surfaces (Reid et al., 1995; Ryan et al., 1997, Yermiyahu et al., 1997b), and Kinraide et al. (1994) predicted that under conditions of sufficiently low Ca²⁺, the addition of Al³⁺ may induce a state of cell-surface Ca²⁺ insufficiency.

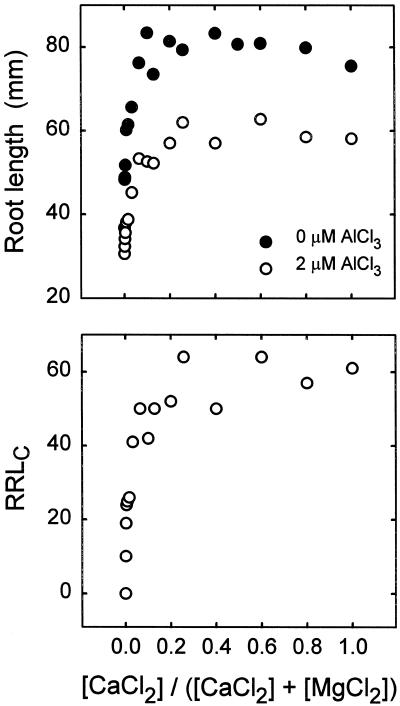
To test that hypothesis, new experiments were performed to assess Al³⁺ intoxication in a Ca²⁺-Mg²⁺ replacement series in which [CaCl₂] + [MgCl₂] = 1 mm (Fig. 1). This experimental design eliminated mechanism I as a variable because of the similar effects of Ca²⁺ and Mg²⁺ on ψ₀ (Kinraide et al., 1998). Figure 1 (top panel) demonstrates that [CaCl₂] > 0.1 mm ([MgCl₂] < 0.9 mm) supported full root elongation in the absence of Al, but in the presence of 2 μm AlCl₃, [CaCl₂] > 0.2 mm was required. As [CaCl₂] declined below 0.2 mm, RRL_C also declined. This indicates that Al³⁺ caused a Ca²⁺ insufficiency between 0.1 and 0.2 mm CaCl₂, and that Al³⁺ aggravated the Ca²⁺ insufficiency already expressed in the controls below 0.1 mm CaCl₂. Alleviation of toxicity by Ca²⁺ restoration of toxicant-displaced Ca²⁺ will be referred to as mechanism II. The use of {Ca²⁺}₀ instead of {Ca²⁺}_∞ in Equation 2 is an attempt to express that mechanism. Mechanism II is related to the Ca²⁺-displacement hypothesis for toxicity, which states that a cation is toxic because it displaces Ca²⁺ from the cell surface.

Figure 1.

Root elongation in response to CaCl₂, MgCl₂, and AlCl₃ in the rooting medium. [CaCl₂] + [MgCl₂] = 1 mm and pH = 4.6. RRL_C is the root length in Al solutions relative to Al-free solutions with similar CaCl₂ and MgCl₂. The data were compiled from six experiments, with each point on the graph based on one to six values. Each of these values was based on the measured lengths of 10 roots, as described in Methods.

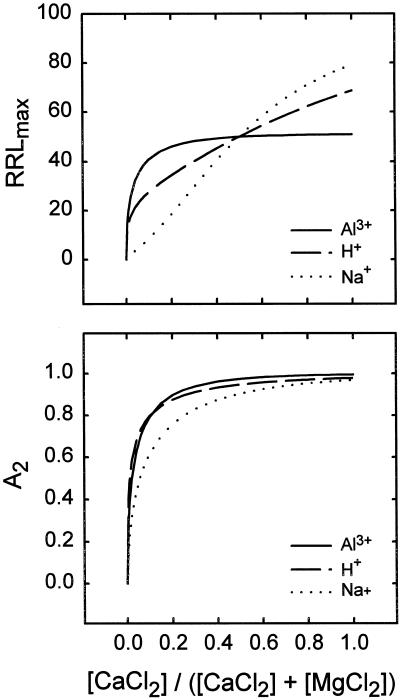
If mechanisms I and II both operate in the alleviation of Al³⁺ toxicity, then Equation 3 (not incorporating Eq. 4) should be appropriate. The experiments presented in Figure 1 were pooled with the new experiment presented in Table I. Because the pH was only moderately low in these experiments (4.6) and the sum of the divalent cations was moderately high (1 mm), the roots were under no H⁺ stress (Kinraide et al., 1992; present study). Regression analysis according to Equation 3 yielded the results presented for Al³⁺ in Table II. When Equation 4 was incorporated into Equation 3, a nonsignificant value for a₄ was obtained. Figure 2 presents model-generated curves for RRL_max and 1 − 1/exp[(a₂{Ca²⁺}₀)^{b₂] based on the coefficients in Table II. Because all solutions for a given toxicant are electrostatically similar, mechanism I does not influence the trends in Figure 2.}

Table I.

Effects of Al³⁺, Ca²⁺, and Mg²⁺ on root elongation in cv Scout 66 seedlings

AlCl3	CaCl2	MgCl2	Measured RRLmax	A1	A2	Computed RRLmax
μm
0	10	990	54	1	0.56	56
0	20	980	60	1	0.70	70
0	40	960	85	1	0.82	82
0	80	920	95	1	0.91	91
0	160	840	93	1	0.97	97
0	320	680	100	1	0.99	99
2	10	990	24	0.60	0.42	25
2	20	980	29	0.60	0.55	32
2	40	960	47	0.60	0.68	40
2	80	920	70	0.60	0.78	48
2	160	840	58	0.60	0.90	54
2	320	680	65	0.60	0.96	57
3	10	990	16	0.47	0.39	18
3	20	980	41	0.47	0.51	24
3	40	960	33	0.47	0.64	30
3	80	920	42	0.47	0.77	36
3	160	840	41	0.47	0.88	41
3	320	680	41	0.47	0.95	45
4	10	990	11	0.38	0.37	14
4	20	980	21	0.38	0.49	19
4	40	960	28	0.38	0.62	24
4	80	920	28	0.38	0.75	29
4	160	840	34	0.38	0.86	33
4	320	680	25	0.38	0.94	36

Each solution was adjusted to pH 4.6 with HCl. RL_max = 75.5 mm and RL_S = 34.0 mm. Two of the column headings are terms taken from Equation 3; A₁ = 1/exp[(a₁{T}₀)^{b₁] and A₂ = 1 − 1/exp[(a₂{Ca2+}₀)b₂]. The computed RRL_max = 100 A₁ · A₂. The data are from a single experiment representative of several similar but not identical Al3+-Ca2+-Mg2+ experiments; the coefficients for the computation of RRL_max are based on 57 measurements (see Table II).}

Table II.

Summary of statistics from regression analyses according to the equation RRL_max = 100(1/exp[(a₁{T}₀)^{b₁])(1 − 1/exp[(a₂{Ca2+}0})^b₂])

Toxicant	r2	n	a1	a3	a4	a7	b1	a2	b2
Al3+	0.944	57	120				2.71	10.3	0.520
H+	0.893	117		7.57	0.0863		6.23	13.7	0.379
Na+	0.842	105		0.00669	0.579		6.59	12.6	0.467
Na+	0.886	105		0.0107	2.04	0.247	3.51	12.4	0.555

{T}₀ is the activity of the toxicant and {Ca²⁺}₀ is the activity of Ca²⁺ at the PM surface expressed in millimolar. In some cases a₁ = a₃/(a₄{Ca²⁺}₀ + 1) or a₁ = a₃/(a₄{Ca²⁺}₀ + a₇ {Mg²⁺}₀ + 1). All values are significantly different from 0 at the 5% level. Simple correlation coefficients for {Ca²⁺}₀ versus {T}₀ were −0.341, −0.330, and −0.428 for Al³⁺, H⁺, and Na⁺, respectively.

Figure 2.

Calculated root responses to CaCl₂, MgCl₂, and toxicants in the rooting medium. [CaCl₂] + [MgCl₂] = 1 mm and pH = 4.5, except where H⁺ was the designated toxicant. Toxicant levels (AlCl₃ = 3.06 μm, pH = 4.12, and NaCl = 132.2 mm) were chosen so that RRL_max = 50 at [CaCl₂]/([CaCl₂] + [MgCl₂]) = 0.5. ψ₀ was −14, −15, and −10 mV for the added Al³⁺, H⁺, and Na⁺, respectively. The constancy of ψ₀ for a toxicant means that electrostatic displacement of toxicant by Ca²⁺ (mechanism I) played no role in the computed trends. A₂ = 1 − 1/exp[(a₂{Ca²⁺}₀)^{b₂] and is an expression of mechanism II alleviation. The continued increase in} RRL_max for Na⁺ and H⁺ in the top panel signifies the action of mechanism III.

Ca²⁺ Alleviation of H⁺ Toxicity

Ca²⁺ alleviates H⁺ toxicity, and mechanism I appears to operate because toxicity is also alleviated by Na⁺, Mg²⁺, and Tris(ethylenediamine)cobalt³⁺ and other cations whose effectiveness increases with increasing charge (Kinraide et al., 1992). Nevertheless, the pattern of Ca²⁺ alleviation is different from that of the Ca²⁺ alleviation of Al³⁺ toxicity because Ca²⁺ is a more effective ameliorant than Mg²⁺, even at relatively high [Ca²⁺]_∞, where mechanism II would not be expected to operate. In Ca²⁺-Mg²⁺ replacement experiments, RRL_C continued to increase with increasing [Ca²⁺]_∞ (Kinraide et al., 1994). Growth experiments with H⁺ indicate that the effectiveness of the toxicant may be reduced by Ca²⁺ by mechanisms beyond those already described. For that reason, we introduce a third class of mechanisms: the alleviation of toxicity by Ca²⁺ by one or more mechanisms other than I and II will be referred to as mechanism III. The incorporation of Equation 4 into Equation 3 is an attempt to express these mechanisms.

If mechanism III does operate, then Equation 3 (not incorporating Eq. 4) will be incomplete, and incorporation of Equation 4 into Equation 3 may improve the description of root elongation. These ideas were tested by pooling results from several published experiments (Kinraide et al., 1994) with results from new experiments such as those presented in Table III. The data were evaluated in terms of Equation 3 (incorporating Eq. 4). The results of the regression analysis are presented in Table II and Figure 2, where the effects of mechanism III on H⁺ toxicity can be seen in the continued increase of RRL_max for H⁺.

Table III.

Effects of pH and Ca²⁺ on root elongation in cv Scout 66 seedlings

RL_max = 68.5 mm and RL_S = 23.2 mm. A₁ = 1/exp[(a₃/(a₄{Ca²⁺}₀ + 1){T}₀)^{b₁], A2} = 1 − 1/exp[(a₂{Ca²⁺}₀^{b₂], and computed RRL_max = 100 A1} · A₂. The data are from an experiment performed twice. The coefficients for the computation of RRL_max are based on 117 measurements (see Table II).

pH	CaCl2	Measured RRLmax	A1	A2	Computed RRLmax
	μm
3.6	200	8	0.00	0.70	0
3.9	200	8	0.00	0.84	0
4.2	200	30	0.17	0.94	16
4.5	200	90	0.82	0.98	81
4.8	200	100	0.99	0.99	99
3.6	400	4	0.00	0.78	0
3.9	400	0	0.01	0.90	1
4.2	400	58	0.48	0.97	46
4.5	400	93	0.95	0.99	94
4.8	400	86	1.00	1.00	100
3.6	800	4	0.00	0.86	0
3.9	800	16	0.08	0.94	8
4.2	800	77	0.78	0.98	77
4.5	800	100	0.99	0.99	98
4.8	800	88	1.00	1.00	100

Ca²⁺ Alleviation of Na⁺ Toxicity

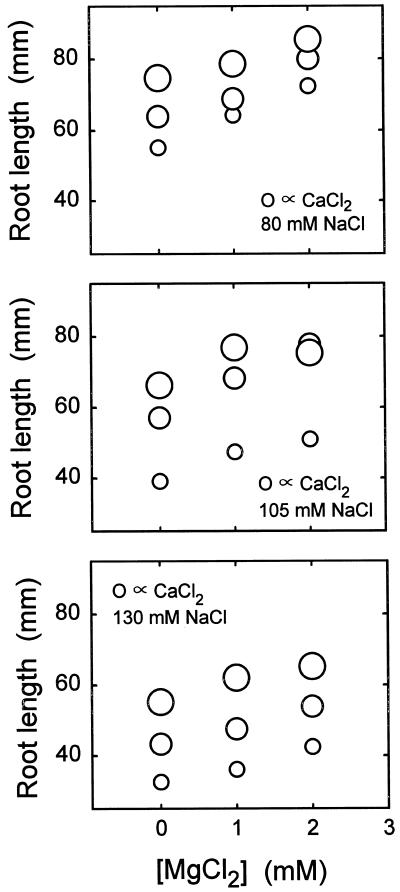
Ca²⁺ alleviates Na⁺ toxicity, but a preliminary inspection of the data indicates that Ca²⁺ alleviation is not dominated by mechanism I to the extent that it is in Al³⁺ toxicity or even H⁺ toxicity. The diagnostic feature of mechanism I alleviation is that cations other than Ca²⁺ are effective ameliorants. Mg²⁺ and Sr²⁺ do reduce Na⁺ toxicity, but the effects are weak compared with the effect of Ca²⁺ (Fig. 3). Furthermore, high Na⁺ can impose an osmotic stress that Ca²⁺ is unable to relieve.

Figure 3.

Effects of NaCl, CaCl₂, and MgCl₂ on root elongation. A factorial array of 27 solutions contained 80, 105, or 130 mm NaCl, 0.15, 0.30, or 0.45 mm CaCl₂, and 0, 1, or 2 mm MgCl₂ (all at pH 5.0). Areas of circles are proportional to [CaCl₂]. The data are from a single experiment representative of several similar but not identical Na⁺-Ca²⁺-Mg²⁺ experiments.

Data from several experiments were pooled (including the data from Fig. 3, which were published previously [Kinraide, 1994]), and data from some new experiments in which [Na⁺]_∞ ranged from 0 to 200 mm were also used. In addition, data were examined from an experiment in which mannitol ranged from 0 to 400 mm. Mannitol concentrations < 250 mm were not inhibitory, and Ca²⁺ could relieve Na⁺ toxicity completely when the [NaCl] was <135 mm, indicating that osmotic stress was not a factor in root elongation in solutions with an osmolarity <250 mm. Consequently, only data from solutions with [NaCl] < 135 mm were retained in the pool. Regression analysis of these data yielded the results presented in Table II and Figure 2, where strong mechanism III effects can be seen in the steep and continuous increase of RRL_max for Na⁺.

The coefficient a₁ can be defined to include a Mg²⁺ term. If the equation:

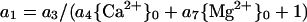5

is incorporated into Equation 3, regression analysis yields six statistically significant coefficients (Table II, last line). Use of Equation 5 for the analysis of Al³⁺ or H⁺ toxicity resulted in nonsignificant values for coefficients.

A Reevaluation of a H⁺-Toxicity Study in an Attempt to Discern Mechanism II

The analytical techniques described above were also applied to several published studies in which a role for mechanism II was asserted or implied. In most cases mechanism I accounted for most of the alleviation, and mechanism II could not be confirmed. The following example illustrates some important points of experimental design and analysis.

In a study of H⁺ toxicity, Yan et al. (1992) concluded that the inhibition of corn root elongation was likely to have been a consequence of H⁺ influx inadequately compensated for by H⁺ secretion, resulting in the acidification of the cytoplasm. H⁺ displacement of Ca²⁺ was thought likely to have enhanced H⁺ influx, an effect that could be offset by the addition of Ca²⁺ to the medium.

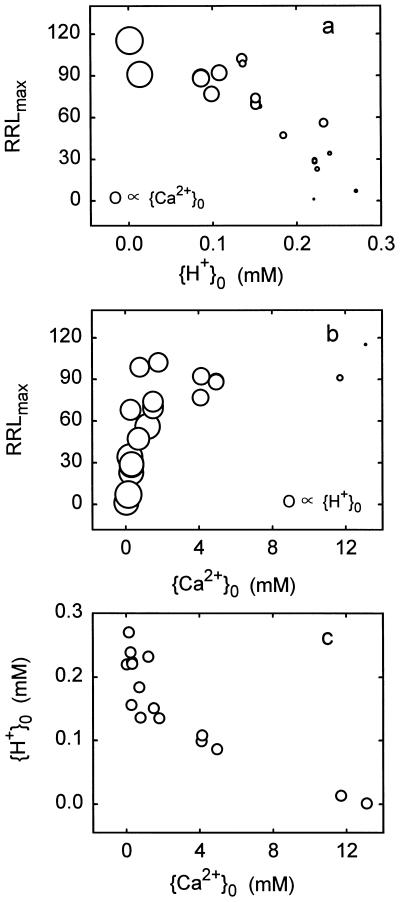
To determine whether inhibition of corn-root growth by H⁺ was demonstrably a function of Ca²⁺ displacement, data were pooled from the figures and tables of Yan et al. (1992). Growth was scaled to RRL_max, {H⁺}₀ and {Ca²⁺}₀ were computed, and RRL_max was plotted against the surface ion activities in Figure 4. Growth appeared to be inhibited by {H⁺}₀ and enhanced by {Ca²⁺}₀, but in this study, as in most others, {H⁺}₀ and {Ca²⁺}₀ were intercorrelated (Fig. 4c), so an effect of Ca²⁺ other than the mechanism I effect is difficult to discern. Analysis in terms of Equation 3 (incorporating Eq. 4) yielded statistically significant values for a₁ (4.38), b₁ (3.00), and a₂ (5.68). b₂ and a₄ could not be evaluated so they were deleted (effectively setting b₂ equal to 1). Apparently, the correlation of {H⁺}₀ with {Ca²⁺}₀ was not strong enough to prevent the evaluation of both a₁ and a₂, so one may conclude, in agreement with Yan et al. (1992), that H⁺-induced Ca²⁺ displacement accounts for some of the intoxication. Nevertheless, the data set is inadequate for extensive analyses, mainly because of {H⁺}₀ and {Ca²⁺}₀ intercorrelations.

Figure 4.

Growth of corn seedling roots in response to H⁺ and Ca²⁺. Data were taken from Yan et al. (1992). Growth measurements were scaled to RRL_max, and activities in the medium and at the PM surface were computed as described elsewhere in the present study. Areas of circles are proportional to {Ca²⁺}₀ or {H⁺}₀, as indicated.

DISCUSSION

The coefficients shown in Table II quantitatively express several characteristics of the studied toxicities and the ameliorative effects of Ca²⁺. Coefficients a₁ and a₃ relate to the strength of the toxicants. Therefore, Al³⁺ is at least 10 times more toxic than H⁺, and H⁺ is about 1000 times more toxic than Na⁺ to short-term root elongation in seedlings of cv Scout 66. These relative toxicities may be termed intrinsic because they refer to toxicant activities at the PM surface. Coefficients a₂ and b₂ refer to the requirement for {Ca²⁺}₀ modeled as though it were independent of {T}₀. The coefficient a₄ indicates interactions between {Ca²⁺}₀ and {T}₀ that are toxicant specific. {Ca²⁺}₀ and {T}₀ do not interact in the case of Al³⁺ toxicity, and the interaction in Na⁺ toxicity is at least 6-fold greater than in the case of H⁺ toxicity. The coefficient a₇ indicates that {Mg²⁺}₀ and {Na⁺}₀ also interact and that Ca²⁺ is about 8 times more effective than Mg²⁺ as a mechanism III ameliorant.

Electrostatic principles make it almost inevitable that mechanism I would play an important role in the Ca²⁺ alleviation of toxicity by cations, especially multivalent cations. It is surprising, therefore, that such a role for Ca²⁺ has been stated only rarely (Foy, 1983; Kinraide et al., 1992, 1994; Ryan et al., 1997; Yermiyahu, 1997a). This statement by Foy (1983) clearly differentiates toxicant displacement from Ca²⁺ replacement: “Beneficial effects of increased concentrations of these elements [Ca, Mg, K, and Na] were probably due to a competitive reduction in Al-root contact, rather than supplying deficient nutrients.” In contrast, mechanism II has been invoked frequently as an explanation for the ameliorative effectiveness of Ca²⁺ (LaHaye and Epstein, 1969; Hanson, 1984; Cramer et al., 1985; Lynch et al., 1987; Shortle and Smith, 1988; Schulze, 1989; Läuchli, 1990; Rengel, 1992; Yan et al., 1992; Yermiyahu et al., 1997a). However, the present study indicates that mechanism I plays a much more significant role than mechanism II, as illustrated in the following computational analysis (Table IV).

Table IV.

Components of toxicity computed for media supplemented with Al³⁺, H⁺, and Na⁺

AlCl2	pH	NaCl	MgCl2	CaCl2	A1	A2	RRLmax
mm		mm
	4.5	3.5		0.5	0.98	0.98	96
0.0043	4.5	3.5		0.5	0.52	0.96	50
0.0043	4.5	3.5		1.0	0.66	0.99	65
0.0043	4.5	3.5	0.5	0.5	0.66	0.96	63
	4.124	3.5		0.5	0.53	0.94	50
	4.124	3.5		1.0	0.75	0.97	73
	4.124	3.5	0.5	0.5	0.63	0.93	58
	4.5	126		0.5	0.55	0.91	50
	4.5	126		1.0	0.85	0.97	82
	4.5	126	0.5	0.5	0.61	0.91	55

The basal medium contained 0.5 mm CaCl₂ and 3.5 mm NaCl acidified to pH 4.5 with HCl. A₁ = 1/exp[(a₁{T}₀^{b₁], A2} = 1 − 1/exp[(a₂{Ca²⁺}₀)^{b₂], and computed RRLmax} = 100 A₁ · A₂. The coefficient a₁ is defined by Equation 4 at the lower pH or by Equation 5 at the higher NaCl concentration.

An infertile, moderately acidic soil may have a soil solution with a [Ca²⁺] of 0.5 mm, a pH of 4.5, and an ionic strength of 5 mm (Wright and Wright, 1987) (simulated by 0.5 mm [CaCl₂] and 3.5 mm [NaCl] acidified with HCl; Table IV). Three stresses were imposed: addition of 4.3 μm AlCl₃, reduction of pH to 4.124, or elevation of NaCl to 126 mm. Each change reduced RRL_max to 50 (computed using the coefficients in Table II), but the stress imposed by Ca²⁺ displacement was minor (A₂ ranged from 0.91 to 0.99). Elevation of CaCl₂ relieved the stress, but only insignificantly by mechanism II. MgCl₂ was almost as effective as CaCl₂ in the alleviation of Al³⁺ toxicity (compare rows 3 and 4 in Table II), where Mg²⁺ alleviation can be attributed only to mechanism I. Although trivial, mechanism II contributed more to the alleviation of Na⁺ toxicity than to the alleviation of H⁺ or Al³⁺ toxicities (the increase in A₂ from 0.91 to 0.97 in rows 8 and 9 is greater than comparable increases for the other toxicants). Mechanism III was a large component of the alleviation of Na⁺ (A₁ declined from 0.85 to 0.61 in rows 9 and 10).

Results presented by Cramer et al. (1985) can be interpreted as evidence that Ca²⁺ is displaced from the root-cell PM surface by high Na⁺, and Yermiyahu et al. (1997a) measured directly the displacement of Ca²⁺ by Na⁺ from the surfaces of PM vesicles. Thus, Na⁺ toxicity appears to correlate negatively with {Ca²⁺}₀, as do other toxicities (Fig. 4). However, these correlations need not be interpreted as evidence that intoxication is mainly the consequence of Ca²⁺ displacement. Two alternative explanations for negative correlations between {Ca²⁺}₀ and toxicity are possible. First, high incidental negative correlations between {Ca²⁺}₀ and {T}₀ are likely (Yermiyahu et al., 1997a; Fig. 4c) but can be avoided (present study; see Table II). Second, a negative correlation between toxicity and {Ca²⁺}₀ is likely to occur whenever mechanism III alleviation is important. It is important to realize that these correlations do not necessarily demonstrate a mechanism II alleviation. Consequently, correlations between Ca²⁺ displacement and toxicity may be observed even if Ca²⁺ displacement plays a small role.

The toxicant-specific nature of mechanism III is not surprising. Consider, as a possibility, that the PM is not very permeable to Al³⁺, so Al³⁺ exerts its principal effects at the cell surface, that H⁺ has major effects at the cell surface and in the cell interior, and that Na⁺ exerts its principal effects intracellularly. If Ca²⁺ reduces PM leakiness in general (Fawzy et al., 1954; Hanson, 1984; Cramer et al., 1985) and blocks Na⁺-permeable channels in particular (for reviews and new data, see a special collection of articles by Amtmann et al., 1997; deBoer and Wegner, 1997; Maathuis and Sanders, 1997; Roberts and Tester, 1997; Tyerman et al., 1997; White, 1997), then a differential effectiveness of mechanism III is likely (Fig. 2).

When Ca²⁺ and toxicant are considered in terms of their bulk-phase intensities, interactions are generally observed, but much of that interaction is indirect and can be attributed to mechanisms I and II. The unmasking of more specific interactions can occur only after these mechanisms have been taken into account. The following steps were used in the present study and may be helpful to others: (1) compute {Ca²⁺}₀ and {T}₀; (2) use experimental designs that ensure an adequate range of values for {Ca²⁺}₀ and {T}₀ without introducing unwanted correlations between those variables (Ca²⁺-Mg²⁺ replacement solutions may be used to vary {Ca²⁺}₀ without varying {T}₀); and (3) use statistical methods that incorporate reasonable, descriptive models such as sigmoidal growth responses rather than linear responses, which extrapolate to absurd values.

Mechanisms I, II, and III have been presented in terms of ionic responses at the PM surface, but ion activities in the cell walls may respond similarly, and some of the intoxication and alleviation may originate from that phase. Additionally, the cell wall and the PM may interact to influence ion activities at the PM surface. Almost certainly, the cell surface is the initial site of ionic perturbations, but intoxication and alleviation may be implemented by Ca²⁺-dependent processes in the cell interior (Rengel, 1992).

CONCLUSIONS

Ca²⁺ appears to alleviate the effects of rhizotoxic cations by multiple mechanisms. First, the electrostatic displacement of toxicant from PM surfaces may be the most important mechanism in most cases, although it is less important for Na⁺ toxicity than for Al³⁺ and H⁺ toxicities. Second, the restoration of toxicant-displaced Ca²⁺ at PM surfaces is unlikely to be an important mechanism in most cases, although it is more important for Na⁺ toxicity than for Al³⁺ and H⁺ toxicities. Third, a class of interactions between Ca²⁺ and toxicants is highly specific and may reflect in part the Ca²⁺ blockade of PM channels that admit toxicants. These conclusions are based on short-term root-growth experiments with wheat seedlings. Growth by other species or organs or growth over longer periods may exhibit other patterns of Ca²⁺ alleviation of toxicity. Forest decline has been attributed to an insufficient supply of divalent cations to leaves or other tree parts induced by high Al³⁺ and H⁺ in soils (Shortle and Smith, 1988; Schulze, 1989). Shoots and roots respond differently to Na⁺ stress. In the present study leaf and coleoptile stunting persisted after the total alleviation by Ca²⁺ of root-growth inhibition at high Na⁺ concentrations, indicating a greater sensitivity of shoot growth to osmotic stress (data not presented). Therefore, roots that express few signs of intoxication may fail to provide adequate water, nutrients, or other growth factors to the shoots.

Abbreviations:

ψ₀

electrical potential at the PM surface

{I^Ζ}₀ and {I^Ζ}_∞

activity of ion I with charge Ζ at the PM surface and in the bulk-phase medium, respectively

[I^Ζ]₀ and [I^Ζ]_∞

concentration of ion I with charge Ζ at the PM surface and in the bulk-phase medium, respectively

PM

plasma membrane

RRL_max

root elongation in toxicant-bearing solutions relative to maximum elongation in toxicant-free, Ca²⁺-sufficient solutions

{T}₀

activity of toxicant at the PM surface