Microscopic variations in interstitial and intracellular structure modulate the distribution of conduction delays and block in cardiac tissue with source–load mismatch

Abstract

Aims

Reentrant activity in the heart is often correlated with heterogeneity in both the intracellular structure and the interstitial structure surrounding cells; however, the combined effect of cardiac microstructure and interstitial resistivity in regions of source–load mismatch is largely unknown. The aim of this study was to investigate how microstructural variations in cell arrangement and increased interstitial resistivity influence the spatial distribution of conduction delays and block in poorly coupled regions of tissue.

Methods and results

Two-dimensional 0.6 cm × 0.6 cm computer models with idealized and realistic cellular structure were used to represent a monolayer of ventricular myocytes. Gap junction connections were distributed around the periphery of each cell at 10 μm intervals. Regions of source–load mismatch were added to the models by increasing the gap junction and interstitial resistivity in one-half of the tissue. Heterogeneity in cell shape and cell arrangement along the boundary between well-coupled and poorly coupled tissue increased variability in longitudinal conduction delays to as much as 10 ms before the onset of conduction block, resulting in wavefront breakthroughs with pronounced curvature at distinct points along the boundary. Increasing the effective interstitial resistivity reduced source–load mismatch at the transition boundary, which caused a decrease in longitudinal conduction delay and an increase in the number of wavefront breakthroughs.

Conclusion

Microstructural variations in cardiac tissue facilitate the formation of isolated sites of wavefront breakthrough that may enable abnormal electrical activity in small regions of diseased tissue to develop into more widespread reentrant activity.

Introduction

Cardiac arrhythmias in the heart caused by both ectopic and reentrant mechanisms have been linked to pathological changes in cardiac structure such as reduced gap junction coupling, fibrotic scar tissue, and increased collagen fibrosis between cardiac bundles.^1–4 In most cases, these architectural changes can be subdivided into two major categories: changes that occur in the intracellular space of the heart and changes that occur in the interstitial (extracellular) space. The intracellular space refers to the structure of the interconnected myocytes, including both the region inside the cell and the gap junction coupling between cells, while the interstitial space refers to the blood vessels and extracellular matrix proteins surrounding the myocytes.^5,6 Despite the increasing experimental evidence supporting the relationship between structural heterogeneity and arrhythmogenesis, there still remain fundamental questions about how inherent microstructural discontinuities caused by cell arrangement, gap junction distribution and expression, and the distribution of extracellular matrix proteins affect macroscopic conduction properties in critical regimes close to the onset of conduction block.^7,8 These questions have been difficult to answer using either experimental studies of cardiac tissue, where it is hard to systematically control the heterogeneity, or using continuous computer models that do not include details about cell structure and instead average much of the microheterogeneity that is present in cardiac tissue.⁹

Discrete computer models that incorporate specific details about cardiac microstructure in healthy and diseased tissue have shown that microstructural heterogeneity can modulate subcellular electrical properties such as maximum upstroke velocity, local conduction velocity, and the foot of the action potential.^10,11 Additional structural heterogeneity caused by abrupt changes in coupling between healthy and diseased tissue or tissue expansion and branching can create source–load mismatches, which occur when current provided by excited tissue upstream (source) does not balance the current necessary to activate unexcited tissue upstream (load).¹² Several in vitro experimental studies have shown that even small variations in source–load conditions can lead to conduction block and wavefront reentry when conduction velocity is slowed.^13,14 In one of the few microstructural modelling studies, Spach et al.¹⁵ found that wavefront shifts and microreentry created by S1–S2 stimulation in ageing human atrial bundles correlated with spatial non-uniformity in sodium current and directional differences in incremental and decremental propagation that were not evident in continuous models. These studies suggest that in diseased and ageing tissue, where propagation is close to the onset of conduction block, microscopic source–load mismatches created by discrete cellular structure may play a role in the formation of more complex patterns of propagation. Similarly, to cardiac microstructure the effect of the interstitial structure on conduction abnormalities in poorly coupled tissue is often neglected in modelling studies; however, several recent studies have also demonstrated that increasing the interstitial resistivity or restricting the size of the extracellular space at sites of source–load mismatch can alter conduction delays and conduction velocity in inhomogeneous cardiac tissue.^16–19 In this study, we use detailed discrete computer models to investigate the effect of both microheterogeneity and interstitial resistivity on conduction delay and conduction block at the boundary between well-coupled and poorly coupled tissue.

Methods

Description of the models of cardiac tissue

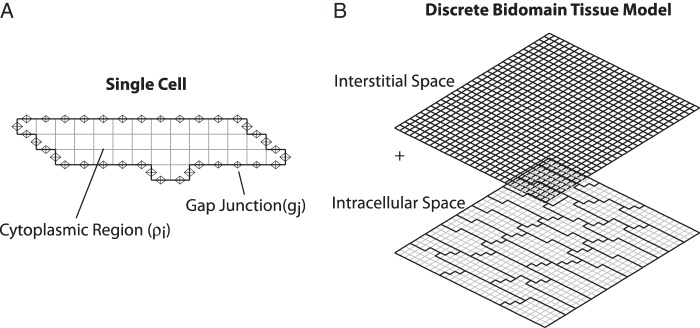
Classical modelling studies that incorporate both the intracellular and interstitial structure often use a bidomain computer model, which represents the intracellular and interstitial spaces as separate but overlapping spaces (Figure 1B).²⁰ As the bidomain model can be computationally expensive, especially for the detailed discrete models that are used in this study, we developed an equivalent two-dimensional (2-D) approximate discrete monodomain model that preserves the intracellular cardiac microstructure but combines the interstitial and the intracellular resistances into a single space.¹⁷ The properties of the interstitial space are represented by the effective interstitial resistivity (ρ_oeff) which is a measure of the specific resistivity of the interstitial space (ρ_e) and the fraction of cross-sectional area occupied by the interstitial domain (f_e). In this study, ρ_oeff is set equal to 0.5 kΩ cm in normal tissue. Similar to earlier versions of the discrete microstructural model, the cytoplasmic area inside of the cell is represented by low resistances with a given intracellular resistivity (ρ_i = 150 Ω cm) and the gap junction connection between adjacent cells is represented by a reduced conductance (g_j).¹¹ Gap junctions are distributed uniformly around the periphery of each cell as shown in Figure 1A to mimic the lateralization observed in diseased tissue and to limit the variability in the pattern of gap junction coupling. The 2-D approximate discrete model described in this study is extended from a 1-D mathematical modelling approach developed by Hubbard and Henriquez.¹⁷

Figure 1.

(A) Single cell with gap junctions distributed around the periphery. (B) Discrete bidomain tissue model composed of interconnected cells. The interstitial space is overlaid on top of the microstructural model of the intracellular space.

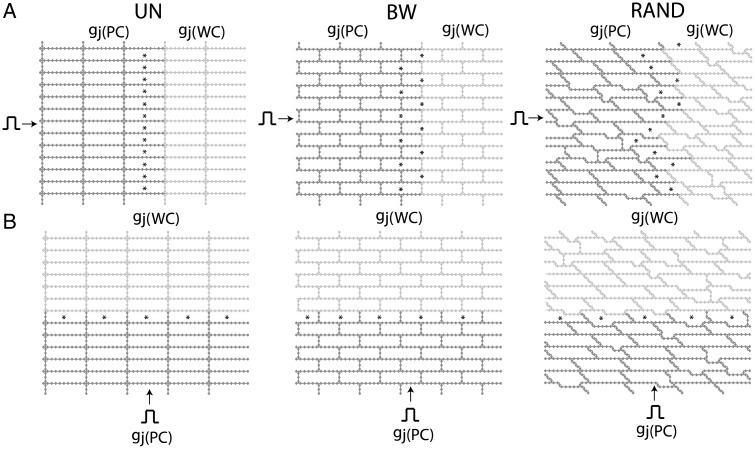
In order to investigate the effect of cell arrangement on conduction delay and maximum sodium current in regions of tissue with significant source–load mismatch, we created three inhomogeneous approximate discrete microstructural models (0.6 cm × 0.6 cm) with idealized uniform cell arrangement (UN), idealized brick wall cell arrangement (BW), and a randomly generated cell arrangement (RAND) shown in Figure 2. In the first part of this study, inhomogeneity was introduced into each of the models by decreasing the gap junction conductance (g_j(PC)) in half of the tissue while keeping the interstitial resistivity constant at a nominal value of ρ_oeff = 0.5 kΩ cm. The gap junction conductance in the well-coupled half of the tissue was set equal to g_j(WC) = 0.10 μS, and the gap junction conductance in the poorly coupled tissue was set equal to g_j(PC) = 0.01 μS, g_j(PC) = 0.005 μS, or g_j(PC) = 0.003 μS. The stars in Figure 2 indicate relative observation points in cells along the transition boundary between the well-coupled and poorly coupled tissue where propagation is most likely to fail. Homogeneous versions of these three types of microstructural models were described in a earlier study by Hubbard et al.²² In a previous 1-D study, we found that increasing ρ_oeff can reduce source–load mismatch and reduce conduction delays at the boundary between poorly coupled and well-coupled regions.¹⁷ To determine the effect of increased interstitial resistivity on conduction delay and block in inhomogeneous UN, BW, and RAND models, ρ_oeff was increased to 2.5 kΩ cm in the second part of this study.

Figure 2.

Schematics of the inhomogeneous discrete monodomain tissue models used during (A) longitudinal and (B) transverse propagation. The poorly coupled region is denoted by g_j(PC) and the well-coupled region is denoted by g_j(WC). UN, uniform cell arrangement; BW, brick wall cell arrangement; RAND, random cell arrangement. The stars indicate the cells that are most likely to experience failure.

Simulation of electrical propagation and data measurement

The Luo Rudy dynamic model of guinea pig myocytes was used to calculate the ionic current.²³ A semi-implicit scheme with a conjugate gradient solver was used to solve the system of equations.²⁴ The time step was kept constant at 5 μs, output data were recorded every 10 μs, and the data for the activation maps were recorded every 10 μs. All simulations used the CardioWave software platform.²⁵

Longitudinal and transverse plane waves were generated in the inhomogeneous tissues shown in Figure 2 by stimulating the cells intracellularly along the left border or the bottom border of the sheet, respectively, with transmembrane current pulses that were 2 ms in duration and two times threshold. Measurements were taken from points within the centre of the well-coupled and poorly coupled regions of the tissue to minimize boundary effects and the effect of stimulus artefact. Activation times were recorded at the time the membrane voltage initially reached −40 mV, and recovery times were recorded at the time the membrane voltage returned to −60 mV. The intracellular delays were computed by taking the difference of the activation times between two nodes located at the beginning and the end of a single cell along a single row or column. Gap junction delays were computed by taking the difference of activation times between two nodes located at the beginning of one cell and the end of the cell immediately preceding it along a single row or column. The magnitude of the maximum sodium current, I_Na,max, was measured at the centre of the cell. Means and standard deviations are reported for gap junction delays and maximum sodium current.

Results

Effect of intracellular microheterogeneity on conduction properties in a poorly coupled region of tissue

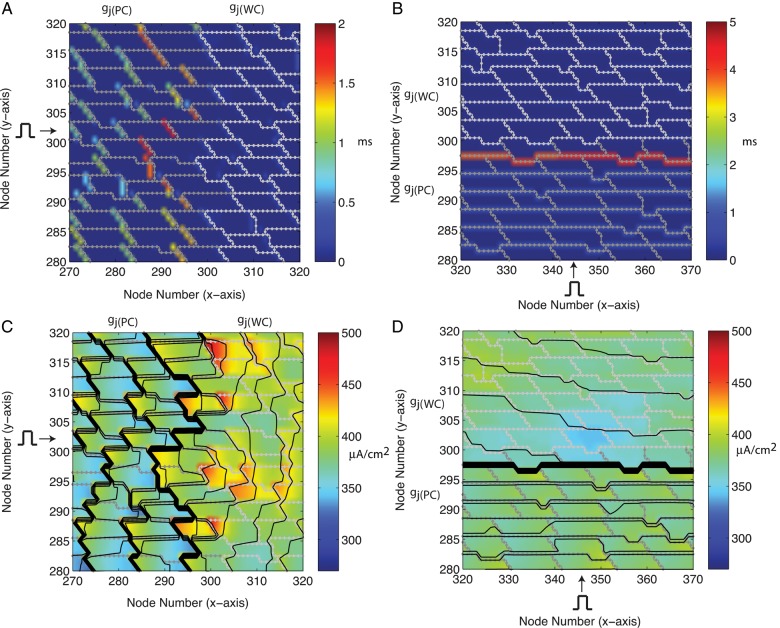
In the first part of the study, ρ_oeff was set equal to a nominal value of 0.5 kΩ cm and we investigated the effect of cell arrangement on conduction delays and maximum sodium current in tissue with neighbouring well-coupled and poorly coupled regions. With the idealized UN cell arrangement, the longitudinal and the transverse delays at transition boundary of the two regions (where the source–load mismatch was greatest) were 10.37 and 4.36 ms, respectively (Table 1). Changing from a UN cell arrangement to a BW cell arrangement decreased the longitudinal conduction delay at the boundary between the well-coupled and poorly coupled region (P < 0.01) but had no effect on the transverse conduction delay in the idealized UN and BW tissues (Table 1). The BW and RAND cell arrangements had similar average longitudinal conduction delays along the boundary, but consistent with the additional variation in cell shape in the RAND tissue, the variability in conduction delay was higher in the RAND tissue than the BW tissue (P < 0.01). As shown for the RAND tissue in Table 2, myocytes located at the transition boundary between the well-coupled and poorly coupled regions showed more variability in longitudinal conduction delay than myocytes located inside the poorly coupled region and the well-coupled region (P < 0.01). During transverse propagation in RAND tissue with g_j(PC) = 0.01 μS, the transverse gap junction delay for cardiac myocytes located directly on the transition boundary (3.76 ± 0.20 ms) also showed greater variation than myocytes located in the poorly coupled region (0.70 ± 0.05 ms) and the well-coupled region (0.17 ± 0.02 ms) (P < 0.01). The variability in longitudinal and transverse conduction delays can be observed in Figure 3A and B. Myocytes located slightly to the right of the transition zone in the RAND tissues showed greater variation in I_Na,max compared with the myocytes that were located inside the poorly coupled and well-coupled regions (P < 0.01). The variability in I_Na,max along the transition boundary during longitudinal and transverse propagation in RAND tissue with g_j(PC) = 0.01 μS can be observed in Figure 3C and D, where the thick black lines indicate an accumulation of activation lines at sites of conduction slowing.

Table 1.

Longitudinal (L) and transverse (T) conduction delays at the transition boundary between the well-coupled and poorly coupled regions in uniform (UN), brick wall (BW), and randomly (RAND) arranged tissues with g_j(WC) = 0.10 μS and g_j(PC) = 0.01 μS

	ρoeff = 0.5 kΩ cm	ρoeff = 2.5 kΩ cm
UN	L: 10.37 ± 0 ms	L: 5.48 ± 0 ms
	T: 4.36 ± 0 ms	T: 4.52 ± 0 ms
BW	L: 1.29 ± 0.03 ms	L: 0.99 ± 0.08 ms
	T: 4.36 ± 0 ms	T: 4.52 ± 0 ms
RAND	L: 1.36 ± 0.41 ms	L: 0.84 ± 0.21 ms
	T: 3.76 ± 0.20 ms	T: 3.58 ± 0.32 ms

Effective interstitial resistivity (ρ_oeff) was set equal to either 0.5 and 2.5 kΩ cm. Italicized data are expanded in Table 2 to give conduction delays in RAND tissue for a range of g_j(PC).

Table 2.

Longitudinal conduction delays (bold) and maximum sodium current, I_Na,max, in the poorly coupled, transition, and well-coupled regions in randomly (RAND) arranged tissues with decreasing gap junction conductance (g_j(PC)) and effective interstitial resistivity (ρ_oeff) equal to 0.5 kΩ cm

	Poorly coupled region	Transition region	Well-coupled region
gj(PC) = 0.01 μS	0.816 ± 0.23 ms	1.36 ± 0.41 ms	0.15 ± 0.03 ms
	370 ± 21 μA/cm2	387 ± 18 μA/cm2	392 ± 12 μA/cm2
gj(PC) = 0.005 μS	1.43 ± 0.42 ms	3.38 ± 1.23 ms	0.15 ± 0.03 ms
	364 ± 14 μA/cm2	360 ± 26 μA/cm2	392 ± 12 μA/cm2
gj(PC) = 0.003 μS	2.21 ± 0.66 ms	11.50 ± 4.9 ms	0.15 ± 0.03 ms
	358 ± 10 μA/cm2	300 ± 51 μA/cm2	392 ± 12 μA/cm2

This table gives extended data for the RAND tissue italicized in Table 1.

Figure 3.

(A and B) Magnification of a 500 μm × 400 μm region at the transition boundary of the randomly generated cell arrangement tissue showing conduction delays during longitudinal and transverse propagation, and (C and D) magnification of the same region of tissue to show the distribution of I_Na,max with an overlay of a contour map of activation times (isochrones shown every 0.36 ms). Dark grey outline: poorly coupled tissue. Light grey outline: well-coupled tissue.

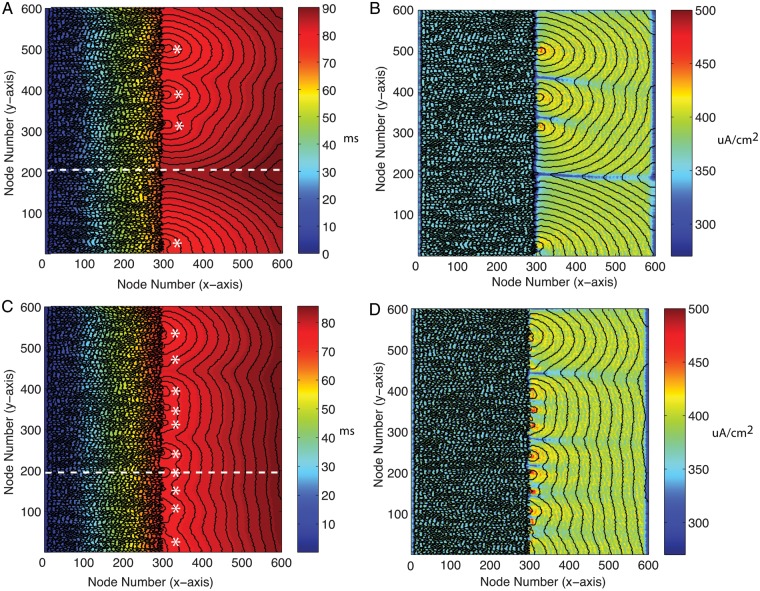
As the level of coupling in the RAND tissue was decreased from g_j(PC) = 0.01 to g_j(PC) = 0.003 μS, the variation in longitudinal gap junction delay along the transition boundary reached as high as 10 ms and the variation in sodium current reached as high as 102 μA/cm² before the onset of conduction block (Table 2). At g_j = 0.003 μS, propagation began to fail after long conduction delays at the transition border and asymmetries in the onset of conduction block occurred because of microstructural variations along the transition boundary. As shown in Figure 4A, wavefront breakthrough occurred at four distinct focal points along the transition boundary and showed pronounced curvature similar to that observed during point stimulation or during propagation through a narrow isthmus.^26,27 In the map of the distribution of sodium current shown in Figure 4B, the regions of highest I_Na,max correlate with the sites in the tissue that showed the highest wavefront curvature. The regions of lowest I_Na,max correlate with sites in the tissue that had long conduction delays or wavefront collisions between neighbouring wavefront breakthroughs.

Figure 4.

(A) Contour map of activation times (isochrones shown at 1 ms intervals) showing wavefront breakthrough at four distinct focal points (*) in tissue with g_j(PC) = 0.003 μS and ρ_oeff = 0.5 kΩ cm. (B) Map of I_Na,max for the same tissue with contour map of activation times overlaid. (C) Contour map of activation times (isochrones shown at 1 ms intervals) showing wavefront breakthrough at 10 distinct focal points (*) in tissue with g_j(PC) = 0.003 μS and ρ_oeff = 2.5 kΩ cm and (D) map of I_Na,max of the same tissue with a contour map of activation times overlaid. The dashed line represents a line of observation points along the longitudinal axis.

Effect of increased interstitial resistivity on conduction delays and wavefront breakthroughs in poorly coupled tissue

In the second part of the study, we investigated the combined effect of cell arrangement and increased ρ_oeff in regions of tissue with source–load mismatch. As shown in Table 1, increasing ρ_oeff from 0.5 to 2.5 kΩ cm in UN, BW, and RAND tissues with g_j(PC) = 0.01 μS caused the longitudinal conduction delay at the transition boundary to decrease by 46, 23, and 38%, respectively (P < 0.01). In UN and BW tissues, the transverse conduction delay increased by 4%; in contrast, the transverse conduction delay in RAND tissues decreased by 5% when ρ_oeff was increased (P < 0.01).

We then investigated the effect of increased ρ_oeff in tissue with g_j(PC) = 0.003 μS, close to onset of conduction block. The average conduction delay along the transition boundary decreased from 11.5 ± 4.9 to 4.36 ± 1.6 ms and the maximum sodium current at the transition boundary increased from 300 ± 51 to 360 ± 29 μA/cm². The decrease in conduction delay at discrete sites along the boundary facilitated propagation and caused the total number of breakthrough sites during longitudinal propagation to increase from 4 to 10 as shown in Figure 4C. At one site along the longitudinal axis (node number = 200), a long conduction delay of 18.7 ms almost at the point of block in Figure 4A decreased to 2.6 ms, resulting in wave breakthrough in Figure 4C. Similarly, to the case with normal ρ_oeff, the pattern of breakthroughs as well as the pattern of sodium current at the boundary between the two regions remained heterogeneous (Figure 4C and D). Increasing interstitial resistivity in regions with source–load mismatch may allow abnormal ectopic activity that would normally be contained in small regions of tissue to breakthrough and cause widespread reentry in a larger mass of tissue.

Discussion

In this study, we used inhomogeneous 2-D microstructural computer models to investigate the effect of microscale changes in intracellular and interstitial architecture on variability in conduction properties and conduction block. A key finding of this study is that close to the onset of conduction block, microstructural heterogeneity leads to large spatial variations in maximum sodium current and conduction delay and to long conduction delays followed by localized wavefront breakthroughs along the border between well-coupled and poorly coupled tissue. The size scale of the microheterogeneity created by variations in cell shape and cell arrangement was on the order of a single cell or smaller (30–100 μm). The sharp increase in the sensitivity of wavefront propagation to microheterogenity in cardiac structure near the onset of conduction block is consistent with a study by Shaw and Rudy²⁸ that showed that the change in maximum upstroke velocity and I_Na,max as a function of gap junction conductance in homogeneous fibres steepens sharply for large gap junction conductances because of the long period of subthreshold depolarization which inactivates sodium channels. Studies in inhomogeneous 1-D fibres have also shown steep decreases in the maximum sodium current and large increases in conduction delay at the transition region between well-coupled and poorly coupled fibre segments.¹² As shown in earlier studies, the variation in sodium current across the poorly coupled cell is highly dependent on the length of the cell and the resistance of the cell, which suggests that near the onset of conduction block in poorly coupled tissue, small inherent variations in cell size and shape may also modulate the transition to conduction block.^11,17,29 In this 2-D study, the sharp decrease in I_Na,max near the transition region was accompanied by high levels of I_Na,max close to the sites of wavefront breakthrough (Figure 4B and D). This decrease in I_Na,max followed by an increase in I_Na,max along the axis of propagation has been observed in 2-D computer studies of wavefront propagation through an expansion site and has been attributed to a decrease in the driving force during the expansion of the wavefront into an area of increasing load.³⁰ Increased variation in conduction delay and maximum sodium current in regions of tissue with source–load mismatch leads to isolated wavefront breakthroughs similar to that observed at expansion sites and may increase the likelihood of unidirectional conduction block and reentrant circuits in small areas of diseased tissue.²⁶

The co-localization of regions of increased interstitial resistivity with regions of reduced gap junction coupling in tissue with source–sink mismatch leads to a paradoxical improvement in conduction and an increase in the number of sites of wavefront breakthrough. Increasing the interstitial resistivity reduces source–load mismatch at the gap junction level, which creates small isthmuses for wavefronts to breakthrough and activate healthy surrounding tissue. This finding is consistent with a study by Rohr et al.,³¹ which investigated the onset of conduction block caused by structural discontinuities and showed that partial uncoupling of the current load or both the current source and current load can improve conduction. Continuous models that incorporate variations in resistivity in regions of tissue with source–sink mismatch may also be able to capture the complex dynamics at the boundary but may not be able to effectively account for the paradoxical effects caused by increasing effective interstitial resistivity in the regions of tissue with high resistivity caused by gap junction uncoupling. A more detailed explanation of the differences between continuous and discrete models in the case of increased interstitial resistivity can be found in a recent study by Hubbard and Henriquez.¹⁷ Although this cited study primarily focuses on 1-D propagation, many of the qualitative findings about the effect of cell size and increased interstitial resistivity on propagation are applicable in 2-D as well. As shown in recent computational studies, the BW observed in 2-D tissue improves conduction in model tissues by reducing the effective resistivity.^22,32 Lateral decoupling increases the effective resistivity and increases the influence of the gap junction on longitudinal propagation, which may also account for some of the stronger effects of gap junction distribution and increased interstitial resistivity on longitudinal conduction in poorly coupled tissue.^22,33

The tissue resistances, cell arrangements, and cell shapes used in these studies were randomly created so that we could observe conditions of slow conduction and the onset of conduction block. In real tissue preparations, additional heterogeneity in gap junction expression and distribution and fibre orientation will also affect the complexity of the pattern of conduction and block.³⁴ However, we believe that the general findings of this study provide a qualitative insight into how interstitial and intracellular microstructural architecture influence wavefront breakthrough in regions of tissue that have significant source–sink mismatch. Additional studies using in vitro cardiac monolayers that correlate with large-scale microstructural computer models may provide valuable information about the behaviour of ectopic activity in critical regimes and the mechanisms underlying cardiac arrhythmias.

Conflict of interest: none declared.

Funding

This work was supported by the National Institutes of Health (HL093711-01A2 to C.H.) and the United Negro College Fund/Merck (Graduate Dissertation Fellowship to M.L.H.).