Mechanical discoordination increases continuously after the onset of left bundle branch block despite constant electrical dyssynchrony in a computational model of cardiac electromechanics and growth

Abstract

Aims

To test whether a functional growth law leads to asymmetric hypertrophy and associated changes in global and regional cardiac function when integrated with a computational model of left bundle branch block (LBBB).

Methods and results

In recent studies, we proposed that cardiac myocytes grow longer when a threshold of maximum fibre strain is exceeded and grow thicker when the smallest maximum principal strain in the cellular cross-sectional plane exceeds a threshold. A non-linear cardiovascular model of the beating canine ventricles was combined with the cellular growth law. After inducing LBBB, the ventricles were allowed to adapt in shape over time in response to mechanical stimuli. When subjected to electrical dyssynchrony, the combined model of ventricular electromechanics, haemodynamics, and growth led to asymmetric hypertrophy with a faster increase of wall mass in the left ventricular (LV) free wall (FW) than the septum, increased LV end-diastolic and end-systolic volumes, and decreased LV ejection fraction. Systolic LV pressure decreased during the acute phase of LBBB and increased at later stages. The relative changes of these parameters were similar to those obtained experimentally. Most of the dilation was due to radial and axial fibre growth, and hence altered shape of the LVFW.

Conclusion

Our previously proposed growth law reproduced measured dyssynchronously induced asymmetric hypertrophy and the associated functional changes, when combined with a computational model of the LBBB heart. The onset of LBBB leads to a step increase in LV mechanical discoordination that continues to increase as the heart remodels despite the constant electrical dyssynchrony.

Introduction

In patients, left bundle branch block (LBBB) leads to asymmetric hypertrophy, in which the septal-to-left ventricular (LV) free wall (FW) volume ratio decreases over several weeks to months.^1–5 This ventricular remodelling is characterized by overall LV dilation, accompanied by a reduction in LV ejection fraction (EF) and septal hypoperfusion.

Previously, we have proposed a stimulus for myocyte axial growth driven by an imbalance between maximum fibre strain and a homeostatic set-point, whereas myocyte radial growth was driven by an imbalance between the smallest maximum principal strain in the cellular cross-sectional plane and a homeostatic set-point value.⁶ This growth law reproduced most observed hypertrophic and physiological responses, including both acute and chronic changes in structure and function, when combined with two comprehensive computational models of the pressure-overloaded (by aortic stenosis) and volume-overloaded (by mitral regurgitation) canine heart.

In the current study, we tested whether the previously proposed growth law⁶ incorporated into a computational model of ventricular canine electromechanics with a closed-loop circulation would lead to physiological structural and functional changes as observed during experimental chronic LBBB in the dog. We compared our results with the chronic dog studies of the Prinzen group at Maastricht University¹ whose findings resembled those of changes in the human. Briefly, in their studies, LBBB was induced in dogs by radio frequency ablation. Electrocardiogram, haemodynamic measurements, and two-dimensional echocardiography of the LV were obtained at baseline and every 2 weeks up to 16 weeks of LBBB, whereas magnetic resonance imaging tagging experiments were performed at baseline, 3 ± 1 weeks and 15 ± 1 weeks after induction of LBBB.

Methods

The cardiovascular model used in this study has been published previously.⁶ Briefly, a non-linear finite-element model of the beating canine right and left ventricles with realistic fibre anatomy was used. Passive material properties were described by a transversely isotropic strain energy law proposed by Guccione et al.⁷ and was slightly compressible.⁸ The contractile properties were described by a Hill-type model⁹ that was slightly modified.¹⁰ The finite-element model was coupled to a lumped-parameter model of the circulation.¹¹ Peripheral resistance was regulated to obtain a cardiac output of 1.8 L/min and mean aortic pressure was regulated by continuously varying total blood volume.¹¹ The effect of constant vs. variable blood volume on LV dilation was tested with additional simulations. Regional electrical activation times were prescribed to match those during LBBB, and were computed by a model of cardiac electrophysiology.^10,12 The electrical activation initiated myofibre contraction in the mechanics model at a basic cycle length of 750 ms. The range of electrical activation times in the LBBB simulation (similar to QRS width) was 109 ms.

The same mechanical stimuli formulation for fibre axial and radial growth as we have proposed previously⁶ was used in the current study. All parameter values from the previous study were also duplicated, except that in the current study the values for the maximum rates for fibre axial and radial growth were lower than those in the previous study and the maximum axial-to-radial growth rate ratio was nine times lower than in the previous study (see Discussion). Tissue growth was modelled by the multiplicative decomposition of the deformation gradient F first proposed by Rodriguez et al.,¹³ which decomposes the deformation gradient tensor into plastic (growth) and elastic (from which strains and stresses are calculated) components. During a 16-week growth simulation, the model ventricles adapted in shape (see Supplementary material online) due to the dyssynchronous electrical activation and hence altered mechanical stimuli imposed at the cellular level.

Numerical implementation

The simulations were solved with Continuity 6.4b (http://www.continuity.ucsd.edu) in parallel using 12 processors, on a Linux cluster with dual Intel XeonX5650 6-core 2.66 × GHz processors. A time step of 1 ms was used for the simulations of the cardiac cycles, whereas 10 days were used for the growth simulation time step. The non-linear finite-element models were solved with a modified Newton–Raphson iteration scheme. Integration was performed with 3 × 3 × 3 Gaussian quadrature points. Convergence was reached when both the sum of incremental displacements and the sum of the residuals were lower than 10^–5 mm and 10^–8 N, respectively. The system of linear equations was solved with SuperLU.¹⁴

Results

Model validation

Global function and structure

Model predictions for both acute and chronic changes in global cardiac function were in good agreement with published experimental results (Figure 1 and Table 1). After onset of LBBB, the LV pressure–volume loops shifted to the right (Figure 1), increasing both LV end-diastolic and end-systolic volumes (LVEDV and LVESV, respectively), which decrease LVEF (Figure 2). In the simulations, both LV end-diastolic pressures (LVEDP) and LV dP/dt_max decreased during LBBB throughout the time period simulated. In published experiments,¹ LVEDP and LV dP/dt_max increased in the chronic stage, albeit these changes were not significant. In both model and experiment, systolic LV pressure decreased during the acute phase of LBBB and increased at later stages. Cardiac output decreased in the acute phase and increased back to the initial value in the chronic phase. The relative changes in LVEDV and LV wall mass during LBBB were similar between simulations and experiments (Table 1 and Figure 2). The septal-to-lateral wall mass ratio decreased faster in the simulations than in the experiments (Figure 2). In the case where total blood volume was kept constant, LV wall mass also increased, but LVEDV and LVEF remained virtually unchanged (Figure 2).

Figure 1.

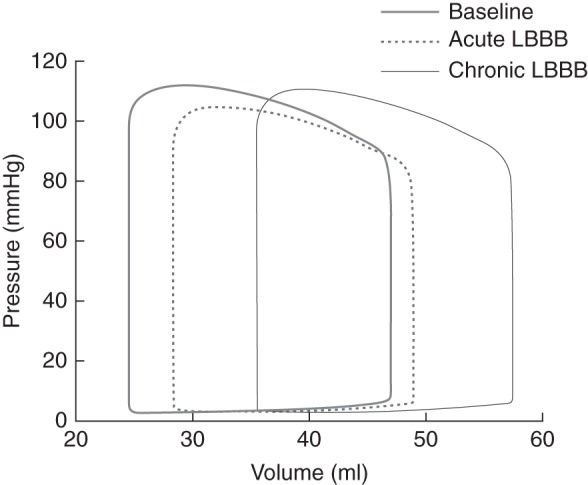
Pressure–volume loops of the normal heart (baseline at 0 weeks), acute left bundle branch block (2.9 weeks), and chronic left bundle branch block (15.7 weeks) simulations.

Table 1.

Haemodynamics and structure from baseline, acute, and chronic left bundle branch block simulations and experiments^1,15

	Baseline		Acute LBBB (2 weeks)		Chronic LBBB (16 weeks)
	Simulation	Experiment	Simulation	Experiment	Simulation	Experiment
Heart rate (b.p.m.)	80	101 ± 171	80	121 ± 471	80	88 ± 301
			0%	+20%	0%	−27%
LV dP/dtmax (mmHg/s)	2167	1803 ± 9091	2017	1313 ± 4461	1964	1552 ± 5801
			−7%	−35%	−9%	−23%
LVPmax (mmHg)	112	105 ± 415	105	100 ± 515	109a	111 ± 4a15
			−6%	−5%	+4%	+6%
LVEDP (mmHg)	6.7	8 ± 61	5.9	6 ± 71	5.8	8 ± 51
			−12%	−25%	−28%	0%
Cardiac output (L/min)	1.8	3.3 ± 1.11	1.7	2.0 ± 0.9*1	1.8	3.2 ± 1.31
			−6%	−39%	0%	−3%
LVEDV (mL)	46.9	104 ± 311	49.6	110 ± 361	57.8	135 ± 53*1
			+6%	+6%	+23%	+30%
LVEF (%)	48	43 ± 41	42	37 ± 8*1	38	33 ± 6*1
			−13%	−14%	−21%	−23%
LV wall mass (g)	98	126 ± 311	101	135 ± 371	118	145 ± 30*1
			+3%	+7%	+20%	+15%

Values from experiments are mean ± standard deviation. Per cent changes are with respect to baseline.

LV, left ventricular; dP/dt_max, maximal rate of pressure rise; EDP, end-diastolic pressure; EDV, end-diastolic volume; EF, ejection fraction; P_max, peak cavity pressure.

^aChronic LBBB at 8 weeks.

*P < 0.05 compared with baseline.

Figure 2.

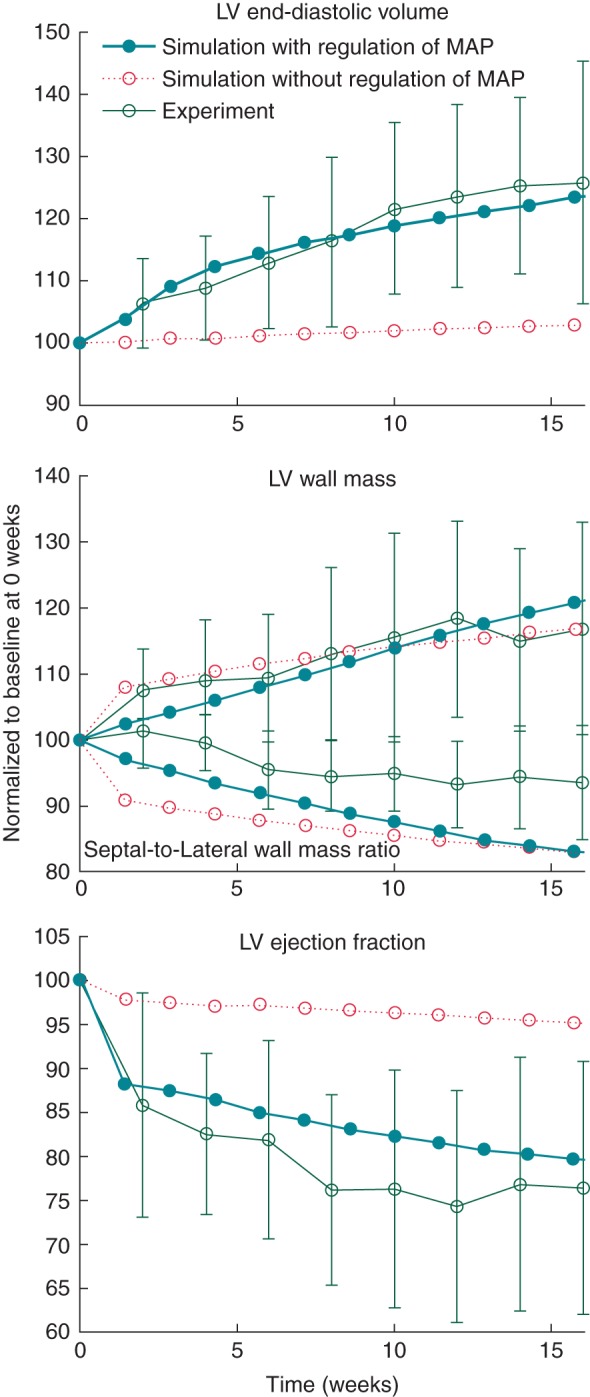
Changes in left ventricular end-diastolic volume (top), left ventricular wall mass and septal-to-lateral wall mass ratio (middle), and left ventricular ejection fraction (bottom) for the simulations in which total blood volume regulated mean aortic pressure (MAP), and in which total blood volume was kept constant (with unregulated mean aortic pressure). The experimental results are redrawn from Ref.¹

Regional function and structure

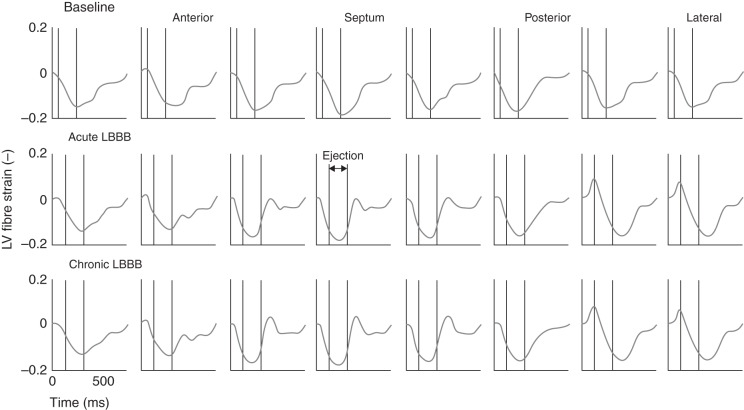
Left ventricular fibre shortening patterns during the baseline, acute and chronic LBBB phases in the simulations were also similar to those from experiments and simulations from previous studies¹⁰ (Figure 3). Compared with normal activation in the baseline heart, fibre shortening during ejection became distributed more non-uniformly during LBBB. As shown in our previous study,¹⁰ early-activated fibres in the septum shortened during isovolumic contraction, continued to shorten during the first part of ejection, and stretched during the late ejection, with a small net effect of shortening during ejection. In the late-activated lateral wall, fibres were stretched during isovolumic contraction (pre-stretched) and shortened during ejection (more than early-activated fibres) exhibiting post-systolic shortening. During chronic LBBB, when the LV has dilated, fibre shortening became distributed more non-uniformly compared with acute LBBB (mechanical discoordination increased as indicated by the indices internal stretch fraction, circumferential uniformity ratio estimate, and coefficient of variation of regional work; see Table 2). Early-activated fibres in the septum exhibited a larger net effect of stretching during ejection, as indicated by the fraction of septal tissue that is being stretched during ejection (fraction of wall tissue stretched during ejection, Table 2). Mean external regional work and circumferential systolic shortening (CS_sys) in the septum continued to decrease during LBBB, whereas the experimental¹ values for septal CS_sys and regional work switched from negative to positive between acute and chronic LBBB, albeit these changes were not significant.

Figure 3.

Left ventricular mid-wall fibre strain during the cardiac cycle around the left ventricular circumference in the baseline heart, during acute (2.9 weeks) and chronic left bundle branch block (15.7 weeks). Note the stretching of septal fibres after aortic valve closure in the left bundle branch block phases (‘septal flash’ or ‘paradoxical septal motion’) which gets exacerbated in the chronic phase compared with the acute one.

Table 2.

Regional left ventricular function from baseline, acute, and chronic left bundle branch block simulations

	Baseline	Acute LBBB (2 weeks)	Chronic LBBB (16 weeks)
Septal CSsys (%)	15.6	4.4	1.8
LVFW CSsys (%)	15.4	17.6	15.6
Mean septal external regional work (kPa)	5.1	1.7	1.1
Mean LVFW external regional work (kPa)	3.9	4.5	4.6
Septal FTS (%)15	0.0	20	38
LVFW FTS (%)15	0.0	0.0	1.4
ISF (−)16	0.002	0.09	0.13
CURE (−)17	0.98	0.77	0.71
COVW (−)10	0.52	0.97	1.09

ISF, internal stretch fraction; CS_sys, systolic circumferential shortening; CURE, circumferential uniformity ratio estimate; COVW, coefficient of variation of regional work; FTS, fraction of wall tissue stretched during ejection.

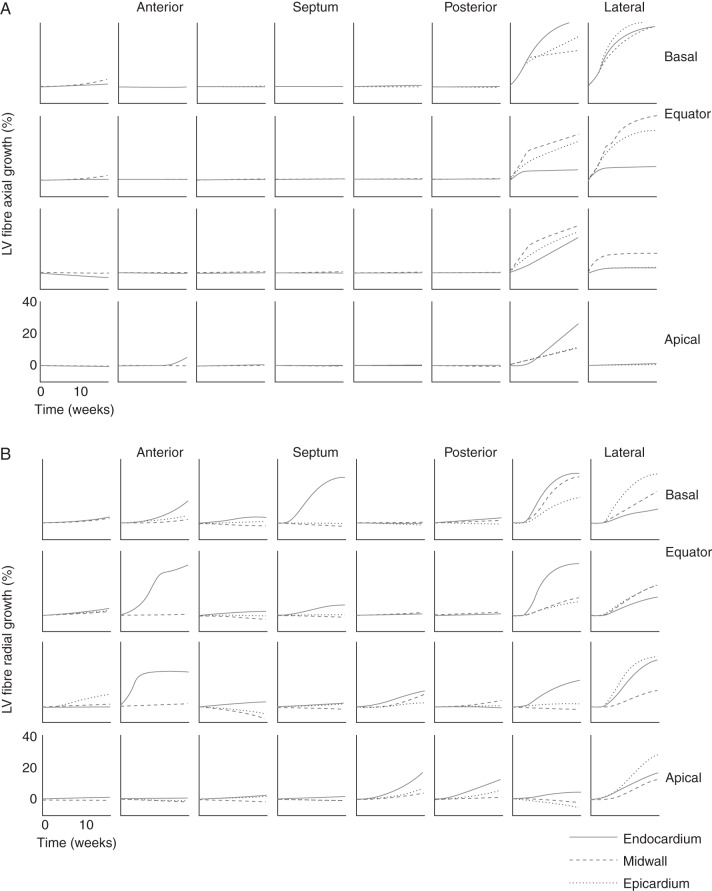
Left ventricular dilation was mostly caused by axial growth of fibres in the postero-lateral wall (Figures 4A and 5), whereas in the septum and anterior wall, fibre axial growth was virtually absent. Fibres also grew in the radial direction for the most part in the postero-lateral wall (Figures 4B and 5). In the septum and anterior walls though, mid-wall fibres decreased in radius to some extent, whereas endocardial fibres grew radially in some regions. These fibre dimensional changes were dependent on electrical activation time (Figure 6), which also has been demonstrated experimentally with LVFW pacing.¹⁸ After 16 weeks of LBBB, LV fibre volumes increased up to 61 ± 35% in the latest activated regions. There was a larger variation in fibre diameter change compared with fibre length change in the early-activated regions (Figure 6).

Figure 4.

Growth of fibres in axial (A) and radial (B) direction throughout the left ventricular wall over the 16 weeks time-course of left bundle branch block starting from baseline at 0 weeks.

Figure 5.

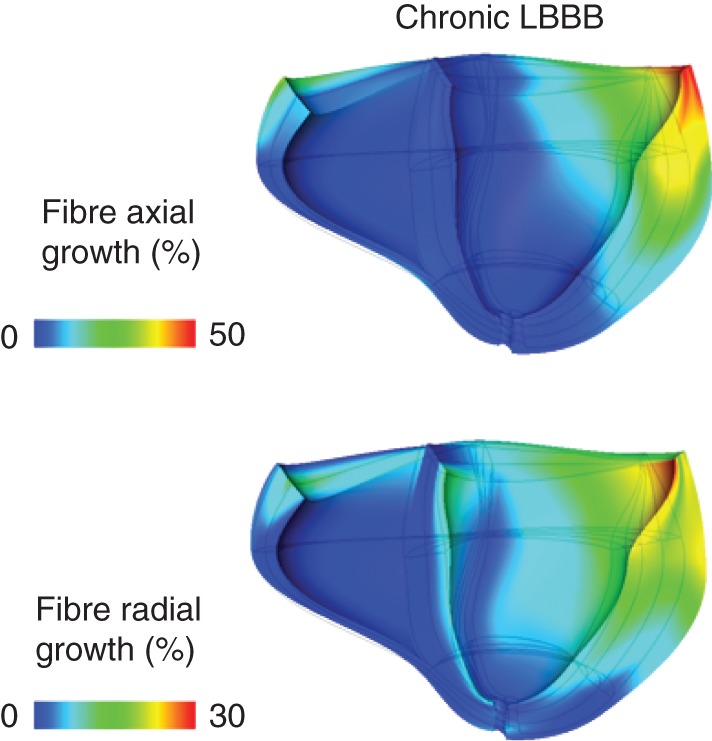
Anterior view of a longitudinal cross-section of the ventricles after 15.7 weeks of left bundle branch block at end-diastole, depicting percentages of fibre axial (top) and radial (bottom) fibre growth. The mesh overlay shows the shape of the ventricles at end-diastole at baseline.

Figure 6.

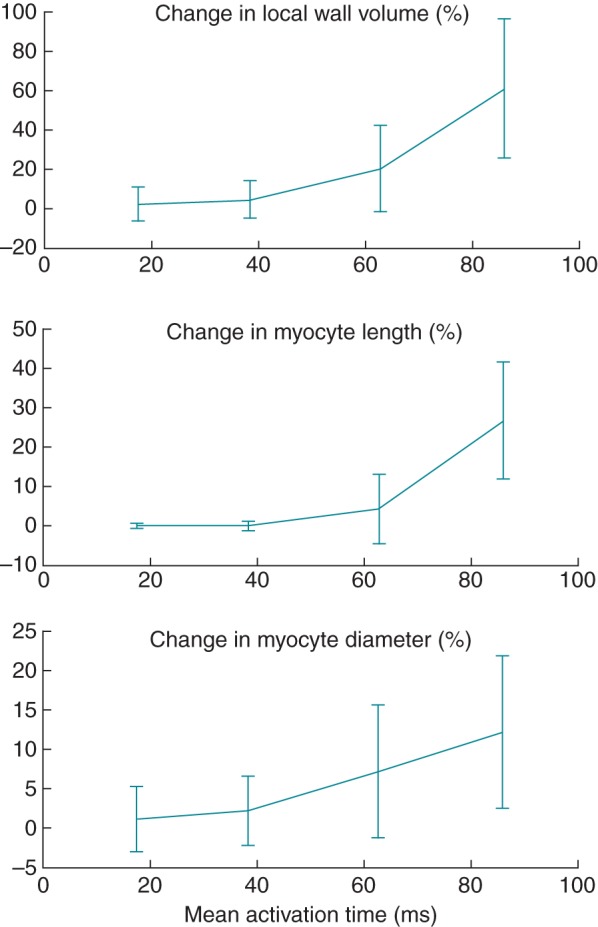
Cell dimension changes in the left ventricular as a function of electrical activation time after 16 weeks of left bundle branch block.

Discussion

The main findings from this study were that (i) our previously proposed growth law, which led to realistic eccentric and concentric hypertrophy in simulations of the volume- and pressure-overloaded heart, is also able to reproduce functional and structural changes in simulations of the LBBB heart. In the present study, hypertrophy was asymmetric—depending on electrical activation times—with an overall eccentric growth of the LV, which is in agreement with canine LBBB experiments. (ii) With acute LBBB, LV mechanical discoordination increased stepwise, and increased continuously thereafter during chronic LBBB, despite constant electrical dyssynchrony, over the time period simulated.

Left bundle branch block has been shown to be an independent risk factor for cardiac mortality.¹⁹ In patients, LBBB is often accompanied by LV dilation, reduced EF, and septal perfusion defects: the canine study by Vernooy et al.¹ showed that these accompanying pathologies can be induced solely by chronic LBBB. In the current study, electrical dyssynchrony (LBBB) caused thickening and dilation in the LVFW, because homeostatic set-points for myocyte growth were exceeded. Dilation and reduced EF were accelerated by inclusion of regulation of mean aortic pressures, for which an increase in total blood volume was required. Mechanical discoordination continued to increase over a period of 16 weeks despite the constant electrical dyssynchrony, and was caused by the combination of electrical dyssynchrony, increase in total blood volume, and ongoing dilation. The interactive effects of dilation and electrical dyssynchrony on mechanical discoordination agree with our previous finding.¹⁰ In that previous computational study, stepwise changes in (symmetric) eccentric hypertrophy and electrical dyssynchrony were prescribed, whereas in the current study a more mechanistic approach was followed in which the electrical dyssynchrony drove the hypertrophic remodelling through a cellular-based growth law.

There were several differences in model setup and growth law parameter values between the current study and our previous computational study of growth induced by pressure and volume overload.⁶ In the current study the values for the maximum rates for fibre axial and radial growth were lower than those in the previous study, and the maximum axial-to-radial growth rate ratio was nine times lower than in the previous study. In addition, in the current study, total blood volume was variable, whereas in the previous study⁶ total blood volume was kept constant during all simulations. These two sets of combinations were necessary in order to match experimental results (lower growth rates and blood volume changes vs. higher growth rates and constant blood volume), and are presumably more realistic. Therefore, in order to maintain the definition of a growth law that exhibits structural and functional changes due to various pathologies that are in agreement with experiments, we performed further simulations of growth in the pressure- and volume-overloaded heart with the parameters from the current study. Structural and functional changes in the volume overload simulation matched well with known experimental results (see Supplementary material online). Although the pressure overload simulation exhibited concentric hypertrophy, the rate of LV mass increase was slower than measured experimentally. Hence, the growth rate for fibre radial growth may still be underestimated, and/or the severities of the aortic stenoses in the experiments and model were not equivalent.

Although we make the assumption that a stimulus for cellular radial growth is associated with a cellular cross-sectional strain, there are other possible candidate stimuli that have been proposed in the literature.^11,20,21 For example, from a set of isometric and shortening experiments with rat right ventricular papillary muscles, Guterl et al.²¹ concluded that myocyte shape is regulated by systolic shortening and/or diastolic lengthening and they found that systolic stress played little or no role in the growth process. Whereas diastolic extension has been used in the current study as a stimulus for fibre axial growth, systolic shortening as a stimulus for fibre radial growth could also be maintaining a minimum sarcomere length or change of sarcomere length¹¹ in a cardiac cycle.

Patient-specific modelling is the development of computational models of human pathophysiology that are individualized to patient-specific clinical measurements.²² Most patient-specific models however only predict acute outcomes, thus ignore chronic changes (for exceptions, see Refs.^23,24). Combining growth models with patient-specific organ models (e.g. cardiovascular system, skeletal muscle, and bone²²) will become invaluable in predicting long-term effects of medical devices, surgeries, and therapies,⁶ in which reverse remodelling is key, for example, in valve replacement/repair,^25,26 cardiac resynchronization therapy,²⁷ cardiac restraint device therapy,^28,29 and cardiac assist device therapy.^30,31

In the current study, we modelled the progression to compensated hypertrophy. In the future, cell-level growth models can serve as a framework for implementing increased mechanistic detail in (defective) mechanotransduction pathways³² and microstructural models. This will allow for multi-scale simulation studies of decompensated heart failure by investigating effects of altered remodelling pathways at the subcellular level to cell, tissue, organ, and systems levels.

Limitations

We did not include electrophysiological remodelling mechanisms in our study. Dyssynchronous activation leads not only to asymmetric wall thickness changes and a redistribution of coronary perfusion,^1,33 but also to changes in cellular electrophysiology. For example, Jeyaraj et al.³⁴ showed that in dogs, electrophysiologically remodelled regions remote from the pacing site correlated best with increased circumferential strain and thus suggested strain was part of a mechanoelectric feedback mechanism. As electrophysiological remodelling affects mechanics, it will be interesting to include electrophysiological remodelling mechanisms^35,36 in our current ventricular model of electrical dyssynchrony and growth.

In the model, the baro-reflex effects on heart rate were not taken into account. The experiments showed that heart rate varied over the course of the measured time period: it increased at 2 weeks of LBBB and dropped below baseline at 16 weeks of LBBB. Variability however was high and rates were not significantly different with time compared with baseline. Since we did not know how heart rate varied at all time points, in the model we chose to keep heart rate constant. Inclusion of more acute control systems, however, would be an interesting future study.

We employed a so-called weak model of electromechanics, in which electrical activation times are pre-computed by a ventricular model of electrophysiological conduction and used as input in the mechanics model to initiate fibre contraction. Hence, for each calculated cardiac cycle and during growth evolution, the activation pattern remained unchanged. In reality however, dilation due to long-term pacing may result in a greater dispersion of activation and repolarization, especially in combination with electrophysiological remodelling and in the transition to heart failure. Hence, increasing electrophysiological dispersion may exacerbate mechanical discoordination over time.

In conclusion, our previously proposed growth law interacted with a computational mechanics model of the contracting heart and reproduced measured asymmetric hypertrophy in response to LBBB in the heart. With acute LBBB, LV mechanical discoordination increased stepwise, and increased continuously thereafter during the simulation period of chronic LBBB, despite constant electrical dyssynchrony. Hence, tissue growth further exacerbates mechanical discoordination in response to electrical dyssynchrony.

Supplementary material

Supplementary material is available at Europace online.

Conflict of interest: J.H.O and A.D.M. are co-founders of Insilicomed, Inc., a licensee of University of California San Diego-owned software (Continuity) used in this research. R.C.P.K. is a consultant to Insilicomed. Insilicomed was not involved in this research.

Funding

This work was supported by grants from the National Center for Research Resources (5P41RR008605-19), the National Institute of General Medical Sciences (P41 GM103426-19), from the National Institutes of Health and National Institutes of Health grant (R01 HL96544 to A.D.M.).