Abstract
Identifying significant determinants of groundwater nitrate contamination is critical in order to define sensible agri-environmental indicators that support the design, enforcement, and monitoring of regulatory policies. We use data from approximately 1200 Austrian municipalities to provide a detailed statistical analysis of (1) the factors influencing groundwater nitrate contamination and (2) the predictive capacity of the Gross Nitrogen Balance, one of the most commonly used agri-environmental indicators. We find that the percentage of cropland in a given region correlates positively with nitrate concentration in groundwater. Additionally, environmental characteristics such as temperature and precipitation are important co-factors. Higher average temperatures result in lower nitrate contamination of groundwater, possibly due to increased evapotranspiration. Higher average precipitation dilutes nitrates in the soil, further reducing groundwater nitrate concentration. Finally, we assess whether the Gross Nitrogen Balance is a valid predictor of groundwater nitrate contamination. Our regression analysis reveals that the Gross Nitrogen Balance is a statistically significant predictor for nitrate contamination. We also show that its predictive power can be improved if we account for average regional precipitation. The Gross Nitrogen Balance predicts nitrate contamination in groundwater more precisely in regions with higher average precipitation.
Keywords: Nitrate concentration, Groundwater quality, Gross Nitrogen Balance, Agriculture, Regression analysis, Austria, Land use and nitrate contamination, Nitrate policy, OECD agri-environmental indicators
Highlights
► We provide a statistical analysis of determinants of groundwater nitrate levels. ► We assess the capacity of the Gross Nitrogen Balance to predict nitrate levels. ► High average temperature and precipitation decrease groundwater nitrate levels. ► The Gross Nitrogen Balance is a stat. significant predictor for nitrate levels. ► Its capacity can be improved if precipitation is taken into account.
1. Introduction
Nitrogen fertilizers are applied extensively in agriculture to increase crop production, but excess nitrogen supplies can cause air, soil, and water pollution. Arguably one of the most widespread and damaging impacts of agricultural overapplication of nitrogen fertilizers is the degradation of groundwater quality and contamination of drinking water supplies, which can pose immediate risks to human health (Lord and Anthony, 2002; Schroeder et al., 2004). The EU Directive 91/676/EEC, which protects waters against pollution caused by nitrates from agricultural sources, sets the acceptable threshold of nitrate concentration in groundwater at 50 mg/l as nitrate. The EU Directive 2006/118/EC also attempts to protect groundwater against pollution and deterioration by suggesting that Member States establish quality standards, develop methodologies for assessing and monitoring groundwater quality, and implement measures supporting groundwater protection, including changes to farming and forestry practices.
An assessment of the impact and magnitude of nitrate leaching from agricultural activities is necessary in order to design and implement appropriate regulatory policies that support these goals. Consequently, a meaningful indicator is needed to allow governments to implement effective policy measures and monitor policy compliance (de Ruijter et al., 2007; Lord and Anthony, 2002; Watson and Atkinson, 1999). The most commonly used indicator to monitor and assess nitrogen use across countries is the Gross Nitrogen Balance (EEA, 2001; OECD, 2007; Parris, 1998).
These concerns about groundwater nitrate contamination have led to the following research questions: (1) What are the factors that determine nitrate contamination in groundwater? In particular, which agricultural practices tend to contaminate groundwater and what is the influence of external factors such as weather conditions and soil characteristics? (2) Is the Gross Nitrogen Balance a good predictor of groundwater contamination and is its frequent use in guiding policies justified?
Researchers have identified several factors affecting nitrate groundwater contamination, including fertilizer levels and build-up of soil organic matter, which can result in a large mineral nitrogen pool and thus in a higher risk of nitrate leaching (Korsaeth and Eltun, 2000; Sieling and Kage, 2006). Furthermore, manure management, crop cultivation practices (Lord and Anthony, 2002; Rankinen et al., 2007), soil texture (de Ruijter et al., 2007), and precipitation surpluses (Boumans et al., 2001; Elmi et al., 2002; Fraters et al., 1998; Salo and Turtola, 2006) have been found to influence the extent of agricultural nitrate leaching. Potential determinants of nitrate leaching have been investigated using several methods. For instance, farm and field experiments have been performed (Boumans et al., 2001; de Ruijter et al., 2007), controlling for alternative cropping systems (Korsaeth and Eltun, 2000), management practices (Rankinen et al., 2007; Sieling and Kage, 2006), and soil types (Salo and Turtola, 2006). Even though these experiments provide precise results and insights, they have the disadvantage of being limited in scale and time such that routine applications may not be feasible, or the data is not suited for generalization (Buczko et al., 2010). Devising measures of groundwater contamination on a national scale can be cumbersome and difficult. Groundwater sampling is costly and nitrate concentration often responds slowly to changes in agricultural management practices (Lord and Anthony, 2002; OECD, 2008), making it difficult to determine causality. Additionally, direct measurements and long-term monitoring are often influenced and distorted by weather events (Lord and Anthony, 2002). Bio-physically based process models are often used to simulate the nitrogen cycle at field to watershed scale (Buczko et al., 2010; Cannavo et al., 2008; van der Laan et al., 2010). However, data requirements, model parameterizations and initial assumptions may limit their use (Buczko et al., 2010; Cannavo et al., 2008).
Alternatively, risk indicators or agri-environmental indicators, such as the Nitrogen Balance, are often used to predict nitrate leaching in groundwater (OECD, 2007). Nitrogen Balances are appreciated for being objective, transparent, and readily verified agri-environmental indicators (Lord and Anthony, 2002). As such, they raise awareness about nutrient use issues and support the enforcement of regulatory nutrient management policies (Oenema et al., 2003). Nitrogen Balances can be assessed at different degrees of complexity and can be computed on a farm as well as national scale (Oenema et al., 2003; Watson and Atkinson, 1999). There are three types of Nitrogen Balances commonly in use: (i) the farm-gate balance accounts for nutrients in all kinds of products which enter and leave a farm. This method allows researchers to obtain precise results but is difficult to compute on the regional level (Lord and Anthony, 2002; OECD, 2007; Schroeder et al., 2004); (ii) the soil surface balance, such as the Gross Nitrogen Balance as suggested by the Organisation for Economic Co-operation and Development (OECD), lists inputs and outputs to the soil (Lord and Anthony, 2002; OECD, 2007; Schroeder et al., 2004); and (iii) the soil system balance accounts for inputs and outputs to the soil as well as for recycling of nutrients within the system and changes in the soil nutrient pool (Oenema et al., 2003). The OECD suggests the Gross Nitrogen Balance methodology as the appropriate indicator to calculate comparable nitrogen balances on a regional or national scale (OECD, 2007).
However, the degree to which the indicator is capable of reflecting actual nitrate leaching effects is unclear (de Ruijter et al., 2007; Lord and Anthony, 2002; Sieling and Kage, 2006), because the Gross Nitrogen Balance is a theoretical concept and as such only captures the potential for groundwater contamination. This is an important point when extrapolating from nutrient balance trends to actual environmental impacts (OECD, 2008). Much of the scientific literature agrees that Nitrogen Balances perform rather poorly when predicting observable nitrate concentration levels (Buczko et al., 2010; Korsaeth and Eltun, 2000; Oenema et al., 2003; Rankinen et al., 2007; Salo and Turtola, 2006; Schroeder et al., 2004; Sieling and Kage, 2006). For instance, de Ruijter et al. (2007) could not find clear results concerning the appropriateness of the Nitrogen Balance as an indicator of nitrate contamination. Research studies assess the concordance of actual nitrate leaching and predictions made by the Nitrogen Balance by correlation analysis (Buczko et al., 2010; Lord and Anthony, 2002). Rankinen et al. (2007) performed an analysis of covariance to investigate the potential of the Nitrogen Balance to predict nitrate leaching. Many researchers have also used regression analyses to explain nitrate leaching with a limited number of explanatory variables, such as the Nitrogen Balance and annual precipitation sums (Buczko et al., 2010; Korsaeth and Eltun, 2000; Rankinen et al., 2007; Salo and Turtola, 2006; Sieling and Kage, 2006). These statistical analyses have two important weaknesses. First, they are often limited geographically as well as temporally. Second, they usually do not take into account (i.e. do not “control for”) all relevant external factors that could potentially influence nitrate contamination. This can result in a so-called omitted variable bias, or the wrong attribution of effects to certain factors.
We employ a regression approach to systematically investigate the determinants of groundwater nitrate contamination as well as the effectiveness of the Gross Nitrogen Balance as a predictor of nitrate contamination in groundwater. We construct an extensive and detailed panel dataset on the Austrian situation that includes time series of nitrate concentration levels in groundwater, land cover types, land uses, as well as soil and weather data for around 1200 Austrian municipalities between 1992 and 2007. The temporal and geographical magnitude of our analysis is larger than in other studies. Additionally, our dataset allows us to account for many potential explanatory variables, which makes our analysis less prone to omitted variable bias than other statistical investigations. We are able to quantify the marginal effects of several potential explanatory variables and their relative and absolute magnitude. In addition, our framework allows us to forecast potential nitrate contamination in groundwater given agricultural practices as well as weather and soil conditions (i.e. counterfactual experiments).
2. Materials and methods
2.1. Data sources and manipulation
Concentrations of groundwater nitrate in mg/l were obtained from the Federal Environment Agency Austria (Umweltbundesamt, 2010b). This data is available on a quarterly basis from 01/1992 to 04/2008 for 1238 Austrian municipalities. The number of observations in each time period varies (i.e. nitrate concentration is not available for every time period and municipality). In the course of this analysis we aggregate the quarterly values to annual average values for each municipality.
Data on daily precipitation (in millimeters) and maximum temperature (in degrees Celsius) between 1975 and 2007 were provided by the Central Institute for Meteorology and Geodynamics (ZAMG) (Strauss et al., 2012). The weather observations stem from 34 weather stations, which we assign to the respective municipalities. We have aggregated the daily weather observations to annual average values for each municipality.
Data on land cover in Austria was taken from the CORINE Land Cover database 2006 (Umweltbundesamt, 2010a). Land covers, such as buildings, cropland, grassland, and forests have been computed as a proportion of total size of the municipality. For our analysis, we assume land covers to be time-constant.
Detailed agricultural information on crop cultivation, permanent grassland, number and category of livestock is provided by the Integrated Administrative and Control System (IACS) database (BMLFUW, 2010b). The data is available on a farm level and on an annual basis for 1999–2008. The IACS database provides information on cropland (in hectares) for approximately 70 crops. We aggregate these crops into four crop groups: (i) oilseed and protein crops, (ii) cereal and maize crops, (iii) row crops and vegetables, and (iv) forage crops. These groups are aggregated on municipality level and included into our regression models as proportion of total municipality territory. The sum of the proportion of permanent grassland and the proportion of cropland is referred to as agricultural land. The IACS database also provides information on conventional and organic farming systems. We calculate the proportion of organic and conventional farming system per municipality by weighting with the agricultural land of each farm. The resulting indicator takes on a value between 1 and 2, where 1 represents organic and 2 conventional farming systems.
Finally, we integrate two indicators of soil quality into our analysis: Field water capacity at 33 kPa in topsoil (cm3/cm3) and the volume of stones in topsoil. Both variables are taken from the European digital soil map (Balkovic et al., 2007), which provides several data entries per municipality. We aggregate these values on the municipality level and assume the values to be time-constant. Both, field water capacity and volume of stones are proxies for the ability of the soil to retain water.
2.2. Calculating the Gross Nitrogen Balance
Using the described data, we calculate the Gross Nitrogen Balance on the municipality level according to the OECD and EUROSTAT Gross Nitrogen Balance Handbook (2007). The Gross Nitrogen Balance is computed as total nitrogen inputs minus total nitrogen outputs. Inputs to the Gross Nitrogen Balance are (i) biological nitrogen fixation in the soil, (ii) atmospheric deposition of nitrogen compounds, (iii) livestock manure, and (iv) mineral fertilizer. Total nitrogen input is given by the sum of (i) through (iv) (OECD, 2007).
According to OECD (2007), input components are calculated as follows: The quantity of nitrogen fixed in the soil by symbiotic bacteria in kilogram on the municipality level is calculated by multiplying the municipality's total area under cultivation (in hectares) by a nitrogen fixation coefficient for a given crop in kilograms of nitrogen per hectare. The coefficient is provided by the Austrian Agri-environmental Programme (ÖPUL) (OECD, 2010). The atmospheric deposition of nitrogen compounds in kilogram on the municipality level is calculated by multiplying cultivated agricultural area by the nitrogen deposition rate, which is provided by the Federal Environment Agency Austria (OECD, 2010). The quantity of nitrogen excreted by livestock, used as organic fertilizer, is based on the number and category of livestock and calculated using the respective manure coefficient provided by the Austrian Central Statistical Office (OECD, 2010). Calculating the amount of synthetic fertilizer is more challenging. Therefore, OECD (2007) suggests using data on sales of inorganic fertilizer in terms of nitrogen content. We use data on sales of synthetic nitrogen fertilizer for each of the nine Austrian provinces for the years 1998–2007 (except 2000) provided by the Grüner Bericht issued by the Federal Ministry of Agriculture, Forestry, Environment and Water Management (BMLFUW) (BMLFUW, 2010a). To account for the total quantity of fertilizer applied in a municipality, we add the sales of synthetic fertilizer per province and the estimated quantity of nitrogen in livestock manure per province. The total quantities are then distributed among the municipalities within a province according to the hectare size of agricultural land. The sum of organic as well as synthetic fertilizer serves as a proxy of total nitrogen fertilization.
Total nitrogen output as defined by OECD (2007) includes the amount of nitrogen removed per tonne of crop yield. The amount of nitrogen in kilograms removed from harvested crops is estimated by multiplying crop production with coefficients for each major crop category provided by OECD (2010). To calculate total crop production, we rely on average yields per hectare per province as published in the Grüner Bericht (BMLFUW, 2010a), which are available for 2003 through 2008.
Computing total nitrogen input minus total nitrogen output allows us to calculate the Gross Nitrogen Balance in kilograms of nitrogen per hectare of agricultural land on a municipality level for the years 2003 through 2007.
2.3. Descriptive statistics
Table 1 lists the variables we use in our analysis, their measurement unit and source. Table 2 lists detailed descriptive statistics, including average annual nitrate concentration in groundwater; average daily precipitation amounts and average daily maximum temperature; proportion of agricultural land, land cover, and land uses; the Gross Nitrogen Balance and its components; and soil characteristics.
Table 1.
Definitions of variables and source.
| Variable | Definition | Measurement unit | Data source |
|---|---|---|---|
| Nitrate | Annual average content of nitrate in groundwater per municipality | mg/l | Umweltbundesamt (2010b) |
| Precip | Average daily amount of precipitation per year per municipality | mm | ZAMG (Strauss et al., 2012) |
| Temp | Average daily maximum temperature per year per municipality | °C | ZAMG (Strauss et al., 2012) |
| vs | Average volume of stones in the topsoil per municipality | % | European digital soil map (Balkovic et al., 2007) |
| fwc | Average field water capacity at 33 kPa in the topsoil per municipality | cm3/cm3 | European digital soil map (Balkovic et al., 2007) |
| NBal | Gross Nitrogen Balance per municipality | kg/ha | Own calculation according to OECD Handbook (2007) |
| Fert | Total amount of Fertilizer per municipality | kg/ha | Own calculation according to OECD Handbook (2007) |
| Withd | Total amount of nitrogen withdrawal per municipality | kg/ha | Own calculation according to OECD Handbook (2007) |
| Landuse_grassland | Proportion of grassland per municipality | % | CORINE Land Cover database 2006 |
| Landuse_crops | Proportion of cropland per municipality | % | CORINE Land Cover database 2006 |
| Landuse_buildings | Proportion of buildings per municipality | % | CORINE Land Cover database 2006 |
| Landuse_forest | Proportion of forest per municipality | % | CORINE Land Cover database 2006 |
| PropAL | Proportion of agricultural land per municipality | % | IACS database (1999–2008) |
| Landcover_oilseed & proteins | Proportion of oilseed and protein crops per municipality | % | IACS database (1999–2008) |
| Landcover_forage crops | Proportion of forage crops per municipality | % | IACS database (1999–2008) |
| Landcover_cereal & maize | Proportion of cereal and maize per municipality | % | IACS database (1999–2008) |
| Landcover_row crops & veg | Proportion of row crops and vegetables | % | IACS database (1999–2008) |
| Farming_system | Weighted indicator for organic/conventional cultivation per municipality | 1 (org.)–2 (conv.) | IACS database (1999–2008) |
Table 2.
Summary statistics.
| Variables | Observations | Time period | Mean | Standard deviation | Min | Max |
|---|---|---|---|---|---|---|
| Nitrate | 15,423 | 1992–2008 | 20.62 | 28.69 | 0.00 | 801.21 |
| Precip | 14,169 | 1975–2007 | 2.78 | 1.30 | 0.96 | 10.84 |
| Temp | 14,169 | 1975–2007 | 12.58 | 2.65 | 3.22 | 23.54 |
| Landuse_oilseed & protein | 9974 | 1999–2008 | 0.03 | 0.04 | 0.00 | 0.33 |
| Landuse_forage crops | 7856 | 1999–2008 | 0.04 | 0.04 | 0.00 | 0.61 |
| Landuse_cereal & maize | 7856 | 1999–2008 | 0.19 | 0.21 | 0.00 | 3.57 |
| Landuse_row crops & veg | 7856 | 1999–2008 | 0.02 | 0.05 | 0.00 | 0.80 |
| PropAL | 9974 | 1999–2008 | 0.46 | 0.31 | 0.00 | 5.20 |
| Farming_system | 9228 | 1999–2008 | 1.87 | 0.21 | 1.00 | 2.00 |
| Landcover_grassland | 1087 | Time constant | 0.09 | 0.13 | 0.00 | 0.79 |
| Landcover_cropland | 1087 | Time constant | 0.24 | 0.29 | 0.00 | 0.97 |
| Landcover_buildings | 1087 | Time constant | 0.09 | 0.12 | 0.00 | 0.98 |
| Landcover_forest | 1087 | Time constant | 0.45 | 0.28 | 0.00 | 0.96 |
| fwc | 1087 | Time constant | 0.38 | 0.04 | 0.27 | 0.47 |
| vs | 1087 | Time constant | 8.63 | 4.07 | 1.00 | 15.00 |
| Nbal | 4870 | 2003–2007 | 39.99 | 24.05 | −28.24 | 143.69 |
| Fert | 4870 | 2003–2007 | 99.20 | 42.98 | 0.08 | 181.92 |
| Withd | 4870 | 2003–2007 | 99.76 | 29.88 | 0.02 | 172.61 |
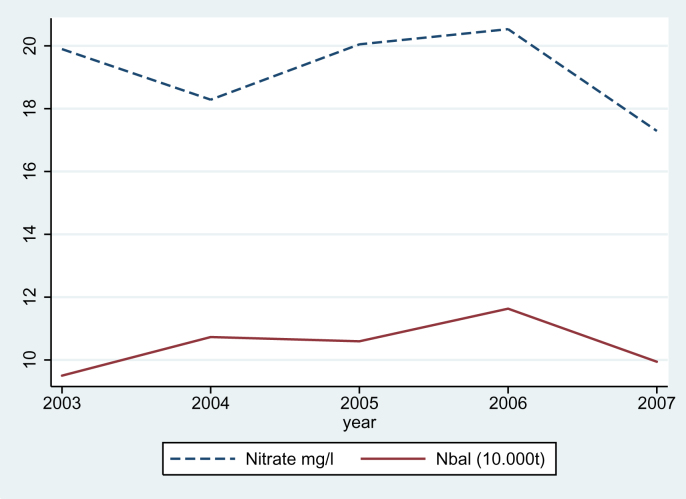
Fig. 1 shows the correlation between annual average nitrate concentration in Austrian groundwater (mg/l) and the Gross Nitrogen Balance (in 10.000 t). It is apparent that the trends are similar – a high value of the Gross Nitrogen Balance correlates with a relatively high concentration of nitrate in groundwater. This is confirmed by the Spearman rank correlation coefficient, which has a value of 0.22. A p-value of zero rejects the null hypothesis that the Gross Nitrogen Balance is statistically independent of nitrate concentration in groundwater. There is a downward trend of average nitrate concentration in groundwater in Austria. Nitrate concentration in the entire country has on average decreased over the past years from 26 mg/l in 1992 to 21 mg/l in 2008. The 50 mg/l acceptable threshold of nitrate concentration in groundwater (EU Directive 91/676/EEC) is rarely reached in Austrian municipalities on average. However, there is a high variation among the nine provinces of Austria. Nitrate concentration is traditionally low in the provinces of Salzburg, Tirol, and Vorarlberg, whereas the concentration is relatively high in Wien, Niederösterreich, and Burgenland.
Fig. 1.
Average nitrate concentration (in mg/l) in Austrian groundwater and the Nitrogen Balance (in 10.000 t).
Data on the soil characteristics field water capacity and volume of stones in topsoil is available for the year 2007 and assumed constant in all analyses. The average field water capacity at 33 kPa is 0.38 cm3/cm3 with a standard deviation of 0.04 cm3/cm3 (Table 2). Field water capacity exhibits a statistically significant negative Spearman rank correlation coefficient with nitrate concentration in groundwater of −0.47. The second soil characteristic included in our analysis is the volume of stones in topsoil. The average volume of stones in topsoil is 8.63% for all of Austria with a standard deviation of 4.07% (Table 2). The Spearman rank correlation for volume of stones in topsoil and nitrate concentration is statistically significant and takes on the value 0.23.
2.4. Empirical method
Given the panel structure of our data, we employ fixed effect estimators (Section 3.2.1) as well as pooled Ordinary Least Squares (OLS) estimators with White standard errors, clustered by the cross section dimension (Sections 3.1 and 3.2.2) in our analyses.
The advantage of using panel data estimation techniques is that the partial effects of the observed explanatory variables can be estimated in the presence of an unobserved effect, which would otherwise be omitted. We employ a fixed effects model in which the unobserved variable is treated as a time-constant parameter to be estimated for each cross-section observation. In this setting, the effect of time-constant observed variables cannot be distinguished from the effect of time-constant unobserved variables, and variation among the dependent variable is explained by time variation within each cross section (Baltagi, 2001; Greene, 2007; Wooldridge, 2001).
In several regression analyses (Sections 3.1 and 3.2.2), we include explanatory variables, such as soil type and land cover type, which are assumed to be time-constant. To estimate the marginal effects of these variables, we resort to the pooled OLS estimator to explain variations in nitrate concentration over years and municipalities. We use White standard errors to account for possible heteroscedasticity in the data. In addition, standard errors are clustered by the cross-section dimension to account for the fact that observations are not independent of time in any given municipality (Wooldridge, 2001).
We include several extensions in the proposed regression models to consider additional effects. When assuming that the partial effect of an explanatory variable depends on another explanatory variable, we include interaction terms in the regression model (Section 3.2.2). These are derived by multiplying the respective explanatory variables. To allow for non-linear effects of the explanatory variable, we include squared terms in the regression equations (Section 3.1). We also consider whether variations in the dependent variable are due to aggregate changes over time. We therefore include year dummies (i.e. a binary variable which takes on the value of 1 if the observed variables take place in a specific year and 0 otherwise). We perform an F-test for each regression, to ensure that the chosen coefficients are jointly statistically significant.
We use the software Stata 10 for all operations.
3. Models
3.1. Determinants of nitrate concentration in groundwater
3.1.1. Site-specific characteristics
We investigate the relationship between nitrate concentration in groundwater and various site-specific characteristics such as land cover, weather conditions, and soil quality. The time dimension (t) is given by years and the cross-sectional dimension (i) represents municipalities. Year dummies are included to control for aggregate annual shocks. These are defined as follows:
The regression equation takes the form:
| (1) |
where j ∈ {buildings; cropland; grassland; forest} and k ∈ {1992,…,2007}.
Based on the literature, we conjecture that precipitation plays an important role in explaining variations in nitrate concentration. Schweigert et al. (2004) found that average September precipitation may fill soil reservoirs with water and lead to higher nitrate leaching. Similarly, several studies found that increasing precipitation might positively affect nitrate concentration in groundwater (Davis and Sylvester-Bradley, 1995; Korsaeth and Eltun, 2000; Rankinen et al., 2007). Conversely, higher average precipitation could foster the uptake of nitrogen by crops (Schweigert et al., 2004; Sieling and Kage, 2006) or support the dilution of nitrates (Hofreither and Pardeller, 1996) and thus decrease potential nitrate leaching. These opposing effects suggest that the coefficient of precipitation could have either a negative or a positive sign.
Another important weather effect concerns average daily maximum temperature, which can have opposing effects on nitrate concentration in groundwater. On the one hand, maximum temperature controls for geographic location of municipalities. We find that alpine municipalities (mostly located in the provinces of Salzburg, Tirol, or Kärnten) have lower average annual maximum temperature than the Austrian average as a result of their altitude. As there is less agricultural activity at high altitudes, we expect lower nitrate concentrations in these regions. Thus, high average maximum temperature should imply higher nitrate concentration in groundwater. Similarly, Schweigert et al. (2004) suggest that high average temperature can lead to higher soil mineralization rates, which could subsequently increase nitrate concentration in groundwater. On the other hand, they suggest that high temperatures favor evapotranspiration. Additionally, high temperatures often correlate with dryness, which slows the process of mineralization (Schweigert et al., 2004). Both processes could thus reduce leaching of nitrates into groundwater.
Concerning the different types of land cover, higher proportions of cropland are expected to have a clear positive effect on nitrate leaching (Schroeder et al., 2004), since higher fertilization rates may lead to excesses of soil nitrates that can leach into groundwater. Conversely, we expect grasslands and forests to have negative impacts on nitrate concentration. Additionally, we expect the proportion of area with buildings in a municipality to have a positive effect on nitrate concentration.
Soil types and composition are important determinants of nitrate concentration in groundwater (Buczko et al., 2010; D'Haene et al., 2003; de Ruijter et al., 2007). Soil texture, drainage, climate, vegetation, and long-term land use lead to a gradual build up of soil organic carbon (Davis and Sylvester-Bradley, 1995; Sieling and Kage, 2006). Moist soils in late summer and autumn and low plant demand favor the mineralization of soil organic matter, which can result in a large mineral nitrate pool and higher risk of leaching (Sieling and Kage, 2006). Microbial denitrification processes, which depend on the availability of carbon sources in soil, can remove nitrate from groundwater. Therefore, a high degree of soil organic carbon could correlate with low nitrate levels in groundwater (Schipper and Vojvodić-Vuković, 2000, 2001). However, we only have a limited number of observations for soil organic carbon, such that it is not possible to include it in our analysis. Instead, we use field water capacity as a proxy in our regression analyses. Field water capacity is positively correlated with soil organic carbon (Huntington, 2006), and high levels of water storage capacity have been found to decrease nitrate leaching (Wong et al., 2006). We also control for volume of stones in topsoil. A high volume of stones is usually found in coarse-textured soils, which are generally more prone to nitrate leaching (Donner et al., 2004). Thus, we expect the sign of the estimated coefficient on field water capacity to be negative, because a higher field water capacity implies less leaching. Conversely, higher proportions of stones in the soil might positively affect groundwater nitrate.
3.1.2. Land use and farming systems
Regression (2) focuses on the effect of land use and farming systems and estimates a model of the form:
| (2) |
where j ∈ {oilseed & protein, forage crops, cereal & maize, row crops & veg, grassland} and k ∈ {1999,…,2007}.
As discussed, we classify crops into four groups: oilseed and proteins, forage crops, cereal and maize, and row crops and vegetables. We expect the coefficients of the various crop categories to be positive and the coefficient of the proportion of grassland to be negative. Additionally, we control for the relative amount of farming systems (organic or conventional) in each municipality. We expect nitrate concentration in groundwater to increase with the proportion of conventional farming systems.
3.2. The Gross Nitrogen Balance indicator and actual contamination
The Gross Nitrogen Balance is often used to capture environmental pressures on soil, water, and air originating from nitrate surpluses. As a theoretical concept, it only indicates the potential for environmental pressures. We link potential contamination to actual contamination by comparing the Gross Nitrogen Balance to detailed data on actual nitrate concentration in groundwater.
3.2.1. Fixed effects
We perform a fixed effect panel estimation to determine how well the Gross Nitrogen Balance and its components predict nitrate contamination in groundwater. Typically for fixed effect estimations, municipality-specific constants, αi, are included to account for site-specific characteristics such as soil quality or land cover types. Equations (3) and (4) are estimated for the years 2003–2007, the time span for which the Gross Nitrogen Balance has been calculated. The first regression model (Equation (3)) assesses the effect of the Gross Nitrogen Balance on nitrate contamination. We then review the composition of the indicator and assess the effect of its separate components (Equation (4)). For reasons of multicollinearity, we concentrate on the measure of total fertilization (nitrogen input) as well as withdrawal by harvested crops and forage (nitrogen output):
| (3) |
| (4) |
3.2.2. Accounting for fixed effects
As a next step, we account for the fixed effects of the previous regressions by including several site-specific characteristics, such as proportion of agriculturally used land, soil characteristics, and farming systems of the municipality. We therefore estimate the following regression equations using the technique of clustered pooled OLS:
| (5) |
where k ∈ {2003,…,2007}.
Including site-specific characteristics is especially valuable within our analysis, because it allows us to assess whether the Gross Nitrogen Balance performs better as a proxy for actual groundwater contamination once these characteristics are considered. We expect, that some of these variables could play an important role in determining the predictive power of the Gross Nitrogen Balance. We introduce interaction terms into the regression equation to test this hypothesis:
| (6) |
where k ∈ {2003,…,2007}.
The variable Feat captures characteristics such as precipitation, temperature, farming systems, volume of stones, or field water capacity. To test all possible interactions, we perform several regressions of the above form.
4. Results and discussion
The results of the introduced models are presented in Table 3. We firstly investigated the factors influencing nitrate concentration in groundwater. Table 3 (column 1) illustrates the results of Equation (1), through which the effect of land covers and site specific characteristics have been estimated. Our expectations of the effect of soil and land cover types on nitrate concentration in groundwater have been verified. Except for the effect of the share of area with buildings on nitrate concentration, we find statistically significant non-monotonous effects of all land cover types. As expected, cropland has an exponential positive effect on nitrate concentration. The opposite is found for the proportion of grassland, as well as proportion of area with buildings, for which an initially negative effect on nitrate concentration is found, but which seems to weaken with increased coverage. Also, high forest coverage has a negative effect on nitrate concentration in groundwater. Further, soil quality is important when explaining nitrate concentration in groundwater. The effect of the field water capacity on nitrate concentration is, as expected, negative. As water retention capacity of the soil rises, less fertilizer leaches into groundwater. However, higher proportions of stones in topsoil have a positive effect, confirming our assumption that soil with high stone content favors nitrate leaching into groundwater.
Table 3.
Results of the regression analysis.
| Dependent variable: | Equation (1) Nitrate |
Equation (2) Nitrate |
Equation (3) Nitrate |
Equation (4) Nitrate |
Equation (5) Nitrate |
Equation (6) Nitrate |
|---|---|---|---|---|---|---|
| Precip | −0.838*** | −0.649** | −0.274*** | −0.286*** | −2.287*** | −3.546*** |
| Temp | −0.635* | −1.022*** | −0.257*** | −0.246*** | −1.310*** | −1.294*** |
| Landcover_grassland | −19.91** | |||||
| Landcover_grassland2 | 27.06** | |||||
| Landcover_cropland | 11.73 | |||||
| Landcover_cropland2 | 40.83*** | |||||
| Landcover_buildings | −18.12 | |||||
| Landcover_buildings2 | 41.29* | |||||
| Landcover_forest | 44.91*** | |||||
| Landcover_forest2 | −51.68*** | |||||
| fwc | −71.26*** | −104.5*** | −203.3*** | −202.7*** | ||
| vs | 0.445*** | 0.119 | 0.164 | 0.175 | ||
| Farming_system | 2.949* | 6.149*** | 5.708*** | |||
| Landuse_oilseed & protein | 65.60* | |||||
| Landuse_forage | 24.21 | |||||
| Landuse_cereal & maize | 24.61*** | |||||
| Landuse_row crops & veg | 56.63** | |||||
| Landuse_grassland | −15.94*** | |||||
| Nbal | 0.0347*** | 0.0654*** | −0.0275 | |||
| Fert | 0.0350*** | |||||
| Withd | −0.0261** | |||||
| Prop_AL | 18.36*** | 18.28*** | ||||
| Precip*Nbal | 0.0366** | |||||
| Constant | 43.27*** | 60.39*** | 20.17*** | 20.59*** | 95.52*** | 98.94*** |
| Observations | 14,169 | 7036 | 4811 | 4811 | 4423 | 4423 |
| Adjusted R-squared | 0.289 | 0.297 | 0.949 | 0.949 | 0.240 | 0.242 |
| F-test | F(12, 1205) = 51.56 | F(10, 1041) = 28.11 | F(3, 3689) = 12.59 | F(4, 3688) = 9.77 | F(7, 1044) = 42.65 | F(8, 1044) = 39.45 |
| Prob > F = 0.0000 | Prob > F = 0.0000 | Prob > F = 0.0000 | Prob > F = 0.0000 | Prob > F = 0.0000 | Prob > F = 0.0000 | |
*p < 0.1, **p < 0.05, ***p < 0.01.
The F-test tests whether all regression coefficients are jointly equal to zero.
In all regression equations we control for the effect of average daily maximum temperature and average daily precipitation levels per year. Referring to findings in the literature, presented in Section 3.1.1, our initial expectations of the effect were ambivalent. Our findings provide clear indications that average daily precipitation as well as average daily maximum temperature have a negative effect on nitrate concentration. Municipalities with high average daily precipitation levels experience lower groundwater nitrate concentration. Thus, increased rainfall fosters crop growth and subsequent nitrogen uptake as well as dilutes soil nitrates. The results of Equation (1) indicate that a 1 mm increase in average daily precipitation levels implies, ceteris paribus, a 0.84 mg/l decrease in observed average nitrate concentration in groundwater. If we compare a municipality with average daily rainfall of 2.78 mm with one that experiences a daily average of 10.8 mm, our estimate implies that, ceteris paribus, the nitrate concentration in the municipality with higher rainfall will be lower by 6.75 mg/l. Considering that the average nitrate concentration level is around 20 mg/l, we conclude that the impact of precipitation is highly relevant. Similarly, average daily maximum temperature also exhibits a negative effect on nitrate concentration, which suggests that in municipalities with higher temperatures, higher rates of evapotranspiration and biomass production occur that in turn reduce nitrate leaching into groundwater. The difference between municipalities with the highest and lowest average daily maximum temperature is 20.3 °C. This implies, ceteris paribus, a decrease in nitrate concentration of groundwater of 12.9 mg/l, again a sizable result. These qualitative observations for precipitation and temperature are confirmed in all estimated models, though they vary in magnitude as the datasets used vary in size.
Observing the positive effect of cropland, we investigate the degree to which particular crop types are related to nitrate concentration in groundwater. Table 3 (column 2) reports the results of Equation (2), in which we investigate the effects of land use and farming systems on nitrate concentration. We find that all crop types exert a statistically significant positive effect on nitrate contamination of groundwater, except for proportion of forage crops. We find that municipalities with more conventional farming systems experience significantly higher levels of groundwater nitrates. This is expected due to more intense use of mineral fertilizer in conventional agriculture. We find, ceteris paribus, an increased nitrate level of almost 3 mg/l in a municipality growing crops conventionally over a municipality producing crops exclusively organic. Further, the relative amounts of grassland, precipitation, maximum temperature, and soil characteristics are found to be significant with the same signs as previously discussed (Table 3, column 2). This result suggests a direct link between the degree of nitrogen fertilization and the amount of nitrate leaching. Though some scholars have criticized this conclusion for being too simplistic (Addiscott et al., 1991), there is additional evidence in the literature that corroborates this fact (for example, see Davis and Sylvester-Bradley, 1995).
The results of our analysis also indicate that the Gross Nitrogen Balance is a suitable indicator for predicting actual nitrate contamination of groundwater. The results of Equation (3) are presented in Table 3 (column 3). The positive sign of the regression coefficient indicates that high values of the Gross Nitrogen Balance are associated with high nitrate concentration in groundwater. Quantitatively, however, the Gross Nitrogen Balance explains relatively little of observed nitrate concentration in groundwater. The estimated coefficient of β3 implies that an increase in the average Gross Nitrogen Balance indicator by 10 kg of nitrogen results in an increase of only 0.35 mg/l in groundwater nitrate concentration. The results of Equation (5) indicate that the Gross Nitrogen Balance remains a statistically significant indicator when accounting for site-specific characteristics (Table 3, column 5).
The effects of separate components of the Gross Nitrogen Balance on nitrate concentration were estimated in regression model (4), the results are presented in Table 3 (column 4). We find that, as expected, nitrogen input has a positive influence and nitrogen output has a negative influence on observed nitrate concentration. As discussed previously, average daily precipitation and maximum temperature are statistically significant for explaining nitrate concentration in groundwater.
Finally, we analyzed whether the predictive power of the Gross Nitrogen Balance could be increased, if factors such as the type of farming systems, soil characteristics or precipitation and temperature, were accounted for (Equation (6)). Of all the exogenous factors, only precipitation is statistically significant in determining the explanatory potential of the Gross Nitrogen Balance (Table 3, column 6). If high average precipitation is observed, the Gross Nitrogen Balance does particularly well in predicting nitrate concentration in groundwater. Hence, precipitation levels significantly influence the marginal effect of the indicator. To see this formally, note that the marginal effect of the Gross Nitrogen Balance on the nitrate concentration in groundwater is given by:
| (7) |
The marginal effect is positive if Precip > 0.75 mm; since this is always the case, it corroborates the previously discussed results. Because the indicator captures the theoretical potential for environmental pressure, it appears that the degree to which this potential translates into actual contamination depends significantly on precipitation levels (Sieling and Kage, 2006), which is intuitive considering leaching effects. Assuming the Gross Nitrogen Balance correctly captures the pressure of nutrient surpluses on the soil, the degree to which this translates into nitrate contamination of groundwater is determined by the degree of leaching effects, which are stronger with higher precipitation (Rankinen et al., 2007). Note that even though is positive, the overall marginal effect of precipitation which is given by:
| (8) |
is negative on average. These results suggest that an indicator that portrays potential nitrate leaching as well as actual environmental degradation in a region should take into account specific environmental conditions, in particular the amount of precipitation.
5. Conclusion
Nitrogen is a crucial input in agricultural production, but it puts environmental pressure on (ground)water, soil and air. We identify the likely factors influencing nitrate contamination in Austrian groundwater. We find that on average, increased agricultural activity (especially in conventionally cultivated crops) leads on average to higher nitrate contamination in groundwater. Additionally, environmental factors such as precipitation and temperature play an important role. Higher average maximum temperatures lead to lower nitrate pollution of groundwater, possibly as a result of increased evapotranspiration. Additionally, higher average precipitation increases crops' nitrogen uptake as well as the dilution effect and thus lowers nitrate concentration.
Nitrate leaching from agricultural land uses is usually considered a non-point source pollution problem, making the specific polluter hard to identify. Consequently, indicators that establish the functional relationship between pollution and agricultural activity in the context of site characteristics are necessary to allow effective policy regulation.
The Gross Nitrogen Balance has been identified by the OECD as a priority agri-environmental indicator, meant to measure the potential damage to the environment resulting from excess nitrogen. The second contribution of this work lies in assessing the explanatory power of the Gross Nitrogen Balance as a measure of actual pollution levels, such as nitrate contamination in groundwater. In our statistical analysis, we find that the indicator exerts a positive influence on nitrate concentration in groundwater, and thus conclude that it is an appropriate predictor for nitrate contamination.
In addition, we investigated whether the explanatory power of the indicator can be improved by accounting for weather conditions or soil qualities. We find that the indicator is more useful as a predictive tool in regions with higher average precipitation. Our analysis suggests that the Gross Nitrogen Balance should be enriched with information on precipitation sums if its purpose is to predict actual contamination. This finding calls for a more sophisticated approach, which becomes especially relevant when the Gross Nitrogen Balance is used to design and evaluate environmental policy. The importance of site-specific characteristics in assessing nitrate contamination has also been recognized by several scholars (Buczko et al., 2010; Lord and Anthony, 2002; Schroeder et al., 2004). For instance, Schroeder et al. (2004) note that similar agricultural inputs can result in different outputs as a result of variations in soil, climate, management and crop characteristics, even when applied on the same type of farm or crop. Also, de Ruijter et al. (2007) mention that how nitrate surplus in soils translates to nitrate contamination of groundwater depends critically on soil drainage potential. Thus, the maximum feasible amount of nitrogen that does not impede groundwater quality critically depends not only on agricultural activities but also on external factors.
Acknowledgments
We thank Ulrich Morawetz, Michael Weichselbaumer, Franz Sinabell and Amy Johnson for their support. This research has been realized within the project CC – Tame (Climate Change – Terrestrial Adaptation & Mitigation in Europe; www.cctame.eu) funded by European Commission within the 7th Framework and the programme proVISION introduced by the Austrian Federal Ministry of Science and Research (BMWF; http://www.provision-research.at/).
References
- Addiscott T.M., Whitmore A.P., Powlson D.S. CAB International; Oxford, UK: 1991. Farming, Fertilisers and the Nitrate Problem. [Google Scholar]
- Balkovic J., Schmid E., Moltchanova E., Skalsky R., Poltarska K., Müller B., Bujnovsky R. Data processing for bio-physical process modelling in EU 25. In: Stolbovoy V., Montanarella L., Panagos P., editors. Carbon Sink Enhancement in Soils of Europe: Data Modelling, Verification. European Communities; Luxembourg: 2007. pp. 74–139. (JRC Scientific and Technical Reports). [Google Scholar]
- Baltagi B. John Wiley & Sons; 2001. Econometric Analysis of Panel Data. [Google Scholar]
- BMLFUW . 2010. Gruener Bericht.www.gruenerbericht.at (March, 2010) [Google Scholar]
- BMLFUW . 2010. IACS Database. Vienna, Austria. [Google Scholar]
- Boumans L.J.M., Fraters B., van Drecht G. Nitrate in the upper groundwater of ‘De Marke’ and other farms. Netherlands Journal of Agricultural Science. 2001;49:163–177. [Google Scholar]
- Buczko U., Kuchenbuch R.O., Lennartz B. Assessment of the predictive quality of simple indicator approaches for nitrate leaching from agricultural fields. Journal of Environmental Management. 2010;91:1305–1315. doi: 10.1016/j.jenvman.2010.02.007. [DOI] [PubMed] [Google Scholar]
- Cannavo P., Recous S., Parnaudeau V., Reau R. Modeling N dynamics to assess environmental impacts of cropped soils. Advances in Agronomy. 2008;97:131–174. [Google Scholar]
- Davis D.B., Sylvester-Bradley R. The contribution of fertiliser nitrogen to leachable nitrogen in the UK: a review. Journal of the Science of Food and Agriculture. 1995;68:399–406. [Google Scholar]
- de Ruijter F.J., Boumans L.J.M., Smit A.L., van den Berg M. Nitrate in upper groundwater on farms under tillage as affected by fertilizer use, soil type and groundwater table. Nutrient Cycling in Agroecosystems. 2007;77:155–167. [Google Scholar]
- D'Haene K., Moreels E., de Neve S., Chaves Daguilar B., Boeckx P., Hofman G., van Cleemput O. Soil properties influencing the denitrification potential of Flemish agricultural soils. Biology and Fertility of Soils. 2003;38(6):358–366. [Google Scholar]
- Donner S., Kucharik C.J., Foley J. Impact of changing land use practices on nitrate export by the Mississippi River. Global Biochemical Cycles. 2004;18:1–21. [Google Scholar]
- EEA . European Environment Agency; Copenhagen: 2001. Environmental Signals 2001. European Environment Assessment Report No. 8. [Google Scholar]
- Elmi A.A., Madramootoo C., Egeh M., Liu A., Hamel C. Environmental and agronomic implications of water table and nitrogen fertilization management. Journal of Environmental Quality. 2002;31:1858–1867. doi: 10.2134/jeq2002.1858. [DOI] [PubMed] [Google Scholar]
- Fraters D., Boumans L.J.M., van Drecht G., de Haan T., de Hoop W.D. Nitrogen monitoring in groundwater in the sandy regions of the Netherlands. Environmental Pollution. 1998;102:479–485. [Google Scholar]
- Greene W.H. Prentice Hall; 2007. Econometric Analysis. [Google Scholar]
- Hofreither M., Pardeller K. Ökonometrische Analyse des Zusammenhanges zwischen Agrarproduktion und Nitratbelastung des Grundwassers in Österreich. Die Bodenkultur. 1996;47(4):279–289. [Google Scholar]
- Huntington T.G. second ed. 2006. Available Water Capacity and Soil Organic Matter. Encyclopedia of Soil Science.http://www.tandfonline.com/doi/abs/10.1081/E-ESS-120018496 (accessed 01.07.11.) [Google Scholar]
- Korsaeth A., Eltun R. Nitrogen mass balances in conventional, integrated and ecological cropping systems and the relationship between balance calculations and nitrogen runoff in an 8-year field experiment in Norway. Agriculture, Ecosystems and Environment. 2000;79:199–214. [Google Scholar]
- Lord I., Anthony S.G. Agricultural nitrogen balance and water quality in the UK. Soil Use and Management. 2002;18(4):363–369. [Google Scholar]
- OECD . 2007. OECD and EUROSTAT Gross Nitrogen Balance Handbook.www.oecd.org/tad/env/indicators (March, 2010) [Google Scholar]
- OECD . 2008. Environmental Performance of Agriculture in OECD Countries since 1990.www.oecd.org/tad/env/indicators (March, 2010) [Google Scholar]
- OECD . 2010. Stat. Extracts.http://stats.oecd.org/ [Google Scholar]
- Oenema O., Kros H., de Vries W. Approaches and uncertainties in nutrient budgets: implications for nutrient management and environmental policies. European Journal of Agronomy. 2003;20:3–16. [Google Scholar]
- Parris K. Agricultural nutrient balances as agri-environmental indicators: an OECD perspective. Environmental Pollution. 1998;102:219–225. [Google Scholar]
- Rankinen K., Salo T., Granlund K., Rita H. Simulated nitrogen leaching, nitrogen mass field balances and their correlation on four farms in south-western Finland during the period 2000–2005. Agricultural and Food Science. 2007;16:387–406. [Google Scholar]
- Salo T., Turtola E. Nitrogen balance as an indicator of nitrogen leaching in Finland. Agriculture, Ecosystems and Environment. 2006;113:98–107. [Google Scholar]
- Schipper L., Vojvodić-Vuković M. Nitrate removal from groundwater and denitrification rates in a porous treatment wall amended with sawdust. Ecological Engineering. 2000;14(3):269–278. [Google Scholar]
- Schipper L., Vojvodić-Vuković M. Five years of nitrate removal, denitrification and carbon dynamics in a denitrification wall. Water Research. 2001;35(14):3473–3477. doi: 10.1016/s0043-1354(01)00052-5. [DOI] [PubMed] [Google Scholar]
- Schroeder J.J., Scholefield D., Cabral F., Hofman G. The effect of nutrient losses from agriculture on ground and surface water quality: the position of science in developing indicators for regulation. Environmental Science & Policy. 2004;7:15–23. [Google Scholar]
- Schweigert P., Pinter N., van der Ploeg R. Regression analyses of weather effects on the annual concentrations of nitrate in soil and groundwater. Journal of Plant Nutrition and Soil Science. 2004;167(3):309–318. [Google Scholar]
- Sieling K., Kage H. N balance as an indicator of N leaching in an oilseed rape – winter wheat – winter barley rotation. Agriculture, Ecosystems and Environment. 2006;115:261–269. [Google Scholar]
- Strauss F., Schmid E., Moltchanova E., Formayer H., Wang X. Modeling climate change and biophysical impacts of crop production in the Austrian Marchfeld region. Climatic Change. 2012;111(3–4):641–664. [Google Scholar]
- Umweltbundesamt . 2010. CORINE Land Cover.http://www.umweltbundesamt.at/umwelt/raumordnung/flaechennutzung/corine/ (March, 2010) [Google Scholar]
- Umweltbundesamt . BMLFUW, Sektion VII/Abteilung Nationale Wasserwirtschaft; Ämter der Landesregierungen; 2010. Erhebung der Wassergüte in österreich gemäß Hydrographiegesetz i.d.F. des BGBl. Nr. 252/90 (gültig bis Dezember 2006) bzw. Gewässerzustandsüberwachung in österreich gemäß Wasserrechtsgesetz, BGBl. N 123/06. [Google Scholar]
- van der Laan M., Stirzaker R.J., Annandale J.G., Bristow K.L., du Preez C.C. Monitoring and modelling draining and resident soil water nitrate concentrations to estimate leaching losses. Agricultural Water Management. 2010;97:1779–1786. [Google Scholar]
- Watson C.A., Atkinson D. Using nitrogen budgets to indicate nitrogen use efficiency and losses from whole farm systems: a comparison of three methodological approaches. Nutrient Cycling in Agroecosystems. 1999;53(3):259–267. [Google Scholar]
- Wong M.T.F., Asseng S., Zang H. A flexible approach to managing variability in grain yield and nitrate leaching at within-field to farm scales. Precision Agriculture. 2006;7:405–417. [Google Scholar]
- Wooldridge J.M. The MIT Press; 2001. Econometric Analysis of Cross Section and Panel Data. [Google Scholar]