Phase retrieval using polychromatic illumination for transmission X-ray microscopy

Abstract

An alternative method for quantitative phase retrieval in a transmission X-ray microscope system at sub-50-nm resolution is presented. As an alternative to moving the sample in the beam direction in order to analyze the propagation-introduced phase effect, we have illuminated the TXM using X-rays of different energy without any motor movement in the TXM system. Both theoretical analysis and experimental studies have confirmed the feasibility and the advantage of our method, because energy tuning can be performed with very high energy resolution using a double crystal monochromator at a synchrotron beam line, and there is zero motor error in TXM system in our approach. High-spatial-resolution phase retrieval is accomplished using the proposed method.

1. Introduction

Thanks to the availability of Fresnel zone plates designed for use at X-ray wavelengths [1–3], Transmission X-ray Microscopy (TXM) is currently in use at many facilities all over the world [4–12]. Different research areas ranging from material science [10,13] to biomedical studies [11,14] have benefitted from this technique. In cases that investigate weakly absorbing samples (mainly with low Z elements), phase contrast imaging (PCI) and, subsequently, quantitative phase retrieval are especially important.

Many different methods have been proposed to achieve quantitative phase retrieval in X-ray imaging, including propagation-based PCI [15–17], structured-illumination based PCI [18,19], differential enhanced imaging [20,21] and grating interferometer based PCI [22–24]. Quantitative phase retrieval in a TXM system was accomplished by Yin et al. [25] using a propagation-based scheme (collection of multiple images at different sample positions along the optical axis) in order to extract quantitative phase information. In this contribution, we present a different strategy to perform phase retrieval in a TXM system by tuning the energy of the incident X-ray for illumination instead of moving any motors in the TXM optical system. With images recorded at different energies, a modified hybrid input-output (HIO) algorithm [26,27] is utilized to recover the phase and amplitude map iteratively. Tuning of the X-ray energy is easy to do at a synchrotron beam line and can be done with very fine energy resolution. Therefore, our method is capable of high-spatial-resolution phase retrieval.

2. Beamline and microscope arrangement

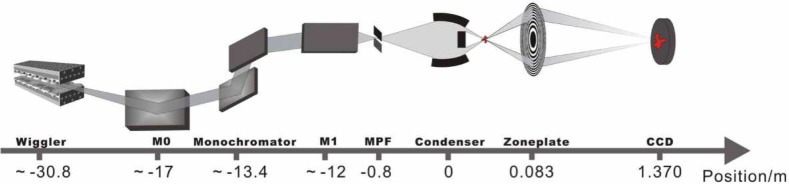
The X-ray transmission images with sub-50 nm resolution were recorded using the TXM system installed at beam line 6-2 of Stanford Synchrotron Radiation Lightsource [11]. The schematic experimental setup is demonstrated in Fig. 1. The X-ray generated from a 56 pole 0.9 Tesla wiggler passes through a vertically collimating mirror (M₀) followed by a monochromator, and a toroidal mirror (M₁) to focus the beam to a spot with size down to a few hundreds of microns (about 200μm × 500μm at 5.4 keV), which acts as the virtual source for the microscope. The monochromator installed at BL6-2 is a liquid-Nitrogen-cooled double-Si(111)-crystal system, which selects a narrow band pass from the incident broad-band spectrum (ΔE/E ≈ 5 ×10⁻⁴). It operates over a 2.1 keV-17.0 keV range while vertically offsetting the beam 6.39 mm to 19.9 mm. For stabilizing the beam, a mirror pitch feedback (MPF) system is install to monitor the micron-level beam movement and to adjust the toroidal mirror (M₁) accordingly. The beam line is operated through the SSRL control software known as “SUPER”. The TXM makes use of a Fresnel zone plate with 200 micron diameter and 30 nm outermost zone width to achieve a magnification factor of around 50. A 2048 × 2048 pixels Peltier-cooled charge-coupled device (QImaging Retiga-4000RV CCD) is used to collect the projection images. The field of view (FOV) at the objective plane is approximately 32μm × 32μm depending on the incident energy configuration. A TXM image of a Siemens calibration standard with 30 nm minimum features is shown in Fig. 2(a). As shown in the blowup [Fig. 2(b)], the 30 nm features are clearly resolved, confirming the spatial resolution of the TXM system. It should be mentioned that the pixel size in the projection image is about 15.6 nm, however the resolution of TXM imaging system is limited by the objective zone plate.

Fig. 1.

Schematic experimental setup of the Transmission X-ray Microscopy installed at beamline 6-2c of Stanford Synchrotron Radiation Lightsource.

Fig. 2.

TXM image of a Siemens calibration standard with 30 nm minimum features. Panel (b) is the magnified view of the highlighted area in panel (a). Scale bar in panel (a) is 5 microns.

3. Experimental strategy and phase retrieval algorithm

The focal length f of a Fresnel zone plate is a function of the energy of the incident X-ray as given by Eq. (1).

$$f=\frac{2\cdot R\cdot {\Delta }_{\mathit{outermost}}}{h\cdot c/E_{\mathit{incident}}}$$ (1)

In Eq. (1), R is the radius of the Fresnel zone plate; Δ_outermost is the outermost zone width of the zone plate; h is the Planck’s constant; c is the speed of light; and E_incident is the energy of the incident beam. When tuning the incident energy, the recorded images are equivalent to those taken at a sample position that is out of focus under the corresponding energy. The distortion effect of the image is similar to that from the propagation-based phase effect. In this contribution, we propose to perform phase retrieval by tuning the energy of the incident X-ray without moving the sample in the beam direction. Fresnel number [given in Eq. (2)] is used to determine the experimental parameters.

$$F=\frac{a^2}{L\cdot \lambda }=\frac{a^2}{2\cdot R\cdot {\Delta }_{\mathit{outermost}}}\cdot \frac{E_{\mathit{incident}}}{\Delta E_{\mathit{incident}}}$$ (2)

In Eq. (2), a is the feature size; L is the distance of propagation; λ is the wavelength of the X-ray; ΔE_incident is the energy tuning range in the experiment. The size of the feature under investigation is typically at least one order of magnitude larger than the spatial resolution limit (30 nm). In order to keep the Fresnel approximation valid (F ≥ 1), the energy tuning range should satisfy ΔE_incident < E_incident · 10⁻² = 54eV. The lower limit of the energy tuning range is estimated by submitting the spatial resolution as the feature size in Eq. (2) and calculating the energy range which satisfies F = 1. As a result, in theory, energy tuning range should be larger than 1 eV and smaller than 54 eV. In reality, there are a few more factors that would affect the performance of the phase retrieval when the selected energy points are too close to (or too far away from) each other, such as the variation of the zone plate efficiency versus energy change, the spatial coherence and the temporal coherence which may lead to a point spread function, blurring the fringe-like pattern and complicating the phase retrieval.

In our simulation and experiment, projection images were acquired using TXM at 5.39 keV, 5.40 keV and 5.41 keV, while maintaining the focus position optimized for 5.40 keV, satisfying the condition given above. In this case the Fresnel diffraction formula [28] is a good approximation for simulating the phase effect. It should be noted that the magnification factor changes while the incident energy is tuned. Thus, in our calculation, cubic interpolation was applied for magnification factor correction prior to any further phase retrieval calculations.

The proposed algorithm for extracting phase information can be described using Eq. (3).

$$E^{i+1}=I_{\mathit{corr}}^{{\lambda }_0}\left(i\mathit{Fresnel}\left(I_{\mathit{corr}}^{\lambda }\left(\mathit{Fresnel}\left(E^i,\lambda ,f_{\lambda }-f_{{\lambda }_0}\right)\right),\lambda ,f_{{\lambda }_0}-f_{\lambda }\right)\right)$$ (3)

In Eq. (3), Eⁱ denotes the estimated wave field after i iterations; $I_{\mathit{corr}}^{\lambda }$ represents for the amplitude correction function, i.e. replacing the amplitude of the estimated wave field using the experimentally measured data under the illumination of X-rays with wavelength λ; Fresnel and iFresnel are the functions of forward and backward Fresnel diffraction calculations respectively; and f_λ is the focal length of the Fresnel zone plate under the illumination of X-rays with wave length λ. As indicated in Eq. (3), in theory, images taken at two different energy points are sufficient for phase retrieval. However, in our experiment and calculation, we make use of images recorded at three different energy values for better convergence of the iterative phase retrieval algorithm.

4. Results and discussion

Computer simulation was performed using test patterns, with the real part of the refractive index decrement [Fig. 3(a)] ranging from 0 to 10⁻⁵ and the imaginary part [Fig. 3(b)] ranging from 0 to 10⁻⁶, for evaluating the proposed experimental scheme and algorithm. The sample size was set to 32μm × 32μm with a thickness of 10μm. The spatial resolution for our calculation was set to 15nm. The calculated intensity distribution recorded with illuminations of 5390 eV and 5410 eV X-rays are demonstrated in Fig. 3(c) and Fig. 3(d) respectively. The image taken at 5400 eV is not shown because it is identical to the distribution of the absorption coefficient [Fig. 3(b)]. Refining on Fig. 3(b), Fig. 3(c) and Fig. 3(d), both the phase map and the amplitude map are recovered successfully using the algorithm described by Eq. (3), and are presented in Fig. 3(e) and Fig. 3(f) respectively.

Fig. 3.

Computer simulation for the proposed experimental scheme and the phase retrieval algorithm. The distribution of the real and imaginary part of the refractive index are presented in panels (a) and (b) respectively. Panels (c) and (d) are the intensity distributions at the detector plane under X-ray illumination at 5390 eV and 5410 eV respectively. The retrieved phase map and amplitude map are shown in panels (e) and (f).

Al₂O₃ balls were used as test samples for the experimental study of the proposed phase retrieval scheme. The TXM system was optimized for imaging at 5.4 keV and transmission images were recorded at 5.40 keV, 5.39 keV, and 5.41 keV [as shown in Figs. 4(a), 4(b) and 4(c)]. Applying the modified HIO algorithm [Eq. (3)] to these recorded intensity distributions, an amplitude map and a phase map at the exit plane of the sample were retrieved [Fig. 4(d) and Fig. 4(e)].

Fig. 4.

TXM imaging results for quantitative phase retrieval. Raw data collected at 5.40 keV, 5.39 keV, and 5.41 keV are presented in panels (a) (b) and (c), respectively. The retrieved amplitude map and phase map are demonstrated in panel (d) and (e). The scale bar in panel (e) is 3 microns.

The energy tuning at a synchrotron beam line can be performed at very high resolution. The finest energy tuning step at beam line 6-2 of SSRL is better than 0.05 eV. Submitting this value in Eq. (1), the resolution of the focal length while tuning the incident energy is finer than 0.16 microns. This is much better than the repeatable movement of the motors installed for the TXM system (around 1 micron). The beam movement caused by the tuning of the monochromator is compensated by the Mirror Pitch Feedback system and the reference image correction procedure. With all the optical elements in the microscope fixed, including the sample, motor errors in TXM system are eliminated completely in our approach.

One concern about our approach for phase retrieval is that the refractive index of a given material is actually a function of the X-ray energy. When tuning the incident energy, the wave field at the exit plane of the sample may be slightly different due to the variation of the refractive index. However, considering that the energy is tuned within a relatively small range (±10 eV), the variation of the refractive index is very small (the refractive index variation of the Al₂O₃ balls is around 1% in the presented experiment) as long as we are working at an energy which is NOT close to the absorption edge of the material under study. Typically, phase contrast methods and phase retrieval studies are applied to soft material with low Z elements. The absorption edges of these low Z elements are much lower than the energy of the X-ray that were utilized for illumination (5.4 keV). Furthermore, our method can be applied straightforwardly to TXM imaging experiments performed at higher X-ray energy. The variation of the refractive index will be even smaller when working at a higher X-ray energy.

5. Conclusion

In conclusion, we have presented a novel experimental scheme for quantitative phase retrieval in a TXM system by illuminating with X-rays of differing energy. Using a modified HIO algorithm, both the phase map and the amplitude map have been retrieved successfully. Without any motor motion in the TXM system, the proposed phase retrieval method can be done easily and accurately.