In vivo depth-resolved oxygen saturation by dual-wavelength photothermal (DWP) OCT

Abstract

Microvasculature hemoglobin oxygen saturation (SaO₂) is important in the progression of various pathologies. Non-invasive depth-resolved measurement of SaO₂ levels in tissue microvasculature has the potential to provide early biomarkers and a better understanding of the pathophysiological processes allowing improved diagnostics and prediction of disease progression. We report proof-of-concept in vivo depth-resolved measurement of SaO₂ levels in selected 30 µm diameter arterioles in the murine brain using Dual-Wavelength Photothermal (DWP) Optical Coherence Tomography (OCT) with 800 nm and 770 nm photothermal excitation wavelengths. Depth location of back-reflected light from a target arteriole was confirmed using Doppler and speckle contrast OCT images. SaO₂ measured in a murine arteriole with DWP-OCT is linearly correlated (R²=0.98) with systemic SaO₂ values recorded by a pulse-oximeter. DWP-OCT are steadily lower (10.1%) than systemic SaO₂ values except during pure oxygen breathing. DWP-OCT is insensitive to OCT intensity variations and is a candidate approach for in vivo depth-resolved quantitative imaging of microvascular SaO₂ levels.

1. Introduction

Depth-resolved in vivo quantification of hemoglobin oxygen saturation (SaO₂) in tissue microvasculature can advance the understanding, monitoring and prediction of the progression of a number of malignant, inflammatory, ischaemic, infectious and immune diseases including cancer, stroke, diabetic retinopathy, glaucoma, atherosclerosis, and vascular dementia [1,2]. Early detection and longitudinal study of pathologies that involve angiogenesis are of great interest to clinical investigators and biomedical engineers.

A number of approaches have been developed to assess microvascular oxygen saturation with varying levels of spatial and temporal resolution. Microvascular oxygenation profiles can be measured using an oxygen-sensitive microelectrode [3–7]. Although oxygen-sensitive microelectrodes have high spatial resolution (10 µm) and can provide oxygen saturation in a selected tissue layer, the micro-environment is irreversibly disturbed, the measurement is one-dimensional and cannot be translated to humans. Magnetic resonance imaging (MRI) has been used to investigate relative and absolute tissue oxygenation with depth resolution and a large field of view [8–12], insufficient temporal and spatial resolution, however, limit ability to visualize individual small vessels.

Minimally invasive or non-invasive optical methods that measure tissue oxygenation in the microvasculature are of interest due to potential high spatial and temporal resolution. Reflection spectroscopic oximetry [13–18] and phosphorescence quenching (PQ) imaging of exogenous oxygen sensitive dyes [17,19–24] provide tissue microvasculature oxygenation information with high transverse resolution but with limited depth specificity. Retinal PQ imaging is capable of providing tens of microns of depth resolution using line-focused illumination on a rodent retina [25,26]. In this approach, fluorescence observed at deeper depths is continuously shifted transversely and the resolution is limited to approximately 50 µm. Clinical translation of retinal PQ imaging is hindered because no FDA approved oxygen sensitive dyes are available.

Spectroscopic Fourier Domain Optical Coherence Tomography (SFD-OCT) [27,28] has been reported to measure depth-resolved microvasculature SaO₂ levels in phantoms [29–33] and tissue [34] by tracking changes in the intensity spectra of backscattered light. However, the variation and complexity of light scattering by blood and tissue limits SaO₂ sensitivity of intensity-based SFD-OCT and complicates clinical translation [35]. Recently, we reported a Dual Wavelength Photothermal (DWP) OCT approach to measure depth-resolved microvasculature SaO₂ levels in phantoms [36]. In DWP-OCT, incident photothermal excitation light at two distinct wavelengths is absorbed by target chromophores in a sample resulting in thermally-induced optical pathlength (op) variations that are measured with a phase-sensitive OCT system. Relative concentration of the two target chromophores can be estimated from the normalized ratio (χ₁₂) of op variations at the photothermal excitation wavelengths. Previously reported DWP-OCT instrumentation utilized for phantom studies [36] was constrained and incapable of recording in vivo measurements; major constraints included: 1) phantom vessel was probed from the top while excitation light was incident from bottom – limiting measurements to thin (few millimeters) specimens; 2) each of the two photothermal excitation wavelengths (765 nm or 800 nm) was incident on the sample at different times – limiting measurements to motionless specimens with stable parameters; and 3) to facilitate co-location of DWP-OCT probe and excitation beams on the phantom, photothermal excitation light was expanded to 0.9 mm diameter – limiting measurements to blood vessels specimens with a lumen diameter greater than 150 µm. In the present study, we extend DWP-OCT to depth-resolved in vivo measurement of SaO₂ levels in microvessels in a murine animal model.

2. Materials and methods

2.1 DWP-OCT system for in-vivo measurements

The experimental setup for our DWP-OCT system (Fig. 1 ) to measure SaO₂ levels contains two major components: a) photothermal excitation lasers at 800 nm and 770 nm to induce nanometer-scale optical pathlength (op) changes in murine tissue; and b) a Phase Sensitive (PhS) OCT system [37] to measure SaO₂-dependent op changes induced by photothermal excitation laser light.

Fig. 1.

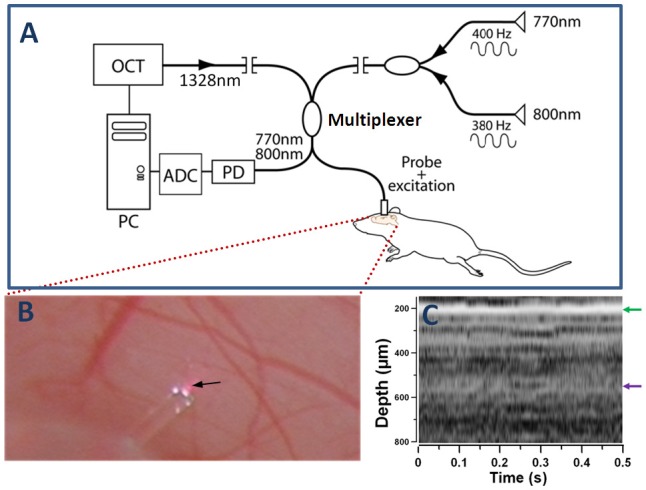
DWP-OCT for in vivo SaO₂ measurements (A), exposed brain cortex and the probe on top of an indicated by arrow 30-µm diameter arteriole (B) and M-mode OCT image recorded from a probed site (C). Optical pathlength changes (op) in a selected arteriole induced by photothermal excitation wavelengths 770 nm (op₁) and 800 nm (op₂) are measured by DWP-OCT and converted to SaO₂ levels. Red spot under the probe (B) is specular reflection of photothermal excitation light from tissue. White spots on the fiber probe are photographic artifacts due to multiple reflections between the fiber and aluminum fiber holder. OCT-signal intensity A-scans of the M-mode image (C) calculated as a 20Log of Fourier transformation of one laser sweep interference fringes between SMF-28 fiber end face and brain tissue. The green arrow (C) indicates position of the cover glass/cortex boundary, while the purple arrow indicates depth location of the arteriole (350 µm below the glass cortex boundary, 550 µm below fiber endface) extracted from speckle contrast and Doppler M-mode images (Fig. 2).

Depth-resolved phase measurements in tissue provided by DWP-OCT are associated with op changes in response to dual-wavelength (770 nm and 800 nm) photothermal excitation of blood in a target microvessel. Optical pathlength changes (op=φλ/(4π)) in the murine brain are induced by light absorption of oxy- and deoxy-hemoglobin in a microvessel, where φ is measured phase change at a specific depth and λ=1328 nm is central wavelength of the tunable laser source. Simultaneous measurement of op in response to 770 nm and 800 nm laser photothermal excitation wavelengths is used to compute SaO₂ levels in blood using an analytical model for χ₁₂ described in phantom studies [36] and in sections 2.1.2 and 3.1 below.

2.1.1. Phase sensitive (PhS) OCT system

A common-path Phase Sensitive (PhS) OCT system was used to measure nanometer scale changes in optical pathlength (op) in the murine brain in response to laser photothermal excitation. The PhS-OCT system has been described in details previously [37]. Briefly, the PhS-OCT system uses a 20 kHz polygon mirror tunable laser (HSL-2000, Santec USA Corp., Hackensack, NJ) with a central wavelength of 1328nm, bandwidth of 100 nm and a measured depth resolution of 16 µm in air. The system provides excellent phase stability in transparent (65 pm at a 280 µm depth) and scattering media (less than 1 nm up to 864 µm depth) and low degradation of optical pathlength sensitivity with increasing depth (0.16 nm/mm in transparent and 2.8 nm/mm in scattering media).

The PhS-OCT system used SMF-28 fiber (Corning Inc., Corning, NY) and contains four subsystems: (1) common-path sample and (2) reference interferometers; (3) a gas-cell based spectral trigger; and (4) real-time Mach–Zehnder external clock interferometer. In the signal interferometer interference fringes formed between light reflected from the end-face of a right-angle cleaved single-mode fiber and the murine brain tissue. A Hydrogen fluoride (HF) fiber-coupled gas-cell (HF-50, Wavelength Reference, Corvallis, OR) provided a temperature/pressure-independent trigger wavelength (λ_st = 1272.97030 nm) for each A-scan. A repeatable and fixed trigger wavelength guaranteed a fixed phase φ=opλ_st/(4π) for each A-scan for a fixed optical pathlength (op) in the sample up to an uncertainty of one external clock period. A reference interferometer was implemented to remove the one clock period uncertainty.

A uniform-frequency external clock was implemented to compensate for dispersion effects associated with the nonlinear sweep rate of the tunable laser that would have resulted in degradation of the point spread function and reduced SNR with increasing scan depth [38,39]. Since the tunable laser used in this study has a 65% duty cycle, uninterrupted real-time acquisition and display of intensity (Fig. 1(C)) and speckle contrast (Fig. 2(A) ) M-mode data (39 frames/s of 512x400 [intensity] and 128x400 [speckle contrast] pixels) was realized by timely substitution (over 35% of duty cycle off-time) of the uniform-frequency optical clock with single-frequency electrical pseudo-clock [37].

Fig. 2.

In-vivo murine brain M-mode image. Speckle contrast (A) and Doppler (B) OCT image. Speckle contrast and Doppler images are presented in color coded arbitrary units and radians correspondingly. Both images consist of 128 (time) x 400 (depth) pixels. The 30-µm diameter target arteriole (purple arrow on left, 15-20 µm lumen diameter) at 550 µm optical depth is visualized in both speckle contrast and Doppler M-mode images. Three cardiac cycles are distinguished in the speckle contrast image. The maxima of the arteriole expansion in a cardiac cycle are indicated with orange arrows. Glass-tissue interface is at approximately 200 µm.

2.1.2. Laser photothermal excitation and photothermal OCT signal

Photothermal excitation beams at 770 nm and 800 nm were combined with the 1328 nm DWP-OCT probe beam in a common optical fiber (Corning SMF-28) using a 800/1310 nm wavelength-division multiplexer (WDM-1300-800-SP, Thorlabs, Newton, NJ). SMF-28 optical fiber is single-mode at 1328nm (OCT) and supports propagation of a few modes at photothermal excitation wavelengths (770 nm and 800 nm). Photothermal excitation light emitted from two 100 mW single-mode fiber pigtailed laser diodes (QPhotonics, LLC, Ann Arbor, MI: QFLD-780-100S for 770 nm and QFLD-808-100S for 800 nm) were combined in a fiber coupler (Optowaves Inc., San Jose, CA). To maintain a stable emission wavelength at 770 nm and 800 nm, temperature of the diode lasers was fixed at aproximately 278 K with 0.01 K precision using temperature controllers (TED200C, Thorlabs, Newton, NJ). Emission wavelength of the diode lasers were verified by an optical spectrometer (USB2000, Ocean Optics, Dunedin, FL).

To study in vivo microvasculature, DWP-OCT photothermal excitation and probe beams must be incident on tissue from a common side. The common path photothermal excitation/probe geometry insured single-sided and co-registration of photothermal excitation and probe beams on a target arteriole in the murine brain and increased DWP-OCT signal amplitude compared to phantom experiments [36]. Probe and photothermal excitation beams were incident on the target arteriole directly from the endface of the SMF-28 fiber without any intervening optics. The DWP-OCT probe fiber was cleaved at a right angle to provide a 4% backreflection that was used as the reference signal for the commonpath sample interferometer [37].

Computation of SaO₂ levels in the microvessel are based on the assumption of a linear relationship between optical pathlength variations (op) and fluence of photothermal excitation light absorbed by microvessel blood over a period (τ₁₍₂₎) of laser excitation [40]:

$$\begin{array}{l}o{p}_1=k{\tau }_1{I}_1\left(1-e^{-{\mu }_{a1}l}\right),\\ o{p}_2=k{\tau }_2{I}_2\left(1-e^{-{\mu }_{a2}l}\right),\end{array}$$ (1)

where τ₁₍₂₎ is the period of photothermal excitation (subscript 1 denote laser excitation at λ₁ = 770 nm and subscript 2 at λ₂ = 800 nm); Φ₁₍₂₎ = I₁₍₂₎τ₁₍₂₎ – fluence and I₁₍₂₎ intensity amplitude of excitation light on the microvessel, l = 20 µm is the microvessel’s lumen diameter (please refer to the Fig. 2), op₁₍₂₎ is amplitude of optical pathlength variation, k - a constant depending on mechanical properties of the tissue, µ_a1(2) – absorption coefficient of the blood: µ_a1(2) = α_d1(2)c_d + α_o1(2)c_o, where c_o and c_d are concentrations of oxygenated and deoxygenated hemoglobin (mM), α_o1(2) and α_d1(2) are tabulated molar extinction of oxygenated and deoxygenated hemoglobin (cm⁻¹mM⁻¹): α_o1 = 0.650 cm⁻¹mM⁻¹, α_o2 = 0.816 cm⁻¹mM⁻¹, α_d1 = 1.312 cm⁻¹mM⁻¹, α_d2 = 0.762 cm⁻¹mM⁻¹ [41].

The parameter µ_a1(2)l achieves its maximal value of α_d1c_dl = 4.6 × 10⁻³ (c_d = 1.77 mM is typical concentration of hemoglobin in mammalian blood) when 770 nm photothermal excitation laser induce op variations in a totally deoxygenated microvessel (SaO₂ = 0%). Hemoglobin concentration in mM was calculated from the conversion value of 11.4 g/dL [42] using hemoglobin molecular weight MW = 64500 g/mole. Since µ_a1(2)l << 1 for microvessels we obtained SaO₂ = c_o/(c_o + c_d) from the op₁/op₂ ratio as [36]:

$$Sa{O}_2=\frac{{\alpha }_{d1}-{\chi }_{12}{\alpha }_{d2}}{{\chi }_{12}\left({\alpha }_{o2}-{\alpha }_{d2}\right)-\left({\alpha }_{o1}-{\alpha }_{d1}\right)},$$ (2)

where χ₁₂ = (op₁/Φ₁)/(op₂/Φ₂) is the normalized ratio of op variation. The Eq. (2) shows that SaO₂ levels can be computed directly by measuring op at two wavelengths normalized by incident excitation light fluences.

To remove ambiguity in calculation of SaO₂ levels associated with temporal variation in the blood layer thickness (microvessel lumen, l) and total hemoglobin concentration (THb = c_o + c_d) in the target arteriole, we implemented simultaneous dual-wavelength (770 nm and 800 nm) photothermal excitation (Fig. 1). As can be seen from Eq. (3) in the case when l and THb are functions of time (l = l(t) and THb = THb(t)) the parameter χ₁₂ used for calculation of SaO₂ levels in Eq. (2) can vary unpredictably over time (Δt = t₂ - t₁):

$$\begin{array}{l}o{p}_1/{\Phi }_1=k\left[Sa{O}_2\left({\alpha }_{o1}-{\alpha }_{d1}\right)+{\alpha }_{d1}\right]THb(t)l(t),\\ o{p}_2/{\Phi }_2=k\left[Sa{O}_2\left({\alpha }_{o2}-{\alpha }_{d2}\right)+{\alpha }_{d2}\right]THb(t)l(t),\end{array}$$ (3)

where t₁₍₂₎ is time of measurement of op₁₍₂₎. Equation (3) is Eq. (1) written in terms of SaO₂ and Thb after simplification.

Temporal variation of in vivo blood layer thickness [l = l(t)] is due to arteriole pulsation associated with cardiac and respiratory motion. Respiratory motion may lead to temporal variation in l by lateral movement of the target arteriole with respect to DWP-OCT probe and photothermal excitation beams. Total hemoglobin concentration (THb) can vary with time in response to an intravascular injection due to transient blood dilution. Separation between op₁ (770 nm) and op₂ (800 nm) was achieved using frequency encoding by intensity modulation of the two photothermal excitation beams (770 nm at f₁ = 400 Hz and 800 nm at f₂ = 380 Hz). Modulation of photothermal excitation beams was achieved by modulating laser diode driver’s current (505B, Newport Corp., Irvine, CA) with a pure sinusoidal voltage waveform using two distinct arbitrary waveform generators (33250A, Agilent Technologies Inc., Santa Clara, CA).

2.2 Animal preparation and arteriole identification

2.2.1 Animal preparation

Experiments were performed in accordance with the University of Texas at Austin IACUC protocols. Adult male mice (30 g, strain: CD-1, Charles River Laboratories International, Inc., Wilmington, MA) were anesthetized with 2% isoflurane in a 70/30 N₂O/O₂ gas mixture and kept at a regulated temperature of 37°C using a heating pad. Aseptic surgery was performed to implant a cranial window providing optical access to cortical microvessels. In brief, a craniotomy (5x5 mm) was performed over the somato-sensory cortex and buffered with artificial cerebral spinal fluid. The craniotomy was sealed with a 150 µm cover glass and dental cement over the surrounding skull edge. The craniotomy protocol employed in studies reported here is commonly employed in cerebral blood flow studies and allows routine optical imaging of the murine brain while retaining physiological control [43]. Different SaO₂ levels (51%, 57%, 71.5%, 80.6%, 92% and 99%) were achieved by varying the oxygen flow rate in a gas mixture composed of oxygen and nitrogen oxide. The DWP-OCT fiber probe was placed on top of the cover glass and directed at a target microvessel and data collected over a 10 second time period. The measurement protocol was repeated 5 times for each SaO₂ level.

Before DWP-OCT measurements, systemic blood oxygenation was stabilized at a fixed SaO₂ level for at least 5 minutes within ±2% using a MouseOx system (STARR Life Science Corp., Oakmont, PA) with the probe attached to the hindpaw of the mouse.

2.2.2. Selecting target arteriole in the murine brain

Real-time data display together with small DWP-OCT probe diameter (125 µm) was utilized to record data from a target arteriole. OCT intensity including intensity M-mode images (Fig, 1C) do not directly detect location of murine brain microvessels [44]. We developed a multistep protocol that allowed us to first, point DWP-OCT probe at a target arteriole, second maximally overlap the arteriole with DWP-OCT beams and third verify amplitude of the DWP-OCT signal was sufficient to provide meaningful SaO₂ measurements. First the DWP-OCT probe was pointed at the arteriole under the guidance of the surgical microscope (OMS-75, Topcon Medical Systems Inc., Oakland, NJ). Identification of the arterioles was conducted by ascertaining the correct direction of branching which are predominantly opposite to the draining venules in this region and by smaller arteriole diameters due to higher order branching. This region is supplied by third- to fourth-order branches of the middle cerebral artery (MCA), which branch from the temporal lobe of the brain towards the medial to supply the cortical layers and drain into the venules. Further confirmation was obtained by visual inspection of the color of the surface microvasculature during pure oxygen inhalation, where a lighter red is associated with oxygenated hemoglobin versus dark crimson of deoxygenated hemoglobin in venous blood. Since the common-path interferometer employed here had a limited working distance (3.8 mm) precise placement of the DWP-OCT probe on the target arteriole was greatly facilitated by a miniature aperture (bare fiber cladding) and transparency of the probe. Next, the DWP-OCT probe was moved to maximize real-time speckle contrast from the target arteriole. The last step of insuring maximal overlap between photothermal excitation/OCT probe beams and the target arteriole was maximizing the amplitude of op variation at the modulation frequency of the 800 nm photothermal excitation beam. After obtaining maximal overlap between the target arteriole and DWP-OCT probe beams, the probe was fixed for the remainder time period for data acquisition from the arteriole. Optical pathlength (op) variations at the modulation frequency of phothermal excitation beams was not observed when the DWP-OCT probe was directed onto a murine brain region free of blood vessels.

3. Results

3.1 Calculation of SaO₂ levels

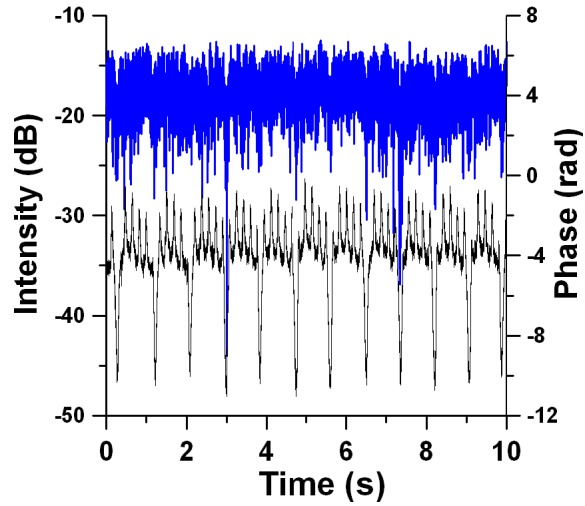
DWP-OCT phase data recorded over a 10 s time period (Fig. 3 ) corresponding to light reflected from the posterior side of a 30 µm diameter target arteriole was used to calculate SaO₂ levels.

Fig. 3.

DWP-OCT intensity (blue) and phase (black) vs. time at fixed probe depth at the posterior side of a 30-µm diameter arteriole. Phase signal contains a fast (5.9 Hz) component due to heart beat and a slow (1.2 Hz) component due to respiration.

Diameter of the arteriole was measured from a recorded digital image (Fig. 1(B)). Depth location of the back reflected light from the target arteriole was determined from Doppler [45,46] and speckle contrast [47,48] images (Fig. 2). Speckle contrast M-mode images were acquired using the Mariampillai [48] et al algorithm. Each A-scan in the speckle contrast M-mode image was calculated as a standard deviation between four adjacent OCT-signal (intensity) A-scans. The Doppler M-mode image was acquired using the Leitgeb et al algorithm [46]. To calculate each A-scan in the Doppler M-mode image we start from 512 phase A-scans and calculate the average difference between five consecutive phase A-scans.

Modulations observed in recorded phase data (Fig. 3) were those of murine heart and breathing rates. To acquire op variations associated with absorption of photothermal excitation light by blood the 10 s segment of phase data was divided into 21 segments each 5 s long and separated by 0.25 s: the first 5 s segment starts at 0 s while 21st segment starts at 5 s within the 10 s segment. Fast Fourier transformation of the 5 s phase data segments (Fig. 4 ) revealed op variations with amplitude ranging 1-2 nm at f₁ = 400 Hz and f₂ = 380 Hz due to absorption of photothermal excitation light by blood in the target arteriole. The normalized op₁/op₂ ratio (χ₁₂ = (op₁/Φ₁)/(op₂/Φ₂) = I₂f₁op₁/(I₁f₂op₂)) was used to calculate SaO₂ levels (Eq. (2)). The ratio I₂/I₁ was determined from the average power of photothermal excitation light at 770 nm and 800 nm. Average radiant power at the DWP-OCT probe was measured with a calibrated power meter (1936-C, Newport, Irvine, CA) to give 8.7 mW at 770 nm and 10.7 mW at 800 nm.

Fig. 4.

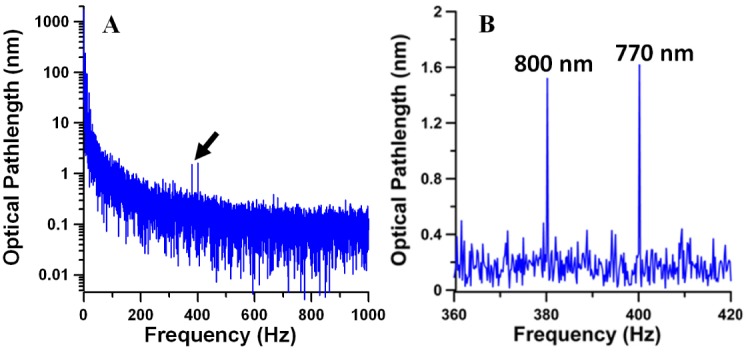
(A) Power spectrum of optical pathlength (op) variations at a fixed 350 µm tissue optical depth (550 µm from the fiber endface). The op power spectrum was acquired by converting time domain phase data presented at the Fig. 3 to op variation [(op(t) = φ(t)λ/(4π)] and using a Fast Fourier Transformation (FFT) of the first 5 s of the data. (B) Laser-induced op variations at 380 Hz (800 nm) and 400 Hz (770 nm) indicated by arrow in A.

Phase data in each 5 s segment was processed when OCT intensity signal variation was less than 15 dB (Fig. 3). SaO₂ level determined from DWP-OCT was calculated as a mean of 21 values from each of the 5 s time segments.

3.2 Optimizing intensity modulation frequencies

Selection of optimal intensity modulation frequencies was required for robust SaO₂ measurement. Optimal modulation frequency (f_mopt = 400 Hz) was experimentally determined based on the maximal ratio of op_SNR/op_SD (Fig. 5 ), where op_SNR = op₂/op_noise and op_noise was standard deviation (n = 20) of op background amplitude, op_SD is standard deviation of op_SNR over five consecutive measurements. Here, op₂ was used to determine optimal intensity modulation frequency since light absorption at 800 nm had a much weaker dependence on SaO₂ levels compared to op₁ (770 nm). Signal-to-noise ratio of optical pathlength variation (op_SNR) at f_mopt = 400 Hz was nearly equal to maximal op_SNR (f_m = 600 Hz) only with a substantially smaller standard deviation (Fig. 5).

Fig. 5.

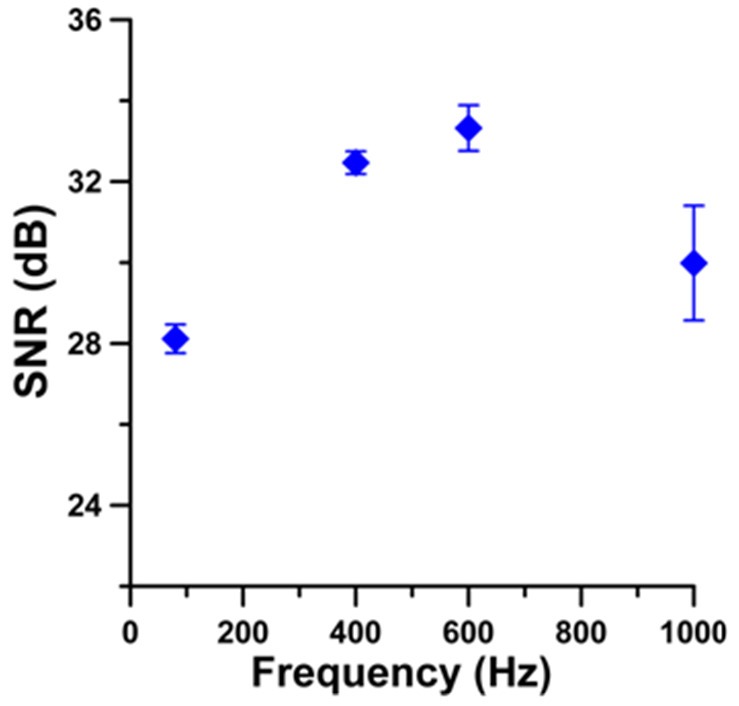
OP amplitude signal-to-noise ratio (op_SNR) vs. laser (800nm) photothermal excitation frequency. Error bars are op_SNR ± op_SD, n=5.

3.3 Gas challenge verification of DWP-OCT in murine brain arteriole

Calculated SaO₂ levels from DWP-OCT phase data for each of the twenty one 5-s segments measured in a target arteriole in the murine brain are shown in Fig. 6 . Systemic SaO₂ levels measured with a pulse-oximeter are indicated in each plot. Calculated SaO₂ levels from DWP-OCT phase data revealed oscillatory temporal dynamics during every time segments at fixed reference SaO₂ levels. Average DWP-OCT SaO₂ values are plotted versus systemic pulse-oximeter SaO₂ values (Fig. 7 ).

Fig. 6.

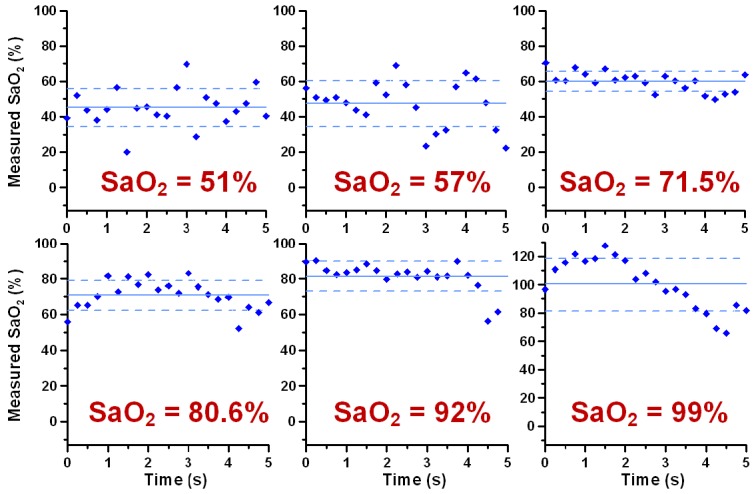
Computed SaO₂ levels from DWP-OCT op measurement. Each data point is calculated from op measured over a 5 s time period at fixed probe depth. Successive data points are separated by 0.25 s. Solid lines indicate mean DWP-OCT values, dashed lines - means ± standard deviations. Systemic SaO₂ levels measured with pulse oximeter indicated in red. Probe depth is on the posterior side of 30 µm diameter arterioles.

Fig. 7.

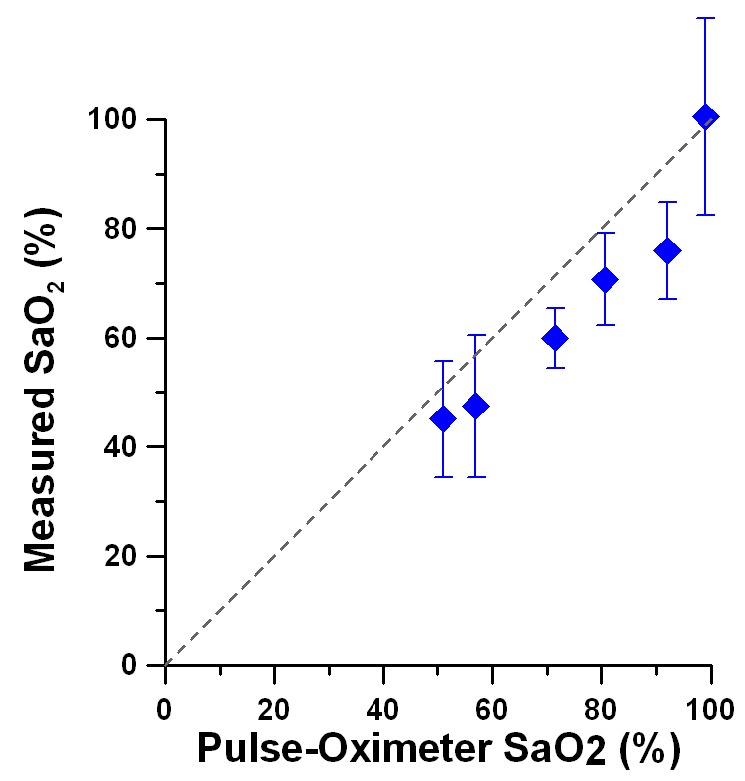
DWP-OCT vs. pulse oximeter SaO₂ values. Average difference between DWP-OCT and pulse oximeter SaO₂ values is 10.1%. Error bars are standard deviations (n=21).

The DWP-OCT SaO₂ values were linearly correlated (R² = 0.98, n = 5) and slightly and systematically lower than arterial blood-gas SaO₂ except for the blood-gas SaO₂ = 99% when the animal inhaled pure oxygen. In calculations of R² blood-gas SaO₂ value of 99% was excluded. Systemic arterial SaO₂ values are known to be higher than brain arteriole’s SaO₂ values due to gas exchange between arteriole blood and surrounding tissue [49]. When the animal breathed pure oxygen the DWP-OCT (100.4%) as well as blood-gas (99%) SaO₂ values showed that the systemic and arteriole’s blood hemoglobin were totally oxygenated within experimental error. We hypothesize that during pure oxygen inhalation, blood plasma contains excess dissolved oxygen sufficient to both diffuse to surrounding tissue and saturate (100%) arteriole hemoglobin. The averaged difference between DWP-OCT and systemic pulse-oximeter SaO₂ values was 10.1% with the pure oxygen breathing measurement included and 11.1% without. The standard error of measurements of 2.1% is estimated from 4.3% residual mean square of a linear fit of the 5 lowest SaO₂ values presented in Fig. 7.

4. Discussion

Because DWP-OCT is based on thermally induced changes in the target tissue the method is valid when thermal energy dissipation from the heated region (d_e = 50 µm - photothermal excitation beam diameter at target arteriole) is slower than heating rate (τ_e = 1/2f_mopt = 1.25 ms - half period of photothermal excitation light modulation). Thermal energy is dissipated by two mechanisms: 1) thermal diffusion, where thermal relaxation time τ_th should be longer than τ_e (τ_th > τ_e) which was satisfied in our experiments. In experiments reported here, ${\tau }_{th}=d_e^2/\left(16\alpha \right)$ = 1.42 ms and is longer than τ_e = 1.25 ms. Here α=1.1×10⁻³ cm²s⁻¹ [50] is thermal diffusivity of blood. 2) blood flow heat transfer, where the time of red blood cell traveling across photothermal excitation beam diameter (τ_bf) should be longer than τ_e (τ_bf > τ_e) which was also satisfied in our experiments. Here ${\tau }_{bf}=d_e/v_{bf}$ = 2.5 ms is longer than τ_e = 1.25 ms, where v_bf = 20 mm/s is a maximal blood velocity in 30 µm diameter arteriole [51]. According to the second condition, a modulation frequency of 400 Hz used in our experiments allows probing SaO₂ levels in arterioles with a maximal velocity of 40 mm/s corresponding to arterioles with beam diameters between 50 µm [52] and 70 µm [51].

Safety considerations for in vivo application of DWP-OCT require a small temperature increase due to absorption of photothermal excitation light below few degrees Celsius. Slow temperature increase observed in phantom experiments [36,53,54] was not observed in our in vivo experiments; raw DWP-OCT phase data showed no monotonic increase associated with a cumulative heating effect (Fig. 3). We attribute absence of cumulative heating effects in vivo to effective thermal energy dissipation in the probed murine arteriole. In experiments reported here, we estimate temperature increase was below 0.04 K. The estimate is based on comparison between the maximum op amplitude observed in phantom experiments [36] and that in the current in vivo study. Temperature increase over one-half period of photothermal excitation modulation in phantom studies was ΔT_ph = 0.033 K corresponding to maximum optical pathlength amplitude, op_ph = 1.74 nm. Temperature increase over one-half period of photothermal excitation modulation in the current study is:

$$\Delta T_a=\frac{o{p}_a}{o{p}_{ph}}\Delta T_{ph}= 0.0\text{38} \text{K,}$$ (4)

where op_a = 2 nm is maximum op amplitude measured at the target arteriole.

Competitive optical modalities proposed for depth-resolved microvascular SaO₂ investigation [29–34] are based on spectroscopic detection of intensity of backscattered probe light from different tissue layers. These methods face difficulties to achieve clinically relevant precision (below 10%) for measuring SaO₂ levels in vivo associated with uncontrolled changes in signal intensity due to complex hemodynamics, scattering and speckle variations [34,35]. Single wavelength excited optical pathlength (op) variations measured in Photothermal OCT [53,54] are not influenced by scattering or speckle dynamics and depend only on light absorption by targeted chromophores. Dual Wavelength Photothermal (DWP) OCT took advantage of intensity independent spectrally resolved op measurements induced by hemoglobin absorption to achieve preliminary estimated precision in the SaO₂ levels measurements of 2.1%. Actual precision of in vivo DWP-OCT need further investigation.

In experiments reported here the DWP-OCT probe was used without any intervening optics. This configuration allowed precise aiming of the DWP-OCT probe and photothermal excitation beams at a target arteriole using a surgical microscope. Although in our non-focusing system (1328 nm) beam divergence from a 9.2 µm mode-field diameter at the fiber endface is 63 µm in diameter at 550 µm from the fiber endface below in the brain tissue and can influence intensity OCT signal-to-noise-ratio (SNR), phase sensitivity is not affected. Measured op changes are only sensitive to amount of light absorbed by blood in the target microvessel which may include both singly and multiply scattered light. Intensity SNR will not influence measurements as long as phase sensitivity is significantly below contribution from physiological op noise (40 nm in time-domain mode, Fig. 3). Intensity SNR in our system at a depth of 350µm in brain tissue was 35 dB (Fig. 1(C)) and sufficient to provide a time-domain phase sensitivity of 1.7 nm [37,55] substantially less than amplitude of physiological and motion noise in the murine model.

DWP-OCT for measuring SaO₂ can be customized for applications in specific tissues and pathologies by implementing system changes including, introduction of scanning optics for recording B-scan images and optimizing the intensity, spot size and modulation profile of photothermal excitation light. Although one-dimensional M-mode images presented here have some diagnostic value, many applications require recording B-scan images of tissues with introduction of appropriate scanning optics. Another candidate DWP-OCT optimization is reducing intensity of photothermal excitation light at 770nm (8.7 mW) and 880nm (10.7 mW). First, in studies reported here photothermal excitation as well as probe light is not focused on the target arteriole. In our measurements, optical distance between the DWP-OCT probe (SMF-28 fiber) and arteriole was 550 µm. Gaussian beam divergence of the 1328 nm beam waist from the probe fiber tip (9.2 µm diameter) gives a 63 µm DWP-OCT probe beam diameter at the target blood vessel. Far field (170 mm) measurement of the 800 nm beam diameter (24.4 mm) suggests photothermal excitation beam diameter at the arteriole was d_e = 50 µm using a Gaussian beam approximation. Focusing of photothermal excitation light to 5 µm could increase op variation amplitude by as much as 100 times [36]. DWP-OCT signal-to-noise ratio can be increased with better focusing of the probe light in the tissue. Second, SMF-28 fiber is multimode supporting a few modes at 770 nm and 800 nm which decreases overlap of probe and photothermal excitation light and leads to faster divergence of photothermal excitation light. Launching only the fundamental mode of photothermal excitation light at the output of the multiplexer [56] (Fig. 1) will additionally increase the DWP-OCT signal. Third, different modulation profiles of photothermal excitation light may be used to optimize the DWP-OCT signal. For example, by varying the duty cycle at a fixed fluence, the averaged power is modified and op_SNR/op_SD can be optimized.

The development of non-invasive imaging technologies that can detect early depth-resolved changes in microvascular blood oxygenation can drive the discovery of new biomarkers and provide a better clinical understanding and prediction of the progression of many diseases with an etiology that includes a vascular component such as retinal diseases, stroke and cancer. This approach can also be applied for depth-resolved oxygenation imaging in multi-layered tissues including retina, skin and other epithelial tissues. Resolution of depth-resolved SaO₂ measurements that DWP-OCT is capable of providing in multi-layered tissues requires further investigation and will be reported in the future. Proof-of-concept experiments reported here using DWP-OCT for in vivo measurement of SaO₂ did not employ a scanning system and were limited to point measurements at selected tissue depths. Incorporation of a two- and three-dimensional scanning system will facilitate anatomical identification of tissue microvasculature for blood oxygenation measurements. In summary, we have reported for the first time a DWP-OCT method to probe depth-resolved SaO₂ levels in microvasculature in vivo in selected murine brain arterioles.