An Empirical Bayesian Approach for Identifying Differential Coexpression in High-Throughput Experiments

Summary

A common goal of microarray and related high-throughput genomic experiments is to identify genes that vary across biological condition. Most often this is accomplished by identifying genes with changes in mean expression level, so called differentially expressed (DE) genes, and a number of effective methods for identifying DE genes have been developed. Although useful, these approaches do not accommodate other types of differential regulation. An important example concerns differential coexpression (DC). Investigations of this class of genes are hampered by the large cardinality of the space to be interrogated as well as by influential outliers. As a result, existing DC approaches are often underpowered, exceedingly prone to false discoveries, and/or computationally intractable for even a moderately large number of pairs. To address this, an empirical Bayesian approach for identifying DC gene pairs is developed. The approach provides a false discovery rate controlled list of significant DC gene pairs without sacrificing power. It is applicable within a single study as well as across multiple studies. Computations are greatly facilitated by a modification to the expectation–maximization algorithm and a procedural heuristic. Simulations suggest that the proposed approach outperforms existing methods in far less computational time; and case study results suggest that the approach will likely prove to be a useful complement to current DE methods in high-throughput genomic studies.

1. Introduction

A common goal of microarray and related high-throughput genomic experiments is to identify genetic signatures that provide insight into understanding, diagnosing, and/or treating disease. A multitude of effective methods have been designed for this purpose, almost all of which focus on identifying genes or gene sets showing average expression levels that vary across biological condition. Applications of the most effective approaches for identifying so called differentially expressed (DE) genes or gene sets have proven useful (for a review, see Newton et al., 2007; Barry, Nobel, and Wright, 2008; Yakovlev, Klebanov, and Gaile, 2010). However, in spite of notable successes, major insights have resulted far less frequently than expected (Pollack, 2007; Zilliox and Irizarry, 2007). This is due to the immense complexity of most diseases, and in particular to the fact that manifestation of disease can result from a de- or reregulation of genes that does not significantly affect each gene’s average expression level.

An important example is given in a study of endometrial cancer (Kato et al., 2003), where the expression of two genes known to be involved in cellular proliferation and genome replication (Ki-67 and MCM3, respectively) demonstrated significant positive coexpression in normal cells, but not cancer cells, suggesting a deregulation between the two genes that potentially results in cancer development or maintenance. The identification of Ki-67 would not have been made if only the average levels of expression had been considered, because Ki-67 abundance did not change between the two groups. Chan et al. (2000) highlight a similar result in a study of ovarian cancer, where no coexpression between Bcl-2 and p53 expression was found in normal ovaries, but significant negative coexpression in malignant ovaries is evidenced. Another example concerns a study of cell cycle regulation in islet (Keller et al., 2008), where investigators showed that p16 and a group of cyclins (genes that control progression of cells through the cell cycle) are negatively coexpressed in lean mice, but positively coexpressed in obese mice suggesting a reregulation of the cell cycle pathway related to obesity. As in the other aforementioned examples, p16 and many of the cyclins were not shown to be DE between the lean and obese mice and would have therefore been missed had DE measures been applied in isolation. Numerous additional examples abound further suggesting that identification of other types of differential regulation, above and beyond DE measures, may increase one’s ability to distinguish between groups and provide insight into their distinct etiologies (for a discussion and additional examples, see de la Fuente, 2010). In particular, the discernment of differentially coexpressed (DC) gene pairs from their equivalently coexpressed (EC) peers may prove useful to this end (de la Fuente, 2010). As noted in de la Fuente (2010), the term coexpression often refers to some measure of correlation, and hereinafter we will use the term to refer specifically to Pearson’s correlation unless otherwise noted.

The simplest methods for identifying DC gene pairs conduct pair-specific tests for selected pairs within a condition, identify those pairs that are strongly or significantly coexpressed, and define DC pairs as those coexpressed in one condition but not another. Approaches for doing so both within (Watson, 2006) and across (Choi et al., 2005) experiments exist. Although useful, these approaches sacrifice considerable power by conducting analyses separately within condition, they do not provide probabilistic statements regarding the likelihood that a particular pair is DC, and they cannot identify important types of DC pairs (e.g., those showing significant coexpression in both conditions that differs in magnitude or sign). These concerns are largely addressed by the approach of Lai et al. (2004) who propose an extension of the traditional F-test to accommodate not only changes in means but also correlations. The determination of exact thresholds is computationally prohibitive in their model, and as a result they propose an approach to approximate false discovery rate (FDR), which is shown to be conservative in most cases. Also, because the test statistic quantifies both DE and DC, selection of a pair provides no information about whether the pair is DE, DC, or both.

It is worth noting a few other approaches that have been developed for coexpression analysis. The liquid association method of Li (Li, 2002) investigates changes in coexpression among pairs of genes in a single condition conditional on the expression of some other single gene; we note that this approach does not aspire to analyzing differential coexpression across biological conditions. Two approaches by Hu and colleagues (Hu et al., 2009; Hu, Qiu, and Glazko, 2010) do look for differential coexpression across biological conditions, by assessing DC at the gene as opposed to the gene pair level. These two approaches highlight DC arising from different variances as well as correlations across conditions, without separating the two sources. As our article concerns DC inference at the gene pair level, these three methods will not be further examined.

To address a number of the limitations presented by previous methods, we here present an empirical Bayesian approach for identifying DC gene pairs from a high-throughput experiment measuring expression in two or more conditions within a single study or across multiple studies. The approach provides an FDR controlled list of interesting pairs along with pair-specific posterior probabilities that can be used to identify particular types of DC. Section 2 details the underlying model and its assumptions with specific emphasis on computational efficiency and meta-analysis. The simulation studies presented in Section 3 suggest an improvement in power over comparable approaches with reasonable runtimes. Finally, case study results and a Discussion are presented in Sections 4 and 5, along with examples highlighting ways in which the derived posterior probabilities may be used in practice.

2. Methods

2.1 Description of the Model

Consider normalized expression levels in a study indexed by s, profiled from m genes in n_s subjects, where the n_s subjects are partitioned into K conditions, each with $n_s^k$ chips ( ${\sum }_k{n}_s^k=n_s$). For every pair of genes, Fisher’s Z-transformation (Fisher, 1928) is applied to sample correlations calculated within condition, ${\rho }_s^1,\dots ,{\rho }_s^K$, to yield ${\mathbf{y}}_s=(y_s^1,\dots ,y_s^K)$, where the pair subscript has for the moment been suppressed for simplicity of notation. As noted by Bartlett (1993), this transformation has several advantages, including symmetry, homogeneous and known variance, and approximate normality when moderately large sample sizes are available. As a result, $y_s^k$, the transformed correlation for a pair within condition k, is assumed to arise from a normal distribution with mean ${\lambda }_s^k$ and variance $\frac{1}{n_s^k-3}$.

The distribution of latent levels of correlation across pairs is also modeled in terms of normal distributions, using the following density, which we will call ψ_s:

$${\psi }_s(·)=\sum _{g=1}^{G_s}[w_{sg}\times \phi (·;{\mu }_{sg},{\tau }_{sg}^2)],$$ (1)

where G_s is the number of mixture components, w_sg is the weight of the g^th component, φ is the univariate normal density, and μ_sg and ${\tau }_{sg}^2$ are component-specific means and variances, respectively. This specification accommodates fluctuation in the latent levels of correlation across pairs and allows for information sharing across pairs as well as conditions within the study. In practice, the one-component distribution is often too simplistic to describe the data while distributions with needlessly many components increase runtime without an accompanying increase in performance. Therefore, we will only consider 1 ≤ G_s ≤ 3.

Of primary interest is identifying those pairs for which ${\lambda }_s^k$ differs across conditions, or, more generally, defining the DC class. For example, when K = 2, there is a single way in which a pair could be classified as $\text{DC}({\lambda }_s^1\ne {\lambda }_s^2)$, referred to hereinafter as a DC class. When K = 3, there are four DC classes: ${\lambda }_s^1\ne {\lambda }_s^2={\lambda }_s^3;{\lambda }_s^2\ne {\lambda }_s^1={\lambda }_s^3;{\lambda }_s^3\ne {\lambda }_s^1={\lambda }_s^2$; and a DC class where ${\lambda }_s^1,{\lambda }_s^2$, and ${\lambda }_s^3$ are all distinct. The number L of EC/DC classes (there is always a single EC class) increases with increasing K, as prescribed by the Bell exponential number (Bell, 1934); EC/DC classes will be indexed by l = 1, …, L.

The preceding yields the following multivariate setup for a correlation vector ${\mathbf{y}}_s=(y_s^1,\dots ,y_s^K)$ in study s:

$${\mathbf{y}}_s\mid {\mathit{\lambda }}_s\sim \mathit{MVN}({\mathit{\lambda }}_s,{\mathbf{\sum }}_{\sigma }),$$ (2)

$${\mathit{\lambda }}_s\mid l,\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\}\sim \sum _{g=1}^{G_s}[w_{sg}\times \mathit{MVN}({\mathit{\mu }}_{sg},{\mathbf{\Psi }}_{sg}^l)],$$ (3)

where ${\mathit{\lambda }}_s=({\lambda }_s^1,\dots ,{\lambda }_s^K)$, the K-vector μ_sg = (μ_{s g}, …, μ_sg ) contains K copies of μ_sg, Σ_s is a K-by-K diagonal matrix with diagonal entries $d_{kk}=\frac{1}{n_s^k-3}$ (note that this is equivalent to the vector elements arising from independent normals), and the ${\mathbf{\Psi }}_{sg}^l$ are (possibly singular) matrices particular to the EC/DC class of the gene pair in question. For example, when there are two conditions, ${\mathbf{\Psi }}_{sg}^1$ (EC case) and ${\mathbf{\Psi }}_{sg}^2$ (DC case) are, respectively, given by

$${\mathbf{\Psi }}_{sg}^1=\left(\begin{array}{ll}{\tau }_{sg}^2\hfill & {\tau }_{sg}^2\hfill \\ {\tau }_{sg}^2\hfill & {\tau }_{sg}^2\hfill \end{array}\right)\text{and}{\mathbf{\Psi }}_{sg}^2=\left(\begin{array}{ll}{\tau }_{sg}^2\hfill & 0\hfill \\ 0\hfill & {\tau }_{sg}^2\hfill \end{array}\right).$$

Combining equations (2) and (3) gives the joint conditional distribution of y_s and λ_s under a specific EC/DC class l and in turn the intermediate marginal distribution of y_s for that class is obtained by integrating over λ_s. Because the specified model is a mixture of conjugate quantities and hence conjugate itself, as Σ_s and all ${\mathbf{\Psi }}_{sg}^l$ are known, we get:

$${\mathbf{y}}_s\mid l,\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\}\sim \sum _{g=1}^{G_s}[w_{sg}\times \mathit{MVN}({\mathit{\mu }}_{sg},{\mathbf{\sum }}_s+{\mathbf{\Psi }}_{sg}^l)].$$ (4)

It is worth noting that the density of a $\mathit{MVN}({\mathit{\mu }}_{sg},{\mathbf{\sum }}_s+{\mathbf{\Psi }}_{sg}^l)$ can be evaluated as the product of the densities of one or more multivariate normals (MVN) with a particular covariance structure, D + uu′, where D is a diagonal J -by-J matrix (J ≤ K) and u is a J -vector, both containing only positive entries. This fact contributes greatly to computational efficiency, because any particular MVN density with covariance as given above can be stated without using determinants or inverses, via application of the matrix determinant lemma (Harville, 1997) and the Sherman–Morrison formula (Bartlett, 1951) and hence evaluated using only linear algebra. To highlight this point (and simplify notation a bit later on) the likelihood obtained from equation (4) is stated as

$$L({\mathbf{y}}_s\mid l,\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\})=f_l({\mathbf{y}}_s;\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\}),$$ (5)

where f_l refers to the appropriate mixture of products over MVN densities with covariance structure D + uu′ for study s.

2.2 Combining Information from Multiple Studies

Suppose that we have S studies, indexed by s. Furthermore assume that they contain expression information pertaining to the same m genes over K conditions. For a given gene pair, it is assumed that it follows one pattern with respect to the K conditions under consideration; that is to say, it belongs to a particular EC/DC class l.

Let the (K×S)-vector y refer to the concatenation of the K-vectors y_s in order. Given a class l, the y_s are assumed to arise from their study-specific distributions in a (conditionally) independent manner. Under this assumption, we may take products of (5) to obtain:

$$L(\mathbf{y}\mid l,\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\})=\prod _{s=1}^S{f}_l({\mathbf{y}}_s;\{{\mu }_{sg}\},\{{\tau }_{sg}\},\{w_{sg}\}).$$ (6)

Assuming the y arise from a mixture over EC/DC classes, with mixing proportions π₁, …, π_L, ${\sum }_{l=1}^L{\pi }_l=1$ and defining ϑ = ({μ_sg }, {τ_sg }, {w_sg }) and θ = (π₁, …, π_L, ϑ), the observed likelihood is derived:

$$L(\mathbf{y};\mathit{\theta })=\sum _{l=1}^L\left[{\pi }_l\times \prod _{s=1}^S{f}_l({\mathbf{y}}_s;\mathit{\vartheta })\right].$$ (7)

The vectors of transformed correlations, y, are assumed to arise from equation (7) in an independent manner, conditional on the system-wide hyperparameters of θ. Although this is obviously not true in practice, as pairs that involve common genes are not independent, correlations among such pairs are less dependent than the genes contained in the pair, and are therefore only strongly dependent when the genes in question are strongly correlated (Langford, Schwertman, and Owens, 2001). As a result, this violation is less severe than that made in many gene-specific analyses (Broet, Richardson, and Radvanyi, 2002; Kendziorski et al., 2003; Smyth, 2005); and empirical results suggest that the violation is not severely detrimental in practice (see Section 3).

Adding this assumption to equation (7) and liberating the suppressed gene pair subscript i = 1, …, p, where p is the number of pairs, yields

$$L({\mathbf{y}}_1,\dots ,{\mathbf{y}}_p;\mathit{\theta })=\prod _{i=1}^p\sum _{l=1}^L\left[{\pi }_l\times \prod _{s=1}^S{f}_l({\mathbf{y}}_{si};\mathit{\vartheta })\right].$$ (8)

Note that when S = 1 this meta-analysis framework simplifies into a framework for DC analysis within a single study.

2.3 Parameter Estimation

Consider the complete data likelihood for the model described above:

$$L_C(\mathit{\theta };{\mathbf{y}}_1,\dots ,{\mathbf{y}}_p,\{z_{il}\})=\mathit{exp}\left[\sum _{i=1}^p\sum _{l=1}^L\mathcal{I}\{z_{il}=1\}\times \left(log{\pi }_l+\sum _{s=1}^{S}log{f}_l({\mathbf{y}}_{si};\mathit{\vartheta })\right)\right],$$ (9)

where each z_il ∈ {0, 1} denotes whether or not the true EC/DC class of pair i is l.

An expectation–maximization (EM) algorithm (Dempster, Laird, and Rubin, 1977) can be used to obtain estimates of θ = (π₁, …, π_L, μ₁, …, μ_S, τ₁, …, τ_S ) from the data. Specifically, on the t^th iteration, the E-step consists of calculating the complete data sufficient statistics {ω_il } = {E[z_il ]|y₁, …, y_p, θ^(t)} for all i and l via equation (5) and Bayes theorem, under the current value of θ, θ^(t), to obtain the Q-function

$$\begin{array}{l}Q(\mathit{\theta }\mid {\mathbf{y}}_1,\dots ,{\mathbf{y}}_p,{\mathit{\theta }}^{(t)})=E_{\{z_{il}\}\mid {\mathbf{y}}_1,\dots ,{\mathbf{y}}_p,{\mathit{\theta }}^{(t)}}[log{L}_C(\mathit{\theta };{\mathbf{y}}_1,\dots ,{\mathbf{y}}_p,\{z_{il}\})]\\ =\sum _{i=1}^p\sum _{l=1}^L{\omega }_{il}\left(log{\pi }_l+\sum _{s=1}^{S}log{f}_l({\mathbf{y}}_{si};\mathit{\vartheta })\right)\\ =\sum _{i=1}^p\sum _{l=1}^L{\omega }_{il}log{\pi }_l+\sum _{i=1}^p\sum _{l=1}^L{\omega }_{il}\sum _{s=1}^{S}log{f}_l({\mathbf{y}}_{si};\mathit{\vartheta }).\end{array}$$ (10)

We will use Ω to refer to the p-by-L matrix {ω_il }.

The M-step then maximizes the Q-function for θ. In this context, maximization can be divided into two parts as equation (10) is separable into two summands, one a function of the mixing proportions and the other a function of ϑ. Closed-form maximizers π̂₁, …, π̂_L are obtained by taking column-wise means of Ω. Closed-form solutions for the constituents of ϑ are not available, but can be obtained numerically, subject to the constraints that ∀s, G_s is known, τ_gs > 0, and Σ_g w_sg = 1. In the current implementation, bobyqa in R/minqa is used (Powell, 2009) for this numerical optimization.

For each study s, knowledge of G_s is essential to proper execution of the framework; good initial estimates of ϑ are also helpful to speed convergence. Both are estimated from the data in this empirical Bayesian framework. Although a number of methods may be used for this purpose, we prefer the M-clust algorithm (Fraley and Raftery, 2002, 2006) as implemented in R/mclust: When properly queried using the transformed correlations from the data as inputs, M-clust will return good values for G_s, the {μ_sg }, and the {τ_sg }. M-clust also returns a mixture component classification and a measure of classification uncertainty for each datum, which can be used to estimate the w_sg via averaging the uncertainty values.

Although the use of the Fisher Z-transform along with assumptions of parametric forms and conditional independence of pairs produce likelihoods that can be quickly evaluated, there is still a considerable computational burden for even modestly large m, as the number of pairs is quadratic in the number of genes; the M-step is by far the most expensive in terms of runtime. Noting this, as well as the fact that the mixing proportions take much longer to converge than the estimates of ϑ, a modification to the standard EM is used, as detailed below. Also provided is a heuristic which can be used to further cut runtime.

2.3.1 A special case of the two-cycle alternating expectation-conditional maximization (TCA-ECM)

This modified EM consists of running an E-step to calculate the Q-function, then calling the numerical optimizer to update ϑ. Then, a cycle of calculating the E-step and maximizing to obtain estimates of the mixing proportions, π̂₁, …, π̂_L, keeping the current estimate of ϑ fixed, is performed until estimates of the mixing proportions converge. This process replaces a single iteration of the standard EM, and repeats until convergence of θ is achieved.

In other words, one iteration of the standard EM is replaced by:

1. Calculate {ω_il } given π and ϑ.

2. Maximize Q w.r.t ϑ given the {ω_il } (note that due to the separable nature of Q, the derived argmax does not depend on π). Update the members of ϑ with their respective components of the joint argmax.

3. Calculate {ω_il } given π and this updated ϑ.

4. Maximize Q w.r.t. π given {ω_il } (note that this step likewise does not depend on ϑ). Update π with the argmax.

5. Repeat 3 and 4 until π converges

Technically speaking, this modification to the standard EM is not novel. It can be construed as an incarnation of the TCA-ECM algorithm presented by Meng and van Dyk in 1997 (personal communication). However, it is a special case of that rather general framework and can dramatically reduce runtimes if the following conditions hold:

1. Good initial estimates for one subset of θ may be computed using the data (and hence estimates for this subset converge quickly during the EM), while only poor or uninformed estimates exist for the other, and

2. The M-step is computationally cheap for the latter subset (e.g., closed-form maximizers exist) but expensive for the former (e.g., numerical optimization is required).

When these conditions hold, this modification to the standard EM (referred to hereinafter as the TCA-ECM) requires fewer iterations than the standard EM, is considerably faster, and provides the same estimates of θ, up to specified convergence and iteration tolerances (simulations not shown; see also Meng and van Dyk, 1997). Executions of our algorithm with only one iteration of this modification will be referred to as one-step incarnations.

2.3.2 A helpful heuristic

To further reduce runtime, one can use a random subset of the data (e.g., 0.1% of all gene pairs) to perform computations related to ϑ, specifically while either calling M-clust or the pertinent portion of the TCA-ECM. This heuristic is exceedingly beneficent when the number of pairs is large, because the number of data points p (which number in the hundreds of thousands if not millions when m > 500) is far greater than the number of free parameters being estimated. The validity and efficacy of this heuristic will be illustrated in Section 3.

Our approach has been implemented in an add-on extension package for the R statistical computing language (R Development Core Team, 2009), where the most computationally intensive portions of the code are dynamically outsourced to code written in C, to improve runtime speed. All simulations were run on a standard DELL Xeon 5670 with 1600 Mhz and 48 GB of RAM.

3. Simulations

The proposed methodology provides a way to identify DC gene pairs, but it relies on numerical approximation methods and it assumes conditions that are never fully satisfied in practice (e.g., assumptions of conditional independence). To assess the methodology we performed a small set of simulation studies. These provide some, albeit limited, insight into the quality of parameter estimates from the TCA-ECM algorithm and associated heuristics, potential gains in computational time, and how violations of assumptions affect inference. Perhaps most importantly, the simulation results also provide information on error rates related to DC inference and facilitate a comparison to related approaches.

We consider four simulations in three scenarios. The first simulation (SIM I) is designed to assess relative performance among the modified EM algorithms when the model described in Section 2.1 holds. A simulated data set consists of 10,000 observations (which represent transformed correlations) simulated in two conditions, where the normal mixture prior takes a specified form. Five different priors are considered; their descriptions and density plots (Web Supplement Figures 1a–e) are provided in the Web Supplement. For each form of the prior, 20 simulated data sets are generated.

The other sets of simulations (SIMS II-A, II-B, and III) are designed to assess performance when model assumptions are violated. A single data set in SIM II-A contains three groups of 100 genes, simulated in each of two conditions. Within each group and condition, the genes are all correlated; genes in different groups are uncorrelated. Two covariance matrices, one for each of two conditions, are created such that the strengths of the correlations in the first group are not the same between conditions, but all other correlations are unchanged. SIM II-B is identical except that the three groups now have 1000, 1000, and 2000 genes, respectively, rather than each having 100 genes as in SIM II-A. SIM III contains two groups of 1500 genes where DC pairs exhibit changes in sign and the majority of intergroup correlations are not zero. Further details for the setup of SIMS II-A, II-B, and III are given in Web Supplement Appendices A and B.

For each simulated data set in SIMS II-A, II-B, and III, Fisher Z-values were obtained from correlations calculated using the biweight midcorrelation that was used to minimize the effect of potential outliers (Wilcox, 1997). A single simulation consists of 200 chips, 100 in each condition; data are drawn from a MVN distribution with mean zero and covariance as dictated by condition. As in SIM I, 20 simulations are considered in each of these.

A gene pair is identified as DC using our approach under a soft thresholding mechanism if the posterior probability of DC exceeds a critical value that controls the posterior expected FDR at 5% (Berger, 1980, p. 164). A gene pair is identified as DC under a hard thresholding mechanism if the posterior probability of DC exceeds 0.95. This threshold conservatively controls the posterior expected FDR at 5%.

Our approach is compared to an FDR-controlled pairwise application of Box’s M-test (Mardia, Kent, and Bibby, 1979) and to the ECF (expected conditional F) approach of Lai et al. (2004). For the M -test, the p-values obtained from each pair of genes are converted into q-values (Storey, 2002) and thresholded to get a list of pairs with FDR of 5%. In the ECF approach, the distribution from which the null is drawn is data independent once the number of subjects (microarrays) in each condition is known. Using the code from the ECF web-site and details provided in personal communications, we simulate from this null one million times to obtain ECF thresholds corresponding to multiple comparison adjusted p-values ranging from p = 10⁻¹ to 10⁻⁴, following the approach used in (Lai et al., 2004) (see Table 2).

Table 2.

SIM II-A

Approach	Obs. FDR	Obs. power	Time*
1-step TCA-ECM (soft threshold)	0.054 (0.021)	0.952 (0.099)	549(195)
1-step TCA-ECM (hard threshold)	0.0004 (0.0003)	0.869 (0.162)	549(195)
ECF w/p = 10−1	0.277 (0.028)	0.932 (0.064)	134+(1)
ECF w/p = 10−2	0.037 (0.012)	0.718 (0.141)	134+(1)
ECF w/p = 10−3	0.006 (0.004)	0.452 (0.154)	134+(1)
ECF w/p = 5 × 10−3	0.004 (0.003)	0.381 (0.145)	134+(1)
ECF w/p = 10−4	0.001 (0.001)	0.240 (0.116)	134+(1)
Box’s M -test	0.084 (0.035)	0.856 (0.067)	27(1)

Average FDR and power from the proposed approach with hyperparameters estimated using the one-step versions of the TCA-ECM under soft and hard thresholding. Values are means calculated over 20 simulated data sets; standard deviations are shown in parentheses. Results from the ECF approach of Lai et al. (2004) and Box’s M -test Mardia et al. (1979) are also shown. Computational time is given in seconds. Should the reader desire them, means and standard deviations for the observed false and true positives for SIM II-A can be found in Web Supplement Table 1.

^*Times for the ECF results do not include the runtime required for the simulation of the ECF null, which depends linearly on the number of null simulations. When using one million null simulations (as was the case here) this adds an additional 795 seconds to the ECF’s runtime.

3.1 Results

Table 1 provides timing, parameter, and deviance estimates derived from data generated under SIM I for both the full and one-step TCA-ECM approaches. Averages across 20 data sets are shown with standard deviations given in parentheses. There are two conditions, so there are two EC/DC classes. The proportion of DC was set to 0.05 (π₂ = 0.05; so π₁ = 0.95) in these simulations. Deviance is defined here as 1000 × ||f_t − f_e ||₂, where f_t and f_e are the true and estimated densities for the distribution from which the transformed correlations are generated. This is done to compare the estimated ϑ to the truth in situations where a model of different complexity is deemed best for the simulated data (e.g., a two-component f_e is chosen when f_t truly uses three components). The results in Table 1 indicate that the one-step version of the TCA-ECM provides performance and accuracy that are very close to those obtained from the full TCA-ECM in a fraction of the time. Therefore, we will not include the full approach in subsequent simulations where data set size is computationally prohibitive.

Table 1.

SIM I

	A1	B1	B2	C1	C2
Time
TCA-ECM	68(3)	529(84)	3600(6366)	735(108)	2933(402)
1-step TCA-ECM	26(3)	153(2)	184(22)	216(1)	218(3)
π̂1
TCA-ECM	0.949(0.003)	0.949(0.003)	0.949(0.004)	0.950(0.002)	0.949(0.003)
1-step TCA-ECM	0.949(0.003)	0.948(0.003)	0.948(0.004)	0.949(0.002)	0.948(0.003)
Deviance*
TCA-ECM	0.1(0.1)	1.2(0.8)	2.3(0.7)	0.7(0.4)	2.7(2.0)
1-step TCA-ECM	0.1(0.1)	1.1(0.7)	0.5(0.4)	0.8(0.4)	10.5(6.6)

Hyperparameters estimated using the full and one-step versions of the TCA-ECM under five different true distributions of transformed correlations (see Web Supplement Figure 1). The proportion of DC was set to 0.05 (π₂ = 0.05; so π₁ = 0.95) in these simulations. Values shown are means calculated over 20 simulated data sets; standard deviations are shown in parentheses. Computational time is given in seconds.

^*Defined as 1000 × ||f_t − f_e ||₂, where f_t and f_e are the true and estimated densities for the distribution from which the transformed correlations are generated.

Power, FDR, and runtime for the proposed approach, the ECF procedure of Lai et al. (2004) and Box’s M -test (Mardia et al., 1979) evaluated using the data from SIM II-A are shown in Table 2. The results suggest that the proposed approach has well-controlled FDR, with power that is increased over that obtained from ECF for each of the thresholds considered (including one corresponding to p = 10⁻¹).

Given the results from SIM II-A, as well as the fact that computation in the ECF approach is prohibitive over many simulations when p (the number of pairs) is relatively large, we only consider our approach in SIMS II-B and III, with the one-step TCA-ECM restricted to 0.1% of the pairs for parameter estimation. Note that for 4000 genes, this restriction still leaves ~ 8000 pairs from which the relatively few parameters (there are at most eight hyperparameters and mixing proportions) are estimated. Table 3 reports power, FDR, and runtime for results derived from 20 runs of SIMS II-B and III for this restricted version of the one-step TCA-ECM, suggesting that while the use of the restricted algorithm reduces runtime considerably, it does not detrimentally impact observed FDR or power.

Table 3.

SIM II-B and SIM III

Approach	FDR	Power	Time
SIM II-B
1-step TCA-ECM (soft threshold; 0.1% pairs)	0.058 (0.015)	0.985 (0.011)	3734 (362)
1-step TCA-ECM (hard threshold; 0.1% pairs)	0.0006 (0.0003)	0.913 (0.049)	3734 (362)
SIM III
1-step TCA-ECM (soft threshold; 0.1% pairs)	0.122 (0.034)	0.975 (0.022)	3086 (195)
1-step TCA-ECM (hard threshold; 0.1% pairs)	0.008 (0.007)	0.903 (0.055)	3086 (195)

Average FDR and power from the proposed approach in SIMS II-B and III with hyperparameters estimated using the one-step version of the TCA-ECM under soft and hard thresholding and the subset heuristic with 0.1% of pairs. Values are means calculated over 20 simulated data sets; standard deviations are shown in parentheses. Computational time is given in seconds.

4. Prostate Cancer Case Study

As an application of this approach, we considered three studies of prostate cancer for which microarray expression data were available for normal and diseased subjects. These studies will be referred to as the Monzon, Taylor, and Roth studies, respectively. They are described in detail in Web Supplement Appendix C. In short, each study utilized a different Affymetrix microarray platform, and each data set is available at the Gene Expression Omnibus (with GEO accession ids GSE6919, GSE21034, and GSE7307, respectively). The Monzon study considers samples from 18 normal and 65 diseased prostates; Taylor considers 29 normal and 150 diseased; Roth considers 7 normal and 17 diseased.

The three studies have 8631 genes in common, many of which are homologues within gene families. From the 8631, we selected 5765 genes representing unique genes from the families. For all three studies, any gene for which two or more probes existed was represented by a single probe, which was chosen by calculating the average intensity across all arrays within that study for all probes corresponding to that gene and then taking the probe with the median such average. Background correction of the intensities contained in the raw (.CEL) files was performed using Robust Multi-array Average (RMA; Bolstad et al., 2003). Quantile normalization was not done due to issues concerning unpredictable alterations of correlations across samples (see Discussion). Rather, chip-specific intensities were normalized to have the same median across studies.

With condition defined by disease status (K = 2), the proposed approach was used to identify DC gene pairs separately for all three studies and together in a meta-analysis. Over 16.6 million gene pairs were considered. As in the simulation studies, biweight midcorrelation (Wilcox, 1997) was used prior to Fisher’s Z-transformation to minimize the effects of outliers.

4.1 Results

When analyzing the studies individually, 14,954 and 115,279 gene pairs were declared DC by the approach for the Monzon and Taylor studies, respectively; 408 of these pairs were in common across the two studies. No pairs were flagged in the much smaller Roth study. We note that lack of common identifications is often observed in studies of differential expression due to differences in sample quality, subtle differences in sample type (assayed tumors can be at different stages, for example, and this information is not often available), technical differences in sample processing, and differences in microarray platforms. Indeed, this type of discrepancy motivated much of the work on gene set enrichment analysis (Subramanian et al., 2005). In contrast, the meta-analysis yields 141,678 DC gene pairs, including the 408 gene pairs identified by both Monzon and Taylor separately. In addition, 8,055 of 14,954 and 97,064 of 115,279 pairs carried over their DC identification to the meta-analysis.

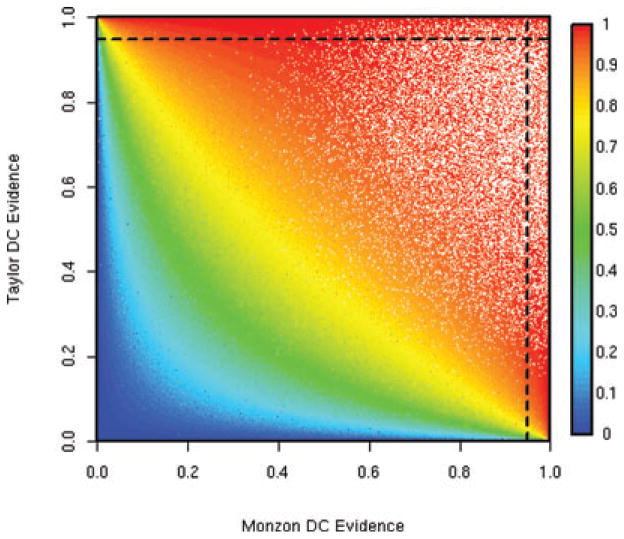
Figure 1 shows posterior probabilities of DC obtained from the Monzon and Taylor individual analyses for all 16.6 million pairs. The color of each pair’s point corresponds to the posterior probability of DC generated by the meta-analysis, ranging from blue (nil evidence of DC) to red (high evidence of DC). Dashed lines indicate the 0.95 cutoffs used in the individual analyses; those points boxed into the upper right-hand corner reflect the 408 pairs taken by both studies. Lest the reader think that Figure 1 indicates that Roth’s study did not contribute to the meta-analysis results, consider Web Supplement Figure 2. The structure is similar to Figure 1, except that now only those 141,678 pairs taken by the meta-analysis are plotted (in red). Although the curve largely describes the results of Monzon and Taylor, note the handful of points that lie far beyond the curve. These pairs are taken by the meta-analysis due to the Roth study. For emphasis, pairs for which the posterior probability of DC obtained from the Roth study is greater than 0.5 are circled.

Figure 1.

Shown are the posterior probabilities of differential coexpression obtained from all 16.6 million gene pairs in the Monzon and Taylor individual analyses. Their color corresponds to the meta-analysis evidence; see the color bar. Dashed lines indicate the 0.95 cutoffs used in the individual analyses; those points boxed into the upper right-hand corner reflect the 408 pairs taken by both studies. This figure appears in color in the electronic version of this article.

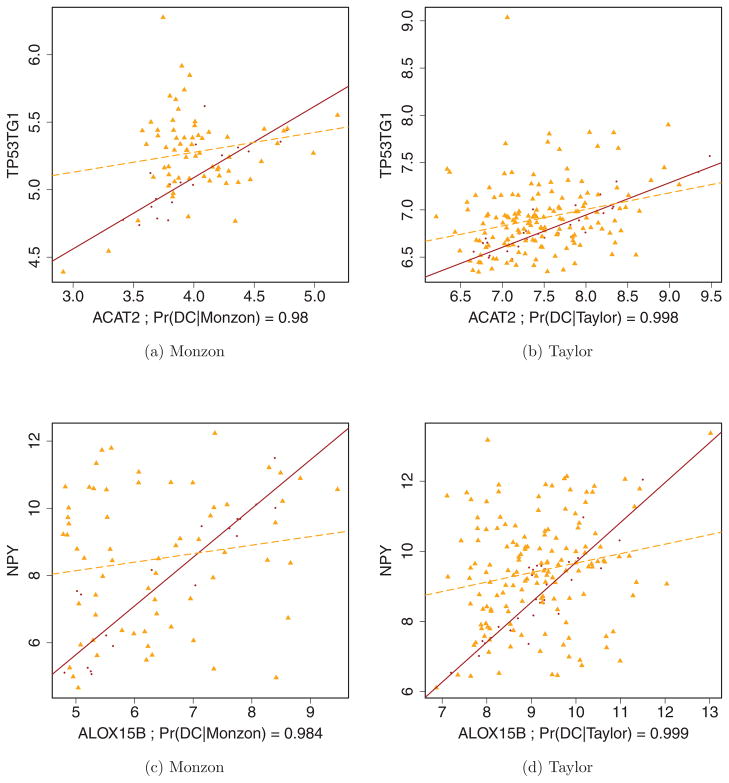
Figure 2 shows two gene pairs identified by the meta-analysis as well as the separate Monzon and Taylor analyses. The plotted points are colored by condition, with noncancerous subjects in purple and cancerous subjects in orange. A robust regression line (i.e., one based on only those points used internally by the biweight midcorrelation calculation) is overlaid for each condition as a visual aid. When viewing these regression lines as proxies for correlation, it is important to note tightness around the line as well as slope; however, because these lines were fit using least squares, their trajectories are driven by vertical (y-axis) deviations. Web Supplement Figure 3 similarly highlights two other pairs chosen as DC by the meta-analysis, but neither of the individual studies. Although there appears to be a clear DC relationship, the individual studies are underpowered (relative to the meta-analysis) to identify these pairs as DC at an FDR of 5%.

Figure 2.

Two gene pairs deemed DC by Monzon, Taylor and the meta-analysis. The processed expression values for ACAT2~TP53TG1 are plotted using data from (a) Monzon and (b) Taylor in the first two plots; ALOX15B~NPY is similarly depicted in (c) and (d). Colors and shapes indicate condition; noncancerous subjects are indicated by dots, cancerous subjects by triangles. A robust regression line (see Methods) is superimposed for each condition (cancerous is dashed). These figures appear in color in the electronic version of this article.

5. Discussion

Understanding the genetic basis of disease requires identifying genes that are differentially regulated between healthy and affected conditions. For over a decade, thousands of investigations utilizing high-throughput expression data have focused on identifying DE genes. Although tremendously powerful in many settings, it is becoming increasingly clear that overlooking other types of differential regulation, such as DC, can be critically limiting and in some cases can lead to incorrect inference (Mentzen, Floris, and de la Fuente, 2009).

The empirical Bayesian approach presented here provides a much needed method for identifying DC pairs while controlling a specified FDR. The pair-specific posterior probability distributions facilitate classification of each pair into its most likely EC/DC class. The approach does not restrict DC gene pairs to those that are highly correlated in at least one condition, it allows for the identification of DC pairs that change in magnitude but not sign across conditions, and it does not involve tests for DE. This last point is important because many of the best methods for normalization prior to a DE analysis change the correlation structure between genes in a significant way and so are not optimal when performing DC identification is of interest (Qiu et al., 2005). In other words, the most appropriate method for normalization depends in part on whether subsequent analysis involves tests for DE or DC, and it is not yet clear how best to normalize measurements prior to applying methods that aim to do both simultaneously.

Although our approach does not involve identification of DE genes, the hierarchical framework presented here is conceptually similar to our previous work, which proposed a log-normal normal hierarchical model for identifying DE genes (Kendziorski et al., 2003). A main difference is that here we introduce a more flexible prior that accommodates the structure of transformed correlations observed in practice. More importantly, the normal observation component is used here to describe Fisher Z-transformed correlations calculated from gene pairs rather than log-transformed expression from individual genes as in a DE analysis. We note that the Z-transformation is required as raw, nontransformed correlations do not exhibit the desired variance properties described by Bartlett (1993) and assumed by our model; however, care must be taken in postprocessing when correlations are very large in magnitude as the Z-transformation is exceedingly nonlinear as raw correlations approach −1 or 1. In addition to providing a more flexible model that can accommodate the distribution of coexpressions observed in practice, these differences have important implications computationally. In particular, estimation of hyperparameters via the EM algorithm as previously described becomes arduous in studies of coexpression even when the number of genes is modest (because all pairs are considered). To address this, we have proposed a modification to the EM algorithm referred to as the TCA-ECM along with a heuristic that provides reliable parameter estimates in substantially reduced computing time. As the conditions specified in Section 2.3.1 are not specific to this application, the TCA-ECM as implemented here should prove advantageous in other more general mixture model settings where the conditions hold.

As with any modeling framework, the proposed approach makes a number of assumptions that should be checked in practice. A main one is that transformed correlations can be well approximated by a normal mixture; our code provides such a diagnostic. The biweight midcorrelation or Spearman’s correlation provide estimates that are largely robust to outliers; and the biweight midcorrelation was used here as it has been shown to be superior to Spearman’s correlation in many regards (Wilcox, 1997). A second assumption concerns conditional independence of the correlations (equation (8)). The simulation study suggests that this violation results in slight increases in FDR with little change in power. Further work is required to more completely assess the impact on inference when the model assumptions are violated.

A few notes on computational limitations: Because our approach is making probabilistic statements about all (m choose 2) gene pairs, it is not suited for direct applications to extremely large numbers of genes, such as whole-genome analyses (~20,000 genes leading to ~200M gene pairs). Even in analyses where the number of genes is not this big, some prefiltering of genes is usually beneficent, such as filtering genes with very low (~1–2 on the log₂ scale; Irizarry et al., 2003) or constant expression. Although such filtering will probably change the overall underlying distribution of correlations across the system, this will not adversely affect the ability of our approach to properly control FDR as long as the distribution can be approximated by our flexible prior; this is something that can be assessed via diagnostics, as in Web Supplement Figure 4.

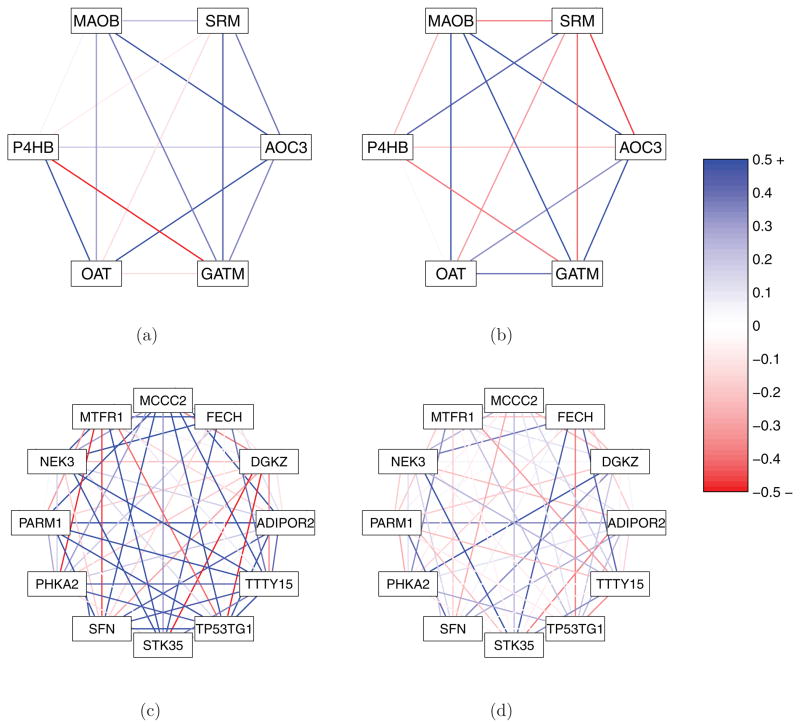
Although the proposed methodology does not make use of (and is hence not constrained by) previously defined sets of genes, the pair-specific posterior probabilities of DC provided by the approach can augment an analysis that has identified a group of genes as interesting a priori. The upper panel of Figure 3 shows six genes identified in Gorlov et al. (2009) as being individually significant in the transition from normal prostate to localized prostate cancer. No information is provided in Gorlov et al. (2009) on the relationships among the genes, but as one can see in Figure 3, there are a number of interesting features among the pairs. Notably, SRM appears to be a DC hub within this gene set.

Figure 3.

In the upper panels, a graphical depiction of relationships within and across conditions for a small pathway related to prostate cancer identified by a recent paper (Gorlov et al., 2009) is shown. The two networks in (a) and (b) show biweight midcorrelations observed among these genes within this pathway in noncancerous and cancerous subjects, respectively, using the Monzon data. In the lower panels, relationships within and across conditions for a network of 12 genes greedily built up from a seed of PARM1 are shown, based on meta-analysis posterior probabilities of DC (but again illustrated using the Monzon data for (c) noncancerous and (d) cancerous subjects). In both sets of panels, deepness of color indicates strength of correlation, where correlations of magnitude 0.5 or greater receive the deepest hue; see the color bar. These figures appear in color in the electronic version of this article.

It may also be of interest to construct groups of genes strongly DC with a gene of interest. Such a gene could be identified a priori or could be chosen from a list rank ordered by overall DC. Take, for instance, PARM1. PARM1 is believed to play a role in prostate cancer progression, as it is thought to enable certain cells in the prostate to resist apoptosis (The Human Gene Compendium, 2011). Additionally, it is in the top 20 genes when one rank orders the genes by their upper 0.00001 quantile of meta-analysis posterior probabilities of DC, across all m − 1 pairs involving themselves. The lower panel of Figure 3 shows 12 genes greedily chosen to form a DC subnetwork, using PARM1 as a seed. Specifically, each gene was added sequentially into the subnetwork by virtue of having the highest average meta-analysis posterior probability of DC with respect to pairs involving genes already in the subnetwork. The result is a novel subnetwork of genes that exhibits strong DC patterns among its members. The network shows strong correlation among members in the noncancerous condition that is lost when cancer is present, suggesting a deregulation among members. A number of prostate and/or cancer related genes are identified. Perhaps most interesting is TP53TG1, which has been shown to play an important role in signaling of TP53, a well-known tumor-suppressor gene (Takei et al., 1998).

In summary, it is becoming increasingly clear that important types of differential regulation are missed by traditional tests for DE genes; DC measures are one such type. The proposed approach is computationally efficient and should prove to be a useful complement to a traditional DE analysis. However, unlike most DE methods, the approach utilizes correlations as opposed to gene-specific expression measures, and as a result it is directly applicable to other types of high-throughput studies where correlations are of some interest. Integrating multiple types of high-throughput studies at once requires extending the framework. Current efforts in this direction are underway.