Nhs: Network-based Hierarchical Segmentation for Cryo-EM Density Maps

Abstract

Electron cryo-microscopy (cryo-EM) experiments yield low-resolution (3–30Å) 3D-density maps of macromolecules. These density maps are segmented to identify structurally distinct proteins, protein domains, and sub-units. Such partitioning aids the inference of protein motions and guides fitting of high-resolution atomistic structures. Cryo-EM density map segmentation has traditionally required tedious and subjective manual partitioning or semi-supervised computational methods, while validation of resulting segmentations has remained an open problem in this field. Our network-based bias-free segmentation method for cryo-EM density map segmentation, Nhs (Network-based hierarchical segmentation), provides the user with a multi-scale partitioning, reflecting local and global clustering, while requiring no user input. This approach models each map as a graph, where map voxels constitute nodes and edges connect neighboring voxels. Nhs initiates Markov diffusion (or random walk) on the weighted graph. As Markov probabilities homogenize through diffusion, an intrinsic segmentation emerges. We validate the segmentations with ground-truth maps based on atomistic models. When implemented on density maps in the 2010 Cryo-EM Modeling Challenge, Nhs efficiently and objectively partitions macromolecules into structurally and functionally relevant sub-regions at multiple scales.

Introduction

Cryo-EM reconstructions of macromolecules are increasing in resolution (1), extending their application from rigid-body docking to generation of atomistic structural models independent of prior structural information (1–3). Specifically, secondary structure can be annotated for resolutions better than 9Å, and for resolutions better than 4Å, de novo structure determination is possible. At lower resolutions, cryo-EM density maps still convey general macromolecular shape and assist the fitting of atomistic structures within the molecule, useful especially when cryo-EM maps suggest a novel functional state (2). Because this multi-scale organization of macromolecular components can give structural information, suggest hypotheses of molecular motions, or offer functional cues, locating individual sub-units within density maps is critical for subsequent analysis.

Segmentation of individual sub-units within cryo-EM density maps is a challenging problem that has traditionally been accomplished by tedious and subjective manual partitioning. Recently, automatic and semi-automatic segmentation techniques, where some former structural insight is employed, have improved upon manual partitioning (31). The watershed diffusion method of Pintillie et al. provides fast segmentations given a small amount of user guidance (4,5). Bajaj’s multiseeded fast-matching method likewise produces reliable segmentations when provided with symmetry information (6–8). An unsupervised method is thus necessary for those cases where such prior structural information is not available.

We propose a simple Markov diffusion framework to segment cryo-EM density maps into meaningful sub-regions (9). Our segmentation algorithm for locating structural sub-regions within molecules is termed Nhs: network-based hierarchical segmentation. The hierarchical nature of Nhs generates an increasingly coarser set of segmentations ranging from locally interacting regions to globally connected molecules (Fig. 1) with no user supervision. The segmentation at the appropriate level of detail can then be used for fitting atomic models, identifying secondary structure, detecting structural homologues, etc. This approach is an adaptation of our earlier work developing spectral graph partitioning algorithms for segmenting natural images, understanding protein dynamics and allosteric propagation, and relating signal propagation on a protein structure to its equilibrium dynamics (10–11). We present our results on the cryo-EM maps used in the 2010 Cryo-EM Modeling Challenge (1).

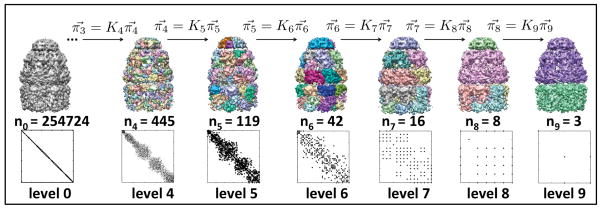
Figure 1. Network-based hierarchical segmentation of GroEL+GroES at 7.7Å.

The affinity map and cluster assignments are shown for each hierarchy level. The number of nodes in the network is given for each level. Importantly, in level t there are n_t nodes, thus the segmented map has n_t clusters and the affinity matrix A_t is (n_t × n_t). At level 1, each of the 254,724 voxels in the map are assigned to their own cluster, however, the map is shown in gray for visualization purposes. Levels two and three are left out of the diagram due to space considerations.

We model the cryo-EM map, a three-dimensional voxel-grid of intensities, as a weighted undirected graph and build an unsupervised hierarchical elastic network model. Each density map voxel is represented as a graph vertex, and edges are defined between the 26 voxels in its standard neighborhood. Edge weights, or affinities, between neighboring vertices are a function of intensity difference. By modeling the density map as a graph, we can divide the graph into clusters such that vertices within clusters have high affinity edges, and vertices between clusters have low affinity edges. We perform this partitioning by constructing a Markov transition matrix over the edge weights and initiating Markov diffusion (or random walk) on the graph. As Markov probabilities homogenize through diffusion, an implicit segmentation emerges. By choosing a set of nodes representative of each segment, and initiating Markov diffusion again from each coarser set of nodes, a hierarchical network model is built. Together, subsequent levels of the hierarchy constitute a multi-resolution representation of map sub-regions. Unlike many existing segmentation algorithms, no a priori predictions for the total number of segments are required.

Results

Nhs produces a hierarchy of increasingly coarser map segmentations for each Challenge cryo-EM map, where each level provides a segmentation based on more global interactions than the previous level. Figure 1 shows the hierarchy of segmentations, along with the affinity maps used in computation of the hierarchy, for GroEL+GroES at 7.7Å. Results on a synthetically generated map are presented in Figure 2. A summary of our results on the cryo-EM maps used in the 2010 Cryo-EM Challenge is provided in Figure 3.

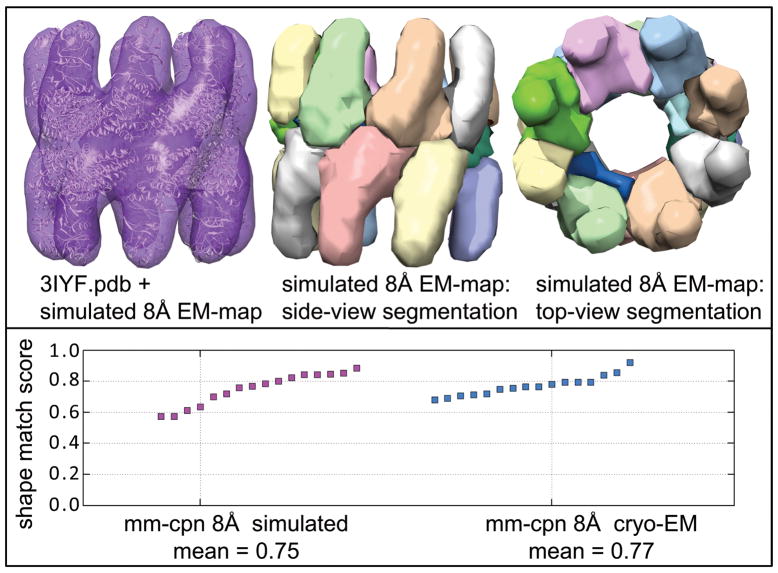
Figure 2. Segmentation of simulated 8Å cryo-EM-map.

An 8Å cryo-EM map was simulated by isotropic smoothing of the Mm-cpn PDB structure: 3IYF.pdb (12,30). In the top panel, the left image shows the PDB structure (white) inside the simulated map. The middle and right images shows the side and top views of the map segmentation at hierarchy level 6/8. All maps are shown at the intensity threshold (τ) at which they were segmented. In the bottom panel, the shape-match score for each of the 16 Mm-cpn chains is shown for the simulated and the experimental 8Å Mm-cpn cryo-EM maps. The mean score is reported for each map below the graph.

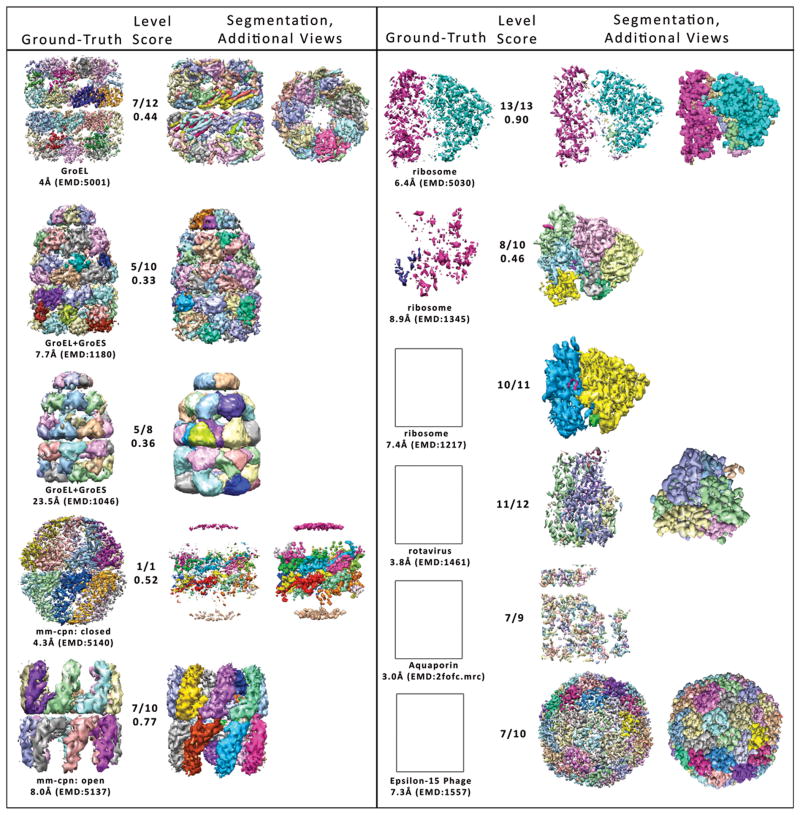
Figure 3. Segmentations of Challenge maps.

Colored regions correspond to unique clusters. For each map, the hierarchy level with the highest scoring segmentation is shown (third column). In the second column, the hierarchy level is given out of the total number of hierarchy levels for that Nhs segmentation, as well as the shape-match score for this segmentation. In the first column, the ground-truth partitioning of the map, for which the shape-match score was calculated is shown. Ground-truth maps and predicted segmentations are shown at the intensity threshold used for the segmentation. For GroEL at 4Å and Rotavirus, top-views of the segmented map are shown in the fourth column. For Mm-cpn at 4.3Å, Ribosome at 6.8Å, and Epsilon-15 Phage at 7.3Å, the map is shown at a lower intensity threshold for clarity in the fourth column. Figures generated in Matlab and Chimera with TOM Toolbox (26).

Validation

Following the method described by Pintilie et al. (5), we synthesized ground truth maps for each cryo-EM map using atomistic coordinates contained in the corresponding PDB file, and used these maps to evaluate our segmentations. That is, this validation protocol requires a cryo-EM density map whose subunit arrangement is known and whose subunit structures have been solved atomistically. Each cryo-EM density map voxel within 2Å of an atom in the corresponding PDB structure was assigned to that atom, in keeping with the practice that molecular surfaces extend approximately this distance from constituent atoms. Note that a ground-truth map so constructed is only an approximation. For example, a voxel’s intensity can be impacted by peripheral atoms with masses greater than that of the closest atom, causing misclassified intensity. According to protein and subunit assignments for individual atoms found in the literature (12,14–18), each voxel assigned to a particular atom was labeled as belonging to the region that the atom belonged to, to form a ground truth partitioned map.

Determining the ground-truth partitioning

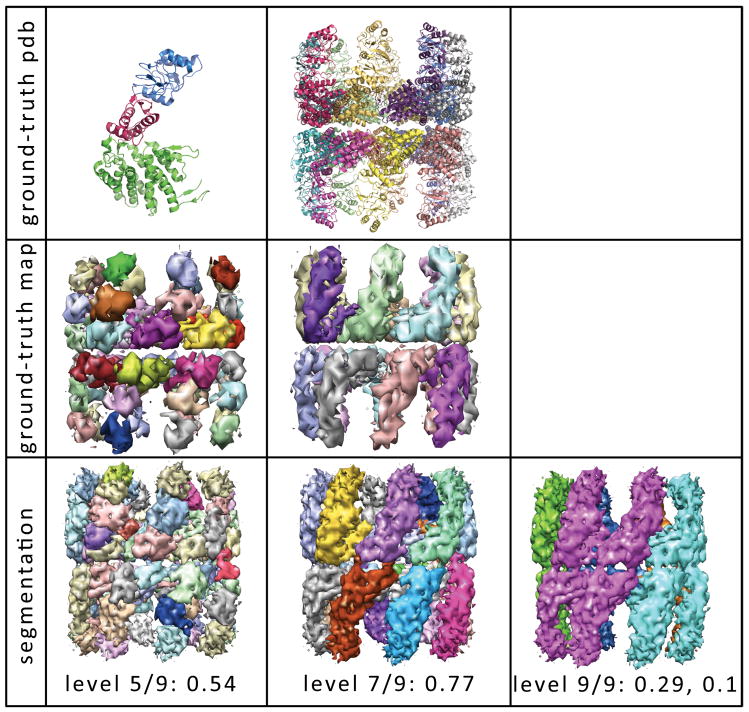
As a macromolecular structure can be partitioned in multiple ways (by sub-units, monomers, domains), there is no unique and objective ground truth segmentation for each map. For example, Figure 4 shows two informative partitionings of the 8Å Mm-cpn map. In the first column, each monomer is segmented into its apical, intermediate, and equatorial domains yielding 48 segments (12,24). The ground-truth map for this partitioning is shown in the second row, and the hierarchy level with segmentation closest to this domain-based partitioning is shown in the third row. In the second column, the 8Å Mm-cpn map has been partitioned into individual monomers, and the hierarchy level with the closest segmentation to the monomer-based partitioning is shown in the bottom row. As the hierarchy progresses, the individual monomers are grouped together lengthwise (third column). This lengthwise grouping might reflect inter-ring communication between aligned sub-units. The adaptive nature inherent to Nhs’ hierarchical protocol is thus highly valuable for maps with structural and functional features at various scales.

Figure 4. Segmentation of the 8Å Mm-cpn map at three hierarchy levels.

The ground-truth partitioning of Mm-cpn can be defined structurally at two levels. The first row shows the atomistic partitioning in the PDB structure (3IYF) at the domain level (column one) and the monomer level (column two). In the upper-left hand corner, the apical domain is shown in blue, the intermediate domain in pink, and the equatorial domain in green (12). The second row shows the ground truth map derived from the above atomistic partitioning. In the third row, segmentation of the Mm-cpn map is shown at three hierarchy levels, along with the shape-match score. The first column shows the segmentation at hierarchy level 5 out of 9, which scored highest with respect to the above domain-based ground truth partitioning. The second column show the segmentation at hierarchy level 7, which scored highest with respect to the monomer-based ground truth partitioning. The third column show the segmentation at hierarchy level 9 out of 9, and its scores with respect the domain-based and monomer-based partitionings, respectively.

Scoring

The shape-match score for each sub-unit i of the ground-truth map is computed according to the equation ${\partial }_i=\frac{\mathit{vol}(G_i\mid P_i)}{\mathit{vol}(G_i\cup P_i)}$, where G_i corresponds to the i^th known sub-unit in the ground-truth segmentation, and P_i corresponds to the most similar segment in the predicted segmentation to known sub-unit i (13,5). The overall shape-match score for a map is given as $s=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\partial }_i$, where n is the number of known sub-units.

In Figure 2, we present a segmentation by Nhs on a simulated 8Å cryo-EM map based on 3IYF.pdb (12, 29,30). In the bottom left panel, the shape match score for each of the 16 monomers is shown (highest possible score is 1.0). We see that Nhs performs well on this synthetic map. Encouraged by results on simulated maps, such as the one shown here, we tested our method on the Challenge maps.

Segmentation of Challenge Maps

In Figure 3, segmentation results are shown for eleven of the thirteen cryo-EM maps from the 2010 Challenge: GroEL at 4 Å (14), GroEL+GroES at 7.7 Å (15), GroEL+GroES at 23Å (16), Mm-cpn at 4Å (12), Mm-cpn at 8Å (12), ribosome complex at 6.4 Å (17), ribosome complex at 8.9Å (18), ribosome complex at 7.4 Å (19), VP6 from rotavirus at 3.8 Å (20), Aquaporin at 3.0 Å (21), and Epsilon-15 phage capsid at 7.3 Å (22). Corresponding PDB files were used to create ground-truth partitionings for each map.

For the GroEL and GroEL+GroES maps, Nhs identifies the individual domains of the monomers (Fig. 3) (25). In the GroEL map at 4Å resolution, Nhs receives the highest shape-match score for its segmentation of each monomer into apical, intermediate, and equatorial domains. Because of the high resolution of this map, it has many disconnected high intensity regions at the intensity threshold used (see Methods). These small isolated regions were each assigned to their own cluster, lowering the shape-match score. However, as can be seen from the top view, the overall segmentation into seven monomers in each ring is clear. The GroEL+GroES 7.7 Å map was segmented into 9 levels (see also Fig. 1). The highest scoring non-trivial segmentation level was Level 5, whose shape-match score with respect to the domain-based ground truth partitioning received a low segmentation score due to moderate over-segmentation. The next (coarser) hierarchy level (Level 6) captures the equatorial and apical domains of each monomer, but does not assign most intermediate domains to unique clusters. We suspect that the intermediate domains were not captured as independent segments because of the low electron density in these regions resulting from the flexibility of this domain. For the GroEL+GroES 23.5Å map, the shape-match score again reflects the lack of recognition of intermediate domains due to low intensity in these regions.

The segmentations of the Mm-cpn maps by Nhc received relatively high shape-match scores (Fig. 2,3). Due to the low intensity threshold at which segmentation was performed, the lid regions of the 4.3Å Mm-cpn map were separated from their monomers, and thus were assigned to a different region, reducing the shape-match score for this map. For the 8 Å Mm-cpn map, the only misclassification was in the interior regions of the equatorial domains, which have a high degree of connectivity between monomers and thus are difficult to distinguish by a network-based model.

The hierarchical network model was able to resolve the small and large ribosomal subunits for each ribosome complex map (Fig. 3). For the 6.4Å map, PDB structures 3FIN and 3FIC were available to use as ground-truth models for each subunit, resulting in a high segmentation score. Small segments are visible between the two sub-units, possibly representing densities from the elongation factor complex trapped in the ribosome complex. The 8.9Å ribosome segmentation that has the highest shape-match score to the ground truth map derived from 2P8W has several components, possibly representing proteins contained in this complex. By visual inspection, the 7.4 Å ribosome was correctly segmented, however the PDB file for the signal recognition particle receptor was not conducive to scoring because the protein captured by the PDB was mainly outside of the high density ribosome region, and these voxels were thresholded out due to low intensity.

The segmentation of the rotavirus captured the three interconnecting regions (Fig. 3). Since a PDB map was only available for a single VP6 monomer, the shape-match score was not applicable here (23). Similarly, in Aquaporin and Epsilon-15 phage, PDB files corresponding to the entire cryo-EM map were not available at the time of this submission, so a ground-truth map was not generated for these maps. In the case of Aquaporin, Nhs found individual sub-units of the map. For Epsilon-15, Nhs was able to find domains approximately representative of the icosahedral symmetry, without any user input outside of the map.

Discussion

Symmetry

In Step 3 of the Nhs Algorithm, a set of representative nodes is chosen to be carried on to the next hierarchy level (see Material and Methods). These nodes are chosen based on the stationary distribution of the Markov chain on the network at that hierarchy level, which relates to the degree of connectivity of each node. As such, the representative nodes are currently not chosen in a way that directly reflects the natural symmetry of the cryo-EM map (e.g. 7-fold symmetry in GroEL, 8-fold symmetry in Mm-cpn). That is, nodes are chosen based on local environment, without using global information such as symmetry. Thus, the resulting segmentations have no guarantee of symmetry. This can be seen in Figure 1, by comparing the segmentations between each of the GroEL monomers, as well as by comparing the shape-match scores between the Mm-cpn monomers in Fig. 2. Enforcing symmetry should improve the accuracy of the segmentations, as the average connectivity of each voxel over each of the symmetric monomers would be used to select representative nodes, resulting in a stronger signal of the underlying structure. Because an asset of Nhs is its ability to reasonably segment maps without any user input or prior knowledge of structure, we have chosen not to incorporate user provided symmetry information at this stage. Future work will involve implementing an unsupervised symmetry detection step, to ensure that representative nodes are chosen symmetrically in each hierarchy level.

Comparison to other segmentation tools

By visual inspection, segmentations by Nhs capture multi-scale structural organization of macromolecules. However, the shape-match scores of our segmentations seem low when compared to segmentation scores received by semi-supervised methods (4–8). It is important to note that many previously reported segmentation scores were for simulated cryo-EM maps, as well as experimental maps. Nhs segmentation scores fall in a similar range as other methods on experimental cryo-EM maps (for example, Fig. 2). Lower scores for experimental maps versus simulated maps could reflect difficulties in accurately scoring cryo-EM maps using PDB structures. Noise in experimental maps that is not present in simulated maps also contributes to the discrepancy in scores between the two map types.

Cryo-EM map resolution

Nhs performed similarly on an array of map resolutions for the same macromolecule (Fig. 3). For GroEL and GroEL+GroES at 4, 7.7, and 23.5Å resolutions, Nhs detected individual domains of the Hsp60 monomers. For ribosomes of varying resolution, Nhs identified the small and large sub-units, as well as complexed proteins. Since Nhs finds segments using connectivity within the map, and not the actual map shape or intensities, resolution does not affect its ability to detect underlying structures.

Future Work

As the sub-regions found in each level of the hierarchy highlight the core structural regions of the protein, they can also be used as anchor points for fitting high-resolution structures into cryo-EM maps. Other future work involves inference of secondary structure from characteristic patterns in affinity maps. We also seek to improve the segmentation by identifying symmetry in the cryo-EM maps and using the symmetry to guide kernel selection. Incorporation of symmetry information has proven beneficial in past implementations of hierarchical network segmentation for atomistic structures (32).

Conclusion

Nhs provides reliable segmentations of cryo-EM maps without requiring user knowledge of the underlying map structure. Several segmentation methods are available which provide useful segmentations, given some user input. The advantage of our method is that it provides a hierarchy of reasonable segmentations of the map with no input from the user except the map. The output from this method can, for instance, provide user knowledge which can then guide more accurate segmentation methods requiring more input. Future improvements to this method will detect map symmetry and choose nodes in each level based on symmetric regions, with the goal of producing high accuracy, unsupervised segmentations of cryo-EM maps.

Material and Methods

We use a hierarchical method based on a Markov diffusion process to find a representative set of nodes with which the density map can be represented as a graph (9–11). We approach segmentation as a graph clustering problem where each density map voxel is associated with a graph vertex (node), and edges are defined by the standard 26-neighborhood of each voxel. Edge weights (affinities) between neighboring vertices are a function of intensity difference. From the computed edge weights, we construct a Markov transition matrix, which gives the probability of signal-travel between any two voxels (nodes). Using this transition matrix, we build a hierarchical network model, in which subsequent hierarchy levels contain increasingly coarser sets of nodes, giving a multi-resolution network model of the density map. Nodes within the same cluster are connected by strong edges over many paths, while nodes between clusters are connected by only few paths along weak edges.

Preprocessing

Input: cryo-EM map

We begin by thresholding small voxels in the density maps to reduce the total number of voxels, thereby decreasing computation time and memory expense. Thresholds are chosen by default as a function of the maximum map value (see below). All remaining non-zero voxels are considered nodes in a graph, and we construct an edge between each voxel and its 26 neighbors in 3D-space. The edge weights are defined by: $(a_{ij})=e^{\frac{-{(v_i-v_j)}^2}{{\sigma }_i{\sigma }_j}}$, where v_i gives each voxel intensity and σ_i = 1.5 × median (|v_i − v_j|), ∀j neighbors of i, describes the local environment around each voxel. A high edge weight means that a voxel pair has a low Euclidean distance and similar intensities, thus indicating the likelihood that the voxel pair belongs to the same structural subunit. The affinities together define a (n_voxel × n_voxel) non-negative affinity matrix A = (aij), where n_voxel is the number of non-zero voxels. The affinity matrix is extremely sparse in that it only contains distances between adjacent voxels; each row i has at most 26 non-zero entries.

We next determine each connected component of the network. Connected components are sets of nodes in which each node can be reached by every other node along a connected path. If two nodes are in unique connected components, then there is no path between them, and they will not be assigned to the same cluster. Typically, our small-value threshold is low enough that the entire map remains one connected component. However, since matrix operations become more expensive as matrix size increases, we can greatly increase computational efficiency by segmenting disconnected sections of the network separately.

Network-based hierarchical segmentation

For each dominant connected component, we perform hierarchical diffusion to iteratively reduce the network into increasingly coarser sets of representative nodes. Consider each voxel from this connected component as a node. Let n₀ be the number of nodes in the connected component. Take the rows and columns from A corresponding to the nodes in this connected component to build an affinity matrix A₀ of size (n₀ × n₀).

Algorithm: Nhs

Input: A₀, n₀.

Initiation: Compute the initial degree matrix $D_0(i,j)=\{\begin{array}{cc}{\displaystyle \sum _{j=1}^{n_0}}{A}_0(i,j)& :i=j\\ 0& :i\ne j\end{array}$ and the stationary distribution ${\overrightarrow{\pi }}_o(i)=\frac{D_0(i,i)}{{\displaystyle \sum _j}{D}_0(j,j)}$ of the Markov chain. The degree matrix reflects the connectivity of the graph in that its diagonal contains the total weight of connections with each node. Nodes with high degree can be seen as hubs, and nodes with very low degree can be seen as isolates. The stationary distribution, which is the normalized degree vector, gives the probability of a Markov Chain residing in a particular node after infinite random walk steps.

For example, in Figure 1, the hierarchical segmentation of the GroEL+GroES 7.7Å map with Nhs is shown. The far left figure shows the density map after thresholding intensities less than the computed threshold, 0.75. The initial affinity matrix A₀ is shown beneath the map. For this map, there were n₀ = 254724 voxels in the single dominant connected component. At this zoon, the matrix appears diagonal because each voxel only has edges to its 26 neighboring voxels.

Iteration:

For t = 1 until done:

1. Compute the diagonal degree matrix D_t−1, with entries

   $$D_{t-1}(i,j)=\{\begin{array}{cc}\sum _{j=1}^{n_{t-1}}{A}_{t-1}(i,j)& :i=j\\ 0& :i\ne j\end{array}$$

   and the Markov transition matrix $M_{t-1}=A_{t-1}{D}_{t-1}^{-1}$.

2. Diffuse the Markov transition matrix by repeated multiplication M_t−1 = M_t−1 × M_t−1. Diffusion reveals distant connectivity and promotes cluster behavior by homogenizing probabilities within natural clusters.

3. Prepare a kernel matrix K_t to carry network information from level (t −1) of the hierarchy to level (t). First, select nodes a set of nodes corresponding to local peaks of the stationary distribution such that no selected node has probability greater than p_t of being reached from any other selected nodes according to M_t−1. Then, use the columns (kernels) of the diffused Markov transition matrix (M_t−1) corresponding to these selected nodes to form the (n_t−1 × n_t) kernel matrix K_t, where n_t is the number of kernels found with n_t ≪ n_t−1. The probability bound p_t is determined in each iteration based on the degree of similarity of nodes between the previous two hierarchy levels. It is adjusted to encourage a high degree of network coarsening between iterations.

4. Solve τ⃗_t−1 = K_t τ⃗_t for τ⃗_t with an expectation-maximization algorithm to find a low-dimensional representation τ⃗_t of the stationary distribution τ⃗_t−1 [10].

5. Compute new affinity and Markov matrices A_t and M_t, each of size (n_t × n_t)using τ⃗_t [10]: $M_t=\text{diag}({\overrightarrow{\pi }}_t)K_t^T\text{diag}{(K_t{\overrightarrow{\pi }}_t)}^{-1}{K}_t$ and $A_t=\text{diag}({\overrightarrow{\pi }}_{\text{t}}){\text{K}}_{\text{t}}^{\text{T}}\text{diag}{({\text{K}}_{\text{t}}{\overrightarrow{\pi }}_{\text{t}})}^{-1}{\text{K}}_{\text{t}}\text{diag}({\overrightarrow{\pi }}_{\text{t}})$, where $K_t^T$ is the transpose of K_t and diag(τ⃗_t) indicates a diagonal matrix formed from the vector τ⃗_t.

6. t → t + 1.

Termination: End if n_t ≤ 5. Let T = t. At this point, the component has been divided into less than six segments.

At each hierarchy level, the model gives a probability distribution for the likelihood that a voxel belongs to any distinct sub-region of the structure and thus provides a soft partitioning of the density map. This soft partitioning is elicited by iterating backwards along the hierarchy in order to compute an n_t−1 × n_t ownership matrix W_t for each hierarchy level t, in which W_t (i,j) gives the probability that node i in the connected component belongs to segment j at level t of the hierarchy, t = 1,…,T: $W_t(i,j)=\frac{K_t(i,j){\pi }_t(j)}{{\displaystyle \sum _{k=1}^{n_t}}{K}_t(i,k){\pi }_t(k)}$, where ${\displaystyle \sum _{j=1}^{n_t}}{W}_t(i,j)=1$. To project the ownership map onto the original set of nodes, compute W₀ = W₁ × W₂ × … × W_T, where W₀ is a (n₀ × n_T)matrix.

For segmentation visualization, assign each voxel to the segment for which it has maximal ownership probability to determine a hard partitioning. For the segmentation results shown in Figures 1–5, the hard partitioning is used.

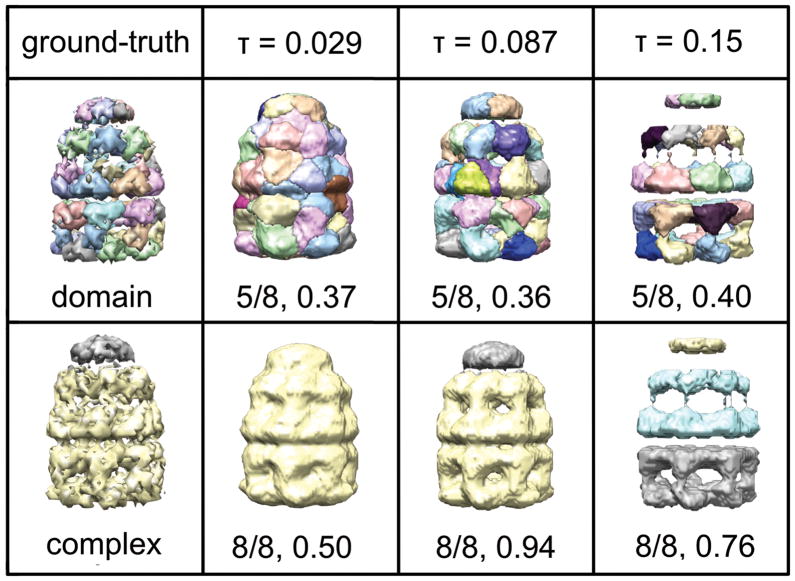
Figure 5. Segmentation of GroEL+GroES at 23.5 Å at three intensity thresholds, τ.

The threshold τ = 0.087 is our computed default threshold for this map. The threshold τ = 0.029 is the contour level recommended for visualization in the EMBD (1046). The first rows shows the resulting segmentation at the hierarchy level scoring highest for the domain-based ground truth partitioning of GroEL+GroES, and the second row shows the resulting segmentation at the hierarchy level scoring highest for the component-based ground truth partitioning of GroEL+GroES. For each segmentation, the hierarchy level out of the total number of levels is given.

Output: Hierarchy of affinity matrices and ownership matrices, A₀, …, A_T and W₀, …,W_T.

Intensity threshold

Before creating the affinity matrix, all small values are removed from the map. Since many voxels in the areas of the map containing no actual molecular density (e.g. the region of the map surrounding the molecule) are non-zero due to noise, small-value thresholding significantly reduces the number of non-zero voxels in the map, which in turn reduces the size of the initial affinity matrix (n_voxels × n_voxels). The intensity threshold τ for small values is a tunable parameter. In this paper, we used the default threshold determined for each map as .315 × em_max, where em_max is the maximum intensity found in the em map. An alternative intensity threshold is the recommended viewing contour level from the EMBD. Our default threshold was determined heuristically, and typically captures approximately the same set of voxels as the recommended contour level (Table 1).

Table 1. Intensity thresholds for pre-processing Challenge cryo-EM density maps.

For each cryo-EM map, the suggested contour level for visualization is given (column 2), as well as our computed threshold for small voxels (column 4). The percent of voxels larger than each threshold is provided (column 3: suggested contour level, column 5: computed threshold), as well as the absolute difference between these two thresholds (column 6). The percent of voxels larger than the threshold is equivalent to the percent of voxels from the cryo-EM map that are used in constructing the affinity matrix, A.

map	EMDB contour	% voxels > τ	computed τ	% voxels > τ	difference in %
AQPO	NA	NA	2.49	5	NA
Epsilon-15 7.3 Å	1.6	6	1.32	9	3
GroEL 4 Å	0.60	11	0.77	7	4
GroEL+GroES 7.7Å	0.61	37	0.75	27	9
GroEL+GroES 23.5Å	.029	5	.087	3	2
Mm-cpn 4.3 Å	0.38	2	0.45	1	1
Mm-cpn 8.0 Å	0.78	7	0.95	11	4
Ribosome 6.4 Å	3.5	2	5.5	1	1
Ribosome 7.4 Å	0.17	13	0.49	5	8
Ribosome 8.9 Å	70.4	5	88.5	4	1
Rotavirus 3.8 Å	1.04	4	0.98	5	1

Choosing a high intensity threshold for segmentation allows the algorithm to run faster and require less memory, as the affinity matrix is (n_voxels × n_voxels). However, the threshold should be low enough that significant details in the map are still present. In Figure 5, we show the segmentation of GroEL+GroES at 23.5Å using three different intensity thresholds τ. Highest scoring intensity maps are shown for two ground-truth partitionings of the GroEL+GroES maps. By visual inspection, the accuracy of the segmentation with respect to domains increases slightly with increasing τ (see row one), however as the threshold increases, the amount of intensity left in the region corresponding to the intermediate domains decreases. Thus, τ should not be chosen so high that significant densities voxels disappear. Overall, the change in shape-match score with respect to intensity threshold is small, indicating that the accuracy of the resulting segmentation is not very sensitive to intensity threshold. The major improvement by choosing a higher intensity threshold is in speed, not accuracy.

Choosing a hierarchy level

Determining which hierarchy level (or levels) to use for further analysis is left to the user. Metrics are available for determining the best level of clustering based on number of graph edges between clusters versus number of graph edges within clusters, e.g. normalized cut (9). As discussed above, different levels of the hierarchy can give different insight into structural and functional organization of the macromolecule.

Ground truth maps

The ground truth maps were determined using the PDB IDs indicated by the Challenge. For GroEL and GroEL+GroES, residues 6–133 and 409–523 were assigned to the equatorial domain, residues 134–190 and 377–408 were assigned to the intermediate domain, and residues 191–576 were assigned to the apical domain (27,14–16). For the 4Å closed Mm–cpn structure, residues 1–141 and 400–523 were assigned to the equatorial domain, 142–210 and 362–399 to the intermediate domain, and 211–361 to the apical domain (12,24,28). For the 8Å open Mm-cpn structure, residues 1–141 and 378–521 were assigned to the equatorial domain, 142–210 and 340–377 to the intermediate domain, and 211–339 to the apical domain (12,24,28). For the 6.4Å and 8.9Å ribosome maps, each PDB chain was considered a domain (17,18). For the remaining maps, no PDB structure was found that covered the majority of the map, hindering scoring with our method.

Implementation

A Matlab implementation of Nhs with a worked example is available by emailing the authors. Required input is the cryo-EM map. Optional input is the intensity threshold, τ, for small values. The algorithm outputs a hierarchy of increasingly coarser map segmentations, with soft and hard cluster assignments at each hierarchy level, as well as MRC files for visualization of each hierarchy level. TOM Toolbox (26) is required for reading and writing MRC file. Depending on cryo-EM map size and sparseness, segmentation takes between 30 minutes and 12 hours on an eight-core, 2.7GHz, 2Gig RAM linux-based desktop workstation.