Abstract
The open state of voltage-gated potassium (Kv) channels is associated with an increased stability relative to the pre-open closed states and is reflected by a slowing of OFF gating currents after channel opening. The basis for this stabilization is usually assigned to intrinsic structural features of the open pore. We have studied the gating currents of Kv1.2 channels and found that the stabilization of the open state is instead conferred largely by the presence of cations occupying the inner cavity of the channel. Large impermeant intracellular cations such as N-methyl-d-glucamine (NMG+) and tetraethylammonium cause severe slowing of channel closure and gating currents, whereas the smaller cation, Cs+, displays a more moderate effect on voltage sensor return. A nonconducting mutant also displays significant open state stabilization in the presence of intracellular K+, suggesting that K+ ions in the intracellular cavity also slow pore closure. A mutation in the S6 segment used previously to enlarge the inner cavity (Kv1.2-I402C) relieves the slowing of OFF gating currents in the presence of the large NMG+ ion, suggesting that the interaction site for stabilizing ions resides within the inner cavity and creates an energetic barrier to pore closure. The physiological significance of ionic occupation of the inner cavity is underscored by the threefold slowing of ionic current deactivation in the wild-type channel compared with Kv1.2-I402C. The data suggest that internal ions, including physiological concentrations of K+, allosterically regulate the deactivation kinetics of the Kv1.2 channel by impairing pore closure and limiting the return of voltage sensors. This may represent a primary mechanism by which Kv channel deactivation kinetics is linked to ion permeation and reveals a novel role for channel inner cavity residues to indirectly regulate voltage sensor dynamics.
INTRODUCTION
Voltage-gated potassium (Kv) channels are responsible for repolarizing the membrane and regulating firing rates in electrically excitable cells (Hille, 2001). Activation of Kv channels relies on the coupling of a voltage-sensing domain (VSD; transmembrane segments S1–S4) to a highly selective potassium (K+)-conducting pore domain (S5–S6; Long et al., 2005b). The pore creates an energetically permissible route for charged K+ ions across the hydrophobic membrane bilayer. Selectivity filter binding sites stabilize dehydrated K+ ions to confer K+ selectivity, and an aqueous inner cavity funnels hydrated K+ ions to the selectivity filter (Y. Zhou et al., 2001; Long et al., 2005b). The conduction pathway becomes accessible to intracellular ions from the cytosol only when the intracellular gate opens and allows the passage of ions into the cavity (Liu et al., 1997).
Voltage-dependent activity is generated through VSD movements that couple to the pore and displace charge before the channel opens. These movements comprise several kinetically distinct and nonconductive closed states that are occupied before the channel pore opens at the intracellular gate (Zagotta et al., 1994b; Schoppa and Sigworth, 1998; Ledwell and Aldrich, 1999; del Camino et al., 2005). The coupling of the VSD to the pore gate is mediated largely by a strong interaction between the S4–S5 linker and the cytosolic end of S6, where the activation gate resides (Lu et al., 2002; Long et al., 2005a,b). Gating charge, which reflects the movements of the VSD, has been shown to be slower to return from voltages at which the channel pore opens than from potentials where the open state has not been populated (Perozo et al., 1993; Zagotta et al., 1994b; Chen et al., 1997; Olcese et al., 1997; Batulan et al., 2010; Lacroix et al., 2011). It appears that the channel pore must close before any of the gating charges can return, as the open pore prevents the return of the tightly coupled voltage sensor to its resting conformation, a process referred to as voltage sensor immobilization (Armstrong, 1971; Bezanilla et al., 1991). The kinetics of the return of the gating charge are therefore controlled by two factors: the force exerted by negative voltage, pulling the positively charged residues in the voltage sensor down, and the opposing force conferred by the stability of the open channel pore, which has to close before the voltage sensor can return.
The factors that affect the stability of the open pore fall broadly into two categories: extrinsic (or allosteric), in which elements disparate from the pore impact pore stability, and intrinsic, in which the stability is determined by the local peptide conformation. Extrinsic mechanisms include the inhibition of activation gate closure by the N-terminal peptide in wild-type (WT) Shaker channels, which immobilizes gating charge while it prevents pore closure (Bezanilla et al., 1991). Intracellular applied quaternary ammonium ions greatly slow the recovery of ionic and gating currents and stabilize the open pore in a similar way (Armstrong, 1971; Choi et al., 1993; Melishchuk and Armstrong, 2001), and both of these examples highlight the rate-limiting nature of the first transition away from the open state. Alternatively, if an open state has an intrinsic conformation that is more stable than the closed state, the rate of leaving that state will be slowed. Processes such as slow inactivation have been linked to the slow return of gating charge, suggesting that conformational rearrangements, associated with C-type inactivation processes, might physically stabilize the voltage sensor in the activated state (Bezanilla et al., 1982; Fedida et al., 1996; Olcese et al., 1997; Wang et al., 1999). More recently, stabilization of the VSD after depolarization has been observed in noninactivating HCN (hyperpolarization activated cyclic nucleotide gated) channels (Bruening-Wright and Larsson, 2007) and a Ciona intestinalis voltage-sensitive phosphatase, which lacks a pore (Villalba-Galea et al., 2009). These studies suggest that the voltage sensor might “relax” by itself and adopt an intrinsically distinct, stable conformational state (Villalba-Galea et al., 2008). Even in the absence of inactivation, or quaternary ammonium ions, or prolonged depolarizations that induce VSD relaxation, a slowing of the return of charge is still observed after depolarization. Gating currents recorded from nonconducting Shaker IR W434F channels in K+ internal solutions still display a slowing of IgOFF after brief depolarizations to potentials at which the channels open (Perozo et al., 1993), and varying the major monovalent cation in intracellular and extracellular solutions has been shown to influence the rate of return of gating charge (Chen et al., 1997; Wang et al., 1999; Melishchuk and Armstrong, 2001; Varga et al., 2002; Goodchild and Fedida, 2012). It is clear that both extrinsic and intrinsic factors can impact directly on the stability of the open state and the subsequent rate of channel deactivation, but their relative contributions, although currently unknown, are often dependent on specific conditions and the channel type.
In this study, we sought to understand the mechanism of open-state stabilization in Kv1.2 channels by varying the intracellular ionic composition and mutating pore residues. Although Kv1.2 gating currents have not previously been studied, we used Kv1.2 rather than Shaker channels for two reasons: (1) Kv1.2 is resistant to inactivation as a result of a valine residue at position V381 (T449 in Shaker), which allowed us to investigate gating independently from inactivation processes; and (2) the availability of a high resolution crystal structure of the open-state channel allowed us to interpret our results from a structural perspective. Our results show that the stabilization of voltage sensors associated with the open state is critically regulated by the occupancy of a specific site in the inner pore. This suggests that the open pore is not intrinsically more stable than the closed pore, but that it is controlled extrinsically by the occupancy of the inner pore by both permeant and nonpermeant ions, which create an energy barrier to pore closure.
MATERIALS AND METHODS
Cell culture and molecular biology
WT Kv1.2 channel cDNA were mutated within the mammalian expression vector pGW1. Point mutations were generated using the QuikChange II Site-Directed Mutagenesis kit (Agilent Technologies) and confirmed by sequencing. Channels were expressed in mammalian tsA201 cells grown and maintained in MEM (Invitrogen) at 37°C in an air/5% CO2 incubator. Media contained 10% bovine serum (Gibco) with 100 U/ml penicillin and 100 µg/ml streptomycin (Invitrogen). On the day before transfection, cells were washed with MEM, treated with trypsin/EGTA for 1 min, and plated on 25-mm2 glass coverslips. WT Kv1.2-pGW1 and green fluorescent protein–pcDNA3 cDNA were then transiently cotransfected using Lipofectamine 2000 transfection reagent according to the manufacturer’s instructions (Invitrogen). 24–48 h after transfection, coverslips with adherent cells plated on the surface were washed in external solution and then placed in a recording chamber containing the external bath solution. All recordings were performed at room temperature (∼20°C).
Patch-clamp electrophysiology
Whole-cell current recording and data acquisition were performed using an amplifier (Axopatch 200B) controlled with pClamp10 software (Molecular Devices). Patch electrodes were pulled from thin-walled borosilicate glass (World Precision Instruments) on a horizontal micropipette puller (Sutter Instrument) and fire polished before use. Electrodes had resistances of 1–2 MΩ when filled with internal solutions. Liquid junction potentials were calculated using the junction potential calculator function in pClamp10. Membrane potentials were corrected for junction potentials >3 mV that arose between the pipette and bath solution by applying the appropriate offset potential before recording, unless otherwise stated. Leak subtraction was routinely applied using a −P/8 or −P/6 protocol from the holding potential unless otherwise stated. Currents were filtered at 10 kHz and sampled at 100 kHz for gating currents and deactivation tail current recordings or filtered at 2–5 kHz and sampled at 25 kHz for other ionic current recordings. Only isolated, unconnected cells were used for recording, and ≥80% series resistance compensation was applied in all whole-cell recordings to minimize any error in membrane voltage and low-pass filtering effects resulting from series resistance and cell capacitance.
Solutions
Gating current recordings.
The extracellular bath solution contained the following (mM): 140 TEACl, 10 HEPES, and 1 CaCl2, pH adjusted to 7.4 with HCl. Intracellular pipette solution contained the following (mM): 140 NMG+, 10 HEPES, and 5 EGTA, pH adjusted to 7.2 with HCl. For TEA+-, Cs+-, and K+-based internal solutions, NMG+ was replaced with 140 mM TEACl, CsCl, or KCl. For K+ internal recordings, 2.8 mM K+ was added to the external TEA+ to set the K+ reversal potential at −100 mV to avoid potential contamination of OFF gating currents by any endogenous K+ currents.
Whole-cell ionic current recordings.
The extracellular solution contained the following (mM): 135 NaCl, 5 KCl, 1 MgCl2, 2.8 Na-acetate, 10 HEPES, and 1 CaCl2, pH adjusted to 7.4 with NaOH. Intracellular pipette solution contained the following (mM): 130 KCl, 5 EGTA, 1 MgCl2, 10 HEPES, 4 Na2-ATP, and 0.1 GTP, pH adjusted to 7.2 with KOH.
Data analysis
Charge-voltage (Q-V) measurements were obtained by integrating the ON gating (IgON) or OFF gating currents (IgOFF) over an 11-ms period, unless otherwise stated. Conductance-voltage (G-V) relationships were constructed from isochronal tail current measurements at −40 mV after families of 50-ms depolarizing prepulses were applied to activate the channels, from a holding potential of −100 mV. Q-V and G-V relationships were normalized to the maximum value and fit with a single Boltzmann function of the form A/Amax = (1 + exp(zF(V − V0.5)/RT))−1, where A/Amax is the normalized conductance (G/Gmax) or charge (Q/Qmax), z is the equivalent charge, V0.5 is the half-activation voltage, F is Faraday’s constant, R is the gas constant, and T is the temperature in kelvin. Fitting was performed on data from individual experiments using Microcal Origin software (version 8), and the fit parameters quoted in the text are the means ± SEM of the individual fits. In figures, curves are fit to mean data for display purposes. Statistical significance was assessed using unpaired Student’s t tests and considered significant for P < 0.05.
Kinetic modeling
Our experiments suggested that the kinetics of NMG+ dissociation (koff) was voltage dependent (see Fig. 3 C) and was therefore modeled using rate constants of the form
where kon(0 mV) and koff(0 mV) are the voltage-independent rate constants reflecting the intrinsic chemical binding energy of the interaction, [B+] is the concentration of NMG+i, z is the NMG+ charge, and δ is the fraction of the membrane field sensed by the ions. As the majority of charge is carried during transitions between closed states (Ledwell and Aldrich, 1999), occupancy of the O:B+ state will trap channels in the open state and voltage sensors in the activated state. The dissociation and association rate of NMG+ ions entering and leaving the cavity will then determine the rate-limiting step in voltage sensor return and thus be reflected in the kinetics of IgOFF.
Figure 3.
Voltage dependence of the rate of return of stabilized charge. (A) Representative current traces from a paired-pulse protocol with extending durations between test pulses reveals the slow recovery of IgON at −100 mV. A 12-ms depolarizing pulse to 30 mV was given to move all the charge and induce charge stabilization. This was followed by an extending recovery period, after which a test pulse to 30 mV was reapplied to assess the amount of charge that had returned. (B) The recovery of charge was plotted against the recovery pulse intervals at different holding potentials (HP) and fit with a single exponential. (C) The mean IgOFF rates were plotted against the recovery potential and fit with an exponential function of voltage (Eq. 1). The time constants of the fitted exponential functions were, at −100 mV, τ = 17.2 ± 1.7 ms (n = 5); at −90 mV, τ = 31 ± 0.6 ms (n = 3); and at −80 mV, τ = 62.4 ± 0.6 ms (n = 5). Error bars represent SEM.
We could not measure IgOFF at 0 mV, as voltage sensors are in the activated state at that voltage. Instead, we derived a rate constant for koff(0 mV) of 0.11 s−1 and voltage dependence zδ of 1.6 based on the voltage dependence of the IgOFF rate between −80 and −100 mV, where the channel pore is shut and the voltage sensors are in the deactivated state (see Fig. 3). The rate of relaxation to a new equilibrium between two states is defined by 1/(kon + koff) and at 0 mV, therefore, simplifies to 1/(kon(0 mV) × [NMG+] + koff(0 mV)). Substituting our estimate of the rate of onset of the development of slow charge return (1/τ) at 0 mV of 270.27 s−1 (see Fig. 2 C), an apparent kon(0 mV) of 1,929.71 M−1 s−1 for NMG+i association was calculated. This is likely to represent a lower limit, as the derivation of the rate of onset of the slow OFF gating would be dependent on channel opening and therefore be rate limited by the opening transition, which may be slower than NMG+i association. These experimentally predicted kon(0 mV) and koff(0 mV) values were then used in the model. The voltage dependence of the dissociation rate of NMG+ from the pore in the model was set at zδ = 1.6, thus assuming an equivalent voltage dependence of the association and dissociation rates.
Figure 2.
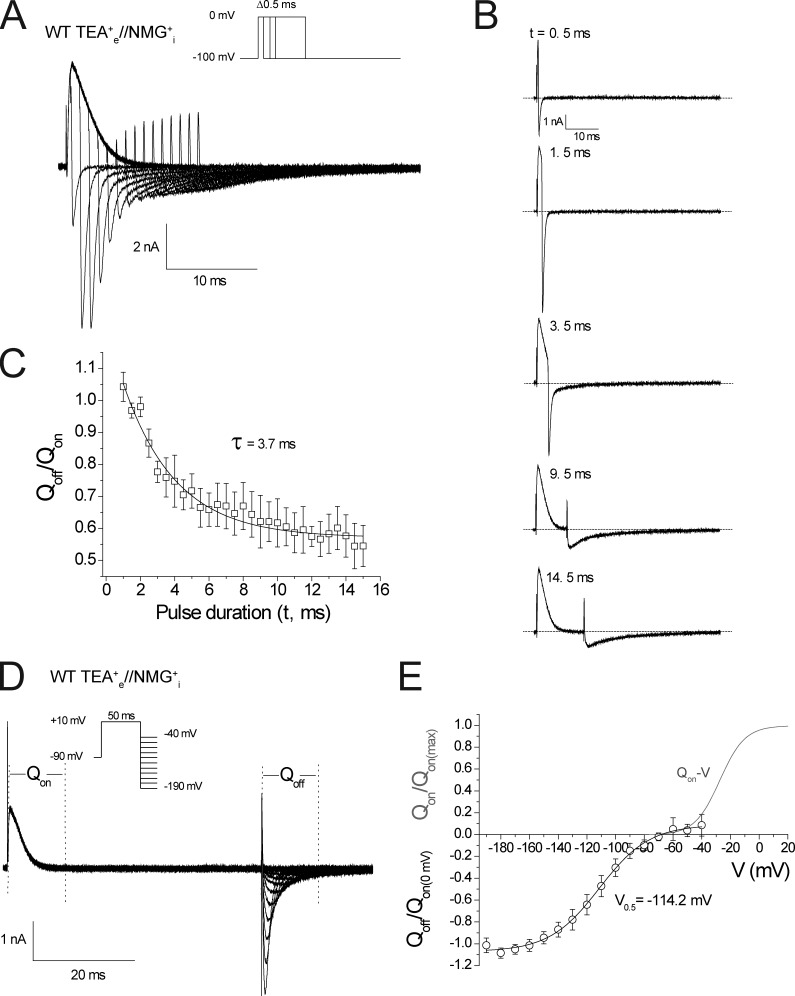
Rate of induction of the slowing of Kv1.2 charge return and the voltage dependence of return of stabilized voltage sensors. (A) Representative gating current demonstrating the slowing in the kinetics of IgOFF currents at a repolarizing voltage of −100 mV as the duration of depolarization to 0 mV was extended in 0.5-ms increments (n = 4). (B) Isolated traces from A after depolarization of 0.5, 1.5, 3.5, 9.5, and 14.5 ms. (C) Plot of the Qoff/Qon as a function of pulse duration. Qoff was calculated by integrating the first 11 ms of IgOFF. (D) Representative gating currents obtained using the two-pulse protocol shown. Return of charge was observed after a 50-ms depolarizing pulse to 10 mV by a series of hyperpolarizing pulses in 10-mV increments from −40 to −190 mV. Linear membrane leak was subtracted online using a −P/8 leak subtraction protocol from a subtraction holding potential of −140 mV (n = 6). (E) The first 11 ms of IgOFF were integrated, and the values were plotted against voltage and compared with the Qon-V relationship from Fig. 1 D. Error bars represent SEM.
Simulations were performed using the program IonChannelLab (De Santiago-Castillo et al., 2010) and Berkeley Madonna with the integration period set at 10 µs (100 kHz). Simulated gating currents were low-pass filtered at 10 kHz in Clampfit (Molecular Devices), and Q-V curves were generated using the same integration periods as that for experimental data (11 ms). The voltage-dependent rate constants α, β, γ, and δ governing the transitions between resting and activated voltage sensor states were based on a previously described Shaker IR gating model, ZHA (Zagotta Hoshi Aldrich; Zagotta et al., 1994a). The transitions between states were governed by rate constants exponentially dependent on membrane voltage of the form
where k is the rate constant, k(0 mV) is the 0-mV rate, z is the equivalent electronic charge in e0, V is the voltage, and F, R, and T have their normal thermodynamic meanings (stated in the previous section). The rate constants used in the model were based on the ZHA model as follows: (k (s−1), z (e0)), α: 1,120, 0.25; β: 370, −1.6; γ: 2,800, 0.32; δ: 21.2, −1.1; kon(0 mV): 1,929.71, 1.6; koff(0 mV): 0.11, −1.6.
Online supplemental material
Fig. S1 demonstrates the resistance of Kv1.2 to inactivation over the time course of the gating current experiments and the insensitivity of this inactivation to the presence of intracellular NMG+. Supplemental materials and methods for this experiment and the docking simulation are also available. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210823/DC1.
RESULTS
Striking slow OFF gating current of the Kv1.2 channel voltage sensor
As stated in the Introduction, it is the stability of channel open states relative to the closed states that determines the rate of return of gating charge when channels close (Armstrong, 1971; Bezanilla et al., 1991; Melishchuk and Armstrong, 2001). The first observation that was made from WT Kv1.2 channels was that the OFF gating currents at −100 mV displayed fast kinetics when returning from pulses up to −30 mV (Fig. 1, A and B). However, at more positive pulse potentials, a slow component in the IgOFF kinetics emerged along with a decrease in the peak amplitude, illustrated by individual traces in Fig. 1 B. These gating currents are measured with the permeant K+ and Na+ ions in standard physiological solutions replaced by NMG+ and TEA+. What is most obvious is the lack of symmetry between the ON gating currents that represent the movement of the charged voltage sensor from resting to activated and the OFF gating currents. The ON gating currents rise rapidly and show typical voltage-dependent kinetics as increasing depolarization increases the rate of charge movement, whereas the OFF gating currents become slowed and blunted after larger depolarizations. The Qoff-V relationship was normalized to the maximum Qon and illustrates that only around 70% of the Qon had recovered within 11 ms as a result of the slowing of IgOFF (Fig. 1 C). The normalized peak IgOFF was plotted against the pulse potential in Fig. 1 D and clearly illustrates that after depolarizations more positive than −30 mV, the fast IgOFF was replaced by a diminished and slowed IgOFF representing the return of stabilized voltage sensors. A simple comparison of the G-V with the Qoff-V and peak IgOFF plot illustrates that slowing of the OFF gating current correlates with potentials at which the open probability (Po) of the channels rapidly increases, thus linking the process of the slowing of charge return to the open pore.
Figure 1.
Kv1.2 gating currents display slow OFF gating currents after depolarization to potentials that populate the open state. (A) Representative gating currents recorded from tsA201 cells transfected with Kv1.2 using intracellular NMG+ and extracellular TEA+ solutions with the displayed voltage protocol. The leak currents were subtracted using a −P/8 leak subtraction protocol from a subtraction holding potential of −100 mV (n = 9). (B) Individual representative gating current traces isolated from the same recording to illustrate the onset of slowing of the IgOFF current recorded at −100 mV after depolarizing steps from −50 to 10 mV in 20-mV increments. (C) Q-V relationships obtained from integrating IgON (□, Qon-V) and IgOFF (○, Qoff-V) for 11 ms. The normalized Qon-V was fit with a Boltzmann equation that gave fitted values of V0.5 = −28.6 ± 1.3 mV and z = 3 ± 0.2 (n = 9) for the Qon-V. Also shown is the G-V relationship (Δ) constructed from isochronal tail current measurements at −40 mV for Kv1.2 currents recorded in standard ionic conditions, which gave fitted values of V0.5 = −4.4 ± 2.8 mV and z = 1.9 ± 0.1 (n = 4) with a representative family of current traces from the displayed protocol inset. (D) The peak IgOFF currents from each cell were normalized and plotted against the voltage of the preceding depolarizing pulse. Error bars represent SEM.
Entry of the voltage sensor into the stabilized state occurs over the time course of channel openings
In these first recordings of OFF gating currents from Kv1.2, not only is a slowing of charge return extensive, but the onset is extremely rapid, and the voltage dependence of charge return is displaced to very negative potentials. The time course of the onset of the slow OFF gating (Fig. 2 A) was comparable with that of channel opening rather than an inactivation process that is limited in scope and occurs over a much longer time scale in Kv1.2 (Fig. S1 A) and that is not perturbed by the presence of intracellular NMG+ ions replacing K+ (Fig. S1 B). The emergence of the slow IgOFF is clearly visible in the isolated traces shown in Fig. 2 B and represents a stabilization of the voltage sensor in the activated state. Fig. 2 C shows a plot of Qoff/Qon that was fit with a single exponential function, giving a time constant for the stabilization of the voltage sensor at 0 mV of 3.7 ± 1.1 ms (n = 4).
The rate of the return of stabilized charge displayed a marked hyperpolarizing shift in the voltage dependence of the charge return (V0.5 = −114.2 ± 4.5 mV, z = 1.8 ± 0.1; n = 6; Fig. 2 E) compared with the Qon-V (Fig. 1 C) and suggested that to return charge to the resting state from this state over a fixed period of time required significantly more energy than was required to move the charge into the activated state in the first place. To accurately resolve the kinetics of charge recovery, we used a double pulse recovery protocol as shown in Fig. 3 A. The plots of charge recovery over time were fit with a single exponential function at holding potentials between −80 and −100 mV, where the channels are fully closed (Fig. 3 B). Now,
| (1) |
where IgOFF(0 mV) represents the theoretical rate of gating charge return at 0 mV and zδ is the voltage dependence of the IgOFF rate, where z represents the electronic charges and δ is the fraction of the membrane field experienced by the charges. Fitting the mean data to Eq. 1 gave fitted value of koff(0 mV) = 0.11 s−1 and zδ = 1.6 (Fig. 3 C). The successful fitting with a single exponential term suggested that the rate-limiting step of charge return after channel opening was dominated by transitions from a single state.
Intracellular ions, including physiological concentrations of K+, alter voltage sensor dynamics
We next sought to investigate the basis for the stability of the open state in Kv1.2. Slow OFF gating in Shaker channels is caused by the N-terminal region of the channel entering the pore in the same way as intracellular TEA+, through blockade of pore closure (Bezanilla et al., 1991; Perozo et al., 1992). More recently, a slowing of OFF gating has been correlated with the ionic radii of group 1 cations used in the internal solution, with larger cations causing more severe slowing (Wang et al., 1999). Here, we have examined the effect of two cations with previously described disparate effects in Kv channels: a large blocking cation, TEA+, which causes severe slowing, and a small cation, Cs+, that previously caused an increase in the rate of charge return (Fig. 4).
Figure 4.
The effects of varying intracellular cations on rate of charge return. (A) Representative current traces recorded using an intracellular TEA+ solution were evoked by 12-ms depolarizing pulses applied in 10-mV increments from a holding potential of −100 mV. (B) Gating currents recorded with Cs+i. (C) Representative currents obtained by depolarizing the membrane to 0 mV for 50 ms before repolarization to a series of pulses from −40 to −190 mV with TEA+i. Linear membrane leak was subtracted online using a −P/8 leak subtraction protocol from a subtraction holding potential of −140 mV. (D) Return of charge in the presence of intracellular TEA+ and Cs+ was measured during an 11-ms charge integration period after the depolarizing pulse and plotted against voltage. The Qoff-V for Cs+I had V0.5 = −38 ± 1.8 mV, z = 2.8 ± 0.2 (n = 3). Using intracellular TEA+i did not significantly affect IgON (Qon-V: V0.5 = −30.3 ± 1.4 mV, z = 2.3 ± 0.3; n = 5). The Qoff-V for TEAi (Δ) gave fitted values of V0.5 = −125.9 ± 3.9 mV and z = 2 ± 0.2 (n = 3). Error bars represent SEM.
TEA+i (Fig. 4, A and C) caused a severe slowing of IgOFF at potentials that correlated with channel opening and a comparable Qoff shift to NMG+i (Figs. 1–3). Using Cs+i solution (Fig. 4 B), we observed a small outward ionic current, as a result of slight Cs+ permeability through Kv1.2 channels, that masked IgON. We were, however, able to resolve IgOFF at −100 mV in these cells by adding 3.1 mM Cs+ to the extracellular solution, setting the reversal potential for Cs+ to −100 mV to eliminate any contamination from ionic tail currents at that voltage (Chen et al., 1997). The Cs+i OFF gating currents were slowed after depolarizations more positive than −30 mV but recovered fully within the integration period (Fig. 4 B). In this situation, little shift of Qoff was seen with Cs+i (Fig. 4 D), suggesting that because TEA+i and NMG+i internal solutions required a greater energy to recover gating charge than Cs+i, the voltage sensor was stabilized in the activated state by the larger cations more effectively than by Cs+.
To answer the question of whether physiological concentrations of intracellular K+ ions could slow voltage sensor return in Kv1.2, we created a nonconducting mutant Kv1.2 W366F-V381T, analogous to the P-type inactivated Shaker W434F nonconducting channel. Fig. 5 A shows representative gating currents from this mutant recorded with K+i solution. The mutant channel displayed fast IgOFF kinetics after subopening threshold depolarization but became dominated by a slow component at voltages where the Kv1.2 channel pore opens (Fig. 5, A and B) and showed a Qoff-V typical of a dominant OFF charge slowing process where Qoff saturates before all the Qon gating charge is recovered because of the slowing of IgOFF. The transition from fast to slow IgOFF is clearly shown by the plot in Fig. 5 D, where the peak IgOFF currents are seen to decline rapidly at voltages greater than −40 mV, at which the slow component becomes dominant. These data suggest that physiological concentrations of internal K+ ions are able to interact with the open channel pore to cause a stabilization of the open state of the voltage sensor. We performed the same experiment using intracellular Cs+ ions to examine whether Cs+ would still have the effect of slowing OFF gating currents. Representative traces from an experiment using intracellular Cs+ is displayed in Fig. 5 (E and F) and shows clearly that Cs+ ions were also sufficient to slow charge return. The plot of peak IgOFF shows that the slowing occurs with Cs+i after depolarizations to potentials that would open the pore (n = 4; Fig. 5 G).
Figure 5.
The nonconducting mutant Kv1.2 W366F,V381T shows slow OFF gating currents with intracellular K+ and Cs+. (A) Representative current traces recorded using K+i solution were evoked by 12-ms depolarizing pulses applied in 10-mV increments from a holding potential of −100 mV. (B) Individual representative gating current traces isolated from the same recording to illustrate the onset of slowing of the IgOFF current recorded at −100 mV after depolarizing steps from −50 to 10 mV in 20-mV increments. (C) Q-V relationships obtained from integrating IgON (Qon-V: V0.5 = −39.4 ± 1.7 mV, z = 4.4 ± 1.3; n = 3) and IgOFF (Qoff-V) for 11 ms and fit with a Boltzmann function (n = 3). (D) Plot of the normalized peak IgOFF amplitude against voltage with a WT G-V curve in gray for comparison. (E) Representative current traces recorded using Cs+i solution. (F) Individual representative gating current traces isolated from the same recording from −50 and −10 mV. (G) Plot of the normalized peak IgOFF amplitude with internal Cs+ solution. Error bars represent SEM.
An inner cavity pore lining S6 residue I402 contributes to the interaction site for ionic stabilization of the voltage sensor
Based on the previous experiments, we considered the hypothesis that all intracellular ions that can occupy the Kv1.2 inner cavity will stabilize the open state of the channel and prevent voltage sensor return until they are expelled and, thus, that cations are a significant extrinsic regulator of open-state stability, channel pore closing, and charge return. In Shaker IR channels, a mutation of an inner pore cavity lining residue, I470, to the smaller C residue has previously been shown to allow TEA+ to reside in the closed inner cavity as a result of pore enlargement (Holmgren et al., 1997; Melishchuk and Armstrong, 2001).
In Kv1.2, a homologous mutation was made (Kv1.2-I402C). Gating currents recorded from Kv1.2-I402C with intracellular NMG+ no longer displayed slow OFF gating currents (Fig. 6 A). The OFF gating currents remained fast at all potentials, and the normalized Qoff-V showed saturating charge return. The Qon-V V0.5 was not significantly different from Kv1.2 WT channels (Fig. 6 B), and the Kv1.2 transmembrane currents, the G-V relation, and the G-V0.5 were not different from WT Kv1.2, suggesting that the activation and coupling of the voltage sensors to pore opening was unaltered by this mutation in S6. The absence of a discernable rising phase in IgOFF after pulses that would open the pore suggested that the first open to closed transition was much faster in this mutant than in WT Kv1.2.
Figure 6.
Mutation of an S6 residue to enlarge the cavity relieved slowing of charge return and increased the rate of ionic deactivation kinetics. (A) Representative gating currents recorded from Kv1.2-I402C in the same conditions as Kv1.2 WT (Fig. 1 A) with NMG+i. (B) Qon-V and Qoff-V relationships with values for the Qon-V of V0.5 = −24.4 ± 2.3 mV, z = 2.9 ± 0.8 (n = 7) and for the Qoff-V of V0.5 = −25.6 ± 2.3 mV, z = 1.7 ± 0.1 (n = 6). (C) Representative ionic currents recorded from Kv1.2-l402C. The G-V relationship for Kv1.2-I402C was plotted with the WT (gray dashes) for comparison. Kv1.2-I402C, V0.5 = −1.1 ± 2.2 mV, z = 2.4 ± 0.1 (n = 5); P > 0.05 compared with WT. (D) To quantify the IgOFF rate, channels were depolarized to 0 mV for 50 ms to open channels, and the decay of IgOFF upon repolarization was fit with single exponential functions at potentials between −100 and −80 mV. Off rates (1/τ) were as follows: −80 mV, 1/τ = 369.8 ± 35.7 s−1; −90 mV, 1/τ = 441 ± 25.7 s−1; and at −100 mV, 1/τ = 511.2 ± 62.2 s−1. The voltage dependence of the rate of charge was assessed by plotting the IgOFF rate against membrane voltage and fit with an exponential function of voltage (Eq. 1). (E) Representative normalized ionic tail currents recorded in 140 mM external K+ from Kv1.2 WT (black traces) and Kv1.2-I402C (gray traces) channels at −120 mV and −80 mV. Currents were recorded between −50 and −120 mV after a 50-ms pulse to 30 mV to open channels fully. The t0.5 decay was plotted against the voltage to quantify the increased rate of Kv1.2-I402C deactivation kinetics. Error bars represent SEM.
To compare Kv1.2-I402C IgOFF kinetics with the WT channel, IgOFF tracings at potentials between −80 and −100 mV were fit with a single exponential function to estimate the rate of charge return. Representative IgOFF currents at negative potentials after a 50-ms depolarizing step to 0 mV to open channels are shown in the inset to Fig. 6 D. The mean IgOFF rates were plotted against voltage and then fit with Eq. 1 to give the fitted values koff(0 mV) = 103.1 s−1 and zδ = 0.4. The reduced zδ of IgOFF rates observed in the I402C mutant result from the removal of a voltage-dependent rate-limiting transition, such as the exit of a charged intracellular ion. This observation is consistent with the mutant pore being able to close unimpeded around a blocking ion, or a significant reduction in the affinity of those ions for the mutant inner pore, increasing their dissociation rate such that they no longer limit the pore closing rate.
Ionic deactivation kinetics is rate limited by K+ ion occupancy of the inner pore
We have established that voltage sensor return is slowed in the presence of internal K+ ions (Fig. 5) and hypothesize that this is caused by the inability of the inner pore gate to shut when the cavity is occupied by an ion. To examine whether K+ ions in permeant ionic conditions could have a similar effect, we examined the deactivation kinetics of ionic currents in WT channels compared with Kv1.2-I402C channels. Deactivation tail currents recorded in 140 mM external K+ at −120 or −80 mV clearly show a faster rate of deactivation in Kv1.2-I402C (Fig. 6 E). The time for half the peak current to decay (t0.5 decay) demonstrated that deactivation kinetics are threefold more rapid in Kv1.2-I402C at all voltages tested (n = 7–10). These data confirm that there is a rate-limiting step in Kv1.2 channel deactivation that is reliant on a specific ionic coordination site within the inner cavity that must be vacated before the pore can shut.
Kinetic model of intracellular cation modulation of pore closure
To test the possibility that NMG+i acts as a limiting regulator of pore closure, we used a Markov state model to simulate IgOFF. The model was based on an established Shaker IR gating model in which the channel opens only once all four subunits have moved through two closed transitions into an active state (ZHA; Zagotta et al., 1994a). This model includes a modifying factor θ, which was set at 9.4, to slow the exit from the open state and reflect the cooperativity of the final concerted opening step and/or the combination of extrinsic and intrinsic open-state stability. The fast closed state present in the ZHA model to account for flickering single-channel openings was omitted in our model. The model, depicted in Fig. 7, was modified to incorporate an NMG+-bound open channel state, O:B+. In this scheme, if the rate of NMG+ unbinding is significantly slower than the first open to closed transition (4δ/θ), it will become the dominant rate-limiting transition for pore closure and the subsequent return of gating charge. This is similar to the “foot in the door” mechanism known to operate in Shaker K+ channels (Armstrong, 1971; Choi et al., 1993; Perozo et al., 1993).
Figure 7.
Kinetic modeling of intracellular NMG+ binding can account for the observed slowing of IgOFF kinetics. (A) Schematic of the Markov model used to simulate gating currents. (B, left) Simulated gating currents with the depicted voltage protocols and a slowing factor θ of 9.4 as in the original ZHA model. (right) Normalized Q-V relationships calculated by integrating gating current for 11 ms after the depolarizing pulse (Qon/Qon(max)), repolarization (Qoff/Qon(max)), or hyperpolarization after 50 ms at 0 mV (Qoff/Qon(0 mV)). (C) Repeat of simulations in B, but with the removal of the slowing factor (θ = 1). (D) Repeat of simulations in B, but with the addition of 140 mM NMG+i. Error bars represent SEM.
Simulated OFF gating currents evoked by sequential depolarizations increasing by 20 mV from a holding potential of −100 mV generated from the original ZHA model with θ = 9.4 are shown in Fig. 7 B. The Qon and Qoff-V relationships are symmetrical, with a V0.5 of −47 mV indicating that all charge that had moved during the activation of the voltage sensors was returned within the integration period. However, when the Qoff was measured after depolarization to 0 mV for 50 ms to open channels, the V0.5 was somewhat hyperpolarized to –60 mV. This left shift reflected the slowing of IgOFF as a result of stabilization of the voltage sensor in the activated state by the slowed transition away from the open state. When compared with our data displayed in Fig. 2 E, it is apparent that Kv1.2 gating currents recorded with NMG+i displayed a greater left shift in Qoff(0 mV)-V than the ZHA Shaker model. To simulate the gating currents in the absence of any intrinsic stabilization, the open-state stabilizing factor θ was set to 1 as shown in Fig. 7 C. In this case, the V0.5 for each Qoff-V curve was very similar to the Qon (−46 mV). This model recapitulated the data we gathered for the mutant channel Kv1.2-I402C, which showed a relief of open-state stabilization, suggesting that we might consider this channel’s kinetics consistent with an NMG+-independent gating scheme (Fig. 6).
To assess the effect of internal NMG+ ions binding to the open state on the Qoff -V curves, we simulated the addition of 140 mM NMG+i ions into the model depicted in Fig. 7 using θ = 1; that is, a channel that has no intrinsic open-state stabilization. Addition of internal NMG+ slowed IgOFF after depolarization to potentials at which the channel pore opens, recapitulating our observations for Kv1.2 gating currents (Fig. 1, A and B). The Qoff-V relationship shows that ∼60% of the Qon is returned (Fig. 7 D), similar to the ∼70% we observed in Kv1.2 gating current recordings (Fig. 1 C). In addition, the Qoff(0 mV)-V curve was left shifted to −101 mV as a result of the stabilization of the open state and consequent slowing of IgOFF, analogous to the Kv1.2 gating currents recorded in the presence of NMG+i (Fig. 2 E). This simulation demonstrates that the effect of an intracellular cation trapping channels in the open state and rate-limiting voltage sensor return can quantitatively account for the slow OFF gating and resultant left shift in Qoff-V that we have observed in Kv1.2 gating currents.
DISCUSSION
Deactivation kinetics of Kv channels are critically important in controlling membrane repolarization and influencing the frequency of action potential firing in excitable cells, yet the underlying mechanisms have remained unresolved. Here, we have demonstrated that the kinetics of deactivation and the associated voltage sensor return are controlled allosterically by ions occupying the inner cavity of open Kv1.2 channels, rather than by the intrinsic structural stability of the open pore domain alone.
Evidence for an occupancy theory of open pore stability
We found that intracellular ions affect IgOFF without substantially altering IgON, suggesting that an activated state of the voltage sensor was stabilized. Slowing of IgOFF correlated with depolarization to voltages at which the channel Po rapidly increases (greater than −30 mV; Fig. 1 C), strongly favoring the interpretation that slowing was mediated through the open pore. In addition, the time course of the onset of the slow OFF gating current was fast and approximated the time course of channel activation (Fig. 2 A), indicating that pore opening was the critical step, rather than inactivation, which was minimal and much slower in this channel (Fig. S1 A). We assessed the voltage dependence of charge return and found that the Qoff-V was markedly left shifted with respect to the Qon-V (Fig. 2). This left shift is the result of stabilization of the activated state of the voltage sensor, as more negative voltages are required to return the sensors from activated positions than was originally needed to move them into the activated states (Lacroix et al., 2011). These data support the conclusion that ions within the open pore stabilized the voltage sensor in the activated state. A clue to the underlying mechanism emerged upon observing that the species of intracellular cations could critically regulate the presence or absence of slow OFF gating current (Fig. 4).
The mechanism of open pore stabilization
The inner pore cavity of Kv channels contains a binding site for permeating ions located at approximately the same position as the quaternary ammonium binding site, just below the selectivity filter (Choi et al., 1993; M. Zhou et al., 2001; Y. Zhou et al., 2001; Lenaeus et al., 2005). Occupancy of this site by inactivation peptides or intracellular blockers causes slow return of gating charge (Bezanilla et al., 1991; Perozo et al., 1992; Melishchuk and Armstrong, 2001). In Kv channels, the pore of the channel must close before the voltage sensors can deactivate; thus, intracellular pore blockers have the effect of slowing the return of voltage sensors, which is supported by kinetic studies of Kv channels that place an open state accessed from the last closed state that imposes pore closure as a requirement before voltage sensors can transition back to resting states (Bezanilla et al., 1994; Zagotta et al., 1994a; Schoppa and Sigworth, 1998). For Kv1.2 specifically, voltage clamp fluorometry studies of gating support this model because return movement of S4 follows the kinetics of ionic current deactivation (Horne et al., 2010) and is slowed by the Kvβ1.2 subunit. which confers N-type inactivation (Peters et al., 2009).
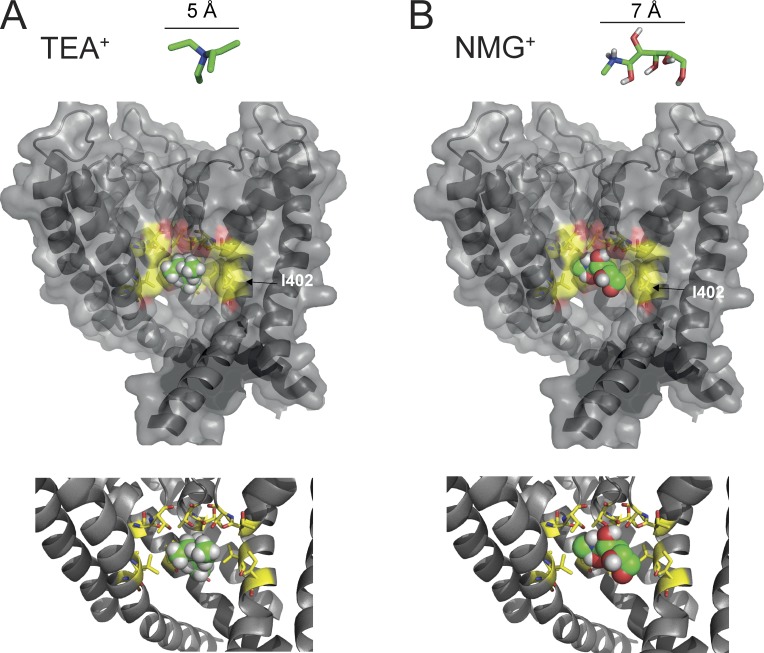
We used the Kv1.2 open-state crystal structure to investigate the possibility of TEA+ or NMG+ binding in the inner cavity through a docking simulation (Fig. 8, A and B). The docking demonstrated that both NMG+ and TEA+ can interact in a binding pocket within the inner cavity. To test this model, we mutated Kv1.2-I402 to cysteine. This mutation has previously been shown to enlarge the cavity, allowing TEA+ to be trapped in closed Shaker channels, as opposed to WT channels where the TEA+ molecule must dissociate before the pore can shut (Holmgren et al., 1997; Melishchuk and Armstrong, 2001). The Kv1.2-I402C mutation removed the slow OFF gating current with intracellular NMG+ and suggests that NMG+ was either no longer able to bind effectively with the Kv1.2-I402C channel or that the pore was able to close relatively unimpeded around the NMG+ ion occupying the inner cavity.
Figure 8.
Docking of large intracellular cations within the inner cavity of the crystal structure of the Kv1.2 open pore. (A and B) A cutaway view of the pore (S5–S6) of Kv1.2, with one subunit of the tetramer cut away for viewing with TEA+ (A) or NMG+ (B; carbon atoms are colored green) ions docked deep in the inner cavity of the channel. (bottom) Close up of binding pocket. Residues forming the binding pocket (defined as within 4 Å of the ligand) are displayed as sticks (carbon atoms are yellow). (Images were generated with PyMol.) Residues within a 4-Å radius were as follows: the intracellular cavity facing V399 and I402 in S6, and T373 and T374 at the intracellular entrance to the selectivity filter. I402 is labeled. The interaction of the ligands with both polar and aliphatic residues suggested a mixed contribution of hydrophobic and electrostatic contributions to the binding.
The scheme of this proposed mechanism in which a blocking ion enters the open pore and causes pore closure to be rate limited by the exit rate of the ion is depicted in Fig. 9. We tested this scheme with a kinetic model (Fig. 7) that recapitulated the emergence of a slow component in IgOFF that became dominant after greater depolarizations. This reflected the stabilization of the voltage sensor and also resulted in a left shift of the Qoff-V relation, confirming that the stabilization of the open channel pore by NMG+ or another intracellular ion could account for the slowing of IgOFF we observed.
Figure 9.
Schematic diagram illustrating the proposed mechanism of open pore stabilization. (A) Channels in the absence of permeant ions or nonconductive mutant Kv1.2 W366F,V381T have vacant or collapsed selectivity filters. Upon depolarization, the channel activation gate opens, and intracellular ions can enter the inner cavity. Upon hyperpolarization, the pore cannot shut until the inner cavity is vacated, which rate limits the voltage sensor return. (B) In the presence of permeant ions K+ or Cs+, the selectivity filter is occupied. As the channel pore opens, the hydrated ions can enter the inner cavity, but the binding site is less stable because of strong ion–ion repulsive forces from the other ions in the selectivity filter. Upon hyperpolarization, the exit rate of the hydrated ions is faster as a result of repulsive forces, and the pore can shut faster than in the absence of permeant ions in the conduction pathway. SF, selectivity filter.
The affinity of ions for the inner cavity binding site is the basis of open pore stabilization
We expected the affinity of NMG+ and TEA+ to be comparable because of the similar left shift in Qoff-V we observed (Qoff(0 mV)-V0.5 NMG+, −114.2 mV vs. TEA+, −126 mV; Figs. 2 E and 4 D). The Kd of NMG+ binding (koff(0 mV)/kon(0 mV)) derived from our kinetic model was 57 µM (Fig. 7), a higher affinity than the reported Kd for internal TEA+ in Shaker channels of 390 µM (Choi et al., 1993). The increased affinity of our interactions could be explained by the lack of any competing permeant ions in our experiments, which would lead to a unique high affinity binding environment at the inner cavity site (Fig. 9 B). It has already been demonstrated in Shaker that increasing external K+ or Rb+ concentrations effectively lowers the affinity of intracellular quaternary ammonium ions and NMG+ ions for the inner cavity binding site (Armstrong, 1971; Melishchuk and Armstrong, 2001). Repulsive electrostatic interactions between the positively charged ions within the conduction pathway critically regulate the affinity of individual binding sites to allow high flux rates in a conducting channel (Hille and Schwarz, 1978). Considering these repulsive forces, we predict that the removal of positively charged permeant ions stabilized the TEA+/NMG+ binding site in Kv1.2 and enabled a higher affinity interaction than would normally be present with permeant ions in the pore.
This mechanism could explain the apparent paradox that the nonconducting P-type inactivated mutant channel in internal K+ has significantly slower IgOFF (Fig. 5, A and B) than ionic deactivation (Fig. 6 E). The removal of K+ ions from the selectivity filter in the P-type inactivated channel prevents the repulsive ion–ion interactions normally created within the highly occupied selectivity filter from displacing the intracellular K+ ion from its binding site, thus creating an atypical high affinity K+ binding site in the intracellular cavity (Fig. 9 A). This effect may also contribute in general to the increased slowing of IgOFF observed in channels that have undergone a pore-collapsing mutation or a P-type/slow inactivation process. Interestingly, internal Cs+ ions caused a similar rate of slowing in the conducting and nonconducting channels, which would suggest that the binding interactions of Cs+ ions within the inner cavity are not as strong as that of K+ but are still sufficient to be rate limiting to pore closure.
Although the ionic deactivation kinetics for K+ conductance are several-fold faster than the return of IgOFF in gating current experiments, the requirement for ions to vacate the pore in K+-containing solutions before closure is verified by our observation that ionic deactivation kinetics in the Kv1.2-I402C channel are threefold faster than the WT channel (Fig. 6 E). Therefore, the I402C channel also decreases any stabilizing effect that K+i and NMG+i ions occupying the pore may have produced.
Considering these data leads to a position in support of the occupancy hypothesis (Matteson and Swenson, 1986; Melishchuk and Armstrong, 2001) and provides a mechanistic basis for this effect. It follows that the critical determinant of open pore stability is not intrinsic intraprotein structural interactions but the allosteric effects of ionic occupancy of the inner cavity binding site creating an energy barrier to pore closure that has to be overcome.
The nature of the ion binding site in the inner cavity
It would be extremely informative in understanding our data to be able to examine a closed-state structure of a channel pore, but no crystal structures are currently available for closed Kv channels. Unfortunately, the KcsA closed-state structures are not a good model for the closed state of the Kv channel. KcsA has a considerably larger inner cavity than Shaker, as indicated by the fact that TBA, with a diameter of ∼10 Å, has been crystallized and trapped in the inner cavity of the closed-state KcsA (Y. Zhou et al., 2001), but TEA (with a diameter of ∼5 Å; Fig. 8 A) cannot be trapped in the closed cavity of the Shaker channel (Holmgren et al., 1997). In addition, cysteine modification experiments in the presence of intracellular TEA and TBA have demonstrated a pattern of reactivity in Shaker channels inconsistent with the linear pore lining helices of the KcsA channel, postulated to be related to the lack of a P-X-P helix breaking motif in the S6 of KcsA (del Camino et al., 2000). The KcsA structure does show that a fully hydrated K+ ion with eight water molecules resides in this cavity, indicating the possibility of a relatively stable site within a large cavity (Y. Zhou et al., 2001). The diameter of a hydrated K+ ion has been estimated at around 5.4 Å, a comparable size to the TEA+ ion, with a hydration energy of ±85 kcal/mol (Hille, 2001). The free energy difference between the open and closed states of the Shaker channel is estimated to be ∼2 kcal/mol (Yifrach and MacKinnon, 2002). Energetically, a hydrated K+ ion residing in an open channel cavity could offer a significant barrier to channel pore closing because of the energetic costs associated with reorganizing the hydration shell.
The mechanism of slowing of Kv1.2 IgOFF kinetics is distinct from a voltage sensor conformational rearrangement
Slowing of IgOFF and the consequent left shifts in the Qoff-V relationship after prolonged depolarization have previously been linked to inactivation processes and a phenomenon known as voltage sensor relaxation, where the slowing of voltage sensor return is suggested to indicate a different pathway of voltage sensor transit from the relaxed state (Villalba-Galea et al., 2008; Lacroix et al., 2011). In our Kv1.2 experiments, however, the left shift of Qoff-V (Fig. 2) is unlikely to be associated with a relaxation process, as the durations of our depolarizing pulses are at most 50 ms, which is much slower than the time course over which relaxation is reported to occur (τ = ∼1.8 s; Lacroix et al., 2011), and, indeed, we found no evidence of the Kv1.2 channel significantly inactivating over a greater time course than of our gating current recordings (Fig. S1 B). This leads to the conclusion that relaxation and/or inactivation cannot be the sole cause of slow return of OFF gating currents in Kv channels after depolarization.
Ion binding in the inner cavity offers an extrinsic mechanism by which channel deactivation kinetics are modulated
In summary, our results suggest that ion occupancy of the inner cavity of Kv1.2 channels impairs pore closure by slowing the open to closed transition and is therefore the cause of slowed IgOFF after depolarizations that open channels. The affinity of the ion for the cavity then becomes a primary determinant of pore closure, as depicted in Fig. 9 (A and B). Our data highlight the role that the channel inner cavity may play in fine-tuning deactivation kinetics of different channels, as variation in ion binding affinities and/or dissociation rates significantly affect deactivation kinetics. In essence, this represents an allosteric mechanism, separate from the VSD, through which it is possible for Kv channels to display varied deactivation kinetics.
Supplementary Material
Acknowledgments
We wish to thank Dr. David Steele for helpful contributions to the docking simulation.
This work was supported by the Canadian Institutes of Health Research and the Heart and Stroke Foundation of Canada. S.J. Goodchild is supported by a postdoctoral fellowship from the Heart and Stroke Foundation of Canada.
Christopher Miller served as editor.
Footnotes
Abbreviations used in this paper:
- VSD
- voltage-sensing domain
- WT
- wild type
References
- Armstrong C.M. 1971. Interaction of tetraethylammonium ion derivatives with the potassium channels of giant axons. J. Gen. Physiol. 58:413–437 10.1085/jgp.58.4.413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batulan Z., Haddad G.A., Blunck R. 2010. An intersubunit interaction between S4-S5 linker and S6 is responsible for the slow off-gating component in Shaker K+ channels. J. Biol. Chem. 285:14005–14019 10.1074/jbc.M109.097717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F., Taylor R.E., Fernández J.M. 1982. Distribution and kinetics of membrane dielectric polarization. 1. Long-term inactivation of gating currents. J. Gen. Physiol. 79:21–40 10.1085/jgp.79.1.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F., Perozo E., Papazian D.M., Stefani E. 1991. Molecular basis of gating charge immobilization in Shaker potassium channels. Science. 254:679–683 10.1126/science.1948047 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., Perozo E., Stefani E. 1994. Gating of Shaker K+ channels: II. The components of gating currents and a model of channel activation. Biophys. J. 66:1011–1021 10.1016/S0006-3495(94)80882-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruening-Wright A., Larsson H.P. 2007. Slow conformational changes of the voltage sensor during the mode shift in hyperpolarization-activated cyclic-nucleotide-gated channels. J. Neurosci. 27:270–278 10.1523/JNEUROSCI.3801-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F.S., Steele D., Fedida D. 1997. Allosteric effects of permeating cations on gating currents during K+ channel deactivation. J. Gen. Physiol. 110:87–100 10.1085/jgp.110.2.87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi K.L., Mossman C., Aubé J., Yellen G. 1993. The internal quaternary ammonium receptor site of Shaker potassium channels. Neuron. 10:533–541 10.1016/0896-6273(93)90340-W [DOI] [PubMed] [Google Scholar]
- del Camino D., Holmgren M., Liu Y., Yellen G. 2000. Blocker protection in the pore of a voltage-gated K+ channel and its structural implications. Nature. 403:321–325 10.1038/35002099 [DOI] [PubMed] [Google Scholar]
- del Camino D., Kanevsky M., Yellen G. 2005. Status of the intracellular gate in the activated-not-open state of shaker K+ channels. J. Gen. Physiol. 126:419–428 10.1085/jgp.200509385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Santiago-Castillo J.A., Covarrubias M., Sanchez-Rodriguez J.E., Perez-Cornejo P., Arreola J. 2010. Simulating complex ion channel kinetics with IonChannelLab. Channels (Austin). 4:422–428 10.4161/chan.4.5.13404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedida D., Bouchard R., Chen F.S. 1996. Slow gating charge immobilization in the human potassium channel Kv1.5 and its prevention by 4-aminopyridine. J. Physiol. 494:377–387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodchild S.J., Fedida D. 2012. Contributions of intracellular ions to Kv channel voltage sensor dynamics. Front. Pharmacol. 3:114 10.3389/fphar.2012.00114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. 2001. Ionic channels of excitable membranes. Third edition. Sinauer Associates Inc., Sunderland, MA: 814 pp [Google Scholar]
- Hille B., Schwarz W. 1978. Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72:409–442 10.1085/jgp.72.4.409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren M., Smith P.L., Yellen G. 1997. Trapping of organic blockers by closing of voltage-dependent K+ channels: Evidence for a trap door mechanism of activation gating. J. Gen. Physiol. 109:527–535 10.1085/jgp.109.5.527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horne A.J., Peters C.J., Claydon T.W., Fedida D. 2010. Fast and slow voltage sensor rearrangements during activation gating in Kv1.2 channels detected using tetramethylrhodamine fluorescence. J. Gen. Physiol. 136:83–99 10.1085/jgp.201010413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix J.J., Labro A.J., Bezanilla F. 2011. Properties of deactivation gating currents in Shaker channels. Biophys. J. 100:L28–L30 10.1016/j.bpj.2011.01.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledwell J.L., Aldrich R.W. 1999. Mutations in the S4 region isolate the final voltage-dependent cooperative step in potassium channel activation. J. Gen. Physiol. 113:389–414 10.1085/jgp.113.3.389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenaeus M.J., Vamvouka M., Focia P.J., Gross A. 2005. Structural basis of TEA blockade in a model potassium channel. Nat. Struct. Mol. Biol. 12:454–459 10.1038/nsmb929 [DOI] [PubMed] [Google Scholar]
- Liu Y., Holmgren M., Jurman M.E., Yellen G. 1997. Gated access to the pore of a voltage-dependent K+ channel. Neuron. 19:175–184 10.1016/S0896-6273(00)80357-8 [DOI] [PubMed] [Google Scholar]
- Long S.B., Campbell E.B., Mackinnon R. 2005a. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 309:897–903 10.1126/science.1116269 [DOI] [PubMed] [Google Scholar]
- Long S.B., Campbell E.B., Mackinnon R. 2005b. Voltage sensor of Kv1.2: structural basis of electromechanical coupling. Science. 309:903–908 10.1126/science.1116270 [DOI] [PubMed] [Google Scholar]
- Lu Z., Klem A.M., Ramu Y. 2002. Coupling between voltage sensors and activation gate in voltage-gated K+ channels. J. Gen. Physiol. 120:663–676 10.1085/jgp.20028696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matteson D.R., Swenson R.P., Jr 1986. External monovalent cations that impede the closing of K channels. J. Gen. Physiol. 87:795–816 10.1085/jgp.87.5.795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melishchuk A., Armstrong C.M. 2001. Mechanism underlying slow kinetics of the OFF gating current in Shaker potassium channel. Biophys. J. 80:2167–2175 10.1016/S0006-3495(01)76189-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olcese R., Latorre R., Toro L., Bezanilla F., Stefani E. 1997. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J. Gen. Physiol. 110:579–589 10.1085/jgp.110.5.579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo E., Papazian D.M., Stefani E., Bezanilla F. 1992. Gating currents in Shaker K+ channels. Implications for activation and inactivation models. Biophys. J. 62:160–168, discussion: 169–171 10.1016/S0006-3495(92)81802-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo E., MacKinnon R., Bezanilla F., Stefani E. 1993. Gating currents from a nonconducting mutant reveal open-closed conformations in Shaker K+ channels. Neuron. 11:353–358 10.1016/0896-6273(93)90190-3 [DOI] [PubMed] [Google Scholar]
- Peters C.J., Vaid M., Horne A.J., Fedida D., Accili E.A. 2009. The molecular basis for the actions of KVbeta1.2 on the opening and closing of the KV1.2 delayed rectifier channel. Channels (Austin). 3:314–322 10.4161/chan.3.5.9558 [DOI] [PubMed] [Google Scholar]
- Schoppa N.E., Sigworth F.J. 1998. Activation of Shaker potassium channels. III. An activation gating model for wild-type and V2 mutant channels. J. Gen. Physiol. 111:313–342 10.1085/jgp.111.2.313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga Z., Rayner M.D., Starkus J.G. 2002. Cations affect the rate of gating charge recovery in wild-type and W434F Shaker channels through a variety of mechanisms. J. Gen. Physiol. 119:467–485 10.1085/jgp.20028520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villalba-Galea C.A., Sandtner W., Starace D.M., Bezanilla F. 2008. S4-based voltage sensors have three major conformations. Proc. Natl. Acad. Sci. USA. 105:17600–17607 10.1073/pnas.0807387105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villalba-Galea C.A., Sandtner W., Dimitrov D., Mutoh H., Knöpfel T., Bezanilla F. 2009. Charge movement of a voltage-sensitive fluorescent protein. Biophys. J. 96:L19–L21 10.1016/j.bpj.2008.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Zhang X., Fedida D. 1999. Gating current studies reveal both intra- and extracellular cation modulation of K+ channel deactivation. J. Physiol. 515:331–339 10.1111/j.1469-7793.1999.331ac.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yifrach O., MacKinnon R. 2002. Energetics of pore opening in a voltage-gated K(+) channel. Cell. 111:231–239 10.1016/S0092-8674(02)01013-9 [DOI] [PubMed] [Google Scholar]
- Zagotta W.N., Hoshi T., Aldrich R.W. 1994a. Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J. Gen. Physiol. 103:321–362 10.1085/jgp.103.2.321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta W.N., Hoshi T., Dittman J., Aldrich R.W. 1994b. Shaker potassium channel gating. II: Transitions in the activation pathway. J. Gen. Physiol. 103:279–319 10.1085/jgp.103.2.279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M., Morais-Cabral J.H., Mann S., MacKinnon R. 2001. Potassium channel receptor site for the inactivation gate and quaternary amine inhibitors. Nature. 411:657–661 10.1038/35079500 [DOI] [PubMed] [Google Scholar]
- Zhou Y., Morais-Cabral J.H., Kaufman A., MacKinnon R. 2001. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution. Nature. 414:43–48 10.1038/35102009 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.